Motion Artefacts in MRI: a Complex Problem with Many Partial Solutions

Abstract

Subject motion during magnetic resonance imaging (MRI) has been problematic since its introduction as a clinical imaging modality. While sensitivity to particle motion or blood flow can be used to provide useful image contrast, bulk motion presents a considerable problem in the majority of clinical applications. It is one of the most frequent sources of artefacts. Over 30 years of research have produced numerous methods to mitigate or correct for motion artefacts, but no single method can be applied in all imaging situations. Instead, a ‘toolbox’ of methods exists, where each tool is suitable for some tasks, but not for others. This article reviews the origins of motion artefacts and presents current mitigation and correction methods. In some imaging situations, the currently available motion correction tools are highly effective; in other cases, appropriate tools still need to be developed. It seems likely that this multifaceted approach will be what eventually solves the motion sensitivity problem in MRI, rather than a single solution that is effective in all situations. This review places a strong emphasis on explaining the physics behind the occurrence of such artefacts, with the aim of aiding artefact detection and mitigation in particular clinical situations.

INTRODUCTION

Compared to other imaging modalities, such as ultrasound or computed tomography, MRI has always been particularly sensitive to subject motion. This is primarily due to the prolonged time required for most MR imaging sequences to collect sufficient data to form an image. This is far longer than the timescale of most types of physiological motion, including involuntary movements, cardiac and respiratory motion, gastrointestinal peristalsis, vessel pulsation, and blood and CSF flow. The effects of motion have been well known since the early days of MRI and include blurring and ghosting in the image (1, 2).

Recent technological improvements have improved the situation in some cases, but have exacerbated it in others. On one hand, incremental performance gains in hardware (e.g. higher performance gradients) have enabled faster imaging, as have breakthroughs such as parallel imaging. Faster imaging means that some scans can be performed in a shorter time, leading to a smaller chance of involuntarily subject motion. On the other hand, hardware improvements have improved the achievable resolution and signal-to-noise ratio (SNR), and the sensitivity to motion has therefore increased. Stronger gradients also mean greater phase accumulation for moving spins. Higher main field strengths and stronger gradients also mean that a typical MR scan is generally louder than it was in the early days of MRI, which reduces the chance of infants sleeping through the procedure. This is particularly true for diffusion-weighted or diffusion tensor imaging, as was reviewed recently by Le Bihan (3).

At present, there is no sign that the problem of subject motion during MRI examinations will be resolved through hardware improvements. The potential of accelerated imaging seems to be increasingly limited by biologic constraints: peripheral nerve stimulation limits gradient switching speeds; specific adsorption rate (SAR) limits the use of RF excitation pulses; and T1 and T2 relaxation times constrain the sequence repetition and echo times, depending on the required contrast.

Furthermore, it seems increasingly likely that there is not, and will not be, a single methodological solution to the problem of motion in MRI; rather, a toolbox of solutions exists. The choice of which tool to apply depends on the task at hand, namely, the imaging situation and type of motion in question. Some prevention or correction techniques are highly effective in particular circumstances, but useless in others. Other techniques are relatively general, but are not completely effective. It is therefore extremely important to recognize and understand motion artefacts in order to identify the physical cause of the problem in a particular clinical situation and use the best possible tool for the problem.

In this review, we first examine the physical origins of motion artefacts and then summarize the main motion prevention and correction tools currently in use or in development. Our aim is to provide a condensed guide to the function, application and limitations of these methods.

PHYSICAL PRINCIPLES BEHIND MOTION ARTEFACTS

The appearance of motion artefacts in an image is a result of a complicated interaction between the image structure, the type of motion, the specifics of the MR pulse sequence and the k-space acquisition strategy. In this section we briefly revisit the most important physical mechanisms affecting the appearance of motion artefacts.

K-space and the image acquisition process

Spatial encoding in MRI is an intrinsically slow and sequential process. For the appreciation of the effect of motion on MR images it is important to realize that the data acquisition occurs not directly in image space, as is the case in photography, but rather in frequency or Fourier space, which is commonly termed ‘k-space’.

K-space corresponds to the spectrum of the spatial frequencies of the imaged object and depending on the imaging situation can be two- or three-dimensional. Spatial frequency spectra of objects with small number of contrast features and with smooth intensity variations are predominantly defined by the components close to the k-space origin. Objects or organs with sharp high-contrast edges contain a significant spectral density at the k-space periphery. The majority of biological samples show very local spectral density in k-space centred around k=0. Some organs and tissues, such as brain cortex, have a fractal-like nature (4) and therefore show a slower decay of spectral density in k-space.

To understand the properties of k-space and its relation to image/object space, it is important to develop an intuition regarding the local and global properties of these two spaces. This topic is reviewed in detail by Paschal and Morris (5). K-space describes the object using a set of global planar waves. Every sample in k-space describes the contribution of the wave with a corresponding frequency to the entire image. Therefore a change in a single sample in k-space affects theoretically the entire image. Similarly, a change in the intensity of a single pixel (e.g. in a dynamic process) generally affects all k-space samples. However, when such change can be allocated to a larger cluster of pixels, predominantly the centre of k-space is affected. The latter phenomenon is the basis of a range of data-sharing techniques, which achieve a higher apparent temporal resolution in dynamic imaging by updating the central region of k-space more frequently (6-9).

Different strategies to populate k-space with measured data are termed “k-space sampling trajectories” or “k-space trajectories”. The most common and clinically relevant approach collects data on a rectilinear grid in k-space (so-called ‘Cartesian’ sampling), because it allows for a computationally efficient image reconstruction using the fast Fourier transform (FFT). Even though we primarily consider the Cartesian sampling strategy, it is necessary to distinguish between the multitude of k-space trajectories, which differ from each other in the way and the order the nodes of this rectilinear 2D or 3D k-space grids are visited. Other popular data acquisition schemes include radial (5, 10), PROPELLER (11) and spirals (12).

Typical motion-induced deterioration effects observed in MR images consist of a combination of the following basic effects:

• Blurring of sharp contrast or object edges (intuitively similar to photography)

• Ghosting (both coherent and incoherent) originating from moving structures

• Signal loss due to spin dephasing or undesired magnetization evolution

• Appearance of undesired strong signals

The first two points are related to the signal readout process, whereas the latter two are related to the signal generation and contrast preparation within the pulse sequence. Here we refer to ghosting as a partial or complete replication of the object or structure along the phase-encoding dimension, or along multiple phase-encoding dimensions for 3D imaging. Periodic motion synchronized with the k-space acquisition results in a coherent ghosting with the number of replicas corresponding to the frequency of k-space modulation: two ghosts result if every second line is altered, four if every fourth, etc. Deviations from perfect periodicity in k-space result in incoherent ghosting, appearing as multiple overlapped replicas, and sometimes seen as stripes in the phase-encoding dimension.

The main cause of readout-related motion artefacts is the inconsistency between the various portions of the k-space data used for the image reconstruction or between the data and the signal model assumed in the reconstruction. Simple reconstruction using an inverse FFT (iFFT) assumes the object has remained stationary during the time the k-space data were sampled. A violation of this assumption results in artefacts.

To demonstrate possible motion artefact appearance we have simulated a range of motions and k-space reordering schemes. Figure 1a shows the digital phantom used based on the Shepp-Logan phantom with altered intensities and a grid of small objects added. Figures 1b-d demonstrate the range of simulated motions (continuous rotation to 10°, continuous translations by 10 pixels in vertical and horizontal directions (Figs. 1b-d, respectively) and a periodic sinusoidal oscillation in the horizontal direction with the same amplitude (not shown). To provide a reference of image quality, a photography-like image acquisition has been simulated, averaging the motion in image space (Figs. 1e-1h). It is noteworthy that the image 1h appears more blurred than 1g, because for periodic motion the object spends more time in proximity of the terminal positions.

Fig. 1.

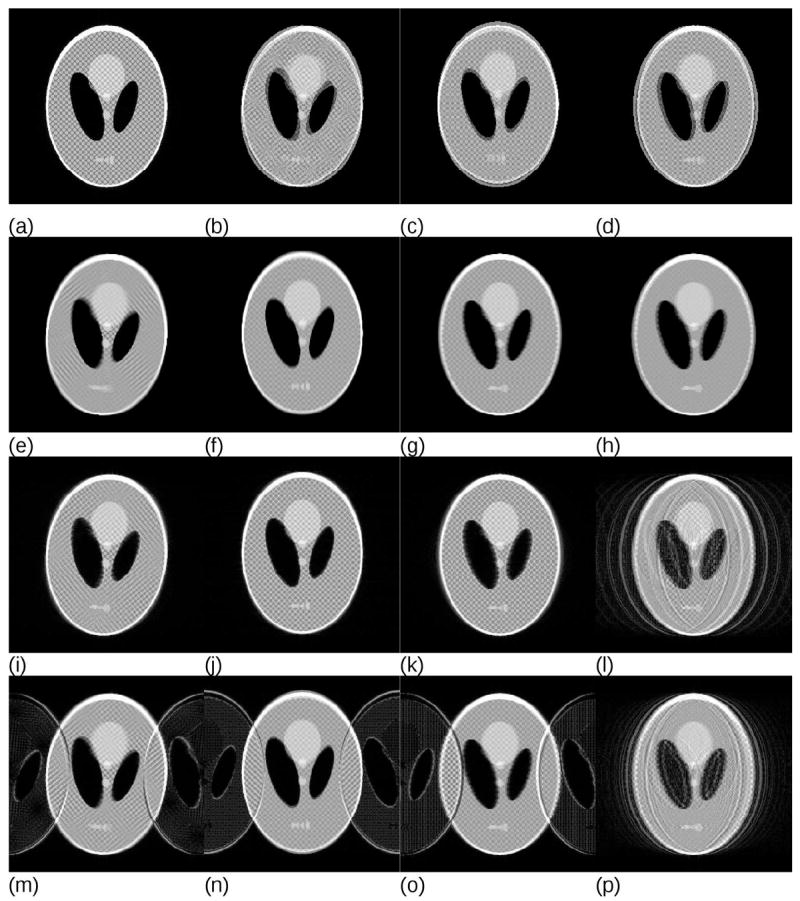
(a) Original FFT reconstruction without motion, (b-d) sum of first and last source images to show the range of simulated motions for (b) continuous monotonic rotation to the total angle of 10°, (c) continuous vertical translation and (d) continuous horizontal translation (in both cases 10 pixels for a matrix of 256×256). Periodic horizontal translation has the same amplitude and is not shown. Images (e-h) demonstrate the results of averaging the motion as would correspond to photography with an equivalently long exposure time; (e) rotation, (f) vertical translation, (g) horizontal translation and (h) periodic horizontal translation. Note the loss of detail and edge information due to the motion blur and the enhanced blurring in (h) due to the fact that with sinusoidal motion the object spends more time close to the terminal positions. Images (i-l) show simulated MRI acquisitions with linear k-space ordering. Images (m-p) show simulated two-shot interleaved MRI acquisitions. Plots of the motion as a function of k-space position for the representative images are presented in Fig. 2.

It is common knowledge in the imaging community that MRI is particularly sensitive to motion. However, in the case of slow continuous drifts and sequential k-space ordering, Fourier acquisition is actually significantly less motion-sensitive than a corresponding “photographic” image taken with the same “exposure time” (Fig s 1i-1k). Periodic motion however produces very strong ghosting (Fig. 1l). In the case of interleaved multishot k-space ordering, even slow continuous drifts produce significant ghosting (Figures 1m-1o). Note that ghosting reduces for the periodic motion in Figure 1p in comparison to Figure 1l because the interleaved acquisition scheme traverses k-space faster, which reduces the number of full oscillations effectively seen in the complete k-space data set. If the interleaving scheme is synchronized with the underlying periodic motion, the artefacts reduce further to the level comparable with that in Figure 1k. This phenomenon is often exploited in cardiac imaging and is discussed in more detail below. Plots of the motion as a function of k-space position for the representative images in Fig. 1 are presented in Fig. 2.

Fig. 2.

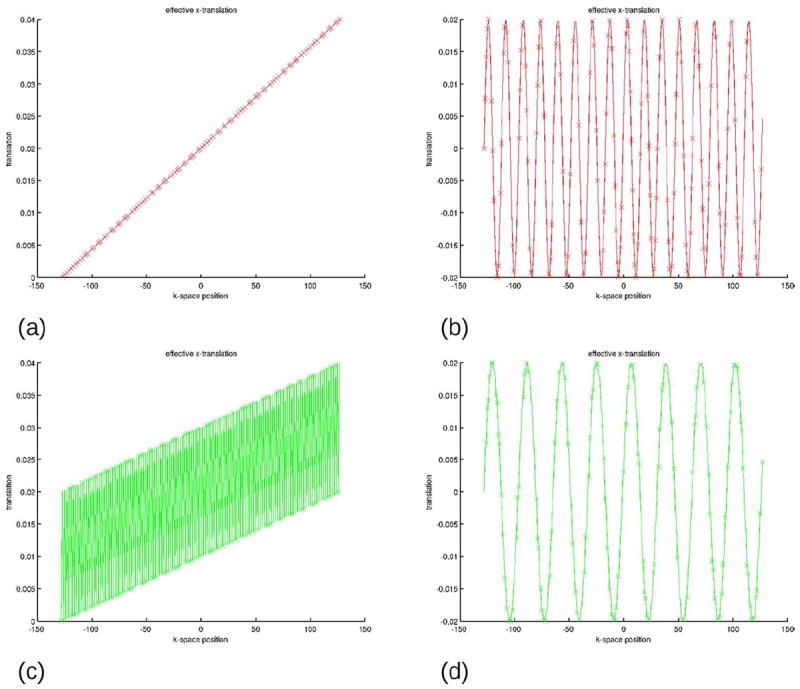
Effective translation (as a fraction of the FOV) as a function of the k-space position for (a) Fig. 1j and 1k, (b) Fig. 1l, (c) Fig. 1n and 1o and (d) Fig. 1p. As seen, if the external disturbance oscillates as a function of k-space position, e g. in cases (b), (c) and (d), ghosting will result (see corresponding images in Fig. 1). Reduced ghosting in Fig. 1p can be explained by the effective reduced frequency of oscillation of the position as a function of the k-space coordinate (compare plots (b) and (d)). Plots of rotations are omitted due to their similar appearance.

Although slow continuous motions do occur in clinical settings, for example due to the gradual relaxation of the neck muscles in head imaging, they only strongly affect sequences relying on interleaved k-space acquisitions, e.g. T2-weigted TSE/FSE (Turbo/Fast Spin Echo) imaging. In addition to periodic processes (e.g. breathing, cardiac motion, blood pulsation and tremors), sudden position changes, for example due to swallowing in head imaging or insufficient breath hold capability in abdominal scanning are the effects that often lead to artefacts. The effect of sudden motion on the Fourier acquisition is visualized in Figure 3. Here, single 10° rotation events have been simulated, with the motion occurring at different time points, leading to varying proportions of k-space data that are inconsistent. Figures 3a-3d and Figures 3e-3h assume linear and interleaved k-space ordering, respectively. In both cases 12.5% (1/8th) of the inconsistent k-space data result in a negligible effect; however, image quality deteriorates much faster for the interleaved acquisition. Centric k-space reordering demonstrates even higher resistance against artefacts (Figures 3i-3l).

Fig. 3.

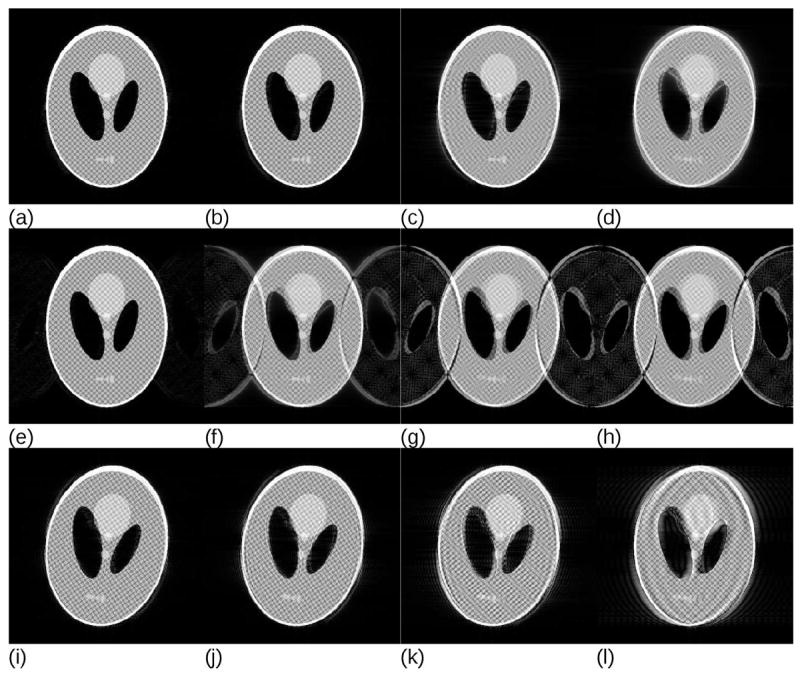
Simulations of a single sudden orientation change during the k-space acquisition for different k-space acquisition strategies and different amounts of inconsistent k-space data. For a linear k-space ordering, images reconstructed from datasets containing (a) 12.5%, (b) 25%, (c) 37.5% and (d) 50% inconsistent data have been simulated. Hardly any artefacts are visible if the corruption occurs outside of the ½ of the maximum k-space distance to the centre. Similar conclusions follow for the two-shot interleaved k-space acquisitions with (e) 12.5%, (f) 25%, (g) 37.5% and (h) 50% of inconsistent data. Images (i-l) present a similar simulation for the centric reordering with (i) 50% of inconsistent with respect to the k-space centre data, (j) 62.5%, (k) 75% and (l) 87.5%, respectively. The precise threshold at which visually detectable artefacts start to appear strongly depends on the image, primarily on the presence of small high-contrast features, but the overall tendency is that below a certain distance from the k-space centre a single motion event produces only negligible artefacts.

The following conclusions can be drawn from these simulations:

1. MRI with a sequential k-space ordering is fairly insensitive to slow continuous motion;

2. motion as a function of k-space position is the most relevant parameter for the appearance of artefacts;

3. it is important where in k-space fast motion occurs, as data corruption near the centre of k-space produces stronger artefacts than data corruption near the k-space periphery;

4. repeated modulation in k-space amplifies artefacts and should be avoided.

Types of motion

The different types of motion relevant for in vivo MRI can be loosely separated into the following categories: rigid body motion, elastic motion and flow.

Rigid body motion, or ‘bulk motion’, includes one-dimensional translations (requiring a single parameter for its mathematical representation), multi-dimensional translations (requiring several parameters), or completely unconstrained rigid motion (requiring six parameters). For example, diaphragm motion is sometimes approximated using a one-dimensional translation, but involuntary head motion normally requires six degrees of freedom, comprising three translations and three rotations.

Elastic motion typically includes stretching, compression and shearing along three axes, in addition to rigid body motion. It requires 12 degrees of freedom for its complete representation. Elastic motion is observed in the abdomen, where various locations experience different displacements and deformations. Flow can in some cases be assumed to be one-dimensional, for example for laminar blood flow in small or medium-sized vessels or CSF flow in the cervical spine. It then requires only a single parameter (velocity) for its complete representation. More complex flow is observed in the heart and aorta. This requires a two- or three-dimensional velocity vector field for its complete description.

The most complete description is provided by the displacement field, which consists of the trajectories of each particle within the object as a function of time. Although being complete, the displacement field is often not measurable with sufficient precision. Luckily, for the vast majority of practical situations this description is too detailed. Physical, mechanical and physiologic constraints placed on the human body (e.g. incompressibility of liquids and a majority of tissues, presence of bones and joints, etc.) allow for a drastic reduction of the number of parameters required for the description of motion.

Data corruption mechanisms

Several physical mechanisms contribute to the appearance of the motion artefacts. The most important and relevant for in vivo MRI are the following:

• Incorrect phase accumulation due to tissue motion during the periods in the pulse sequence where gradients are switched on. MRI relies on the ability to create gradient echoes, and typically assumes that tissues are stationary during imaging. As seen in Fig. 4, spins moving in the direction of the gradient acquire additional phase. If this phase varies for different phase-encoding steps, inconsistencies in k-space arise;

• The so-called excitation history effect appears when slice-selective RF pulses are used for excitation, saturation or refocusing. As seen in Fig. 5, out-of-plane motion between such pulses affects the desired evolution of the signal and typically results in generation of signals that are too strong or too weak, or causes alternations in image contrast. For multi-shot imaging this results in magnitude inconsistencies in k-space;

• Motion of the tissues and body parts often affects magnetic fields used in MRI. The B0 field within the imaging volume changes significantly if the orientation of the body part changes but may also be affected by motion of relatively distant body parts due to long-ranging magnetic susceptibility effects (13, 14). Both transmit and receive B1 fields may also change depending on the body position or due to the motion of the surface coils themselves.

• Rotations during the k-space data acquisition process in multi-shot imaging produces inconsistencies between the effective readout directions for different k-space lines (see Fig. 6). Even if the true motion during the acquisition is known and compensated for, the resulting k-space is not sampled homogeneously, which may result in ghosting or streaking artefacts.

• Cardiac or respiratory motion leads to so-called ‘physiologic noise’ in fMRI. Because the fMRI signal is very small (15), any other dynamic changes caused by, for example, periodic blood flow, appears as a confounding factor in the analysis. The situation is further exacerbated by the realively low temporal resolution of typical fMRI acquisitions leading to a spectral aliasing of the physiologic signals.

Fig. 4.

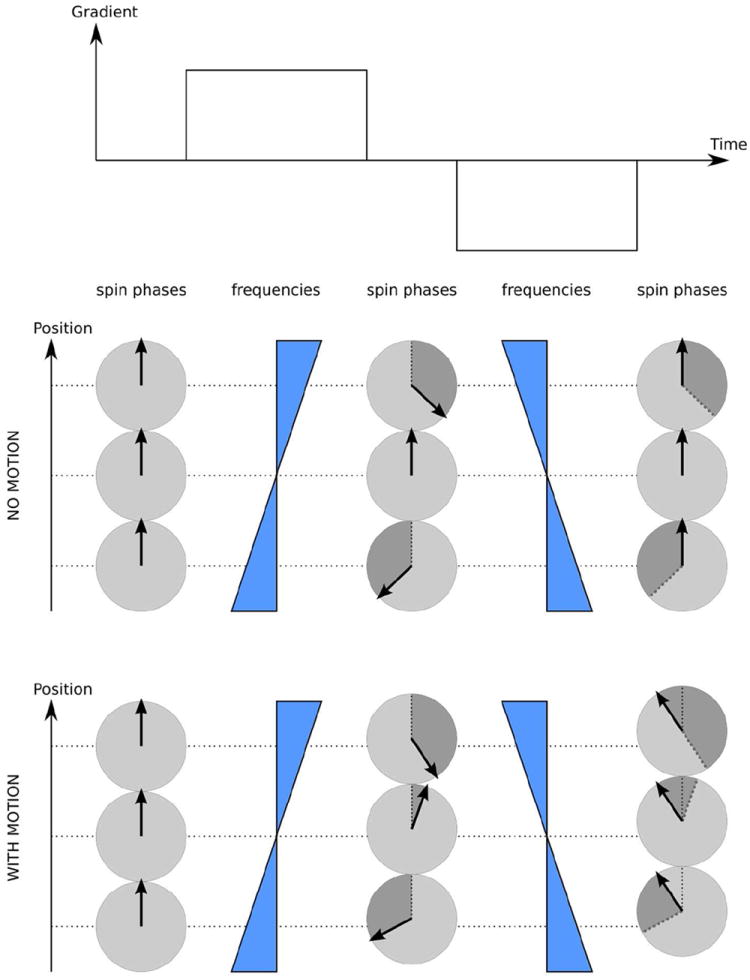
Velocity effects on the phase of MR signals. Stationary spins can be refocused with a pair of gradient pulses of equal area and opposite polarity, which is a basis of gradient echo. Spins moving along the gradient direction acquire additional phase due to the fact that dephasing and refocusing occur at different physical locations where the same gradient indices different frequency shifts, leading to different amounts of the phase acquired during dephasing and refocusing periods. Greyed segments on the corresponding phase circles mark the amount of phase acquired by the moving spins during the last gradient pulse.

Fig. 5.

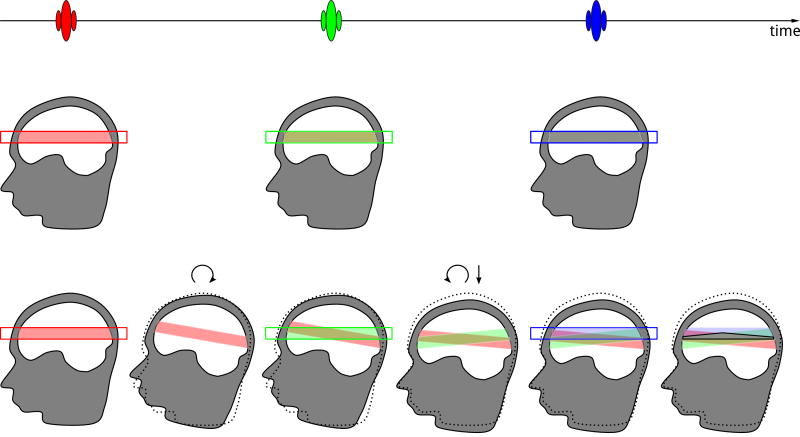
Excitation history effects visualized for a 3-pulse MR pulse sequence. In the case of no motion, regions excited by all three pulses overlap resulting in the desired signal evolution. The respective brain regions are marked using half-transparent bands with the colour of the corresponding slice-selective RF pulse. Overlap of red and green results in light brown. When light brown is followed by an overlap with blue, a grey colour results, which indicates the desired spin evolution. In the case of motion, (rotation after the first pulse, followed by a combination of rotation and translation after the second pulse, original position is shown as dotted line) the grey region corresponding to the desired spin evolution is substantially reduced, while coloured regions with undesired signal evolution appear. Therefore desired signals are decreased, and undesired signals are produced, resulting in artefacts, such as ghosting or signal disturbances. The unwanted signals may also cancel some of the desired signals, causing signal voids.

Fig. 6.

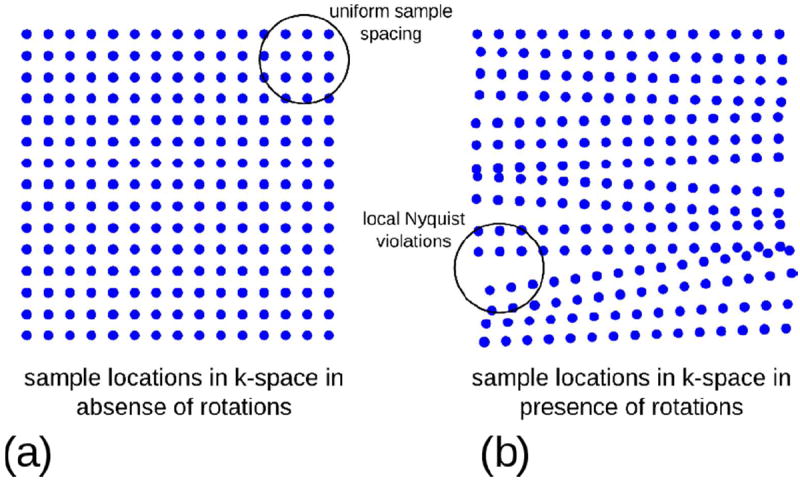
The effect of rotations on the k-space sample locations in object coordinates. In the absence of rotations (a) the k-space samples are arranged on a uniform grid fulfilling the Nyquist criterion. Rotation of the object during the image acquisition rotates the spatial frequency components associated with the object with respect to the encoding gradients, which effectively redistributes the samples in k-space (b). This leads the sampling density in some areas of k-space to fall below the Nyquist criterion and results in streaking and ghosting artefacts in the images, which are difficult to correct for in reconstruction even if the motion is known.

Data inconsistencies between k-space lines or segments in multi-shot imaging typically result in ghosting or blurring. Most of the above mechanisms may also affect the contrast preparation modules (e.g. diffusion weighting or inversion) and thus generate undesired contrast variations without visible ghosting artefacts. This occurs particularly in single-shot imaging.

ARTEFACT MITIGATION STRATEGIES

As discussed above, there are many types of motion and many possible mechanisms for data corruption resulting from each motion type. It follows, therefore, that many different strategies have been developed to address these challenges. In the following, we categorize these methods into three distinct groups: motion prevention, artefact reduction and motion correction (Table 1).

Table 1.

Common notion artefact mitigation strategies

Motion prevention	Artefact reduction	Motion correction
Training	Faster imaging	Navigators
Distraction	Insensitive sequences	Self-navigated trajectories (PROPELLER and alike)
Feed and wrap (for babies)	Gradient moment nulling
Foam restraints	Saturation bands	Prospective correction
Sedation	Triggering and gating	Retrospective correction
Bitebars/head holders	Phase reordering
Breathhold

Motion prevention is the most obvious method of suppressing motion artefacts. If motion can be avoided, then the effects discussed early in the review are prevented and other, more complex, strategies become redundant. Unfortunately, preventing motion is not always practical and so artefact reduction or motion correction strategies must often be employed. Artefact reduction is defined in this review as acquisition strategies that reduce artefacts in the resulting image or replace them with those with a less dramatic appearance, when compared to standard Cartesian acquisition methods. Motion correction, on the other hand, normally involves the explicit estimation and compensation of motion. Combinations of all three methods are possible, just as multiple tools may be used together in a complementary fashion in the toolbox analogy mentioned above.

Motion prevention

Prevention is the most commonly attempted approach to avoid motion artefacts in clinical MRI. The main prevention tools available are briefly summarized here.

For young children, training with a mock MRI is useful to avoid bulk motion by reducing anxiety. However, this method is not widely available and is not particularly cost effective. In infants, imaging can be timed after feeding to take advantage of sleeping. Babies can be well wrapped, which also encourages sleeping. Foam restraints or special inflatable devices are in common use, the latter particularly in the case of infants. However, these methods are only partially effective. Nevertheless, Windram et al. have recently reported failure-free imaging of 20 young patients with a congenital heart disease using the feed-and-sleep technique (16).

Moderate sedation, or in some cases, general anaesthesia, is often employed (17, 18) when imaging young children. Surprisingly enough, sedation is not always effective, with occurrence of motion artefacts in about 12% of cases (17) and an increased prevalence of failures in older children. According to (17), general anaesthesia is more reliable, as it has a much lower incidence of motion artefacts (about 0.7%) but is associated with much greater costs (in part due to the requirement of a presence of an anaesthetist), more severe side effects and greater health risks.

In the early days of MRI, bite bars mounted on head coils (19, 20) were deemed an effective means of avoiding head motion. However, due to their cumbersome set up and significant discomfort, these approaches have not found wide acceptance in clinical practice. The same applies to other immobilizing systems, such as a personalized plaster cast head holder (21). Vacuum immobilizer cushions, which are available from several suppliers, address the set-up issues, but, in the experience of the authors, are perceived as very uncomfortable after a time period of 10 to 30 minutes.

In the case of abdomen or cardiac imaging, breath-holding is an obvious, and effective, methods of suppressing motion artefacts due to breathing (see Chapter 12.3 in (22)). Breath-holding, however, restricts scan duration severely (between 10 and 20 seconds in clinical settings), which in turn limits the image quality, resolution and coverage. Image quality is further restricted by the quality of breath-hold (e.g. presence of drifts or tremour). To overcome time limitations multiple breath-holds are often employed despite limitations associated with breathing hysteresis and limited reproducibility of breath-hold positions.

Artefact reduction

The basic remedial approaches and tools to reduce motion artefacts were devised about 30 years ago, in the early days of MRI. A 1986 review article by Bellon (23), lists strategies such as shortening imaging time, optimizing the phase encoding direction and ordering, and reducing flow sensitivity. These basic approaches remain valid to date, but new ways of achieving the same goals have appeared. Therefore, for the sake of completeness, we review the current artefact reduction strategies below.

Faster imaging

In analogy to photography, shortening the image acquisition time below the typical time scale of motion is the most straightforward approach to reduce motion artefacts. The wider availability of fast imaging techniques is largely responsible for the improvements seen in MRI with regard to the immunity to motion, rather than the more complicated motion correction techniques discussed below. In the case of spontaneous movements, shorter scan times mean that the patient is less likely to become uncomfortable and move. In the case of cardiac or breathing motion, fast sequences acquire more data within a single period. An early example of fast gradient echo imaging is the FLASH (fast low-angle shot) sequence (24), which uses low-angle excitation and spoils transverse magnetization between TRs. Progress in gradient hardware has resulted in the wide availability of fully-refocused gradient echo sequences (25) (so-called balanced steady-state free precession, bSSFP). For the same reason, echo planar imaging (EPI) (26), which was initially deemed barely feasible, has became a workhorse in functional neuroimaging. T2-weighed imaging has became clinically feasible due to the adoption of the echo-train principles (27), but still remains too slow for certain applications, such as breathhold abdominal imaging. In such cases a single-shot fast spin-echo (a.k.a. HASTE) is often employed as a means of freezing motion at expense of a moderate loss in spatial resolution.

Parallel imaging (28-30) has revolutionized many MRI applications by shortening acquisition times, typically by a factor of 2 to 3. More recently, these approaches have been extended to acceleration in two encoding dimensions (31, 32) leading to even higher gains for 3D imaging or novel approaches, such as simultaneous multi-slice imaging (33). The introduction of compressed sensing MRI (34) in 2007 has provided a further tool for acceleration of MRI acquisitions and has paved a way to new motion-compensated applications (35).

Fast imaging, however, compared to the standard counterpart, frequently represents a compromise between the acquisition time and other confounding issues. Single-shot imaging typically has a limited spatial resolution. EPI suffers from geometric distortions and chemical-shift artefacts. Parallel imaging methods rely on the accuracy of the coil calibration data and may result in new types of artefacts if motion happens during the acquisition of the reference data (36-38). Compressed sensing is often criticized for the introduction of the new types of artefacts (e.g. patchiness, synthetic appearance), which may mask important anatomic features in some cases (39).

Gradient moment nulling

Gradient moment nulling is a widely used method to reduce artefacts produced by objects or tissues moving with a near-constant velocity. It is particularly useful for the suppression of flow-related artefacts. The method attempts to minimize the phase shifts acquired by both stationary and moving spins at the echo time. Without gradient moment nulling (Fig. 7a), stationary spins are refocused, but spins moving along the direction of the applied gradient are not. With gradient moment nulling (Fig. 7b), both stationary spins, and spins moving with a constant velocity, are refocused. Mathematically this is equivalent to minimizing both the 0th gradient moment (area under the gradient waveform) and the 1st gradient moment at the echo time. The gradient moment nulling condition is exactly or approximately fulfilled for a range of multi-echo imaging sequences (40) such as multi-gradient echo or turbo spin echo, but only for even echoes within the echo train. This phenomenon is termed “even echo refocusing” in the literature.

Fig. 7.

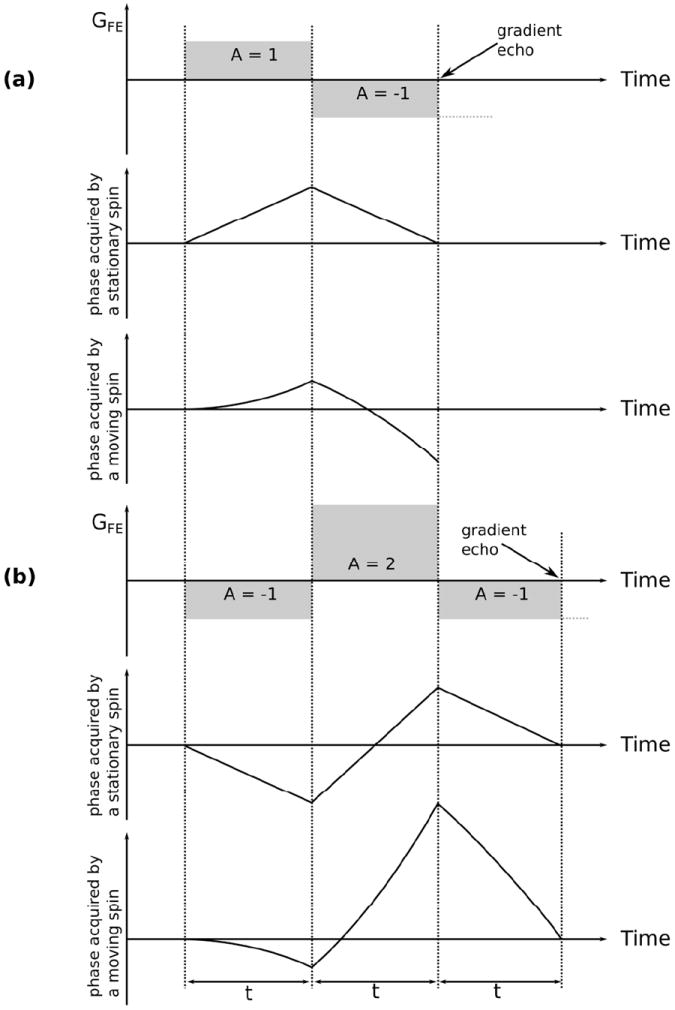
The effect of linear motion on the phase acquired by the spins under the action of the encoding gradients (frequency encoding in this example). A bipolar gradient (a) refocuses the stationary spins at the moment when the net area under the gradient arrives to zero. This is because the phase accrual in this case is proportional to a product of the gradient amplitude and the time duration. Contrary to that, the phase acquired by a spin moving along the gradient direction is proportional to the gradient amplitude, duration and the displacement of the spin. Because the displacement under the continuous motion is proportional to the time, the phase shows a quadratic dependency on time. Therefore, a bipolar gradient fails to refocus moving spins. Consequently, such spins will be poorly located and a motion artefact will be seen in vascular structures and moving fluids. It is possible to account for the quadratic behaviour of the phase by introducing a third gradient lobe, as shown in (b). Here, in order to keep the polarity of the frequency encoding gradient the sign of the two preceding lobes has been adjusted. The gradient area ratio of 1:-2:1 does not induce additional dephasing for the stationary spins and allows for refocusing the spins moving with a constant velocity. Other gradient schemes are possible taking into account gradient amplitude and slew rate limits, but velocity compensation always increases the minimal echo time.

Incorporation of gradient moment nulling almost always slows down the sequence as it requires additional gradient lobes to be added. Currently the majority of scanner vendors provide this feature for one or several encoding dimensions as an option amongst the sequence parameters, typically referred to as “flow compensation”.

Motion insensitive sequences

Imaging methods relying on spiral or radial encoding strategies are often more motion-tolerant than Cartesian sequences, in that the motion artefacts have a more benign appearance in the images (41). The reason for this is that these strategies typically oversample the centre of k-space, which either smears out the artefacts, due to the inherent averaging (41-44) or may further be employed for more advanced correction in post-processing (45-49). Furthermore, if the readout starts at or close to the centre of k-space, it is easier to achieve gradient moment nulling, which reduces phase errors between the shots.

Phase reordering

The order of acquisition of k-space lines can make a substantial difference to the appearance and severity of motion artefacts when imaging a moving object. Changing the ordering to minimize artefacts is particularly common to prevent artefacts from respiratory motion. An early example of this is respiratory-ordered phase encoding (ROPE) (50), where neighbouring lines in k-space are acquired at points in the respiratory waveform that are also close together. This minimizes side lobe peaks in the point-spread function (PSF), which reduces ghosting. Such techniques are often generally referred to as ‘respiratory compensation’. A major advantage of respiratory compensation over respiratory gating is a much shorter scan time.

Respiratory compensation requires information about motion caused by the patient breathing. Typically, respiratory bellows are used to obtain a waveform that gives information about the patient’s chest position via measurement of the movement of air in the bellows. It is important that the bellows are correctly attached in order to measure the full range of respiratory motion. MR navigators that track breathing motion are also often used as a source of information for the phase reordering (51).

Spatial saturation bands

Movement of parts of the anatomy (e.g. blood flow from arteries, breathing motion in abdominal imaging, etc.) can generate motion artefacts that overlay the organ of interest (52, 53). Spatial saturation bands can be used to suppress signal from such moving tissue. To achieve this, one or more spatially selective 90° RF pulses are applied prior to the actual excitation pulse. The transverse magnetization is then dephased by spoiler gradients. Moving spins from the saturated region are therefore prevented from contributing to artefacts in the imaged volume. However, the additional RF pulses lead to an increase in SAR and measurement time – clinically, this results in a decreased number of slices for a given TR.

Triggering and Gating

Patient motion resulting from physiologic effects such as heartbeat or breathing is generally periodic. This is an advantage for motion correction, as MR data acquisition can be timed to the different points within the cardiac cycle (54) or breathing position (55).

There are two general approaches to enforce consistency of the data acquired in presence of (quasi-) periodic motion. Data can either be collected at the same point in the cycle (triggering) or acquired continuously and then reordered retrospectively (gating). Triggering is often easier to implement and it has the advantage of a more precise synchronization with the underlying motion. On the other hand triggering by necessity introduces a delay, which both disrupts the signal steady state and misses some part of the dynamic cycle in applications like cardiac cine imaging. Gating is free of these shortcomings, but it has to sacrifice some scanning efficiency and allow for a certain degree of redundancy to ensure that sufficient data are available for retrospective image reconstruction.

Both triggering and gating rely on an additional signal or several signals correlated to the physiologic motion in question. For cardiac imaging, electrodes are normally placed on the subject’s chest to record the electrocardiogram (ECG). This has the drawback of slower patient workflow and has some safety implications (56). At higher field strengths (3T and above) the quality of the ECG trace may be reduced substantially, so it is therefore important to optimize the placement of the EEC electrodes and leads (57). Another possibility is to use a pulse oximeter, typically attached to subject’s finger. However, peripheral signals are less sharp and precise and are more suitable for gating because of the delay associated with a limited velocity of the pulse wave in the human body. Respiratory gating and triggering can rely on respiration sensors, such as belts or bellows typically affixed to the subject’s chest or belly, as discussed above. However, the reliability of such devices and the relation to the breathing-induced motion of the internal abdomen organs are substantially lower than in the case of cardiac motion. Therefore MR navigators following the position of the diaphragm or directly the organ of interest are often preferred. Navigators are discussed in more detail in a separate section below. Another popular approach acquires one or several non-encoded samples following the RF excitation. This is commonly referred to as FID-gating or self-gating (58, 59).

Generic limitations to both triggering and gating arise from the violation of the two basic assumptions behind these techniques: periodicity of the disturbing motion and stationarity of the imaged object or organ. Therefore cardiac MR imaging in patients with arrhythmia remains challenging. In paediatrics both breathing and heartbeat may be very irregular, which limits the achievable image quality severely. Also in adults free-breathing exams fail sporadically, due to breathing position drifts and changes in breathing patterns. Imaging of fast non-stationary and irreproducible events, such those observed in cardiac perfusion is an area of active research (e.g. (60)).

Motion correction

MR Navigators

MR navigator methods acquire the required position information during an imaging sequence using the MR scanner itself ((61-63). This is achieved by frequently playing out ultra-short (on the order of milliseconds) navigator sequences during the imaging process. These navigator sequences allow for determination of the object’s position by comparing each acquired navigator signal to a reference.

Generally, navigators can be separated into two categories: those that work in k-space and those that work in image-space. They can be further classified in terms of their dimensionality: 1D, 2D, or 3D. Since any additional information encoded by the navigator comes at a cost of increased acquisition and processing times, and increased complexity, navigators are typically simplified to an extent acceptable for the target application. Therefore, 1D and 2D navigators are popular especially in abdominal and cardiac imaging to correct for breathing motion, by tracking the position of the diaphragm (64, 65). In brain imaging, 2D navigators allow for a correction of rigid body motion in the navigator plane (66-69). In DWI even the smallest movements caused by brain pulsation can lead to phase changes due to the strong gradients used for diffusion weighting. Variations of the image phase leads to substantial image artefacts in multishot-DWI. MR-navigators measuring the image phase after diffusion weighting (in 2D) allow the correction of these phase instabilities (70, 71).

3D navigators allow for the correction of patient motion in up to 6 degrees of freedom (66, 72-74). They also require substantial time to be available in the host sequence, on the order of hundreds of milliseconds. This time is available in many sequences, due to contrast preparation or recovery delays; therefore, 3D navigators have become increasingly popular, especially in brain structural imaging. Spectroscopic acquisitions offer even more ‘empty space’ within the sequence, which is sufficient to acquire several navigator echoes, or even specialized shim navigators to correct for shim alterations due to motion (75, 76). Recently, substantially faster 3D navigators, relying on parallel imaging or multiband excitation (33), have been presented at various conferences and workshops.

To improve the accuracy of the navigation sequence, and to reduce interference with the imaging process, it is possible to use additional spatial-frequency-tuned markers (77), miniature radio-frequency probes (78, 79), or signals of the endogenous fat (80, 81). However, many of these methods were so far restricted to 1D (80) and 2D (77, 81), and are generally only used in research applications.

An alternative to the navigator methodology is self-navigated methods, which allow the determination of motion from the MR imaging data themselves (45-47, 49, 58). All of these methods are very specific to a particular imaging scheme and are often limited to 2D acquisitions. One popular variant of self-navigated sequences is PROPELLER, which is discussed in detail in the next section. Self-navigation methods can also be extended to 3D, for example in conjunction with a three dimensional radial imaging scheme (48).

Navigator information can be used either retrospectively to correct the acquired imaging data (82), or prospectively to adapt the imaging scan to the patient’s position. Note that for prospective motion correction, motion parameters need to be extracted from the navigator data in real time. Advantages and disadvantages of both prospective and retrospective approaches are discussed below.

A detailed overview of different navigator approaches can be found in Chapter 12.2 of Bernstein (22).

PROPELLER

The acronym ‘PROPELLER’ is an abbreviation for ‘periodically rotated overlapping parallel lines with enhanced reconstruction’ (11). PROPELLER imaging, and all its variants, follow a strategy similar to that of radial imaging. However, instead of acquiring the data projection-by-projection, strips of several parallel k-space lines are collected. This can be realized using different readout strategies like RARE (83), EPI(84, 85), or GRASE (84). This strip is rotated around the k-space origin in the subsequent acquisition cycles until a disc of k-space is filled.

This sampling scheme provides substantially reduced motion sensitivity due to the strong oversampling of the k-space centre and its radial character. In addition, during the reconstruction the robustness to motion can be further improved (86). Low-resolution images reconstructed from single blades can be used to quantify in-plane translations and correct for the resulting inconsistencies between the blades prior to the final image reconstruction. Additionally, the central disc of k-space - which is acquired by all strips - can be used to detect and correct in plane rotations of the single k-space strips. By cross-correlating the central disc of the corrected strips, through-plane motion can be detected. Such motion cannot be corrected for retrospectively; however, by introducing factor that puts less weight on corrupted blades, the influence of through-plane motion can be reduced.

The PROPELLER sampling strategy can be combined with undersampling techniques (87). It can also be used to introduce diffusion weighting to the RARE readout module (88), which was shown to be of interest for DTI at high fields(89).

The PROPELLER methodology has been shown to be a very useful tool in clinical settings (90) and is available on the majority of imaging platforms (under different names). Drawbacks of PROPELLER are the increased image acquisition time, due to the strong oversampling around the k-space centre, the limitation to 2D imaging and a limited robustness against through-plane motions.

Prospective correction

Prospective motion correction is an intuitive approach where the relative spatial position and orientation between scanning coordinates and the object of interest is kept constant. For the correction of head motion, a rigid object is assumed, moving in 6 degrees-of-freedom. If the position and orientation of such an object can be measured in real time, the magnetic gradients, RF pulses, and receiver frequency and phase can be adjusted accordingly. Rotations of the object require a rotation of the encoding gradients; translations require a change of transmit and receive frequency and phase (91).

In the case of head motion, head pose can be measured using MR navigators, working either in image space (e.g. PROMO (92, 93), PACE (94)), or k-space (e.g. cloverleaf, spherical or orbital navigators (66, 67, 73)). Alternatively, an external tracking device can be used, including stereo camera systems (95), miniature RF probes (78, 79, 96), in-bore camera systems (97-99), or ultrasound systems (100). Navigators need to be compatible with the sequence timing and typically have a low temporal sample rate. On the other hand, external tracking typically requires an MR compatible design and accurate calibration to the scanner coordinate system. Furthermore, the majority of the external approaches require a tracking device to be mounted on the subject, which is a concern for routine applications.

The topic of prospective motion correction has gained popularity in the last few years resulting in numerous new applications including fMRI (101, 102), DWI (103, 104), and spectroscopy (105-107). Although it is an extremely promising approach for neuroimaging, it does have some limitations, including practical considerations (e.g., marker fixation for external tracking systems) and uncorrectable effects (e.g., motion-related B0 distortions (108)). Covering this topic in detail is beyond the scope of this paper; interested readers are referred to a recent review article (109).

Post-processing techniques & retrospective correction

While prospective correction methods aim at maintaining data quality during the acquisition, retrospective techniques attempt to improve data consistency afterwards, by modifying the collected data or the reconstruction model. This can be done by either including the exact knowledge about the motion during the scan (e.g. using navigator data) or with iterative algorithms (e.g. optimizing image entropy, gradient entropy or other measures of artefacts (110-112)).

The basic idea behind these methods is to undo the motion-related changes occurring to the MR data. For rigid body motion these are described according to the Fourier theorems: a translation of the object leads to a phase ramp in the acquired k-space, an object rotation corresponds to a rotation of k-space (113). While translations are relatively easy to correct by applying a phase change to the acquired data, the correction of rotations requires the use of non-Cartesian reconstruction methods (114,115) and includes some sophisticated algorithms (116-119) which are computationally intensive.

In 3D imaging, arbitrary rigid body motion can be corrected, as long as the acquired signals are only damaged but not lost (e.g. there are no signal dropouts due to intra-voxel dephasing). For 2D imaging these correction methods are limited to in-plane motion, as through-plane motion during the scan results in inconsistencies, which cannot be corrected.

Elastic motion remains a major challenge for both prospective and retrospective correction approaches. Especially in abdominal and cardiac MRI, the complexity of the underlying motion restricts the current concepts to a combination of gating/triggering followed by a correction of affine motion within the gating window (60, 120).

An alternative approach to retrospectively improve the quality of datasets which are only partially affected by motion is described in (121). By discarding motion corrupted data and filling the resulting parts of k-space using parallel imaging techniques, the quality of the reconstructed images could be increased at a cost of SNR and possibly some residual blurring.

By including a general description of motion into the MR signal equation (122) using measured or estimated displacement fields (123) free-breathing cardiac imaging has been demonstrated. Recently this approach has been extended to incorporate compressed sensing methodology (35). Unfortunately such retrospective image reconstruction methods are extremely computation-intensive, which presently restricts their clinical acceptance.

CONCLUSIONS

Due to peculiarities of the image acquisition process in MRI, motion causes a varying range of artefacts, including blurring, ghosting, signal dropouts and unwanted signal enhancement. The large variety of image contrasts and k-space sampling methods in MRI causes these artefacts to appear differently from scan to scan. This, coupled with a large range of motion types that occur in vivo, means that there is no single motion correction tool that can be applied to every motion problem. Instead, there is a toolbox of techniques, where different tools are applicable in particular situations. In some cases, powerful tools are already available; in other cases, tools still need to be developed. Nonetheless, it is likely that developing dedicated tools for specific situations will be what eventually solves the motion problem in MRI, rather than a single approach that solves all problems.