Skip to main content
PMC home page
Nature Portfolio logoLink to Nature Portfolio
. 2015 Jul 16;6:7666. doi: 10.1038/ncomms8666

Determination of band alignment in the single-layer MoS2/WSe2 heterojunction

Ming-Hui Chiu 1,*, Chendong Zhang 2,*, Hung-Wei Shiu 3, Chih-Piao Chuu 1, Chang-Hsiao Chen 1, Chih-Yuan S Chang 1, Chia-Hao Chen 3, Mei-Yin Chou 1,4,5, Chih-Kang Shih 2,a, Lain-Jong Li 1,6,b
PMCID: PMC4518320  PMID: 26179885

Abstract

The emergence of two-dimensional electronic materials has stimulated proposals of novel electronic and photonic devices based on the heterostructures of transition metal dichalcogenides. Here we report the determination of band offsets in the heterostructures of transition metal dichalcogenides by using microbeam X-ray photoelectron spectroscopy and scanning tunnelling microscopy/spectroscopy. We determine a type-II alignment between MoS2 and WSe2 with a valence band offset value of 0.83 eV and a conduction band offset of 0.76 eV. First-principles calculations show that in this heterostructure with dissimilar chalcogen atoms, the electronic structures of WSe2 and MoS2 are well retained in their respective layers due to a weak interlayer coupling. Moreover, a valence band offset of 0.94 eV is obtained from density functional theory, consistent with the experimental determination.

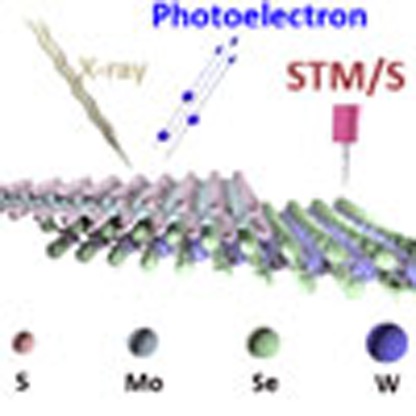Inline graphicThe alignment of the bandgap of adjacent materials in a heterostructure largely determines the electronic properties of a device. Here, the authors measure the conduction and valance band offsets at the interface between two two-dimensional materials: molybdenum disulphide and tungsten diselenide.

Transition metal dichalcogenides (TMDs) have emerged as a new platform for atomic layer electronics1 and optoelectronics2,3,4,5. Many proposed novel devices are based on heterostructures formed between dissimilar TMDs6,7,8,9,10,11,12,13. Heterojunction band offset is the key parameter for designing HJ-based electronic/photonic devices and accurate determination of this parameter is of critically important. In conventional semiconductor heterojunctions (HJs), one commonly used technique to determine the valence band offset (VBO) is XPS14,15,16,17. This method relies on finding the core-level alignment of two constituent semiconductors across the HJ. Then with additional information on the core-level position relative to the valence band maximum (VBM) measured separately for individual semiconductors, the VBM alignment across the HJ can be determined. The application of this technique to TMD HJs, however, faces two technical challenges. First, the HJ is formed only locally with a lateral lengthscale of only a few microns, owing to the limited lateral size of available TMD monolayer samples. It is thus necessary to locate such locally formed HJs and measure the core-level alignment across the junction. The second challenge is the determination of the VBM position. In conventional semiconductors, the valence bands primarily comprise of sp orbitals, with a smooth density of states (DOS). This allows for a precise determination of the VBM through curve fitting. In single-layer (SL) TMDs, the DOS near VBM has a complicated line shape due to the different characteristics of the states near Γ and K.

In the following, by using microbeam X-ray photoelectron spectroscopy (μ-XPS) where the photon spot can be focused down to sub-microns (spot size ∼100 nm), we are able to measure the core-level alignment across the TMD HJs at the local scale. Moreover, by using scanning tunnelling microscopy/spectroscopy (STM/S) to measure individual TMDs we determine the quasi-particle gaps and the fine structures involved, such as the energy difference between the VBM at Γ and K. The special combination of μ-XPS and STM/S measurements allow us to deduce the precise band offset values including both the VBO and conduction band offset (CBO). In addition, the first-principles calculations are performed to elucidate the interlayer interaction.

Results

The μ-XPS measurements

For μ-XPS measurements, the single-crystalline monolayer TMDs were synthesized using chemical vapour deposition on sapphire substrates18,19,20. These as-grown TMDs were then detached from sapphire substrates and transferred onto Si wafers with native oxides to form the HJ stacks (see the Methods section). It has been shown recently that with the presence of a thin native oxide (∼2 nm) layer the photoemission measurement can be carried out without the charging effect, but the oxide is also thick enough to ensure that the Si band structure is suppressed so the valence band structure detected is only from SL-TMDs21. For STM measurements, SL-TMDs are grown on highly oriented-pyrolytic-graphite (HOPG) directly to provide enough conductivity for STM imaging.

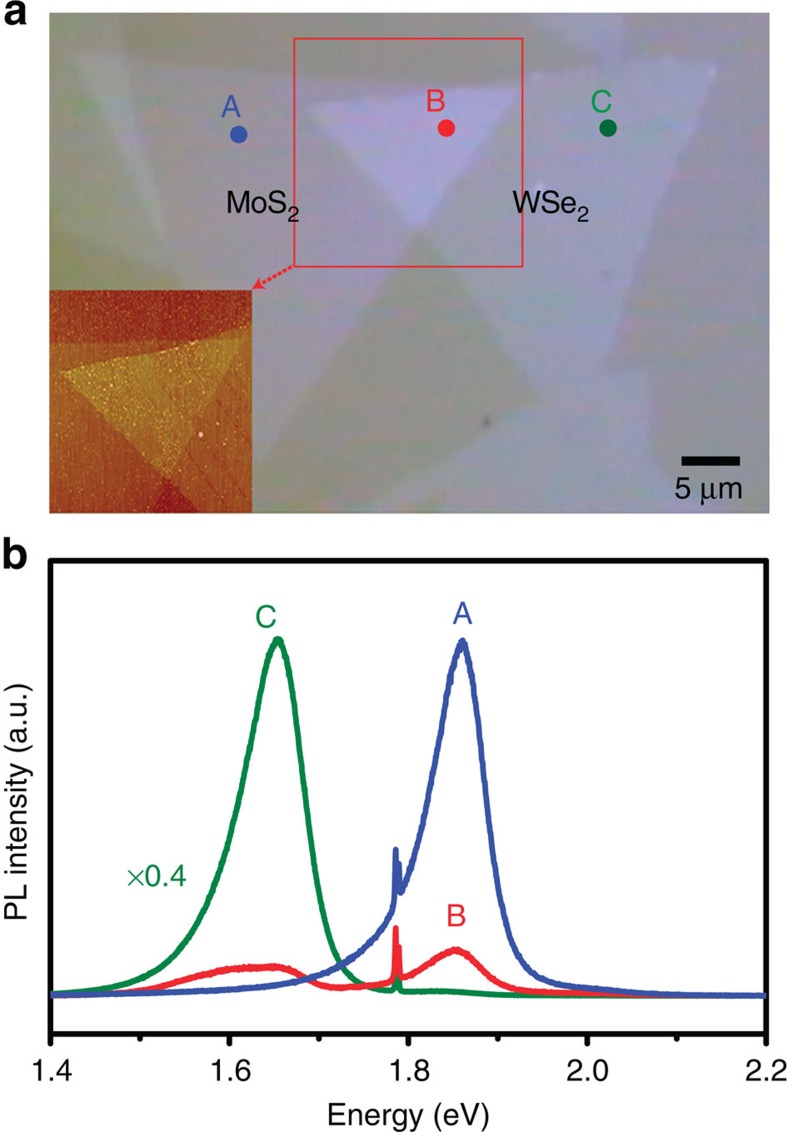
Figure 1a shows the optical micrograph and atomic force microscopy images for the WSe2/MoS2 heterostructure stacked on a sapphire substrate. The characterizations by atomic force microscopy, optical gap measurements and Raman spectroscopy (Supplementary Fig. 1 and Supplementary Table 1) indicate that they are single-layer TMDs flakes22,23. Figure 1b shows the photoluminescence (PL) spectra for the selected sites including MoS2 only (A), WSe2 only (C) and WSe2/MoS2 (B) areas. The PL intensity of both MoS2 and WSe2 for the overlapped area (B) is significantly lower than that from WSe2 or MoS2 alone, indicating that the photoexcited carriers are quenched through other routes than the emission from individual WSe2 or MoS2 band edges. The surface adsorbates on these two-dimensional (2D) materials are removed by vacuum annealing at an elevated temperature23. Herein, these flakes are annealed in a high vacuum chamber (2 × 10−10 Torr) at 300 °C for over 8 h before the scanning photoelectron microscopy (SPEM) scans.

Figure 1. Optical microscopy images and photoluminescence spectroscopy taken on the staked WSe2/MoS2 heterostructure.

Figure 1

Open in a new tab

(a) Optical micrograph and atomic force microscopy images for the WSe2/MoS2 heterostructural stacked flakes on a sapphire substrate. (b) Photoluminescence spectra for the selected sites including MoS2 only (A), WSe2 only (C) and WSe2/MoS2 (B) stacked areas.

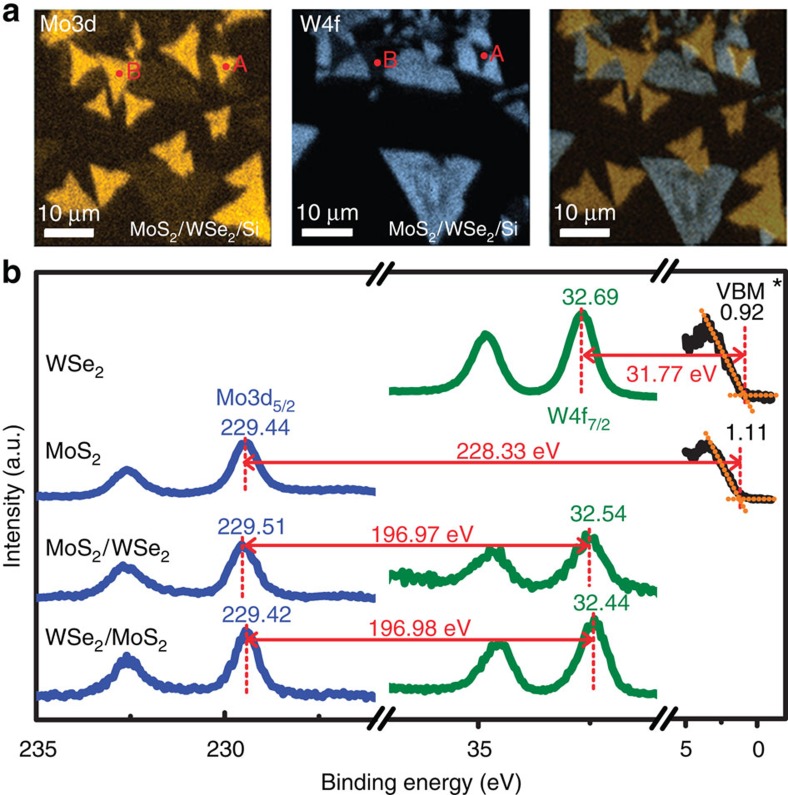
Figure 2a shows the spatial mapping of Mo3d5/2 (left), W4f7/2 (middle) and their composite (right) respectively using μ-XPS. Such an elemental mapping allows us to identify isolated SL-WSe2, SL-MoS2 and locally stacked HJ bilayer unambiguously. The corresponding core-level spectra of W4f and Mo3d in isolated SL-WSe2, isolated SL-MoS2, the WSe2/MoS2 stack and the MoS2/WSe2 stack are shown in Fig. 2b. Also shown are the corresponding valence band (VB) spectra in isolated SL-WSe2 and SL-MoS2 flakes. The energy splittings and relative intensities due to the spin–orbit coupling for W4f (4f7/2 and 4f5/2) and Mo3d (3d5/2 and 3d3/2) doublets remain unchanged before and after forming 2D stacked films. Furthermore, their energy locations are independent of the X-ray beam flux, confirming the absence of the charging effect.

Figure 2. μ-XPS measurements on the stacked MoS2/WSe2 and WSe2/MoS2 heterostructures.

Figure 2

Open in a new tab

(a) The Mo3d and W4f mappings for the same physical area. The right figure is the overlapped mapping that allows the identification of MoS2/WSe2 stacked areas. A and B points are the typical stacking area where the XPS are taken. (b) The spectra for the selected isolated WSe2 and MoS2 flakes, the stacked MoS2/WSe2 and WSe2/MoS2 heterostructure. All numbers are quoted in electron volt. There is an uncertainty of ±0.04 eV when determining the energy levels for all peaks.

The core-level separation between the W4f7/2 and Mo3d5/2 is determined to be 196.97±0.04 eV across the HJ. In reverse stacking (that is, WSe2/MoS2), this value becomes 196.98±0.04 eV, essentially unchanged within the experimental error. To determine the VBO, we also need the respective quantities of core level relative to the VBM in individual SL-WSe2 and SL-MoS2. With a least-square fit of the leading edge of the VB spectra (shown in Fig. 2b), the apparent VBM locations are determined to be 0.92 eV for WSe2 and 1.11 eV for MoS2 (Supplementary Fig. 2). We recognize, however, that this fitting procedure may not lead to the correct value of VBM value due to the complicate line shape in the DOS (discussed further in Supplementary Note 1). We thus label this ‘apparent' VBM position as VBM*. Using this procedure, we determine that the Mo3d5/2 relative to the VBM* in MoS2 to be 228.33±0.04 eV and the W4f7/2 relative to the VBM* in WSe2 to be 31.77±0.04 eV. Assuming that the energy difference between the VBM* and the core level remains unchanged after stacking, the apparent VBO* for MoS2 and WSe2 and in the stacked film MoS2 on WSe2 can be determined as:

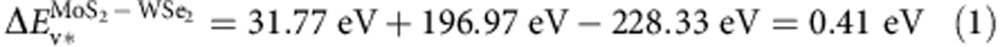graphic file with name ncomms8666-m1.jpg

Here the notation MoS2−WSe2 in the superscript indicates that this is the potential step moving from MoS2 into WSe2. The error bar in the determination of the VBO* is estimated to be 0.07 eV. The consistent core-level separation of 196.98±0.04 eV between W4f and Mo3d in reverse stacking also implies the validity of VBO commutativity in TMD HJs. Following similar procedures, we determine the VBO* between WS2 and MoS2 as 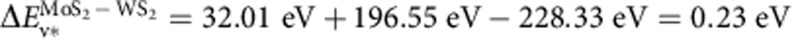Inline graphic using the W and Mo core-level alignment; and the VBO* of WS2/WSe2 HJ as 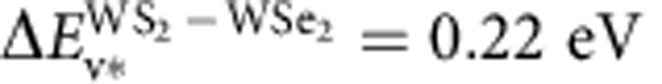Inline graphic using the S and Se core-level alignment. One very interesting result is that the transitivity is satisfied. Namely VBO* (MoS2−WSe2) is essentially the same as VBO*(MoS2−WS2)+VBO*(WS2−WSe2) within the experimental error bar.

Determination of band-edges by STM/S

Theoretical calculations show that the DOS near the VBM is dominated by the states near the Γ point with much less contribution from those near the K point where the true VBM is located (as shown in Supplementary Fig. 3b, and the generic band structures can also be seen in the Supplementary Fig. 3a.). Since XPS is unable to resolve the Γ-K splitting, the measured VBM* likely corresponds to the location of the Γ point. Thus, the resulting VBO* would not correspond to the true VBO. This shortcoming is overcome by using STS to accurately determine the quasi-particle gaps, and the Γ−K VBM energy splitting, ΔΓ−K. With these additional pieces of information, the band alignment (both valence band and conduction band) can be accurately determined.

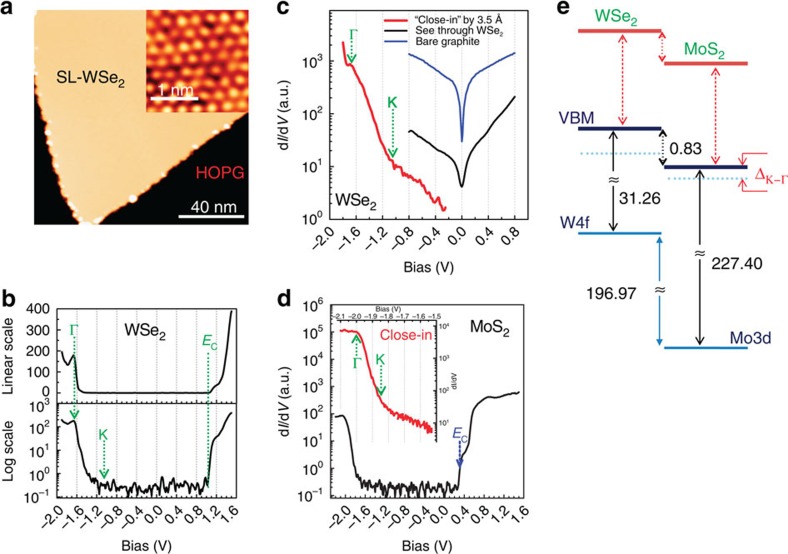
Figure 3a shows the STM image of SL-WSe2 grown on HOPG, with a typical tunnelling spectrum shown in Fig. 3b. In the negative bias range, there is sharp peak at about −1.65 V then vanishes quickly as the bias is increased. In the positive sample bias range, an onset of conductivity occurs at +1.03 V. To determine the VBM and CBM positions, the conductivity is displayed in the logarithmic scale (lower panel in Fig. 3b) where the sharp onset at 1.03 V can be unambiguously identified as the CBM. The determination of the VBM using such a dI/dV spectrum, however, encounters some ambiguity. An extrapolation of the leading edge would yield a threshold being located somewhere between −1.4 and −1.3 V. Detailed examination, however, reveals that the global VBM at the K point is located at a significantly higher energy location (at −1.05 V) and the peak at the −1.65 V corresponds to the local VBM at the Γ point. In the WSe2 region, as long as the junction stabilization voltage (namely, the applied bias before the interruption of the feedback) is between −1.65 and −2.0 V, the spectrum does not have enough sensitivity to detect the global VBM position. To enhance the ability to observe these states, we acquire another spectrum by reducing the tip-to-sample distance by ∼3.5 Å, shown as the red curve in Fig. 3c. In this ‘close-in' distance, tunnelling from the states of the underlying graphite can also be detected. Moreover, there is a threshold at −1.05±0.05 V separating the states derived from graphite and those from WSe2. This threshold is assigned as the global VBM at the K point. By using a stabilization voltage of −0.8 V (well into the gap region of WSe2), the underlying graphite electronic states can be ‘seen through SL-WSe2' and the spectrum is essentially the same as the spectrum acquired in the bare graphite surface (shown as the black and blue curves in Fig. 3c). This also confirms our assignment of the threshold at −1.05 V to be the global VBM position at K point. More detailed discussions on the determination of energy location of different thresholds and their origins in the Brillouin Zone can be found in ref. 24. In Fig. 3d, we show a close-in spectrum for MoS2 where the Γ point can be identified at −2.0 V while the VBM is located at −1.84±0.05 eV. The CBM location of MoS2, can also be resolved as 0.31±0.05 eV.

Figure 3. STM images and the tunnelling spectra of WSe2 and MoS2 grown on HOPG.

Figure 3

Open in a new tab

(a) STM image of single layer WSe2 grown on HOPG. The inset shows the atomic resolution image taken on the SL-WSe2. For the inset, U=−1.4 V, I=10 pA. (b) The dI/dV-V spectrum taken on the SL-WSe2 flake. The tunnelling conductance dI/dV (with arbitrary unit) is plotted in both the linear scale (upper panel) and the logarithmic scale (lower panel). The green dashed arrows indicate the positions of the local VBM at Γ and K points, which are equal to −1.65 eV and −1.05 eV, respectively. The CBM is assigned at +1.03 eV. (c) The clear threshold, corresponding to VBM at K, can be seen in the dI/dV spectrum taken with much more close tip-sample distance (∼3.5 Å closer than b). For comparison, the spectra taken with the stabilization bias with the gap (−0.8 V) is shown in black, while the one taken on bare graphite is in blue. The similar dI/dV (in black) and ‘close-in' (red in inset) spectra of SL-MoS2 are displayed in d, while the valence band maxima at Γ and K are marked in the inset. The EC (blue arrow) corresponds to the CBM. (e) The diagram of band alignments among single-layer MoS2 and WSe2. The local VBM at Γ and global VBM at K are shown in cyan and red, respectively.

To determine the core-level position relative to the true VBM in SL-TMD, we carry out μ-XPS on similarly prepared single-layer MoS2 and WSe2 on HOPG (Supplementary Fig. 4). The measurements yield a binding energy of 229.24±0.03 eV for Mo3d5/2, corresponding to a separation of 227.40 eV to the true VBM (at the K point) in MoS2. Similarly, W4f7/2 in SL-WSe2 on graphite has a binding energy of 32.31±0.03 eV, corresponding to a value of 31.26 eV when referenced to the true VBM. With these two binding energies relative to their individual VBM determined, we can reapply the same algorithm and obtain a true VBO of

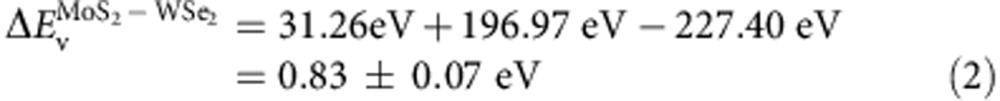graphic file with name ncomms8666-m4.jpg

One can immediately see that the VBO measured is 0.42 eV larger than the apparent VBO* of 0.41 eV measured using XPS alone. This is due to the fact that in WSe2, the K point is 0.60 eV higher than the Γ point while in MoS2, it is only about 0.16 eV higher. With these STS energy data, the VBO* value can be deduced as 0.39 eV, very close to the XPS values of 0.41 eV. This affirms our earlier conjecture that the XPS measurement of VBM* is dominated by the high DOS at the Γ point. STS measurements of quasi-particle gaps (2.15±0.1 eV for MoS2 and 2.08±0.1 eV for WSe2) also allow us to deduce a CBO of 0.76±0.12 eV, affirming a type-II band alignment as illustrated in Fig. 3e.

Another very interesting observation is that for individual SL-MoS2 and WSe2 on graphite the binding energy difference between Mo3d5/2 and W4f7/2 is 229.24−32.31=196.93±0.04 eV, essentially the same as the core-level separation (196.97±0.04 eV) across the HJ stack. This means that ‘the supporting graphite substrate is a good common energy reference' for TMDs when we consider the problem of band alignment. In fact, if we take directly the VBM measured in STS for SL-TMD on graphite (−1.05 eV for WSe2 and −1.84 eV for MoS2), a VBO of 0.79 eV is deduced when we choose graphite as the energy reference. Why does this work? If we treat SL-TMD on graphite as a semiconductor–semimetal heterojunction, then the measured VBM position of SL-TMD on graphite also represents the VBO of the TMD/graphite heterojunction. If we then use the VBOs determined for SL-MoS2/graphite and SL-WSe2/graphite, and apply the transitivity we will deduce a VBO of 0.79 eV for MoS2/WSe2 heterojunction system, essentially the same as the VBO measured using XPS. We suggest that the reason this transitivity holds is related to the weak van der Waals interactions between TMDs and graphite and between different TMDs.

First-principles calculations of the TMD HJs

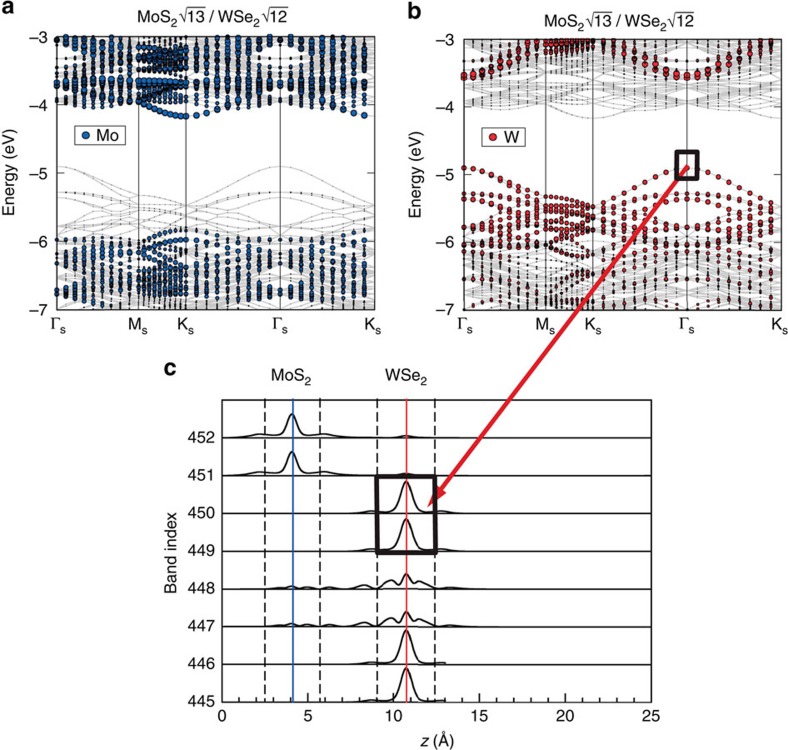
One fundamental question to address is whether or not individual layers retain their respective electronic structures even after stacking. The definition heterojunction would be meaningful only if this is true. To address this issue, we have carried out theoretical density functional theory (DFT) calculations for the electronic structures of the composite system formed by two dissimilar SL-TMD layers. Shown in Fig. 4 is the case for MoS2/WSe2 calculated using a 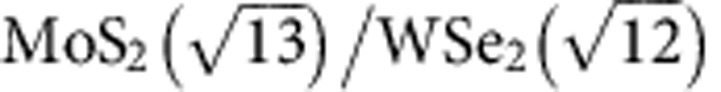Inline graphic supercell to accommodate the difference in lattice constants. The direct bandgap at the original K point in the isolated MoS2 layer remains at K for the Brillouin zone of the supercell (labelled as Ks in Fig. 4), while the direct bandgap at the original K point in the WSe2 layer is folded to the Γs point. As can be seen, the electronic structures can be nicely projected into their respective MoS2 and WSe2 layers that are the same as the isolated layers, confirming the validity of treating the MoS2/WSe2 as a heterojunction. Moreover, a numerical value of 0.94±0.1 eV for the VBO is obtained in the DFT calculation which agrees very well with the 0.83±0.07 eV measured experimentally.

Figure 4. First-principles calculations for the electronic structures of the composite system formed by two dissimilar SL-TMD layers.

Figure 4

Open in a new tab

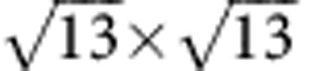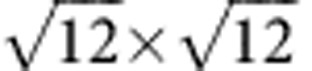(a,b), Energy band structure of the MoS2/WSe2 bilayer calculated using a supercell containing rotated Inline graphic and Inline graphic unit cells of MoS2 and WSe2, respectively, to minimize the strain in individual layers due to lattice mismatch. The labelling of the symmetry points is referenced to the Brillouin zone of the supercell. Note that the original K point in the MoS2 SL remains at Ks, while the original K point in the WSe2 SL is folded to Γs. The projected bands onto Mo and W atoms are shown in a,b, respectively, with the amount of Mo (W) projection represented by the size of blue (red) circles. (c) One-dimensional charge density (integrated over the horizontal direction) illustrating that the states at the band edges belong to a distinct layer.

Theoretically, we have also carried out the calculations for heterostructures with other combinations of TMDs. The interlayer interaction between two TMD layers with the same chalcogen species turns out to be significant enough to change the characteristics of the states at the VBM. As an example, the MoS2/WS2 heterostructure is presented in Supplementary Note 2, and the energy bands are shown in Supplementary Fig. 5. We find that the band offset at the K point remains well defined and appears to be independent of the stacking pattern. However, the interlayer coupling moves the VBM position in the WS2 layer from K to Γ point, creating an indirect gap about 0.1–0.2 eV smaller than the direct gap6 (see Supplementary Fig. 5). Thus, for optical property that is dominated by the direct transition at the K point, the band offset concept may remain valid6,25, but one has to take into account the indirect bandgap in transport measurements.

Discussion

In summary, by using μ-XPS, in conjunction with scanning tunnelling spectroscopy, we have shown the capability to determine the band alignment in locally formed TMD heterostructures. We determine a type-II alignment in WSe2/MoS2 with a VBO of 0.83±0.07 eV and a CBO of 0.76±0.12 eV. We further discover that the TMDs and the supporting graphite also form a semiconductor/semimetal heterostructure such that the transitivity hold for different heterostructures formed between SL-TMDs and TMD/graphite. Theoretical investigations show that the electronic band structure of the stacked TMD bilayers containing different chalcogen species resembles a superposition of the energy bands of individual layers, upholding the definition of semiconductor heterojunction. Quantitative agreement of VBO value is found between theoretical calculations and experimental measurements.

Methods

Growth and characterizations of 2D monolayers

The direct growth of MoS2 or WSe2 monolayer crystal flakes on a sapphire substrate by the vapour-phase reaction has been reported in our previous reports19,20. In brief, high-purity metal trioxides MO3 (M=Mo, W) was placed in a ceramic boat at the heating centre of the furnace. A sapphire substrate was placed in the downstream side adjacent to the ceramic boat. Sulfur or Selenium powder was heated by a heating tape and carried by Ar or Ar/H2 to the furnace heating centre. The furnace was then gradually heated from room temperature to desired temperature for reaction. After the reaction process, furnace was naturally cooled down to room temperature. These monolayers were characterized atomic force microscopy (Veeco Dimension-Icon system) and a confocal Raman /photoluminescence system (NT-MDT equipped with a 473-nm laser with the spot size of ∼0.5 μm).

Scanning tunnelling microscopy

All STM investigations reported here were acquired at 77 K in ultra-high-vacuum (UHV; base pressure <6 × 10−11 Torr). Electrochemically etched W-tips were cleaned in situ with electron beam bombardment. The tunnelling bias is applied on sample. Before STM investigations, the samples were cleaned in situ by heating it up to 250 °C for an extended time (typically longer than 2 h). The conductance spectra were taken by using a lock-in amplifier with a modulation voltage of 10 mV and at a frequency of 724 Hz.

Preparation of stacking layers

To stack the MoS2 (WSe2) monolayer flakes on the undoped Si substrate, a layer of PMMA thin film was coated on the as-grown MoS2 (WSe2) on sapphire as a transfer supporting layer26. After dipping in an aqueous NaOH (HF) solution, the PMMA-supported MoS2 (WSe2) monolayer was detached from sapphire substrates and transferred to the Si(111) substrate (Sheet resistance >300 Ohm sq−1), followed by the removal of PMMA using acetone. Various 2D heterostructural stacking films such as WSe2 on MoS2 or WSe2 on MoS2 can be obtained by transferring desired 2D flakes onto the other flake.

Microbeam SPEM

The synchrotron radiation-based SPEM system is located at beam line 09A1 of National Synchrotron Radiation Research Center, Taiwan. The system is composed of a 16-channel hemisphere electron energy analyser (model 10–360, PHI), a sample scanning stage, and Fresnel zone plate optics to focus the monochromatic soft X-ray down to 100 nm. By synchronized raster scanning the sample relative to the focused soft X-ray, the excited photoelectrons (PE) were collected and analysed by the analyser. The PE intensity of specific core-level line can be converted into a two-dimensional surface chemical state distribution image27. SPEM can also be operated in μ-XPS mode to acquire high-resolution PE spectra. Combining the imaging and μ-XPS modes makes SPEM a suitable instrument to study the heterostructure of novel 2D materials28. The photon energy utilized in this study was 400 eV, which was calibrated every 8 h with the Au 4f core-level line of a clean gold foil electrically contacted with the samples to ensure the measurement reproducibility.

Theoretical calculations

First-principles calculations were carried out within DFT using the Vienna Ab initio simulation package (VASP)29,30. The interactions between electrons and ions is described by the projector augmented wave method31, and the exchange-correlation potential is described by the Perdew–Burke–Ernzerhof-generalized gradient approximation32, with vdW corrections incorporated with vdW-DF functionals33. A supercell size of 25 Å is used to eliminate the spurious image interaction in the slab calculation, and the energy cutoff of plane waves is 600 eV. The lattice constants of monolayer MoS2 and WSe2 used in the simulation are 3.17 and 3.31 Å, respectively. The interlayer spacing is 6.67 Å between MoS2 and WSe2. More detail can be seen in Supplementary Note 3.

Additional information

How to cite this article: Chiu, M.-H. et al. Determination of band alignment in the single-layer MoS2/WSe2 heterojunction. Nat. Commun. 6:7666 doi: 10.1038/ncomms8666 (2015).

Supplementary Material

Supplementary Information

Supplementary Figures 1-5, Supplementary Table 1, Supplementary Notes 1-3 and Supplementary References

ncomms8666-s1.pdf (830.2KB, pdf)

Acknowledgments

This research was supported by Academia Sinica, National Science Council Taiwan (NSC-102-2119-M-001-005) and AFOSR BRI. The work at UT Austin is support with grants from the Welch Foundation (F-1672), and the US National Science Foundation (DMR-1306878), and the theoretical work at Georgia Tech is supported by the US Department of Energy, Office of Science, Basic Energy Sciences, under Award No. DE-FG02-97ER45632. C.-K.S also thanks the National Science Council, Taiwan for financial supports for a visiting chair professorship at the National Tsing Hua University, Taiwan (NSC 102-2811-M-007-034). C.-P.C. acknowledges the support from the Thematic Project at Academia Sinica.

Footnotes

Author contributions C.-K.S. and L.-J.L. conceived the experiment. L.-J.L. coordinated the growth and XPS effort, C.-K.S. coordinated the STM effort and M.-Y.C. directed the theoretical simulation effort. C.-H.C. and C.-Y.S.C. performed the growth and M.-H.C. prepared the CVD stacked films and carried out the Raman and PL characterizations. H.-W.S. and C.-H.C. performed the XPS measurement. C.Z. carried out the STM measurement. C.Z. and C.-K.S. analysed the STM data. C.-P.C. carried out the theoretical simulation. L.-J.L., C.-K.S. and M.-Y.C. wrote the papers with inputs from the other co-authors.

References

  1. Radisavljevic B., Radenovic A., Brivio J., Giacometti V. & Kis A. Single-layer MoS2 transistors. Nat. Nanotechnol. 6, 147–150 (2011) . [DOI] [PubMed] [Google Scholar]
  2. Splendiani A. et al. Emerging photoluminescence in monolayer MoS2. Nano Lett. 10, 1271–1275 (2010) . [DOI] [PubMed] [Google Scholar]
  3. Mak K. F., Lee C., Hone J., Shan J. & Heinz T. F. Atomically thin MoS2: a new direct gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010) 136805 . [DOI] [PubMed] [Google Scholar]
  4. Wu S. F. et al. Electrical tuning of valley magnetic moment through symmetry control in bilayer MoS2. Nat. Phys. 9, 149–153 (2013) . [Google Scholar]
  5. Xiao D., Liu G. B., Feng W. X., Xu X. D. & Yao W. Coupled spin and valley physics in monolayers of MoS2 and other Group-VI dichalcogenides. Phys. Rev. Lett. 108, 196802 (2012) . [DOI] [PubMed] [Google Scholar]
  6. Rivera P. et al. Observation of long-lived interlayer excitons in monolayer MoSe2–WSe2 heterostructures. Nat. Commun. 6, 6242 (2015) . [DOI] [PubMed] [Google Scholar]
  7. Tongay S. et al. Tuning interlayer coupling in large-area heterostructures with CVD-grown MoS2 and WS2 Monolayers. Nano Lett. 14, 3185–3190 (2014) . [DOI] [PubMed] [Google Scholar]
  8. Lee C.-H. et al. Atomically thin p–n junctions with van der Waals heterointerfaces. Nat. Nanotechnol. 9, 676–681 (2014) . [DOI] [PubMed] [Google Scholar]
  9. Cheng R. et al. Electroluminescence and photocurrent generation from atomically sharp WSe2/MoS2 heterojunction p–n diodes. Nano Lett. 14, 5590–5597 (2014) . [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Hong X. P. et al. Ultrafast charge transfer in atomically thin MoS2/WS2 heterostructures. Nat. Nanotechnol. 9, 682–686 (2014) . [DOI] [PubMed] [Google Scholar]
  11. Fang H. et al. Strong interlayer coupling in van der Waals heterostructures built from single-layer chalcogenides. Proc. Natl Acad. Sci. USA 111, 6198–6202 (2014) . [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Britnell L. et al. Strong light-matter interactions in heterostructures of atomically thin films. Science 340, 1311–1314 (2013) . [DOI] [PubMed] [Google Scholar]
  13. Withers F. et al. Light-emitting diodes by band-structure engineering in van der Waals heterostructures. Nat. Mater. 14, 301–306 (2015) . [DOI] [PubMed] [Google Scholar]
  14. Franciosi A. & Van de Walle C. G. Heterojunction band offset engineering. Surf. Sci. Rep. 25, 1–140 (1996) . [Google Scholar]
  15. Bratina G., Sorba L., Antonini A., Biasiol G. & Franciosi A. AlAs-GaAs heterojunction engineering by means of Group-IV elemental interface layers. Phys. Rev. B 45, 4528–4531 (1992) . [DOI] [PubMed] [Google Scholar]
  16. Kowalczyk S. P., Cheung J. T., Kraut E. A. & Grant R. W. CdTe-HgTe Inline graphic heterojunction valence-band discontinuity: a common-anion-rule contradiction. Phys. Rev. Lett. 56, 1605–1608 (1986) . [DOI] [PubMed] [Google Scholar]
  17. Shih C. K. & Spicer W. E. Determination of a natural valence-band offset: the case of HgTe- CdTe. Phys. Rev. Lett. 58, 2594–2597 (1987) . [DOI] [PubMed] [Google Scholar]
  18. Cong C. X. et al. Synthesis and optical properties of large-area single crystalline 2D semiconductor WS2 monolayer from chemical vapor deposition. Adv. Opt. Mater. 2, 131–136 (2014) . [Google Scholar]
  19. Huang J. K. et al. Large-area synthesis of highly crystalline WSe2 mono layers and device applications. ACS Nano 8, 923–930 (2014) . [DOI] [PubMed] [Google Scholar]
  20. Lee Y. H. et al. Synthesis of large-area MoS2 atomic layers with chemical vapor deposition. Adv. Mater. 24, 2320–2325 (2012) . [DOI] [PubMed] [Google Scholar]
  21. Jin W. C. et al. Direct measurement of the thickness-dependent electronic band structure of MoS2 using angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 111, 106801 (2013) . [DOI] [PubMed] [Google Scholar]
  22. Tonndorf P. et al. Photoluminescence emission and Raman response of monolayer MoS2, MoSe2 and WSe2. Opt. Express 21, 4908–4916 (2013) . [DOI] [PubMed] [Google Scholar]
  23. Zhang C. D., Johnson A., Hsu C. L., Li L. J. & Shih C. K. Direct imaging of the band profile in single layer MoS2 on graphite: quasiparticle energy gap, metallic edge states and edge band bending. Nano Lett. 14, 2443–2447 (2014) . [DOI] [PubMed] [Google Scholar]
  24. Zhang C. D. et al. Probing critical point energies of transition metal dichalcogenides: surprising indirect gap of single layer WSe2. Preprint at http://arxiv.org/abs/1412.8487 (2014) . [DOI] [PubMed]
  25. van der Zande A. M. et al. Tailoring the electronic structure in bilayer molybdenum disulfide via interlayer twist. Nano Lett. 14, 3869–3875 (2014) . [DOI] [PubMed] [Google Scholar]
  26. Lebegue S. & Eriksson O. Electronic structure of two-dimensional crystals from ab initio theory. Phys. Rev. B 79, 115409 (2009) . [Google Scholar]
  27. Chiou J. W. X-rays in nanoscience: spectroscopy, spectromicroscopy, and scattering techniques Ch. 4 Weinheim : Wiley-VCH (2010) . [Google Scholar]
  28. Shiu H. W. et al. Graphene as tunable transparent electrode material on GaN: layer-number-dependent optical and electrical properties. Appl. Phys. Lett. 103, 081604 (2013) . [Google Scholar]
  29. Kresse G. & Furthmuller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp. Mater. Sci. 6, 15–50 (1996) . [DOI] [PubMed] [Google Scholar]
  30. Kresse G. & Furthmuller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996) . [DOI] [PubMed] [Google Scholar]
  31. Blochl P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994) . [DOI] [PubMed] [Google Scholar]
  32. Perdew J. P., Burke K. & Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996) . [DOI] [PubMed] [Google Scholar]
  33. Klimes J., Bowler D. R. & Michaelides A. Van der Waals density functionals applied to solids. Phys. Rev. B 83, 195131 (2011) . [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Figures 1-5, Supplementary Table 1, Supplementary Notes 1-3 and Supplementary References

ncomms8666-s1.pdf (830.2KB, pdf)

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES