Accelerated Molecular Dynamics and Protein Conformational Change: A Theoretical and Practical Guide Using a Membrane Embedded Model Neurotransmitter Transporter

Abstract

Molecular dynamics simulation provides a powerful and accurate method to model protein conformational change, yet timescale limitations often prevent direct assessment of the kinetic properties of interest. A large number of molecular dynamic steps are necessary for rare events to occur, which allow a system to overcome energy barriers and conformationally transition from one potential energy minimum to another. For many proteins, the energy landscape is further complicated by a multitude of potential energy wells, each separated by high free-energy barriers and each potentially representative of a functionally important protein conformation. To overcome these obstacles, accelerated molecular dynamics utilizes a robust bias potential function to simulate the transition between different potential energy minima. This straightforward approach more efficiently samples conformational space in comparison to classical molecular dynamics simulation, does not require advanced knowledge of the potential energy landscape and converges to the proper canonical distribution. Here, we review the theory behind accelerated molecular dynamics and discuss the approach in the context of modeling protein conformational change. As a practical example, we provide a detailed, step-by-step explanation of how to perform an accelerated molecular dynamics simulation using a model neurotransmitter transporter embedded in a lipid cell membrane. Changes in protein conformation of relevance to the substrate transport cycle are then examined using principle component analysis.

1 Introduction

Classic molecular dynamics (cMD) simulations are used to study the kinetic behavior of proteins. By implementing fundamental laws of motion, the technique is able, on an atom-by-atom basis, to accurately predict the dynamic behavior of proteins in various modeled environments. The technique effectively samples conformational space in a time-dependent manner, and if conducted for a sufficient number of time-steps, produces an accurate representation of a system's potential energy landscape. The resulting trajectories can then be analyzed, allowing for insight to a wide variety of dynamic processes, including protein conformational change.

This technique is invaluable given that proteins are complex structures, interacting dynamically with their environment in response to a variety of thermodynamic, ionic, and other factors. While experimentally determined structures provide valuable three-dimensional information and often a necessary starting point for modeling a given protein, the experimental process provides a single snapshot of a protein, frequently in a non-physiological environment. In order to obtain a detailed mechanistic understanding of protein function, as it is necessary for rational drug development for example, a detailed understanding of dynamic protein conformational change in an environment representative of defined physiological or pathological conditions and under parameters amenable to subtle molecular change is necessary.

While cMD simulations are highly beneficial in this regard, simulation time is limited to the nanosecond or microsecond timescale at best, despite implementation of state-of-the-art supercomputers with highly advanced processing ability. Although processing ability continues to improve, the limit in achievable timescale is further reduced as an increased understanding of biological systems results in the need to model more accurate and complex systems, containing multimers of large proteins in various contexts for example.

Given these limitations, cMD simulations often fall short of effectively exploring the full energy landscape. Exceedingly large numbers of computational steps are required for rare events to occur allowing systems to overcome energy barriers and transition from one potential energy minima to another. Furthermore, the energy landscape for proteins often consists of multiple potential energy wells separated by high free energy barriers. Still, by means of exceedingly long all-atom cMD simulations, often conducted on special-purpose machines using specialized force fields, investigators have achieved timescales far in excess of those previously accessible to computational study, gaining insight into a variety of complex dynamic protein behavior, including protein folding and conformational change within the folded state [1, 2].

In order to avail a more widely available and expeditious technique to simulate the infrequent transition between potential energy minima and therefore realistically capture protein dynamics, alternate computational approaches are necessary. One such approach, termed steered molecular dynamics (SMD), involves applying external forces to a system to explore its mechanical responsiveness [3]. While this approach has proven effective in a number of contexts [4–8], it relies on user defined forces most accurately applied given prior knowledge of the conformational state of interest.

In contrast, accelerated molecular dynamics (aMD) provides a straightforward and effective way to simulate infrequent events required for protein conformational change without previous knowledge of conformational states, potential energy wells, or barriers. The aMD method alters the amount of computational time a system spends in a given potential energy minima by adding a bias potential, ΔV(r), to the true potential in such a way that potential surfaces in vicinity of the minima are raised, while those closer to the barrier or saddle point are not affected. This allows for a reduction in computational time spent at a potential energy minima and an increase in the ability of a system to move over potential barriers. The effect of the bias is removed by correcting statistics sampled on the biased potential. The method results in preservation of the underlying shape of the potential energy surface and converges to the correct canonical probability distribution, allowing for an approach that efficiently and accurately explores conformational space [9].

Today, aMD simulations are routinely performed to assess time-dependent protein conformational change [10–15] and are fully integrated into commonly used software packages including NAMD [16, 17] and Amber [18, 19]. Performing aMD simulations is straightforward and consists of steps similar to those in cMD simulations, with the addition of defining aMD specific variables.

2 Theory

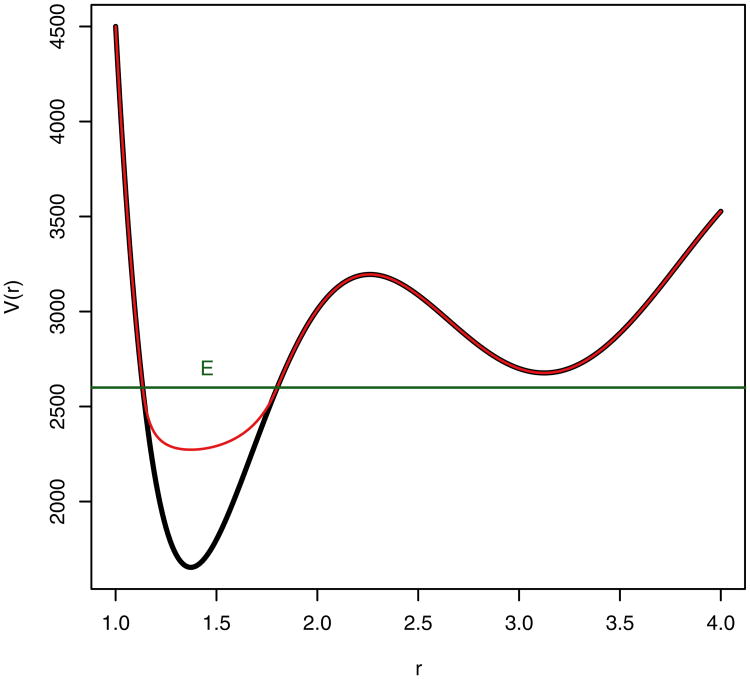
Expanding on a previous hyperdynamics method explored by Voter [20, 21], the aMD method allows for assessment of protein conformational change by reducing the computational time a simulated protein spends in a potential energy basin, allowing the system to transverse potential energy barriers more readily. This is accomplished by adding a bias potential to the true potential when the systems potential energy falls below a threshold level (Fig. 1). While Voter's method of implementing the bias potential requires the Hessian matrix to be diagonalized at each time step in order for identification of transition state regions, the aMD method is based on a simpler bias potential proposed by Steiner et al. [22] and implemented by Rahman and Tully [23]. In this “puddles” method, the bias potential is selected so that the produced modified potentials near the minima remain constant if the true potential of the system falls below a selected threshold level. Accordingly, diagonalization of the Hessian matrix is not required at each step, allowing for the simulation method to be applied to larger systems such as proteins.

Fig. 1. Graphical representation of the biased potential, the threshold boost energy, E, and the normal potential.

Specifically, a nonnegative, continuous bias boost potential function ΔV(r) is defined such that when the true potential of a system, V(r), falls below a specified boost energy, E, the simulation is carried out using the modified potential V*(r) = V(r) + ΔV(r), while when V(r) is greater than or equal to E, the simulation is carried out using the true potential such that V*(r) = V(r). The relationship between the true potential, modified potential, boost energy, and bias boost potential is

$$V^{\ast }(\mathbf{r})=\{\begin{array}{c}V(\mathbf{r}),V(\mathbf{r})\ge E,\\ V(\mathbf{r})+\mathrm{\Delta }V(\mathbf{r}),V(\mathbf{r})<E\end{array}$$ (1)

aMD provides a robust method that, in comparison to cMD simulation, accelerates the state to state transition of large molecules such as proteins. By using the bias potential to modify the true potential of the system, the transition of the system from one state to another takes place at an accelerated rate with a timescale Δt* that is nonlinear, such that

$$\mathrm{\Delta }{t}_i^{\ast }=\mathrm{\Delta }t{e}^{\beta \mathrm{\Delta }V[\mathbf{r}(t_i)]}.$$ (2)

Accordingly, the clock is advanced at each step based on the strength of the bias potential, where Δt represents the actual time step on the unmodified potential. If the bias potential, ΔV(r) = 0, as is the case when V(r) is greater than or equal to the boost energy E, the system is on true potential and Δt* = Δt. Statistics can then be used to estimate the total simulation time based on the following equations:

$$t^{\ast }=\sum _i^N\mathrm{\Delta }{t}_i^{\ast }=\mathrm{\Delta }t\sum _i^N{e}^{\mathrm{\beta }\mathrm{\Delta }V[\mathbf{r}(t_i)]},$$ (3)

$$t^{\ast }=t\langle e^{\mathrm{\beta }\mathrm{\Delta }V[\mathbf{r}(t_i)]}\rangle ,$$ (4)

where 〈e^{βΔV[r(t_i)]}〉 is the boost factor, a measure of the simulation acceleration extent, and N is the total number of simulation steps.

Importantly, the aMD method converges to the canonical distribution, allowing for accurate determination of equilibrium and other thermodynamic properties. The phase space for the modified potential can be reweighted at each point by multiplying individual configurations by the bias strength at each configuration, resulting in a corrected ensemble average equivalent to that observed with the normal potential [24, 25]. This approach as well as other reweighting approaches allowing for accurate free energy calculation of the resulting trajectories continue to be explored.

In the original method described by Rahman and Tully, the boost potential ΔV(r) is defined as E − V(r). With this method, when the true potential energy is below the threshold boost energy E, the modified potential energy, V*(r) = E. This produces flat regions or “puddles” at potential energy basins. While this method is computationally inexpensive, complications due to the discontinuity at points where the unmodified potential meets the modified potential result in the need for special computations which increase the computational burden overall. More importantly, at a high boost energy, the flat modified potential exists at a level higher than most transition state regions. As a result the system may undergo a “random walk” and is slow to converge.

Alternatively, the aMD method utilizes a “snow drift” approach which fills the minima, producing a more smooth landscape. The shape of the underlying potential energy surface is maintained even at a high boost energy E. The method results in a smooth transition where the unmodified potential energy above the boost energy meets the modified potential energy. In order to accomplish this, ΔV(r) is defined by the equation

$$\mathrm{\Delta }V(\mathbf{r})=\frac{{(E-V(\mathbf{r}))}^2}{\mathrm{\alpha }+(E-V(\mathbf{r}))},$$ (5)

The tuning parameter α determines the depth of the modified potential energy basin, such that when α = 0, the energy basin is flat, just as in the method described by Rahman and Tully, while as α increases the depth of the modified potential energy basin decreases.

It is important that the values for E and α be selected carefully in the course of an aMD simulation, as these values determine how aggressive a given simulation is accelerated and how accurately the energy landscape is maintained respectively. The value of E should be selected such that it is larger than the minimum V(r), V_min, at the beginning of the simulation. Consider for example a situation in which E is selected such that it is lower than a system's potential energy minimum. Where V(r) > E, V*(r) = V(r), the energetics of the system will be maintained just as in a typical molecular dynamic simulation. Alternatively, E can be selected such that it is greater than a system's potential energy minimum, V*(r) = V(r) + ΔV(r). Since proteins tend to have several potential energy minima spaced closely together, it is advisable to calculate the average true potential energy of a protein over a short period of cMD simulation, and to use this value as the minimum potential energy from which E can be determined.

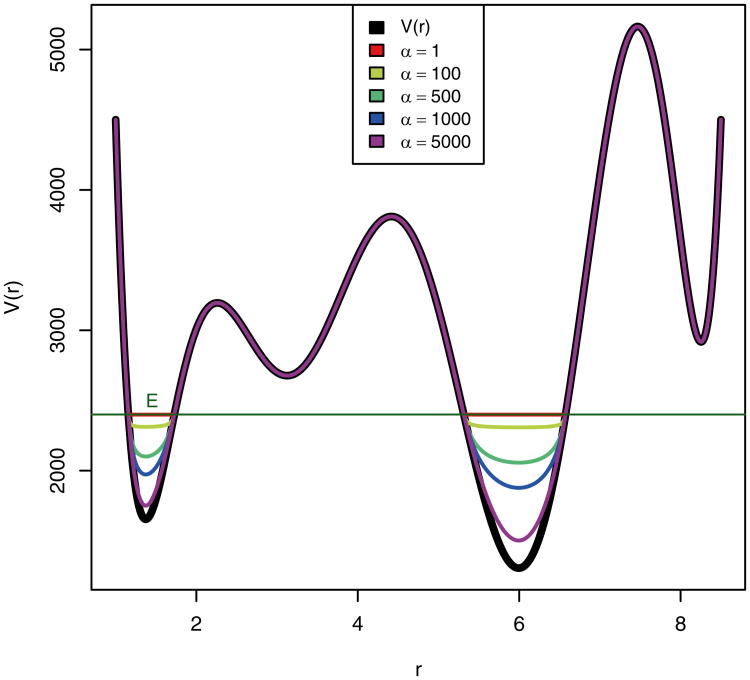
When the value of E is set low, the modified potential energy remains below the transition state regions and the probability of overcoming energy barriers and enhanced energy sampling is diminished (Fig. 2). In this situation the value of α is of lesser importance to protein conformational sampling and the aMD simulation as a whole, providing that α is large enough so that the modified potential energy basins are not flat (“puddles”) since this would result in the calculated force becoming discontinuous where the modified potential energy equals the boost energy.

Fig. 2. Graphical representation of a hypothetical potential energy function and different bias potentials plotted at various α values and at a relatively low threshold boost energy, E.

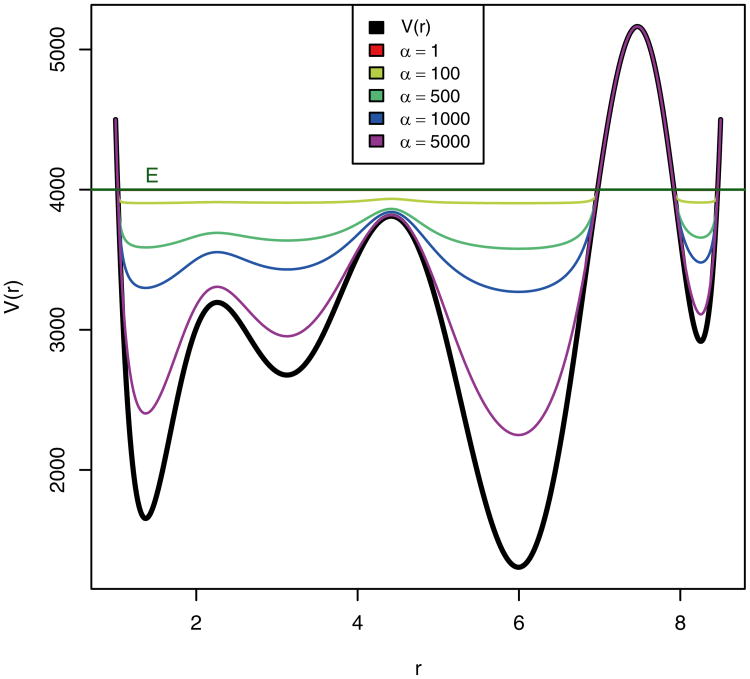
Alternatively, when the value of E is set to be high, the value of α becomes much more significant (Fig. 3). If the value of E is set high and the value of α is set low, the modified potential becomes equivalent in most places and the system undergoes a random walk. In order to prevent this and to maintain the basic shape of the underlying unmodified potential energy, when the value of E is set high, the value of α must likewise be set high.

Fig. 3. Graphical representation of a hypothetical potential energy function and different bias potentials plotted at various α values and at a relative high threshold boost energy, E.

Taken together, as indicated above, the first step in determining the correct values for E and α is to determine the minimum potential energy of a given system, which is best determined by calculating the average potential energy of the true potential over a short period of cMD simulation, and then using this value as the minimum potential energy (V_min). The value of E should then be chosen so that it is greater than the minimum potential energy. The magnitude by which E is greater than V_min will determine the aggressiveness of acceleration in the simulation. In practice, the value of E is usually selected so that it equals V_min plus 2.5–3.0 times the number of amino acids in the simulation. The value of α should then be set so that it is equal to E−V_min. At this value the modified potential energy will preserve the landscape of the underlining unmodified potential energy wells and will merge with the original potential in a smooth fashion [9].

While aMD simulation allows rapid sampling of multiple conformational states, analyzing the resultant trajectories can be problematic due to the large amount of data produced. While the traditional root mean square deviation (RMSD) method can be used to distinguish between different conformational states, this method is not as effective as the system undergoes transitions between subtle yet significant conformational states yielding low RMSD values. Instead, principal component analysis (PCA) can be used as a more sensitive method to distinguish between different conformational states.

PCA reduces the dimensionality of large data sets by calculating a covariance matrix and it eigenvectors. Vectors with the highest eigenvalues become the most significant principal components. When principal components are plotted against each other, similar structures cluster. Each cluster then theoretically represents a different protein conformational state.

Since PCA can be calculated using coordinates from any subset of atoms within a given protein, atom selection can have a large effect on observed outcomes. A common protocol used to avoid sample noise from random fluctuations is to calculate the PCA only for backbone carbon atoms. Alternatively, specific residues or segments of a given protein can be selected based on experimental observations and isolated in a PCA analysis. For example, following aMD simulation of the leucine transporter, the combination of coordinate positions for the backbone carbon atoms of the transmembrane helical domains 1b and 6a was a better discriminator of conformations than the calculations of either the whole structure or any other helical domains alone or in combination [15].

3 Methods

Below we present a protocol for performing aMD simulation and assessing protein conformational change. As an example, we highlight our recent work modeling the bacterial leucine transporter (LeuT), a homologue of the eukaryotic Na⁺/Cl⁻-dependent neurotransporters responsible for terminating synaptic transmission by driving the cellular uptake of neurotransmitters, including the biogenic amines. These proteins are the targets of numerous pharmacological compounds and their dysfunction is associated with disorders of the nervous system. Through the use of aMD simulation, we have gained insight to the function of this class of proteins [26, 15].

In order to provide the reader with a guide such that an equivalent technique can be extended to the study of any protein of interest, we will discuss (1) building a simulation environment suitable for aMD simulation and the study of protein conformational change, (2) preparatory energy minimizations, heating the system, cMD equilibration, and aMD production runs, and (3) analysis of protein conformational change using PCA.

3.1 Computer Software

A text editor is useful for many of the manipulations described below. Helpful functions include the ability to quickly copy and paste several lines of text, search and replace functionality with features such as wild-cards and line number restrictions and the ability to quickly move to a given line number or string of text. More complicated tasks are often facilitated by the use of a procedural programing language such that complex edits to a PDB file are straightforward. UCSF Chimera [27] is a program for visualization, analysis, and manipulation of molecular structures and when used in conjunction with MODELLER [28] is useful in this context for adding missing residues during the initial preparation of the system. The Visual Molecular Dynamics (VMD) package [29] offers robust molecular visualization as well as a variety of molecular building and manipulation options; it will be used here for visualization, the creation of lipid membrane starting coordinates, and embedding the protein in the lipid membrane. AMBER [18] offers highly scalable code designed for high- performance simulation of large molecular systems; it will be used in the following example for placing hydrogen atoms, solvation, energy minimization, heating the system, cMD equilibration, and aMD production runs. The Bio3D utility package in the R statistical computing software environment [30] will be used to perform PCA analysis.

3.2 Obtain the Starting Protein Coordinates

Prior to performing an aMD simulation, it is necessary to obtain starting coordinates for the protein of interest. These may come from crystal structures, nuclear magnetic resonance (NMR) structures, or various computational models. In the case of LeuT, the crystal structure coordinates [31] can be downloaded from the Protein Data Bank, entry 2A65 (www.rcsb.org; MMDB accession no. 34395). When working with a new PDB file, it is a good practice to open the PDB file with a text editor to carefully review the header information in order to gain an overall understanding of the types of residues present, both those that are part of the protein and otherwise, potential limitations of the model, and any other pertinent information.

3.3 Build Coordinates for a Lipid Membrane

For many membrane proteins, the surrounding lipid membrane structure plays a critical role in influencing protein dynamics. In order to realistically model and most accurately capture transporter dynamics we will embed the LeuT in a lipid bilayer. Here we will demonstrate this by using the VMD Membrane Plugin 1.1 to generate the starting coordinates for a lipid membrane and then use VMD's graphic user interface (GUI) front end to align the newly generated membrane with the existing crystal coordinates.

The VMD Membrane Plugin 1.1 uses pre-built patches of lipid bilayers to generate a rectangular membrane of the necessary size. The algorithm used to build the lipid bilayer patches creates two lipid layers, with each layer consisting of a two-dimensional hexagonal lattice of lipids. In order to allow for straightforward insertion of proteins, the lipid tails are nearly fully extended. The distance between the layers and the lattice period is set to correspond with experimental data corresponding to actual membrane thickness and surface density respectively. In order to introduce some disorder to the patches, each lipid is placed in the lipid plane in a random orientation and a truncated Gaussian spread is used in the perpendicular direction. Additional disorder is introduced by a 1 picosecond equilibration in vacuum, serving the additional function of eliminating steric collisions while still leaving most of the lipid tails extended. Finally, the VMD Membrane Plugin 1.1 properly hydrates the lipid head groups, simplifying downstream solvation and equilibration of the protein-membrane system. A more detailed description of the VMD Membrane Plugin 1.1 can be found at: http://www.ks.uiuc.edu/Research/vmd/plugins/membrane/.

In the following steps, we build the membrane coordinates in VMD:

1. Select Extensions → Modeling → Membrane Builder to launch the VMD Membrane Plugin.

2. Under Lipid, select POPE. This defines the lipid composition. Currently, POPE and POPC lipid structures are supported. The lipid composition should be selected to most closely match the lipid composition in vivo as guided by experimental data. Here we selected POPE as this is compatible with the phosphatidylethanolamine-predominant monoamine transporter protein milieu.

3. Under Membrane X Length and Membrane Y Length we specify the membrane dimensions in Ångströms. For this system, we enter 110 for both dimensions.

4. The Output Prefix and Topology can be left as the default settings. Click Generate Membrane to create the specified membrane.

3.4 Align the Membrane and Protein Coordinates

Positioning the membrane properly must be done carefully and with appropriate consideration for the underlying biology. One way to accomplish this is to position the membrane such that polar head groups and hydrophilic lipid tails make contact with specific residues of the transmembrane protein, as guided by experimental data. If this data is not available, an alternate method involves calculating the center of mass of the main center vestibule of the transmembrane protein and aligning this with the center of mass of the generated membrane. This process is explained in detail in the VMD Membrane Proteins Tutorial by Alek Aksimentiev et al. [33]. Here, we position the LeuT based on a combination of experimental data and an analysis of the polarity of the residues at the transporter-lipid interface as follows:

After generating the membrane and water coordinates as detailed in Subheading 3.3, without closing VMD, load the LeuT crystal structure file (PDB 2A65).

1. Load PDB 2A65 by selecting File → New Molecule. Under Load Files for: ensure that New Molecule is selected. Click on Browse and navigate to the folder where the coordinates are saved. Selected the correct file and click Open. Under Determine file type: PDB should be selected automatically if the file was given the correct extension (.pdb). Select Load.

2. In the VMD Main window, the currently loaded molecules are listed in the Molecule List Browser. Two separate molecules should be listed in this window: one containing the generated membrane and water coordinates and a second containing the 2A65 coordinates.

In order to better visualize our protein, membrane, and water molecules, we will alter the graphical representation. Select Graphics → Representations and adjust the representation as follows:

1. Under Selected Molecule select the molecule corresponding to the lipid membrane. Under selected atoms type resname POPE and not hydrogen and click on Apply.

2. Click on Create Rep. This creates a second representation for the molecule containing the lipid coordinates. Under Selected Atoms type resname TIP3 and click Apply. This creates two separate representations for the coordinates generated by Membrane Builder 1.1, one representation for the lipid molecules (without hydrogen atoms) and a second representation for the water molecules. In the white box under Create Rep, where the two separate representations are listed, double click on the representation containing the water molecules. The text should turn red and the water molecules should disappear from the OpenGL Display. While the water molecules are important to the simulation, positioning the membrane correctly in relation to the protein is facilitated by hiding the water molecules.

3. Under Selected Molecule click on the dropdown menu and select the molecule containing the LeuT coordinates. Change the Coloring Method to ResType and Drawing Method to Cartoon and click Apply. This allows us to distinguish between nonpolar residues (white), polar residues (green), basic residues (blue), and acidic residues (red). This information will be helpful in properly positioning the lipid membrane.

4. In the VMD Main window, select Display → Orthographic.

We are now ready to move the crystal structure coordinates while holding the newly generated membrane coordinates fixed.

1. In the VMD Main window select Mouse → Move → Molecule. All the coordinates within the 2A65 crystal structure are now moved by clicking with the left mouse button on the transporter in the OpenGL Display window and dragging. Holding the shift key and moving the mouse allows the membrane and water coordinates to be rotated about the point on the screen that is clicked. Using the left mouse button rotates about the x or y axis of the screen, while using the middle or right button rotates the coordinates about an axis perpendicular to the screen.

2. Using the keyboard and mouse commands indicated above, we now move the crystallized coordinates such that the transporter is positioned correctly in relation to the membrane. The general orientation of the transporter in the lipid membrane is described based on experimental data obtained by Yamashita et al. [31]. More exact placement is obtained by positioning to the greatest extent possible (1) the nonpolar residues (white) at the membrane interface in contact with the hydrophobic lipid tails of the POPE membrane and (2) the polar residues (green) at the membrane interface either in contact with the polar head groups our out of the transverse plane of the lipid bilayer (Fig. 4).

3. When satisfied with the placement of the transporter in relation to the membrane coordinates, in the VMD Main window select File → Save Coordinates. Under Save data from use the dropdown menu to select the molecule containing the correctly positioned 2A65 coordinates. Under Selected atoms select all. Ensure pdb is selected under File type. Click Save, navigate to an appropriate directory and enter a file name to save the lipid coordinates. Finally, click Save again. The PDB and PSF files generated for the membrane and membrane solvation are automatically saved to the VMD working directory when the membrane structure is generated. Since no modifications were made to the membrane it is not necessary to re-save these files.

Fig. 4.

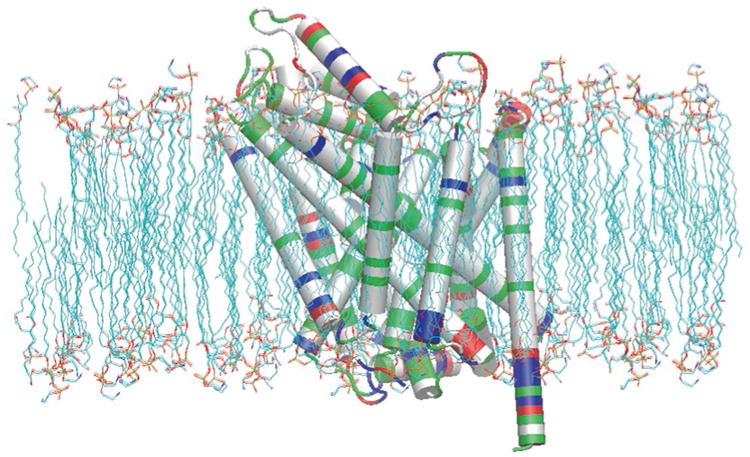
LeuT positioned within the POPE lipid membrane. Nonpolar residues (white) at the membrane interface in contact with the hydrophobic lipid tails of the POPE membrane and polar residues (green) at the membrane interface either in contact with the polar head groups our out of the transverse plane of the lipid bilayer

3.5 Prepare the Starting Protein Coordinates

In the case of 2A65, in addition to including the coordinates for the amino acids that make up the transporter, the Protein Data Bank entry includes crystallized coordinates for ions found in the binding pocket, the substrate leucine, water molecules, and a B-octylglucoside (BOG) residue. In our simulation, we wish to include the crystallized transporter with ions, but remove the substrate, water molecules, and B-octylglucoside residues. The substrate is removed in this example in order to sample transporter conformations that occur in the absence of substrate. The B-octylglucoside residues are removed since they are not likely to influence the dynamic process of substrate transport, the interest of this study. It is important that decisions in regard to experimental design, such as that mentioned previously, be made with consideration for underlying biology and specific study objectives.

In order to accomplish this, we will use a text editor to modify the crystal coordinates saved after alignment with the membrane in Subheading 3.4. While it is not essential, it can be helpful from an organizational perspective to save the coordinates for each individual subunit/chain in new separate PDB files, keeping only lines containing coordinate information. If several chains are to be included in a single coordinate file, it is necessary to add the TER keyword between each chain, although this is not needed between water molecules. In the case of LeuT (PDB 2A65), we create two new separate PDB files from the membrane aligned coordinates, one containing the coordinate lines for the residues of the transporter and one containing the coordinate lines for the binding pocket ions (with each line of ion coordinate information separated by the TER card).

At this stage it is also important to consider special residues with modifiable protonation states, such as cysteine and histidine residues. When PDB coordinate files are initially read into LEaP to produce input files for production calculations in AMBER, regular protonated cysteine residues should be named CYS, deprotonated or metal atom bound cysteine residues should be named CYM, and cysteine residues involved in disulphide bridges should be named CYX. Similarly, histidine residues should be named HIE when protonated in the epsilon position, HID when protonated in the delta position, and HIP when protonated in both the epsilon and delta positions. In the LeuT crystal structure, there are no cysteine residues, however, we replace the residue name HIS with the residue name HID.

It is helpful also to remove all hydrogen atoms included in the newly made coordinate files. Coordinates for hydrogen atoms in NMR structures may be inaccurate. Furthermore, NMR naming conventions are different from PDB naming conventions. Still, if needed, it is possible to use LEaP to correct the nonstandard hydrogen names. In the present example, all hydrogen atoms will be positioned using LEaP and then energy minimized prior to cMD simulation.

Finally, note that some PDB files contain alternate coordinates for specific residues. When these coordinates are read into AMBER using LEaP, only the A conformation is used. If a different coordinate set is needed, this can be accomplished by modifying the PDB file to contain only the coordinates of interest.

3.6 Build Missing Residues

Review of the headers in the 2A65 PDB file indicates that the four most N- and C-terminal residues and residues N133 and A134 are missing. We will build the missing non-terminal residues (N133 and A134) into our structure, but leave out the terminal residues. This task can be accomplished in UCSF Chimera and MODELLER as follows:

1. In UCSF Chimera load the membrane aligned 2A65 PDB file by selecting File → Open and navigating to the PDB structure. While it is often not necessary to specify the “file type” it is a good practice to do so to avoid any potential unexpected errors.

2. Select Tools → Structure Editing → Model/Refine Loops. This brings up sequence information for the protein. Missing residues are highlighted with red boxes. Selecting Model/Refine Loops will also open UCSF Chimera's interface to MODELLER.

3. In the Model Loops/Refine Structure window select non-terminal missing structure. This selects residues that are found in the PDB SEQRES record, but missing from the PDB file coordinates. This selection only selects residues constrained at both ends by existing structures, so the N- and C-terminal missing residues will not be built.

4. Other building parameters can also be modified. In this example, we allow 0 residues adjacent to the missing regions to move, generate 1 model, use the Discrete Optimized Protein Energy (DOPE) energy score [32], and run MODELLER using the Web service. After selecting Ok, progress toward completion of this step can be tracked in the lower left hand side of the main UCSF Chimera window.

5. The new coordinates can be saved by selecting File → Save PDB. Give the file a new name by adding text in the box to the right of File name, select the newly created model in the box to the right of Save models and select Save.

6. Using a text editor, open the newly saved PDB file containing the missing residues, navigate to and highlight the newly created residues and cut/paste the new ATOM information into the appropriate place in the previously prepared PDB file containing only the transporter coordinates. Note that since we have not built the N-terminal residues, the PDB file output by UCSF Chimera has renumbered the residues beginning in the first position. Be careful to select and copy the correct residues.

7. Renumber the new residues and atoms appropriately in the transporter coordinate file being prepared for input to AMBER. While renumbering the two newly created residues is straightforward to accomplish manually, renumbering the atoms manually is a daunting task. To assist in doing this, the Fortran 90 source code provided below can be used to compile a program that reads in a PDB file containing 4056 atoms and outputs a PDB file with identical information but appropriately numbered atoms. Different PDB manipulation scripts can be written in any procedural programing language of choice to assist in performing more complex alterations to various components of a PDB file.

program renumber_atoms

implicit none

character (len = 5) ∷ first

character (len = 6) ∷ old

character (len = 64) ∷ last

integer ∷ i = 1

do i = 1, 4056

read (5,“(a5,a6,a64)”), first, old, last

write (6,“(a5,i6,a64)”), first, i, last

end do

end program

3.7 Remove Overlapping Membrane Structures

In Subheading 3.4 PDB and PSF files were generated for a lipid bilayer with solvated polar head groups. In Subheadings 3.5 and 3.6 the LeuT transporter and binding pocket ions were correctly positioned within the bilayer and the missing transporter residues were built respectively. There are still, however, lipid and water molecules that overlap with the transporter structure. In this section VMD will be used to delete any lipid or water residues that overlap or are too close to the transmembrane protein.

First, a protein structure file (PSF) is generated from the LeuT only PDB file created in Subheading 3.6. This is done in VMD using the automatic PSF generator as follows:

1. Open VMD and in the VMD Main window select Extensions → Tk Console. In the VMD TkConsole that opens, navigate to the directory where the LeuT PDB file generated in Subheading 3.6 is located by using the “cd” command followed by the path to the appropriate directory and pressing enter.

2. Load the PDB file by entering the command “mol new file-name.pdb” and pressing enter.

3. In the VMD Main window select Extensions → Modeling → Automatic PSF Builder.

4. Under “Step 1: Input and Output Files” ensure the PDB file loaded in step 2 is selected under “Molecule” and that the “Output basename” is “leut_autopsf”.

5. Under “Step 2: Selections to include in the PSF/PDB” make sure that “Everything” is selected.

6. Under “Step 3: Segments Identified” select “Add a new chain”. Under “Chain Name” enter “LeuT”. The “First Atom” and “Last Atom” should be changed to the first and last LeuT atom number in the PDB file that was loaded (1 and 4057 respectively). Under “N terminal patch” and “C terminal patch” add “NTER” and “CTER” respectively. Finally select “Add chain”.

7. Under “Step 4: Patches” select “Apply patches and finish PSF”. This will create in the current working directory a PSF and PDB file with the name entered under “Output basename”.

Next, the previously generated membrane.psf and membrane. pdb files are loaded, the membrane and transporter structures are combined into a single PSF and PDB to allow for comparison, lipid and water molecules that are within a specified distance from the protein are deleted, and the resulting PDB and PSF files for the system with overlapping residues deleted are output. All of these steps are easily accomplished with the following script that can be run from the VMD Tk Console:

# Load package

package require psfgen

# Load starting structures

resetpsf

readpsf membrane.psf

coordpdb membrane.pdb

readpsf leut_autopsf.psf

coordpdb leut_autopsf.pdb

# Output a combined structure

writepsf leut_mem.psf

writepdb leut_mem.pdb

# Load combined structure

mol load psf leut_mem.psf pdb leut_mem.pdb

# Delete lipid and water molecules within 1.2 A of protein

# Get segids to check

set check_sel [atomselect top “resname POPE or water”]

set check_sel_segs [lsort -unique [$check_ sel get segid]]

foreach list_seg $check_sel_segs {

# find atoms

set current_atom [atomselect top “segid $list_seg and within 1.2 of protein”]

# delete residues

set current_res [lsort -unique [$current_ atom get resid]]

foreach res $current_res {

delatom $list_seg $res

}

}

# Output modified structure

writepsf leut_mem_no_overlap.psf

writepdb leut_mem_no_overlap.pdb

# Load modified structure for viewing

mol load psf leut_mem_no_overlap.psf pdb leut_mem_no_overlap.pdb

The above script is executed in VMD by inserting the commands in a text document and saving the file to VMD's current working directory. Within the Tk Console, the script is then run by executing the command “source filename”, where “filename” is the name of the file the above script is saved as.

Next, assess the resulting structure. The script above can be modified such that the cutoff distance at which residues are deleted is changed. When satisfied with the resulting structure, save PDB files for the membrane alone and the membrane solvation alone as follows. In the VMD Main window select File → Save Coordinates. Under Save data from use the dropdown menu to select the correct molecule. Under Selected atoms select resname POPE and not hydrogen. Ensure pdb is selected under File type. Click Save, navigate to an appropriate directory and enter a file name to save the lipid coordinates. Finally, click Save again. Repeat this process again to save the water molecules alone by changing the Selected atoms to waters and not hydrogen.

3.8 Generate a Nonstandard POPE Lipid Unit Using Antechamber

If we loaded the files generated thus far into AMBER's LEaP program using a standard protein force field, the POPE lipid residue would not be recognized. In this next section we will use the Antechamber tool set that comes with AMBER in order to generate an input file that is necessary in order to include the POPE lipid structure in our simulation. The Antechamber tool set works in conjunction with the general AMBER force field (GAFF), a force field that is designed to have general atom types such that it can provide broad applicability to a variety of different molecules. It can also be used in conjunction with traditional AMBER force fields that may be more appropriate for the rest of the molecules in a simulation. As such, Antechamber and GAFF are highly useful entities. The Antechamber tool set automatically identifies atom and bond types, judges atomic equivalence, provides a residue topology file, and suggests reasonable alternatives for any resulting missing force field parameters. Given the highly automated nature of this process, however, it is critical to carefully evaluate the resulting output to verify suitability.

Here we will use Antechamber to assign atom types and charges for the POPE residue. To begin, open the PDF file generated previously containing the coordinate information for the POPE lipid membrane. Copy and paste all the lines that together make up a single POPE residue (there are 125 ATOM lines that together represent a single POPE residue) into a new text file called pope.pdb. Next, in order to use antechamber to create the “prepin” file necessary to define the new POPE unit in LEaP, run the following command:

$AMBERHOME/bin/antechamber -i pope.pdb -fi pdb -o pope.prepin -fo prepi -c bcc -s 2

The “$AMBERHOME/bin/antechamber” command initiates the antechamber utility. The “-i” command specifies the name of the input file and the “-fi” command specifies the format of the input file; antechamber accepts several other input file formats. The “-o” command specifies the name of the output file and the “-fo prepi” command tells antechamber to output the file in the PREP format used internally by LEaP. “-c bcc” directs antechamber to calculate the atomic point charges using the BCC charge model. Finally, “-s 2” specifies the level of verbosity that antechamber is to provide.

Completion of this step will result in several new files in the directory where the script is executed. The files in capital letters are intermediate files useful for troubleshooting; should analysis of the following produce the intended results they can safely be deleted. The divcon.out file results from quantum mechanics calculations necessary in order to determine the point charges for individual atoms. It is useful to assess this file to ensure that this process has completed without error. Finally, the “pope.prepin” file is the file necessary to load the new POPE unit into LEaP. This file contains a definition of the POPE unit including connectivity, charges, and atom type information. Importantly, the atom types in this file (column 3) are all listed in lower case; this is intended to distinguish from the atom types to be evaluated using traditional AMBER force filed parameters, which are defined in upper case.

The GAFF is designed to be extensive and therefore include parameters for a large combination of parameters. It is possible, however, that a new unit defined in Antechamber may contain a combination of atom types that have not been parameterized. In order to check for this the parmchk executable is called:

$AMBERHOME/bin/parmchk -i pope.prepin -f prepi -o pope.frcmod

This command compares the parameters that are necessary for the new POPE unit to those that are available in the GAFF. Should any parameter be missing antechamber will either empirically calculate the parameter or find a similar, analogous parameter; the results of which are then listed in the “.frcmod” file. Should it be impossible to define parameters in this way, Antechamber will add a place holder and a comment indicating that revision is required, in which case other methods of parameterization should be pursued. It is important to carefully assess the rational that is used for any parameters obtained in the “.frcmod” file. The “pope.frcmod” file obtained here is shown below:

remark goes here

MASS

BOND

ANGLE

DIHE

IMPROPER

c3-o -c -os 10.5 180.0 2.0 General improper torsional angle (2 general atom types)

c2-c3-c2-ha 1.1 180.0 2.0 Using default value

NONBON

3.9 Solvate the System, Add Missing Atoms, and Generate Input Files for Production Calculations

Prior to performing production calculations such as energy minimizations or MD simulations in AMBER, it is necessary to define: (1) a “prmtop” file that contains the required force field parameters and a description of the molecular topology and (2) an “inpcrd” file that contains the atomic coordinates. An “inpcrd” file can also contain atomic velocities and periodic box information if defined. Here, AMBER's LEaP program will be used to generate the files necessary for production calculations.

In order to realistically model protein behavior, it is furthermore necessary to solvate the system with water molecules and ions. Any missing atoms including hydrogen atoms and N- and C-terminus specific atoms which have not previously been included can be added at this point. Conveniently, LEaP will perform all of these tasks. The molecular coordinates and parameter information developed as described above will be used as a starting point.

Here, tleap, the command line version of LEaP will be used. The script provided below will read in the coordinate and parameter information generated thus far and define a periodic box. Next, water molecules will be added, maintaining a 1.5 Å or greater distance from any existing solute and forming a box that extends 12 Å in the Z axis from any existing solute. Sodium and chloride atoms will then be added within the box surrounding solute. The Coulombic potential on a grid will be used to determine placement and should steric conflict occur with a water molecule, the water molecule will be removed and the ion will be added in its place. The number of sodium and chloride ions are selected to mimic physiological ion concentrations and also to meet the requirement of an overall neutral system. Finally, the resulting system is evaluated for errors and a PDB file as well as the necessary “prmtop” and “inpcrd” files are output for the system as a whole.

# Load force field parameters

source leaprc.gaff

source leaprc.ff99SB

# Load Antechamber files - from 3.8

loadAmberPrep pope.prepin

loadAmberParams pope.frcmod

# Load positioned binding pocket ions - from 3.5

bpions = loadpdb “bp_ions_positioned.pdb”

# Load positioned LeuT with missing residues - from 3.6

leut = loadpdb “leut_positioned_allres.pdb”

# Load lipids and lipid solvation - from 3.7

pope = loadpdb “pope.pdb”

popewater = loadpdb “pope_water.pdb”

# Combine into one unit

system = combine {bpions leut pope popewater}

# Set periodic box

setBox system vdw

# Solvate the system along the z axis; maintain a distance of 1.5 A from solute

solvateBox system TIP3PBOX {0 0 12} 1.5

# Add ions to produce a neutral system

addIons system Na+ 56 Cl- 60

# Examine the final unit

check system

charge system

desc system

# Output files

savePdb system leut_system.pdb

saveamberparm system leut_system.prmtop leut_system.inpcrd

quit

With all the necessary files in the current working directory and the above script saved to a text file called “leap.in”, the following command is used to execute the script:

tleap –f leap.in

3.10 Perform Energy Minimizations

Next energy minimizations are performed in order to “relax” the system. This is necessary to eliminate any energetically unfavorable interactions that may occur in the process of building the system. For example, hydrogen atoms added as described above are positioned according to a predefined geometry and therefore the resulting coordinates may have steric conflicts or overlap with other residues. The minimization steps eliminate such problems, providing an energetically favorable, more stable starting point for molecular dynamics simulation.

Using the “prmtop” and “inpcrd” files generated in Subheading 3.9, AMBER's sander can be used to perform the energy minimization. The following “minimize.in” file is used to direct sander to perform an energy minimization:

Minimization of solvent

&cntrl

imin = 1,

maxcyc = 1000,

ncyc = 400,

ntb = 1,

ntr = 1,

cut = 12

/

Hold protein and lipids fixed

250.0

RES 1 636

END

END

The “&cntrl” command must begin with a leading black space and specifies the type of namelist that follows. The minimization starts at step 1 (imin = 1) and continues for 1,000 steps (maxycy = 1,000). The first 400 steps utilizes the steepest decent algorithm, appropriate for quickly reducing the largest strain, and the remaining 600 steps utilizes the conjugate gradient algorithm which is more appropriate for converging to a minima (ncyc = 400). Constant volume periodic boundary conditions will be used (ntb = 1). Position restraints will be used (ntr = 1) using a force constant of 250 kcal/mol/Ų to restrain the lipid and protein residues (residue numbers 1–636).

The following command will execute the energy minimization:

$AMBERHOME/bin/sander -O -i minimize.in -o minimize.out –c leut_system.inpcrd -p leut_system.prmtop -r leut_system_min.rst

Where “-O” specifies that output files should be overwrite any existing files, “-I” specifies the name of the “mdin” file, “-o” specifies the name of the output file, “-c” specifies the starting “inpcrd” file, “-p” specifies the “prmtop” file, and “-r” specifies the name of the final coordinates following minimization.

Beginning with the “rst” file from the previous minimization, the following “mdin” file can be used to minimize the lipids as well:

Minimization of solvent and lipids

&cntrl

imin = 1,

maxcyc = 1000,

ncyc = 400,

ntb = 1,

ntr = 1,

cut = 12

/

Hold protein fixed

250.0

RES 1 511

END

END

Finally, all atoms in the simulation are minimized with the following “mdin” file:

Minimization of all atoms

&cntrl

imin = 1,

maxcyc = 1000,

ncyc = 400,

ntb = 1,

ntr = 0,

cut = 12

/

3.11 Heat the System and Perform an Initial cMD Equilibration

Following energy minimization the system is ready for cMD equilibration. The system temperature is linearly increased from 0 to 310 K (tempi = 0.0; temp0 = 310.0) in order to prevent excessive and sudden solute fluctuations. A weak restraint is placed on the protein and lipid residues to further aid in this regard. A Langevin temperature equilibration scheme (ntt = 3) will be used to equalize and maintain the system temperature using a collision frequency of 1.0 ps⁻¹ (gamma_ln = 1.0).

While equilibration will ultimately be performed using constant pressure and temperature parameters, as the system is heating up the pressure that is calculated can be inaccurate, leading to issues if constant pressure parameters are employed. The use of restraints with constant pressure parameters further causes problems. Accordingly, the system is initially equilibrated at constant volume (ntb = 1) and then later transitioned to constant pressure parameters. Furthermore, since the hydrogen atom motion in solute is unlikely to affect the overall protein dynamics, a SHAKE algorithm is used which fixes all bonds involving hydrogen (ntc = 2; ntf = 2), reducing computational burden and allowing the time step to be increased to 2 fs without introducing any instability (if hydrogen atoms were allowed to oscillate the would provide the highest frequency oscillation in the system and therefore determine the maximum time step).

The following “heat.in” script can be used to heat the system:

cMD heating of the system with restraints on protein and lipid residues

&cntrl

imin = 0, irest = 0, ntx = 1,

ntb = 1,

cut = 12.0,

ntr = 1,

ntc = 2, ntf = 2,

tempi = 0.0, temp0 = 310.0,

ntt = 3, gamma_ln = 1.0,

nstlim = 20000, dt = 0.002

ntpr = 2000, ntwx = 2000, ntwr = 2000

/

Keep protein and lipids fixed with weak restraints

10.0

RES 1 636

END

END

In the “heat.in” script above the minimization is turned off (imin = 0) and initial velocities are randomly assigned from a Boltzmann distribution (irest = 0; ntx = 1). A cutoff of 12 Å is used (cut = 12). 20,000 cMD steps will be performed (nstlim = 20,000) using a time step of 2 fs per step (dt = 0.002), resulting in a total simulation time of 40 ps. The output file (ntpr), trajectory file (ntwx) and restart file (ntwr) will be written to every 2,000 steps. Finally, weak position restraint (ntr = 1) using a force constant of 10 kcal/mol/Ų will be used to minimize lipid and protein residues movement (residue numbers 1–636). The following command will initiate heating of the system:

$AMBERHOME/bin/sander -O -i heat.in -o heat. out –c leut_system_min3.rst -p leut_system. prmtop -r leut_system_heated.rst

After heating the system, a short cMD equilibration using constant temperature and pressure parameters in necessary to obtain information about the system that will be required for aMD production runs.

The following “cMD.in” script can be used to accomplish this:

cMD equilibration to obtain parameters necessary for aMD production runs

&cntrl

imin = 0, irest = 1, ntx = 7,

ntb = 2, pres0 = 1.0, ntp = 2, taup = 2.0,

cut = 12.0,

ntr = 0,

ntc = 2, ntf = 2,

tempi = 310.0, temp0 = 310.0,

ntt = 3, gamma_ln = 1.0,

nstlim = 500000, dt = 0.002

ntpr = 2000, ntwx = 2000, ntwr = 2000

/

In the “cMD.in” script above, the parameters that have changed in comparison to the “heat.in” script are defined as follows. Since the simulation is being restarted, the time step is read in from the previous run (irest = 1) and the coordinates being read in are in ASCIII restart format (ntx = 7). Anisotropic pressure scaling will be used (ntp = 2) to maintain a constant pressure (ntb = 2) with an average pressure of 1 atm (pres0 = 1.0) and a relaxation time of 2 ps (taup = 2.0). No position restraints are used (ntr = 0). One nanosecond of simulation time will be obtained (nstlim = 500000, dt = 0.002). The following command can be used to execute the script:

$AMBERHOME/bin/sander -O -i cMD.in -o cMD. out –c leut_system_heated.rst -p leut_system. prmtop -r leut_system_cMD_equil.rst

3.12 Perform aMD Production Runs

The cMD equilibrated system and data obtained from the cMD equilibration can now be used for aMD production runs. aMD production runs are conducted in a very similar fashion to the cMD equilibration described in Subheading 3.11, with the only difference being the definition of additional aMD specific parameters. The following “aMD.in” script can be used for aMD production runs:

aMD production run

&cntrl

imin=0, irest=1, ntx=7,

ntb = 2, pres0 = 1.0, ntp = 2, taup = 2.0,

cut = 12.0,

ntr = 0,

ntc = 2, ntf = 2,

tempi = 310.0, temp0 = 310.0,

ntt = 3, gamma_ln = 1.0,

nstlim = 500000, dt = 0.002

ntpr = 2000, ntwx = 2000, ntwr = 2000

iamd = 3,

alphaD = 357.7,

EthreshD = 12988.9,

alphaP= 10494.2,

EthreshP = -94241.8

/

In the “aMD.in” script above, the simulation parameters are the same as in the previously used “cMD.in” with the addition of the following aMD specific parameters. The aMD implementation in AMBER allows for the possibility of boosting the torsional terms of the potential only (iamd = 2), the whole potential (iamd = 1), or the whole potential with an additional boost to the torsions (iamd = 3). alphaD is defined as the product of 0.2, 3.5 kcal/mol/residue, and the number of protein residues (511 residues are in the LeuT example here). EthreshD is defined as the product of 3.5 kcal/mol/residue and the number of protein residues, added to the average dihedral based on cMD equilibration (11,200.4 for the system in this example). alphaP is defined as the product of 0.2 and the total atoms (52,471 total atoms in this example). EthreshP is defined as the sum of alphaP and the average EPtot from cMD equilibration (−104,736 for the system in this example).

The following command can be used to execute the “aMD.in” script:

$AMBERHOME/bin/sander -O -i aMD.in -o aMD_01. out –c leut_system_cMD_equil.rst -p leut_system.prmtop -r leut_system_aMD_01l.rst

Several additional aMD production runs can be performed, each time beginning with the restart coordinates output from the previous run.

3.13 Prepare Data for PCA Analysis

When sufficient aMD production runs have completed, principal component analysis is used to analyze the results from the aMD simulations. The statistical program R is a platform for performing statistical calculations with large data sets. Through the use of the Bio3D add on package, R is able to perform analysis of PDB and DCD files. To start using the Bio3D package with R to analyze the data, the data must be formatted into a Bio3D useable style. The first thing to note is that Bio3D works best with protein only data, so any other molecules will need to be removed (lipids, waters, ions, etc.). The second note is that Bio3D does not utilize parameter-topology files from AMBER (PRMTOP) or protein structure files from NAMD (PSF); instead, Bio3D uses information from the PDB file to determine the protein structure. The final note on Bio3D is that it requires DCD trajectories for processing (the default binary for NAMD), so AMBER trajectories will need to be converted.

1. Use VMD and load in the structure file (PSF or PRMTOP): File → New Molecule then load in the PRMTOP file. VMD will recognize that it is an AMBER topology file but not whether or not it is one with a periodic boundary conditions. For our LeuT simulations, and probably under most circumstances, it will be necessary to change the file type to AMBER coordinates with Periodic Box.

2. Load the trajectories into the created molecule: Right click the molecule and select Load data into molecule. Select the trajectory file and load in. Depending on the size of the trajectory and available computer resources, this may need to be broken into smaller steps or trajectory frames will need to be skipped.

3. Change the visualization to show the protein only: Graphics → Representations. Select the molecule and change the atom selection to the desired atoms. Replacing the selection all with the phrase protein will usually be sufficient, however this may change depending on the configuration of the topology file.

4. Save a PDB file of the first frame of the trajectory: Right click the molecule from the main window and click Save Coordinates. Change the type to PDB and change the first and last frame to 0. Use the drop down menu to select the atom selection specified in step 3 above. This will be the PDB Bio3D will use to determine the protein structure.

5. Create a DCD file of the trajectory frames: Follow the steps above to Save coordinates, but change type to DCD and make sure the first frame is 0 and the last frame is the last frame loaded into the system.

3.14 Using Bio3D and R to Calculate the PCA

In an R terminal, load in the Bio3D library (ensure the package has previously been installed). Read in the PDB file of the first frame as the structure and then the trajectory from the DCD file.

library(bio3d)

pdb <-read.pdb(“LeuT_frame1.pdb”)

dcd <- read.dcd(“LeuT_trj.dcd”)

Select the atoms of interest for the PCA analysis. The atom.select command pulls the indices of atoms which correspond to the atom selection. For our analysis, we choose to use all alpha carbon positions of select residues. The elety parameter of the atom.select command specifies the atom type (“CA” = alpha carbon), and the resno parameter can be used to select residues by number.

ca.ind <- atom.select(pdb, elety=“CA”)

In order to eliminate translations and rotations the trajectory structures will need to be fitted and superposed to the PBD structure. The fit.xyz command can be used to accomplish this. The fit.xyz command takes two necessary input parameters—the structure to use as a reference and the structures to fit to the reference. It should be noted that the fit.xyz command only takes coordinates as input, so the $xyz object of the PDB will need to be used. The bracket argument pulls the atom selections from above as the coordinates to fit. The output of the fit.xyz command will be a superposed trajectory of the selected atoms only.

trj.fit <- fit.xyz(pdb$xyz[ca.ind$xyz], dcd[,ca.ind$xyz])

The PCA of the coordinates can be taken based on the trajectory with the pca.xyz command.

trj.pca <- pca.xyz(trj.fit)

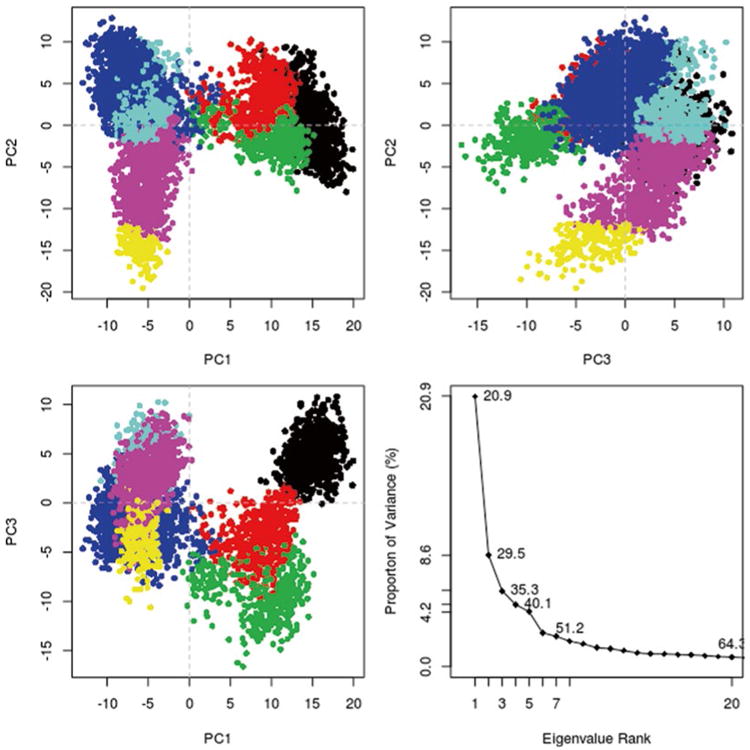
With the Bio3D package installed, the plot command has been overloaded to create a default PCA plot with four graphs. Three are the z-scores of the first three principal components plotted against each other in two dimensions. The last is a scree plot representing how much of the variance of the data set is captured by each principal component (Fig. 5).

Fig. 5. Bio3D plot of principal component data.

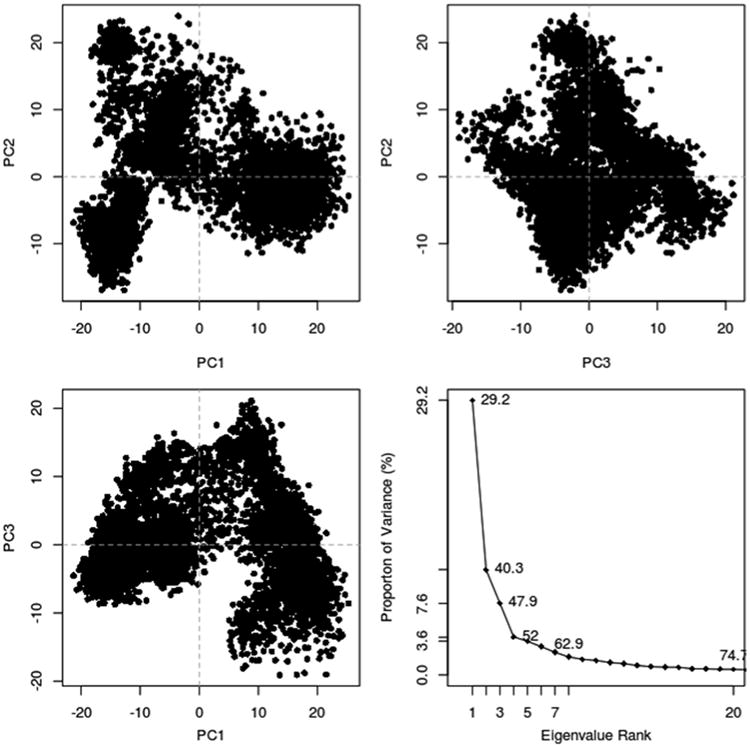
plot(trj.pca)

The plot points can be computationally clustered and colored by cluster. This can be done by creating a distance matrix of the principal components of interest (principal components 1, 2, and 3 were used in this analysis).

d <- dist(trj.pca$z[,1:3])

A dendrogram of the distance matrix can be calculated and plotted for visualization. The plot of the dendrogram can be used to determine the number of clusters desired from the analysis.

hc <- hclust(d)

plot(hc)

The cutree command can be used to create a color vector which will color each point based on the number of groups desired. It takes two arguments, the dendrogram and k which is the desired number of clusters. Here, the LeuT data appeared to fall into seven clusters. The PCA plots can be colored by replotting the PCA and using the output from the cutree command as an argument to the col parameter (Fig. 6). For structure analysis, representative structures from each cluster can be isolated and analyzed in molecular visualization software of choice like VMD.

Fig. 6. Bio3D plot of PCA data colored by cluster after calculation of cluster groups.

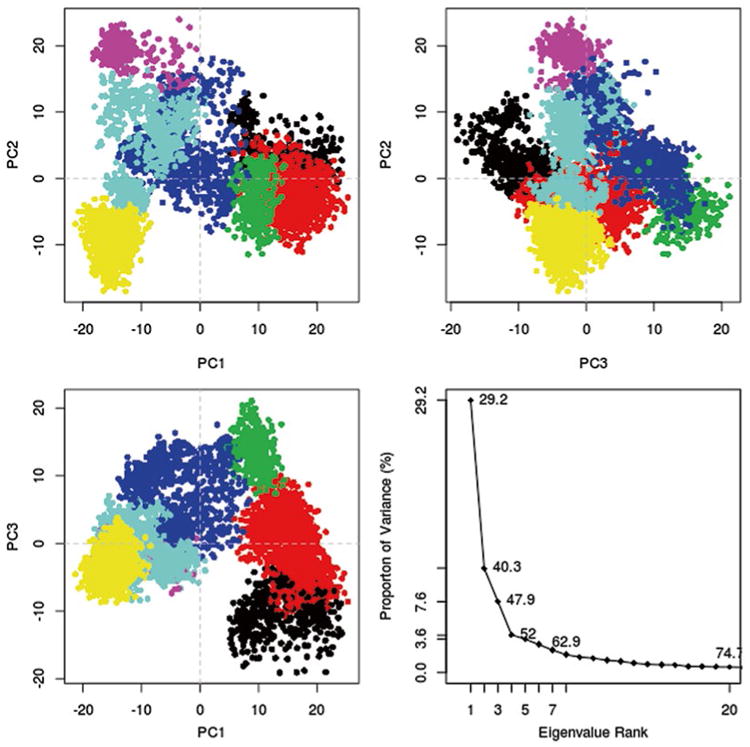
grps <- cutree(hc,k=7)

plot(trj.pca,col=grps)

3.15 Validation and Use of the PCA

PCA of aMD data is useful for finding protein segments that are most involved in structural changes. The RMSF (root mean square fluctuations) calculation can be used to determine how much each residue moves during the trajectory.

rf <- rmsf(trj.fit)

The pca.xyz command calculated a matrix with as many principal components as number of data frames entered into it, but the question of how many principal components to use remains. One tool for determining how many to use is the scree plot which shows how much of the data is captured by each principal component, but for the LeuT analysis described here, less than 50 % of the variance is captured after the three most influential principal components. The RMSF can also be utilized in order to determine whether all of the captured fluctuations within those first three components is a sufficient representation of the structural changes involved.

The RMSF can be used to validate the principal components by overlaying the RMSF with the $au object from the PCA calculation. The $au object is the atomic vector which shows how much each residue contributes to a principal component. The goal is to obtain a graph where each residue's RMSF value is captured by at least one of the selected principal components. If a residue shows on the RMSF but is not captured in one of the $au objects, then another principal component will need to be used (Fig. 7).

Fig. 7. Root mean square fluctuations graph superposed with the $au vectors representing the amount of variance captured by each principal component. This graph has all residues included, and the carboxy terminus appears to dominate the principal component.

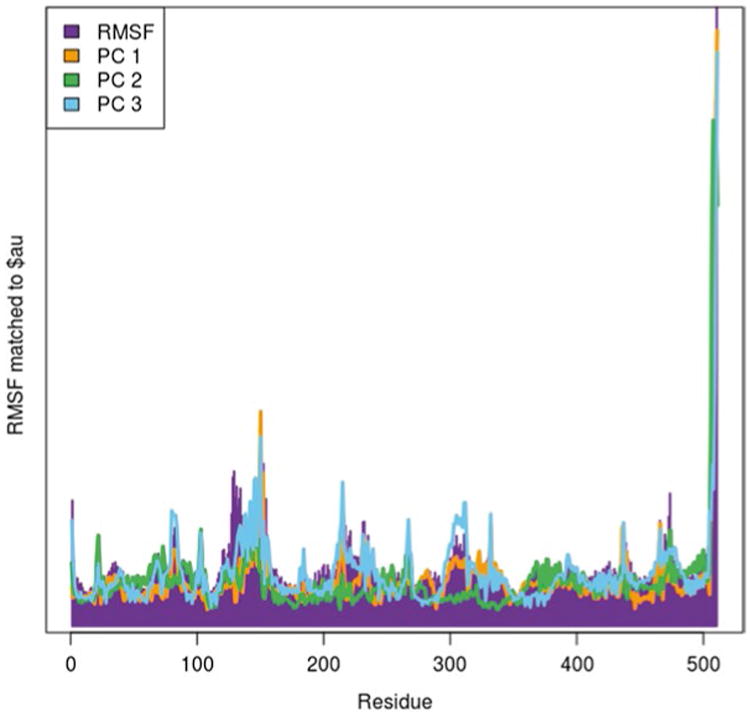
barplot(rf,col=“purple”,border=“purple”)

par(new=TRUE)

plot(trj.pca$au[,1],type=“l”,col=“orange”, lwd=3)

points(trj.pca$au[,2],type=“l”,col=“green”, lwd=3)

points(trj.pca$au[,3],type=“l”,col=“skyblue”,lwd=3)

legend.labels = c(“RMSF”, “PC 1”, “PC 2”, “PC 3”)

legend.cols = c(“purple”, “orange”, “green”, “skyblue”)

legend(“topleft”,legend.labels, fill = legend.cols)

Looking at Fig. 7 from the above example, sometimes a single residue or group of residues may dominate the entire PCA and prevent the PCA from capturing other residue fluctuations. In the LeuT example here, it appears that the last few residues of TM12 at the carboxy terminus of the protein contribute a large portion of the PC. However, these residues mostly just vibrate in the cytosol, and we can therefore exclude these residues from the analysis and rerun the PCA. This can be done by editing the indices used with the atom.select command. Then check the $au object with the RMSF again (Fig. 8).

Fig. 8. RMSF graph superposed with the $au vectors of the principal components after adjusting the PCA by removing residues 506–512.

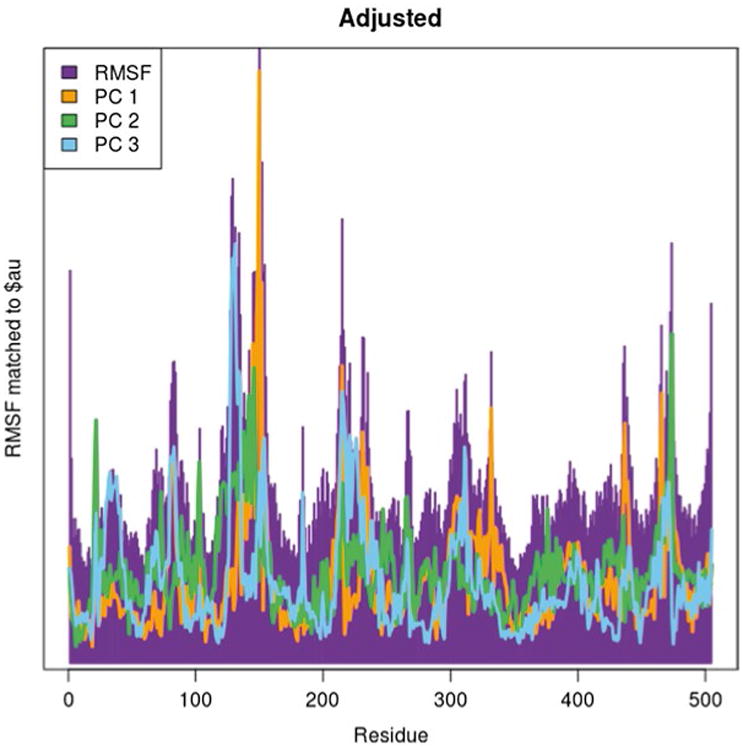
ind.adj <- atom.select(pdb,elety=“CA”,re sno=1:505)

trj.fit.adj <- fit.xyz(pdb$xyz[ind.adj$xyz], dcd[,ind.adj$xyz])

trj.pca.adj <- pca.xyz(trj.fit.adj)

rf.adj <- rmsf(trj.fit.adj)

barplot(rf.adj,col=“purple”,border=“purple”,main=“Adjusted”)

par(new=TRUE)

plot(trj.pca.adj$au[,1],type=“l”,col=“orange”,lwd=3)

points(trj.pca.adj$au[,2],type=“l”,col=“green”,lwd=3)

points(trj.pca.adj$au[,3],type=“l”,col=“sky blue”,lwd=3)

Once a suitable RMSF plot has been obtained, the PCA can be reclustered and replotted to visualize the new PCA result (Fig. 9).

Fig. 9. Adjusted PCA plot of LeuT with residues 506–512 removed and each point colored by cluster.

d <- dist(trj.pca.adj$z[,1:3])

hc <- hclust(d)

grps <- cutree(hc,k=7)

plot(trj.pca.adj,col=grps)

The fluctuations captured by each principal component can also be visualized as a trajectory in VMD. Use the mktrj.pca command to generate a VMD trajectory for visualizing captured fluctuations in each principle component desired. Load the PDB file into VMD and change the representation to Trace or Tube since the PCA only printed out the alpha carbons.

mktrj.pca(trj.pca,pc=1,mag=1, file=“PC1.pdb”)

As mentioned above in the background, it may be necessary to reweigh the PCA plots to determine the validity of each point. The following steps are necessary in order to accomplish this:

1. Extract the βΔV[r(t_i)] for each structural point from the simulation log files using text manipulation tools like grep and awk.

2. Load these values into R.

3. Calculate e^{βΔV[r(t_i)]} for the vector.

4. Plot any two desired principal components against each other and generate a contour plot using the e^{βΔV[r(t_i)]} vector as a coloring parameter (or any other desired method of plotting three dimensional data in R).

3.16 Compare the Resulting Conformations with Additional Structural Data

Additional structural coordinates, such as various crystallized LeuT structures thought to be representative of portions of the substrate transport cycle, can be projected into the PCA space using the homology functionality within Bio3D. To start, read the structures to be projected onto the PCA into R and align to the reference PDB.

crys <- pdbaln(c(pdb,other pdb files))

The alignment of the crystal files and the alignment of the trajectory files must match. Unfortunately, since the alignment changes the index values of the reference PDB to match the sequence, it is necessary to match the index values of the aligned sequence to the trajectory. There is a function (pdb2aln) to do this planned for new releases of Bio3D; however, at the time of this writing, this function is not yet available in the general Bio3D package.

Gap inspection (for missing residues) may be necessary using the gap.inspect command. In this case, the PCA may need to be recalculated if residues previously used have gaps. One way to avoid having to recalculate the PCA is to do the PCA of the crystals alone and project the trajectory into the crystal PCA space. The following example will assume projecting the crystals onto the trajectory PCA space.

1. Run a fit to the reference PDB:

   crys.fit <- fit.xyz(crys$xyz[1, any index values such as gap positions or specific residues], crys $xyz[2:length(crys$xyz[,1]),same index values])

2. Project the crystals into the trajectory PCA space:

   crys.pca <- pca.project(crys.fit, trj.pca)

   plot(trj.pca)

   points(crys.pca[,1],crys.pcs[,2], col= “black”)