Population representation of visual information in areas V1 and V2 of amblyopic macaques

Abstract

Amblyopia is a developmental disorder resulting in poor vision in one eye. The mechanism by which input to the affected eye is prevented from reaching the level of awareness remains poorly understood. We recorded simultaneously from large populations of neurons in the supragranular layers of areas V1 and V2 in 6 macaques that were made amblyopic by rearing with artificial strabismus or anisometropia, and 1 normally reared control. In agreement with previous reports, we found that cortical neuronal signals driven through the amblyopic eyes were reduced, and that cortical neurons were on average more strongly driven by the non-amblyopic than by the amblyopic eyes. We analyzed multiunit recordings using standard population decoding methods, and found that visual signals from the amblyopic eye, while weakened, were not degraded enough to explain the behavioral deficits. Thus additional losses must arise in downstream processing. We tested the idea that under monocular viewing conditions, only signals from neurons dominated by – rather than driven by – the open eye might be used. This reduces the proportion of neuronal signals available from the amblyopic eye, and amplifies the interocular difference observed at the level of single neurons. We conclude that amblyopia might arise in part from degradation in the neuronal signals from the amblyopic eye, and in part from a reduction in the number of signals processed by downstream areas.

Introduction

Amblyopia is a developmental disorder in which abnormal visual experience early in life leads to lasting impairment of visual sensitivity in one eye. The search for the neural basis of this visual deficit has led to the conclusion that information from the affected eye suffers multiple stages of abnormal processing in the brain (Kiorpes, 2006, Levi, 2013). This cascade begins in primary visual cortex (V1), where signals from the two eyes first combine, but the role of this area in limiting amblyopic vision is not yet fully understood. Animal studies have shown that visual information from both eyes is faithfully relayed through the retina to visual thalamus, LGN, suggesting that relatively normal inputs are available to visual cortex (Blakemore & Vital-Durand, 1986, Levitt, et al., 2001, Movshon, et al., 1987). However, single neurons in V1 appear to process inputs from each eye differently, exhibiting lower sensitivity and altered spatial selectivity to stimuli presented to the amblyopic eye (Eggers & Blakemore, 1978, Kiorpes, et al., 1998, Movshon et al., 1987) While consistent with an ocular imbalance in visual sensitivity, these single-cell differences are too small to account for behaviorally measured amblyopic deficits (Kiorpes et al., 1998, Kiorpes & Movshon, 2004)

Amblyopia is also accompanied by a disruption of binocular cortical organization (Hubel & Wiesel, 1965, Kiorpes & Movshon, 2004, Smith, et al., 1997, Wiesel, 1982). Excitatory binocular convergence in V1 is reduced, with most neurons receiving input predominantly from one eye. In some cases the balance of inputs from the two eyes is maintained, with each innervating similar numbers of monocular neurons. In other cases an eye dominance emerges, with fewer cells responding preferentially to stimulation of the amblyopic eye. Animals raised with unilateral blur as a model of anisometropia tend to show eye dominance favoring the unblurred eye in V1, while those raised with unilateral strabismus tend to show more balanced ocular dominance (Crawford & von Noorden, 1978, Crawford, et al., 1993, Crawford & von Noorden, 1979, Kiorpes et al., 1998, Movshon et al., 1987, Smith et al., 1997, Wiesel, 1982). However, those suffering the most severe amblyopic deficits show large shifts in eye dominance regardless of origin of the abnormality (Kiorpes et al., 1998, Movshon et al., 1987). Interestingly, some studies of strabismic amblyopes have found no evidence for an eye dominance bias in V1 while shifts in preference toward the untreated eye were found in area V2 (Bi, et al., 2011). Thus, while it is clear that there is a disruption of binocularity in V1 in amblyopic macaques, the relative dominance of one eye over the other does not directly predict the presence or depth of amblyopia.

It remains unclear what implications the reorganization of eye dominance may have for amblyopic vision. One possibility is that the small differences in single-neuron sensitivity mentioned above are amplified in the pooled activity of neural populations in which relatively few units represent the amblyopic eye. The aggregate sensitivity of such population-level responses increases as more units are incorporated in the pooling, and a shortage of neurons carrying signals from the amblyopic eye could limit sensitivity independently of single-neuron deficits. Stated more generally, normal functioning of a cortical network may be impaired at the single-unit level by weak signals, or by network-level factors affecting the integration of information across a population of neurons. Understanding the role of early visual cortex in limiting amblyopic vision may rely on characterizing neural responses at both of these levels.

We recorded the activity of large neural populations in parallel, with electrode arrays placed in parts of V1 and V2 representing the fovea and near retinal periphery of each hemisphere in amblyopic macaques. We measured the eye dominance and sensitivity of populations of neurons as well as the ability of these populations to support the monocular detection of visual stimuli similar to those used to measure behavioral deficits in amblyopia. We used simple decoding algorithms to measure the performance of neural populations tested through each eye, and used them to ask whether the deficit in visual signaling through the amblyopic eye is due to reduced numbers of neurons or to abnormal response properties. We found that the reduced strength of inputs from the amblyopic eye does not by itself lead to the deficit, which derives instead from abnormalities in the distribution of responses elicited through that eye in the cortical population.

Methods

Subjects

We studied 7 adult female macaque monkeys (Macaca nemestrina), 6 behaviorally verified amblyopes and 1 visually normal control. Amblyopia resulted from rearing with either unilateral blur, a model for anisometropic amblyopia, or experimental strabismus, leading to strabismic amblyopia. Methods for inducing the development of amblyopia have been described in detail previously (Kiorpes, Kiper & Movshon, 1993, Kiorpes, Tang & Movshon, 1999). Briefly, strabismus was induced surgically in three animals at two to three weeks of age by resection of the medial rectus muscle and transection of the lateral rectus muscle of one eye. Developmental anisometropia was produced by rearing with extended-wear soft contact lenses (Contact Lens Precision Labs, Cambridge, England; MedLens Innovations, Front Royal, VA, USA). A strong blurring lens (−8 or −10 diopters) was placed in one eye, the fellow eye wore a plano lens. One untreated animal served as a control. See Table 1 for treatment details and ages of intervention. All animal care and experimental procedures were performed in accordance with protocols approved by the New York University Animal Welfare Committee and conformed to the NIH Guide for the Care and Use of Laboratory Animals.

Table 1.

Animal	Treatment	Age at onset (days)	Age at test (years)	Age at recording (years)
S1*	Strabismus	26	1.8	18.9
S2	Lens-reared (−8D)	24	5.7	7.1
S3	Lens-reared (−10D)	24	9.4	17.2
S4	Lens-reared (−10D)	20	4.5	17.4
S5	Strabismus	17	1.5	10.3
S6	Strabismus	23	3.2	10.8
Control	None		1.4	7.7

^*Note: At the test age, the treated eye was mildly amblyopic; physiological recording showed the untreated eye to be deficient in cortex suggesting that the eye preference switched in the intervening years. We therefore take the untreated eye as the amblyopic eye for physiological results.

Behavioral testing

Behavioral assessment of visual deficits was conducted using standard methods for our laboratory (Kiorpes et al., 1993, Kiorpes et al., 1999). We measured contrast sensitivity as a function of spatial frequency for each eye of each amblyopic animal; the control animal was tested binocularly. Visual sensitivity was tested using a 2-alternative, forced-choice detection task in which a Gaussian-vignetted sinusoidal grating was presented on the left or right side of a computer display. Apple juice was delivered for correctly indicating the location of the grating target. Animals freely viewed the display, with optical correction provided as needed. We tested four to six spatial frequencies depending on the animal’s resolution range with the viewing eye. Sensitivity was assessed using method of constant stimuli at four to five contrast levels per spatial frequency in pseudorandom order. For each spatial frequency, a psychometric function was obtained based on at least 40 trials per contrast condition; a maximum-likelihood fitting procedure was used to compute a contrast detection threshold at 75% correct. We then fit each contrast sensitivity function with a descriptive model,

$$s(\omega )=a{\omega }^b{e}^{-c\omega }$$

which expresses sensitivity as a double exponential function of spatial frequency (ω), with fitted parameters a, b, and c. The relative difference in sensitivity between the two eyes across all spatial frequencies was quantified as a measure of the depth of amblyopia, Amblyopia Index (AI) (Kiorpes et al., 1998).

Surgical preparation

Physiological recordings were performed between 2 and 17 years after behavioral testing. Preparation for acute recording followed standard protocols described previously (Cavanaugh, Bair & Movshon, 2002, Graf, et al., 2011). Animals were anesthetized using continuous intravenous infusion of the opiate sufentanil citrate (6 µg/kg/hr, initial dose). Heart rate, end-tidal pCO₂, EEG, and body temperature were monitored continually to confirm adequate anesthesia and physiological stability. Muscle paralysis by infusion of vecuronium bromide (100 µg//kg/hr) ensured stable position of the eyes. The eyes were treated with topical atropine sulfate to dilate the pupils, and protected with gas-permeable contact lenses.

Visual stimulation

We estimated refractive error and determined direction of gaze using direct ophthalmoscopy. Appropriate lenses were used to make the retinas conjugate with stimuli presented on a gamma-corrected cathode ray tube (CRT) monitor (Eizo T966), with spatial resolution 1280 × 960 pixels, temporal resolution 120 Hz, and mean luminance 35 cd/m². Viewing distance was 1.14 m or 2.28 m depending on array placement (foveal or peripheral), at which distances the screen subtended 21 deg × 16 deg or 10.5 deg by 8 deg. A binocular mirror system allowed independent alignment of each eye’s fovea to any point on the display. We placed the foveas so that receptive fields of neurons driven by each eye were separated by at least half the screen’s width and stimuli placed on one eye’s receptive fields were remote from the other’s. We generated stimuli using an Apple Macintosh computer running Expo (http://corevision.cns.nyu.edu). Visual stimuli were samples of bandpass-filtered spatiotemporal noise. Each sample was created from an array of 512×512×60 values drawn randomly from a Gaussian distribution; we then applied a spatiotemporal filter defined over spatial frequency (bandpass Butterworth filter with high and low cutoff spaced 1 octave apart), orientation (raised cosine with bandwidth 60 deg), and temporal frequency (Butterworth filter with passband 2–8 Hz). Filtered noise samples had mean luminance equal to that of the unmodulated display and root-mean-square contrast of 33%. Center spatial frequencies of 0.5, 1, 2, 4, and 8 c/deg (at 1.14 m, twice those values at 2.28 m) and center orientations of 0, 45, 90, and 135 deg were used to create 20 different filters. We created 60 unique samples of noise, each presented once to each eye per trial. Stimuli were presented monocularly in a 4- or 8-deg circular aperture while the other eye viewed a blank (mean-luminance) portion of the screen. Samples from each filter were randomly interleaved, along with 600 blank trials in which both eyes viewed mean luminance for 700ms. Stimulus duration was 500ms with a 200ms inter-stimulus interval, and stimulation alternated between eyes every 6 minutes. Figure 1 shows single frames taken from three different samples of noise.

Figure 1.

Visual stimuli were samples of bandpass spatiotemporal noise, with power spread over 1 octave of spatial frequency and 60 deg of orientation. Three single frames taken from different noise movies are shown as examples, representing a subset of the center spatial frequencies and orientations tested. The noise was dynamic, containing temporal frequencies spanning 2–8 Hz. Stimuli were presented monocularly for 500 ms in a circular aperture (typically 8 deg).

Multielectrode recording

A craniotomy over occipital cortex and resection of the dura allowed visualization of the cortical surface for placement of recording arrays relative to anatomical landmarks. After visualizing the lunate sulcus, we implanted a 96-electrode "Utah" array (Blackrock Systems) over the estimated location of the V1/V2 border. Electrodes in the arrays were 1 mm long, 400 µm apart, and formed a regular, rectangular grid parallel to the cortical surface. We pneumatically inserted the array to a depth of 500 to 1000 µm. After the initial recording, the array was removed and either a new array or the same array was implanted at a different border location. In each animal, we performed 2 implantations in each cortical hemisphere: one medial, in cortex representing the parafoveal visual field, and one lateral, close to the cortical representation of the fovea. Raw voltage signals were bandpass filtered between 300 and 6000 Hz and then squared to obtain a measure of instantaneous power. The response of a multiunit cluster on a single trial was defined as the instantaneous power averaged over a 500 ms window aligned to stimulus onset. On a few occasions we also recorded well-isolated single neurons based on usual criteria (Kelly, et al., 2007), and measured firing rate as well as multiunit power. The number of such sites was small, so the intrusion of large single unit signals into our measures of multiunit power was minimal. To compare single-unit and multiunit responses, we also removed isolated spikes from the filtered voltage signals by subtracting the average waveform of each unit at time points where a spike was identified. The remaining multiunit signal was then squared and averaged as described above.

Histology

At the end of the recording session, the animal was killed with an overdose of sodium pentobarbital, and perfused transcardially with heparinized 0.01 M phosphate-buffered saline (PBS, pH 7.4), followed by 4% paraformaldehyde (PFA) in 0.1 M phosphate buffer (PB, pH 7.4). Blocks of visual cortex containing the recording sites were removed and either flattened between glass slides while postfixing in 4% PFA or postfixed without flattening. A vibratome was used to cut 50 µm sections parallel to the cortical surface. Sections from one animal were Nissl stained; sections from all other animals were reacted overnight at 37°C in a solution containing 0.03% cytochrome c, 0.02% catalase, and 0.05% diaminobenzidine (DAB) in 0.01 M PBS to stain for cytochrome oxidase (CO). To determine the visual area sampled by each electrode, the border between V1 and V2 was identified based on the pattern of CO or Nissl staining and traced in register with the electrode reconstruction, using either camera lucida or Neurolucida (MBF Bioscience).

Ocular dominance

For each electrode, responses to sixty unique noise samples were averaged to yield a mean response for each orientation, spatial frequency, and eye of presentation. After subtracting the spontaneous activity level measured during blank trials, the largest mean response elicited through the fellow eye by any stimulus condition (R_f) was compared to the largest response elicited through the amblyopic eye (R_a) to compute an Ocular Dominance Index, defined as ODI = (R_f-R_a)/(R_f+R_a). This comparison was not always between responses to the same stimulus, as the neurons driven through the two eyes sometimes responded best to different stimuli. The index varied between −1 and 1, with negative and positive values indicating larger responses through the amblyopic or fellow eyes, respectively. We excluded recording sites from which no stimulus in either eye elicited a response more than a 10% above spontaneous activity.

Decoding the responses of neural populations

The pattern of responses elicited from a given neural population by a particular stimulus type was characterized using linear discriminant analysis. Using responses recorded simultaneously on N electrodes, we defined the N×1 discriminant vector s = C⁻¹*(r – r₀) where the vector r contained each electrode’s mean response to the 60 stimuli of a single type, and r₀ the mean responses to 600 blank trials. The N×N covariance matrix, C was derived by averaging the between-electrode covariances computed using blank trials with those computed from stimulus trials, weighted by the relative number of trials in each. We converted the population response to each trial, represented as an N-element vector containing each electrode’s response, to a scalar value by projection onto the discriminant vector. We compared the set of projected values resulting from stimulus trials to those from blank trials by computing

$$d\text{'}=\frac{u-u_0}{\sqrt{v+v_0}},$$

where u and v represent the mean and variance of projections from stimulus trials, and u₀ and v₀ projections from blank trials. For each neural population considered, we computed a separate discriminant and d’ for each spatial frequency, orientation, and eye.

Neural performance and population size

To test the performance of neural populations of different size, we first rank ordered all 96 electrodes based on their individual performance on detection of a given stimulus type, quantified as d’ between single-electrode responses to stimulus and blank trials. We then defined subpopulations based on this ordering, considering only the best N electrodes (N = 1,6,11,…,96). For each subpopulation, we repeated the linear discriminant analysis to obtain a measure of sensitivity, d’, as a function of subpopulation size. We fit the resulting curves, one for each stimulus condition, describing performance as a function of population size, with two descriptive models of differing complexity. To compare models, we used cross-validation: the raw data were randomly split in half into a training set and a validation set, each of which was used to compute a d’ at each population size, using the rank ordering and discriminant vectors derived from the whole data set. Each model was fit to the d’ values obtained from the training set, and these fits were evaluated against the holdout data. We define the evidence for a model as

$$L=\sum _n-{({d\text{'}}_n-{\widehat{d}\text{'}}_n)}^2$$

where n represents population size, and d'_n and d̂'_n are the sensitivity values for that population size derived from the holdout data and from the model fit to the training data, respectively. This measure is proportional to the log likelihood of the data given the model prediction under an assumption of Gaussian noise. We repeated this process 100 times with different random divisions of the data set. This method is designed to test for overfitting: a more complex model will almost always provide a better fit to the training set, but possibly only by capturing random fluctuations in the data. We compared the average evidence for both models, and rejected the more complex model if it failed to provide a better prediction for holdout data compared to simpler model.

Bootstrap estimates of central tendency

We used a nonparametric bootstrap analysis to describe the central tendency of a distribution, whether of eye dominance over many multiunit sites or of model parameters fit to many stimulus conditions and neural populations. We resampled from the empirical distribution randomly, with replacement, 1000 times, computing the mean of each random sample. We report the average of these 1000 estimates, as well as the 95% confidence interval derived from the distribution of mean estimates. When analyzing the eye dominance of individual recording sites in detail, we resampled individual trials to derive a mean, variance, and confidence interval from an empirical distribution of ODI values for each neuron or multiunit cluster.

Declaration

All the work reported in this paper was carried out in accordance with the Code of Ethics of the World Medical Association (Declaration of Helsinki).

Results

We measured visual responses to monocular presentation of structured noise stimuli (Figure 1, see Methods). Multiunit responses were robust and generally well tuned for the spatial characteristics of the stimuli. For each of 5 spatial frequencies and 4 orientations, we averaged responses to 60 unique samples of noise and subtracted spontaneous activity to obtain a mean response measure for each eye. Figure 2 plots response as a function of spatial frequency for each site of one implantation of a recording array in an anisometropic monkey (Subject 2), in cortex contralateral to the amblyopic eye, representing approximately 5 deg eccentricity. For ease of viewing, responses to 4 orientations were averaged, and responses from each electrode were separately normalized to 1. White and black curves represent responses elicited through the fellow and amblyopic eyes, respectively; in most cases, one eye evoked clearly stronger responses. Histological reconstruction confirmed that this array straddled the V1/V2 border, and assigned most electrodes unambiguously to one of these two areas as indicated by the shading. In V1, the eye that dominated responses alternated row by horizontal row of electrodes, as expected from the usual pattern of eye dominance columns orthogonal to the V1/V2 border (Hubel & Freeman, 1977, Hubel, Wiesel & LeVay, 1977).

Figure 2.

Multiunit responses recorded with 96 electrodes of a single array placement (Animal S2, contralateral hemisphere, 5 deg eccentricity). Responses of each multiunit site to stimulation of the amblyopic eye (black) and fellow eye (white) were averaged over orientation and normalized to reach a maximum of 1; the unstimulated baseline response was taken as 0. Normalized response is shown as a function of center spatial frequency at each site (scale at lower left). Most sites responded preferentially to one or the other eye. This array placement spanned the border of V1 (light gray background) and V2 (dark gray background). Histological reconstruction allowed assignment of most electrodes to one of these two areas, while a minority of sites near the border were undetermined (intermediate gray background).

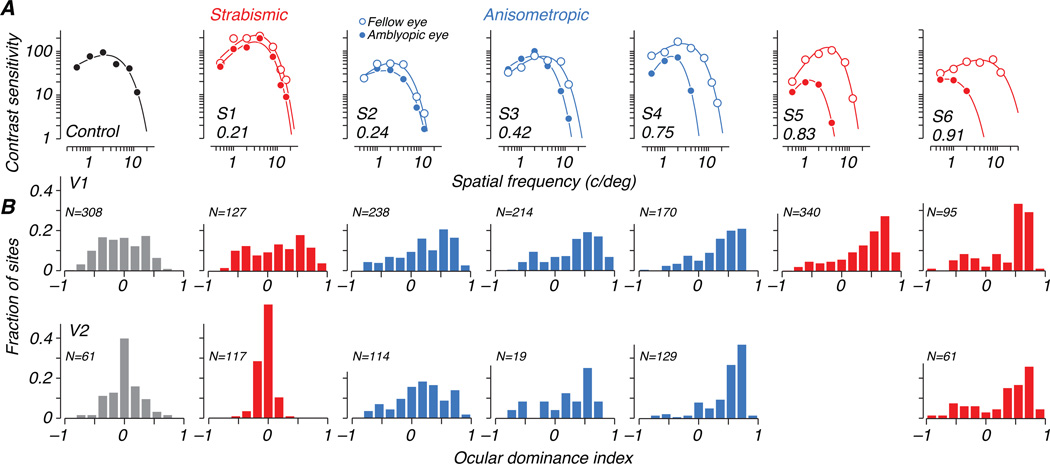
Behavioral characterization of the amblyopic deficit for each experimental animal is shown in Figure 3A. Contrast sensitivity functions (CSFs) for each eye of each animal are plotted; open symbols represent fellow eye data and filled symbols represent amblyopic eye data. In this and all other plots, we use red when presenting data from strabismic amblyopes and blue for anisometropic amblyopes. Binocular data for the control animal are shown in black in the first panel. As is typical, the relative sensitivity of the two eyes of the amblyopes depended on spatial frequency, and varied widely across the 6 amblyopes. To capture the depth of amblyopia, we computed an amblyopia index (AI) as the difference in area between curves fitted to each eye, normalized by the area under the fellow eye curve (Kiorpes et al., 1998). This index is zero when sensitivity is equal in the two eyes, and reaches a 1 if the amblyopic eye is completely blind. Values of AI for the treated animals ranged from 0.21 to 0.91, and are indicated in the lower left corner of each panel of Figure 3A. We ordered the amblyopes by AI, labeling the least severe case S1 and the most severe case S6.

Figure 3.

(A) Contrast sensitivity (inverse of threshold contrast) is plotted as a function of spatial frequency of a sinusoidal grating, separately for the amblyopic eye (filled symbols) and fellow eye (open symbols). Behavioral sensitivity loss in the amblyopic eye was quantified using an amblyopia index (AI) that ranges from 0 (no deficit) to 1 (monocular blindness). All treated animals showed visual deficits in the amblyopic eye. Subjects 1–6 are ordered by severity of deficit and AI values are shown in the lower left of each panel. Strabismic amblyopes are plotted in red, and anisometropic amblyopes in blue. (B) Distributions of ocular dominance obtained for recording sites in V1 (top row) and V2 (bottom row) are shown for each animal below its behavioral contrast sensitivity data. Eye preference of each multiunit site was described using an ocular dominance index (ODI). Positive values of ODI represent dominance of the fellow eye, and negative values amblyopic-eye dominance. Neural populations recorded in amblyopic animals responded more strongly to stimulation of the fellow eye, while ODI histograms for the control animal are centered near zero. As noted under Table 1, the amblyopic eye of S1 was reassigned based on the neural data; the reassignment was used for all physiological measures for this animal.

Ocular dominance

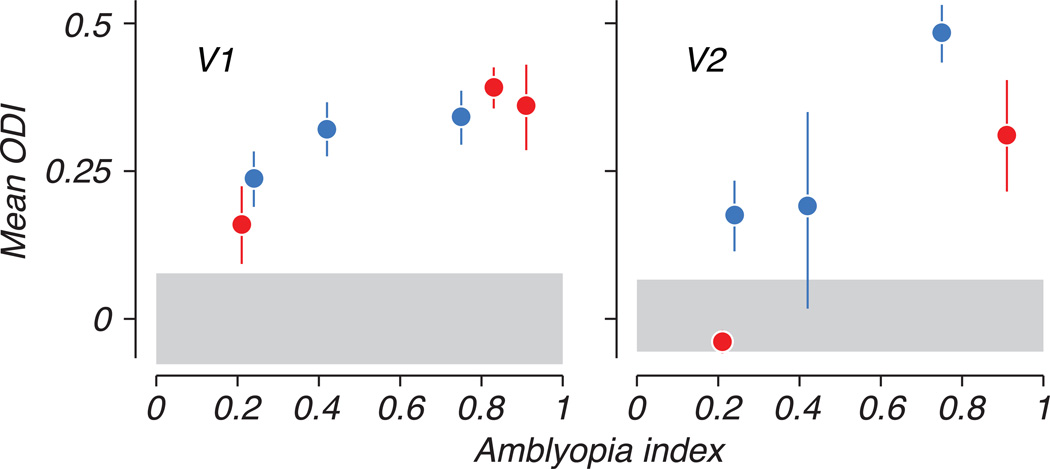
A variety of neural response patterns was observed across arrays and animals, with some multiunit clusters responding to stimulation of either eye but many showing a strong preference for one eye over the other (e.g., Fig. 2). We quantified eye preference using an ocular dominance index (ODI), which varied between −1 and 1, with negative and positive values representing stronger responses elicited through the amblyopic or fellow eyes, respectively (see Methods). We excluded from this analysis recording sites for which no stimulus in either eye elicited a significant response. Distributions of ODI for each animal are shown in Figure 3B, for V1 and V2 separately, below the corresponding animal’s behavioral contrast sensitivity functions in Figure 3A. In the control animal, the ODI distribution showed a range of eye dominance, as is typical, but was centered around the origin indicating a lack of bias in the population toward either eye. In contrast, the neural populations recorded in V1 and V2 of amblyopic animals showed an ocular dominance bias toward positive values – on average, cells responded more strongly to the fellow eye than the amblyopic eye. The degree of ocular dominance bias varied from animal to animal, and correlated with the severity of visual deficits measured behaviorally. Figure 4 compares the mean ODI for each animal to its behavioral amblyopia index. In both V1 and V2, the extent to which the cortical population favored the fellow eye was clearly correlated with relative loss of sensitivity of the amblyopic eye (R² = 0.79 for V1 and 0.71 for V2).

Figure 4.

Mean ocular dominance index (ODI) for each animal is plotted with respect to the behaviorally derived amblyopia index. The degree of bias toward the fellow eye in neural populations correlated strongly with the relative imbalance in sensitivity between the two eyes. This pattern was observed in V1 and V2, in both strabismic (red) and anisometropic (blue) amblyopes. Error bars represent 95% confidence intervals on distribution means, computed from a nonparametric bootstrap (see Methods). The gray bar represents a similar confidence interval on the mean ODI in the control animal.

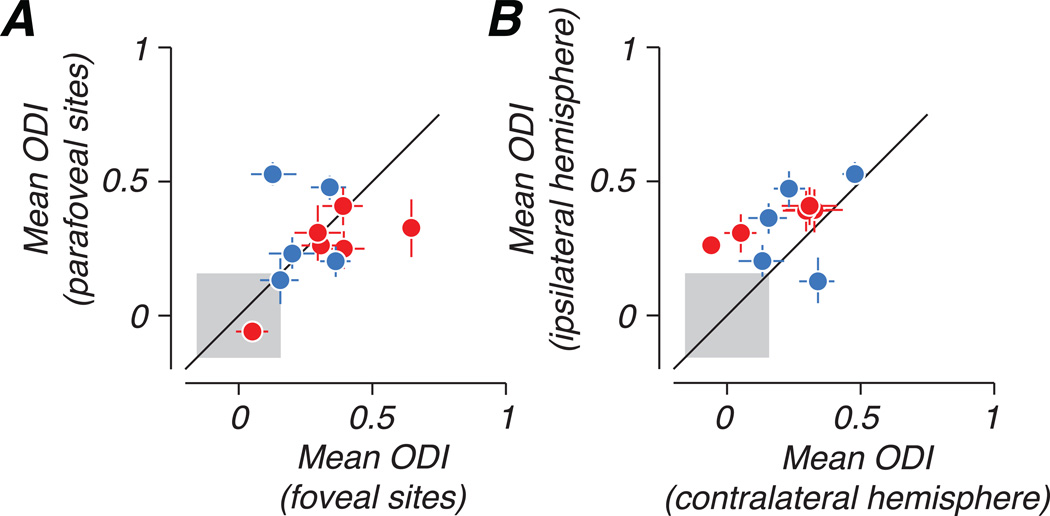
We tested the dependence of ocular dominance bias on eccentricity and hemisphere by implanting multiple arrays in each animal, sampling different locations along the mediolateral extent of the V1/V2 border. In each cerebral hemisphere, array placements targeted cortical representations of different visual eccentricities: one medial, representing parafoveal or near-peripheral visual space (2–7 deg eccentricity), and one lateral, representing the fovea (within the central 1 deg). Figure 5A compares the mean ODI of each foveal population sampled to that of the parafoveal population recorded in the same hemisphere of the same animal. In several cases, the ocular dominance bias toward the fellow eye was seen more strongly in central vision (points falling below the diagonal line); however, the opposite was also observed. The point falling farthest below the identity line represents an interesting case, in which the foveal representation of one strabismic animal showed a nearly complete dominance of the fellow eye, and extremely weak responses elicited through the amblyopic eye by any stimulus. We consider this case further below. Figure 5B compares mean ODI between neural populations approximately matched for eccentricity but recorded from different hemispheres. ODI bias was consistently stronger in the hemisphere ipsilateral to the amblyopic eye, showing that the nasal retina of the amblyopic eye was more strongly represented in cortex than the temporal retina.

Figure 5.

Comparison of ocular dominance bias across eccentricity and hemisphere. (A) Mean ODI is compared between foveal (<1 deg) and parafoveal (2–7 deg) populations recorded in the same hemisphere. In most cases, fellow eye bias was larger in populations representing the fovea. (B) Mean ODI is compared between populations approximately matched for eccentricity but recorded in different hemispheres. The dominance of the fellow eye was stronger in the hemisphere ipsilateral to the amblyopic eye. Error bars represent 95% confidence intervals based on a bootstrap, and the gray square indicates a confidence interval on the magnitude of bias measured in the control animal.

Comparing single-neuron and multiunit responses

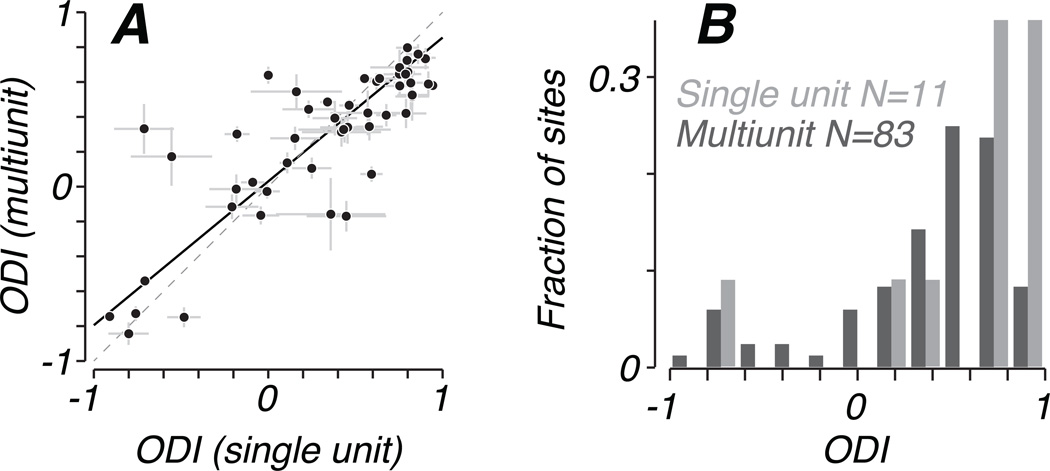
For 51 recording sites, we isolated single neurons based on spike waveform and computed ODI from firing rates. Voltage records from these sites contained background multiunit activity in addition to large spikes belonging to single units. We compared the ocular dominance of a single unit to its accompanying multiunit ensemble by analyzing the multiunit signal as described in Methods, after first removing single-unit spike waveforms from the voltage trace. Figure 6A plots the ODI of these multiunit clusters with respect to the ODI of a single unit recorded on the same electrode. The close agreement suggests that our analysis of multiunit responses reflects the ocular dominance of single units near our recording sites. A linear fit to these data, incorporating estimates of variance for both measures (Press, et al., 2007), revealed a slope significantly less than 1 (0.83 +/− 0.02), indicating that ODI values for single units were more strongly monocular than multiunit activity, as would be expected if the multiunit records include data from neurons of dispersed eye dominance.

Figure 6.

(A) Ocular dominance of 51 single neurons was compared to that of the multiunit activity recorded on the same electrode. Spike waveforms were removed from voltage traces to eliminate the contribution of isolated units to multiunit responses. Single unit ODI generally reflected that of the accompanying multiunit ensemble, but tended to have stronger eye preference, as revealed by the slope of the best-fitting straight line, which was significantly less than 1 (0.83 +/− 0.02) (B) On one array placement in a severe amblyope (S7), we recorded from 11 single neurons in addition to 83 responsive multiunit clusters without isolatable spikes. The distribution of multiunit ODI (dark gray bars) is biased toward the fellow eye, as in Figure 3B. The small sample of single units was similarly biased (light gray bars). Mean ODI did not differ significantly between single and multiunit, but single units were significantly more monocular than the multiunit distribution, taking more extreme ODI values.

This can be seen clearly using data from one array placement (Subject 6, left hemisphere, 7 degrees eccentricity), from which we recorded on 94 visually responsive sites, of which 11 had isolated single neurons and 83 only multiunit activity. Figure 6B shows distributions of ODI separately for multiunit and single unit sites from this array. Although the mean ODI of these 11 neurons (0.57) was greater than that computed from the multiunit sample (0.37), this difference failed to reach significance in a statistical permutation test: Using repeated random sub-sampling of 11 out of 83 multiunit sites, we obtained an empirical distribution of mean ODI values. The mean ODI computed from single units fell within the 95% confidence interval derived from this distribution. The ODI distributions did differ in the degree of binocularity. Repeating the permutation test using the absolute value of ODI, we found that the sample of single units was significantly more monocular, having more extreme ODI values than the multiunit distribution (p<0.005).

Decoding neural population responses

We captured the visual information in the responses of neural populations using a simple decoding algorithm, linear discriminant analysis, which quantified the sensitivity of neural populations to stimuli presented to each eye. This analysis is a concise measure of the separation between stimulus and no-stimulus trials in the space of neural responses, and can also be interpreted in light of a theoretical downstream mechanism that “decodes” the output of a neural population to perform a particular detection task by linearly weighting the responses of different neurons (Abbott & Dayan, 1999, Deneve, Latham & Pouget, 1999, Georgopoulos, Schwartz & Kettner, 1986, Jazayeri & Movshon, 2006, Salinas & Abbott, 1994, Seung & Sompolinsky, 1993). For a given population of simultaneously recorded multiunit clusters, we derived a set of weights, which were used to sum responses across the population, yielding a scalar value describing the population response to each trial. The distribution of responses resulting from stimulus trials was compared to those from no-stimulus trials by computing a d’ value, which defines the best sensitivity achievable by a mechanism that linearly combines responses across the population. The performance of such a decoder will generally depend on the information present in individual neural responses, the number of neural signals included in the pooling, and the extent to which inter-neuronal correlations lead to redundancy among these signals (Averbeck, Latham & Pouget, 2006, Shadlen, et al., 1996, Zohary, Shadlen & Newsome, 1994). We therefore measured the effects of population size on neural performance to explore the relationship between the sensitivity of data from individual recording sites and of the whole population. For each stimulus condition, we subsampled our neural populations by rank-ordering multiunit clusters by their individual sensitivity (d’), and repeating our decoding analysis using only the best N electrodes. This yielded a separate d’ value for each population size, ranging from 1 to 96 multiunit clusters.

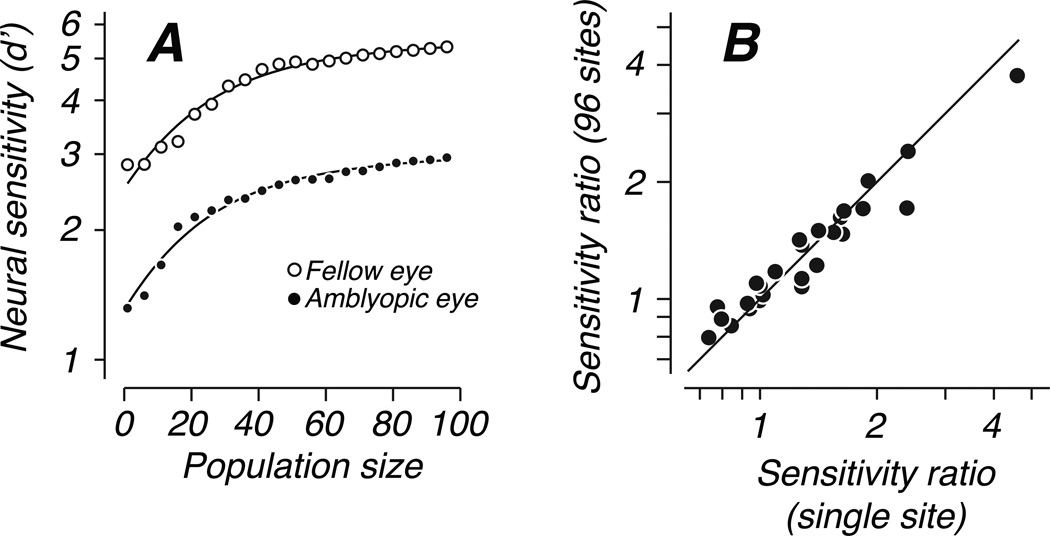
Sensitivity increased in the same way with the number of neurons in the pool for detection through either eye. Figure 7A plots performance of a neural population at detecting one example stimulus as a function of subpopulation size, separately for each eye. The sensitivity of the fellow eye was higher than that of the amblyopic eye for all population sizes; the curves are parallel on a logarithmic axis, showing that sensitivity of the two eyes differed by a constant ratio. Sensitivity in the two eyes of each animal depended on population size in the same systematic way. The example shown in Figure 7 is typical: performance increased with population size in a decelerating manner such that beyond a size of approximately 40 sites, the addition of more multiunit clusters provided relatively little additional information. We characterized the effect of population size by fitting these curves with a simple descriptive model,

$$d\text{'}=a+\frac{bN}{\sqrt{c^2+N^2}}$$

with fitted parameters a, b, and c. The offset parameter a described the performance of the best single unit for the task, while the gain parameter b, in units of d’/neuron, captured the increase in performance achieved with increased population size. The parameter c characterized the saturation of the curves, and its value specified the population size at which the curves reached √2/2 of the difference between the initial offset a and the extrapolated asymptotic performance level. We fit this model to each pair of curves derived from the two eyes’ performance with the constraint that both eyes shared the same saturation parameter, c, while a and b were free to differ between eyes. We then repeated the fitting procedure with the saturation parameter also free to vary between eyes. We used a cross-validation analysis to compare the quality of these two fits and found that the simpler model, with a single saturation parameter, better predicted holdout data not used in the model fitting (see Methods for details). This model also fit extremely well in absolute terms, explaining on average 95% and 97% of the variance in population size curves from the amblyopic and fellow eyes, respectively. For each population, we computed the sensitivity ratio d’_fellow / d’_amblyopic for population sizes of 1 and 96 – the ratio derived from a population size of 1 (the best multiunit site for the task) was very similar to the difference in sensitivity at the level of the whole population (Fig. 7B), suggesting that all pairs of curves were parallel as in the example in Figure 7A. Because the shapes of the curves relating sensitivity to population size were the same for each eye, the responses of our neuronal populations did not suggest any difference in efficiency of pooling neurons driven by the two eyes.

Figure 7.

Decoding analysis. Neural sensitivity was computed from subpopulations of various size. (A) For one array placement and one example stimulus condition, sensitivity is plotted with respect to population size, separately for detection through the amblyopic eye (filled symbols) and fellow eye (open symbols). Data from the two eyes were parallel on a log d’ axis, suggesting a constant ratio of d’ between the eyes. Solid curves show the fit of a simple descriptive model defined in the text (Animal S3, ipsilateral hemisphere, 5 deg eccentricity). (B) The ratio of sensitivity between the eyes (fellow/amblyopic) was similar for a population sizes of 1 (best multiunit site for the task) and 96 (all sites). We computed the geometric mean over stimulus conditions, and represent each array penetration by a single data point.

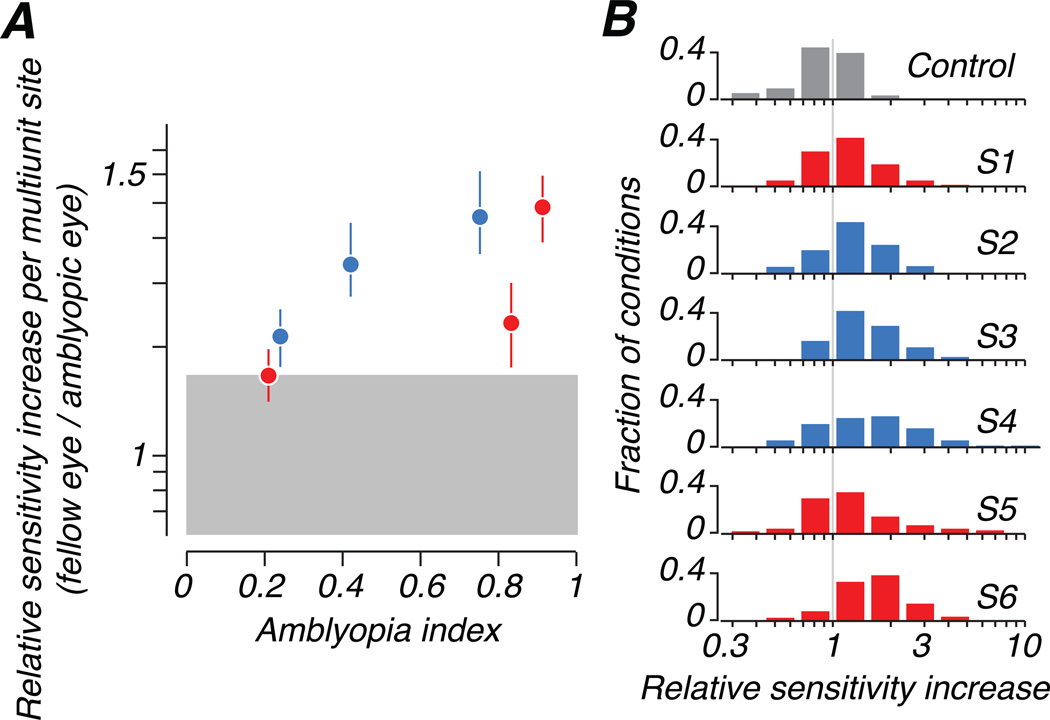
For every stimulus condition, we took the ratio of initial slopes for the two eyes’ responses (fellow/amblyopic) as a function of population size (with the offset parameter a free to vary) to describe the population sensitivity to stimuli delivered to each eye. Figure 8A compares this relative sensitivity across stimulus conditions and populations to the behavioral amblyopia index for each animal; Figure 8B shows full distributions of the measure for each animal, where each entry in the distributions is one combination of recording site and spatial frequency. The difference in contributions of neurons driven by each eye to population sensitivity correlated strongly with the severity of visual deficit measured behaviorally.

Figure 8.

We used the initial slope of each fitted sensitivity curve (example in Figure 6A) as a measure of the average contribution of a multiunit site to population sensitivity. The ratio of slopes from the two eyes is shown (fellow/amblyopic) (A) The relative contribution per site was larger for the fellow eye: the ratio of slopes was greater than 1 when averaged across stimulus conditions. This mean ratio is plotted with respect to amblyopia index. (B) Distributions of the ratio of slopes are shown for each animal. The gray vertical line represents equal contributions per site in the two eyes.

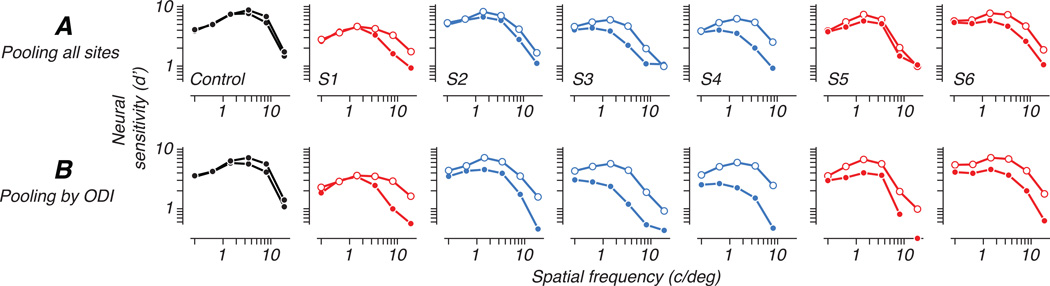
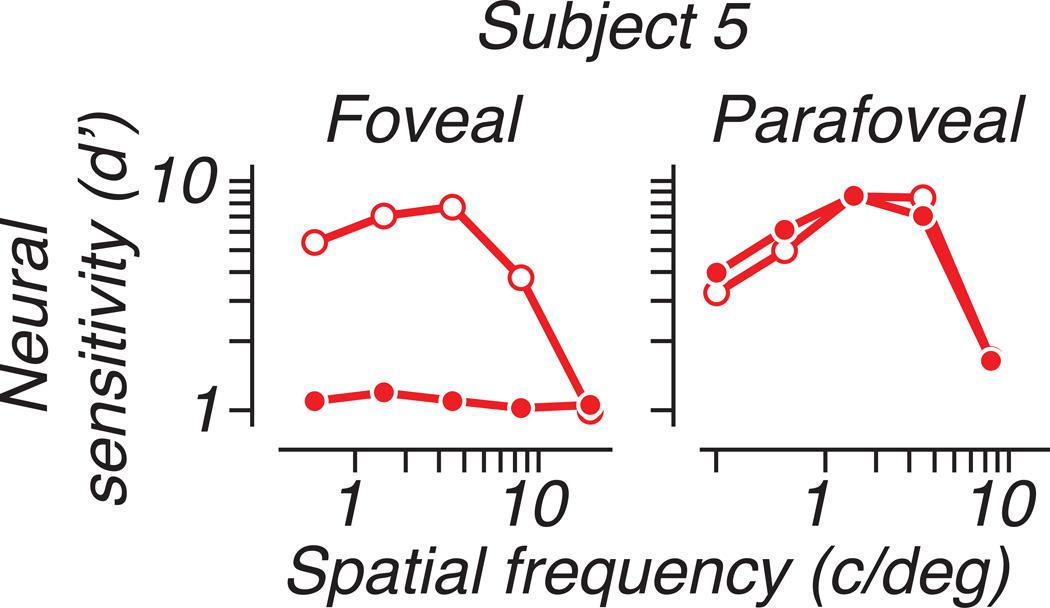
We computed population neural sensitivity for each eye of each animal. Neural performance usually differed between the eyes in a spatial-frequency dependent manner similar to behavioral contrast sensitivity: low spatial frequency stimuli were detected equally well through either eye, while the relative sensitivity of the amblyopic eye decreased at higher spatial frequencies. Figure 9A plots neural sensitivity as a function of spatial frequency, separately for detection through the fellow and amblyopic eyes. For each animal, we averaged d’ over orientation and over the 4 populations recorded from separate array placements. For one animal (S5), which showed a dramatic difference in ocular dominance between foveal and peripheral populations, we separately quantified the neural performance of each recording locus; Figure 10 shows this comparison in the same format as Figure 9. Sensitivity for detection through the amblyopic eye was barely measurable in the population representing the fovea (approximately 0.75 deg eccentricity), while a population recorded in the same hemisphere (contralateral to the treated eye) and representing the parafovea (2.5 deg) showed nearly equal sensitivity for the two eyes; this pattern is suggestive of the specific deficits in foveal vision observed in some human amblyopes (Hess & Pointer, 1985).

Figure 9.

(A) We quantified neural sensitivity as a function of spatial frequency, averaging over stimulus orientation, when pooling all multiunit sites. The amblyopic eye (filled symbols) showed a sensitivity deficit relative to the fellow eye (open symbols) that depended on spatial frequency. Each column represents a different animal, as in Figure 3. (B) We also pooled cortical sites according to ocular dominance index (ODI), pooling signals only over sites preferring the viewing eye. This restriction had little effect on fellow-eye sensitivity, but decreased sensitivity to amblyopic-eye stimulation, mostly by reducing the number of neurons available for decoding.

Figure 10.

One strabismic animal with severe amblyopia showed large neural deficits foveally but not in the near periphery. Neural sensitivity is plotted with respect to spatial frequency as in Figure 8. Results from 2 array placements are shown, one representing the fovea (eccentricity 0.75 deg) and another representing an eccentricity of approximately 2.5 deg, recorded in the same hemisphere (contralateral to the amblyopic eye). Sensitivity of the foveal population to amblyopic-eye stimulation was almost completely absent, while in the parafovea, sensitivity in the two eyes was similar.

While neural sensitivity to amblyopic eye stimulation was generally inferior to fellow eye sensitivity, it greatly exceeded behavioral performance. In S6, for example, contrast sensitivity in the amblyopic eye was impaired to the extent that behavioral thresholds could not be measured above 3 c/deg (refer to Figure 3A). However, neural sensitivity was sufficient to detect a 4 c/deg stimulus with d’ greater than 3. The pooled response of the whole population, therefore, showed differences between the eyes that, like single-neuron deficits reported previously (Kiorpes et al., 1998, Kiorpes & Movshon, 2004), were qualitatively similar to behavioral deficits but too small to fully explain loss of sensitivity in the amblyopic eye.

We wondered whether the large ocular dominance biases seen in these populations might help explain the behaviorally measured visual deficits. In the analyses given so far, we estimated the sensitivity of neuronal populations by including the responses of all neurons driven by that eye, regardless of eye dominance. Suppose, however, that when making visual discriminations under monocular viewing, the animal’s performance was determined only by neurons dominated by the viewing eye. This would sharply reduce the number of neurons available during amblyopic eye viewing, since more neurons were dominated by the nonamblyopic eye (Fig. 3B). We therefore repeated our decoding analysis, using only neurons dominated by the viewing eye. Specifically, we measured sensitivity for detection through the amblyopic eye pooling only over sites favoring that eye (ODI<0), and similarly tested fellow eye sensitivity pooling only over fellow eye dominated sites (ODI>0). The result is shown in Figure 9B. As expected given the fellow eye’s dominance, sensitivity for the fellow eye was similar to that obtained by pooling all sites (Fig. 9A). For the amblyopic eye, in contrast, there was a marked decrease in sensitivity when relying only on the sites where its responses were stronger. This is a natural consequence of pooling over fewer neurons (Fig 7A), and it also shows that when signals were pooled over the entire population, our decoded sensitivity to amblyopic eye stimulation relied substantially on the contribution of multiunit sites that were actually dominated by the fellow eye.

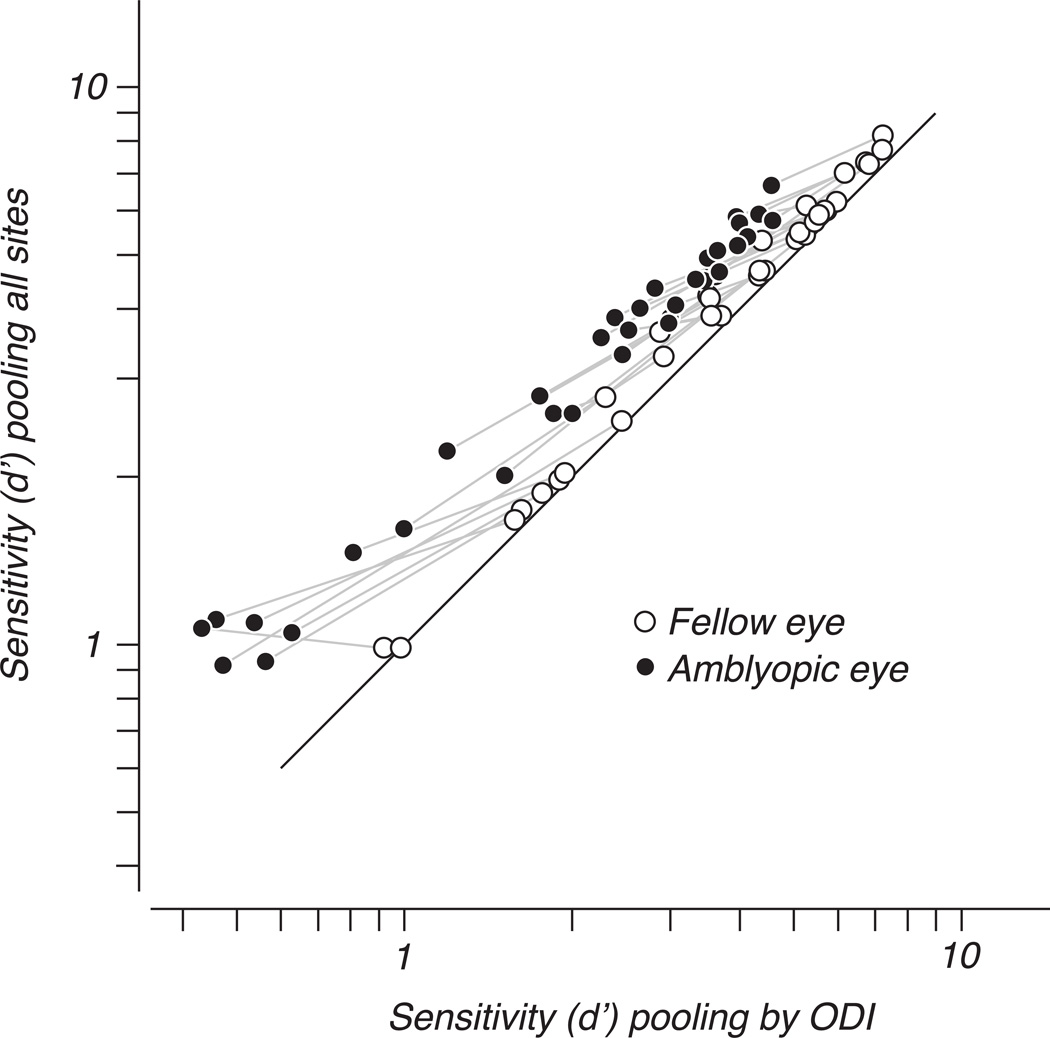
Figure 11 shows this explicitly by re-plotting the data of Figure 9. Sensitivity when pooling all sites is compared to sensitivity when pooling was restricted to cells preferring the viewing eye. Sensitivity of the fellow eye (open symbols) increased slightly by making use of the whole population, but a much larger improvement in amblyopic eye sensitivity resulted from incorporating fellow-eye-dominated sites in the pooling of amblyopic eye signals (filled symbols), especially when the sensitivity of the neurons dominated by the amblyopic eye was poor.

Figure 11.

The data of Figure 8 are re-plotted to show the difference in sensitivity under the two forms of pooling. Compared to the restricted case of pooling by ODI, amblyopic eye performance (filled symbols) benefited from additionally pooling fellow-eye dominated sites. Fellow-eye sensitivity (open symbols) differed less between the two forms of pooling. Gray lines connect points representing the two eye’s sensitivity to the same spatial frequency in the same animal.

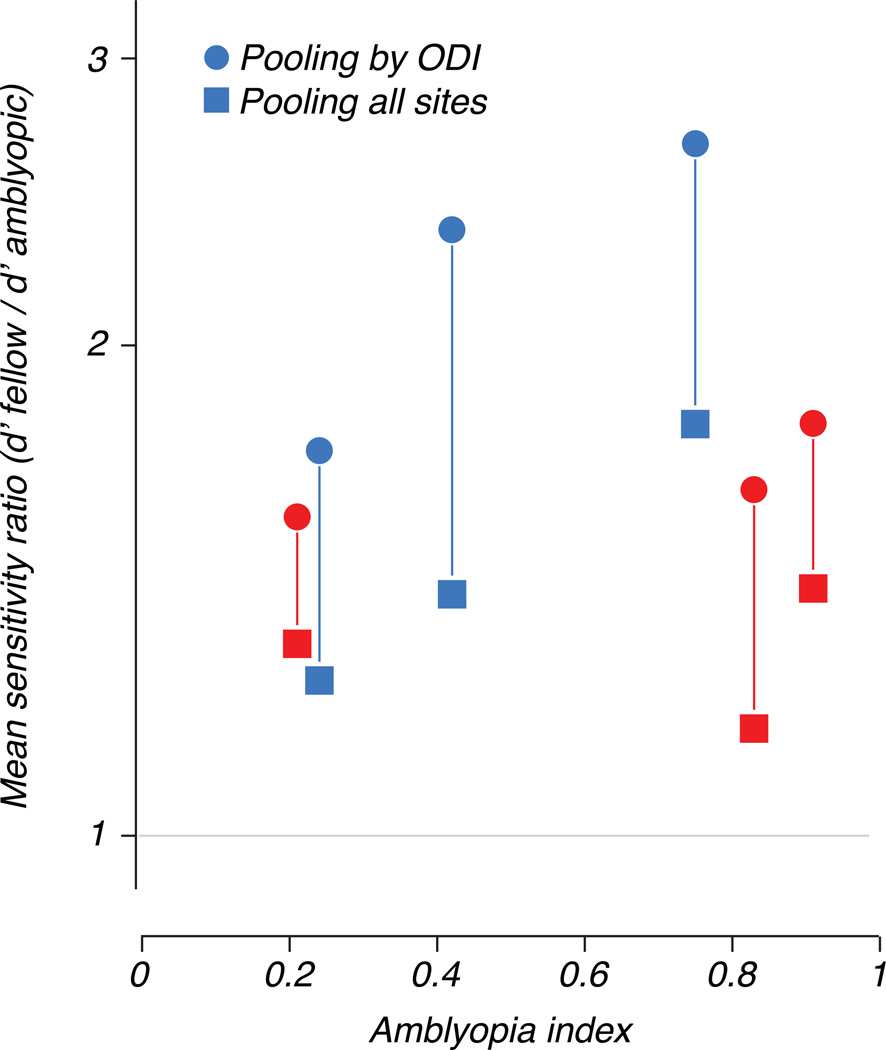
Figures 9 and 11 reveal that restricting the neural sample in this way greatly amplified the difference in sensitivity between the eyes. We computed a sensitivity ratio (fellow/amblyopic) under both pooling methods and averaged over stimulus conditions. Figure 12 plots this ratio against the behavioral amblyopia index and shows, for each animal, a larger amblyopic eye deficit resulting from pooling based on eye preference (circles) compared to pooling signals over the entire population (squares).

Figure 12.

Differences in neural sensitivity between the eyes expressed as a ratio of d’ values (fellow/amblyopic), averaged over stimulus conditions and neural populations. This mean sensitivity ratio is plotted against amblyopia index. Square symbols represent d’ values computed by pooling over all multiunit sites, while circles represent values computed using only those sites whose responses were dominated by the viewing eye.

Discussion

We recorded from visual cortex in 6 amblyopic macaques and one normal control. We analyzed multiunit activity recorded with 96-electrode arrays that straddled the V1/V2 border in the representations of the fovea and near periphery of the visual field of both hemispheres. Using a conventional population analysis of the simultaneously recorded multielectrode responses, we found reduced sensitivity and responsiveness of signals evoked by stimulation of the amblyopic eye, and an overall shift of eye dominance toward the non-amblyopic eye. This confirms our earlier findings of a weak representation of the amblyopic eye in visual cortex (Kiorpes et al., 1998, Movshon et al., 1987). Here we consider the extent to which abnormalities in sensitivity in combination with an under-representation of the amblyopic eye at the population level in early visual cortex might jointly limit the downstream processing of visual signals.

Previous studies have identified primary visual cortex as the first site at which signals from an amblyopic eye are weakened, but the implications of the identified neural abnormalities remain unclear. Single neurons in V1 are less sensitive to stimuli presented to the amblyopic eye than to the fellow eye (Kiorpes et al., 1998, Movshon et al., 1987). These differences are similar in form to behavioral deficits in contrast sensitivity, with high spatial frequencies being most affected, but are too small to explain the behavioral impairment (Kiorpes et al., 1998). The weakened signals in V1 neurons may form the initial substrate for deficits in spatial vision, but subsequent processing must amplify these early effects to provide the ultimate limit on amblyopic visual perception (Kiorpes et al., 1998, Kiorpes & Movshon, 2004). The question of how this amplification occurs is open.

Ocular imbalance in visual cortex

Studies of the distribution of ocular dominance in amblyopic V1 have consistently reported a decrease in binocularity, with larger numbers of neurons receiving input predominantly from one eye (Bi et al., 2011, Crawford et al., 1993, Kiorpes et al., 1998, Movshon et al., 1987, Smith et al., 1997, Wiesel & Hubel, 1963). The responses described in this study were relatively more binocular, both in the control animal and in amblyopes across a wide range of visual impairment. This enhanced binocularity presumably arises from the multiunit measure of neural activity we used. Our approach eliminates bias in the selection of recording sites and in the processing of recorded signals, capturing weak or noisy neural activity that could be overlooked in a search for single neurons. However, neurons with different response properties are averaged within one multiunit cluster. It is also notable that there is evidence for binocular interactions – albeit mainly suppressive ones – in neurons that would be classified as largely monocular by more conventional criteria (Bi et al., 2011, Smith et al., 1997), suggesting that amblyopic cortex may be less monocular than previously claimed.

Previous studies have consistently documented shifts in ocular dominance away from the treated eye of anisometropic amblyopes, with less consistent bias observed in V1 of strabismic animals (Bi et al., 2011, Kiorpes et al., 1998, Movshon et al., 1987, Smith et al., 1997). We found significant bias in the V1 populations recorded from all 3 anisometropic monkeys tested, and in 2 out of 3 strabismics. The magnitude of these shifts in eye dominance and their correlation with behavioral deficits were consistent in both forms of amblyopia. Our approach was unique in that we sampled foveal as well as near peripheral visual field representations in both hemispheres of each animal. We found that the extent of ocular dominance bias varied with both field location and hemisphere, with the foveal sites and ipsilateral hemisphere generally showing the largest bias. This finding is consistent with human psychophysical data showing larger sensitivity losses in amblyopic fovea (Hess & Pointer, 1985, Pardhan & Whitaker, 2000, Sireteanu & Fronius, 1981, Thomas, 1978) and further suggests a specific weakness of the cortical representation of the temporal retina of the amblyopic eye.

The changes in neural circuitry that mediate shifts in ocular balance are not known with certainty. The classical view, based on experiments with monocularly-deprived monkeys and cats (Hubel et al., 1977, Wiesel & Hubel, 1963), is that excitatory connections from one eye are weakened, partially deafferenting the cortex and leading to a shift in dominance. While a simple attenuation of excitatory signals from the amblyopic eye could underlie biases in ocular dominance, there is also evidence that a more complex interplay of excitation and inhibition shapes eye preference over the course of development. Strong interocular suppression has been described in visual cortex of strabismic cats and monkeys (Sengpiel, et al., 1994, Smith et al., 1997), and pharmacological and intracellular evidence suggest that in cat this suppression is mediated by intracortical inhibition (Scholl, Tan & Priebe, 2013, Sengpiel, et al., 2006). The change in the excitatory-inhibitory (E/I) balance of circuits serving normal binocular vision might therefore reflect strengthened inhibition, weakened excitation, or both (see Takesian & Hensch, 2013 for a review) A reduction in excitation may reveal inhibitory components that are present but difficult to observe under conditions of normal E/I balance (Scholl et al., 2013), even if the proximal cause is a loss of excitatory input. A dynamic reorganization of excitatory and inhibitory circuits also occurs in rodents during monocular deprivation (Kuhlman, et al., 2013, Ma, Li & Tao, 2013, Maffei, et al., 2006, Yazaki-Sugiyama, et al., 2009). but the relevance of this to amblyopia in truly binocular animals is uncertain, given the absence of evidence for fused stereoscopic binocular vision in rodents, whose oculomotor behavior suggests that their visual system is optimized for other tasks (Wallace, et al., 2013).

V1 and V2 – similarities and differences

Most earlier studies of cortical effects of amblyopia have concentrated on V1. Our approach here allows us to make a direct comparison of the effects of amblyopia on V1 and V2 under matched conditions. Strong ocular dominance bias was observed in both areas, and correlated with behavioral deficits, more strongly in V1 than V2; the stronger correlation with V1 may reflect the larger number of V1 sites (Figure 2). In cases where V1 and V2 populations were recorded simultaneously, we evaluated differences in neural sensitivity between the eyes in both areas and found no difference in the magnitude of neural deficit (data not shown). This seems to contrast with recent findings suggesting that shifts in eye preference in strabismic animals are absent in V1, arising first in V2 (Bi et al., 2011), but note that in our case we only have data from both areas in two strabismic amblyopes.

Testing for a population-level deficit

The bridge between small abnormalities at the level of single neurons and larger deficits in behavior might be the result of some downstream abnormality, or it may emerge from the structure of signals carried by neural populations in early visual cortex. The ability of large numbers of neurons to process visual information collectively cannot be captured simply in terms of single-unit response properties. Pooling responses across neurons can eliminate noise and increase sensitivity, but there are limits to this advantage, set by factors only evident at the population level. Noise that is correlated across neurons cannot be averaged out, and shapes the way in which neural signals are integrated (Averbeck et al., 2006, Graf et al., 2011, Shadlen et al., 1996, Zohary et al., 1994). The quality of a population representation also depends critically on the number of signals available for pooling. Previously reported population biases in ocular dominance suggest that vision through the amblyopic eye might be limited in part by the smaller number of cortical neurons that evoke strong responses relative to the fellow eye (Bi et al., 2011, Movshon et al., 1987). In the psychophysical literature, this possibility is suggested by analyses that attribute perceptual deficits to cortical “undersampling” of the image (Hess & Field, 1994, Levi & Klein, 1985, Levi & Klein, 1996, Wang, Levi & Klein, 1998). This possibility has not been directly tested previously because methods that characterize single neurons in isolation provide limited insight into the effects of pooling signals across a population.

Our analysis of neural population performance in detecting monocular stimuli revealed a simple relationship between single-unit properties and the sensitivity of large populations – sensitivity increased smoothly with the number of neurons that contributed, and this relationship was similar in form for both eyes, suggesting that there is no difference in the correlated variability that might selectively impair the pooling of signals from the amblyopic eye. Optimally pooling signals from both eyes across a population of any size revealed a constant ratio of sensitivity between the two eyes, reflecting differences in sensitivity found at the level of single neurons (Fig 7). We wondered whether sub-optimal pooling of information might amplify the deficits found at the single-unit level, specifically by reducing the number of neurons available for decoding when the amblyopic eye was viewing. We reasoned that some selection mechanism might restrict the signals available for perceptual judgment to those from neurons dominated by the viewing eye. Simulating this situation revealed a greater ocular imbalance in sensitivity than that seen in single-unit responses (Fig 9, 11), because signals from the amblyopic eye came from a smaller number of neurons. The true extent of this additional loss is difficult to estimate, because it depends on whether the curves of sensitivity vs. population size (Fig 7) truly saturate or merely continue to grow slowly up to the largest available population size. This analysis nonetheless shows that undersampling of the image in the early visual cortex might explain the downstream amplification of the sensitivity loss observed in early visual cortex.

The changes in neural circuits that might lead to abnormal decoding of amblyopic eye signals are unknown. Presumably, decoding is done downstream of V1 and V2, and relies on organized cortico-cortical projection systems. If these systems suffer from the same abnormalities as thalamo-cortical projection systems, then changes in downstream circuits might have the same features as the changes we discussed above in afferent circuits: decreased excitation, enhanced inhibition, and consequently reduced signal transfer. Cascaded changes of this kind as signals pass through the cortical visual pathway would amplify the eye dominance effects seen in early visual cortex. In addition to changes in signal strength, there is also reason to think that the orderliness of neural connections is diminished in amblyopia. Cortical neurons in amblyopic animals have not only weaker responses but also reduced spatial resolution even though their thalamic inputs are normal (Movshon et al., 1987). This must reflect a disordering of afferent connectivity, leading to a disruption of the structure of cortical receptive fields, and serves as a simple example of information loss due to abnormal pooling of normal visual signals. There is similar evidence that fine spatial structure of receptive fields may become disorganized in the transformation between V1 and V2 of amblyopic macaques (Tao, et al., 2014). The performance of our decoding algorithm depends on optimal combination of neural signals, and an instantiation of this algorithm in the brain requires precise connections between early visual cortex and higher areas. If the precision of this pattern is dependent on learning and experience (Law & Gold, 2008), then a behavioral preference for the dominant eye could contribute to a biased decoding strategy that manifests itself as a disorganized pattern of connections among cells carrying signals from the amblyopic eye.

We conclude is that there is information available from the amblyopic eye in early visual cortex which does not drive perceptual judgments. Downstream processing by higher visual areas fails to make full use of this information, but the level of processing and the manner in which information is lost remains unknown. Suboptimal pooling of neural signals represents one simple mechanism that could limit the efficiency with which downstream areas can use the signals from V1 and V2.

Highlights.

• Amblyopic visual cortex has a weak representation of the amblyopic eye

• The weak representation is greater in fovea, ipsilateral to the amblyopic eye

• Neural populations in amblyopic cortex respond to stimuli not visible perceptually.

• Pooled neural output yields better sensitivity than the amblyopic eye

• Reduced visual sensitivity may be explained by subsampling of amblyopic eye neurons