Abstract
Lactic acid fermentation of radish was conducted using various additive and growth stimulators such as salt (2 %–3 %), lactose, MgSO4 + MnSO4 and Mustard (1 %, 1.5 % and 2 %) to optimize the process. Response surface methodology (Design expert, Trial version 8.0.5.2) was applied to the experimental data for the optimization of process variables in lactic acid fermentation of radish. Out of various treatments studied, only the treatments having ground mustard had an appreciable effect on lactic acid fermentation. Both linear and quadratic terms of the variables studied had a significant effect on the responses studied. The interactions between the variables were found to contribute to the response at a significant level. The best results were obtained in the treatment with 2.5 % salt, 1.5 % lactose, 1.5 % (MgSO4 + MnSO4) and 1.5 % mustard. These optimized concentrations increased titrable acidity and LAB count, but lowered pH. The second-order polynomial regression model determined that the highest titrable acidity (1.69), lowest pH (2.49) and maximum LAB count (10 × 108 cfu/ml) would be obtained at these concentrations of additives. Among 30 runs conducted, run 2 has got the optimum concentration of salt– 2.5 %, lactose- 1.5 %, MgSO4 + MnSO4– 1.5 % and mustard- 1.5 % for lactic acid fermentation of radish. The values for different additives and growth stimulators optimized in this study could successfully be employed for the lactic acid fermentation of radish as a postharvest reduction tool and for product development.
Keywords: Lactic acid fermentation, Lactic acid bacteria, LAB, Radish, RSM, Salt, Mustard MgSO4 and MnSO4
Introduction
India is the second largest producer of fruits and vegetables in the world but unfortunately, due to the lack of postharvest infrastructure and processing capabilities, a lot of produce goes waste, resulting in a huge loss of these natural resources (Joshi et al. 2011). Among different vegetables produced and consumed in India, radish (Raphnus sativus), occupies a significant place in Indian diet as salad and cooked food. Radish possesses medicinal value and is even prescribed for patients suffering from piles, liver troubles, enlarged spleen and jaundice (Brar et al. 1972).
Radish in their natural state can be preserved for a very short period only and thus, their availability to the consumers remains seasonal. Among different methods, fermentation is one of the oldest methods of food preservation in the world (Joshi & Somesh 2009). The tremendous increase in consumer demand for fresh-like products containing natural ingredients, changing food patterns and convenience have led to the development of minimally processed products using lactic acid bacterial (LAB) cultures. The lactic fermentation is a natural process brought about by the lactic acid bacteria (LAB) present in the raw food or those derived from a starter culture. Also, its bio-preservation nature has gained increasing attention as natural means for controlling the shelf-life and safety of food products (Joshi et al. 2011).
In our earlier attempt, a process for lactic acid fermentation of radish was standardized in which radish fermentation was successfully carried out at 26 °C and 2.5% salt using Lactobacillus plantarum, Pediococcus cerevisiae and Streptococcus lactis var. diacetylactis in sequence (Somesh & Joshi 2007). However, LAB are only present in the raw vegetables which can be employed for carrying out fermentation by adjusting the proper concentrations of salt, additives and growth stimulators (Daeschal et al. 1987). Hence, fermentation of majority of vegetables is done by naturally occurring lactic acid microflora rather than by defined starter cultures. Various factors such as microorganisms, salt concentration, temperature, chemical additives, amount of fermentable carbohydrates in the vegetables and the availability of nutrients in the brine affect the lactic acid fermentation of vegetables (Joshi et al. 2008). Besides all this, lactic acid fermentation of radish has been successfully used as one of the alternatives for preservation and to provide healthful products for consumers (Joshi and Thakur, 2000; Karovlcova and Kohajdova, 2005; Joshi & Somesh 2009; Joshi & Somesh 2010; Joshi et al. 2011).
Salt has historically been used for directing the fermentation of cucumber, radish and carrot (Hudson and Buescher 1985; Fleming et al. 1987). Many ingredients apart from salt can be used in the preparation of lactic acid fermented fruits and vegetables. These ingredients include a source of nutrients such as sugars (Lactose), mineral salts (MgSO4 + MnSO4). Mustard seeds in powdered form help to restrict the growth of unwanted bacteria either through a regulatory effect on pH or by producing inhibitory substances during fermentation and have a final flavour and taste in fermented vegetables (Montet et al. 1999; Anand and Das 1971).
Response surface methodology (RSM) is a useful approach to identify the optimum operating conditions of a given system. This method is applied to find out how a particular objective is affected by a given set of operating conditions of interest, and identify the optimum operating conditions (Box et al. 1978; Giovanni 1983). The major advantage of RSM is to minimize the load of experiments as well as time (Tzeng et al. 2009). There is no report on the RSM in optimizing the lactic acid fermentation of radish in the documented literature. Taking all these important advantages and uses of lactic acid fermentation of radish into consideration, the aim of the present study was to investigate the effect of salt, additives and growth stimulators on natural lactic acid fermentation of radish at room temperature, employing a central composite design (CCD) and response surface methodology (RSM) in order to optimize the concentration of salt, various additives and growth stimulators for natural lactic acid fermentation of radish.
Materials and methods
Raw materials
Radish, mustard and salt used in the experiments were procured from the local market. The chemicals, viz. Lactose, Magnesium Sulphate (MgSO4), Mangnese Sulphate (MnSO4) used in the study were of analytical grade.
Experimental design for optimization of lactic acid fermentation
Response surface methodology was applied to the experimental data using a commercial statistical package (Design expert, Trial version 8.0.5.2, State Ease Inc., Minneapolis, IN statistical software) for the generation of response surface plot and optimization of process variables. A factorial experiment was used to study the effects of various independent variables viz., salt (A), lactose (B), MgSO4 + MnSO4 (C) and mustard (D) on the response variables such as per cent titrable acidity (Y1), pH (Y2), per cent salt (Y3) and LAB count (Y4) of lactic acid fermentation of radish. The averages from three replicated values of each run were taken as dependent variables or responses. For the statistical analysis, the numerical levels were standardized to −1, 0 and +1. The standard scores were fitted to a quadratic polynomial regression model for predicting individual Y responses by employing at least square technique (Wanasundara and Shahidi 1996). The second order polynomial equation was fitted to the experimental data of each dependent variable as given. The model proposed to each response of Y was:
| 1 |
Where βo, βi, βij are intercepts, quadratic regression coefficient terms Xi and Xj are independent variables (in this case A, B, C and D). The model permitted evaluation of quadratic terms of the independent variables on the dependent variable. The response surface and contour plot were generated for different interactions of any two independent variables, where holding the value of third variables as constant at central level. The optimization of the process was aimed at finding the optimum values of independent variables.
Statistical analysis
Response surface methodology (RSM) was used to estimate the main effects of salt, lactose, MgSO4 + MnSO4 and mustard on lactic acid fermentation process. A central composite design was used with salt (2 %, 2.5 % and 3 %), lactose (1 %, 1.5 % and 3 %), MgSO4 + MnSO4 (1 %, 1.5 % and 3 %) and mustard (1 %, 1.5 % and 3 %) being the independent process variables (Table 1). For the generated 30 experiments, RSM was applied to the experimental data using design expert 8 (Design expert, Trial version 8.0.5.2, State Ease Inc., Minneapolis, IN statistical software). Data were statistically analyzed by using RSM (F test for analysis of variance ANOVA).
Table 1.
Process variables and their levels of experimental design
| Symbols | Independent variable | Range and levels | ||
|---|---|---|---|---|
| −1 | 0 | +1 | ||
| A | Salt (%) | 2 | 2.5 | 3 |
| B | Lactose (%) | 1 | 1.5 | 2 |
| C | Magnesium sulphate + Manganese sulphate (%) | 1 | 1.5 | 2 |
| D | Mustard (%) | 1 | 1.5 | 2 |
Lactic acid fermentation
Fermentation of radish was performed similar to that practiced for sauerkraut fermentation and as done in our earlier studies (Joshi et al. 2008). Optimally mature roots of radish were washed, peeled and grated into shreds. The required concentration of salt (2 %, 2.5 % and 3 %) along with additives and growth stimulators (1 %, 1.5 % and 3 %) were added uniformly throughout the mass of shredded radish. The shredded radish was then, packed tightly into the glass jars and then, weighed down to expel the air in-between the shreds. During fermentation, the surface of radish shreds was covered with a plastic bag filled with water to serve as weight to press done the shredded mass so that the radish shreds slide down into the brine until the surface of the uppermost shreds was covered with the brine. The shreds were allowed to ferment at room temperature (25 ± 2 °C) in the laboratory.
Analytical methods
The radish shreds and brine were monitored for titratable acidity (%), pH and lactic acid bacterial (LAB) count during fermentation according to the standard methods. The pH was determined with digital pH meter (CRISON Instrument Ltd. Spain) that was standardized with buffers of pH 4.0 and 7.0 before pH measurements. Titratable acidity and per cent salt estimation was measured by the method of AOAC (1980) and Ranganna (1986), respectively.
LAB count
Lactic acid bacterial (LAB) count of microorganisms was taken according to the method given by Harrigan and McCance (1966) using MRS agar media having composition [g/L]: Peptic digest of animal tissue [10], yeast extract [5], beef extract [8], dextrose [20], polysorbate 80 [1], ammonium citrate [2], sodium acetate [5], magnesium sulphate [0.2], manganese sulphate [0.05], dipotassium phosphate [2] and agar [12]. pH of the medium at 25 °C was adjusted to 5.7 ± 0.2. Incubation temperature for the cultures was 37 ± 1 °C.
Results
Experimental results of various responses
Table 2 reveals the experimental results of various responses (Y1, Y2, Y3 and Y4). It is discernible from the table that addition of the various additives and growth stimulators alongwith salt, especially mustard has resulted into the desirable characteristics (increased acidity, lowered pH, high LAB count). Among all the 30 runs employed, the range of per cent titrable acidity, pH, per cent salt and LAB count varied from 1.49–1.69 %, 2.49–3.2, 1.43–2.99 % and 6.9–9.9, respectively. The highest per cent titrable acidity, lowest pH and highest LAB count was obtained with the Run 2 having salt- 2.5 %, lactose- 1.5 %, MgSO4 + MnSO4- 1.5 % and mustard- 1.5 %. Addition of lactose at this concentration would have proved a potential energy substrate for lactic acid bacteria. However, the alternation (increase or decrease) in the concentration of the variables resulted in remarkable changes in the responses. For an instance, at salt- 3 %, lactose- 2 %, MgSO4 + MnSO4 - 1 % and mustard - 1 %, the per cent titrable acidity, pH, per cent salt and LAB count were recorded to be 1.49 %, 3.14, 2.87 % and 6.9, respectively which were less in magnitude as desirable. It is also clear from the table that Y3 (per cent salt) remained more or less the same as it was added initially in the fermentation vessel indicating that salt was used for the stimulation of LAB.
Table 2.
Experimental design and results of the central composite design of 30 experiments for lactic acid fermentation of radish
| Factor 1 | Factor 2 | Factor 3 | Factor 4 | Response 1 | Response 2 | Response 3 | Response 4 | |
|---|---|---|---|---|---|---|---|---|
| Run | A | B | C | D | Y1 | Y2 | Y3 | Y4 |
| 1 | 2.00 | 1.00 | 2.00 | 1.00 | 1.52 | 3.11 | 1.9 | 6.9 |
| 2 | 2.50 | 1.50 | 1.50 | 1.50 | 1.69 | 2.49 | 2.45 | 10 |
| 3 | 3.00 | 2.00 | 2.00 | 2.00 | 1.5 | 3.13 | 2.89 | 7 |
| 4 | 3.00 | 1.00 | 1.00 | 1.00 | 1.54 | 3.06 | 2.91 | 7 |
| 5 | 2.00 | 1.00 | 1.00 | 1.00 | 1.61 | 3.18 | 1.75 | 7 |
| 6 | 3.00 | 2.00 | 2.00 | 1.00 | 1.55 | 3.2 | 2.92 | 8.67 |
| 7 | 2.00 | 2.00 | 1.00 | 1.00 | 1.54 | 3.13 | 1.79 | 7 |
| 8 | 2.00 | 1.00 | 1.00 | 2.00 | 1.61 | 3 | 1.91 | 8.33 |
| 9 | 2.50 | 1.50 | 1.50 | 0.50 | 1.58 | 3.14 | 2.39 | 8 |
| 10 | 2.00 | 1.00 | 2.00 | 2.00 | 1.59 | 2.96 | 1.92 | 9.33 |
| 11 | 2.50 | 1.50 | 2.50 | 1.50 | 1.57 | 3.03 | 2.48 | 8 |
| 12 | 2.00 | 2.00 | 2.00 | 1.00 | 1.56 | 3.2 | 2 | 8 |
| 13 | 2.50 | 1.50 | 1.50 | 1.50 | 1.55 | 3.15 | 2.39 | 7 |
| 14 | 3.00 | 2.00 | 1.00 | 2.00 | 1.49 | 3.12 | 2.85 | 7 |
| 15 | 2.50 | 1.50 | 1.00 | 1.50 | 1.6 | 2.79 | 2.45 | 8.33 |
| 16 | 2.50 | 1.50 | 1.50 | 2.50 | 1.61 | 2.99 | 2.38 | 9 |
| 17 | 3.00 | 1.00 | 2.00 | 1.00 | 1.65 | 2.95 | 2.99 | 9 |
| 18 | 2.50 | 1.50 | 1.50 | 1.00 | 1.63 | 2.8 | 2.42 | 9.67 |
| 19 | 2.50 | 1.50 | 1.50 | 1.50 | 1.62 | 2.5 | 2.48 | 9.9 |
| 20 | 3.00 | 1.50 | 1.50 | 1.50 | 1.61 | 2.89 | 2.98 | 9 |
| 21 | 2.50 | 1.50 | 1.50 | 1.50 | 1.63 | 2.69 | 2.45 | 8.67 |
| 22 | 2.00 | 2.00 | 1.00 | 2.00 | 1.6 | 3.06 | 1.99 | 8 |
| 23 | 2.50 | 1.50 | 0.50 | 1.50 | 1.5 | 3.14 | 2.39 | 7 |
| 24 | 3.00 | 2.00 | 1.00 | 1.00 | 1.49 | 3.14 | 2.87 | 6.9 |
| 25 | 2.50 | 1.50 | 1.50 | 1.50 | 1.6 | 2.8 | 2.37 | 9 |
| 26 | 2.50 | 2.50 | 1.50 | 1.50 | 1.5 | 3.15 | 2.49 | 7 |
| 27 | 2.00 | 2.00 | 2.00 | 2.00 | 1.59 | 3.04 | 1.85 | 9 |
| 28 | 3.00 | 1.00 | 2.00 | 2.00 | 1.6 | 3.03 | 2.83 | 9 |
| 29 | 3.00 | 1.00 | 1.00 | 2.00 | 1.57 | 3.01 | 2.92 | 9 |
| 30 | 1.50 | 1.50 | 1.50 | 1.50 | 1.57 | 3 | 1.43 | 8.2 |
A-salt A, B-lactose, C-MgSO4 + MnSO4 and D-mustard, Y1− per cent titrable acidity,Y2-pH, Y3-% salt and Y4-LAB count (cfu X 108)
Fitting models
Experiments were performed according to the CCD experimental design given in Table 2 in order to search for the optimum combination of various parameters for the lactic acid fermentation of radish. The experimental results along with the theoretically predicted values of all the responses are shown in Table 2. The responses of the CCD designs were fitted in the mathematical expression (2–5) of relationship in terms of coded factors with variables as shown below:
| 2 |
| 3 |
| 4 |
| 5 |
where Y1, Y2, Y3 and Y4 are per cent titrable acidity, pH, per cent salt and LAB count (cfu X 108) respectively, and A, B, C and D are the coded values of the test variables, salt, lactose, MgSO4 + MnSO4 and mustard, respectively. The statistical significance of the model equations were evaluated by the F test for analysis of variance (ANOVA). The results of multiple linear regressions conducted for the second order response surface model are given in Tables 3, 4, 5, and 6. The significance of each coefficient was determined by Student's t-test and p-values.
Table 3.
Analysis of variance (ANOVA) for response surface quadratic model for titrable acidity during lactic acid fermentation of radish
| Source | Sum of Squares | Df | Mean Square | F Value | p-value Prob > F |
|---|---|---|---|---|---|
| Model | 0.060 | 14 | 4.267 E-003 | 4.78 | 0.0024 |
| A | 2.658 E-003 | 1 | 2.658 E-003 | 2.98 | 0.1050 |
| B | 9.204 E-003 | 1 | 9.204 E-003 | 10.31 | 0.0058* |
| C | 2.604 E-003 | 1 | 2.604 E-003 | 2.92 | 0.1083 |
| D | 8.263 E-004 | 1 | 8.263 E-004 | 0.93 | 0.3513 |
| AB | 5.256 E-003 | 1 | 5.256 E-003 | 5.89 | 0.0283* |
| AC | 6.006 E-003 | 1 | 6.006 E-003 | 6.73 | 0.0204* |
| AD | 3.306 E-003 | 1 | 3.306 E-003 | 3.70 | 0.0735 |
| BC | 1.563 E-004 | 1 | 1.563 E-004 | 0.17 | 0.6816 |
| BD | 6.250 E-006 | 1 | 6.250 E-006 | 7.000 E-003 | 0.9344 |
| CD | 5.063 E-004 | 1 | 5.063 E-004 | 0.57 | 0.4631 |
| A2 | 4.858 E-003 | 1 | 4.858 E-003 | 5.44 | 0.0340* |
| B2 | 0.017 | 1 | 0.017 | 19.00 | 0.0006* |
| C2 | 0.014 | 1 | 0.014 | 15.36 | 0.0014* |
| D2 | 1.282 E-003 | 1 | 1.282 E-003 | 1.44 | 0.2495 |
| Residual | 0.013 | 15 | 8.929 E-004 | ||
| Lack of fit | 7.913 E-003 | 11 | 7.194 E-004 | 0.53 | 0.8201 NS |
| R-squared | 0.8169 | ||||
| Adj R-squared | 0.6460 | ||||
| Pred R-squared | 0.2298 | ||||
| Adeq precision | 7.450 |
(Df Degree of freedom, NS Not Significant, *- 5 % level of Significance)
Table 4.
ANOVA for response surface quadratic model for pH during lactic acid fermentation of radish
| Source | Sum of Squares | Df | Mean Square | F Value | p-value Prob > F |
|---|---|---|---|---|---|
| Model | 0.86 | 14 | 0.061 | 6.56 | 0.0004 |
| A | 4.238 E-003 | 1 | 4.238 E-003 | 0.45 | 0.5112 |
| B | 0.032 | 1 | 0.032 | 3.37 | 0.0863 |
| C | 9.375 E-004 | 1 | 9.375 E-004 | 0.10 | 0.7560 |
| D | 0.026 | 1 | 0.026 | 2.74 | 0.1185 |
| AB | 2.756 E-003 | 1 | 2.756 E-003 | 0.29 | 0.5953 |
| AC | 7.563 E-004 | 1 | 7.563 E-004 | 0.081 | 0.7801 |
| AD | 7.656 E-003 | 1 | 7.656 E-003 | 0.82 | 0.3800 |
| BC | 1.806 E-003 | 1 | 1.806 E-003 | 0.19 | 0.6667 |
| BD | 1.806 E-003 | 1 | 1.806 E-003 | 0.19 | 0.6667 |
| CD | 1.056 E-003 | 1 | 1.056 E-003 | 0.11 | 0.7416 |
| A2 | 0.14 | 1 | 0.14 | 14.76 | 0.0016* |
| B2 | 0.38 | 1 | 0.38 | 40.67 | < 0.0001* |
| C2 | 0.28 | 1 | 0.28 | 30.19 | <0.0001* |
| D2 | 0.25 | 1 | 0.25 | 26.44 | 0.0001* |
| Residual | 0.14 | 15 | 9.359 E-003 | ||
| Lack of fit | 0.049 | 11 | 4.424 E-003 | 0.19 | 0.9865 NS |
| Pure error | 0.092 | 4 | 0.023 | ||
| Cor total | 1.00 | 29 | |||
| R-squared | 0.8596 | ||||
| Adj R-squared | 0.7286 | ||||
| Pred R-squared | 0.6300 | ||||
| Adeq precision | 7.926 |
(Df Degree of freedom, NS Not Significant, *- 5 % level of Significance)
Table 5.
ANOVA for response surface quadratic model for per cent salt during lactic acid fermentation of radish
| Source | Sum of Squares | Df | Mean Square | F Value | p-value Prob > F |
|---|---|---|---|---|---|
| Model | 5.41 | 14 | 0.39 | 159.37 | <0.0001 |
| A | 4.76 | 1 | 4.76 | 1959.94 | <0.0001* |
| B | 2.204 E-003 | 1 | 2.204 E-003 | 0.91 | 0.3556 |
| C | 0.010 | 1 | 0.010 | 4.12 | 0.0604 |
| D | 9.370 E-006 | 1 | 9.370 E-006 | 3.862 E-003 | 0.9513 |
| AB | 4.556 E-003 | 1 | 4.556 E-003 | 1.88 | 0.1907 |
| AC | 1.406 E-003 | 1 | 1.406 E-003 | 0.58 | 0.4583 |
| AD | 0.012 | 1 | 0.012 | 4.76 | 0.0454* |
| BC | 6.250 E-006 | 1 | 6.250 E-006 | 2.576 E-003 | 0.9602 |
| BD | 5.625 E-005 | 1 | 5.625 E-005 | 0.023 | 0.8810 |
| CD | 0.028 | 1 | 0.028 | 11.56 | 0.0040* |
| A2 | 1.371 E-003 | 1 | 1.371 E-003 | 0.57 | 0.4639 |
| B2 | 1.033 E-003 | 1 | 1.033 E-003 | 0.43 | 0.5240 |
| C2 | 1.498 E-003 | 1 | 1.498 E-003 | 0.62 | 0.4442 |
| D2 | 0.011 | 1 | 0.011 | 4.41 | 0.0530 |
| Residual | 0.036 | 15 | 2.426 E-003 | ||
| Lack of fit | 0.030 | 11 | 2.690 E-003 | 1.58 | 0.3499 NS |
| Pure error | 6.800 E-003 | 4 | 1.700 E-003 | ||
| Cor total | 5.45 | 29 | |||
| R-squared | 0.9933 | ||||
| Adj R-squared | 0.9871 | ||||
| Pred R-squared | 0.9655 | ||||
| Adeq precision | 45.597 |
(Df Degree of freedom, NS Not Significant, *- 5 % level of Significance)
Table 6.
ANOVA for response surface quadratic model for LAB count (cfu X 108) during lactic acid fermentation of radish
| Source | Sum of Squares | Df | Mean Square | F Value | p-value Prob > F |
|---|---|---|---|---|---|
| Model | 23.93 | 14 | 1.71 | 4.54 | 0.0031 |
| A | 2.333 E-003 | 1 | 2.333 E-003 | 6.189 E-003 | 0.9383 |
| B | 0.66 | 1 | 0.66 | 1.76 | 0.2045 |
| C | 3.13 | 1 | 3.13 | 8.31 | 0.0114* |
| D | 2.34 | 1 | 2.34 | 6.20 | 0.0250* |
| AB | 1.48 | 1 | 1.48 | 3.93 | 0.0660 |
| AC | 0.047 | 1 | 0.047 | 0.13 | 0.7281 |
| AD | 1.78 | 1 | 1.78 | 4.71 | 0.0464* |
| BC | 0.047 | 1 | 0.047 | 0.13 | 0.7281 |
| BD | 1.78 | 1 | 1.78 | 4.71 | 0.0464* |
| CD | 0.45 | 1 | 0.45 | 1.18 | 0.2941 |
| A2 | 0.93 | 1 | 0.93 | 2.46 | 0.1374 |
| B2 | 8.56 | 1 | 8.56 | 22.72 | 0.0002* |
| C2 | 5.15 | 1 | 5.15 | 13.66 | 0.0022* |
| D2 | 0.65 | 1 | 0.65 | 1.72 | 0.2091 |
| Residual | 5.65 | 15 | 0.38 | ||
| Lack of fit | 3.45 | 11 | 0.31 | 0.57 | 0.7928NS |
| Pure error | 2.21 | 4 | 0.55 | ||
| Cor total | 29.58 | 29 | |||
| R-squared | 0.8089 | ||||
| Adj R-squared | 0.6305 | ||||
| Pred R-squared | 0.2975 | ||||
| Adeq precision | 6.737 |
(Df Degree of freedom, NS Not Significant, * - 5 % level of Significance)
Model F-values of 4.78, 6.56, 159.37 and 4.54 for Y1, Y2, Y3 and Y4 respectively, imply that the models were significant. Table 3, 4, 5, and 6 reveal that for titrable acidity B, AB, AC, A2, B2, C2 were significant model terms; for pH A2, B2, C2, D2 were significant; for salt estimation A, AD, CD were significant model terms; whereas, in case of LAB count C, D, AD, BD, B2, C2 were significant model terms. The "Lack of Fit F-values" of 0.53, 0.19, 1.58 and 0.57 for Y1, Y2, Y3 and Y4 respectively, imply that the Lack of Fit is not significant relative to the pure error which indicates towards the fitness of models. The goodness of fit of the models were checked by the determination coefficient (R2). All the independent variables showed the values of R2 to be > 0.75 and "Adeq Precision" greater than 4 which indicated aptness of the model and adequate signal, respectively. Hence, the models were used to navigate the design spaces (Box et al. 1978).
3D response surface graphs
Response surface plots as a function of two factors at a time, maintaining all other factors at fixed levels are more helpful in understanding both the main and the interaction effects of these two factors. These plots can be easily obtained by calculating from the model, the values taken by one factor where the second varies with constraint of a given Y value. The response surface curves were plotted to understand the interaction of the variables and to determine the optimum level of each variable for maximum response. The response surface curves for Y1, Y2, Y3 and Y4 are shown in Fig. 1. The nature of the response surface curves shows the interaction between the variables. The elliptical nature of the contour in 3D-response surface graphs depicts the mutual interactions of all the variables in providing significant effect on the responses. In general, all the additives contributed cummutatively towards the fermentation process by increasing the acidity and LAB count; and lowering the pH. However, the analysis of the results and response graphs showed that, in the range studied, only the treatments having ground mustard had an appreciable effect on lactic acid fermentation w.r.t these desirable characteristics.
Fig. 1.
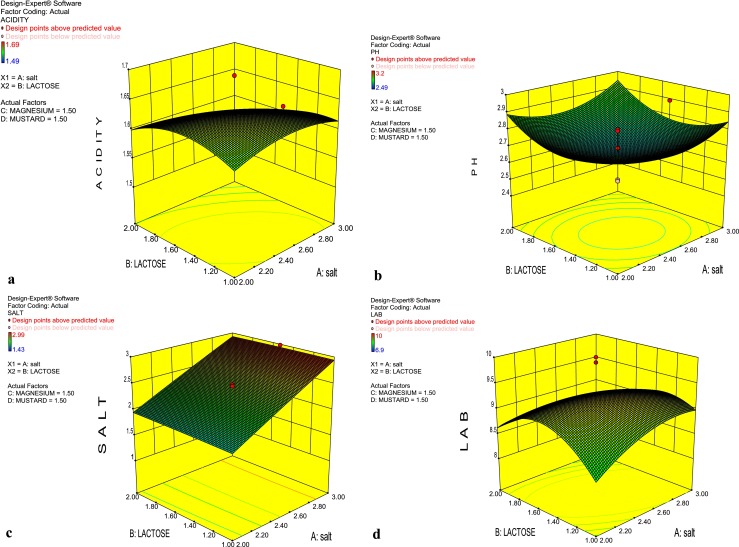
3D Response surface graph of radish fermentation depicting the interactions between Lactose and Salt at 1.5 % Mustard and Mg SO4 + MnSO4 on Acidity (a), pH (b) Salt (c) and LAB count (d)
The response surface graph (Fig. 1a) depicts the main effect and interaction of lactose and salt on titrable acidity while keeping the concentration of mustard and MgSO4 + MnSO4 constant at 1.5 %. It is clear from the shape of the graph that with the increase in the concentration of additives and growth stimulators, there was an increase in the titrable acidity. Maximum acidity was achieved at salt (2.5 %), lactose (2 %), mustard (1.5 %) and MgSO4 + MnSO4 (1.5 %). It is also clear from the graph that the titrable acidity decreased to 1.49 % when lactose and salt were at 1 and 2%, respectively. It is apparent that this concentration of lactose and salt was less and not optimum. This reduced acidity was obtained in our earlier work also (Joshi et al. 2008).
Fig. 1b depicts the interaction of various variables on pH in the form of 3D response graph. It can be easily inferred from the graph that pH was indirectly proportional to the concentration of variables used in the experiments. The lowest value of pH was desirable for the fermentation process. The lowest pH was observed when fermentation was carried out at salt content of 2.5 %, lactose 2 %, mustard 1.5 % and MgSO4 + MnSO4 1.5 %. Lowering of pH helps to prevent the growth of pathogenic and undesirable microorganisms thus, leads to biopreservation.
The interactions between lactose and salt at 1.5 % of mustard and MgSO4 + MnSO4 (1.5 %) on per cent salt estimation is depicted in the form of 3D Response surface graph (Fig. 1c). The flattened and straight slope of response plots indicated that the concentration of salt did not show any specific pattern. However, the equilibrium salt contents are relevant for the LAB to grow and show the activities. The main function of salt is to stimulate the LAB and it can neither be excreted nor synthesized, therefore, its concentration did not vary in the entire process.
Similar but little elliptical graph was observed in case of LAB count as compared to the response graph of titrable acidity which also indicated that the variables under study have significant effect on LAB count (Fig. 1d). Maximum bacterial count was observed when the fermentation was carried out by using salt (2.5 %), lactose (2 %), mustard (1.5 %) and MgSO4 + MnSO4 (1.5 %). However, close to this value of LAB count was observed at lactose, mustard, MgSO4 + MnSO4 (1–1.5 %) and salt (2–2.5 %). Further, it is evident from the magnitude of P and F values that there is maximum positive contribution of all the variables viz., salt, lactose, mustard and MgSO4 + MnSO4 on the various responses: titrable acidity, pH and LAB count during the lactic acid fermentation of radish (Tables 3, 4, 5, and 6).
Optimum concentrations of additives and growth stimulators
Optimum concentrations of salt, additives and growth stimulators for lactic acid fermentation of radish was determined to obtain the best results w.r.t the desirable characteristics i.e. increased titrable acidity, low pH and high LAB count for Lactic Acid Fermentation. Second order polynomial models obtained in this study were utilized for each response in order to determine the specified optimum concentrations of salt, additives and growth stimulators. The sequential quadratic programming using design expert 8.0.5.2 was used to solve the second-degree polynomial regression equation. The optimum values obtained by substituting the respective coded values of variables are: salt – 2.5 %, lactose- 1.5 %, MgSO4 + MnSO4 – 1.5 % and mustard 1.5 %. At this point, all the desirable characteristics were achieved to be the best in fermentation process as these optimized concentrations increased titrable acidity (1.69 % as compared to the lowest value of acidity obtained i.e. 1.48 %), lowered pH (2.49 as compared to the highest value of acidity obtained i.e.3.18) and increased LAB count (10 × 108 cfu/ml as compared to the lowest value of acidity obtained i.e.6.33 × 108).
Discussion
From the results (Table 2), it is revealed that addition of the various additives and growth stimulators alongwith salt, especially mustard has resulted in imparting the desirable characteristics (increased acidity, lowered pH and high LAB count) to the lactic acid fermentation. Mustard seeds are known to stimulate the growth of Lactic Acid Bacteria (LAB) and increases the bacterial count (Sethi and Anand 1984). Mustard seeds contain allyl isothiocynate, a volatile aromatic compound with antibacterial and antifungal properties which may be responsible for imparting the desired characteristics to the fermentation. Ground mustard seeds or oil have been used to increase lactic acid levels during fermentation of turnip in earlier study also (Anand and Das 1971). Addition of mustard (1–2 %) with different salt concentrations (2–12 %) increased the rate of lactic acid production in cauliflower slurry (Sethi and Anand 1984).
The highest per cent titrable acidity, lowest pH and highest LAB count was obtained with the Run 2 (Table 2) having salt- 2.5 %, lactose- 1.5 %, MgSO4 + MnSO4- 1.5 % and mustard- 1.5 % and alternation (increase or decrease) in the concentration of the variables resulted in remarkable changes in the responses. The salt content when optimum results in stimulating of different species of lactic acid bacteria in proper sequence as is known in sauerkraut fermentation (Frazier & Westhoff 1988). Salt in low concentration is used by microorganisms for their normal activity, while, higher concentration resulted in plasmolysis and ultimately death of the microorganism. But, plasmolysis also promotes the growth of lactic acid bacteria by releasing nutrients contained in the plant cells. The dominant bacteria at the outset of fermentation are resistant to high salt concentration. Due to progressive acidification of the medium, acid tolerant bacteria are present in the final stages of the process. A dominant floral sequence over the course of lactic acid fermentation has been identified i.e. successively Pediococcus, Leuconostoc and Lactobacillus (Heubert and Dupuy, 1994). Besides, lactose is the substrate used for lactic acid fermentation and thus, may have stimulated the lactic acid fermentation to obtain the desirable results (Aubert 1985). The addition of salts of magnesium and manganese sulphate (MgSO4 + MnSO4) might have stimulating effect on lactic acid bacteria by their proper growth and ultimately the lactic acid fermentation of radish (Ahmed and Mittal 1986). Hence, it can be inferred that their concentration at a moderate range is favourable for the lactic acid fermentation of radish. This may be due to the favourable conditions being generated inside the fermentation vessel by supporting the development of anaerobic conditions for the growth of LAB and hence, increasing the acidity and lowering the pH (Buckenhuskes et al. 1988). Also, this concentration of salt (2.5 %) has been successfully used in the lactic acid fermentation of radish for shelf - stability and pickling in our earlier study (Joshi & Somesh 2009). But it is optimum concentration of various factors that gain consistent and desirable results on lactic acid fermentation of radish.
To sum up, in this study RSM was used to determine the optimum operating conditions that yielded increased titrable acidity, low pH and high LAB count for Lactic Acid Fermentation of radish. Analysis of variance has shown that the effects of all the process variables including salt, lactose, MgSO4 + MnSO4 and mustard were statistically significant. Second order polynomial models were obtained for predicting per cent titrable acidity, salt, pH and LAB count. Among 30 runs conducted, run 2 has got the optimum concentration of salt – 2.5 %, lactose- 1.5 %, MgSO4 + MnSO4 – 1.5 % and mustard - 1.5 % for lactic acid fermentation of radish. The study has clearly resulted in the optimum parameters for conducting the lactic acid fermentation of radish by using RSM for biopreservation and product development.
Acknowledgments
The authors thank Horticulture Mini Mission for providing the financial support and Dr. Y S Parmar UHF Nauni, Solan (HP) for providing infrastructural facility.
References
- Ahmed B and Mittal BK (1986) Effect of magnesium and manganese on the growth of Lactobacillus acidophilus. In: ICFOCST, Held at Bombay, Abstract No. 3.18, CFTRI, Mysore, India.
- Anand JC, Das L. Effects of condiments on lactic fermentation in sweet turnip pickle. J Food Sci Technol. 1971;8(3):143. [Google Scholar]
- AOAC . Official methods of analysis. 13. Washington DC: Association of Official Analytical Chemists; 1980. [Google Scholar]
- Aubert C. Les aliments fermentes traditionnels: Une richesse meconnue. Paris: Collection Les Vrais Aliments d’ Aujourd’hui et de Demain. Terre Vivante; 1985. p. 263. [Google Scholar]
- Box GEP, Hunter WG, Hunter JS. Statistics for Experimenters. New York NY: John Wiley & Sons; 1978. [Google Scholar]
- Brar JS, Nandpuri KS, Kumar JC. Inheritance studies in radish (Raphanus sativus L.) J Geophys Res. 1972;6(2):901–911. [Google Scholar]
- Buckenhuskes H, Gessler A, Gietrschner K. Analytical characterization of canned and pasteurized sauerkraut. Ind Obst Gemuserverwert. 1988;73:434–463. [Google Scholar]
- Daeschal MA, Andersson RE, Fleming HP. Microbial ecology of fermenting plant materials. FEMS Microbiol Rev. 1987;46:357–367. doi: 10.1111/j.1574-6968.1987.tb02472.x. [DOI] [Google Scholar]
- Fleming HP, Mcfeeters RF, Thompson RL. Effects of sodium chloride concentration on firmness retention of cucumbers fermented and stored with calcium chloride. J Food Sci. 1987;52:653–657. doi: 10.1111/j.1365-2621.1987.tb06695.x. [DOI] [Google Scholar]
- Frazier WC, Westhoff DC. Food Microbiology. 4. New Delhi: Tata McGraw-Hill; 1988. [Google Scholar]
- Giovanni WA. Response surface methodology and product optimization. Food Technol. 1983;37:41–45. [Google Scholar]
- Harrigan WF, McCance EM, editors. Laboratory Methods in Microbiology. 2. London: Academic; 1966. [Google Scholar]
- Heubert JC, Dupuy P. Conservation des fruits et legumes. In: de Roissart H, Luquet FM, editors. Bacteries Lactiques: Aspects Fondamentaux et Technologiques. France: Lorica Uriage; 1994. p. 233. [Google Scholar]
- Hudson JM, Buescher RW. Pectic susbtances and firmness of cucumber pickles as influenced by CaCl2, NaCl and brine storage. J Food Biochem. 1985;9:211–215. doi: 10.1111/j.1745-4514.1985.tb00350.x. [DOI] [Google Scholar]
- Joshi VK, Somesh S. Lactic acid fermentation of radish for self stability and pickling. Natural Product Radiance. 2009;8(1):19–24. [Google Scholar]
- Joshi VK, Sharma S, Thakur NS. Effect of temperature, salt concentration and type of microorganism on lactic acid fermentation of carrot. Acta Aliment. 2008;37:205–219. doi: 10.1556/AAlim.37.2008.2.7. [DOI] [Google Scholar]
- Joshi VK, Somesh S, Neerja R. Preparation and evaluation of appetizers from lactic acid fermented vegetables. Journal of Hill Agriculture. 2011;2(1):20–27. [Google Scholar]
- Joshi VK, Somesh S. Preparation and evaluation of sauces from lactic acid fermented vegetables. J Food Sci Technol. 2010;47(2):214–218. doi: 10.1007/s13197-010-0037-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joshi VK, Thakur S. Lactic acid fermented beverages. In: Verma LR, Joshi VK, editors. Postharvest Technology of Fruits and Vegetables. New Delhi: Indus Publ. Co; 2000. p. 1102. [Google Scholar]
- Karovlcova J, Kohajdova Z. Lactic Acid-Fermented Vegetable Juices: Palatable and Wholesome Foods Chem Paper. 2005;59(2):143–148. [Google Scholar]
- Montet D, Loiseau G, Zakhia N, Mouquet C (1999) Fermented fruits and vegetables. In: Joshi VK, Pandey A (eds) Biotechnology: Food Fermentation, Edu. Publ. Distri, New Delhi, pp 951–969
- Ranganna S. Handbook of Analysis of Quality Control for Fruit and Vegetable Products. 2. New Delhi: Tata McGraw Hill Publ. Co.; 1986. [Google Scholar]
- Sethi V, Anand JC. Effect of mustard and its components on the fermentation of cauliflower. Indian Food Packer. 1984;38(4):41–46. [Google Scholar]
- Somesh S, Joshi VK. Influence of temperature and salt concentration on lactic acid fermentation of radish (Raphanus sativus) J Food Sci Technol. 2007;44(6):611–614. [Google Scholar]
- Tzeng D-I, Tai C-Y, Yi-Chen C, Yeu-Pyng L, Shau-Mei OA. Investigation of fermenting conditions for sugarcane (Saccharum officinarum l.) wine using response surface methodology. J Food Process Preserv. 2009;33:330–346. doi: 10.1111/j.1745-4549.2008.00254.x. [DOI] [Google Scholar]
- Wanasundara PKJPD, Shahidi F. Optimization of hexa metaphosphate-assisted extraction of flaxseed proteins using response surface methodology. J Food Sci. 1996;61(3):604–607. doi: 10.1111/j.1365-2621.1996.tb13168.x. [DOI] [Google Scholar]


