Personalisation of breast cancer follow-up: a time-dependent prognostic nomogram for the estimation of annual risk of locoregional recurrence in early breast cancer patients

Abstract

The objective of this study was to develop and validate a time-dependent logistic regression model for prediction of locoregional recurrence (LRR) of breast cancer and a web-based nomogram for clinical decision support. Women first diagnosed with early breast cancer between 2003 and 2006 in all Dutch hospitals were selected from the Netherlands Cancer Registry (n = 37,230). In the first 5 years following primary breast cancer treatment, 950 (2.6 %) patients developed a LRR as first event. Risk factors were determined using logistic regression and the risks were calculated per year, conditional on not being diagnosed with recurrence in the previous year. Discrimination and calibration were assessed. Bootstrapping was used for internal validation. Data on primary tumours diagnosed between 2007 and 2008 in 43 Dutch hospitals were used for external validation of the performance of the nomogram (n = 12,308). The final model included the variables grade, size, multifocality, and nodal involvement of the primary tumour, and whether patients were treated with radio-, chemo- or hormone therapy. The index cohort showed an area under the ROC curve of 0.84, 0.77, 0.70, 0.73 and 0.62, respectively, per subsequent year after primary treatment. Model predictions were well calibrated. Estimates in the validation cohort did not differ significantly from the index cohort. The results were incorporated in a web-based nomogram (http://www.utwente.nl/mira/influence). This validated nomogram can be used as an instrument to identify patients with a low or high risk of LRR who might benefit from a less or more intensive follow-up after breast cancer and to aid clinical decision making for personalised follow-up.

Background

A locoregional recurrence (LRR) has a high risk of distant metastasis, and thus confers a poor prognosis [1]. LRRs are defined as the reappearance of breast cancer on the same site as the primary tumour, in the chest wall or ipsilateral, infraclavicular, supraclavicular or parasternal lymph nodes after curative treatment [2]. Factors that influence the risk of recurrence include tumour size, age, vascular invasion, multifocality, histological grade, hormone receptor status and treatment of the primary tumour [3–13]. Regular follow-up is aimed at detecting LRRs in an early stage to improve survival [14]. In the Netherlands, patients are followed clinically for at least 5 years after their treatment. Still, most of the recurrences are detected by the women themselves in between follow-up visits and some are detected after the 5 years of clinical follow-up [15, 16]. In a Dutch multicentre study, Geurts et al. [14] found that only 34 % of the LRRs were detected asymptomatically during routine visits. Due to the increase in survival, the burden of follow-up on health care is rising. Even though the risk factors are known, follow-up is the same for all patients and not dependent on the personal risk of the individual breast cancer patient. Since 2012, the national guideline of the Netherlands recommends an individualised follow-up by shared decision making, but does not provide recommendations on how to effectuate it. To achieve this, good insight into time-dependent individual LRR risk is necessary.

Statistical models that are used for predicting the outcomes of patients are called prognostic models. Many prognostic models appear to be adequate at the population level. However, their use to predict risks on the level of the individual patient is questionable. Patients and clinicians need accurate risks on the individual patient level to reach more informed and uniform decision making. Challenges are incomplete knowledge on causality and the existence of various risk factors with only a small effect [17, 18]. For the prediction of breast cancer, the first model was developed by Gail et al. [19]. This model, as well as other well-known models (e.g. BRCAPRO, BOADICEA [20], [21]) is aimed at predicting the general risk of primary breast cancer. To get towards personalised follow-up, models predicting LRRs are required. In this paper, logistic regression is used to calculate the risks. Not only the single risk estimated for the overall follow-up period of 5 years, but also the annual time-dependent risk. To facilitate uptake in clinical practice, ease of use and accessibility are crucial. This can be achieved by using a nomogram: a graphical representation of the underlying model. Our aim is to develop and validate a time-dependent logistic regression model and nomogram suitable for the annual risk prediction of LRRs in individual breast cancer patients. Knowing this individual risk could facilitate the decision on a personalised follow-up plan.

Patients and methods

Study population

Patients were selected from the Netherlands Cancer Registry (NCR), a nationwide population-based registry, which records all newly diagnosed tumours since 1989. The information on patient, tumour and treatment characteristics, as well as data concerning recurrences within the first 5 years following primary breast cancer were recorded from the patient files by specially trained registration clerks.

Women diagnosed with primary invasive breast cancer between 2003 and 2006 without distant metastasis, previous, or synchronous tumours (diagnosed within 3 months after the first tumour [22]), treated with curative intent and without neo-adjuvant systemic treatment were selected from the registry (n = 37,230). Curative intent was defined as surgical removal of the primary tumour without macroscopic residual disease. Adjuvant treatment should have been received in case of microscopic residue. In the first 5 years following primary breast cancer treatment, 950 (2.6 %) of the selected patients developed a LRR as a first event. For external validation, data were used of a cohort of 12,308 patients from a selection of Dutch hospitals (43 out of 91) that developed their primary breast cancer between the years 2007 and 2008. Of these patients, 275 (2.2 %) were diagnosed with a LRR.

Although second primary breast cancers (any epithelial breast cancer with or without lymph node metastasis in the contralateral breast [2]) are also of interest with regard to follow-up care, they are not included in the model. Second primary tumours are a different entity from the primary tumour, and are hard to predict based on the available clinical variables [23–25]. Patients with a known genetic predisposition (estimates vary between 3 to around 7 % [26–28]) are not part of the regular follow-up. Unless they underwent a double mastectomy, they undergo a separate, more intensive follow-up.

Model development

Variables were selected based on literature and availability of the data. As the effect of age on LRR risk is nonlinear, it was discretized into four groups (<50, 50–59, 60–69, ≥70). The patient, tumour and treatment characteristics shown in Table 1 were assessed for their influence on recurrence risk using multivariable binary logistic regression analysis. By means of backward elimination, we deleted variables from the initial model until only variables with a P value of <0.157 (Akaike information criterion) were maintained in the model. A last check was performed by adding and removing the variables one by one. Firstly, a prediction model for the 5-year LRR risk was developed. Secondly, risks were determined per year conditional on not being diagnosed with recurrence in the previous year(s). Interaction was tested by adding interaction terms to the model. A correlation matrix was composed to assess possible correlation between the variables. Variables with a high correlation coefficient (>0.7 or <−0.7) were excluded. With a ratio of around 100:1, there were enough events for the included variables in the model. Based on simulation studies, it was determined that the ratio should be at least 10:1 [29].

Table 1.

Patient and tumour characteristics

	Index cohort		Validation cohort		P		Index cohort		Validation cohort		P
	(2003–2006)		(2007–2008)				(2003–2006)		(2007–2008)
	n	%	n	%			n	%	n	%
Total	37,278		12,318			PR status					0.004
Age category					<0.001	Negative	9580	33.7	3806	32.2
<50	9779	26.2	3006	24.4		Positive	18,877	66.3	8018	67.8
50–59	10,601	28.4	3353	27.2		Unknown	8821		494
60–69	8421	22.6	3101	25.2		Her2-Neu status					0.017
≥70	8477	22.7	2858	23.2		Negative	13,832	85.2	10,238	86.2
Histologic type					0.300	Positive	2405	14.8	1639	13.8
Ductal	29,582	79.4	9795	79.5		Unknown	21,041		441
Lobular	4000	10.7	1271	10.3		Number of surgeries					0.383
Mixed	1552	4.2	551	4.5		1	33,136	88.9	10,926	88.7
Other	2144	5.8	701	5.7		2	3909	10.5	1301	10.6
Grade					<0.001	≥3	233	0.6	91	0.7
I	7628	22.0	2907	24.5		Type of surgery					<0.001
II	15,595	44.9	5253	44.3		Breast conserving	21,049	56.5	7215	58.6
III	11,479	33.1	3700	31.2		Non-breast conserving	16,229	43.5	5103	41.4
Unknown	2576		458			Time from indicence to last OK					0.720
Tumour size					<0.001
≤2 cm	22,611	61.2	7796	63.7		<30 days	27,579	74.0	9098	73.9
2-5 cm	13,243	35.8	4152	33.9		30–60 days	8205	22.0	2742	22.3
>5 cm	1094	3.0	283	2.3		>60 days	1494	4.0	478	3.9
Unknown	330		87			Axillary lymph node dissection					<0.001
Multifocal					0.257
No	23,237	84.8	10,275	84.3		No	18,397	49.4	7315	59.4
Yes	4168	15.2	1907	15.7		Yes	18,881	50.6	5003	40.6
Unknown	9873		136			Chemotherapy					<0.001
Lymph node status					<0.001	No	23,886	64.1	7583	61.6
Negative	22,516	61.3	7809	64.0		Yes	13,392	35.9	4735	38.4
1–3 positive	10,093	27.5	3189	26.2		Radiotherapy					0.001
>3 positive	4119	11.2	1196	9.8		No	12,783	34.3	4026	32.7
Unknown	550		124			Yes	24,495	65.7	8292	67.3
ER status					0.001	Hormone therapy					<0.001
Negative	5417	18.8	2113	17.3		No	21,696	58.2	6563	53.3
Positive	23,433	81.2	10,066	82.7		Yes	15,582	41.8	5755	46.7
Unknown	8428		139

LRR locoregional recurrence, ER oestrogen receptor, PR progesterone receptor, Her2-Neu human epidermal growth factor receptor 2

The percentage of missing values of the included variables ranged between 0 and 24 % (PR status). ER and PR status were not registered by the NCR on a regular basis in 2003 and 2004. The variables of the prediction model with missing values were multiple imputed using a chained equation approach [30–32]. Calculations were performed with the MICE package of R. It was assumed that missing values occurred randomly, which validates the use of imputation. A comparison with the complete case analysis was made, as well as an assessment of the convergence. The analyses were repeated on the imputed data and pooled by using Rubin’s rules.

Validation

Prognostic validity or discrimination refers to the capability to discern between high and low-risk patients [33]. It was measured by the Harrell c-statistic from area under the receiver operating characteristic (ROC). A c-statistic of 1.0 indicates perfect predictive ability, whereas 0.5 represents no predictive discrimination. Calibration, whether the predicted probabilities accord with the observed ones, was evaluated by the Hosmer–Lemeshow goodness-of-fit test in deciles. A P value above 0.05 (indicating no significant difference between the model and the data) is generally considered as a satisfactory goodness-of-fit. Plotting the difference between the observed and predicted probabilities was used for graphical assessment of the calibration.

To see if the model can effectively differentiate between women who will develop a LRR and women who will not, the model was validated. For internal validation, bootstrapping (n = 1000) was used because it provides stable estimates [34]. If the shrinkage factor from the validation is over 0.85, it is considered satisfactory [35]. External validation was performed by regression analyses on the validation cohort. Areas under the ROC curves were compared using the jackknife method proposed by DeLong et al. [36]. A P value < 0.05 was considered statistically significant. Analyses were performed using STATA version 13 and R 3.1.1 software (http://www.r-project.org). The nomogram was developed using HTML and jQuery (JavaScript).

Results

After backward elimination, the model included the variables grade, size, multifocality and nodal involvement of the primary tumour, type of surgery, and whether patients were treated with radio-, chemo- or hormone therapy (Table 2). Assessment of the correlations revealed a high correlation between type of surgery and use of radiotherapy (correlation coefficient -0.8). Since radiotherapy showed a higher influence on the risk, type of surgery was omitted from the model. Due to high correlation between the oestrogen (ER) and progesterone (PR) receptor status, they were combined into one variable (ER/PR negative versus other). Inclusion of interaction terms did not improve the model. The patients in the index and validation cohort had small differences in the included variables age, grade, size, lymph node status, hormone status and treatments (all <3 % per category, Table 1). Healthy convergence was achieved with the multiple imputations.

Table 2.

Logistic regression estimates

		Five year risk						Conditional yearly risk
		2003–2006			2007–2008			2003–2006
		n = 37,230, 950 LRRs			n = 12,308, 275 LRRs			Year 1, 150 LRRs			Year 2, 268 LRRs
		OR	95 % CI	P	OR	95 % CI	P	OR	95 % CI	P	OR	95 % CI	P
Age
<50		Ref.			Ref.			Ref.			Ref.
50–59		0.62	0.49–0.78	<0.001	0.65	0.45–0.93	0.019	0.63	0.33–1.19	0.152	0.83	0.56–1.22	0.340
60–69		0.61	0.47–0.79	<0.001	0.60	0.41–0.89	0.011	0.54	0.26–1.13	0.103	0.64	0.40–1.03	0.065
≥70		0.41	0.31–0.55	<0.001	0.55	0.36–0.85	0.007	0.65	0.31–1.36	0.251	0.40	0.23–0.71	0.002
Tumour size
≤2 cm		Ref.			Ref.			Ref.			Ref.
2–5 cm		1.35	1.10–1.64	0.003	1.57	1.15–2.14	0.005	1.75	1.03–2.98	0.038	1.51	1.06–2.14	0.022
>5 cm		1.08	0.63–1.86	0.780	2.96	1.48–5.93	0.002	2.21	0.83–5.88	0.112	1.32	0.55–3.16	0.539
Nodal involvement
0		Ref.			Ref.			Ref.			Ref.
1–3		1.64	1.32–2.04	<0.001	1.60	1.14–2.24	0.007	2.36	1.32–4.21	0.004	1.53	1.05–2.24	0.028
>3		2.90	2.14–3.94	<0.001	3.10	1.95–4.94	<0.001	8.49	4.31–16.73	<0.001	2.94	1.77–4.90	<0.001
Grade of differentiation
1		Ref.			Ref.			Ref.			Ref.
2		1.92	1.45–2.54	<0.001	1.60	1.10–2.34	0.014	2.76	1.05–7.23	0.039	1.27	0.74–2.17	0.386
3		2.96	2.16–4.05	<0.001	2.38	1.51–3.72	<0.001	4.06	1.34–11.33	0.008	2.24	1.26–3.99	0.006
Hormone status
Other		Ref.			Ref.			Ref.			Ref.
ER & PR negative		1.41	1.08–1.84	0.011	1.44	0.96–2.16	0.076	1.82	0.953.49	0.069	2.57	1.58–4.17	<0.001
Multifocality
No		Ref.			Ref.			Ref.			Ref.
Yes		1.23	0.99–1.54	0.062	1.19	0.85–1.67	0.307	1.19	0.68–2.09	0.543	0.94	0.62–1.43	0.777
Radiotherapy
No		Ref.			Ref.			Ref.			Ref.
Yes		0.51	0.43-0.62	<0.001	0.50	0.38-0.66	<0.001	0.31	0.19-0.52	<0.001	0.36	0.26-0.50	<0.001
Chemotherapy
No		Ref.			Ref.			Ref.			Ref.
Yes		0.43	0.33–0.56	<0.001	0.34	0.23-0.52	<0.001	0.39	0.19–0.79	0.009	0.56	0.35–0.89	0.015
Hormone therapy
No		Ref.			Ref.			Ref.			Ref.
Yes		0.41	0.32-0.53	<0.001	0.35	0.24-0.51	<0.001	0.16	0.08-0.35	<0.001	0.57	0.35-0.92	0.020
Intercept
		0.04	0.03–0.05	<0.001	0.04	0.03–0.07	<0.001	0.00	0.00–0.01	<0.001	0.01	0.01–0.02	<0.001

		Conditional yearly risk
		2003–2006
		Year 3, 203 LRRs			Year 4, 164 LRRs			Year 5, 165 LRRs
		OR	95 % CI	P	OR	95 % CI	P	OR	95 % CI	P
Age
<50		Ref.			Ref.			Ref.
50–59		0.64	0.38–1.08	0.092	0.51	0.31–0.85	0.009	0.45	0.25–0.79	0.006
60–69		0.82	0.47–1.41	0.465	0.44	0.25-0.77	0.004	0.62	0.35–1.09	0.099
≥70		0.59	0.31–1.11	0.101	0.30	0.16–0.56	<0.001	0.31	0.15–0.63	0.001
Tumour size
≤2 cm		Ref.			Ref.			Ref.
2–5 cm		1.20	0.79–1.84	0.393	1.65	1.04–2.64	0.035	0.79	0.47–1.32	0.364
>5 cm		0.36	0.05–2.65	0.314	0.51	0.07–3.85	0.510	0.79	0.18–3.42	0.750
Nodal involvement
0		Ref.			Ref.			Ref.
1–3		2.48	1.58–3.90	<0.001	1.10	0.63–1.92	0.732	0.98	0.55–1.73	0.942
>3		1.92	0.88–4.20	0.102	1.90	0.87–4.14	0.105	1.83	0.82–4.07	0.137
Grade of differentiation
1		Ref.			Ref.			Ref.
2		1.55	0.88–2.71	0.127	3.28	1.71–6.30	<0.001	1.89	1.05–3.40	0.034
3		2.41	1.27–4.57	0.007	4.95	2.33–10.49	<0.001	2.22	1.10–4.51	0.026
Hormone status
Other		Ref.			Ref.			Ref.
ER & PR negative		1.16	0.65–2.07	0.625	0.78	0.41–1.47	0.443	0.63	0.28–1.41	0.261
Multifocality
No		Ref.			Ref.			Ref.
Yes		1.56	0.99–2.47	0.054	2.18	1.38–3.45	0.001	0.68	0.35–1.30	0.244
Radiotherapy
No		Ref.			Ref.			Ref.
Yes		0.58	0.39-0.86	0.008	0.85	0.55-1.30	0.454	0.75	0.47-1.19	0.220
Chemotherapy
No		Ref.			Ref.			Ref.
Yes		0.52	0.29–0.92	0.025	0.26	0.14–0.49	<0.001	0.45	0.23–0.87	0.018
Hormone therapy
No		Ref.			Ref.			Ref.
Yes		0.38	0.22-0.65	<0.001	0.32	0.18-0.57	<0.001	0.96	0.53-1.73	0.891
Intercept
		0.01	0.00–0.01	<0.001	0.01	0.00–0.01	<0.001	0.01	0.00-0.02	<0.001

OR odds ratio, CI confidence interval, LRR locoregional recurrence, ER oestrogen receptor, PR progesterone receptor

Validation

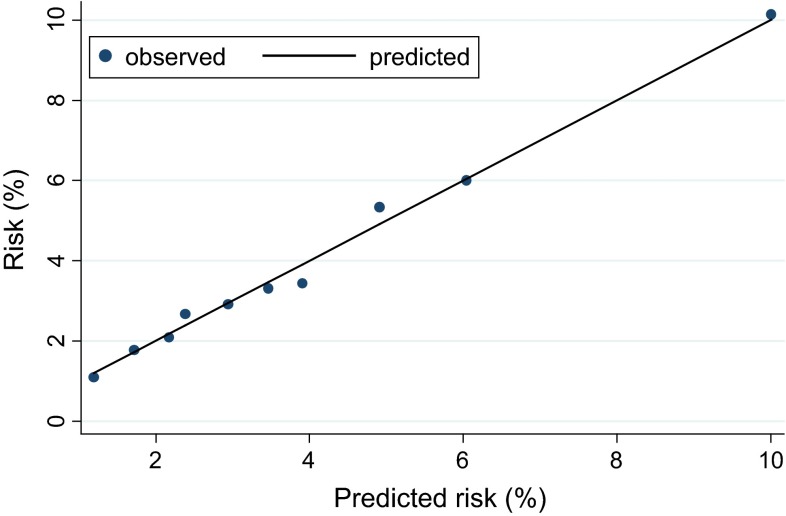
Table 3 details the discrimination and calibration properties of the prediction model. The probability measure of the predictive ability given as the c-statistic was 0.71 for the 5-year risk of LRR (95 % confidence interval [CI] 0.69–0.73); indicating good discriminating ability. Per subsequent year after primary treatment, the index group showed an area under the ROC curve of 0.84, 0.76, 0.70, 0.73 and 0.65, respectively. The predictions were well calibrated, as can be seen in the Hosmer–Lemeshow goodness-of-fit test (Fig. 1). For the deciles, the average expected to observed ratio was 1.05 and the P value 0.28, indicating a high agreement between the predictions and observations.

Table 3.

Model validation

	5 year risk		Yearly risk
	Index cohort 2003–2006	Validation cohort 2007–2008	2003–2006
			Year 1	Year 2	Year 3	Year 4	Year 5
Discrimination
C-statistic	0.71	0.70	0.84	0.77	0.70	0.73	0.62
Calibration
LR test (P value)	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	0.014
Goodness-of-fit testa (P value)	0.2817	0.0897	0.1455	0.1767	0.5504	0.5182	0.8685
Internal validation
Shrinkage factor	0.98	Na	0.95	0.96	0.88	0.88	0.65
Corrected C-statistica	0.70	Na	0.83	0.76	0.67	0.71	0.58

^aAfter bootstrapping

Fig. 1.

Calibration chart

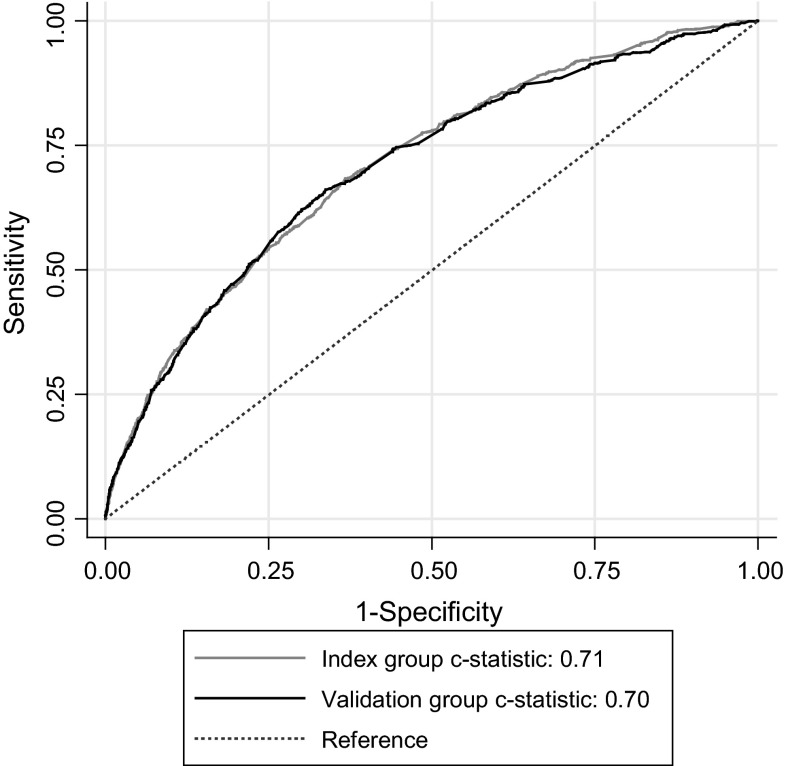
Internal validation in the index group with 1000 times bootstrapping revealed a shrinkage factor of 0.98 for the 5-year risk estimates (Table 3). In the external validation, all effects in the validation group were in the same direction, and the estimates in the validation group did not differ significantly from the index group. Tumour size, chemotherapy and hormone therapy had a slightly higher influence in the validation cohort (Table 2). The comparison between the ROC curves from the index and validation group can be found in Fig. 2.

Fig. 2.

ROC curves of the index (n = 37,230) and validation (n = 12,308) cohort for 5-year LRR risks

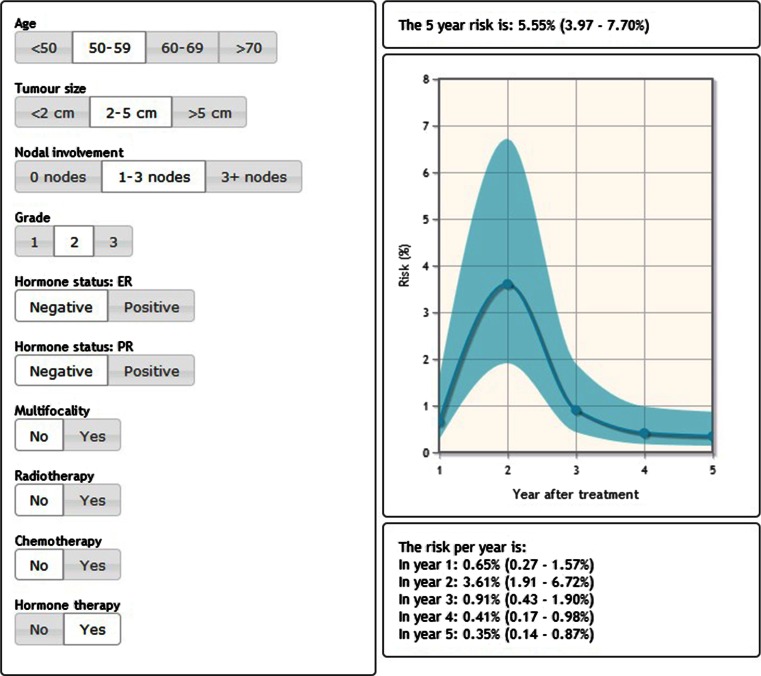
The models based on the imputed data were embedded in the nomogram which is available on http://www.utwente.nl/mira/influence. Figure 3 provides a screenshot of the nomogram which shows the time-dependent risk of a theoretical patient aged between 50 and 59, with a T₂M₀N₁, grade II, hormone status negative primary tumour, who did receive hormone therapy, but no radio- or chemotherapy.

Fig. 3.

Print screen from the nomogram, providing the time-dependent risk of a fictional patient

Discussion

This study describes the development and validation of the first-ever time-dependent logistic regression model for the prediction of the annual risk of LRR of breast cancer, developed based on data from 37,230 patients. The model takes into account the age of the patient, grade, size, multifocality, and nodal involvement of the primary tumour, and whether patients were treated with radio-, chemo- or hormone therapy. The risk factors used in our model are filtered from the population-based registry and are readily available in (Dutch) clinical practice and for use of the nomogram, without extra efforts or data gathering. Validation displayed only a small overestimation of the risk of developing a LRR (as could be expected with large sample sizes [37]).

In a systematic review on primary breast cancer risk prediction models, it was found that calibration of most models was sufficient [38]. However, discriminatory accuracy was considered poor to fair (c-statistic of 0.52–0.66) after internal validation. Reasons provided were lack of knowledge on risk factors, the different subtypes of breast cancer and discrepancies between risk factors across populations [38]. In this study, both calibration and discrimination (c-statistic of 0.71 after validation) were satisfactory. The individual risk estimates do show uncertainty, particularly in the later years. So risk estimates still need to be interpreted with caution. With nodal involvement being the highest risk factor (odds ratio (OR) 2.9 for >3 nodes compared to negative nodes for the 5 year risk, up to OR 8.5 for the risk in the first year), the effects of the included factors are modest. For instance, Thrift et al. [17] advocate that for prediction of individual risks, the relative risk of factors should exceed ten to be a good predictor of individual risk (even though this does not warrant discriminatory accuracy). Subsequently, individual predictions should be improved by decreasing the unexplained variation. Based on the conventional clinical risk factors, this is not to be expected. Hence more research is needed to discover new characteristics with discriminative ability [18].

This study had a number of strengths including data on many variables associated with risk of LRR and a large sample size. Also, the sample size of the validation cohort was appropriately large, as a minimum of 100 events and hundred non-events was proposed by Vergouwe et al. [39] for an external validation population. A correction for possible subsequent recurrences was unfortunately not feasible, while only first and synchronous recurrences are registered in the NCR. Although information on other known risk factors such as vascular invasion and breast density was unavailable and could not be taken into account, the nomogram can be updated to incorporate more variables when they become available in clinical practice and registries [40]. Of note, our analysis showed that Her2-Neu and primary tumour morphology were not independent predictors of LRR. These findings are in contrast to that of previous studies [10, 41]. This could be due to the fact that all Her2-Neu positive patients are treated with herceptin in the Netherlands. Our nomogram was based on data of almost all diagnosed early primary breast cancers between 2003 and 2006; thus, the results should be generalizable to the Dutch population. Another strength is the presentation of the conditional risk through time instead of only a 5-year risk estimate, which enables the clinician to give a better assessment of the risk over time for patients and adjust the follow-up plan accordingly.

The difference in treatment between the index and validation cohort can be attributed to changing guidelines over time. If the risk is of LRR is high, it could be considered to use adjuvant treatment. However, this is outside the scope of this study, the model is targeted at patients who have completed their treatment. The nomogram can be improved with automatic updating: the new patients will cause adjustments of the estimates, and new patients will weigh more than the less recent ones to better tailor the model to the current clinical practice.

User-friendly access through a nomogram is beneficial for both patients and clinicians. Still, it remains important that the users understand the correct interpretation. Therefore, it is of great importance to present the estimates with the corresponding CI [42]. Much used nomograms like for example Adjuvant! Online (adjuvant treatment decisions) [43], the nomograms from Memorial Sloan Kettering Cancer Center (o.a. likelihood that breast cancer has spread to sentinel lymph nodes) [44] or IBTR! (benefit of adjuvant radiotherapy) [45] do not display these intervals, which makes it hard to appreciate the certainty of the risk estimates.

Current guidelines for follow-up after breast cancer aimed at detecting LRRs at an early, asymptomatic stage prescribe equal follow-up for every patient. This research shows there is a great variability in the risk of LRR, underlining the need for an individualised follow-up. With simulation modelling, thresholds can be found for when to assign the visits, so that using the yearly risk predictions, individual follow-schedules can be developed. This will lower the burden on both patients and care providers, as well as health care resources.

Conclusion

This time-dependent logistic regression model for the prediction of the annual risk of LRR of breast cancer nomogram is simple to use and shows a good predictive ability in the Dutch population. It can be used as an instrument to identify patients with a high risk of LRR who might benefit from a less or more intensive follow-up after breast cancer and to aid clinical decision making.

Abbreviations

AUC

Area under the curve

BOADICEA

Breast and ovarian analysis of disease incidence and carrier estimation algorithm

BRCAPRO

Breast cancer probability

CI

Confidence interval

ER

Oestrogen receptor

Her2-Neu

Human epidermal growth factor receptor 2

LRR

Locoregional recurrence

MICE

Multiple imputation by chained equations

NCR

Netherlands cancer registry

OR

Odds ratio

PR

Progesterone receptor

ROC

Receiver operating characteristic

Compliance with Ethical Standards

Conflict of interest

The authors declare that they have no conflict of interest.