Localization of Transcranial Targets for Photoacoustic-Guided Endonasal Surgeries

Abstract

Neurosurgeries to remove pituitary tumors using the endonasal, transsphenoidal approach often incur the risk of patient death caused by injury to the carotid arteries hidden by surrounding sphenoid bone. To avoid this risk, we propose intraoperative photoacoustic vessel visualization with an optical fiber attached to the surgical tool and an external ultrasound transducer placed on the temple. Vessel detection accuracy is limited by acoustic propagation properties, which were investigated with k-Wave simulations. In a two-layer model of temporal bone (3200 m/s sound speed, 1-4 mm thickness) and surrounding tissues, the localization error was ≤2 mm in the tranducer's axial dimension, while temporal bone curvature further degraded target localization. Phantom experiments revealed that multiple image targets (e.g. sphenoid bone and vessels) can be visualized, particularly with coherence-based beamforming, to determine tool-to-vessel proximity despite expected localization errors. In addition, the potential flexibility of the fiber position relative to the transducer and vessel was elucidated.

1. Introduction

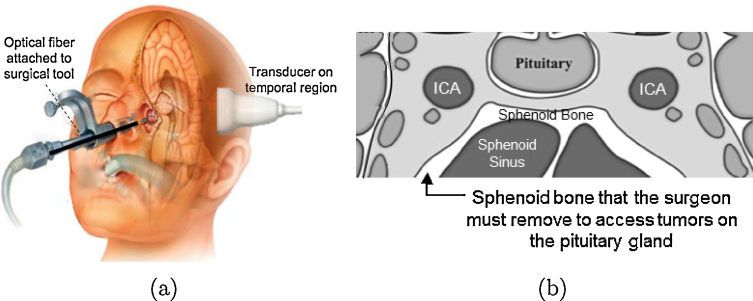
Pituitary tumors cause a variety of hormonal complications, compressing critical nerves and arteries at the base of the brain, and creating a potential for vision loss. Endonasal, transsphenoidal surgery is the most common method for removal of pituitary tumors to reverse endocrine problems and restore normal hormone balance [1]. In this minimally-invasive procedure, an endoscope is used to visualize the surgical field and tools such as a drill for sphenoidal bone removal and a curette for tumor resection are passed through the nostrils and nasal septum to access the sphenoid sinus and resect the tumor, as depicted in Figure 1(a). However, the endoscope is limited to visualizing superficial structures. One of the most significant surgical complications arises from accidental injury to the carotid arteries, located within 1-7 mm on either side of the pituitary gland and hidden by the sphenoid bone [2,3], as illustrated in Fig. 1(b). Accidental injury to these arteries creates a serious surgical setback, resulting in extreme blood loss, thrombosis, neurological deficits, stroke, or possibly death, with 14% morbidity and 24-40% mortality rates [4,5]. It may be treated with emergency interventions, albeit with a high risk of irreversible neurological damage [6].

Fig. 1.

(a) Photoacoustic system concept. (b) Coronal view of the anatomy surrounding the sphenoid bone (adapted from [22]). To visualize the internal carotid artery (ICA) intraoperatively with photoacoustic imaging, light must pass through the sphenoid bone.

This complication occurs most frequently with novice surgeons who have performed fewer than 200-500 of these surgeries and thus are not sufficiently familiar with potential variations in the anatomy surrounding the pituitary gland [7,8]. In addition, this procedure is particularly challenging in pediatric patients who are born with small nasal cavities that mainly develop into their full size after puberty [9,10]. Approximately 75% of hospitals in the United States treat 2-25 cases annually [11], thus, there are generally limited opportunities for novice surgeons to gain necessary caseload experience.

Although intraoperative x-ray or CT may be used to navigate the bony anatomy surrounding a pituitary tumor [12], it does a poor job of visualizing blood vessels and incurs the risks associated with radiation exposure. Intraoperative magnetic resonance (MR) imaging is another option, but it is costly, and generally suffers from low resolution and poor image quality due to the weak magnetic field [13]. MR aniography is a similarly expensive option with poor vessel resolution, and it is not suitable for patients with pacemakers or metal implants [14]. In MR and CT angiography, it is additionally burdensome to synchronize the injection of contrast agents with intraoperative imaging. In addition, none of these options support continuous, real-time, intraoperative vessel visualization.

While transcranial ultrasound provides real-time imaging, it requires low transmit frequencies for skull penetration, which translates to poor spatial resolution and necessitates expert sonographers to interpret images [15]. A real-time Doppler ultrasound probe was developed to assist surgeons with detecting carotid arteries [16], but failure was reported due to the incorrect interpretation of images and Doppler signals, resulting in misjudgment of the carotid artery location [3].

Real-time photoacoustic imaging [17–19] is a faster, safer, less expensive option (compared to CT and MR imaging), implemented by emitting nanosecond light pulses from a laser [20]. When the laser irradiates a target, such as bone or vessels, the target absorbs the light, according to its optical absorption spectrum. Optical absorption causes thermoelastic expansion and generates acoustic waves that are detectable with an ultrasound transducer. Signal detection with photoacoustic imaging is expected to be advantageous over conventional ultrasound imaging because there is less acoustic interaction with the skull. The acoustic waves are only required to pass through the skull once, rather than twice as in pulse-echo ultrasound and as a result, the waves are less susceptible to the sound scattering and aberrations that occur when they encounter the skull. In addition, higher frequency probes (compared to the standard low-frequency transcranial ultrasound probes) may be used to obtain better resolution [21].

We propose to adapt photoacoustic imaging for this task [21] by placing a transducer on the temple of the patient's skull, as shown in Fig. 1(a). The temporal region includes the pterion bone which is the thinnest portion of the human skull measuring 1-4.4 mm thick [23]. An optical fiber, coupled to a laser, would be attached to a surgical tool. During surgery, the tool and fiber will be inserted into the nasal passage where the optical fiber would illuminate the sphenoid bone which has a thickness of 0.4-8.8 mm [24,25]. Intraoperative photoacoustic images will be acquired to visualize blood vessels and sphenoidal bone.

The ability to visualize the distance between sphenoid bone (which could act as a surrogate for the tool tip position) and blood in the photoacoustic images would inform surgeons of their proximity to the carotid artery as the sphenoid bone is being removed. Alternatively, a metal tool tip could possibly be visualized in the photoacoustic image if the attached fiber additionally illuminates it and generates a photoacoustic response from the metal tip [26] that is acoustically coupled to the surrounding cranial environment. In addition, for more accurate navigation and tool-to-vessel orientation, photoacoustic images could be registered with the preoperative CT or MR images that are currently used to guide surgical procedures. Although transcranial photoacoustic imaging was previously demonstrated with neonatal and adult skulls [27–29], the proposed embodiment of this approach is novel.

Potential challenges include uncertainty surrounding target locations (due to acoustic heterogeneities within the skull) and varied image quality with fiber placement (given the flexible separation of light delivery from acoustic reception). Thus, the goals of this paper are to quantify the expected target shift as functions of temporal bone thickness and speed of sound, devise methods to compensate for this target shift, and characterize target visualization as a function of fiber placement. Challenges with acoustic propagation through the temporal bone are investigated with theoretical equations and k-Wave [30] simulations, because it is difficult to experimentally decouple bone thickness and sound speed. However, challenges with target visibility and optical propagation through the sphenoid bone are investigated with phantom experiments. Although these multiple challenges are investigated independently to understand their individual influences, we expect them to coexist during surgery.

2. Methods

2.1. k-Wave Simulations

A k-Wave simulation [30] was designed to explore the effect of temporal bone thickness and speed of sound on the location of targets in reconstructed photoacoustic images. The simulated phantom consisted of a temporal bone layer at the face of the probe and a horizontal, linear photoacoustic target, which could represent the sphenoid bone or a blood vessel. The temporal bone was modeled with a density of 1900 kg/m³ [31]. The target and surrounding medium were modeled with a sound speed of 1540 m/s and a density of 1000 kg/m³.

To investigate the expected variations due to speed of sound and thickness independently, the temporal bone thickness was varied from 1-12 mm (in 1 mm increments) with its sound speed fixed to 3200 m/s [32–34]. Similarly, the speed of sound in the temporal bone was varied from 2000 to 4000 m/s [33] (in 200 m/s increments) with thickness fixed to 7 mm. Note that negligible changes were observed when the density was varied (1000-2200 kg/m³) with sound speed and thickness fixed. A total of five arbitrary target depths were investigated: 6, 9, 12, 15, and 18 mm. These known target depths were compared to target depths measured in the simulated photoacoustic images.

Simulation results were compared to theoretical values using the following expression derived from a two-layer phantom model containing temporal bone located between a transducer and cranial tissue:

$$d_{\mathrm{measured}}=d_{\mathrm{actual}}+t_b\left(\frac{c_0-c_b}{c_b}\right),$$ (1)

where d_measured is the target depth measured in an image (i.e., perceived target depth), d_actual is the true target depth, t_b is the temporal bone thickness, and c_b and c₀ are the sound speeds in temporal bone and the surrounding medium, respectively. Note that the expression $t_b\left(\frac{c_0-c_b}{c_b}\right)$ modifies the actual target depth and can be considered as the expected localization error in the axial probe dimension given the proposed model.

To demonstrate the effects of bone curvature, the linear temporal bone was replaced with curved bone of uniform thickness (4 mm) and varied thickness (1 mm to 6 mm). The image target was 27.3 mm in length, located at a depth of 30 mm, which is within the range of expected target depths for infants [35]. In addition, the temporal bone was replaced with cranial bone segmented from a CT image. This model was used to image two parallel targets, 25 mm in length, located at depths of 70 mm and 80 mm from the transducer, which is within the range of expected target depths for adults [36]. The temporal bone was modeled with a density of 1900 kg/m³. The targets and surrounding medium were modeled with a sound speed and density of 1540 m/s and 1000 kg/m³, respectively.

2.2. Phantom Experiments

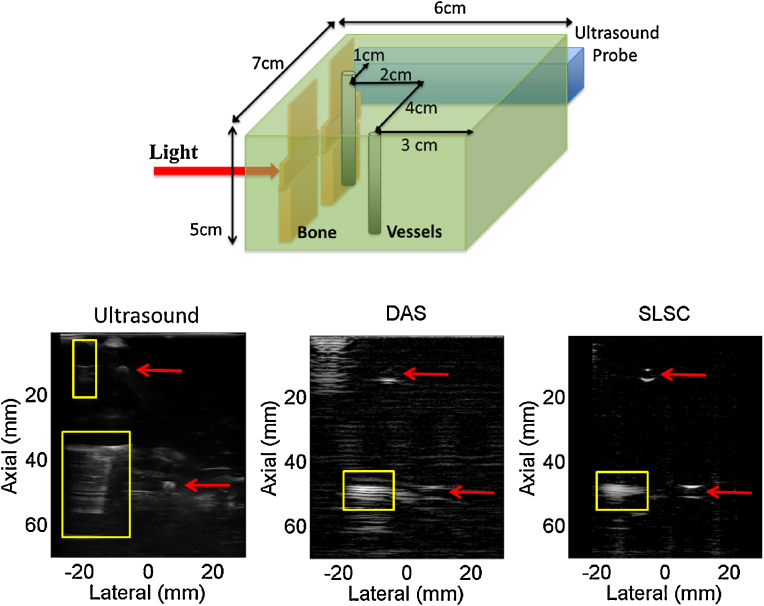
To evaluate visualization of targets with geometries that are relevant to the proposed clinical application, a bovine gelatin phantom was fabricated with two cylindrical targets that were 3.5 mm in diameter, slightly smaller than the reported 3.7-8.0 mm carotid artery diameter for patients age 12 or older [37]. These vessel-mimicking targets were placed 0 cm and 2 cm from 2-mm thick ex vivo bovine bone specimens during the phantom fabrication process, as shown in Fig. 2(a). Light was directed toward the bone and vessel located 5 cm from the probe with a 1 mm core diameter optical fiber (0.37 numerical aperture) coupled to a 1064 nm wavelength Nd:YAG laser. The pulse energy was 14 mJ at the tip of the fiber.

Fig. 2.

Photoacoustic experimental setup for (a) bone visualization and (b) fiber translation.

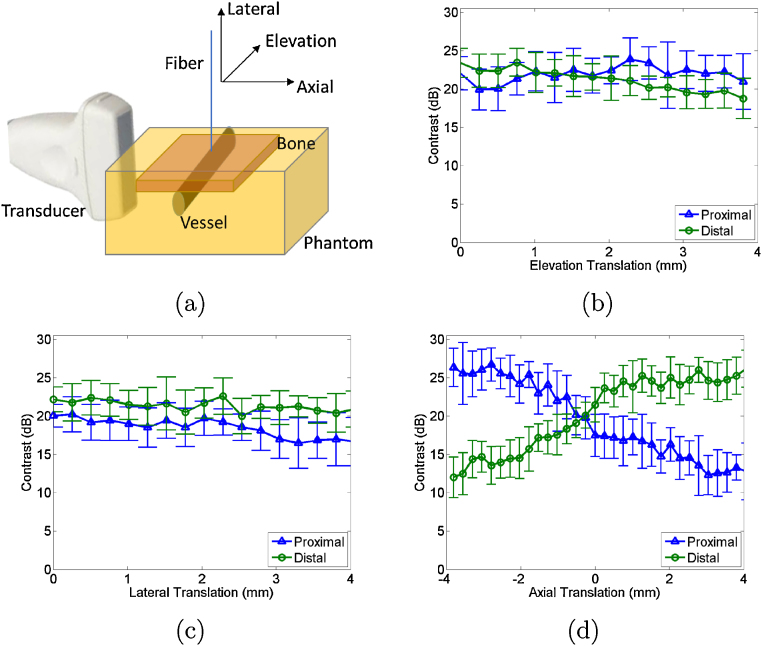
The surgical tool attached to the fiber could either be handheld and manipulated by the surgeon, which is the current standard, or jointly controlled by a robot and surgeon [38]. Hence, to explore the effects of subtle fiber motions in the presence of optical diffusion caused by the sphenoid bone, a second phantom was constructed with the vessel-like target, bone, probe, and fiber placed in the same relative orientations. The vessel target described previously and a 1 mm-thick bovine marrow bone cut to dimensions of 1.2 cm x 1.8 cm were placed during the phantom fabrication process resulting in fully embedded targets located approximately 1 cm from the exposed phantom surface parallel to the axial-elevation plane. A 1 mm core diameter optical fiber (0.37 numerical aperture) was coupled to a 1064 nm Nd:YAG laser and affixed to a manual translation stage. The pulse energy at the tip of the fiber was approximately 10 mJ with 20% optical transmission through the bovine marrow bone (measured prior to phantom construction, using our previously reported methods [39]). The absence of optical or acoustic scatterers enabled visual alignment of the fiber with the center of the bone and vessel, and the fiber was placed in this initial position, approximately 1 mm above the phantom surface. The fiber traversed in 0.3 mm increments from the initial position in the axial, lateral, and elevational probe dimensions, as illustrated in Fig. 2(b). The maximum distances traversed were within the dimensions of the sphenoid sinus [40–42]. Contrary to the fiber's flexibility, we envision that the probe will be fixed to a rigid arm (e.g., after identifying a suitable position with navigation system guidance [43] or transcranial Doppler ultrasound), hence we did not explore the effects of transducer motion.

In both experiments, an Ultrasonix L14-5W/60 linear transducer with a bandwidth of 5-14 MHz was placed with the diameter of the vessel perpendicular to the axial dimension of the probe. When temporal bone was previously placed between a phantom and the transducer, the resulting sound attenuation produced a black region distal to the temporal bone in the ultrasound image [21]. Therefore, temporal bone was not placed between the phantom and transducer for the experiments herein to enable target localization in ultrasound images, which were used as the ground truth for photoacoustic image interpretation. The transducer was connected to a SonixTouch ultrasound scanner, and a SonixDAQ data acquisition unit was triggered by the flashlamp output signal of the laser to access raw, pre-beamformed radiofrequency photoacoustic data. The software framework for this photoacoustic system is described in a previous publication [19].

2.3. Image Reconstruction and Analysis

Simulated images were reconstructed with the Fourier-based method provided by the k-Wave simulation package [30]. Experimental images were reconstructed off-line with delay-and-sum (DAS) and short-lag spatial coherence (SLSC) [44,45] beamformers consisting of 33-element overlapping subapertures. The SLSC image was formed with a short-lag value (M) equal to 5 (i.e., 15% of the receive aperture) and a correlation kernel size (n₂ − n₁) equal to 0.2 mm (i.e., equivalent to the smallest wavelength within the bandwidth of the linear array). The relationship between these parameters and the SLSC photoacoustic image is described in detail in previous publications [21,46,47], however, the following equations for the normalized spatial correlation of received signals ($\hat{R}$) and the short-lag spatial coherence (R_sl) summarize our approach:

$$\hat{R}(m)=\frac{1}{N-m}\sum _{i=1}^{N-m}\frac{{\sum }_{n=n_1}^{n_2}{s}_i(n)s_{i+m}(n)}{\sqrt{{\sum }_{n=n_1}^{n_2}{s}_i^2(n){\sum }_{n=n_1}^{n_2}{s}_{i+m}^2(n)}}$$ (2)

$$R_{\mathrm{sl}}=\sum _{m=1}^M\hat{R}(m)$$ (3)

where N is the total number of elements in the receive aperture, m is the distance (i.e. lag) between two elements of the receive aperture in units of number of elements, s_i(n) is the time-delayed, zero-mean signal received by the ith element, and n is the sample depth in units of samples.

Image contrast was measured as $20{\log }_{10}\left(\frac{S_i}{S_o}\right)$ where S_i and S_o are the means of the image data within regions of interest (ROIs) located inside and outside of the target, respectively.

3. Results

3.1. Target Depth Shifts

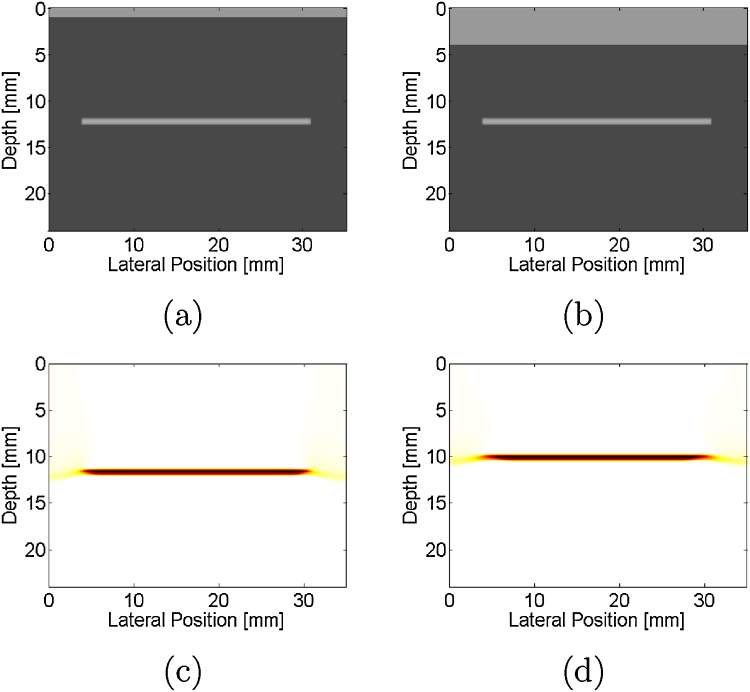
Fig. 3(a) shows a simulated phantom mimicking temporal bone located at the sensor surface and a target located at a depth of 12 mm. The corresponding simulated photoacoustic image shows the target at a depth less than the actual depth, as seen in Fig. 3(c). When the temporal bone thickness was increased to 4 mm, as shown in Fig. 3(b), the target depth in the corresponding simulated photoacoustic image (Fig. 3(d)) was further reduced.

Fig. 3.

Simulated phantom with (a) 1-mm and (b) 4-mm thick temporal bone located at the sensor surface (depth = 0 mm) and horizontal target located at a depth of 12 mm. Corresponding simulated photoacoustic images, demonstrating that as the temporal bone thickness increases from (c) 1 mm to (d) 4 mm, the target appears closer to the ultrasound sensor.

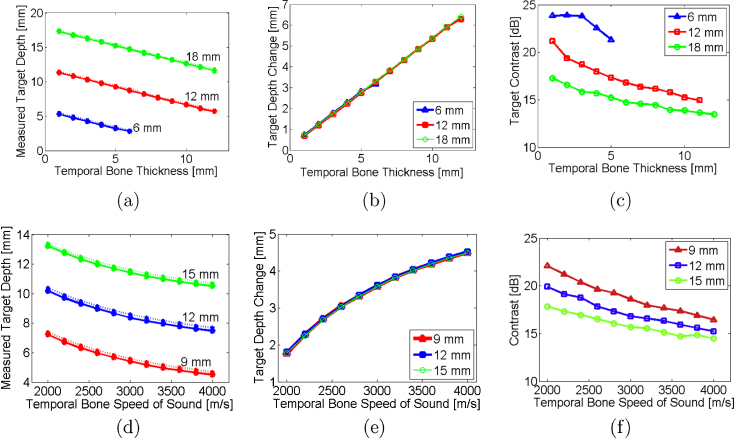
The target depth was measured as thickness was varied from 1-12 mm with the speed of sound constant (3200 m/s) for target depths of 12 mm and 18 mm, as shown in Fig. 4(a). For the 6 mm target depth, the temporal bone thickness did not exceed 6 mm to avoid overlap of the target and temporal bone. The differences between the actual target depth and measured depth (i.e., d_actual − d_measured) ranged from 0.7 mm to 6.4 mm for thicknesses of 1-12 mm, respectively, as demonstrated in Fig. 4(b). These depths were compared to the theory (dashed lines, calculated from Eq. 1) with excellent agreement, showing that the constant of proportionality is $\left(\frac{c_b-c_0}{c_b}\right)$. Thus, as demonstrated in Fig. 4(b), the depth shifts do not depend on the actual target depth, which could range from 21±4 mm in infants [35] to 77±5 mm in adults [36]. Contrast values ranged 13.4-23.8 dB and generally decreased with increasing temporal bone thickness, as shown in Fig. 4(c).

Fig. 4.

(a,d) Depth of target and (b,e) change in target depth quantified as functions of temporal bone thickness and speed of sound, respectively. Each line represents the actual target depth. Theory (dashed lines, calculated from Eq. 1), agrees with simulation results. Target contrast as functions of temporal bone (c) thickness and (f) speed of sound. Legend indicates actual target depths.

As the speed of sound was increased from 2000 m/s to 4000 m/s with the thickness fixed at 7 mm, the target appeared closer to the ultrasound sensor, as quantified in Fig. 4(d). Similar to Fig. 4(b), the actual depth of the targets (e.g. 9, 12, and 15 mm) did not alter the magnitude of the depth shift, as seen in Fig. 4(e). The differences between the actual and measured depths ranged from 1.8-4.5 mm. Depth shifts were compared to the theory (dashed lines, calculated from Eq. 1) with excellent agreement. The contrast of these targets ranged 14.5-22.1, as demonstrated in Fig. 4(f) and generally decreased with increasing sound speed, likely caused by the increase in acoustic heterogeneities.

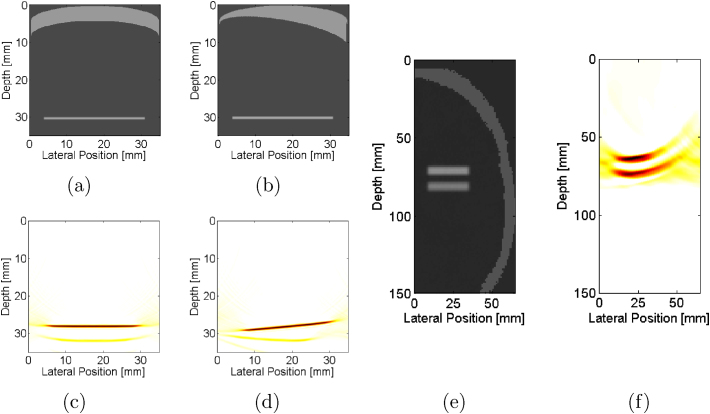
Temporal bone is not always linear and could instead contain curvature with a constant thickness, as illustrated in Fig. 5(a), or varied thickness, as illustrated in Fig. 5(b). In both cases, the presence of the curvature adds additional clutter artifacts in the corresponding simulated photoacoustic images of Fig. 5(c) and (d), respectively. Note also that the curved bone of varied thickness alters the target depth, which could be overcome by visualizing multiple photoacoustic targets in an image. This solution is illustrated in Fig 5(e), which replaces the temporal bone with geometry segmented from a CT image. The corresponding simulated photoacoustic image (Fig. 5(f)) of two parallel targets at a fixed depth from the sensor demonstrates that the distance between the targets is maintained regardless of the acoustic heterogeneities caused by the temporal bone. To successfully implement this approach, the multiple targets would ideally have similar lateral positions relative to the probe, to ensure that the measured photoacoustic signal passes through a section of temporal bone with similar thickness and speed of sound.

Fig. 5.

Simulated phantom of curved bone of (a) constant 4-mm thickness and (b) varying thickness with horizontal target located at 30 mm depth. The acoustic sensor is located at 0 mm depth. Corresponding simulated photoacoustic images, demonstrating that as bone thickness changes from (c) constant to (d) varied, the target location changes, which would complicate vessel localization. (d) Simulated phantom containing skull from a segmented CT image with two parallel targets and (e) corresponding photoacoustic image, indicating that the challenge with the depth shifts could be overcome if more than one target is present in the image.

3.2. Sphenoid Bone Visualization

Fig. 6 shows a schematic diagram of our experimental setup with light directed toward the bone and vessel located 5 cm from the probe. The bone appears at this depth in DAS and SLSC photoacoustic images (yellow boxes), however, the boundaries of the vessels (red arrows) are poorly visualized in the DAS image, because the laser fluence incident on these targets is lower due to decreased optical transmission [39]. For the vessel located 1 cm from the probe, note that only the proximal boundary is visible in the ultrasound image while the distal boundary is primarily visible in the DAS photoacoustic image. The corresponding SLSC image does a better job of visualizing the three separate targets with similar contrast given the similar spatial coherence of photoacoustic signals from these three targets. Results are promising for detecting bone and vessels in the same image with coherence-based beamforming. Similar targets could be visualized during surgery to determine tool-to-vessel proximity despite the target depth shifts observed in Figs. 3-5.

Fig. 6.

Schematic of experimental setup (top), ultrasound image (bottom left) and corresponding DAS and SLSC photoacoustic images (bottom middle and right, respectively). Boxes and arrows indicate signals from bone and vessels, respectively. Photoacoustic DAS and SLSC images (each shown with 30 dB dynamic range) indicate that bone and vessel can be visualized to determine tool-to-vessel proximity despite expected localization errors.

3.3. Fiber Position

As demonstrated in Fig. 6, for typical sizes of the carotid arteries (3.7-8.0 mm [37]), only the proximal and distal boundaries are expected to be visible, due to factors such as the constructive interference from subresolution optical absorbers on the target boundary [48], the limited angle view with the linear array, and the limited bandwidth of the transducer. Therefore, two contrast measurements (one from each boundary) may be obtained from each image of a blood vessel.

The contrast of the signals from each boundary was measured as the fiber was translated in three dimensions, relative to the standard orthogonal probe axes shown in Fig. 7(a). The mean contrast difference between the two boundaries is altered by up to 4 dB along the length of the vessel, as shown in Fig. 7(b). This minimal change indicates that the fiber does not need to be in the same plane as the photoacoustic image to visualize the vessel and obtain contrast measurements. Fig. 7(c) shows similarly minimal change in mean contrast measurements (<6 dB) as the fiber moves within 4 mm from the phantom surface, indicating that the fiber position in this probe dimension minimally affects target localization. Note that translation in this direction increases the surface area of light incident on the target, particularly for larger vessels, given the conical light profile exiting the fiber. For smaller vessels, translation in this direction would cause a decrease in fluence to the target as the fiber moves away from the phantom, as previously demonstrated for cylindrical targets with a 0.8 mm diameter (i.e., brachytherapy seeds) [46].

Fig. 7.

(a) Schematic diagram of phantom and experimental setup. Mean contrast as a function of fiber translation in the (b) elevation, (c) lateral, and (d) axial probe dimensions. Error bars represent ± one standard deviation of twenty measurements. Schematic diagram illustrates fiber translation directions.

The greatest change in contrast is observed with axial translation as shown in Fig. 7(d), although light is diffused after passing through the bone. This result is insightful because it demonstrates that the light diffusion caused by bone is not sufficient to generate equal signal amplitudes for both vessel boundaries when the fiber is slightly offset from the vessel center (an observation similarly supported by the DAS photoacoustic image in Fig. 6). In Fig. 7(d), the mean contrast difference between the proximal and distal vessel boundaries varies by up to 14 dB with fiber translation along the vessel diameter, in the probe's axial dimension. This change appears to be somewhat symmetrical about the initial translation position (0 mm), likely due to the symmetry of the vessel, with larger differences occurring in either direction from this initial position.

In all cases (Fig. 7(b)-(d)), the mean contrast of the proximal and distal vessel boundaries at 0 mm is approximately 21-24 dB, indicating that the manual translation stage sufficiently returned the fiber to its initial position (i.e. within 3 dB contrast error), and the vessel boundaries had <3 dB mean contrast difference at this fiber position.

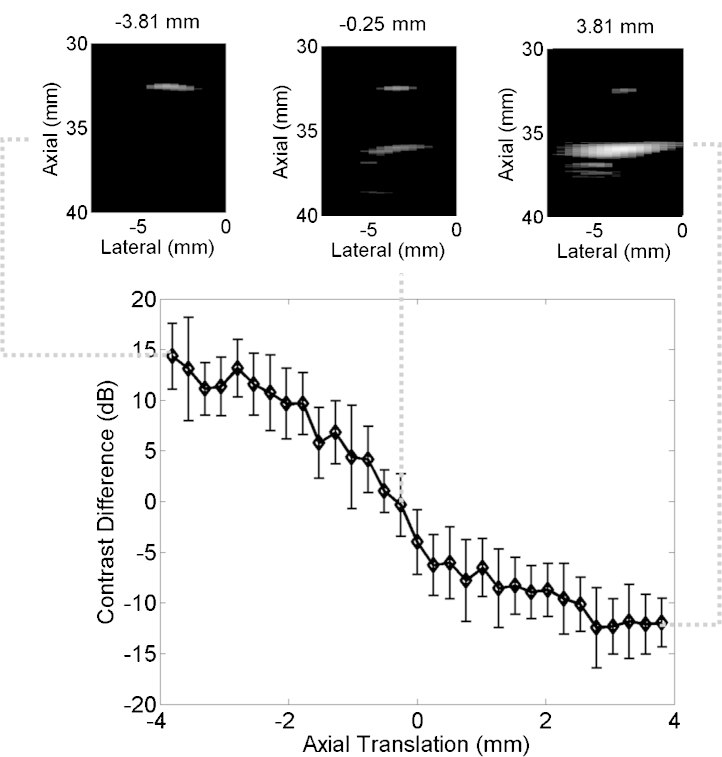
Fig. 8 shows the difference between mean contrast measurements from the proximal and distal vessel boundaries as a function of the axial fiber translation. This difference was closest to 0 dB when the fiber was translated -0.25 mm from the manually determined vessel center, positive for translations toward the probe, and negative for translations away from the probe. Representative photoacoustic images created with the DAS beamformer are shown above the plot. All images are taken from the same axial and lateral positions (defined relative to the probe) with the axial fiber position indicated above each image (defined relative to the manually determined vessel center). Note that positioning the fiber in this direction does not significantly alter the location of the vessel boundaries in each image. Thus, contrast variations are the primary effect of fiber motion in this direction.

Fig. 8.

Mean contrast difference between the proximal and distal vessel boundaries as a function of fiber translation in the axial probe dimension. Error bars represent ± one standard deviation of twenty measurements. The example photoacoustic images show vessel boundaries visualized at fiber positions -3.81, -0.25, and 3.81 mm, from left to right, respectively. All images are shown with 20 dB dynamic range.

4. Discussion

Although both sound speed and thickness can vary within the same bone sample, by decoupling these influences with simulations, we determined that for a fixed speed of sound, the perceived target depth decreased linearly with increased thickness. Conversely, for a fixed bone thickness, the perceived target depth decreased nonlinearly with speed of sound. These results can be used for acoustic sensor placement planning in transcranial photoacoustic imaging (e.g., the choice of left or right temporal region could be based on the amount of regional thicknesses variation, potentially determined from preoperative CT images).

The predicted localization error can be accounted for by adding a bias toward the probe equal to $t_b\left(\frac{c_0-c_b}{c_b}\right)$ when displaying interventional images for the neurosurgeons, or by visualizing multiple structures (e.g., blood and bone or two blood vessels). The first approach assumes that it is sufficient to model the cranial environment as two layers, each with largely differing sound speeds, as represented in the simulations throughout this paper and verified with an experiment described in our previous publication [21]. In this previous experiment, a 4-mm thick human adult cadaveric temporal bone specimen was placed between the phantom and tranducer, resulting in a target that appeared 1 mm closer to the transducer (compared to the target location with no bone present). This shift agrees with theory (Eq. 1) for an assumed sound speed of 2053 m/s, which is within the range of reported values for human skull (2010-3360 m/s [33]).

In a clinical setting, the predicted localization error and associated bias would rely on published (or if possible intraoperative) estimates of sound speed as well as skull thickness estimates from preoperative images. Given the probe orientation shown in Fig. 1(a) and the most recurring values reported in the literature (e.g. ≤3200 m/s and 1-4 mm temporal bone sound speed and thickness, respectively [23,33]), the localization error is expected to be ≤2 mm in the axial dimension of the probe, according to Fig. 4(b). Note that over the lateral width of the probe, bone thickness and speed of sound are not expected to vary by the large ranges shown in Figs. 4 and 5, particularly not with transcranial probes which generally have a small (e.g. 2 x 2 cm²) footprint. Thus, the predicted error could potentially apply to all lateral locations in an image. In addition, this error is expected to be less than or similar to any potential registration errors [49].

Because the optics are separated from the probe, one additional factor affecting target localization is the position of the fiber relative to the target and the probe, which could potentially be controlled with a dedicated navigation system [43]. We observed similar vessel contrast when the fiber was translated along a vessel within 4 mm from the center of the image plane as shown in Fig. 7(b). Thus, perfect fiber alignment with the image plane (i.e. the elevation probe dimension) is not required. In addition, the vessel is not required to be perpendicular to the fiber. Fig. 7(c) indicates that it may tilt away from the fiber (which is expected given the complex anatomy of the internal carotid arteries) without significantly affecting vessel contrast. The largest contrast difference between the proximal and distal boundaries occurs as the fiber is translated across the vessel diameter, as shown in Fig. 7(d). Based on these results, observed differences in vessel boundary visualization during surgery (e.g. Fig. 8) would likely indicate that the fiber is offset from the vessel center. Additional considerations include the vessel size relative to the fiber diameter and illumination surface area.

While drilling the sphenoid bone, an optical field of view (FOV) of ± 4 mm from the fiber axis (Fig. 7(d)) is beneficial for increasing awareness of surrounding vessels. As bone is removed, we expect a decrease in vessel illumination area because less light will be scattered with thinner bone and the fiber will be closer to the vessel, resulting in a reduced size of the incident light profile. Thus, the optical FOV relative to the fiber axis is expected to decrease as the drill and attached fiber approach the vessel. With this decrease in FOV, the surgeon should strive for minimal to no vessel visualization to ensure that the tool-to-vessel separation distance is large enough to avoid carotid artery injury, as vessel visualization could indicate that the tool is too close. This indicator would be effective regardless of sphenoid bone or tool tip visualization, registration errors, or target localization bias.

Our experimental results additionally demonstrate the ability to image both bone and another target in a photoacoustic image (Fig. 6), which agrees with demonstrations by other researchers [27,29,50,51], particularly demonstrations with a 50 μm target comprised of canine blood located approximately 2 cm from the bone surface [27]. Although skull bone has a similar optical absorption spectrum to that of the cranial tissues surrounding a blood vessel [52,31,53], the optical transmission through bone (and hence incident fluence on the underlying vessel) is expected to decrease by 56-80% for bone thicknesses of 1-4 mm [39]. Therefore, after light penetrates bone, the larger optical absorption of the blood vessel is expected to dominate the resulting photoacoustic signals, relative to any negligible photoacoustic response from surrounding tissues.

Fig. 6 builds on our previous success with SLSC beamforming for transcranial photoacoustic images [21] and indicates that this beamformer is beneficial for global target localization, regardless of incident fluence or variations in properties such as optical absorption or the Grüneisen parameter. This result is similar to findings achieved in vivo with prostate brachytherapy seeds serving as the photoacoustic target [54,55], indicating that multiple targets may be visualized with similar contrast with the SLSC beamformer regardless of variations in the incident laser fluence. An amplitude-based beamformer would potentially be preferred when bone thickness is decreasing due to drilling, as the resulting change in contrast may be used to determine the amount of bone that remains [39].

The presented studies do not consider the effects of acoustic aberrations due to the skull, which was previously investigated by Jin et al. [56], nor the effects of shear wave propagation, which was previously modeled by Mitsuhashi et al. [57]. In addition, optical delivery methods within laser safety limits could be achieved by reducing the pulse energy or increasing the surface area of light incident on the bone (e.g., by adding a diffuser to the fiber tip [46,55], increasing the numerical aperture of the fiber [54], surrounding the tool with multiple fibers, and/or maximizing the distance between the fiber and tool tips), however specific details are outside of the scope of this paper. Our primary purpose was to investigate target localization for a novel clinical application with relative light, sound, vessel, and bone orientations unlike previously reported transcranial phototoacoustic imaging examples.

5. Conclusion

To the authors’ knowledge, this work is the first to investigate target localization challenges when using photoacoustic imaging to guide surgical procedures within the skull. The perceived target depth decreased with increased bone thickness or sound speed. To address this challenge, an area of uncertainty may be added to visualized targets. A second option is to visualize multiple targets in the image to achieve accurate localization by relying on the known (e.g. CT-derived) distances between the multiple targets. After the removal of a large majority of bone and a subsequent decrease in the optical FOV, visualization of the carotid artery could potentially indicate that a tool is too close to this blood vessel. To overcome challenges with target visibility due to poor light penetration, the SLSC beamformer may be utilized to display multiple photoacoustic targets with similar contrast and provide a global map of the surgical environment. In addition, we demonstrated large flexibility of the fiber position relative to the probe and vessel to achieve suitable target contrast with amplitude-based beamformers. With these observations and suggestions to overcome expected challenges, the proposed photoacoustic imaging approach has convincing merit for guiding neurosurgical procedures to potentially eliminate the deadly risk of carotid artery injury during surgery.

Conflict of Interest

The authors declare that there are no conflicts of interest.

Biographies

Muyinatu A. Lediju Bell is a postdoctoral fellow at Johns Hopkins University. She completed her PhD in Biomedical Engineering (BME) at Duke University in 2012 and earned her BS degree in Mechanical Engineering (BME minor) from the Massachusetts Institute of Technology in 2006. Her research interests include image quality improvements in ultrasound and photoacoustic imaging, acoustic wave propagation theories, acoustic beamforming, medical device design, and clinical translation of novel medical imaging technologies that improve the standard of cancer patient care.

Anastasia K. Ostrowski is an undergraduate student majoring in Biomedical Engineering at the University of Michigan with a focus on electrical engineering and a minor in entrepreneurship. She completed two summers of the NSF Research Experience for Undergraduates Program at Johns Hopkins University, where she conducted photoacoustic research under the direct mentorship of Dr. Muyinatu A. Lediju Bell.

Ke Li is a second year master's student majoring in Biomedical Engineering at Johns Hopkins University. She obtained her bachelor's degree in Information Engineering (Opto-electronics) from Zhejiang University, China. Ke is interested in optical imaging, image processing and analysis, and machine learning.

Peter Kazanzides received his PhD degree in electrical engineering from Brown University and started working on surgical robotics in 1989 as a postdoctoral researcher at the IBM T.J. Watson Research Center. He cofounded Integrated Surgical Systems in 1990 to commercialize the ROBODOC System for orthopaedic surgery and served as the director of robotics and software. He joined Johns Hopkins University in 2002 and is currently an associate research professor of computer science.

Emad M. Boctor is an assistant professor in the Departments of Radiology, Computer Science, and Electrical Engineering at Johns Hopkins University. His interests encompass medical imaging, ultrasound instrumentation, elasticity/thermal/photoacoustic imaging, image-guided intervention, and robotics.