Characterization of the Dynamics in the Protonic Conductor CsH₂PO₄ by ¹⁷O Solid-State NMR Spectroscopy and First-Principles Calculations: Correlating Phosphate and Protonic Motion

Abstract

¹⁷O NMR spectroscopy combined with first-principles calculations was employed to understand the local structure and dynamics of the phosphate ions and protons in the paraelectric phase of the proton conductor CsH₂PO₄. For the room-temperature structure, the results confirm that one proton (H1) is localized in an asymmetric H-bond (between O1 donor and O2 acceptor oxygen atoms), whereas the H2 proton undergoes rapid exchange between two sites in a hydrogen bond with a symmetric double potential well at a rate ≥10⁷ Hz. Variable-temperature ¹⁷O NMR spectra recorded from 22 to 214 °C were interpreted by considering different models for the rotation of the phosphate anions. At least two distinct rate constants for rotations about four pseudo C₃ axes of the phosphate ion were required in order to achieve good agreement with the experimental data. An activation energy of 0.21 ± 0.06 eV was observed for rotation about the P–O1 axis, with a higher activation energy of 0.50 ± 0.07 eV being obtained for rotation about the P–O2, P–O3^d, and P–O3^a axes, with the superscripts denoting, respectively, dynamic donor and acceptor oxygen atoms of the H-bond. The higher activation energy of the second process is most likely associated with the cost of breaking an O1–H1 bond. The activation energy of this process is slightly lower than that obtained from the ¹H exchange process (0.70 ± 0.07 eV) (Kim, G.; Blanc, F.; Hu, Y.-Y.; Grey, C. P. J. Phys. Chem. C 2013, 117, 6504−6515) associated with the translational motion of the protons. The relationship between proton jumps and phosphate rotation was analyzed in detail by considering uncorrelated motion, motion of individual PO₄ ions and the four connected/H-bonded protons, and concerted motions of adjacent phosphate units, mediated by proton hops. We conclude that, while phosphate rotations aid proton motion, not all phosphate rotations result in proton jumps.

1. Introduction

Solid inorganic acids are a promising class of proton-conducting solid electrolytes for use in fuel cells that operate in an intermediate-temperature range (200–600 °C).¹⁻⁴ In particular, CsH₂PO₄, has been intensively studied because of its desirable operating temperature (230–260 °C⁵) and high protonic conductivity (σ = 2.2 × 10^–2 S cm^–1 at 240 °C⁶) in the so-called superprotonic conducting phase.⁷ One of the key questions remaining for CsH₂PO₄ is the mechanism of proton conduction in the superprotonic phase, proton conductivity arising from structural and dynamic disorder of hydrogen bonds and phosphate anions.⁶ Understanding this is key to engineering novel, improved electrolytic materials for these applications. In this context, mixed compositions of CsH₂PO₄ with other oxyanions,^8,9 other cations,¹⁰ inorganic/organic scaffolds,¹¹⁻¹³ and other known proton conductors¹⁴ have been extensively investigated in the search to improve desired physical properties, such as higher protonic conductivities, better mechanical properties, and improved thermal stability at high temperatures. The proton conduction mechanisms become more complicated in these systems due to the presence of multiple components, and a deeper understanding of the conduction mechanism in the parent phase CsH₂PO₄ should help more generally to enable further development of this important class of materials.

The proton dynamics of CsH₂PO₄ has been investigated by using various spectroscopic studies and techniques such as AC impedance spectroscopy,^6,11 quasielastic neutron scattering,¹⁷ and ¹H and ²H NMR spectroscopy.¹⁷⁻²⁰ However, the local anion (phosphate) dynamics has yet to be fully characterized experimentally, and a clear relationship between this short-range anionic motion and the long-range protonic motion has not been achieved. In a recent Car–Parrinello ab initio molecular dynamics study of the superprotonic phase,²¹ it was suggested that proton hopping is faster than the phosphate ion rotation, but this has not been proven experimentally. By contrast, computational studies of a similar system, CsHSO₄,²²⁻²⁴ predicted that anionic motion was faster than proton hopping.

There are three known polymorphs of CsH₂PO₄. At low temperatures, CsH₂PO₄ exists in a monoclinic structure in space group P2₁ (the ferroelectric phase), transforming into a monoclinic, paraelectric phase with space group P2₁/m above the Curie temperature (−120 °C). At the superprotonic phase transition (230 ± 2 °C),^3,6,25 CsH₂PO₄ transforms into a cubic phase (space group Pm3̅m).^6,7,15,19 This work focuses on the dynamics in the room-temperature paraelectric phase. Accordingly, we start by reviewing the prior structural data for this phase. The crystal structure of the room-temperature paraelectric phase of CsH₂PO₄ has three distinct oxygen sites, where sites O1 and O2 form a conventional O1–H1···O2 hydrogen bond and O3 atoms are linked via hydrogen bonds formed by the H2 protons. Although some studies have found it convenient to treat this hydrogen bond as having a single minimum with the H2 proton located precisely equidistant from the two O3 atoms¹⁵ (Figure 1a), the majority of the evidence indicates that the H2 proton is located in two, equally populated off-center sites (Figure 1b, and Table S1 for more structural details).^16,26,27 In this model the phosphate group exists in two symmetry-related arrangements, with the two equally populated arrangements differing in terms of which O3 oxygen atom acts as the hydrogen bond donor and acceptor. On a local level, this means that any particular phosphate anion in the structure will have two P–O–H hydrogen bond donor groups (O1–H1 and O3^d-H2), and two P–O hydrogen bond acceptor groups (O2···H1 and O3^a···H2), as shown in Figure 1c. Consistent with this, by using ¹⁷O NQR measurements, Seliger et al.²⁸ also proposed that the H2 protons lie in a double minimum potential and are dynamically disordered over the two off-center sites in the symmetric double well. From an NMR perspective, the disorder of the H2 protons is an important consideration, as the two O3 oxygen atoms within a particular phosphate group will exhibit different ¹⁷O NMR parameters depending on the whether they are acting as donors or acceptors. Previous ¹H NMR studies are in qualitative agreement with this model, with the H2 and H1 protons resonating at approximately 14.3 and 10.9 ppm,^5,20 consistent with strong and (relatively) weaker H-bonding, respectively.

Figure 1.

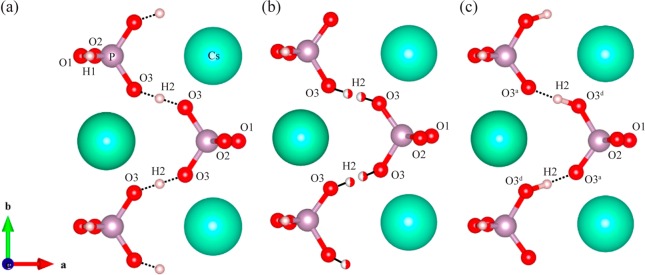
Crystal structures of CsH₂PO₄: (a) an initial structure with a centered O3···H2···O3 hydrogen bond (O3···O3 distance, 2.47 Ź⁵), (b) possible hydrogen-bonding arrangements for the disordered structure proposed in which only one of the two shown H2 ions in the O3···O3 H bond are occupied simultaneously (resulting in O3–H2 distances of 1.00 Å, as determined by neutron diffraction¹⁶), and (c) one possible local hydrogen-bonding arrangement based on the structure shown in part b. Cesium, hydrogen, phosphorus and oxygen atoms are shown in green, pink, purple and red, respectively. The O3^d and O3^a labels in c are used to denote O3 atoms involved in hydrogen bond donor and acceptor, respectively. Half-filled H2 atoms in part b denote a site occupancy of 50%. O1–H1···O2 H-bonds (O1, O2 distance and O1–H distances of 2.53 and 0.90 Å, respectively¹⁵) connect the neighboring tetrahedral PO₄ groups along the c axis.

³¹P NMR spectroscopy can potentially provide insight into the local dynamics of the phosphate ion in these materials.¹⁸⁻²⁰ Previous variable-temperature static ³¹P NMR results on both single crystal¹⁹ and powdered¹⁸ samples of CsH₂PO₄ showed that motion of the phosphate anion in the paraelectric phase could be detected by NMR spectroscopy. However, concerns as to whether the neglect of ¹H–³¹P dipolar interaction (∼3 kHz) affected the extracted motional frequencies¹⁹ and the limited temperature range of the other study (up to 50 °C)¹⁸ motivated our subsequent studies.²⁰ It was, however, difficult to quantify the extent of the reorientation of the phosphate ion in this work since the ³¹P chemical shift anisotropy (CSA), which is a dominant contribution to the static line shape, is not very sensitive to the phosphate motion in this system.²⁰ Similarly, ²H static NMR studies do not provide any direct insight into the nature and time scale of the phosphate ion rotations.²⁰ Thus, alternative NMR probes and/or experiments are required.

The use of ¹⁷O NMR spectroscopy to study local structure²⁹⁻³³ and dynamics in oxide materials^34,35 is well established due to the simple fact that oxygen is ubiquitous in the frameworks of inorganic materials. To date, there are only a few examples of the use of ¹⁷O NMR spectroscopy to probe the dynamics of polyanions (i.e., phosphate, phosphite, sulfate, or arsenate) in solid inorganic acids due to the cost and difficulty of the ¹⁷O isotopic enrichment procedure in these systems, generally required due to the low natural abundance of the ¹⁷O isotope (0.037%), with some notable exceptions including the study of Cs₂WO₄ and KMnO₄,³⁶ Na₃PO₄,³⁷ and crystalline sulfonic acids.³⁸

In this article, we observe and characterize the anion dynamics in ¹⁷O-enriched CsH₂PO₄ by using a combined experimental and computational ¹⁷O NMR approach. We develop a detailed model to describe the reorientation of the phosphate ion and the protonic motion in the paraelectric phase. We correlate the polyanion local rotational motion with the measured protonic motion from our prior study²⁰ to provide insight into proton conduction mechanisms in CsH₂PO₄.

2. Experimental Methods

2.1. Sample Preparation and Characterization

Isotopic ¹⁷O enrichment of CsH₂PO₄ was performed by using a methanol induced precipitation method as described previously⁶ with the starting materials, 20% ¹⁷O-enriched phosphoric acid (Sigma-Aldrich, 80 wt % in 20% ¹⁷O-enriched H₂O) and cesium carbonate (Alpha-Aesar, 99.9%). The synthetic route is identical to that employed for the nonenriched materials except for the use of 20% ¹⁷O-enriched phosphoric acid. The as-prepared ¹⁷O-enriched CsH₂PO₄ was packed and stored in a rotor for the NMR experiments in a dry argon atmosphere to prevent any moisture contamination and exchange with nonenriched oxygen ions (in water). While the enrichment level was not measured post synthesis, it is likely not much lower than the 20% level of the reagents employed due to the rapid precipitation method, which limited exposure to ambient air. The phases present in both pristine and ¹⁷O-enriched CsH₂PO₄ samples were identified by Powder X-ray diffraction (PXRD) measurements obtained on a Panalytical Empyrean X-ray diffractometer using Cu Kα radiation (Figure S1) and by ¹H NMR (δ_iso = 10.9 and 14.3 ppm for H1 and H2 at room temperature, respectively^5,20). The PXRD patterns are consistent with the reported monoclinic phase (space group P2₁/m).¹⁵

2.2. ¹⁷O NMR

All the ¹⁷O magic angle spinning (MAS) NMR spectra were obtained on a 16.4 T Bruker Avance III 700 NMR spectrometer equipped with 1.3 mm HX, 3.2 mm HXY, and 4 mm X MAS probeheads. Variable-temperature Hahn-echo experiments were carried out with a recycle delay of 3–5 s with MAS frequencies of 12.5 and 20 kHz and an rf field strength of 50 kHz. ¹H and ¹⁷O chemical shifts were externally referenced to water at 4.8 and 0 ppm, respectively. The sample temperature was calibrated using the ²⁰⁷Pb resonance of Pb(NO₃)₂ in a separate MAS experiment^39,40 and the sample temperatures quoted have been corrected according to this calibration with a variation of ±5 °C. This variation becomes slightly larger at higher temperatures but even at the highest temperature, 220 °C, it was ±7 °C. To reduce the temperature gradient across the sample, a thick-bottomed 4 mm NMR rotor was used for our NMR measurements.

The oxygen exchange was investigated by using the EXPRESS 3.0 program⁴¹ to simulate the effect of the phosphate rotation on the ¹⁷O NMR line shapes. A ¹⁷O spin–echo experiment at 16.4 T was simulated with the following set of parameters: a spectral width of 50 kHz, 512 points in the free induction decay, a 90° pulse of 1.6 μs, and a MAS frequency of 12.5 kHz. Powder averaging was achieved using the ZCW6765 scheme. For all oxygen sites, δ_iso, C_Q, η_Q, and the Euler angles describing the relative orientations of the electric field gradient (EFG) tensors for the oxygen sites were used as input parameters, the data coming from the results of the first-principles NMR calculations (see section 2.3). The ¹⁷O CSA was neglected in all simulations since it is removed by MAS (see further details in SI). Furthermore, no significant difference was seen when comparing simulated ¹⁷O line shapes with/without the CSA. Simulations were performed to explore the effect of rapid H2 proton exchange between the two sites of the symmetric double potential well hydrogen bond; two different exchange models for oxygen hopping were also used (see further details in the Results section). The simulated ¹⁷O line shapes were generated as a function of exchange frequency, for the various models, and compared with the experimental spectra.

2.3. First-Principles Calculations

First-principles calculations of NMR parameters were carried out using the CASTEP version 6 DFT code,⁴² employing the GIPAW algorithm,⁴³ which allows the reconstruction of the all-electron wave function in the presence of a magnetic field. The generalized gradient approximation (GGA) PBE functional⁴⁴ was employed, and core–valence interactions were described by ultrasoft pseudopotentials.^45,46 NMR parameters were calculated using a planewave energy cutoff of 60 Ry (816 eV) and integrals over the Brillouin zone were performed using a k-point spacing of 0.04 Å^–1. The calculations generate the absolute shielding tensor (σ) in the crystal frame. Diagonalization of the symmetric part of σ yields the three principal components, σ_XX, σ_YY and σ_ZZ. The isotropic shielding, σ_iso, is given by (1/3)Tr{σ}. The isotropic chemical shift, δ_iso, is given by −(σ_iso – σ_ref), where σ_ref is a reference shielding. For ¹⁷O and ¹H, respective reference shieldings of 268 and 30.5 ppm were used. These values are in good agreement with shielding references used in studies of similar oxides.^33,35,55 The quadrupolar coupling constant, C_Q = eQV_ZZ/h and asymmetry parameter, η_Q = (V_XX – V_YY)/V_ZZ are obtained directly from the principal components of the electric field gradient (EFG) tensor, which are ordered such that |V_ZZ| ≥ |V_YY| ≥ |V_XX|, where Q is the nuclear quadrupole moment (for which an experimentally determined value of −25.6 × 10^–31 m² was used⁴⁷). For calculations assuming the centered, single-minimum hydrogen bond model, initial atomic positions were taken from an experimental X-ray diffraction structure.¹⁵ For calculations assuming the disordered two H-site model, two model structures were generated by taking the centered hydrogen bond structure and manually displacing the H2 protons so that they were 0.90 Å from one of the adjacent O3 oxygen atoms (see Figure 1). This O–H separation was based upon the O1–H1 covalent bond length in the X-ray structure.¹⁵ Prior to calculation of the NMR parameters, all structures were fully geometry-optimized, with the unit cell parameters allowed to vary using a cutoff energy of 50 Ry (680 eV) and k-point spacing of 0.04 Å^–1. Of note, an O3–H2 separation of 1.05 Å is obtained from our geometry-optimized structure and this value is in reasonable agreement with a value of 1.00 Å reported from the previous neutron diffraction study.¹⁶ Thermal expansion effects were neglected as the largest change in lattice parameter in CsH₂PO₄ over the temperature range of interest is approximately 3%,⁴⁸ a value that is within the DFT geometry-optimization error: different DFT functionals lead to small expansions/contractions of the unit cell during the geometry optimization, which typically have negligible effect on the calculated NMR parameters.

3. Results

3.1. Room-Temperature ¹⁷O NMR Spectra of CsH₂PO₄: Hydrogen Bond Configuration

The ¹⁷O MAS NMR spectrum of CsH₂PO₄ recorded at 16.4 T (Figure 2a) exhibits a broad signal made up of a number of partially resolved second-order quadrupolar-broadened resonances (see Figure S3 for a comparison between spectra acquired at 16.4 and 20.0 T). The broadest feature centered at 40 ppm is consistent with an oxygen species in a highly asymmetric local bonding environment and can tentatively be assigned to the O1 site, which is covalently bonded to the adjacent P and H1 atoms. The more intense set of resonances centered around 90 ppm are ascribed to overlapping resonances corresponding to the O2 and O3 oxygen atoms.

Figure 2.

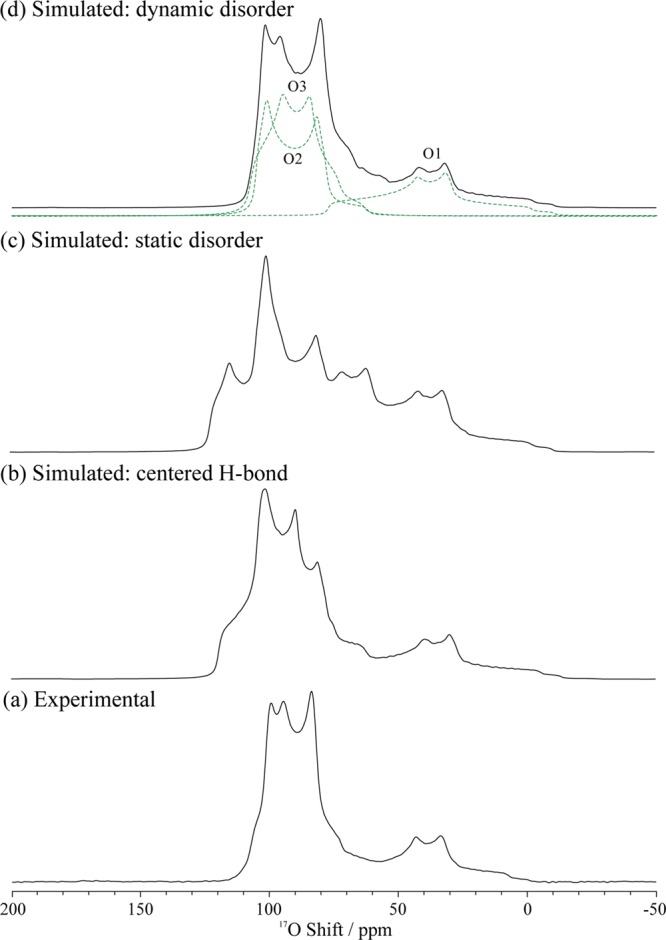
¹⁷O MAS NMR spectra of CsH₂PO₄ (a) obtained at 16.4 T with a MAS rate of 20 kHz, and calculated line shapes at 16.4 T, corresponding to different models for the symmetric O3–H2···O3 hydrogen bond, assuming: (b) a centered H2 hydrogen bond (i.e., with H2 equidistant between the two O3 atoms (Figure 1a), (c) the static disorder model (Figure 1b and c), and (d) the dynamic disorder model with a hopping frequency of ≥10⁷ Hz. These simulations were performed with the NMR parameters extracted from the first-principles calculations (Table 1).

The calculated NMR parameters, listed in Table 1, provide a means of interpreting the spectrum. For the centered hydrogen bond structure (Figure 1a) the large calculated C_Q of −6.97 MHz, the η_Q value of 0.79, and the chemical shift (76.5 ppm) for O1 are all consistent with the broad feature observed experimentally at a lower frequency. For O2 and O3, slightly smaller C_Q values of −5.38 and −5.78 MHz are also consistent with the breadth of the narrower set of resonances at higher frequencies in the experimental spectrum. However, a simulated ¹⁷O MAS NMR spectrum based on the calculated parameters, shown in Figure 2b, does not show good overall agreement with the experimental spectrum. While the O1 resonance is well reproduced by the simulation, poor agreement is observed for the O2/O3 region of the spectrum. This highlights the sensitivity of ¹⁷O NMR to local structural effects and shows that the single-minimum centered hydrogen bond model is not sufficient to fully describe the local environment of the phosphate anion.

Table 1. Calculated ¹⁷O and ¹H NMR Parameters for CsH₂PO₄^a.

	site	δisocalc/ppm	CQcalc/ MHz	ηQcalc
centered hydrogen bond	O1	76.5	–6.97	0.79
O3···H2···O3	O2	109.8	–5.38	0.14
(Figure 1a)	O3	121.3	–5.78	0.53
	H1	11.3
	H2	18.3
off-center hydrogen bond	O1	78.1	–6.94	0.76
O3d–H2···O3a	O2	110.0	–5.36	0.15
(Figure 1c)	O3d	103.1	–6.61	0.77
	O3a	125.7	–5.07	0.30
	H1	11.7
	H2	13.8

^aThe centered and off-center hydrogen bonds refer to static H-bonding configurations (a) and (c) shown in Figure 1.

We therefore consider the proposed models for disorder of the H2 protons across the off-center sites within the O3···H2···O3 hydrogen bonds. To model static disorder of the H2 protons within the hydrogen bond, NMR parameters were calculated for a geometry-optimized unit cell whereby the H2 protons were shifted off-center within the hydrogen bond (Figure 1c). A simulated ¹⁷O MAS NMR spectrum based on the calculated NMR parameters is shown in Figure 2c. Strictly speaking, this representative model removes the inversion and mirror symmetries of the P2₁/m space group known to describe the overall structure of paraelectric CsH₂PO₄. However, because the positions of the other atoms are largely unchanged, the model provides a reasonable means of capturing the loss of local but not global symmetry. It is immediately apparent that this model also gives very poor agreement with the experimental spectrum, as it displays a much more complicated line shape with even more discontinuities in the O2/O3 region of the spectrum. This is a consequence of the lowering of the symmetry, which results in two different local environments for the O3 oxygen atoms (i.e., a hydrogen bond donor (O3^d) and acceptor (O3^a)). The large calculated C_Q and high η_Q values of O3^d are similar to those of O1, which has a similar P–O–H local environment, while the smaller C_Q and lower η_Q values of O3^a are similar to O2, which is also a hydrogen bond acceptor.

We now consider a case whereby protons are dynamically disordered across the H2 sites; that is, they can “hop” or at low temperatures tunnel between the two positions in the double minimum potential. The ¹⁷O MAS NMR spectrum shown in Figure 2d was simulated by assuming rapid dynamic averaging between the corresponding O3 hydrogen bond donor and acceptor pairs, with a rate constant of 10⁷ Hz. The simulation takes into account the changes in both the magnitudes and orientations of the ¹⁷O EFG tensors for each phosphate oxygen as the proton hops from side to side within the O3···H2_1/2 H2_1/2···O3 hydrogen bond (see Supporting Information for further details). A dynamically averaged line shape is now obtained for each of the O1, O2 and O3 oxygen atoms. Since it is not appropriate to describe a dynamically averaged second-order quadrupole broadened line shape with an exchange-averaged tensor⁴⁹ (for example, even isotropic motion that is sufficiently fast to average the second-order quadrupolar effects, but not the first order quadrupolar interaction, will not remove the quadrupolar induced shift⁵⁰), no corresponding NMR parameters for this simulation are given in Table 1. Instead, the simulated spectrum should be directly compared with experiment, the spectrum obtained with this model showing very good overall agreement with experiment, the discontinuities associated with the unresolved O2 and O3 resonances being well reproduced. Of note, the line widths of the resonances appear to be slightly overestimated as compared to the experimental spectrum; indeed, a tendency for the overestimation of ¹⁷O C_Q values has been reported in other studies of inorganic oxide solids.^33,51 The exact rate of dynamic exchange process is difficult to determine from the data presented here, as simulations assuming faster exchange give similar results (i.e., the motion is already in the “fast” motional regime). However, simulations performed with slower exchange rates deviated from the experimental spectrum (see Figure S5). This allows us to place a lower limit of 10⁷ Hz on the dynamic exchange process of the H2 protons at room temperature.

The validity of the dynamic disorder model is further supported by the 2D ¹⁷O MQMAS⁵²⁻⁵⁴ and 2D ¹H–¹⁷O heteronuclear correlation (HETCOR) NMR spectra of CsH₂PO₄ (see Figures S6 and S7), which both clearly show 3 oxygen sites as opposed to 4 sites in the static disorder model. The calculated ¹H chemical shifts are in agreement with the model of a structure with dynamically disordered hydrogen bonds, Table 1. For the single-minimum, centered hydrogen bond model, calculated chemical shifts of 11.3 and 18.3 ppm are both noticeably overestimated as compared to the experimental values of 10.9 and 14.3 ppm.^5,20 The discrepancy is particularly large with respect to the H2 atom, as might be expected for a model that incorrectly captures the behavior of this species. Although a tendency for the overestimation of chemical shifts has been observed in other GIPAW studies,^55,56 the overestimation of the H2 chemical shift by 4.7 ppm is larger than is typically observed, and the calculated difference in chemical shift between the H1 and H2 protons cannot be reconciled with the experimental difference even through the choice of a different reference shielding. In contrast, calculated ¹H chemical shifts of 11.7 and 13.8 ppm for H1 and H2, respectively, are obtained using the dynamic disorder model. Unlike the ¹⁷O case, considering the effect of dynamic averaging of the two off-center H-bonding configurations (see Table S3) does not make a significant difference to the ¹H chemical shifts. These values are in much better agreement with the experimental shifts.

In their totality, the room-temperature ¹⁷O NMR spectra support the generally accepted model of CsH₂PO₄ in which the H2 atom is distributed over two off-center sites in the otherwise symmetric O3···O3 hydrogen bond. The analysis extends our understanding by revealing that the disorder must be dynamic rather than static. That is, the experimental room-temperature ¹⁷O and ¹H NMR²⁰ spectra for CsH₂PO₄ provide conclusive evidence for the dynamic exchange of the H2 protons between the two off-center sites in the O3···H2_1/2 H2_1/2···O3 hydrogen bond on a time scale that is fast with respect to the NMR experiment >10⁷ Hz. Perhaps even more significantly, the analysis demonstrates that NMR methods can be used to directly determine local hydrogen bond features even when multiple oxygen and proton sites are present in the structure.

3.2. Anion Dynamics in the Paraelectric Phase

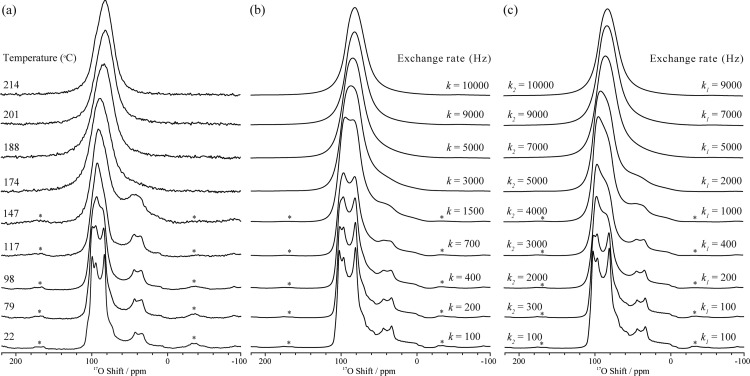
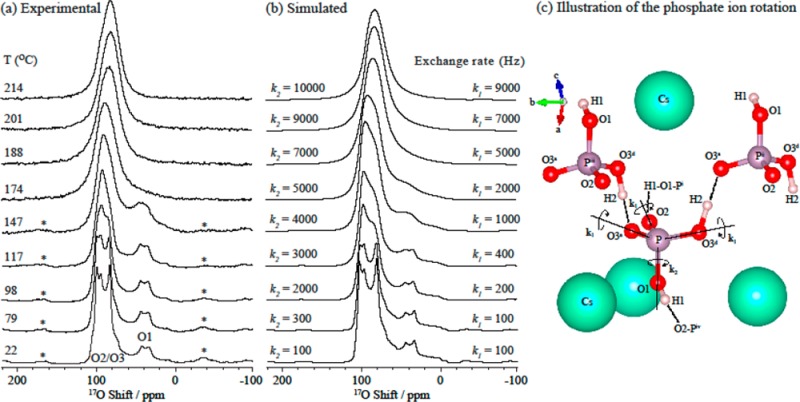
Variable-temperature ¹⁷O MAS spectra of CsH₂PO₄ were recorded from 22 to 214 °C, to probe the high-temperature dynamics in the paraelectric phase (Figure 3a); the results reveal noticeable changes in the line shape across the temperature range studied. The overlapped O2/O3 central-transition line shape starts to change at 79 °C, indicating the onset of a motional process.⁵⁷ At temperatures above 147 °C, the O1 resonance begins to broaden, and upon further heating, the discontinuities associated with the second-order quadrupolar line shapes and spinning side bands gradually disappear (see also Figure S8 showing full spectral width). Complete coalescence of the O1 and O2/O3 line shapes takes place above 180 °C and a single resonance centered at 82 ppm with Δν_1/2 = 2.7 kHz is observed. A gradual shift to lower frequency is observed after the coalescence but the line width remains similar at and above 201 °C.

Figure 3.

(a) Experimental variable-temperature ¹⁷O NMR spectra acquired with a MAS frequency of 12.5 kHz and (b) simulated ¹⁷O line shapes assuming rotations about all four C₃ axes (i.e., four 3-fold rotations) with a single site exchange rate k, and (c) simulated ¹⁷O line shapes assuming a second model with exchange rates k₁ and k₂ as depicted in Figure 4. Asterisks denote spinning side bands. Note that a value for k, k₁, and k₂ of 100 Hz corresponds to motion in the slow exchange limit. 100 Hz simply represents the upper limit for the rates at this temperature.

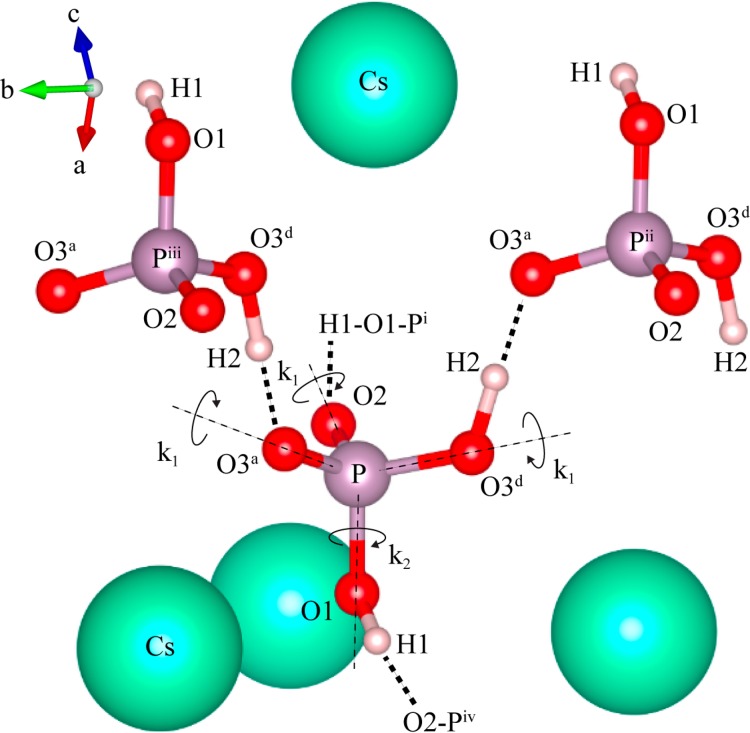
Further simulations were performed to determine the origins of the motional process. Even at the highest temperature, the ¹⁷O resonances are still broad and we do not observe evidence of complete motional narrowing (which would be expected if the exchange process were to enter into a fast mobile regime) in the experimental data. Thus, the motion in this regime is still restricted by the structure or local geometry. On the basis of a previous ¹⁷O NMR study of orthophosphate anion (PO₄^3–) rotation in Na₃PO₄,³⁷ the simplest model for this motional process is to assume phosphate rotations around all four C₃ axes (i.e., four C₃ (3-fold) rotations), resulting in hops between oxygen sites with a single rate constant k (Figure 4). The simulated line shape corresponding to this model, shown in Figure 3b, shows reasonable agreement with the ¹⁷O experimental data. The protons remain fixed in this model (i.e., do not accompany the rotating oxygen atoms), but rapid H2 hopping within the symmetric double well is included. While the rate of the H2 hopping process would be expected to increase with temperature, this H2 hopping is already in the so-called fast regime and was not found to have an effect on the spectrum and so was fixed at 10⁷ Hz in the simulations. The ¹⁷O NMR spectra are not sensitive to presence of H1–H2 hops, to a first approximation. (We confirmed that there is no noticeable difference between the ¹⁷O spectra acquired with and without ¹H decoupling (see Figure S9) and thus the effect of the O–H dipolar coupling is not included in the simulations). The good agreement between the simulated spectra and the experimental VT ¹⁷O MAS NMR spectra clearly indicates that the reorientations around four pseudo C₃ axes of the phosphate group provide a good model for the motional process at high temperatures. At coalescence (∼200 °C), a frequency, k, of 9 kHz is obtained for hops between the oxygen sites. (Note that a jump frequency of k corresponds to a frequency of k for the (approximately) 120° rotation about a P–O bond axis.) However, the match between the experimental and simulated line shapes is not as good at lower temperatures (98–147 °C). Within this temperature range, the second-order quadrupolar-broadened line shape of the O1 oxygen in the experimental spectra remains largely unchanged (even though those of the other oxygen resonances change significantly), and thus this model cannot explain all the details of dynamic process taking place at intermediate temperatures. To account for this discrepancy, we now consider the effect of having different rates for hops about the four pseudo C₃ axes. Since the collapse of the O2/O3 line shape occurs at a slightly lower temperature than that of the O1 line shape, we explored the effect of faster C₃ rotations around a P–O1 axis. This model is illustrated in Figure 4, where the hopping rate k₁ corresponds to rotations about the P–O3^d, P–O3^a and P–O2 bond axes, all of which induce oxygen exchange involving the O1 (and O2/O3) sites, and k₂ corresponds to rotations about the P–O1 bond axis, which results in O2 and O3^d/O3^a exchange only. Again, the possibility that protons accompany the oxygen rotation has not been included in this model, since the ¹⁷O spectra are not directly sensitive to this motion.

Figure 4.

Illustration of the pseudo C₃ rotations around the P–O2, P–O3^d, and P–O3^a axes (with hop rate k₁), and the C₃ rotation around the P–O1 axis (with hop rate k₂) of the phosphate ion (of note, k₁ = k₂ for four identical 3-fold rotations, shown in Figure 3b). The four connected phosphate units Pⁱ to P^iv are shown; the connectivity to Pⁱ and P^iv is simplified for clarity. Cesium, hydrogen, phosphorus and oxygen atoms are shown in green, pink, purple and red, respectively.

The simulations based upon this new model (Figure 3c) are in much better agreement with the experimental data than the previous model (Figure 3b). At the coalescence (200 °C), two characteristic site exchange rates k₁ and k₂ of 7 and 9 kHz are obtained. Although the errors in the determination of k₂ are large, all simulations show that the slower rate k₁ gradually approaches k₂ as the temperature increases.

Figure 5 compares Arrhenius plots of the ¹⁷O four-site exchange, assuming the two different models shown in Figure 3b, c and 4, with that for the ¹H two-site exchange process (k_ex, blue open triangles), the ¹H data coming from our previous study.²⁰ A plot of the ¹⁷O exchange rate versus reciprocal temperature shows a linear relationship through a temperature range of 79–214 °C in the paraelectric phase. An activation energy (E_a) of 0.43 ± 0.05 eV (41 ± 5 kJ mol^–1) is extracted when all hop rates are assumed to be equivalent (red open squares), while activation energies of 0.50 ± 0.07 and 0.21 ± 0.06 eV (48 ± 7 and 20 ± 6 kJ mol^–1, respectively) are obtained for the two distinct rates k₁ (black open circles) and k₂ (orange open diamonds), respectively, for the second model. k is essentially identical to k₁ (within the errors inherent in these simulations) and has a similar, but slightly smaller, activation energy than the value obtained for the proton H1/H2 exchange process (0.70 ± 0.07 eV) in the temperature range of 167–214 °C. The similar activation energy suggests a correlation between the protonic motion and the rotation of the phosphate ions. This will be discussed in the following section.

Figure 5.

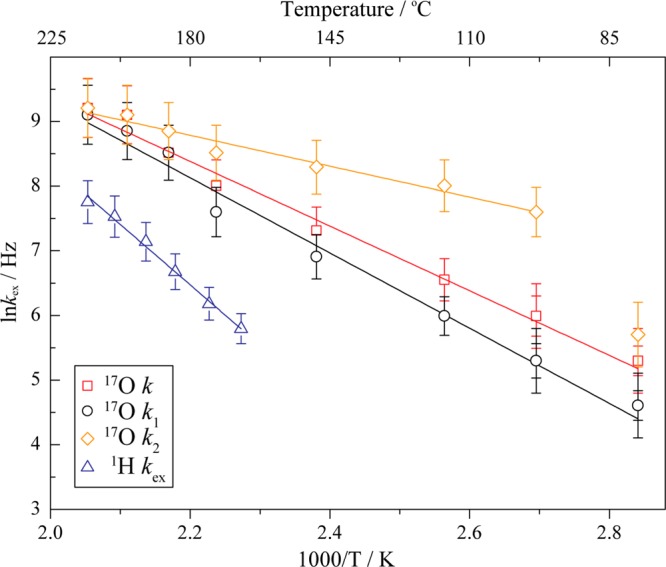
Arrhenius plots for the oxygen four-site exchange process, assuming first, rotations about the four P–O C₃ axes (with identical exchange rates k, red open squares), and second, a faster C₃ rotation about the P–O1 axis (k₂, orange open diamonds), and slower C₃ rotations about the P–O2, P–O3^d, and P–O3^a axes (k₁, black open circles) of the phosphate ion. The red, black, and orange solid lines indicate the Arrhenius equation least-squares fits to the rates k, k₁, and k₂, giving E_a = 0.43 ± 0.05, 0.50 ± 0.07, and 0.21 ± 0.06 eV, respectively, in the temperature range 79–214 °C (for k₂, 98–214 °C). Error bars indicate errors of 5% except 20% for data points at lower temperatures (79 and 98 °C). The blue solid line corresponds to the ¹H two-site exchange data obtained in our earlier study²⁰ (rate k_ex, blue open triangles) with E_a = 0.70 ± 0.07 eV (167–214 °C) which is shown here for comparison.

In summary, the observed changes in experimental variable-temperature ¹⁷O MAS NMR spectra can be explained using a model whereby the phosphate anions undergo restricted reorientation about the P–O bonds. The analysis shows that, at intermediate temperatures, the exchange rate constant describing the C₃ rotations about the O2–P, O3^d-P, and O3^a-P bonds, all of which involve the O1 atom, is significantly smaller than that describing the C₃ rotation about the O1–P bond. As the material approaches the monoclinic-to-cubic (superprotonic) phase transition, the rates of phosphate reorientation about the four P–O bonds become essentially identical.

4. Discussion

Interpretation of the NMR spectra with the aid of atomistic simulations has provided key insights into (1) hydrogen dynamics at room temperature, and (2) phosphate group dynamics as a function of temperature, and earlier work has provided hydrogen dynamics as a function of temperature. Unanswered, however, is the critical question of the relationship (if any) between proton dynamics and phosphate-group dynamics and its connection to long-range proton transport. Here we address this important question by evaluating possible proton transport pathways. In particular, we aim to explain the observation of substantially smaller proton exchange rates than phosphate group reorientation rates (Figure 5), while rationalizing the anisotropy in PO₄ group reorientation rates.

Within the context of the observed phosphate reorientations, there are three possible modes of protonic motion: A, the protons do not hop with the oxygen atoms (i.e., the O and H motions are uncorrelated), B, the protons hop with the phosphate rotation (i.e., the processes are concerted), and C, the processes are correlated, but not every phosphate rotation results in a proton hop. First, assuming case A, where a proton hop does not accompany the phosphate rotation, a C₃ rotation about the O1–P bond will break only the O3^d–H2 bond, a bond which the proton samples dynamically as a consequence of the local disorder. In contrast, rotations about the O2–P and O3^a,d–P bonds will break the stronger O1–H1 bonds (Figure 1 and 4). On the basis of the energetics associated with breaking the O–H bonds, this simple analysis suggests that a C₃ rotation about the O1–P bond with rate k₂ will be easier than the other rotations, providing a qualitative explanation for the differences in k₁ and k₂. However, such a mechanism does not preclude a possible correlation between phosphate and protonic motion; furthermore, it does not explain the similar activation barriers for proton and phosphate motion (as defined by k or k₁).

Case B, in which the protons hop with the phosphate rotation, can occur via two different mechanisms. We define mechanism B(i) as a process which involves simultaneous (concerted) motion of all the H atoms either directly bound or H-bonded to the oxygen atoms of the central phosphate being considered. In contrast to mechanism B(ii) discussed below, it does not involve any concerted rotation of nearby phosphate ions. For example, in the B(i) mechanism, the rotation around the P–O1 bond (i.e., one 120° rotation) results in movement of the three other oxygen atoms to new locations, each accompanied in its motion by a proton. These are the directly bound H2 proton (for which O3^d serves as a donor), and the two hydrogen bonded protons H2 and H1 (for which O3^a and O2, respectively, serve as acceptors). Only two of these three proton hops swap H1 and H2 (which is the process that is detected in the ¹H NMR experiment). Thus, this mechanism results in an H1–H2 exchange rate of 2/3k₂. The effect of rotations about the other three bonds can be similarly evaluated, and these are summarized in Table S4; these all lead to exchange rates of 2/3k₁. Mechanism B(ii) only considers rotations that displace directly bound O–H groups. H-bonded protons, i.e., those linked to acceptor oxygen atoms, do not move with the central phosphate ion. Since such a reorientation will carry the directly bound proton to a location occupied by a hydrogen-bonded proton, this mechanism must be accompanied by concerted rotations of an adjacent phosphate unit Pⁱ, Pⁱⁱ, Pⁱⁱⁱ or P^iv (see Figure 4 for details) to “carry” the H atoms that occupy the target site, into new locations. To illustrate: for a 120° rotation about the P–O1 bond which carries the O3^d–H2 bond to another O (O2 or O3^a) atom, the H atom originally at this new position (O2 or O3^a, either directly bound or H-bonded) will need to move so as to accommodate the new H2 atom. Only one in three oxygen hops results in one H1–H2 exchange, but this hop must be associated with a correlated motion, which also results in H1–H2 exchange. For example, the first O3^d–H2 hop (to the new location, O2···H1) induces a hop/rotation of the adjacent Pⁱ phosphate unit (i.e., a Pⁱ–O1–H1 transfer to the other oxygen sites of the Pⁱ phosphate unit), with 2/3 of the hops resulting in H1–H2 exchange. Similarly, a P–O3^a hop of the central unit (to O3^d–H2) will induce a motion of either Pⁱⁱ–O1–H1 or Pⁱⁱ–O3^d–H2, and thus, 1/2 of the correlated hops will result in the H1–H2 exchange. Importantly, in this albeit complex mechanism, the involvement of many concerted motions provides a way of explaining how protons migrate through the structure by the phosphate rotation. Although this analysis was limited to the directly coordinated (H-bonded) phosphate groups, it is important to stress that this mechanism will involve exchange between phosphates beyond the first coordination sphere considered here. A more detailed analysis of concerted motion was performed (similar to that presented in Table S4, for mechanism B(i)) to quantify the relationship between the rate of proton hops and the phosphate rotation (see Table S5). The most important finding that emerges from this analysis is that concerted motion does not lead to a cascade of events where either the rate of proton hopping ≫ the phosphate rotation rate or vice versa.

We turn to the experimental data to provide further guidance as to which mechanism may be operative. As shown in Figure 5, there is a mismatch in the rates of H1–H2 exchange (from ¹H NMR) and O-reorientation (from ¹⁷O NMR) (∼2 kHz versus 7 kHz at ∼200 °C). Although the exact correlation between H motion and O motion predicted depends on the degree of concerted motion, in both mechanisms B(i) and B(ii), one oxygen hop never results in more than one hydrogen (proton) hop. The ratio of the H and O hop rates varies between 1/3 and 2/3 depending on the mechanism (see Table S4 and Table S5), and thus, the lower rate of proton versus oxygen exchange is only in part explained by this analysis. Hence, neither mechanism B(i) nor B(ii) provides an explanation for why the rate for proton hopping is noticeably smaller than that of phosphate rotation, particularly at lower temperatures. Only mechanism A or C provides an explanation for this observation. The E_a value of 0.50 ± 0.07 eV from the slower O1 exchange rotation (k₁) shows reasonable agreement with the value obtained for the H1–H2 exchange process (0.70 ± 0.07 eV). Within mechanisms B(i) and B(ii), this rotation involves movement of both H1 and H2 protons, providing supporting evidence that the onset of protonic motion in the paraelectric phase is at least partially coupled with reorientation of the phosphate anion, i.e., that mechanism C operates (proton mobility is a correlated processes, but not every phosphate rotation results in a proton hop). In terms of the mechanism for the correlated motion, mechanism B(i), which excludes concerted motion in adjacent phosphate units, is the least likely because it involves the movement of protons that are only H-bonded to the oxygen atom (e.g., O2···H1 protons), although this cannot be concluded on the basis of the experimental data. Note, however, that both mechanisms A and B(i) are consistent with a lower activation energy for P–O1 rotation, since in neither mechanism is an O1–H1 bond broken during rotation. This is not necessarily the case for mechanism B(ii).

5. Conclusions

¹⁷O NMR spectroscopy combined with first-principles calculations has been applied to provide a detailed understanding of the local structure and dynamics of the phosphate ions and protons in CsH₂PO₄. A good match between the experimental and simulated ¹⁷O line shapes was achieved by the use of a dynamic model involving rapid exchange between the two H2 sites in the symmetrical double well. The ¹⁷O line shapes could be simulated as a function of temperature by assuming this rapid exchange between the two H2 sites, and a restricted rotation model of the phosphate group, with two different exchange rates to describe rotation about different P–O bonds. This model provides better agreement with the experimental data than the model that considers a single exchange rate to describe rotation about the 4 P–O bonds, especially for the temperature dependence of the ¹⁷O signal from the O1 resonance, i.e., the oxygen atom bound to the second proton, H1. The faster rate (k₂) corresponds to rotation about the P–O1 bond, a process that does not involve the breakage of the strongest O1–H1 bond, in contrast to rotations about the other P–O bonds. A much lower activation barrier is observed for the P–O1 rotations as compared to other P–O bonds: facile P–O1 rotation is possible without proton motion if both O3 atoms on the phosphate anion of interest behave as acceptors during the reorientation step (instead of one being a donor and one being an acceptor), a mechanism that is enabled by the extremely fast exchange between the two H2 sites of the symmetric H-bond. This mechanism is not possible for rotations about the other P–O (P–O2/3^a/3^d) bonds since they involve both directly bound H1 and H2 protons, this motion being hindered by O1–H1 hydrogen bonding. A similar activation energy is obtained for proton hops and rotations about the P–O2/3^a/3^d axes (with rate k₁) that involve the bound H2 protons, suggesting that phosphate rotations aid the proton hops. However, the rate of proton motion is more than an order of magnitude slower than that of phosphate anion group reorientation, indicating that while phosphate rotation may facilitate proton motion, not all phosphate rotations lead to proton hops at least in the paraelectric phase. A detailed exploration of the relationship between proton jumps and phosphate rotation suggests a mechanism whereby a subset of phosphate rotations carry O1–H1 protons to new locations, this mechanism involving concerted motion of nearby phosphate groups. The concerted motion mechanism is consistent with long-range protonic conduction in CsH₂PO₄.

In summary, ¹⁷O NMR is shown to be a sensitive tool for not only quantifying the phosphate motion but also understanding the nature of the phosphate/protonic motion. This study opens up the possibility of using ¹⁷O NMR to study similar solid inorganic acid systems.

Supporting Information Available

Summary of hydrogen bond configurations in paraelectric CsH₂PO₄ as determined by single crystal neutron diffraction (Table S1), powder XRD patterns of all CsH₂PO₄ samples (Figure S1), simulated 1D spectra with and without the ¹⁷O CSAs (Figure S2 and Table S2), experimental ¹⁷O MAS spectra acquired at different magnetic fields (Figure S3), possible local hydrogen-bonding arrangements (Figure S4 and Table S3), simulated 1D NMR spectra as a function of a hopping frequency (Figure S5), the 2D ¹⁷O MQMAS spectrum (Figure S6), the 2D ¹H–¹⁷O HETCOR spectrum (Figure S7), variable-temperature ¹⁷O MAS spectra with full spectral width (Figure S8), room-temperature ¹⁷O MAS spectra with and without ¹H decoupling (Figure S9), and tables showing the correlations between the rates of phosphate rotation and proton hop rates (Table S4 and S5). This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

^# (F.B.) Department of Chemistry, University of Liverpool, Stephenson Institute for Renewable Energy, Liverpool L69 7ZD, United Kingdom.

The authors declare no competing financial interest.