Tensor scale: An analytic approach with efficient computation and applications

Abstract

Scale is a widely used notion in computer vision and image understanding that evolved in the form of scale-space theory where the key idea is to represent and analyze an image at various resolutions. Recently, we introduced a notion of local morphometric scale referred to as “tensor scale” using an ellipsoidal model that yields a unified representation of structure size, orientation and anisotropy. In the previous work, tensor scale was described using a 2-D algorithmic approach and a precise analytic definition was missing. Also, the application of tensor scale in 3-D using the previous framework is not practical due to high computational complexity. In this paper, an analytic definition of tensor scale is formulated for n-dimensional (n-D) images that captures local structure size, orientation and anisotropy. Also, an efficient computational solution in 2- and 3-D using several novel differential geometric approaches is presented and the accuracy of results is experimentally examined. Also, a matrix representation of tensor scale is derived facilitating several operations including tensor field smoothing to capture larger contextual knowledge. Finally, the applications of tensor scale in image filtering and n-linear interpolation are presented and the performance of their results is examined in comparison with respective state-of-art methods. Specifically, the performance of tensor scale based image filtering is compared with gradient and Weickert’s structure tensor based diffusive filtering algorithms. Also, the performance of tensor scale based n-linear interpolation is evaluated in comparison with standard n-linear and windowed-sinc interpolation methods.

1. Introduction

Scale [1–3] may be thought of as the spatial resolution, or a range of resolutions ensuring a sufficient yet compact data representation facilitating a target knowledge learning process. Scale plays an important role in determining the optimum trade-off between noise smoothing and perception/detection of structures. In image analysis and computer vision literature, the notion of scale evolved from Marr–Hildreth–Koenderink–Witkin scale-space theory [1–4] whose key idea is to represent and analyze an image at various resolutions. This theory aids in breaking a computer vision and image-processing task into a hierarchy of tasks starting with macro-structural properties and gradually progressing toward micro-structures or the inverse. Often, an image representation at a specific scale is obtained by convolving the original image with a Gaussian smoothing kernel whose width is related to the chosen scale. While scale-space theory has been proven to be useful in a wide range of applications [5–17], the notion of “local scale” or “space-variant resolution scheme” [18–22] emerged to overcome two major practical hurdles – (1) lack of a common mechanism unifying knowledge extracted at multi-scale analyses, and (2) absence of optimal scale localization. A knowledge of “local scale” may allow us to spatially tune the neighborhood size in different processes leading to selection of small neighborhoods in regions with fine detail or near an object boundary, versus large neighborhoods in deep interiors [23]. Also, “local scale” may be a vital piece of information leading to developments of effective space-variant parameter controlling strategies [24].

A knowledge of “local scale” may lead to an effective and automatic mechanism to spatially control a process as a function of local scale [23,24]. Towards this direction, Saha and Udupa introduced a local morphometric scale using a spherical model in [23,24] and studied its effectiveness in various image processing applications including image segmentation [23,25–27], filtering [24], registration [28], and removal of partial volume effects in rendering [29]; see [30] for a survey on local scale. However, both the scale-space as well as the local scale theory implicitly utilizes an isotropic model of scales while most structures in the real world are anisotropic justifying the notion of a “tensor scale”, or “t-scale” in short, – a regime of unified and simultaneous representation of local structure size, orientation and anisotropy. T-scale carries the promise of serving as a rich parametric descriptor of local structure and geometry that may benefit several applications including object recognition, image preprocessing, registration and compression. Several applications, including biomedical, geological and satellite imaging, demand quantitative architectural analyses of quasi random mesh-like structures [31,32]. Such applications are likely to directly benefit from the notion of t-scale that provides a unified knowledge of local size, orientation and anisotropy. Previously, we introduced a formulation of t-scale using an ellipsoidal model [30] and studied its usefulness in various image processing applications [30,31,33]. Andaló [33,34] presented an efficient computational solution for t-scale in binary images and demonstrated its usefulness in detecting salient points on a given contour. However, our earlier formulation lacks a precise analytic definition of t-scale and its computational solution in 3- or higher-dimensional images is, often, infeasible. Recently, the theory of generalized and curvature based local scale and their applications have been studied by Udupa and his research group [35–38].

In this paper, we introduce an analytic formulation of t-scale that describes the local structure geometry using a local structure adaptive orthogonal system and presents an efficient computational solution. Also, we demonstrate the applications of t-scale in image filtering and interpolation. Several papers are available in the literature on structure tensor [39–42] computed by convolving tensor products of intensity gradients with a Gaussian kernel. Although, structure tensor is a useful concept, it primarily captures information derived from local gradient field and may not directly relate to local object geometry. For example, in a homogeneous region, structure tensor may not carry meaningful information. Here, we formulate t-scale from a geometric perspective where, at each image point, the tensor provides direct information of local object geometry as opposed to the gradient field and thus provides more precise structural information useful in many applications.

2. Theory and algorithms

In our previous work [30], we introduced the concept of t-scale using an algorithmic approach but without a precise analytic definition. Also, the previous algorithmic framework is unrealistic for 3- and higher-dimensional images due to high computational complexity. In the following, first, we will briefly describe the previous algorithmic definition [30] of t-scale which will be followed by a new analytic approach to define a local morphometric scale using a tensor model [43] and an effective computational solution in two and three dimensions (2-D and 3-D). Also, in the later part of this section, we introduce the theory and algorithms related to applications of t-scale to image filtering and interpolation.

2.1. Earlier algorithmic approach to t-scale

The notion of t-scale was motivated by the thought of representing local structures by an ellipsoid and, in an earlier work, Saha [30] attempted to define t-scale at any image point p in a 2-D plane (or, 3-D space) as the largest ellipse (ellipsoid in 3-D) that is centered at p and is contained inside the same object region defined by the continuity of homogeneity. However, in the previous approach, no analytic definition for the “largest ellipse” or “largest ellipsoid” was provided. Rather, t-scale was defined using an algorithmic approach as follows. Primarily, t-scale at an image point p is computed by locating edge points visible from p along different directions which are then used to compute the t-scale ellipse (ellipsoid in 3-D) at p. Basic steps for t-scale computation are as follows (see Fig. 1):

• Step 1: Trace image intensity along a set of pairs of radially opposite sample lines emanating from p and approximately uniformly distributed over the angular space around p.

• Step 2: Locate the closest edge point on each sample line (triangles and black dots).

• Step 3: Reposition the edge locations on each pair of opposite sample lines according to the axial symmetry of an ellipse (black dots to white dots).

• Step 4: Compute the t-scale at p using the best-fit ellipse derived from the repositioned edge points (triangles and white dots).

Fig. 1.

A schematic description of the algorithmic approach to define t-scale in 2-D. The method starts with edge locations (triangles and black dots) on sample lines emanating from the candidate image point. Following the axial symmetry of an ellipse, the edge points on each pair of radially opposite sample lines are repositioned (black dots to white dots). Finally, t-scale ellipse is computed from repositioned edge points (triangles and white dots).

2.2. T-scale: an analytic definition

Let ℝ denote the set of real numbers and let us consider an image 𝕀 in ℝⁿ where multiple objects are defined as partitions by M number of (n – 1)-D pseudo-Riemannian manifolds, say, m₁, m₂, …, m_M; we refer to these manifolds as partitioning manifolds. Now, let us first consider a point p ∈ ℝⁿ; we will refer to m_i as the nearest partitioning manifold for p if the distance between p and m_i is shorter than that between p and m_j for all i ≠ j. Now, consider p and a set of i orthogonal vectors τ₁, τ₂, …, τ_i; there exists a unique subspace W_i that is parallel to each of the vectors τ₁, τ₂, …, τ_i and passes through the point p. An image is formed over the orthogonal complement $W_i^{\perp }$ of W_i where the partitioning manifolds are: $W_i^{\perp }\cap m_1,W_i^{\perp }\cap m_2,\dots ,W_i^{\perp }\cap m_M$; let us refer to this image as an orthogonal complement image of 𝕀 induced by the vectors τ₁, τ₂, …, τ_i; and the point p. Finally, t-scale at a point p ∈ ℝⁿ in an image 𝕀 is an ordered sequence of n orthogonal vectors 〈τ₁(p), τ₂(p), …, τ_n(p)〉 inductively defined as follows:

1. τ₁(p) is the vector from p to the closest point on the nearest partitioning manifold of 𝕀.

2. Given the first i orthogonal vectors, τ₁(p), τ₂(p), …, τ_i(p), the (i + 1)th vector τ_i+1(p) points from p to the closest point on the nearest partitioning manifold in the orthogonal complement image of 𝕀 induced by τ₁(p), τ₂(p), …, τ_i(p) and the point p.

Thus, although, the nearest partitioning manifold defines the t-scale at a point, the above analytic formulation embrace the case when there are multiple objects. In 2- and 3-D, we refer to τ₁(p), τ₂(p) and τ₃(p) (only, for 3-D) as primary, secondary and tertiary t-vectors of p; in general, “t-vector” will refer to any of the three vectors. The notion of t-scale defined as above is schematically illustrated in Fig. 2 using a 3-D rabbit femur bone surface m₁ (medium dark gray). As illustrated in the figure, t-scale at a given point p (solid black dot) in a 3-D image is an ordered sequence 〈τ₁(p), τ₂(p), τ₃(p)〉 of three orthogonal t-vectors. The primary t-vector τ₁(p) (black) defines the direction and distance to the closest point on the femur surface. The orthogonal complement plane $W_1^{\perp }$ and the 1-D partitioning manifold $W_1^{\perp }\cap m_1$ on $W_1^{\perp }$ are shown in the figure; note that the 1-D partitioning manifold (light gray) is essentially the intersection between the plane $W_1^{\perp }$ (dark gray) and the original partitioning surface m₁ in the 3-D image. The secondary vector τ₂(p) (medium dark gray) is defined by the point on $W_1^{\perp }\cap m_1$ that is closest to p. Once τ₁(p) and τ₂(p) are found, the line (light gray) on which the tertiary vector τ₃(p) lies is confirmed; the final direction and the length of τ₃(p) is defined by finding the closest point on the partitioning surface along the line. It may be noted that, often, projections of the two dotted lines (light and medium dark gray) indicates to two principal directions on m₁ where it meets τ₁(p); this observation is utilized in our computational solution for t-scale in 3-D.

Fig. 2.

An illustration of t-scale using a rabbit femur bone surface (medium dark gray) forming a 2-D manifold m₁. The candidate spel p (solid black dot); the point r on m₁ closest to p gives the primary t-vector τ₁(p) (black). The orthogonal complement plane $W_1^{\perp }$ and the 1-D manifold $W_1^{\perp }\cap m_1$ are shown in dark and light gray, respectively. Secondary t-vector τ₂(p) (solid medium dark line) is defined by the point on $W_1^{\perp }\cap m_1$ closest to p; finally, τ₃(p) (solid light gray line) is given by the closest point on $W_1^{\perp }\cap m_1$ along the line orthogonal to τ₂(p). It may be noted that τ₂(p) and τ₃(p) coincide with principal directions of m₁ at r; this observation is utilized for efficient computation of 3-D t-scale.

Here, we will present a matrix representation T(p) of t-scale at p derived from the ordered sequence of orthogonal t-vectors 〈τ₁(p), τ₂(p), …, τ_n(p)〉 facilitating use of conventional tensor algebra. Let i_j(p) denote the unit vector along τ_j(p) and let λ_j(p) be the magnitude. The matrix representation of t-scale is defined as follows:

$$T(p)=[{\mathbf{i}}_1(p),{\mathbf{i}}_2(p),\dots ,{\mathbf{i}}_n(p)]\left[\begin{array}{lll}{\lambda }_1^2(p)\hfill & \dots \hfill & 0\hfill \\ ⋮\hfill & \ddots \hfill & ⋮\hfill \\ 0\hfill & \dots \hfill & {\lambda }_n^2(p)\hfill \end{array}\right]{[{\mathbf{i}}_1(p),{\mathbf{i}}_2(p),\dots ,{\mathbf{i}}_n(p)]}^T.$$

The above equation represents t-scale using a symmetric positive semi-definite matrix, an equivalence of covariance matrix. Such a compact formulation will facilitate efficient realization of a direction-dependent anisotropic parameter control strategy under a predetermined physical model; see Sections 2.4 for an example. Also, a matrix formulation of t-scale will be helpful in understanding the interaction between local t-scale structure and the scaling, rotation, translation and shear components of local Jacobian matrix of an image deformation field [44–46].

2.3. An efficient computation of t-scale

A direct algorithmic formulation of t-scale computation from its definition faces two major hurdles − (1) object partitions are unknown in real images and (2) high computational complexity in three- or higher-dimensions. Here, we outline our algorithmic solution for 3-D images involving edge detection, distance transform and differential geometric approaches which may be extended to higher dimensions. In an image, often, we do not know the partitioning manifolds used to define t-scale. However, we may realistically assume that detected edge points in an image lie on these hypothetical manifolds. Also, because of the fact that these edge points are dense samples on these manifolds, the distance transform from these edge points is a close approximation to the unknown distance transform from the hypothetical partitioning manifolds. With this understanding, t-scale may be computed by using gradient analyses and computational geometric approaches to the distance transform map from the image edge locations; in the rest of this section, by “distance transform” we will refer to the distance transform from image edge locations.

Based on the above convention, it is observed that the gradient of the distance transform map at any given point provides the direction to the nearest partitioning manifold, i.e., the direction of the primary t-vector. The magnitude of the primary t-vector is defined by the distance transform value at the candidate point. Once the primary t-vector is determined, in 2-D, the secondary t-vector may be computed by locating the closet manifold along the line perpendicular to primary t-vector. However, this computation is not so trivial in 3-D where the first step is to determine the principal directions on the local partitioning manifold (Fig. 2). This task is accomplished using a new algorithm that is based on computational geometric analysis of distance transform. In the following we describe different steps in t-scale computation starting with basic definitions and notations.

In this paper, all computational and algorithmic developments are confined to 2- and 3-D images, although, these methods may generalize to higher dimensions. Let ℤ denote the set of integers. It may be noted that ℝ² and ℝ³ represent a 2-D plane and a 3-D space while ℤ² or ℤ³ denote a digital space in 2- or 3-D, respectively. We will use ℤⁿ as a common reference to ℤ² and ℤ³. An n-D digital image is defined with an image intensity function f : ℤⁿ → ℝ. Each element of an n-D digital space is referred to as a spel (an abbreviation of “spatial element”) whose position is denoted by Cartesian coordinates (x₁, x₂) or (x₁, x₂, x₃) where x₁, x₂, x₃ ∈ ℤ. For any two spels p, q ∈ ℤⁿ, |p – q| denotes the Euclidean distance between the two spels. For any vector v ∈ ℝⁿ, |v| gives its magnitude.

2.3.1. Edge detection and distance transform computation

The purpose of edge detection is to compute sample points on unknown partitioning manifolds in a digital image. Here, we have adopted an edge detection approach combining both Laplacian of Gaussian (LoG) and Derivative of Gaussian (DoG) operators. Specifically, an edge is located at the zero crossing of LoG if absolute value of its DoG exceeds a predefined threshold. It may be noted that edge locations in an image form a set of points in ℝⁿ, therefore, a zero crossing of LoG may not coincide with a spel having integral coordinates. This problem is solved by analyzing topological consistency of sign alteration for LoG values at spels over a 2ⁿ neighborhood; see Fig. 3 for geometric classes of possible alteration patterns over a 2 × 2 × 2 neighborhood. Alteration patterns in a geometric class are identical under mirror reflection and/or rotations by integral multiple of 90°. Topologically consistent cases of LoG sign alterations are shown in Fig. 3a where the points with identical LoG sign are 6-connected [47–49]; a few examples of topologically inconsistent alteration patterns are shown in Fig. 3b. Here, 6-connectivity is enforced for topological consistency as 26-connectivity allows two voxels with identical LoG sign to meet at a vertex and such an object may not be locally separated by a pseudo-Riemannian manifold.

Fig. 3.

Different patterns of LoG sign alteration in a 2 × 2 × 2 neighborhood. Spels in a 2 × 2 × 2 neighborhood are marked with ± or ∓ (light gray) indicating that if the sign of LoG at a spel marked with ± is positive then that at spel marked with ∓ is negative or vice versa. (a) All possible geometric classes of LoG sign alterations with a valid zero crossing. (b) A few examples of topologically inconsistent LoG sign alterations without a valid zero crossing.

A zero crossing of LoG is identified for topologically consistent cases, only. To determine the edge location, first, a zero crossing is located for each pair of points with alternating LoG values in the 2ⁿ neighborhood. Finally, the edge is located at the mean of these zero crossings. The DoG value at the edge location is determined using n-linear interpolation of DoG values at grid locations in the 2ⁿ neighborhood depending upon image dimensionality. To our knowledge, the idea of using topological consistency to locate zero-crossings is new and was not used earlier. Finally, two thresholds thr_high and thr_low of DoG values and a technique similar to hysteresis, originally proposed in Canny’s edge detection algorithm [50], are used to select both strong and weak edges while avoiding noisy zero-crossings. The two thresholds thr_high and thr_low were determined using the hysteresis threshold detection algorithm for the Canny edge detector [51,52]. Saha et al. [53] described an application-dependent training approach to determine different gradient parameters.

Distance transform is defined as a function or an image DT : ℤⁿ → ℝ, where, DT(p)|p ∈ ℤⁿ gives its Euclidean distance from the closest partitioning manifold. Here, the basic idea is to use edge locations in ℝⁿ and then compute an Euclidean distance transform from these locations. Let E denote the set of all edge points in an image; the binding box of an edge location e ε E is the 2ⁿ neighborhood surrounding that point. For every edge location e ε E, a distance transform value is initialized at the 2ⁿ vertices of e’s binding box by directly measuring their distances from e. Following this initialization, the Euclidean distance transform values are perfused inside using a wave propagation algorithm similar to one adopted in [54,55]. See Fig. 4 for results of edge location and distance transform computation.

Fig. 4.

Results of t-scale computation. (a) A 2-D image slice from the Brainweb MR brain phantom data. (b) Computed edge locations (red) and gray scale distance transform. (c) A color coded illustration of 2-D t-scale. (d) Color coding disk at full intensity. (e–g) Same as (a–c) but for 3-D t-scale computation. Results are shown on one image slice; see text for further explanation. (h–j) Same as (e–g) but from another view. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

2.3.2. T-scale computation

As mentioned earlier, the primary t-vector τ₁(p) at a spel p ∈ ℤⁿ is computed by analyzing the gradient of DT map at p as follows:

$$|{\mathbf{\tau }}_1(p)|=\mathit{\text{DT}}(p),$$

and the unit vector i₁(p) along τ₁(p) is

$${\mathbf{i}}_1(p)=\frac{\mathbf{\nabla }\mathit{\text{DT}}(p)}{|\mathbf{\nabla }\mathit{\text{DT}}(p)|}.$$

In this paper, we have used the Sobel gradient operator.

Once, the primary t-vector τ₁(p) is determined, computation of the secondary t-vector τ₂(p) in 2-D is straightforward because the vector lies on the straight line L_p perpendicular to τ₁(p). Thus, τ₂(p) may be computed by locating the closet partitioning manifold along the straight line L_p. However, a difficulty here is that the edge locations representing partitioning manifold form a discrete set of points in ℝⁿ and, therefore, a simple sampling approach along a straight line for locating a manifold may raise the problem of missing the target manifold. This challenge is overcome by modifying the search process as follows. Let p + iΔ_Lp |i = 1,2, … be the sample points on a line L_p; the jth sample point is sufficiently close to the target manifold along L_p if it satisfies the following two conditions:

1. DT(p+jΔ_Lp) ⩽ δ_DT.

2. The angular difference between the two primary t-vectors τ₁(p +jΔ_Lp) and τ₁(p +jΔ_Lp + Δ_Lp) at the two successive sample points p + jΔ_Lp and p +jΔ_Lp + Δ_Lp is close to 180°; in this paper, we have used “⩾ 135°” to account for artifacts due to finite precision and other errors. It may be noted that, if the angular difference is less than 90°, the two points are on the same side of the partitioning manifold. Thus, the threshold of 135° was picked at the middle of the ideal situation of 180° and 90° when the two points fall on the same side of the partitioning manifold.

The value of δ_DT is determined by the density of edge locations and it should also define the sample interval size Δ_Lp; in this paper, we have used δ_DT = 1. Finally, the target manifold is located on the line L_p at a distance of jΔ_Lp + DT(p + jΔ_Lp) from p.

Computation of the secondary t-vector τ₂(p) is more challenging in 3-D as compared to 2-D. The primary reason behind the difficulty is that, the determination of τ₁(p) narrows down τ₂(p) onto a plane P perpendicular to τ₁(p). However, τ₂(p) may lie along any direction on the plane. Although, τ₂(p) is uniquely defined in Section 2.2, its computation demands a search on image geometry on the plane P. To keep the computation of t-scale confined in the local neighborhood, we choose the vector τ₂(p) along the maximum curvature direction at the closest point r on a partitioning manifold (see Fig. 2). A challenge is how to compute the maximum curvature direction at r because an analytic expression of the partitioning surface is unknown; instead, discrete sample points, i.e., edge locations, on the surface are available. The estimation of curvature for discrete 3-D objects has been an important topic in computer graphics, and several methods have been proposed [56–59]. The basic idea behind our algorithm of detecting the maximum curvature direction is to first, determine the primary t-vector τ₁ at every spel in the neighborhood of p. The primary t-vector τ₁ at a neighboring spel of p intersects the partitioning surface at the vicinity of r (see Fig. 5). More importantly, the angular inclination of τ₁ with the plane P, perpendicular to τ₁(p), changes most rapidly along the direction of maximum principal curvature and it changes slowly along the minimum principal curvature direction. In other words, the projection of the unit vector along τ₁ on P takes larger values along the maximum curvature direction and it takes smaller values along the minimum curvature. Although our method is primarily based on this theory, to reduce the effect of noise and discretization, we determine the principal curvature direction using principal component analysis (PCA) of these projection vectors on P as follows. Let q₁, q₂, …, q_m be m points in the neighborhood of p and let i′₁ (q) (solid vectors in Fig. 5b and c) be the projection of the unit vectors i₁(q) on P. To enforce axial symmetry of projection vectors, each projection vector i′₁ (q) (solid line; Fig. 5c) is accompanied with an opposite vector –τ′₁ (q) (dotted line). PCA of the all points represented by these vectors is applied to compute the two principal directions; the eigenvector corresponding to larger eigenvalue gives the direction for maximum principal curvature while the other eigenvector provides the direction of the minimum curvature (see Fig. 5d). The secondary t-vector τ₂(p) is chosen along the maximum curvature direction; the exact value of the t-vector is determined using the same algorithm adopted for detecting τ₂(p) in 2-D. Finally, once the primary and secondary t-vectors are known, the task of finding the tertiary t-vector in 3-D is equivalent to determining the secondary t-vector in 2-D.

Fig. 5.

Computation of the secondary t-vector τ₂(p) in 3-D. (a) A partitioning surface with primary t-vector τ₁(p) (black) at the candidate point p and τ₁(p)s (gray) for several qs in the neighborhood. The plane P orthogonal to τ₁(p) is indicated. (b) τ′₁(q), projection of the unit vectors τ₁(q)/|τ₁(q)| on P, are indicated for several qs in the neighborhood of p along with the curve formed by the intersection of P and the partitioning surface. (c) Computation of principal directions using PCA of τ′₁(q)s (solid) and – τ′₁(q)s (dotted). (d) Projection of principal directions onto partitioning surfaces.

2.3.3. T-scale smoothing

A smoothing filter is often used to reduce noise in intensity images. However, smoothing of a t-scale image may not be as trivial as smoothing a scalar image. First, a matrix representation T(p) of t-scale at p is obtained as described at the beginning of Section 2 to enable various tensor operations and statistical analyses [60]. Weickert [39] has used component-wise Gaussian convolution on local structure tensors to obtain a smooth representation. To avoid producing negative eigenvalues in a component-wise averaging that contradicts the basic definition of t-scale, we have adopted the Log–Euclidean distance (L–E) approach [61]. Effectiveness of the L–E approach in diffusion tensor image (DTI) interpolation has been demonstrated in [61].

Let A = QΛQ^T|Q: unitary matrix, Λ: diagonal matrix with real nonnegative elements, be a symmetric positive semi-definite matrix. The logarithm and the exponential of this matrix are defined as follows:

$$\text{log}A=Q\text{log}\mathrm{\Lambda }{Q}^{\mathrm{T}}=Q\left[\begin{array}{ccc}\text{log}{\lambda }_1& \dots & 0\\ ⋮& \ddots & ⋮\\ 0& \dots & \text{log}{\lambda }_n\end{array}\right]Q^{\mathrm{T}},e^A=Q{e}^{\mathrm{\Lambda }}{Q}^{\mathrm{T}}=Q\left[\begin{array}{lll}{e}^{{\lambda }_1}\hfill & \dots \hfill & 0\hfill \\ ⋮\hfill & \ddots \hfill & ⋮\hfill \\ 0\hfill & \dots \hfill & e^{{\lambda }_n}\hfill \end{array}\right]Q^{\mathrm{T}}.$$

A smoothing function using the L–E approach is defined using a discrete Gaussian kernel G_σ : ℤⁿ → ℝ

$$G_{\sigma }(a)=\{\begin{array}{cc}K{e}^{-\frac{{|a|}^2}{2{\sigma }^2}},& \text{if}a\in G_{\text{support}},\\ 0,& \text{otherwise},\end{array}$$

where G_support is the support of the kernel and K is the scalar normalizing factor ensuring that ∑_a∈GsupportG_σ(a) = 1. Finally, the L–E based tensor smoothing algorithm is designed as follows using the kernel function G_σ defined as above:

$$T_{\text{smooth}}(p)=\text{exp}(\text{log}(T)\ast G_{\sigma }),$$

where ‘*’ is the convolution operator.

2.4. T-scale based image filtering

In this section, we describe a t-scale based diffusive filtering that is primarily developed on the theory of anisotropic diffusion originally proposed by Perona and Malik [62] and subsequently, studied by others [24,63]. The primary objective of the new t-scale based filtering is to govern the diffusion process in a space-variant and orientation-dependent fashion to optimally fit with local image structures captured in the form of t-scale. Anisotropic diffusion [62] was originally described to encourage diffusion within a region (characterized by low intensity gradients) while discouraging it across object boundaries (characterized by high intensity gradients). The anisotropic diffusion process at any spel p may be defined as follows:

$$\frac{\mathit{\text{df}}}{\mathit{\text{dt}}}=\text{div}\mathbf{V}=\underset{\mathrm{\Delta }\tau \to 0}{\text{lim}}{\int }_s\mathbf{V}·d\mathbf{s},$$

where f is image intensity function; t is time variable; “div” is divergence operator; V = GF is diffusion flow vector; G is diffusion conductance function; F is intensity gradient vector; Δτ is the volume enclosed by the surface s surrounding p; and ds = u ds where u is a unit vector which is orthogonal and outward-directed with respect to the infinitesimal surface element ds. The key idea of anisotropic diffusion [62] is to spatially vary the conductance using a nonlinear and non-increasing function of gradient magnitude, e.g. G = exp(–|F²/2σ²|) resulting into a non-monotonic behavior of flow against gradients. Guided by the original theory by Perona and Malik, a diffusive filtering process in a digital image is formulated as an iterative process as follows:

$$f_i(p)=\{\begin{array}{cc}f(p),& \text{if}i=0,\\ f_{i-1}(p)-K_D\sum _{q\in {\mathbb{Z}}^n}{\mu }_{\alpha }(p,q){\mathbf{V}}_{i-1}(p,q)·\mathbf{D}(p,q),& \text{otherwise},\end{array}$$

where f_i represents image intensity at the ith iteration; µ_α is pixel adjacency relation; K_D is a diffusion constant; V_i−1 is intensity flow vector at (i − 1)th iteration (see below for a precise definition); and D(p, q) is unit vector along the direction from p to q and ‘·’ is the vector dot product operator. Assuming a uniform pixel adjacency relation, the diffusion constant K_D should satisfy the following inequality to ensure a monotonic intensity variation with iterations [63]

$$K_D\le \frac{1}{{\sum }_{q\in {\mathbb{Z}}^n}{\mu }_{\alpha }(p,q)},\text{where}p\in {\mathbb{Z}}^n.$$

Using standard 26-adjacency in 3-D, K_D = 1/27. The flow vector V_i is determined by the following equation:

$${\mathbf{V}}_i(p,q)=G_i(p,q){\mathbf{F}}_i(p,q),$$

where

$${\mathbf{F}}_i(p,q)=\frac{f_i(p)-f_i(p)}{|\mathbf{p}-\mathbf{q}|}\mathbf{D}(p,q),$$

and G_i is an orientation- and space-adaptive conductance function at ith iteration. As mentioned before, G_i should be a nonlinear function of local intensity gradient F_i that eventually leads to a non-monotonic behavior of flow with gradients. Gaussian functions, as follows, have popularly been used for G_i

$$G_i(p,q)=e^{-\frac{{|{\mathbf{F}}_i(p,q)|}^2}{2{[\sigma (p,q)]}^2}},$$

where σ is the control parameter determining the degree of filtering. When σ is large, the degree of filtering is high and possibilities of blurring across boundaries and of smearing out regions containing fine details increase. On the other hand, when σ is small, the filtering process performs conservatively and more noise survives after filtering. In conventional diffusive filtering methods [62,63], the diffusion process adapts to local gradient while the controlling parameter σ is kept fixed limiting the fine control on and adaptivity to local image structural properties. Weickert [39] introduced the notion of structure tensor to control the σ parameter and demonstrated its use in along-structure smoothing. The motivation of our work is to use geometric tensor representation of local structures in filtering that facilitates along-structure smoothing while preserving boundary sharpness by discouraging cross-structure diffusion flow; a preliminary version of t-scale based image filtering algorithm was presented in [30] using the old formulation of t-scale. Here, the controlling parameter σ is determined by local t-scale in a space- and direction-variant manner as follows:

$$\sigma (p,q)={\sigma }_{\text{min}}+\chi (\text{max}({\zeta }_p(q),{\zeta }_q(p)))\times {\sigma }_{\psi }.$$

The above formulation ensures a minimum diffusion of σ_min during the filtering process; the second component in the expression on the r.h.s. uses a monotonically non-decreasing function χ to control local diffusion process in a direction-variant manner using the two t-scale derived measures ζ_p(q) and ζ_q(p). The term σ_ψ determines the sensitivity of the diffusion process with local t-scale measures. The t-scale measure ζ_q(p) is defined as follows:

$${\zeta }_p(q)=\sqrt{{\mathbf{i}}_{\mathit{\text{pq}}}^{\mathrm{T}}T(p){\mathbf{i}}_{\mathit{\text{pq}}}},$$

where i_pq is the unit vector along the direction from p to q. Note that, by considering t-scale T(p) as a covariance matrix, the measure ζ_p(q) gives the square root of the variance of the system along the vector i_pq. Here, ζ_p(q) is treated as an approximate measure of the radial length of the ellipsoid T(p) along the direction i_pq. In this paper, we have used the following functional form for χ

$$\chi (x)=1-e^{-\frac{x^2}{2{\sigma }_L^2}},$$

where σ_L is the maximum expected radial length of t-scale ellipse computed as the maximum DT value in the image. In all experimental results presented in Section 4, the parameters σ_ψ is determined as the overall noise level in the image computed in the same way as described in [24]; the value the parameter σ_min is chosen as 25% of the value of σ_ψ. Finally, for all experimental results of the filtering process was run for twenty iterations.

2.5. T-scale based n-linear image interpolation

Linear interpolation is a widely used technique for image resampling [64]. In a one dimensional discrete signal, the linear interpolation in between two successive sample values is defined by the straight line joining the sample points. In an n-D digital image, image intensity values are known at spels p ∈ ℤⁿ with integral co-ordinate values. Following the principle of linear interpolation, the intensity value at a location p_c ∈ ℝⁿ is determined as a weighted sum of intensity values at 2ⁿ vertices of the binding box of p_c = (x₁, x₂, …, x_n). Let ⌊·⌋ and ⌈·⌉ denote the floor and ceiling operators. The vertices of the binding box of p_c are p₁ = (⌊x₁⌋, ⌊x₂⌋, …, ⌊x_n⌋), p₂ = (⌈x₁⌉, ⌊x₂⌋, …, ⌊x_n⌋), …, p_2ⁿ = (⌈x₁⌉, ⌈x₂⌉, …, ⌈x_n⌉). The estimated intensity value at p_c is given as follows:

$$f(p_c)=\frac{{\sum }_{i=1}^{2^n}{w}_{i}f(p_i)}{{\sum }_{i=1}^{2^n}{w}_i},$$

where

$$w_1=\prod _{j=1}^n(\lceil x_j\rceil -x_j),w_2=(x_1-\lfloor x_1\rfloor )\prod _{j=2}^n(\lceil x_j\rceil -x_j),\dots ,w_{2^n}=\prod _{j=1}^n(x_j-\lfloor x_j\rfloor ).$$

The basic idea of using t-scale in n-linear image interpolation is to bring the notion of an anisotropic space where distance increases slower along the direction of the local structure while it increases faster in the cross-structure direction. A smaller value of ζ_pi (p_c) indicates that the vertex p_i is close to the partitioning manifold along the vector i_pjpc and therefore, the weight of p_i in interpolating the intensity value at p_c should be discouraged to avoid cross-region mixing. On the other hand, a larger value of ζ_pj(p_c) means that p_j is relatively far from the partitioning manifold along the vector i_pjpc and therefore a generous value of weight for p_j may be used along-the-edge smoothing. Therefore, the t-scale based weights for linear interpolation are defined as follows:

$$w_i^{\prime }=w_i{\zeta }_{p_i}(p_c).$$

Finally, the t-scale based linear interpolation procedure is defined by the following equation:

$$f(p_c)=\frac{{\sum }_{i=1}^{2^n}{w}_i^{\prime }f(p_i)}{{\sum }_{i=1}^{2^n}{w}_i^{\prime }}.$$

3. Experimental methods

In this section, we describe our experimental methods to examine the performance of the new t-scale computation as well as the performance of t-scale based filtering and interpolation methods. Three different experiments were designed as follows:

1. T-scale computation: To evaluate the accuracy of the new efficient t-scale computation method using 3-D Brainweb phantoms at various levels of noise and blur.

2. T-scale based image filtering: To evaluate the performance of the t-scale based anisotropic diffusive method and compare it with gradient and structure tensor based anisotropic diffusive methods on both 2- and 3-D images.

3. T-scale based n-linear image interpolation: To evaluate the performance of t-scale based n-linear image interpolation method in comparison with standard n-linear and windowed-sinc interpolation methods.

3.1. Accuracy of t-scale computation method

The purpose of our accuracy evaluation study is to examine the difference in t-scale obtained using the efficient differential geometric approach as compared to the true value directly computed as per the definition. To perform this test, we generated phantom images at five different levels of noise (noise: 8–20%) and blurs (σ_blur: 0.5–2.5) from the simulated brain MR image available at brainweb.bic.mni.mcgill.ca/brainweb and a 3-D pulmonary human computed tomography (CT) image. The Brainweb MR phantom data was downloaded with the following parameters – matrix size: 181 × 217 pixels, number of slices: 181, isotropic voxel size: 1 mm, noise: 3% and intensity non-uniformity: 20%. The pulmonary CT images was acquired using the following protocol − 120 kV, 100 effective mAs, pitch factor: 1.0, nominal collimation: 64 × 0.6 mm, image matrix: 512 × 512, number of slices: 518, in-plane resolution: (0.55 mm)² and slice thickness: 0.5 mm.

Following the fact that the definition of t-scale is based on an image representation with partitioning manifold, true t-scale may not be computed from a general image. To define the manifolds, we partitioned the image into three regions, namely, white matter, gray matter and background (Figs. 6b and 7b). True measure of t-scale was obtained from the partitioned image using a sample-line based approach [30] with a high angular sampling of 10 K lines over the 3-D angular space. Test images for t-scale computation using the new differential geometrical approach were derived from the original image after adding a blur and a white Gaussian noise (Figs. 6d and g, and 7d and g).

Fig. 6.

Accuracy of t-scale computation results. (a) An original image slice from the Brainweb MR phantom data. (b) Partitions of white and gray matter regions used for ground true values for t-scale image. (c) True 3-D t-scale image computed by a dense spatial sampling approach on the hard partition image of (b). (d) Phantom image slice with blur and noise. (e) Computed 3-D t-scale image for (d) using the proposed method. (f) Log–Euclidean error map for (e) as compared to (c). (g–i) same as (d–f) but for the phantom at higher noise and blur.

Fig. 7.

Same as Fig. 6 but from the coronal view.

Let W_T(p) be the true t-scale matrix at a spel p computed from the partitioned image and let W_test(p) denote to the t-scale matrix representation obtained from a test image by applying the differential geometric algorithm. Although, t-scale computation methods were applied on entire image, the error analysis was confined to white and gray matter regions only to avoid background; better results were obtained when the background region was included in error analysis. Let Ω denote the region over which the error analysis is performed. The error of t-scale computation is defined as the average normalized Log–Euclidean distance between the true and the computed t-scales over the target region Ω as follows:

$$\mathit{\text{error}}=\frac{2{\sum }_{p\in \mathbf{\Omega }}\Vert \text{log}(W_{\mathit{\text{ss}}}(p))-\text{log}(W_{\mathit{\text{dg}}}(p))\Vert }{{\sum }_{p\in \mathbf{\Omega }}\Vert \text{log}(W_{\mathit{\text{ss}}}(p))\Vert +\Vert \text{log}(W_{\mathit{\text{dg}}}(p))\Vert },$$

‖·‖; is the Euclidean norm of a positive definite symmetric matrix.

3.2. Evaluation of t-scale based image filtering

The purpose of the experiment is to examine the performance of t-scale based filtering methods as compared to intensity based and structure tensor based diffusive filtering algorithms. ITK implementation [65] of gradient-based diffusive filtering and their recommended values of 0.125, 3.0 and 5 were used for the time step, conductance parameter and the iteration number for 3-D image. An algorithm was implemented for structure based diffusive filtering in accordance to the description of [39] and the parameter value settings of 0.001 for regularization parameter α, 1 for threshold parameter C, 0.3 for noise scale σ, 2 for integration scale ρ, and 10 for iteration time t were used as suggested by the author. Three images were used in this experiment − (1) a phantom image generated with geometric structures at various scales, (2) a photographic image of an aquarium and (3) a lung CT image. Both phantom and CT images were corrupted with five different levels of noise (8–20%) and different filtering algorithms were applied to the noisy images to qualitatively evaluate their performance. A measure of residual noise was used to assess the performance a method and also, a measure of structure blurring was examined for the phantom image since the knowledge of structures is needed to define this measure.

Let I be an original phantom or lung image; I was corrupted by adding a zero-mean Gaussian noise n generating a noisy test image I_n = I + n. Noise level was defined over the test region Ω in an image as follows:

$$\mathit{\text{noise}}\%=\sqrt{\frac{{\sum }_{p\in \mathbf{\Omega }}{n}^2(p)}{{\sum }_{p\in \mathbf{\Omega }}{I}^2(p)}}.$$

It may be noted that percent of noise is essentially an inverse measure of signal to noise ratio or SNR widely used as a measure of noise level. Let I_nF denote the image obtained by applying a filtering algorithm to the noisy image I_n. Thus the residual noise in the filtered image is n_r = I_nF – I, and an overall measure of residual noise is defined as follows:

$${\mathit{\text{noise}}}_{\mathrm{r}}\%=\sqrt{\frac{{\sum }_{p\in \mathbf{\Omega }}{n}_{\mathrm{r}}^2(p)}{{\sum }_{p\in \mathbf{\Omega }}{I}^2(p)}}.$$

Relative contrast is defined for the phantom image to measure structure preserving property of a filtering method in terms of object to background contrast relative to residual noise. Let Oj and Bj denote the set of object and background pixels in a phantom image that are no further than m pixels from the object/background interface. Such pixels are identified in a binary image using standard morphological operations. We did not use the entire object/background regions for measure relative contrast as the notion of structure blurring is absent in deep interior and thus, inclusion of such regions in analysis only reduces the sensitivity of the measurement. The performance of different methods was analyzed for two values of 1 and 2 for m. Finally, the relative contrast in an image I is defined as

$$\mathit{\text{RC}}=\frac{|{\mu }_{\mathit{\text{Oj}}}-{\mu }_{\mathit{\text{Bj}}}|}{\sqrt{{\sigma }_{\mathit{\text{Oj}}}{\sigma }_{\mathit{\text{Bj}}}}},$$

where µ_Oj and σ_Oj are the mean and standard deviation of intensities over Oj while µ_Bj and σ_Bj denote same entities over Bj.

3.3. Evaluation of t-scale based n-linear interpolation

The performance of the t-scale based n-linear image interpolation method was evaluated using a phantom image and several medical images from different applications and was compared with standard n-linear and windowed-sinc interpolation methods [64]. A 3-D phantom image of size 512 × 512 × 512 was generated a sinusoidal wavy (along the slice direction) pattern of geometric structures with its scales varying from 5 to 10 voxels. Also, the following sets of medical images were used in our experiment:

1. The Brainweb MR phantom data described in Section 3.

2. Seven human pulmonary multi-detector CT images with voxel size of 0.55 × 0.55 × 0.5 mm³ and in-plane matrix grid size of 512 × 512 with the number of slices varying between 519 and 728.

3. Micro-CT images of four cadaveric distal tibia specimens at 28.8 µm isotropic resolution and 3-D image grid size of 768 × 768 × 512.

4. Five abdominal CT with voxel size of 0.59 × 0.59 × 1.00 mm³ and in-plane matrix grid size of 512 × 512 with the number of slices varying between 64 and 319.

Starting from an original image I, a sub-sampled images I_d was obtained with different sub-sample rates of 2, 3 or 4. A given image interpolation method was applied to each sub-sampled image producing an interpolated image I_int at the original resolution. The performance of the underlying interpolation method is then measured by computing the average normalized absolute difference between the interpolation and the original image as follows:

$${\mathit{\text{error}}}_{\text{int}}\%=\frac{{\sum }_{p\in \mathbf{\Omega }}|I(p)-I_{\text{int}}(p)|}{{\sum }_{p\in \mathbf{\Omega }}I(p)}.$$

4. Results and discussion

In this section, we discuss experiments results of the previous section. Performance of the t-scale computation algorithm is qualitatively illustrated in Fig. 4 using 2-D image slices from the Brainweb MR phantom data and the 3-D pulmonary human CT image. The result of the 2-D t-scale computation algorithm on a Brainweb MR phantom image slice randomly selected from mid-brain region is illustrated in Fig. 4a – d. Results of edge location and gray scale distance transformation are presented in Fig. 4b. The color coding scheme by Saha [30] was adopted to display the 2-D t-scale image at a pixel p that represents an ellipse Г(p). A color value is assigned for the t-scale Г(p) such that the hue component of color indicates its orientation while the saturation and intensity components of the color denote the anisotropy and thickness, respectively. The color coding disk at maximum intensity is shown in Fig. 4d. Results of 3-D t-scale computation on the pulmonary CT image are presented in Fig. 4e – j. 3-D t-scale at a spel p essentially represent an ellipsoid Г(p). Using three components of color-space, we may display an ellipse. Therefore, in 3-D, the intersection between Г(p) and the display plane forming an ellipse is depicted (Fig. 4g and j). Results of both 2-D and 3-D t-scale computation are visually satisfactory. The new algorithm takes 3 s to compute 2-D t-scale for the Brainweb phantom image slice running in a desktop with a 2.53 GHz Intel(R) Xeon(R) CPU and Linux OS; the original sample line based t-scale computation algorithm [30] takes 83 s for the same image. Since a 3-D implementation of the original sample line based t-scale computation algorithm is not available, we calculated the expected computation time as follows. The 2-D sample line based algorithm with 60 sample lines and 60 sample points per line takes approximately 1 min for an image of size 256 × 256. Therefore, in 3-D with 900 sample lines (to maintain a comparable angular sampling rate) the total run time for a 512 × 512 × 518 image should be approximately

$${\left(\frac{512}{256}\right)}^2\times 518\times \left(\frac{900}{60}\right)\times 2=1036\mathrm{h}=43\text{days}.$$

The multiplication by ‘2’ is added to account for tri-linear interpolation in 3-D image instead of bilinear interpolation in 2-D. On the other hand, the new 3-D t-scale computation algorithm takes approximately 50 min to compute t-scale for the 3-D CT image.

4.1. Results of accuracy analysis

Results of accuracy analysis of the efficient t-scale computation algorithm as compared with the results directly obtained from the analytic definition are qualitatively illustrated in Figs. 6 and 7. As observed in both figures, at moderate blur and noise, the agreement of the efficiently computed t-scale with the analytic t-scale computed in absence of noise and blur is visually satisfactory. However, at very high noise and blur, the fine structures are lost in t-scale. Results of quantitative analysis are presented in Table 1. As observed in the table, the performance of the algorithm decreases, i.e., error increases with noise as well as blur. Based on these results, it may be reasonable to conclude that the computational geometric approach to t-scale is efficient and produces acceptable t-scale at moderate blur and noise.

Table 1.

Performance of the 3-D t-scale computation algorithm based on analytic definition at various levels of noise and blurring. Each row indicates a specific noise level that increases from top to bottom and each column indicates a specific blur level that increases from left to right. Results are reported as normalize Log–Euclidean difference (%) to the result generated by space sampling method for the original binary phantom.

	B1	B2	B3	B4	B5
N1	4.07	5.52	6.13	7.20	8.90
N2	4.17	5.63	6.42	7.54	9.11
N3	4.46	5.75	6.59	7.73	9.29
N4	4.62	5.80	6.70	8.21	9.40
N5	5.17	6.10	7.13	8.79	9.78

4.2. Results of t-scale based image filtering

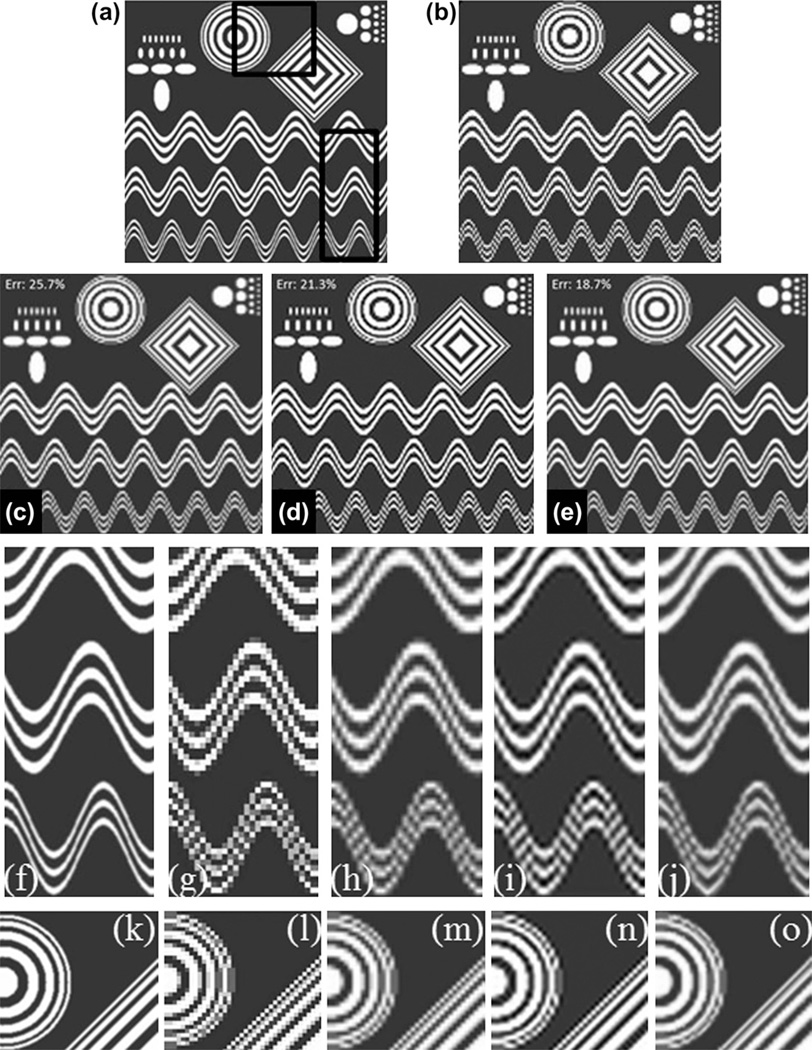
Here we discuss the performance of t-scale based image filtering algorithm with the gradient and structure tensor based methods in both 2- and 3-D. Fig. 8 illustrates results of three filtering algorithms on a photographic image of a fish in an aquarium containing visible noise. Results of application of the three filtering algorithms are presented in Fig. 8b – d. As observed in these figures, among the three results, the maximum visual perceptual noise cleaning and boundary sharpening is achieved using the t-scale based method (Fig. 8d). This observation is confirmed in enlarged views (Fig. 8e – h) of a small box selected from the matching region in the original and the three filtered images. Fig. 9 illustrates results of different filtering methods on a 2-D phantom image. As observed in the figure, at the finest scale, the gradient and structure tensor based filtering algorithms have failed to maintain the separate identity of the three sinusoidal curves at several locations. On the other hand, the t-scale based algorithm has successfully preserved the separation of the three curves at the finest scale while maximally cleaning noise over homogenous regions. The superiority of the t-scale based filtering method on the phantom image is further confirmed in the results of quantitative analysis (Tables 2 and 3) where the t-scale based method has achieved minimum residual noise and maximum enhancement in relative contrast measures among all three method algorithms. In these tables, G-, S- and T-algorithms are used as abbreviations for gradient, structure tensor and t-scale based diffusive filtering algorithms.

Fig. 8.

A qualitative comparison among different diffusive filtering methods. (a) The original digital image with natural noise. (b–d) Smooth images obtained by using gradient (b), structure tensor (c) and t-scale (d) based diffusive filtering methods. (e–h) Zoomed in displays of the matching region cropped from (a–d), respectively. It may be noted that the t-scale based method has outperformed the other two methods in smoothing along the structures while preserving boundaries and effect is more prominent in the zoomed displays in (e–h).

Fig. 9.

Comparative results of image filtering in a 2-D phantom. (a) The original phantom image. (b) Degraded image after adding Gaussian white noise. (c–e) Results of gradient (c), structure tensor (d) and t-scale based (d) anisotropic diffusive filtering methods.

Table 2.

Results of quantitative comparison among three different methods in terms of residual noise after filtering on different images.

Image	Original noise (%)	Residual noise (%)
		G-algorithm	S-algorithm	T-algorithm
3-D Phantom	8.0	7.8	7.7	5.9
	10.0	9.5	9.5	6.8
	12.0	11.1	11.3	7.8
	15.0	13.6	13.7	9.3
	20.0	17.3	17.8	11.4
3-D Lung CT	8.0	7.5	8.7	4.4
	10.0	7.7	9.3	5.3
	12.0	9.5	9.9	5.9
	15.0	11.7	10.9	7.0
	20.0	14.8	14.5	9.4

Table 3.

Results of quantitative comparison among three different methods in terms of relative contrast after filtering on 3-D phantom image.

Radius	Original relative contrast	Relative contrast after filtering
		G-algorithm	S-algorithm	T-algorithm
1 voxel	9.1	8.3	8.1	9.5
	8.6	7.1	7.7	9.0
	8.0	7.3	7.3	8.5
	7.1	6.1	6.7	7.8
	6.0	4.9	5.5	6.7
2 voxels	9.8	8.6	8.4	10.5
	9.2	7.3	8.0	10.1
	8.6	7.7	7.7	9.4
	7.7	6.5	7.1	8.8
	6.5	5.3	5.9	7.6

Fig. 10 illustrates the results of three filtering methods on a 3-D pulmonary CT image. Fig. 10a presents an axial image slice from the original CT data; here, a MIP display of the image region covering ±10 image slices around the target slice is used to depict partial 3-D information of the local pulmonary vasculature. The same image region after adding a 12% white Gaussian noise is shown in Fig. 10b while the results of gradient, structure tensor and t-scale based filtering algorithms are presented in Fig. 10c – e. As observed in these results, the diffusive filtering algorithm has reduced some noise (Fig. 10c) although, it has blurred fine structures at several locations and also the residual noise is visually apparent. While the structure blurring is visually less prominent using the structure tensor based method (Fig. 10d), the presence of residual noise is visible and the peripheral vessels are visually blurred. On the other hand, the t-scale based filtering algorithm has successfully cleaned noise (Fig. 10e) while preserving almost every fine structure visible in Fig. 10a. As mentioned in Section 3.2, relative contrast may not be computed for this experiment and the results of quantitative evaluation of residual noise for different filtering methods at various noise levels are presented in Table 2 where it shows that, at all noise levels, the t-scale-based method has significantly outperformed the other two methods.

Fig. 10.

Results of 3-D image filtering. (a) An original image slice from a pulmonary CT image of a patient. (2) Degraded image after adding Gaussian white noise. (c–e) Results of 3-D image filtering using gradient (c), structure tensor (d) and t-scale (e) based diffusion.

4.3. Results of t-scale based n-linear interpolation

The performance of t-scale based n-linear image interpolation method has been examined and compared with standard linear and windowed-sync interpolation method using a 3-D phantom and a set of medical images selected from different applications. Fig. 11 show the results of applications of the three interpolation methods on the 3-D phantom image after 4 × 4 × 4 down sampling. Improvement in interpolations results using t-scale based interpolation in terms of structure smoothness is visually apparent. The results of application of the three interpolation methods on the Brainweb MR phantom data after 4 × 4 × 4 down sampling is shown in Fig. 12. It appears in the results the t-scale based method reduces the blur along object boundaries and also the ringing effects of windowed-sinc algorithm is absent in the t-scale based interpolation results (Fig. 12e). It may be mentioned that, for all interpolation experiments, t-scale was computed from the sub-sampled images. For quantitative analyses, the three methods were compared under 2 × 2 × 2, 3 × 3 × 3, and 4 × 4 × 4 down sampling rates and the results are presented in Figs. 13–15.

Fig. 11.

Results of image interpolation on a phantom data. (a) An original image slice. (b) Sub-sampled image at the rate 4. (c–e) Result using standard n-linear (c), windowed-sinc (d) and t-scale based n-linear image interpolation. (f–j) Same as (a–e) but for a zoomed part marked in (a). (k–o) Same as (a–e) but for another zoomed region. It may be observed that t-scale helps preserving small structures and it produces smooth edges without causing ringing artifacts which is visible for result produced by the windowed-sinc method.

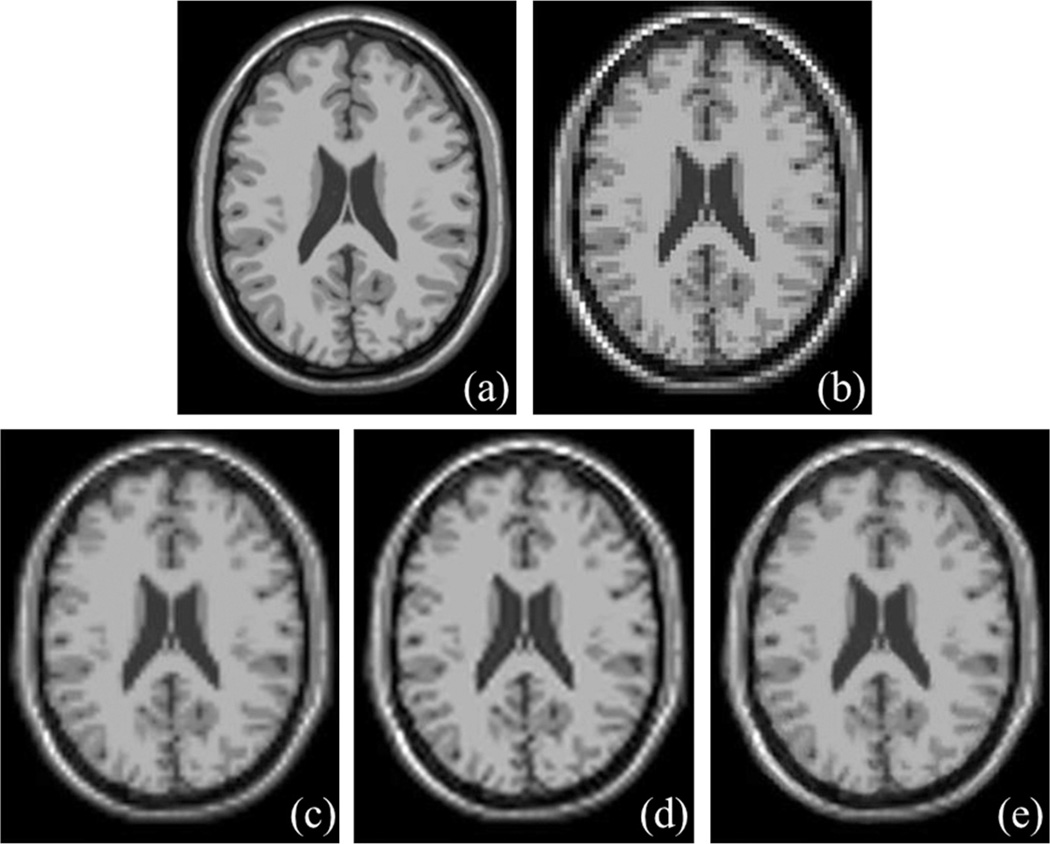
Fig. 12.

Results of image interpolation on the Brainweb MR phantom image. (a) An original image slice. (b) An image slice from sub-sampled image at the rate of 3. (c-e) Results using standard n-linear (c), windowed-sinc (d) and t-scale based n-linear (e) interpolation methods. It may be observed that t-scale has produced crisper edges as compared to the standard n-linear interpolation without causing ringing artifact associated with the windowed-sync method.

Fig. 13.

Performance of three interpolation methods on the different phantom and medical images selected from various clinical applications at sub-sampling rate of 2 × 2 × 2. The percentage error was computed over the entire 3-D image while a paired t-test was performed based on the percentage error from individual slices. As compared with the standard n-linear and windowed-sinc methods, the t-scale based n-linear method has outperformed the first method while comparative performance with the windowed-sinc method varies for different images. An “NS” (non-significant) mark is used to indicate statistical insignificance of difference in results by two methods.

Fig. 15.

Same as Fig. 13 but for subsample rate of 3 × 3 × 3.

The t-scale based interpolation method has improved the interpolation results for datasets at every down sampling rates and the enhancements are statistically significant except for a few cases as indicated in Figs. 13 and 14. As compared to windowed-sinc algorithm, the t-scale based method has improved the interpolation results except for the ankle dataset at 2 × 2 × 2 down sampling. However, for the lung and abdomen datasets, the windowed-sinc interpolation method has performed even worse than basic n-linear method.

Fig. 14.

Same as Fig. 13 but for subsample rate of 3 × 3 × 3.

It general, it may be observed that, as sample rate gets lower, t-scale extends its improvement in results as compared to basic n-linear interpolation while the results using the windowed sinc methods get worse. This observation may be explained by the fact that, the use of structure information in the t-scale method leads to a local context adaptive metric space partially healing for the sub-sampling loss. On the other hand, for windowed sinc method, inclusion of a larger neighborhood may not add further meaningful information and may even worsen the results due to influence by locally disconnected structures falling inside the extended neighborhood leading to increase of ringing artifacts.

5. Concluding remarks

In this paper, we have presented an analytic formulation for t-scale for n-D images and have presented an efficient computational solution in 2- and 3-D. Also, we have provided an efficient computational solution for t-scale in 2-D and 3-D that is based on several new methods including gray scale distance transform and computation of local principal curvature directions on the closest partitioning manifold represented by discrete edge points. Experimental results in comparison with theoretical results derived under the ideal condition of object partitions with no noise and blur have demonstrated that the proposed efficient computation method yields acceptable results at moderate noise and blur with image structures being visually apparent. Applications of t-scale in diffusive image filtering and n-linear interpolation has been presented and the performance of their results in comparison with respective state of art methods has been examined. Specifically, the performance of t-scale based filtering has been compared with gradient and structure tensor based diffusive filtering algorithms and both qualitative and quantitative results have demonstrated improvements in image filtering using t-scale. The performance of t-scale based n-linear interpolation is compared standard n-linear and windowed-sinc interpolation results. Experimental results have shown a clear improvement using t-scale in n-linear interpolation; in comparison with the windowed-sinc interpolation method, the t-scale based n-linear interpolation has shown improved results except for the ankle data set at low sub-sampling. In summary, the new analytic formulation of t-scale captures rich contextual information of local structure with a practical computational solution and may benefit a large class of image processing and computer vision applications including image filtering and interpolation. Currently, we are investigating theoretical properties of t-scale and its applications to other image processing tasks including image segmentation, registration and quantitative morpho-metric analysis.