Functional MRI Using Spin Lock Editing Preparation Pulses

Abstract

A novel approach for detecting blood oxygenation level-dependent (BOLD) signals in the brain is investigated using spin locking (SL) pulses to selectively edit the effects of extravascular diffusion in field gradients from different sized vascular structures. We show that BOLD effects from diffusion amongst susceptibility gradients will contribute significantly not only to transverse relaxation rates (R₂* and R₂) but also to R_1ρ, the rate of longitudinal relaxation in the rotating frame. Similar to the ability of 180-degree pulses to refocus static dephasing effects in a spin echo, moderately strong SL pulses can also reduce contributions of diffusion in large-scale gradients and the choice of SL amplitude can be used to selectively emphasize smaller scale inhomogeneities (such as microvasculature) and to drastically reduce the influence of larger structures (such as veins). Moreover, measurements over a range of locking fields can be used to derive estimates of the spatial scales of intrinsic gradients. The method was used to detect BOLD activation in human visual cortex. Eight healthy young adults were imaged at 3 T using a single-slice, SL-prepped turbo spin echo (TSE) sequence with spin-lock amplitudes ω₁ = 80 Hz and 400 Hz, along with conventional T₂*-weighted and T₂-prepped sequences. The BOLD signal varied from 1.1 ± 0.4 % (ω₁ = 80 Hz) to 0.7 ± 0.2 % (at 400 Hz), whereas the T₂-weighted sequence measured 1.3 ± 0.3 % and the T₂* sequence measured 1.9 ± 0.3 %. This new R_1ρ functional contrast can be made selectively sensitive to intrinsic gradients of different spatial scales, thereby increasing the spatial specificity of the evoked response.

1. Introduction

Blood oxygen level-dependent (BOLD) functional magnetic resonance imaging (fMRI) [1,2] is well established as a non-invasive approach for detecting hemodynamic and metabolic changes secondary to evoked and ongoing neural activity [3–5]. BOLD fMRI data are usually acquired using gradient echo planar imaging (EPI) in which the echo time (TE) is chosen for optimal sensitivity to detect small changes in the transverse relaxation rate R₂* [6–9]. Several factors may contribute to the magnitudes of BOLD signals, including the field strength, TE choice, and physiologic effects from changes in blood volume, flow, and oxygenation. Signal contributions from intravascular blood decrease at higher fields, and a major residual determinant of BOLD effects is the susceptibility induced signal changes in extravascular tissue water. The strength and spatial extent of such susceptibility induced extravascular field gradients, which largely reflect the influence of deoxyhemoglobin, have been shown to affect transverse relaxation [10–14]. Static dephasing effects caused by intrinsic gradients from larger vessels in particular can be reduced using a spin echo acquisition, but extravascular susceptibility contributions caused by diffusion across these gradients are still significant [11,13–19]. It should be emphasized that spin echo sequences with practically achievable values of TE do not completely remove the contributions of protons diffusing through gradients that are caused by large-scale (larger vessel) susceptibility variations [11,14,20]. Importantly, such susceptibility effects are dependent on the magnitude and spatial extent of the causes of the field inhomogeneities, as well as the field and choice of TE [11,21–23] so that in practice at higher fields there are greater relative contributions from microvascular effects in both gradient and spin echo acquisitions.

Here we evaluate the use of spin-locking (SL) prepared acquisitions for selective emphasis of specific (microvascular) scale of magnetic field variations while selectively de-emphasizing large vessel dephasing effects. R_1ρ is the rate of spin lattice relaxation in the rotating frame, and is often measured to characterize relatively slow molecular dynamic processes. Measurements of R_1ρ typically rotate magnetization to the transverse plane where it is then “locked” under the action of a radio frequency field continuously applied along the same direction. The variation of R_1ρ under the action of SL fields of different magnitudes (R_1ρ dispersion) has been previously exploited for studies of chemical exchange, and for quantitative measurements of exchange kinetic parameters [24–26]. Kettunen et al. [27] also quantified R_1ρ dispersion over a broad range of ω₁ to quantify ischemic changes in the mouse brain. For example, in biological samples, exchange between labile protons in various metabolites or macromolecules and solvent water may make major contributions to measured relaxation rates of water, especially at high fields, but the exchange rates involved are quite high (100 s – 1000 s Hz) and significant dispersion of R_1ρ occurs only at relatively high locking field amplitudes. The diffusion of mobile nuclei due to susceptibility induced intrinsic magnetic field gradients may also lead to spin dephasing and alter measured values of R_1ρ, but the time scales involved are generally slower, especially for large scale effects. For example, if the self-diffusion coefficient of water is 2 × 10⁻⁵ cm²s⁻¹, it requires 25 ms to diffuse a distance of 10 μm and 2.5 s to diffuse 100 μm. The variation of R_1ρ with locking field can provide insight into the time-scale of variations of the resonant frequency experienced by nuclei, and thereby their spatial extents. Therefore, judicious choice of the locking field can mitigate the influence of some structures.

Kettunen et al. [28,29], examined the effects of changes in intravascular susceptibility with the use of iron oxide contrast agents and saw little change in R_1ρ at a single locking field but did not measure the dispersion at other fields. However, they did confirm that R_1ρ decreases when blood is oxygenated because of changes in exchange-mediated relaxation by deoxyhemoglobin. Others [30–33] have used SL sequences for fMRI but have used relatively high locking field amplitudes and have interpreted the data in terms of blood volume changes or chemical exchange effects. We recently derived a simple theory that relates variations in R_1ρ at different locking fields to the dephasing caused by protons diffusing across periodically varying intrinsic field gradients of different spatial frequencies [34]. We confirmed these theoretical predictions in experimental studies of beads of different sizes in suspension. For periodically varying local fields, we showed there is a contribution to relaxation given by

$$R_{1\rho }=\frac{{\gamma }^2{g}^{2}D}{{(q^{2}D)}^2+{\omega }_1^2}={\gamma }^2{g}^{2}D\frac{{\tau }_c^2}{1+{\omega }_1^2{\tau }_c^2}$$ (1)

where q is the spatial frequency of the field induced by periodic variations in magnetic susceptibility, D is the self-diffusion coefficient, g² the mean squared gradient strength, γ is the gyromagnetic ratio and ω₁, the spin lock field amplitude. At low values of the locking amplitude the strong, inverse fourth power dependence on q corresponds to a dominant potential effect from large scale structures, in much the same manner as for R₂*. However, those contributions may be rapidly reduced by application of stronger locking fields. A useful parameter to characterize different contributions is a correlation time τ_c given by τ_c = 1/Dq². When the locking field is selected such that 3(ω₁τ_c)² = 5, the variation of relaxation rate with the corresponding value of q is maximized. Here we extend the theory and results of Spear et al. [34] to evaluate the potential of spin locking for selectively emphasizing effects produced by susceptibility variations from vascular structures of different scales and to compare and contrast BOLD signals obtained using conventional gradient echo, spin echo, and R_1ρ prepped fMRI in the visual cortex.

A conventional fMRI acquisition is equivalent to using a spin-lock preparation with locking amplitude = 0, locking period ≈ T₂*, acquisition TE = 0, when the relaxation rate R_2,diff will vary with q⁻⁴ and be dominated by large-scale structures such as draining veins. However, in the presence of a locking field of e.g. 80 Hz, in a simple interpretation, R_1ρ will show maximal rate of change (largest contrast effects comparing different locking amplitudes) in response to structures of radius ≈ 8 μm, corresponding q ≈ 3,950 cm⁻¹. Compared to their contributions when the locking field is 0, the contributions to R_1ρ from diffusion around objects of dimension ≈ 1000 μm should decrease by a factor of more than 10⁸, and for 100 μm by a factor of more than 10⁴, whereas the effects from objects of 5 μm or smaller will be barely affected. Those contributions will be further reduced at higher locking fields. Therefore, the contribution of diffusion around microvasculature structures of interest may be dramatically enhanced relative to larger structures by appropriate selection of the locking frequency.

In this work, we attempt to experimentally determine the effect of applying low locking fields (80Hz) to detect functional contrast and compare it with contrast obtained at high locking fields (400Hz). Based on our previous work [34] and the above theoretical explanation, we hypothesize that at ω1 = 80Hz, functional MR signal will be selectively sensitive to microvasculature. Therefore, we compared it to a T2-weighted spin echo functional contrast and T2* weighted gradient echo functional contrast.

2. Material and methods

Healthy, young, adult subjects (n = 8; age = 29 ± 3 yrs, 5 M, 3 F) provided informed, written consent and were imaged on a 3 T MRI scanner (Philips Achieva, Philips Healthcare Inc., Best, Netherlands) in a protocol approved by our Institutional Review Board. All subjects underwent 7 functional runs of 5 blocks of 36 seconds each of visual stimulation viewing an 8 Hz flickering checkerboard interleaved with an equal duration blank display.

2.1. MRI acquisitions

R_1ρ fMRI: Single slice spin-lock prepped turbo spin echo (TSE) acquisitions were employed at a spatial resolution of 3 × 3 × 4 mm³, matrix size = 96 × 96, TR/TE = 2200/5.3 ms. The oblique axial slice was chosen to pass through the genu and splenium of the corpus callosum to capture the visual cortex. Six functional runs were acquired with spin lock pulse amplitudeω₁ = 80 Hz applied for spin lock durations (TSL) of 20, 50, and 80 ms, and ω₁ = 400 Hz for the same TSLs. T1ρ of GM at 500 Hz has been reported to be ~99 ms [31]. So with these values of TSL, the T1rho decay should be adequately sampled [33]. TE was kept as short as possible (5.3 ms) to minimize additional T₂* contributions to the functional contrast. All six combinations were acquired as separate functional runs with 163 images each. The order of acquisition between ω₁ = 80 Hz and 400 Hz was randomized to reduce any habituation effects or other systematic effects on the evoked activity. The R_1ρ preparation consisted of a 5-pulse cluster designed to reduce effects of B₀ and B₁ imperfections. These were played out as 90° – ω₁ pulse for TSL/2 – 180° –ω₁ pulse for TSL/2 – −90° [35–37]. All pulses were block pulses. T₂-weighted fMRI: T₂-prepped fMRI images were acquired with similar imaging parameters as the R_1ρ data but the T₂ contrast was achieved with TSL = 50 ms and ω₁ = 0 Hz. Gradient echo BOLD fMRI: Conventional gradient echo EPI data were acquired with spatial resolution of 3.5 × 3.5 × 3.5 mm³, matrix size = 96 × 96, TR/TE = 2000/30 ms. Only 3 blocks of the checker board stimulus interleaved with three fixation blocks were used to reduce total acquisition time.

2.2. Analysis

The first and the last two time points during the 36 s blank screen period were not considered in our analyses to avoid signal transition effects between rest and activity. The three TSL data at ω₁ = 80 and 400 Hz were combined into a single time series. Single slice motion correction was performed in AFNI (2dimreg) [38,39]. Maps of R_1ρ at each lock amplitude were evaluated using a linear log fit to the three TSL data. ROIs were drawn in cortical grey matter and white matter and values of R_1ρ were evaluated from the blank presentations between the visual stimuli. For each series, a general liner model (GLM) was fit using FMRI Expert Analysis Tool (FEAT) in FMRI of the Brain’s Software Library (FSL) [40,41]. Voxels, corrected for multiple comparisons, in the visual cortex with an activation threshold z > 4 at a cluster wise threshold of P < 0.05 were considered for further analysis.

Voxels activated in the T₂-prepped sequence as well as the R_1ρ weighted sequences at both, ω₁ = 80 Hz and 400 Hz were selected to evaluate the mean time courses and percent signal changes. In addition, the rate of change of the percent fMRI signal change was assessed within an 11 s interval (5 time points) from the onset of the visual stimulus of flashing checkerboard. The rate of change in signal during this interval was estimated using a linear fit and compared across the different (BOLD, T₂-prep, ω₁ = 80 Hz @ TSL = 50 ms, ω₁ = 400 Hz @ TSL = 50 ms) evoked responses. Significance testing was performed using a paired non-parametric test in MATLAB (signrank). To ensure that the signal response delay independent of the magnitude of signal change in the T2-prepped and R_1ρ –weighted signals, we evaluated the derivative of the time course and the dynamic at which the derivative was maximum was considered as an indicator of the time to peak.

3. Results

The baseline T_1ρ (=1/R_1ρ) values in the gray matter and white matter were 91± 17 ms and 74 ±14 ms respectively at ω₁ = 80 Hz, and 93 ± 16 ms and 77 ± 18 ms respectively at ω₁ =400 Hz. These values were not significantly different (gray matter: p = 0.18, white matter: p = 0.89) at the two locking fields and confirm that at rest there is negligible dispersion in brain tissues at rest at 3 T over the range of low locking amplitudes considered here.

3.1. Visual activation

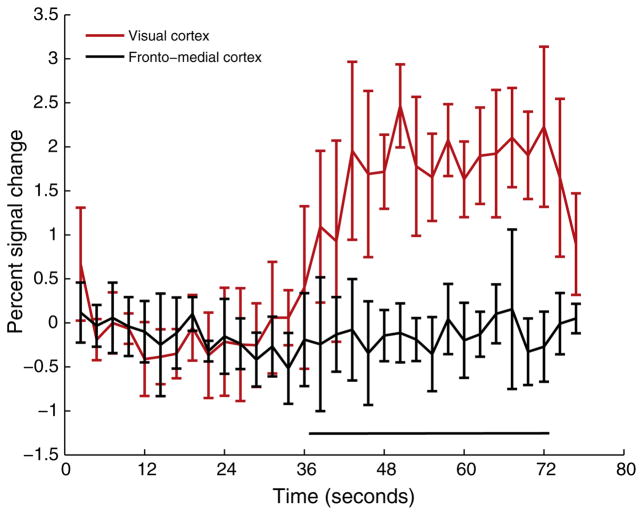
Fig. 1 depicts the activation patterns for different acquisitions for one representative subject (S7). The evoked response is qualitatively similar between the gradient echo T₂* weighted BOLD, T₂-weighted fMRI, and R_1ρ-weighted fMRI sequences. The number of activated voxels and Z-scores were significantly reduced (p < 0.01) in the R_1ρ-weighted fMRI at ω₁ = 400 Hz compared to the other sequences. To check the specificity of the measured response, frontal cortex was chosen as a control region. No change was observed in this region upon presentation of the visual stimulus as shown in Fig. 2 for a representative subject (S1).

Fig. 1.

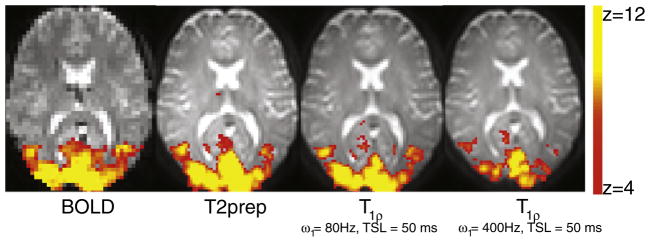
Visual cortex activation following an 8 Hz checkerboard stimulus in subject S7. Activation pattern is similar between BOLD, T2-prep, and R1ρ-weighted fMRI. The % signal change decreases monotonically from left to right.

Fig. 2.

Specificity of evoked response: Time course showing percent signal increases before and during the stimulation interval in the visual cortex and fronto-medial cortex. No activation is expected in the frontal cortex and is confirmed by the reasonably flat response in this representative (same as Fig. 1). Percent signal change in the visual cortex =0.87 %, percent signal change in the frontal cortex = −0.09 %.

Fig. 3a shows the percent signal changes for all acquisitions. Percent signal change with BOLD = 1.9 ± 0.3 %, T₂-prep = 1.3 ± 0.4 %, spin locked (ω₁ = 80 Hz/TSL = 50 ms) = 1.1 ± 0.4 %, spin locked (ω₁ = 400 Hz/TSL = 50 ms) = 0.7 ± 0.2 %. The percent signal change was similar between the T₂-prep sequence and the R_1ρ-weighted fMRI at ω₁ = 80 Hz, and significantly (p < 0.01) lower than the gradient echo BOLD signal change. Further, the percent signal change at ω1 = 400 Hz was significantly (p < 0.01) lower than at ω₁ = 80 Hz. Fig. 3b shows the percent signal changes in T_1ρ for the two locking fields (80 and 400 Hz). Following visual stimulation, the relaxation rates of activated cortex decreased (i.e., T_1ρ increased) as in conventional BOLD fMRI. Increase in T_1ρ at ω₁ = 80 Hz was significantly (p < 0.01) higher than that observed at ω₁ = 400 Hz.

Fig. 3.

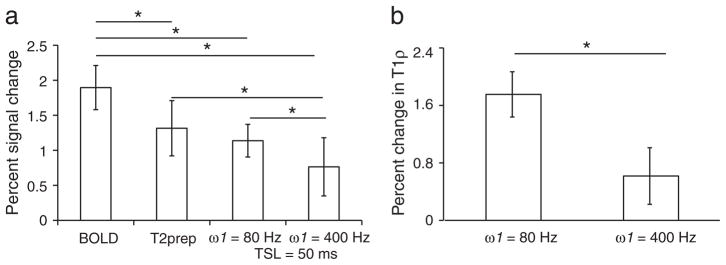
(a) Percent signal changes following visual stimulation using gradient echo BOLD, T2 weighted (T2-prep) sequence, R1ρ-weighted fMRI at ω1 = 80Hz and TSL = 50 ms, and R1ρ- weighted fMRI at ω1 = 400Hz and TSL = 50 ms for all subjects (n = 8). Signal increases were highest in BOLD and lowest in R1ρ-weighted fMRI at ω1 = 400Hz and significantly different from the rest. No significant difference was observed between the T2-prep sequence and R1ρ-weighted fMRI at ω1 = 80Hz. (b) Percent change in the T1ρ (1/R1ρ) values at the two locking fields. * p < 0.01 using paired non-parametric test for significance.

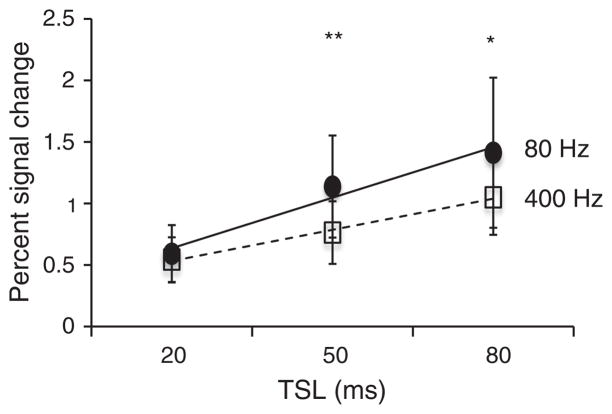
Fig. 4 compares the percent signal change as a function of TSL (20, 50, 80 ms). The percent signal change increased with increase in TSL similar to the increases seen in BOLD signal changes with TE for TE ≤ T₂*, as shown also by Hulvershorn et al. [42] at ω₁ = 400 Hz. However, at TSL of 80 ms, the signal-to-noise ratio (SNR) of the R_1ρ – weighted images reduced significantly (by a factor of 0.71 ± 0.08, p < 0.01 when compared to TSL of 50 ms), causing greater variation in the outcome. SNR for R1ρ –weighted images at ω₁ = 400 Hz at TSL = 50 ms was 86.3 ± 0.70 and at TSL = 80 ms was 63.2 ± 0.72. (See Fig. 3.)

Fig. 4.

Percent signal change in R1ρ-weighted fMRI as a function of spin locking duration (TSL). Similar to BOLD, percent signal change increases with increase in TSL. However, the SNR decreases significantly at TSL = 80 ms compared to TSL = 50 ms causing greater variations in measurement. *p < 0.05, **p < 0.01.

3.2. Time courses

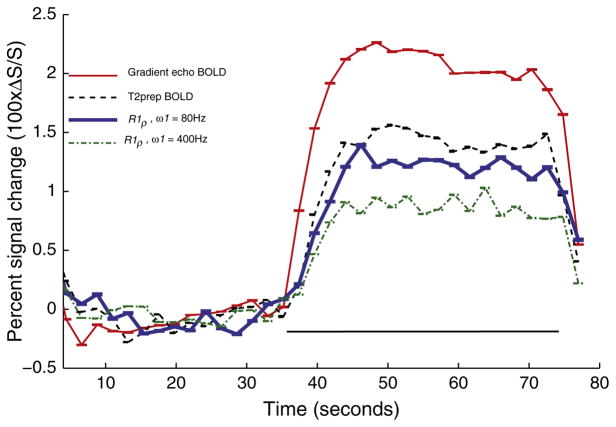
Examination of the activation time courses of all subjects and collapsed across all blocks (Fig. 5) revealed that the rate of signal change (% signal change/s at onset of activation) was significantly (p < 0.05) slower for the T₂-prep signal and R_1ρ –weighted signals compared to gradient echo BOLD signal. The BOLD signal increased the fastest, at a rate 0.25 ± 0.05 %/s. The rate of signal increase was slowest for the R_1ρ –weighted signal when ω₁ = 400 Hz (0.10 ± 0.04 %/s, p < 0.05 compared to others). The rate was higher for R_1ρ at ω₁ = 80 Hz (0.14 ± 0.05 %/s at TSL = 50 ms) and for the T₂-prep sequence (0.17 ± 0.06 %/s) though their difference did not reach statistical significance. For the averaged time-course, the derivative of the BOLD signal peaked immediately at 2 s (17th dynamic), while the derivatives of T2-prepped signal as well as both R_1ρ –weighted signals peaked at 4.4 s (18th dynamic).

Fig. 5.

Temporal characteristics of the evoked response using BOLD (red), T2-prep (broken black line), R1ρ-weighted fMRI at ω1 = 80 Hz (blue dashed line), and at ω1 = 400 Hz (green thick line). Black line denotes the duration of stimulus. Error bars indicate standard error and are collapsed across multiple runs and all subjects. Only the first three blocks were considered for evaluating the time course from the T2-prepped and R1ρ-weighted signals to match the BOLD data. The signal peaked at 4.4 s for T2-prepped and R1ρ-weighted signals after stimulus while it peaked after 2 s for the gradient echo BOLD data.

4. Discussion

Although spin-locking has been used in fMRI before [30,42], the behavior of BOLD signals at different locking fields has not been previously assessed, and the ability to selectively edit diffusion related dephasing effects amongst susceptibility variations of different scales has not been previously explained or exploited. We have shown that R_1ρ–weighted fMRI at low locking fields provides functional contrast in the visual cortex similar to spin echo acquisitions, with lower percent signal changes and longer rise times than gradient echo BOLD signals, and that the BOLD signals decrease in size but rise even slower with higher locking fields. The coarse resolution of this study does not allow us to determine the exact contribution of microvascular signals to the T1rho contrast. We however, interpret these findings in terms of a simple theory that the contribution of diffusion related dephasing to R_1ρ reduces with the application of spin locking fields. This decrease depends on the spin locking amplitude, the average spatial separation of the susceptibility variations, and the spatial gradients of these variations. Intuitively, the spin lock amplitude determines the frequency of precession about the locking field (ω₁), while the correlation time defined earlier (τ_c = 1/Dq²) characterizes the time to diffuse a characteristic dimension (≈1/q) of the medium. The degree of dephasing then depends on whether the product ω₁τ_c is ≫ 1, ≈1 or ≪ 1, defining three regimes in much the same manner as may be derived for spin and gradient echo sequences using Anderson-Weiss mean field theory [11].

We have demonstrated the feasibility of employing R_1ρ contrast to study evoked vascular responses in the visual cortex. Previous studies employed R_1ρ contrast at a single (relatively high) locking field [30,31,42]. Borthakur et al. [30,31] used a combination of R_1ρ and R_2* to enhance image quality, SNR, and functional contrast of MR images using higher locking fields (500 Hz) with longer TEs than the current study. Furthermore, their approach used an EPI readout and thus suffered characteristic signal losses due to field inhomogeneities and image distortions. Our study used a TSE read-out to provide high SNR, distortion free single slice images with only R_1ρ weighted contrast. It is also important to note that in single-slice acquisitions, only in-plane motion can be corrected, while through-plane motion cannot be evaluated. We believe that in our study, through plane motion was minimal as evinced from the activation maps. Significant through-plane motion in the form of artifactual activation/deactivation through the imaging slice was not observed in our study in any subject. Extension of this approach to whole-brain, multi-slice imaging is feasible but will require longer acquisition times. Furthermore, extension of fast spin-echo acquisition is limited due to increased specific absorption rate (SAR) as well as increased magnetization transfer (MT) effects. EPI or other fast acquisitions (e.g. 3D Fast Field Echo with high SENSE factors) [43] are then more feasible options.

Higher spin locking fields have also been used more recently in R_1ρ weighted fMRI. Magnotta et al. (2012) used ω₁ = 400 Hz and attributed the functional contrast to pH changes possibly associated with transient lactate production. However, the production and disappearance of lactate in block paradigms remains controversial, and Magnotta et al. ruled out a BOLD effect in their studies based on the lack of BOLD signals from ex vivo samples. However, we suggest those experiments were not sufficiently definitive because the magnitude of dephasing effects from diffusion is highly dependent on the geometry of the vasculature and is not the same in a homogeneous suspension of blood. Further investigation by [32] concluded that R_1ρ weighted fMRI signals at high fields (>3 T) and spin locking fields in the range of 500 – 2000 Hz, comprise of nonhemodynamic changes related to shifts in metabolite concentrations during functional activity, but those chemical exchange effects occur and are separable at higher locking fields as demonstrated in our recent studies [24,25].

The rate of R_1ρ –weighted signal increases measured by [32] were much faster than BOLD, indicating non-vascular origins of the signal contrast. Previous studies at higher field have shown that spin echo BOLD signals rise more slowly than gradient echo signals because they are more affected by extravascular effects of diffusion around small vessels, compared to gradient echo BOLD signals that include static dephasing and larger vessel contributions. Although our study lacked the requisite temporal resolution, the T₂-prepped data are consistent with the above findings. The slower rates of increase in the R_1ρ –weighted signals, and the further decrease with locking field, suggests that larger vessel contributions are more selectively edited out and that appropriate choice of locking field amplitude can accentuate specific structures.

5. Conclusion

We have extended our previous work on the effects of diffusion in magnetic field inhomogeneities of varying spatial scale on R_1ρ to selectively emphasize the microvascular contribution to functional MRI contrast in vivo. R_1ρ-weighted fMRI produced signal increases similar to spin echo fMRI, offering an alternative to the conventional BOLD EPI acquisitions to increase specificity to the microvasculature. The dispersion of R_1ρ over a range of relatively low spin locking amplitudes may be used to infer the spatial scales of susceptibility gradients.