Inverse Z-spectrum analysis for spillover-, MT-, and T₁-corrected steady-state pulsed CEST-MRI – application to pH-weighted MRI of acute stroke

Abstract

Endogenous chemical exchange saturation transfer (CEST) effects are always diluted by competing effects, such as direct water proton saturation (spillover) and semi-solid macromolecular magnetization transfer (MT). This leads to unwanted T₂ and MT signal contributions that lessen the CEST signal specificity to the underlying biochemical exchange processes. A spillover correction is of special interest for clinical static field strengths and protons resonating near the water peak. This is the case for all endogenous CEST agents, such as amide proton transfer, –OH-CEST of glycosaminoglycans, glucose or myo-inositol, and amine exchange of creatine or glutamate. All CEST effects also appear to be scaled by the T₁ relaxation time of water, as they are mediated by the water pool. This forms the motivation for simple metrics that correct the CEST signal.

Based on eigenspace theory, we propose a novel magnetization transfer ratio (MTR_Rex), employing the inverse Z-spectrum, which eliminates spillover and semi-solid MT effects. This metric can be simply related to R_ex, the exchange-dependent relaxation rate in the rotating frame, and k_a, the inherent exchange rate. Furthermore, it can be scaled by the duty cycle, allowing for simple translation to clinical protocols. For verification, the amine proton exchange of creatine in solutions with different agar concentrations was studied experimentally at a clinical field strength of 3 T, where spillover effects are large. We demonstrate that spillover can be properly corrected and that quantitative evaluation of pH and creatine concentration is possible. This proves that MTR_Rex is a quantitative and biophysically specific CEST-MRI metric. Applied to acute stroke induced in rat brain, the corrected CEST signal shows significantly higher contrast between the stroke area and normal tissue, as well as less B₁ dependence, than conventional approaches.

INTRODUCTION

Chemical exchange saturation transfer (CEST) exploits the chemical exchange of labile protons, either in metabolites or contrast agents, to transfer labeled magnetization to the water pool (1–3). The CEST signal is obtained by water signal acquisition after selective radiofrequency (RF) irradiation at the resonance frequency of an exchanging proton pool. Together with a reference scan, the water signal decrease caused by saturation transfer can be determined. This leads to increased sensitivity mediated by the accumulation of the labeled state in the water pool. As the labeling of the exchanging protons can be performed selectively by RF irradiation at the specific chemical shift, CEST yields biochemical information on living tissue. Several CEST-MRI approaches have been reported that enable the monitoring of cellular metabolites in vivo: amide proton-CEST (4), creatine-CEST (5,6), glutamate-CEST (7), glycosaminoglycan-CEST (8–10), glucose-CEST (11) and also many paramagnetic exogenous agents (3). Some exchange processes are distinctly pH sensitive and allow pH-weighted MRI (4,12–14). This makes CEST imaging interesting for the characterization of ischemic lesions as they occur in stroke where a decrease in the amide proton transfer (APT) peak has been reported (15–17).

However, the RF irradiation used for labeling also excites nearby resonances. Especially for clinical static field strengths and endogenous amide, amine and hydroxyl protons, CEST pools resonate close to the water peak with the consequence that direct saturation of the water protons surpasses the CEST effect. The impact of direct water saturation on the CEST pool resonance is called ‘spillover’. Moreover, magnetization transfer (MT) effects, owing to broad macromolecular resonances, are apparent even far away from the water peak, and overlay the CEST effect. Both spillover and MT effects increase with increasing RF irradiation amplitude B₁ (18,19). Likewise, solute labeling (and hence the possible maximum CEST effect) also increases with B₁ (20). Thus, CEST sequences are often optimized by variation of B₁ to yield maximum contrast (7,10,11), but the signal at optimal B₁ is highly sensitive to spillover (21) and correction is especially required in this optimal case. Finally, as mediated by the water pool, the water T₁ scales with the strength of the whole effect.

To assess the physiological relevance of any MRI contrast, artifacts and sources of non-specific contrast must be identified, explained and eliminated as far as possible. This problem is an active area of research in the CEST community and several approaches have been suggested to correct for the described effect: simple asymmetry analysis (4), Lorentzian line fits (22), Lorentzian differences (23,24) and more sophisticated isolation approaches, such as double-frequency irradiation (25,26) and chemical exchange rotation transfer (CERT) (27,28). However, even CEST signals isolated from concomitant effects, such as T₂ or MT, can still be diluted by them (19,20). Thus, isolation often yields an already diluted effect, and generally does not imply spillover and MT correction: these are different issues.

Therefore, we propose a new evaluation method which is simply applicable to Z-spectrum data and able to both isolate and correct the effects on the CEST signal from spillover, MT and T₁. The approach uses the inverse metric of the Z-spectrum (1/Z) to obtain spillover- and MT-corrected CEST-MRI data. Our approach is based on the equivalence of spin-lock (SL) and CEST experiments (29). By employing a solution of Santyr et al. (30) proposed for pulsed SL, we extend this equivalence to pulsed CEST which is required in applications to clinical MR scanners. As a proof of principle, we present data from creatine–agar model solutions, but expect that this approach will be generally applicable to all types of CEST experiments driven to steady state. We also demonstrate that the inverse metric 1/Z is useful not only for corrections, but also for quantitative CEST-MRI. Finally, we apply the correction to APT imaging in acute stroke, where a pure exchange-weighted contrast might help in the characterization of lesions.

THEORY

The Z-spectrum and useful magnetization transfer ratios (MTRs) for continuous wave (cw)-CEST

We first compile results of cw theory (31,32) for two exchanging pools, the abundant pool ‘a’ (water pool) with thermal magnetization M_0a and the rare pool ‘b’ (CEST pool) with thermal magnetization M_0b. For most metabolite–water systems, an asymmetric population given by the proton fraction f_b = M_0b/M_0a < 1% can be assumed. Both pools undergo longitudinal and transverse relaxation with rates R_1a, R_2a, R_2b. The longitudinal relaxation of pool b, R_1b, is assumed to be small compared with the exchange rate, and is neglected in the following (32). The pools are coupled by the exchange rate k_b and the back exchange rate k_a = f_bk_b. The RF irradiation amplitude (ω₁ = γB₁) and offset frequency from water (Δω) define the off-resonant saturation, which leads to an effective field vector $\stackrel{\rightharpoonup }{{\omega }_{\text{eff}}}=({\omega }_{\text{eff}},0,\mathrm{\Delta }\omega )$ tilted by the angle θ =tan⁻¹(ω₁/Δω) off the z axis (18,22). The steady-state magnetization after saturation M_sat, normalized by the thermal magnetization M_0a, was named the Z-value by Woessner et al. (33). The Z-spectrum or Z(Δω) is given by (32):

$$Z(\mathrm{\Delta }\mathrm{\omega })=\frac{M_{\text{sat}}(\mathrm{\Delta }\mathrm{\omega })}{M_{0\mathrm{a}}}={\text{cos}}^2\theta \frac{R_{1\mathrm{a}}}{R_{1\rho }}$$ [1]

where R_1ρ is the longitudinal relaxation rate of the water pool in the rotating frame:

$$R_{1\rho }=R_{\text{eff}}+R_{\text{ex}}$$ [2]

R_ex is the exchange-dependent relaxation in the rotating frame; R_eff corresponds to R_1ρ of the water pool when there is no exchange and reads:

$$R_{\text{eff}}=R_{1\mathrm{a}}{\text{cos}}^2\theta +R_{2\mathrm{a}}{\text{sin}}^2\theta$$ [3]

This rate arises from the relaxation caused by direct water saturation and is the origin of the spillover effect. If a symmetric MT is also apparent, R_eff can be extended (32,34) by an exchange relaxation for MT to $R_{\text{eff}}=R_{1\mathrm{a}}{\text{cos}}^2\theta +R_{2\mathrm{a}}{\text{cos}}^2\theta +R_{\text{ex}}^{\mathrm{M}\mathrm{T}}$. As we remove R_eff in the following, the exact knowledge of R_2a or $R_{\text{ex}}^{\mathrm{M}\mathrm{T}}$ is not important, as long as we have a reference value with the same R_eff. In agar phantoms, R_eff stays symmetric in Δω and the opposite frequency can be used. In vivo, the baseline can be estimated e.g. by a three-point method [Equation [21]].

The exchange weighting in CEST-MRI is induced by the rate R_ex. Hence, an appropriate evaluation method must provide direct access to R_ex. R_ex can be approximated by (32):

$$R_{\text{ex}}(\mathrm{\Delta }{\omega }_{\mathrm{b}})=k_{\mathrm{b}}{f}_{\mathrm{b}}·\alpha \frac{\frac{{\mathrm{\Gamma }}^2}{4}}{\frac{{\mathrm{\Gamma }}^2}{4}+\mathrm{\Delta }{\omega }_{\mathrm{b}}^2}$$ [4]

where Δω_b is the frequency offset with respect to the CEST pool b. The labeling efficiency can be approximated by (32):

$$\alpha =\frac{{\omega }_1^2}{{\omega }_1^2+k_{\mathrm{b}}(k_{\mathrm{b}}+R_{2\mathrm{b}})}$$ [5]

R_ex is a Lorentzian function of Δω_b with its maximum at Δω_b=0, and linewidth:

$$\mathrm{\Gamma }=2\sqrt{\frac{k_{\mathrm{b}}+R_{2\mathrm{b}}}{k_{\mathrm{b}}}{\omega }_1^2+{(k_{\mathrm{b}}+R_{2\mathrm{b}})}^2}$$ [6]

A useful quantity is the asymmetric MTR (MTR_asym), which attempts to isolate the contributions of CEST effects to the Z spectra using a reference scan without CEST effects, which can be the scan at opposite frequency or the fit of direct water saturation (23,24).

For agar phantoms, we use the opposite frequency signal as a reference. To abbreviate the following relations, we define the label scan around the resonance of pool b as Z_lab = Z(+Δω) and the reference scan at the opposite frequency with respect to water as Z_ref = Z(−Δω). For Z_ref = Z(−Δω), the effective relaxation R_eff (−Δω) is unchanged, i.e. R_eff(−Δω) = R_eff(Δω). Hence, R_ex is only important for the labeling scan and R_ex can be neglected for the opposite frequency. Thus, the opposite frequency can be used as a reference scan Z_ref = Z(−Δω). [This reasoning assumes that: (i) R_eff is symmetric and no MT asymmetry or additional exchanging pools at –Δω are present; and (ii) the width Γ of R_ex (Δω_b) is smaller than the chemical shift (Γ < δ_b) of the corresponding pool.]

For cw steady-state CEST, it has been shown previously (32) that there are different MTR normalizations possible. The most common is the subtraction of the Z-values of the label and reference scan, giving the asymmetry of the Z-spectrum:

$$\mathrm{M}\mathrm{T}{\mathrm{R}}_{\text{asym}}=Z_{\text{ref}}-Z_{\text{lab}}={\text{cos}}^2\theta \frac{R_{\text{ex}}{R}_{1\mathrm{a}}}{R_{\text{eff}}(R_{\text{eff}}+R_{\text{ex}})}$$ [7]

A reported spillover-corrected evaluation proposed by Liu et al. (35,36) normalizes with the reference value:

$$\mathrm{M}\mathrm{T}{\mathrm{R}}_{\text{normref}}=\frac{Z_{\text{ref}}-Z_{\text{lab}}}{Z_{\text{ref}}}=\frac{R_{\text{ex}}}{R_{\text{eff}}+R_{\text{ex}}}$$ [8]

A probabilistic combined model (pcm) for Z-spectra, able to separate CEST from spillover and MT, of Zaiss et al. (22) can also be written as an MTR:

$$\mathrm{M}\mathrm{T}{\mathrm{R}}_{\mathrm{p}\mathrm{c}\mathrm{m}}=\frac{Z_{\text{ref}}-Z_{\text{lab}}}{Z_{\text{ref}}-Z_{\text{lab}}+Z_{\text{lab}}{Z}_{\text{ref}}}=\frac{R_{\text{ex}}}{{\text{cos}}^2\theta ·R_{1\mathrm{a}}+R_{\text{ex}}}$$ [9]

This evaluation easily leads to the ideal proton transfer rate (PTR) = k_a/(k_a + R_1a) (1,37). However, the straightforward way to separate for R_ex is by subtraction of the inverse Z-values:

$$\mathrm{M}\mathrm{T}{\mathrm{R}}_{R\text{ex}}=\frac{1}{Z_{\text{lab}}}-\frac{1}{Z_{\text{ref}}}=\frac{R_{\text{ex}}}{{\text{cos}}^2\theta ·R_{1\mathrm{a}}}$$ [10]

MTR_asym contains a quadratic term of R_eff and MTR_normref contains a linear term of R_eff in the denominator, while MTR_pcm and MTR_Rex are free of R_eff terms and therefore particularly free of R_2a and symmetric MT contributions.

The Z-spectrum and useful MTRs for pulsed-CEST

The assumption of R_1ρ decay during the pulse (pulse duration t_p) and R_1a recovery during RF off (interpulse delay time t_d) leads to the following formula for the steady state in a pulsed SL experiment (30):

$$Z_{\text{pulsed}}^{\mathrm{s}\mathrm{s}}(\mathrm{\Delta }\mathrm{\omega })=\frac{(1-{\mathrm{e}}^{-R_{1\mathrm{a}}·t_{\mathrm{d}}})-\frac{R_{1\mathrm{a}}·\text{cos}\theta }{R_{1\rho }(\mathrm{\Delta }\mathrm{\omega })}(1-{\mathrm{e}}^{R_{1\rho }(\mathrm{\Delta }\mathrm{\omega })·t_{\mathrm{p}}})}{{\mathrm{e}}^{R_{1\rho }(\mathrm{\Delta }\mathrm{\omega })·t_{\mathrm{p}}}-{\mathrm{e}}^{-R_{1\mathrm{a}}·t_{\mathrm{d}}}}$$ [11]

This is the result of Santyr et al. (30) in our notation. Assuming small arguments of the exponential functions, we employ exp(x) ≅ 1 + x and obtain – with the duty cycle (DC) = t_p/(t_p + t_d) – an expression for the normalized steady–state magnetization Z^ss which is similar to the result for the cw case:

$$Z_{\text{pulsed}}^{\mathrm{s}\mathrm{s}}(\mathrm{\Delta }\mathrm{\omega })\approx \frac{R_{1\mathrm{a}}(1-\mathrm{D}\mathrm{C}+\text{cos}\theta ·\mathrm{D}\mathrm{C})}{R_{1\rho }^{\text{pulsed}}(\mathrm{\Delta }\mathrm{\omega })}$$ [12]

where:

$$R_{1\rho }^{\text{pulsed}}(\mathrm{\Delta }\mathrm{\omega })=R_{1\rho }(\mathrm{\Delta }\mathrm{\omega })·\mathrm{D}\mathrm{C}+R_{1\mathrm{a}}·(1-\mathrm{D}\mathrm{C})$$ [13]

Assuming cos θ = 1 and employing Equations [12] and [13] for MTR_pcm [Equation [9]] and MTR_Rex [Equation [10]] leads to the pulsed MTRs:

$$\mathrm{M}\mathrm{T}{\mathrm{R}}_{\mathrm{p}\mathrm{c}\mathrm{m}}=\frac{R_{\text{ex}}·\mathrm{D}\mathrm{C}}{R_{1\mathrm{a}}+R_{\text{ex}}·\mathrm{D}\mathrm{C}}$$ [14]

$$\mathrm{M}\mathrm{T}{\mathrm{R}}_{R\text{ex}}=\frac{R_{\text{ex}}·\mathrm{D}\mathrm{C}}{R_{1\mathrm{a}}}$$ [15]

Therefore, the pulsed MTRs are only altered by the DC as a prefactor of R_ex against the cw case [cf. Equations [9] and [10]]. Thus, these spillover and MT corrections are likewise applicable to pulsed CEST.

Quantitative parameter determination

Equation [10] [with the expected parameter dependences as described in Equation [15]] provides a robust measure for qualitative contrast that avoids the effects from direct water saturation and exchange from symmetric macromolecular MT effects, and is hence superior to the current standard MTR_asym. However, ideally we would like a metric that quantitatively reports on a fundamental sample parameter. To extend this spillover correction method to a quantification method, we define the apparent exchange-dependent relaxation (AREX):

$$\mathrm{A}\mathrm{R}\mathrm{E}\mathrm{X}=\mathrm{M}\mathrm{T}{\mathrm{R}}_{R\text{ex}}{R}_{1\mathrm{a}}$$ [16]

AREX should yield R_ex· DC, which is given by DC, by Equation [4], and the labeling efficiency α [Equation [5]]. We can assume the maximum labeling efficiency (α ≈ 1) as long as the conditions k_b << ω₁ and R_2b << ω₁ hold [Equation [5]]. In this full-saturation limit, when applying irradiation at the b-pool resonance, R_ex = k_bf_b = k_a [Equations [7] and [12]] and hence:

$$\mathrm{A}\mathrm{R}\mathrm{E}\mathrm{X}=k_{\mathrm{a}}·\mathrm{D}\mathrm{C}$$ [17]

Instead of modeling a pulse train by an average B₁ power, we now obtain a DC weighting of an average R_ex during the pulse. The implicit assumption that the average R_1ρ during the pulse equals the cw relaxation rate is discussed below.

In summary, two conditions must be valid for AREX/DC = k_a: First, the full–saturation limit ω₁ >> k_b and, second, R_2b and the peak width [Equation [6]] must be smaller than the chemical shift difference to water (Γ < δ_b). Considering amide protons of proteins at B₀ = 3 T, the CEST pool parameters are k_b ~ 30 s^–1 and δ_b = 3.5 ppm (=447·2π s⁻¹) (1,4). As a model for amide exchange, we employ amine protons of creatine at lower pH (6.2–6.6) to obtain a comparable exchange rate (k_b ~ 30–60 s⁻¹) (19). The smaller chemical shift δ_b = 1.9 ppm (=242·2π s⁻¹) challenges our method for spillover correction and is therefore a crucial test. For 1 µT < B₁ < 5 µT, both conditions are well fulfilled for creatine amine and amide protons:

$$k_{\mathrm{b}}=50{\mathrm{s}}^{-1}<<{\omega }_1=\frac{B_1}{\mu \mathrm{T}}·42.6·2\pi {\mathrm{s}}^{-1}\cong \frac{\mathrm{\Gamma }}{2}<\frac{{\delta }_{\mathrm{b}}}{2}=121·2\pi {\mathrm{s}}^{-1}$$

In general, if peaks are broad and other pools ‘c’ are involved, the reference scan is also contaminated by non-zero exchange-dependent relaxation terms R_ex.ref = R_ex(−Δω) in addition to the on-resonant term R_ex.lab = R_ex(Δω). Thus, AREX yields:

$$\mathrm{A}\mathrm{R}\mathrm{E}\mathrm{X}=R_{\text{ex},\text{lab}}^{\mathrm{b}}-R_{\text{ex},\text{ref}}^{\mathrm{b}}+R_{\text{ex},\text{lab}}^{\mathrm{c}}-R_{\text{ex},\text{ref}}^{\mathrm{c}}$$ [18]

instead of R_ex,lab. Although affected by pool c and therefore no longer being selective, the resulting MTR_Rex is still free from symmetric spillover effects, and hence an apparent R_ex (AREX), which is still a pure exchange-dependent parameter.

pH mapping

Under the assumption of full saturation, AREX/DC is given by k_bf_b. Therefore, AREX of APT can be used to calculate the exchange rate by the formula previously derived by Sun et al. (38):

$$\mathrm{p}\mathrm{H}(\mathit{\text{in vivo}})=6.4+{\text{log}}_{10}\left(\frac{\mathrm{A}\mathrm{R}\mathrm{E}\mathrm{X}/\mathrm{D}\mathrm{C}}{f_{\mathrm{b}}·5.57}\right)$$ [19]

For APT, f_b = 1 : 867 has been reported (38). For amine exchange of creatine, the k(pH) dependence was given by Goerke et al. (39). It can be rearranged to yield the absolute pH employing an AREX map:

$$\mathrm{p}\mathrm{H}(19°\mathrm{C})={\text{log}}_{10}\left(\frac{\mathrm{A}\mathrm{R}\mathrm{E}\mathrm{X}/\mathrm{D}\mathrm{C}}{f_{\mathrm{b}}·1.4615}\right)$$ [20]

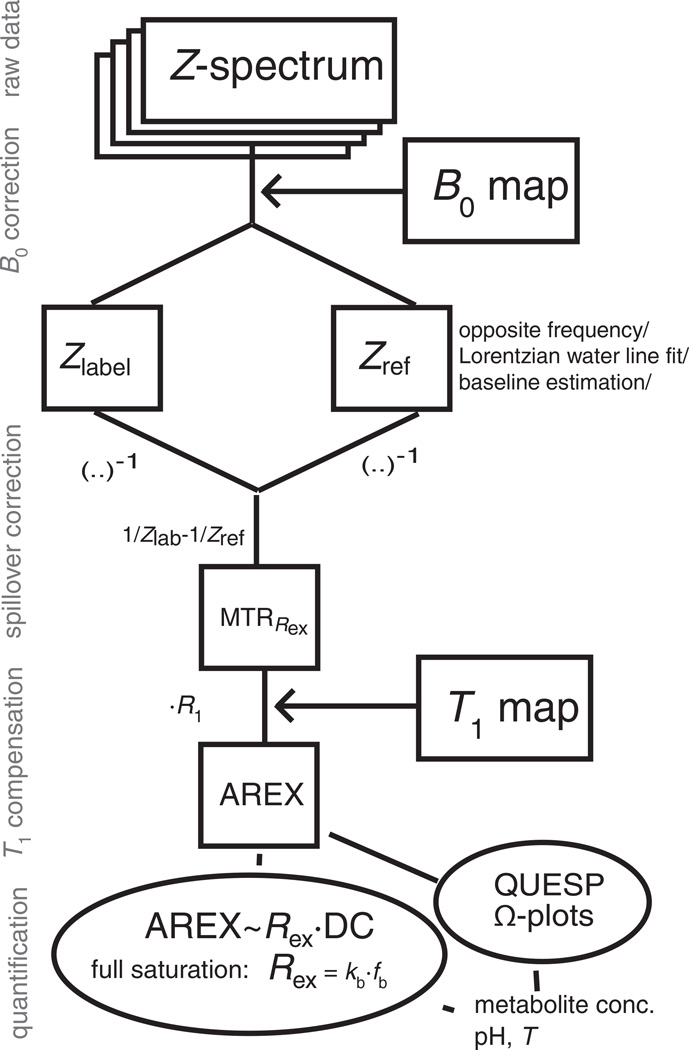
A flow chart of how the theory and evaluation methods are applied to the raw data is given in Fig. 1.

Figure 1.

Scheme of data evaluation for spillover- and T₁-compensated chemical exchange saturation transfer (CEST). Only simple matrix operations are performed to obtain the apparent exchange-dependent relaxation (AREX) contrast. The step of defining a suitable reference value Z_ref is crucial. DC, duty cycle; MTR_Rex, spillover-corrected magnetization transfer ratio yielding R_ex; QUESP, quantification of exchnage by saturation power.

METHODS

The proposed spillover correction based on the inverse metric was tested in CEST experiments with creatine model solutions at B₀ = 3 T, as well as with in vivo rat measurements at 9.4 T.

Phantoms

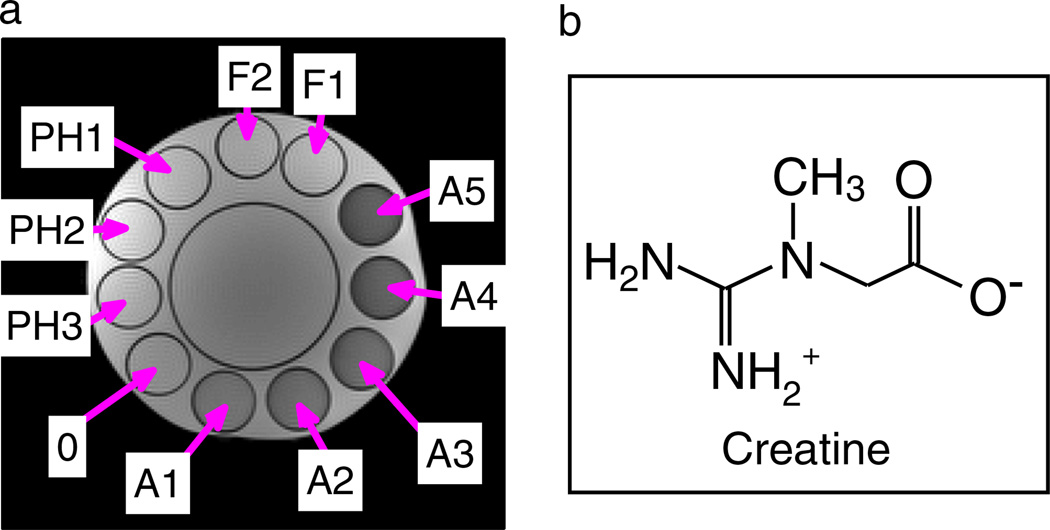
Eleven phantoms containing phosphorus-based sodium–potassium buffer at different pH values were measured. A transverse image is shown in Fig. 2 and their properties are listed in Table 1. Creatine monohydrate (Sigma–Aldrich, Steinheim, Germany) of 55.5mm concentration was added to each 50–mL tube. Two tubes had different creatine concentrations: F1, (2/3) × 55.5mm; F2, (1/3) × 55.5mm.

Figure 2.

(a) Turbo spin echo image of the phantom employed (for details, see Table 1). 0 is the reference solution with 55.5mm creatine and phosphate-buffered saline at pH 6.38 and without agar. The Ax phantoms differ from phantom 0 by increasing agar concentration (0.2–1%). The PHx phantoms differ from phantom 0 by altered pH (6.2, 6.3, 6.6). The Fx phantoms have different creatine concentrations [F1, 1/3 * 55.5 mM; F2, 2/3 * 55.5 mM]. (b) Zwitterionic form of aqueous creatine occurring at low pH.

Table 1.

Phantoms employed, as depicted in Fig. 2, with fitted values from region of interest (ROI) evaluations and exchange rates of creatine predicted by water exchange spectroscopy (WEX) studies (39). Fits by a two-pool Bloch–McConnell simulation were performed simultaneously for five Z-spectra obtained with B₁ = 0.2, 0.4, 0.6, 0.8 and 1.0 µT in each ROI

Phantom/ROI	pH	[Cr] (mm)	[Ag] (%)	kb (WEX) (s−1)	kb (CEST) (s−1)	fb (%)	R2b (s−1)	R2a (s−1)	T1a (s)
0	6.38	55.5	0	35.1	33.8	0.22	40.3	0.60	2.92
A1	6.38	55.5	0.2	35.1	–	–	–	2.47	2.99
A2	6.38	55.5	0.4	35.1	–	–	–	3.57	2.97
A3	6.38	55.5	0.6	35.1	–	–	–	4.82	2.92
A4	6.38	55.5	0.8	35.1	–	–	–	6.23	2.87
A5	6.38	55.5	1.0	35.1	–	–	–	7.58	2.83
F1	6.38	55.5 (1/3)	0	35.1	38.5	0.073	58	0.42	3.00
F2	6.38	55.5·(2/3)	0	35.1	46.5	0.13	53	0.42	2.99
PH1	6.21	55.5	0	23.72	31.6	0.18	49	0.44	2.91
PH2	6.32	55.5	0	30.6	34.8	0.20	48	0.43	2.93
PH3	6.61	55.5	0	59.6	63.0	0.21	54	0.46	2.93

−, missing fitting data when the two-pool model was insufficient.

To vary the conditions for spillover and MT, 0.2–1% agar was added to a 55.5mm creatine solution at pH 6.38 (A1–A5, ‘solidified phantoms’). The pH value did not change during the heating process and addition of agar. Phantom 0 contained no agar, and PH1–PH3 were controls with different pH values of 6.2, 6.3 and 6.6, respectively.

Phantom parameters were estimated for a two-pool model by a full numerical fit of the Z spectra obtained for different RF amplitudes B₁ simultaneously, similar to the Quantification-of-exchange-by-saturation-power-method (QUESP) of McMahon et al. (40).

In vitro MRI experiments

Phantom imaging was performed on a 3-T whole-body MR scanner (Magnetom TIM-TRIO; Siemens, Erlangen, Germany). Z-spectra were obtained after saturation by a train of 80 Gaussian-shaped pulses with a duration t_p = 100 ms for each pulse and an interpulse delay t_d = 100 ms (DC = 50%) at B₁ = flip angle/(γt_p) = 0.2–2 µT, followed by single-shot turbo spin echo imaging (field of view, 220mm²; matrix, 192 × 192; in-plane resolution, 1.1 × 1.1 × 4mm³). Z-spectra were B₀ corrected employing a water saturation shift referencing (WASSR) map (41). After B₀ correction, the MTRs according to Equations [7], [8], [9] and [10] were calculated pixel by pixel and by region of interest (ROI) evaluation, employing the opposite frequency as reference scan Z_ref. MTR_Rex was compared with analytical R_ex and k_a values determined by the numerical fit. Fitting of Z-spectra was performed by stepwise matrix solution (33) of the two-pool Bloch–McConnell equations.

T₁-weighted MR images were acquired by a saturation recovery gradient echo sequence (TE = 4ms; TR = 8ms; 4 shots; 4 averages; field of view, 220mm²; matrix, 256 × 256; in-plane resolution, 0.9× 0.9 × 4 mm³; flip angle, 8°). Altogether, 21 contrasts at different recovery times between 50ms and 5 s were fitted to obtain T₁ maps.

T₂-weighted MR images were acquired by a spin echo sequence with 32 echo delays (TE = 11–352ms; TR= 6 s; field of view, 220 mm²; matrix, 192 × 192; in-plane resolution, 1.1× 1.1× 4 mm³; flip angle, 180°). A pixel-by-pixel logarithmic fit was applied to obtain T₂ maps.

Animal preparation

All animal-related procedures were approved by the Institutional Animal Care and Use Committee at Vanderbilt University. The middle cerebral artery occlusion model was adapted on spontaneously hypertensive male rats (Charles Rivers Laboratory, Wilmington, MA, USA) weighing between 275 and 300 g, as described previously (42). Specifically, rats were anesthetized with isoflurane (3% for induction and 2% during surgery) via a vaporizer with O₂. A midline neck incision was made and the common, external and internal carotid arteries were identified on the right side and isolated from the surrounding structures. The proximal branches of the external carotid artery were ligated and an arteriotomy was made in the external carotid artery. A 0.37-mm-diameter silicon-coated 4–0 nylon suture (Doccol Corporation, Redlands, CA, USA) was introduced into the vessel and routed into the internal carotid artery. The suture was pushed into the internal carotid artery until a mild resistance was felt and the middle cerebral artery was occluded (at a length of 18–20 mm) and the suture was left there. The body temperature was maintained with a heating pad during surgery. The wound was then closed and buprenorphine was administered for post-operative pain management.

In vivo MRI experiments

Animal imaging was performed 48 h after surgery on a 9.4-T horizontal MRI scanner (Varian, Palo Alto, CA, USA). Bite and head bars were used to secure the animal during imaging to reduce respiration-induced motion artifacts. The rectal temperature was kept at 37 °C using a warming air feedback system. Single-shot echo planar imaging was used for acquisition and a triple-reference imaging scheme (43) was used to reduce echo planar imaging artifacts. Measurement parameters were: matrix size, 64; TE = 28 ms. Pulse train parameters were: t_p = 12.5 ms; B₁ = 0.84 µT; DC = 50%; flip angle, 180°; n = 200.

Evaluation

The opposite frequency is a reasonable choice for the reference scan [Z_ref = Z(−3.5 ppm)] for the phantom study. However, in in vivo Z spectra, the opposite side is contaminated by MT and peaks caused by nuclear Overhauser effects.

Therefore, for the in vivo APT signal, the three-point method proposed by Jin et al. (44) was employed on a pixel-by-pixel basis. Using the same Z_ref:

$$z_{\text{ref}}^{*}=\frac{Z(3.0\mathrm{p}\mathrm{p}\mathrm{m})+Z(4.2\mathrm{p}\mathrm{p}\mathrm{m})}{2};Z_{\text{lab}}=Z(3.5\mathrm{p}\mathrm{p}\mathrm{m})$$ [21]

we define the spillover- and MT-corrected parameter MTR_Rex:

$$\mathrm{M}\mathrm{T}{\mathrm{R}}_{R\text{ex}}^{*}=1/Z_{\text{lab}}-1/Z_{\text{ref}}^{*}$$ [22]

and, according to Equation [16], also the T₁ relaxation-compensated parameter AREX*. To enhance sensitivity for ROI evaluations, the MTR values of 3.4, 3.5 and 3.6ppm were averaged using Z_ref from a linear interpolation of the points at 3 and 4.2 ppm.

RESULTS

This section is divided into three parts. First, we present the outcome of Z-spectroscopy of the solidified phantoms and how the different metrics allow for spillover correction. Second, we show the quantitative metric AREX and how the exchange rate and pH mapping can be obtained after compensation for effects of T₁ relaxation. Third, the metrics are applied to in vivo data of stroke in rat brain.

Spillover correction

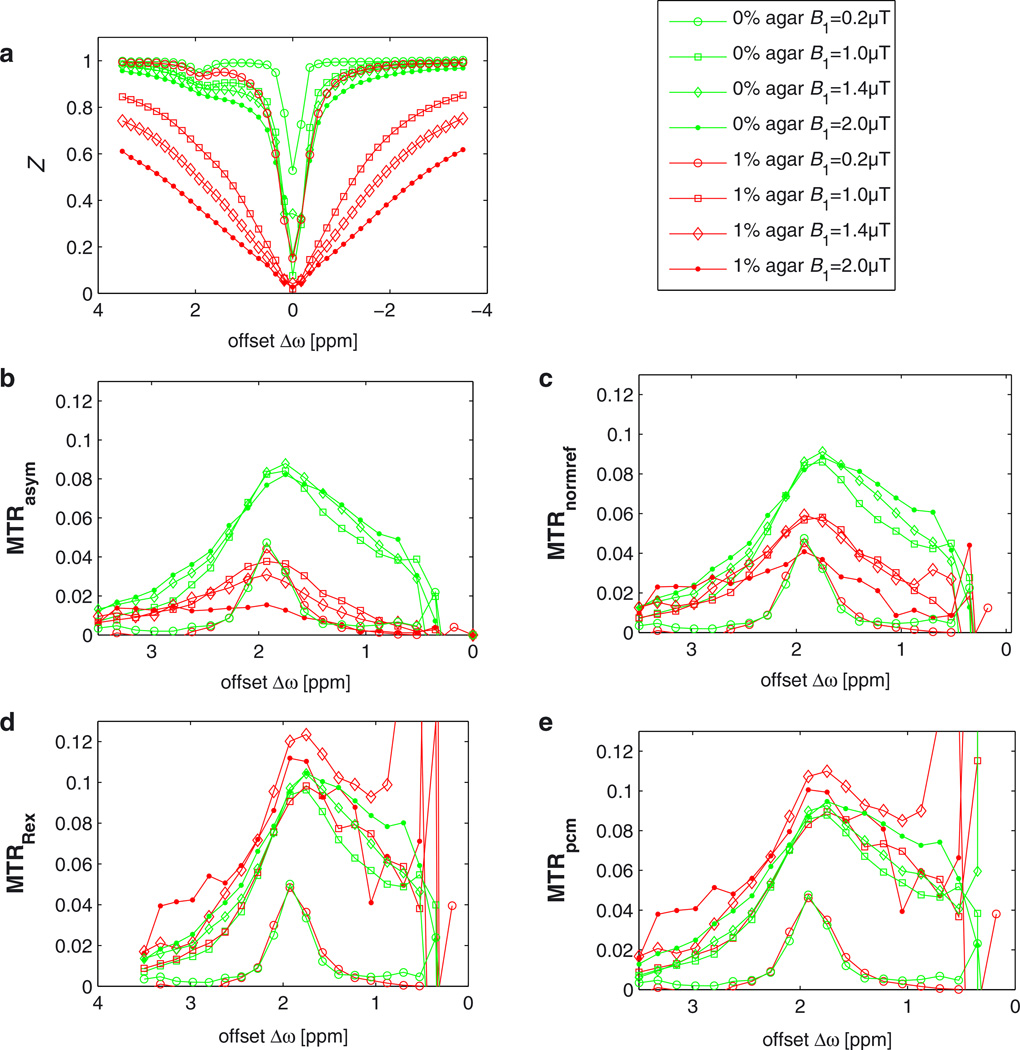
Figure 3a shows distinct effects in the Z-spectrum on addition of 1% agar (phantom A5) in experiments at B₀ = 3 T. The corresponding asymmetry is strongly diluted compared with the creatine solution without agar (phantom 0) (MTR_asym, Fig. 3b). Even in the case of full saturation of the CEST pool (B₁ > 1 µT), we still observe a strong dependence of MTR_asym on B₁ in the solidified phantom. MTR_normref (Fig. 3c) provides an enhancement of the signal of the solidified phantom, but displays an underestimation of the CEST effect by about 30% and a strong dependence on the amplitude B₁ of the saturating field. Both MTR_pcm and MTR_Rex give very similar values for solidified and non-solidified phantoms. This can be seen not only in the case of on-resonant irradiation on pool b, but also the shape of the CEST peak is coherent with the peak of the control measurement in the absence of agar. This proves the validity of our spillover correction for arbitrary frequency offsets. In the case of full saturation, the dependence of MTR_Rex and MTR_pcm on B₁ is less than 15%, producing a small overestimation of the effect. Near the center of the water proton resonance at 0 ppm, all MTRs show considerable deviations, which are even larger for the inverse MTR_pcm and MTR_Rex. Errors increase tremendously, which is discussed in detail below (Fig. 10).

Figure 3.

(a) Z-spectra obtained with different B₁ values from creatine solutions with 1% agar (red lines, A5) and 0% agar (green lines, 0). Labeling increases with B₁, as does the direct saturation effect. For low B₁ of 0.2 µT (circles), the spillover effect is negligible (a), which explains why the curves overlap for all metrics (b–e). (b) MTR_asym shows strong spillover dilution in the solidified phantom (with agar), whereas MTR_Rex (d) and MTR_pcm (e) are able to correct the dilution so that aqueous and solidified phantoms yield almost the same effect. The spillover correction proposed by Liu et al. (35) (c) [Equation [8]] compensates spillover partially. Error bars are omitted for better visibility; they increase strongly for higher spillover correction, as depicted in Fig. 10.

Figure 10.

Error estimation for the inverse metric. Absolute errors increase with increasing spillover effect. This results from the error propagation of the inverse metric. However, relative errors do not change and therefore the contrast-to-noise ratio is not affected. The systematic spillover deviation is traded with a statistical fluctuation. Original errors were scaled by a factor of one-third to improve visibility.

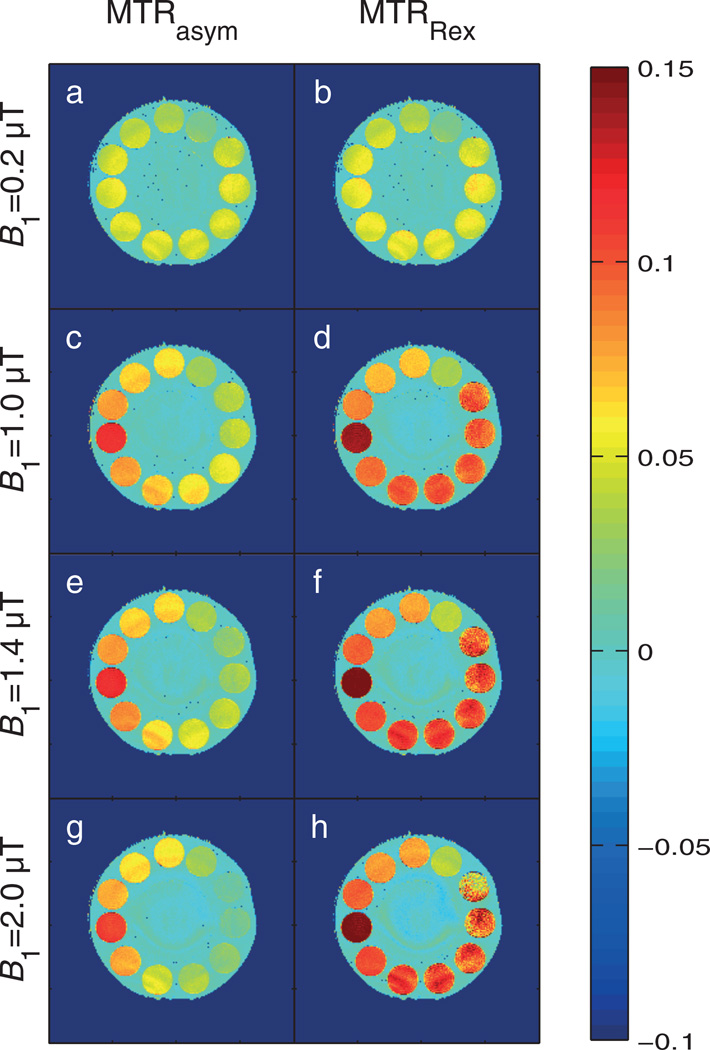
Images of MTR_asym and MTR_Rex at 1.83 ppm display the same relation: Spillover is not critical for small B₁, whereas, for stronger B₁, spillover dilutes MTR_asym significantly. In contrast, MTR_Rex yields a homogeneous contrast up to B₁ = 1.4 µT independent of the agar concentration (Fig. 4). Figure 4 demonstrates the importance of spillover correction, as MTR_asym causes the misinterpretation of diluted signals as changes in pH or concentration. At B₁ = 2 µT, the agar tubes A2 and A3 show a very similar contrast as tube F2 in the presence of one-third of the creatine concentration. For exceedingly high B₁, the contrast-to-noise ratio (CNR) is insufficient and MTR_Rex cannot completely reconstruct the ideal signal from the residual signal. MTR_Rex also enhances the signals from the tubes without agar: different pH and different concentration can therefore be distinguished better after correction.

Figure 4.

Comparison of the normalizations MTR_asym (left column) and MTR_Rex (right column) for B₁ = 0.2, 1.0, 1.4 and 2.0 µT. In each case, the estimation of the chemical exchange saturation transfer (CEST) effect is higher for MTR_Rex. The phantoms with varying agar concentration (0, A1–A5) show similar contrast in MTR_Rex, whereas MTR_asym shows diluted contrast with increasing agar concentration. Differences in pH and creatine concentration are reflected in both magnetization transfer ratios (MTRs). Therefore, MTR_Rex has all the properties of a spillover correction.

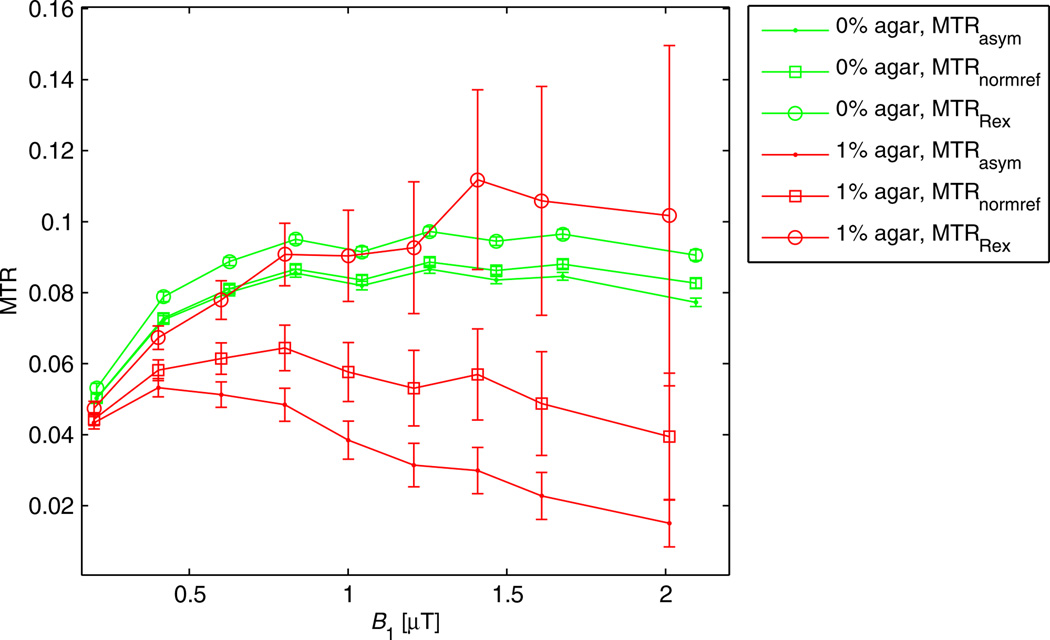
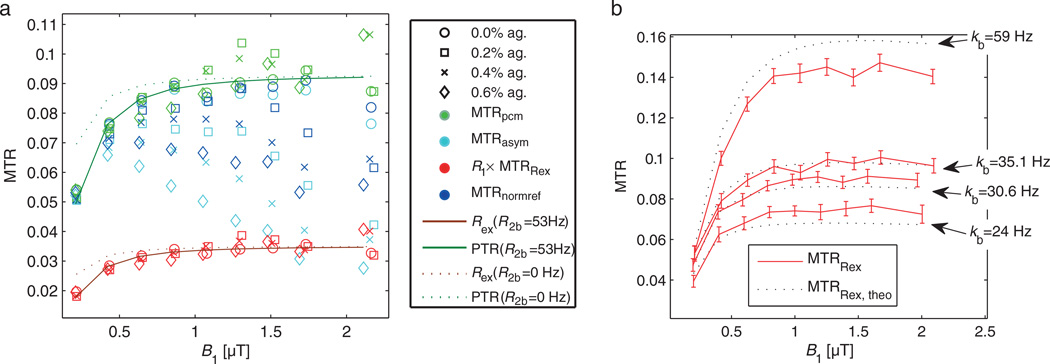
Figure 5 displays MTR as a function of B₁. Using MTR_Rex or MTR_pcm, the plateau of the full-saturation limit is reached, whereas MTR_asym and MTR_normref show the known decrease in the CEST effect caused by spillover dilution induced by MT, T₂ relaxation and B₁. Thus, in the full-saturation limit, a spillover correction is also a first-order B₁ correction.

Figure 5.

(a) Region of interest (ROI) evaluation of ROIs in phantoms 0 and A1–A3 with the proposed spillover corrections. For all agar concentrations and B₁ values, both MTR_pcm (green) and MTR_Rex (red) appear to be in a narrow band around the control without agar (0). MTR_asym (cyan) and MTR_normref (blue) show a much stronger decrease with increasing B₁ and agar. (b) MTR_Rex from data and from theory [Equation [15]] employing parameters of the numerical fit (Table 1, phantoms 0, PH1, PH2, and PH3). The curves match roughly and the dependence on k_b and B₁ is very similar.

Quantification

The numerical Bloch–McConnell fit of ROI-averaged Z spectra for different B₁ values yields the characterization of the phantom parameters listed in Table 1. The values for the exchange rates k_b agree well with water exchange spectroscopy (WEX) data measured by Goerke et al. (39). The relative concentrations f_b are in good agreement with the prepared creatine concentration if the number of exchanging protons per molecule is 4. R_2b values are quite constant at approximately 50 s⁻¹, which is comparable with the exchange rate.

MTR_Rex and MTR_pcm were calculated using B₁, DC, k_b, f_b, R_1a, R_2b and the formula for the rate R_ex [Equation [4]].

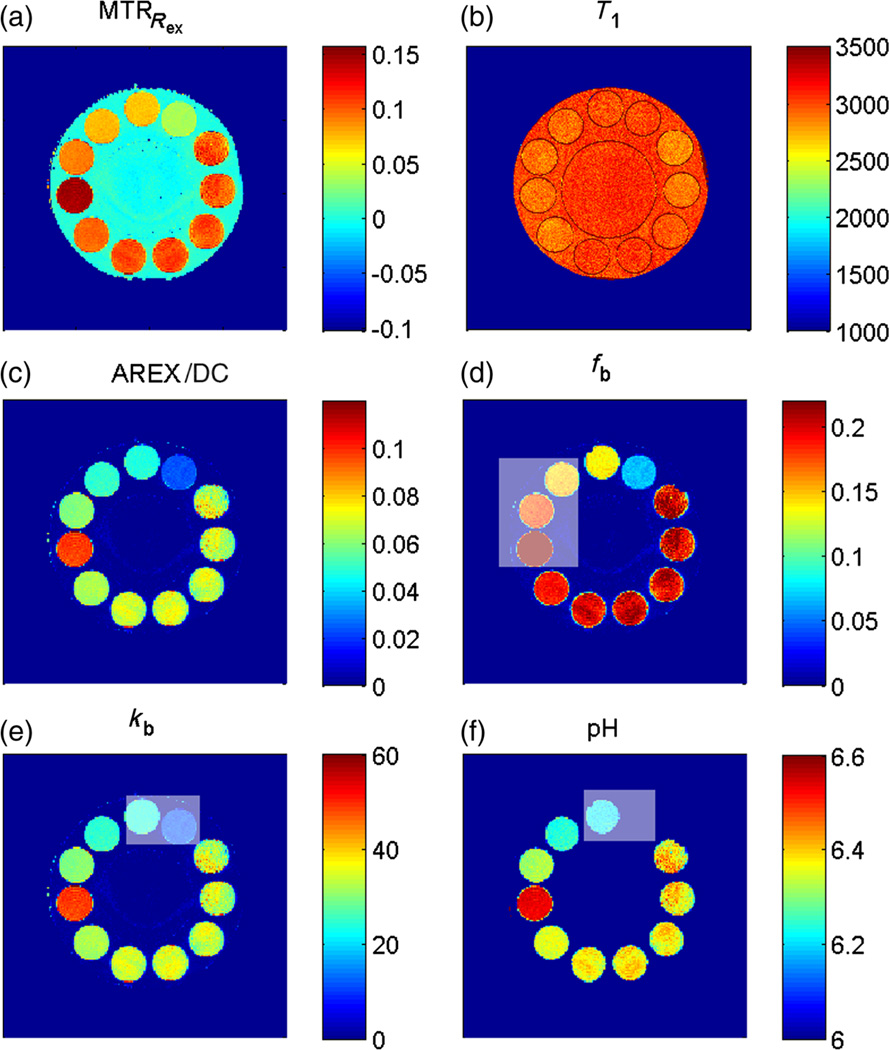
The pulsed approach of Santyr et al. (30) is known to deviate, especially for slow exchange rates (45). Roeloffs et al. (45) showed that a biexponential decay during the break must be modeled to properly extend the model of Santyr et al. (30). For spillover and MT correction, we believe that this is not important as the deviation is still only exchange dependent; for quantification, however, this may have an influence. Nevertheless, the comparison of MTR_Rex calculated from fitting results with MTR_Rex obtained from the data (Fig. 5) shows that the corrected curves can still be interpreted by the analytical solution for MTR_Rex [Equations [10] and [15]] based on the model of Santyr et al. (30). We believe that, because we used 100-ms Gaussian pulses, which end with a low power, the equilibrium between pool a and pool b is not changed greatly directly after the pulse, making the biexponential decay less important. However, this should be studied in detail and may limit our approach for pulsed CEST of slow exchanging systems saturated with different pulse shapes. However, with our pulse parameters, the step from spillover-corrected MTR_Rex to a reliable quantification of the back exchange rate k_a is straightforward by employing Equation [17] (Fig. 6). AREX is therefore proportional to the concentration f_b and the exchange rate k_b. It varies between phantoms F1, F2 and 0, and also between phantoms 0, PH1, PH2 and PH3. AREX yields homogeneous contrast in phantoms 0 and A1–A5. However, a small overestimation of k_a in the agar phantoms compared with the control (0) is observed.

Figure 6.

Quantitative pulsed chemical exchange saturation transfer (CEST)-MRI. (a) MTR_Rex evaluated for B₁ = 1 µT. Employing the T₁ map (b), the spillover-corrected and T₁–compensated apparent exchange-dependent relaxation (AREX) map can be calculated (c). Under the assumption of full saturation, AREX/DC yields a k_a map. (d) f_b map employing the exchange rate for creatine k(pH 6.38, T = 19 °C) = 35 s⁻¹; it suggests that creatine has four exchanging protons. Using f_b = 0.2%, a k_b map (e) can be obtained from AREX, which correlates well with results from water exchange measurements. (f) Therefore, a pH(k_b) map can be obtained using Equation [16]. Gray boxes indicate tubes in which either the concentration or pH was not constant.

Using the exchange rate of creatine protons, k_b(pH 6.38, T= 19 °C) = 35 s⁻¹, measured in WEX experiments (39), a map of the relative proton fraction f_b can be obtained which is valid for the given pH and is in agreement with the fitted results. Together with the prepared creatine concentration (55.5mm), this approach yields the number of labile protons per creatine molecule, N= f_b × [2H₂O]/[Cr]. For pH ≤ 6.4, N is most probably 4, in conformity with the zwitterionic structure of creatine (Fig. 2b) and the pK_a value of the creatine amine groups (pK_a = 6.6 at T = 37 °C) (5). For the phantom at pH 6.6, the proton number might be smaller. Assuming four exchanging amine protons for creatine, the value of f_b can be derived for any creatine concentration. Together with k_a = AREX/DC, we obtain a k_b map. Finally, using the dependence of the creatine amine exchange rate k_b on pH found by Goerke et al. (39), a map of absolute pH values can be calculated. The resulting data are in good agreement with pH values prepared in the phantoms (Fig. 6). This proves that spillover, MT and T₁ relaxation compensation worked well for the creatine–agar phantoms.

Application in vivo

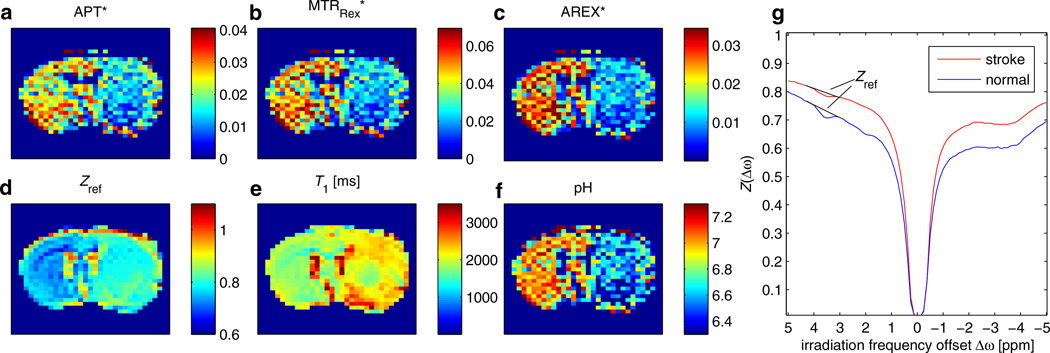
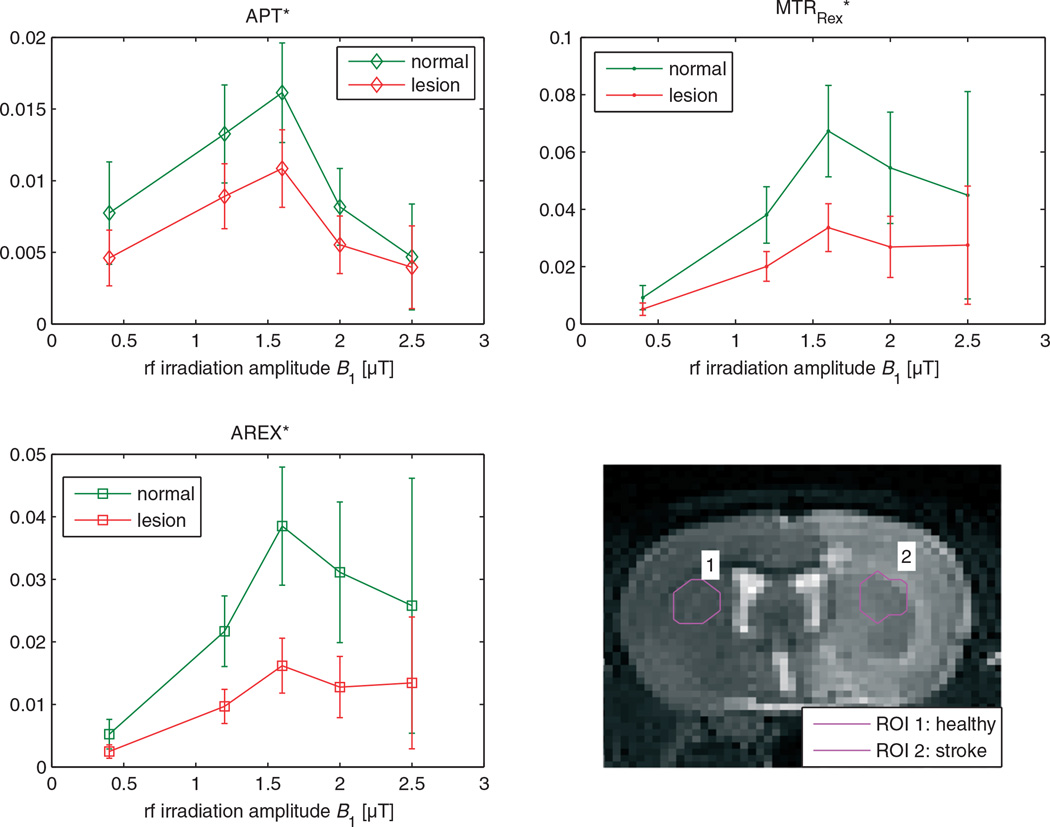
Having demonstrated the validity of the introduced corrections, the formalism can be applied to in vivo data. In a stroke lesion of rat brain, we expect a drop in APT because of the pH drop, which is clearly visible in Fig. 7. The Z-spectrum at 3.5 ppm is contaminated by direct saturation and MT effects (Fig. 7d, g); therefore, the baseline estimation of Jin et al. (44) was employed as a reference. After correction of spillover by MTR_Rex, the CNR between normal and lesion tissue increases from CNR = 1.17 to CNR = 1.44 (values correspond to ROIs in Fig. 8). In addition, the T₁ map (Fig. 7e) shows a difference between lesion and healthy tissue (Fig. 7b). This can be corrected by the AREX evaluation, showing an even higher CNR = 1.62 between normal and pathologic tissue (Fig. 7c). It should be noted that the delay time and rotation transfer effects were taken into account using DC = 1 to calculate k_a. Finally, employing Equation [19] and the reported proton fraction f_b = 0.115%, an absolute pH map can be calculated from AREX. It shows pH values between 7 and 7.2 in normal tissue and a drop to around 6.5 within the lesion (Fig. 7f).

Figure 7.

Amide proton transfer (APT) contrast obtained by pulsed chemical exchange saturation transfer (CEST)-MRI of rat with acute stroke. APT contrast (a) is contaminated by T₁ (e) and spillover effects [visible in the reference image (d)]. After correction of spillover by the inverse metric MTR_Rex, the contrast between lesion and normal tissue increases (b). The T₁-corrected apparent exchange-dependent relaxation (AREX) evaluation yields a pure exchange-weighted contrast which shows even higher signal drop in the stroke lesion compared with normal tissue. (f) From AREX, an absolute pH map can easily be obtained by Equation [19]. For all CEST maps, the average of Z-values at 4.2 and 3 ppm was employed as a reference [Equation [21]], as illustrated by the baselines in the Z-spectra in (g). To achieve good visual comparison of the contrast, each magnetization transfer ratio (MTR) map was windowed from zero to two times the average value of all non-zero pixels. CEST echo planar imaging parameters were: matrix size, 64; TE = 28 ms. Pulse train parameters were: t_p = 12.5 ms; B₁ = 0.84 µT; duty cycle (DC) = 50%; flip angle, 180°; n = 200.

Figure 8.

Region of interest (ROI) evaluation of the three point methods: APT*, the spillover-corrected MTR_Rex and the spillover- and T₁-compensated AREX. Similar to the phantom study, APT* shows a strong decrease with B₁ for values higher than 1.5 µT, whereas MTR_Rex and AREX show a smaller decrease in signal for higher B₁. This pattern is similar to the phantom results (cf. Fig. 5) and indicates validity of the spillover correction. However, the plateau of the full-saturation limit is not reached, probably as a result of contamination of the reference scan. It is important to note that the differences between signals in the stroke lesion and normal tissue are much more significant after spillover correction and T₁ compensation. Under the assumption of equal amide concentrations in stroke and normal tissue, the signal drop reflects a change in exchange rate of about a factor of two. APT, amide proton transfer; AREX, apparent exchange-dependent relaxation; MTR_Rex, spillover-corrected magnetization transfer ratio yielding R_ex.

A further check of the spillover correction is possible by investigating the behavior with increasing B₁, which is shown for the phantoms in Fig. 4. A similar signature in the MTRs as a function of B₁ was observed after spillover correction of ROI-averaged data (Fig. 8b, c): For low B₁, APT*, MTR_Rex* and AREX* show an increase with B₁. After reaching a maximum at 1.6 µT, the signals drop again. However, the decrease for the spillover-corrected methods is less significant and a type of plateau is reached. Again, the APT contrast after spillover correction is shown to be less B₁ dependent. It is important to note the increase in contrast between tissue in the lesion and normal tissue. For AREX, the contrast difference is much larger than the standard deviation. Therefore, AREX leads to a purer but also larger contrast.

DISCUSSION

In this study, we have shown that MTR_Rex, employing the inverse metric of the Z-spectrum, enables the removal of spillover and MT effects from CEST signals.

As depicted in Fig. 1, only simple mathematical operations are needed to obtain a spillover-corrected signal from raw Z-spectra data. Previous studies on spillover by Sun et al. (19,20,46) treated the spillover effect by introducing a spillover coefficient σ of the ideal MTR, i.e. MTR_real = (1 – σ)αMTR_ideal [α is the labeling efficiency, Equation [5]]. In contrast with this approach, we observed that spillover dilution can be better explained by the inverse addition of contributing effects. Spillover dilution of a CEST effect induced by ‘parallel’ saturation of water resembles the ‘dilution’ of a resistor R_b by a parallel circuit to another resistor R_a. If the diluted resistance R_a+b and the resistance of R_a are known, we obtain 1/R_b = (1/R_a+b) – (1/R_a).

The reason why superposition and not inverse superposition of effects in the Z-spectrum was also successful in other treatments originates from the approximation Z = 1/(1 + x) ≈ (1 − x) valid for R_eff ≈ R_1a and small x ≈ R_ex/R_1a. This is also the principal reason why superpositions of Lorentzians can be fitted to steady-state pulsed CEST spectra. According to our results, a superposition of reciprocal Lorentzians should be more suitable. The observation that 1/Z yields basically a R_1ρ spectrum [Equation [1]] further supports the importance of the inverse Z-spectrum. R_1ρ, known from SL experiments, has, as a relaxation rate, the property of being a superposition of the apparent exchange-dependent relaxation effects [Equation [2] (34)].

Some degree of dilution was identified as a spillover effect by Sun et al. (19,20,46). In our approach, this contribution is regarded as a loss in labeling efficiency. The latter can be defined more generally as α = R_ex/k_a, yielding (29):

$$\alpha =\frac{\frac{{({\omega }_{\mathrm{b}}-{\omega }_{\mathrm{a}})}^2}{{\omega }_1^2+\mathrm{\Delta }{\omega }^2}{k}_{\mathrm{b}}+R_{2\mathrm{b}}}{\underset{*}{\underbrace{k_{\mathrm{b}}+R_{2\mathrm{b}}}}}\frac{{\omega }_1^2}{{\omega }_1^2+k_{\mathrm{b}}(k_{\mathrm{b}}+R_{2\mathrm{b}})}$$ [23]

A comparison of Equation [23] with α of Equation [5], which is similar to α given in ref. (37), reveals an additional factor (*) in Equation [23], which decreases with increasing B₁. This factor is maximal at Δω= 0 and can be interpreted as the on-resonance effects induced by the exchange. These effects are employed in on-resonant SL experiments. The loss of labeling is attributed to an interference of off-resonant and on-resonant features of R_ex. Hence, the labeling efficiency is a useful parameter which was extended by the eigenspace approach (29), whereas a spillover coefficient is not appropriate to the inverse metric.

Other than the spillover correction employed by Sun et al. (19) and the ‘isolation’ of R_ex from R_1ρ (R_ex = R_1ρ − R_eff) proposed by Jin et al. (14), which both use additional T₂ and B₁ mapping, our approach employs only the intrinsic metric to correct spillover. This is advantageous because it reduces the scanning time and post-processing efforts. The intrinsic structure was employed in a similar manner in the fitted model of ref. (22) which is the origin of MTR_pcm [Equation [5]].

It is important to note that the isolation and correction of effects are different operations. Although the former approaches, such as MTR_asym, isolate signals from specific effects, these isolated effects can still be diluted (Fig. 3). Therefore, removing the information about parallel effects must be considered carefully, as other contributions may become invisible, but can still be effective as dilutions.

The approach of Liu et al. (35) [Equation [8]] afforded a partial spillover correction which could be explained by the reduction of the quadratic term of R_eff in MTR_asym to a linear one. Their normalization is considered to be appropriate for glutamate-CEST imaging (7,47) and glycosaminoglycan-CEST (48). In particular, these two applications can also benefit from the improvement of the MTR_Rex evaluation.

Next, we discuss our quantitative approach. To the best of our knowledge, there are two different approaches to model the pulsed CEST case: (i) using cw theory with an equivalent cw power (12,49) verified to be valid for slow exchange rates by Tee et al. (50); (ii) the approach of Santyr et al. (30) for SL, which should also be valid for CEST by relying on the equivalence of SL and CEST (29). The SL solution of Santyr et al. (30) takes into account different relaxation during and between the pulses. However, Santyr et al. (30) assume solely a monoexponential decay in the interpulse delay, which cannot explain the modulations as a function of the flip angle observed by CERT (28) or the dependence on the delay time (51). However, for long pulses, as employed in this study, our results suggest that the approach of Santyr et al. (30) is also valid for pulsed CEST. We did not observe a perfect match of the theory of Santyr et al. (30) and the corrected data, which we attribute to the invalid assumption of monoexponential dynamics in the interpulse delay and the assumption of full saturation (R_ex = k_a) during the Gaussian pulse. R_ex obtained by AREX is therefore an effective parameter which incorporates the dependence on pulse shape, as well as processes occurring between the pulses.

The inverse metric is valid only for pulsed CEST/SL if R_1ρt_p << 1 [assumption of Equation [12]], which is not the case for large R₂ and θ or t_p. This could explain why the agar phantoms show slightly different MTR_Rex compared with the solutions without agar (Fig. 4). In principle, this limits the inverse approach to applications with pulses that are much shorter or much longer than 1/R_1ρ(Δω). The latter corresponds to the cw case. In practice, Z-values are directly tunable by B₁ and can be set to values that are not smaller than 0.5; then, R_1ρ ~ 2R_1a and the condition R_1ρt_p << 1 is easier to fulfill.

Pulsed CEST including MT was also studied with similar phantom parameters by Desmond and Stanisz (18), who interpreted their data with numerical Bloch–McConnell simulations. With the addition of agar, T₂ is changed strongly. However, a limitation of our study is that MT was only shown to be corrected up to 1% agar, which corresponds to a fraction of about f_b = 0.3% (52). In contrast, fractions up to f_b = 18% are possible in cartilage (53). For cw simulations, it was shown that the inverse superposition is appropriate up to f_b = 5% (29), but then the assumption of the simple superposition R_1ρ = R_eff + R_ex,CEST + R_ex,MT might be invalid.

The intermediate exchange regime was not explicitly considered in this study. In this case, the spillover correction of MTR_Rex is promising, but still remains to be proven. Although demonstrated so far for amine and amide exchange, we expect that our normalization will work for diamagnetic and paramagnetic CEST in the slow and intermediate exchange regimes, and for the generation of qualitative contrast and quantitative parameter fittings.

Application in the case of non-steady-state and inversion pulses

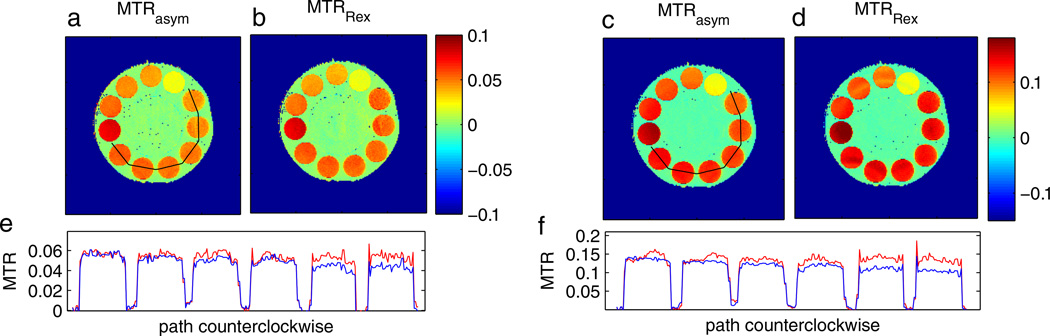
For in vivo protocols, the saturation times are commonly kept shorter, in the range of one or two T₁, to save scanning time or avoid dominant spillover effects (6,7). In addition, more efficient inversion pulses are commonly used (23,24,49,51). Additional measurements in non-steady state with only 3-s irradiation (~1 × T₁) were performed (Fig. 9a, b, e), as well as saturation with a pulse train of 180° pulses (Fig. 9c, d, f), for the phantom described in Fig. 2. In both cases, the homogeneity between the agar phantoms was improved by the inverse evaluation MTR_Rex against MTR_asym. However, within each phantom, the inverse metric induced a less homogeneous contrast. From theory, it is known (32) that the inverse metric is not valid for the transient state. However, near steady state (t_sat≈T₁), it can still be used as an approximation. For inversion transfer or CERT, there is no analytical knowledge, but our results indicate that the general Z-spectrum structure might also be similar for rotation transfer.

Figure 9.

MTR_asym (a, c) and the inverse approach MTR_Rex (b, d) for the practical relevant cases of non-steady-state saturation (t_sat = 3.1 s, B₁ = 0.5 µT, t_p = 100 ms, DC = 50%, n = 16) (a, b) and 180° pulsed saturation (180° pulses; B₁ = 0.48 µT, t_p = 25 ms, DC = 50%, n = 320) (c, d). Profiles along the path (counterclockwise) defined in (a) show that MTR_Rex (red line) corrects the decrease in MTR_asym (blue line) with increasing agar concentration.

Systematic and statistical errors

Figure 10 depicts the increase in errors for MTR_Rex. If we turn to the 1/Z metric, the relative errors are similar, Δ(1/Z)/(1/Z) = ΔZ/Z, but the absolute errors increase, Δ(1/Z) = (1/Z²)ΔZ. For example, R₁=1 s⁻¹ and a dominant direct saturation at the label frequency of R_eff = 2R₁ leads to Z = 0.5. Hence, the statistical error of 1/Z is four times the error of Z.

However, MTR_asym also has a quadratic term of R_eff in the denominator; therefore, MTR_asym~1/Z²·PTR. Thus, the CEST effect estimated by MTR_aysm has a systematic error on the order of 1/Z². This means, by the inverse metric, we trade systematic errors against statistical errors, which can be reduced by averaging. This also indicates that B₁ should not exceed a certain limit to keep Z and the signal-to-noise ratio large. For the estimation of the signal-to-noise ratio, MTR_asym is a good indicator.

Figure 8 indicates that a spillover correction is also a B₁ correction near the full-saturation limit (α ≈ 1). Although MTR_asym shows a strong dependence on B₁ and must be corrected by post-processing, as proposed by Sun et al. (46), MTR_Rex is almost constant up to B₁=2 µT. For faster exchange and partial saturation, the tissue-dependent B₁ correction of Singh et al. (54), reported at B₀ = 7 T, should be performed with spillover-corrected MTR_Rex instead of MTR_normref. We do not recommend the application of a B₁ correction to spillover-diluted data, but suggest that B₁ corrections should be applied directly to R_ex.

Imaging of stroke

In the rat CEST imaging study of Sun et al. (15), APT of normal tissue was reported to be 2.94%, whereas, in the lesion, it dropped to 0.9%. This was stronger than the signal decrease of about a factor of 0.5 observed in our animal study. In addition, in pH mapping, we only saw a drop of 0.5 pH units, whereas a pH decrease of approximately 1 pH unit was reported in ref. (15). In this and other studies (17,38), the correlation with lesions detected by diffusion and perfusion imaging was investigated. In our experiments, the resolution was too low to resolve significant substructures within the lesion. In contrast with other studies, we avoided contaminations of asymmetry analysis by employing a baseline estimation (44). We believe that this is beneficial, especially because significant nuclear Overhauser effects and shifted macromolecular MT effects are apparent in the brain parenchyma. It should be noted that this method can only be applied at higher fields (B₀ ≥ 7 T). For lower B₀, we suggest a Lorentzian line fit of the water resonance as an appropriate reference.

CONCLUSION

We propose a new spillover and MT correction method for the evaluation of Z-spectra which requires no information about T₂ and MT of the system and is easily applied. The validity of the proposed corrected MTR (MTR_Rex) was demonstrated for an in vitro system, yielding high spillover, i.e. creatine, in agar gels at clinical field strengths. MTR_Rex was extended to a T₁ relaxation-compensated metric, called AREX (for ‘apparent exchange-dependent relaxation’), which allowed the quantitative evaluation of Z-spectra and could be verified by numerical fits. The validity, sensitivity and performance of the metric require sufficiently large Z-values (Z>0.5) and an appropriate reference scan. APT-CEST-MRI experiments of acute stroke in rat brain at B₀=9.4 T fulfilled these requirements. The outcome of the evaluation by means of the AREX metric was a significantly higher contrast between the stroke area and normal tissue compared with the contrast obtained using the non-inverse metric. Hence, we propose the application of the AREX metric for the analysis of Z-spectra data of all pathologies in which changes in MT, T₂ or T₁ are observed, in particular in tumors or tissue affected by stroke. With an appropriate reference scan, AREX may help to provide a pure exchange-dependent and exchange site-specific CEST contrast.

Abbreviations used

AREX

apparent exchange-dependent relaxation

APT

amide proton transfer

CEST

chemical exchange saturation transfer

CERT

chemical exchange rotation transfer

CNR

contrast-to-noise ratio

cw

continuous wave

DC

duty cycle

M₀

thermal equilibrium magnetization

MT

magnetization transfer

MTR

magnetization transfer ratio

MTR_asym

magnetization transfer ratio asymmetry

MTR_normref

magnetization transfer ratio normalized by reference scan

MTR_pcm

magnetization transfer ratio of probabilistic combined model

MTR_Rex

spillover-corrected magnetization transfer ratio yielding R_ex

M_z,sat

z magnetization after saturation

PTR

proton transfer rate

QUESP

Quantification of exchange by saturation power

R_eff

effective water relaxation in the rotating frame

R_ex

exchange-dependent relaxation in the rotating frame

ROI

region of interest

RF

radiofrequency

SL

spin-lock

WASSR

water saturation shift referencing.