Accuracy of continuum electrostatic calculations based on three common dielectric boundary definitions

Abstract

We investigate the influence of three common definitions of the solute/solvent dielectric boundary (DB) on the accuracy of the electrostatic solvation energy ΔG_el computed within the Poisson Boltzmann and the generalized Born models of implicit solvation. The test structures include small molecules, peptides and small proteins; explicit solvent ΔG_el are used as accuracy reference. For common atomic radii sets BONDI, PARSE (and ZAP9 for small molecules) the use of van der Waals (vdW) DB results, on average, in considerably larger errors in ΔG_el than the molecular surface (MS) DB. The optimal probe radius ρ_w for which the MS DB yields the most accurate ΔG_el varies considerably between structure types. The solvent accessible surface (SAS) DB becomes optimal at ρ_w ~ 0.2 Å (exact value is sensitive to the structure and atomic radii), at which point the average accuracy of ΔG_el is comparable to that of the MS-based boundary. The geometric equivalence of SAS to vdW surface based on the same atomic radii uniformly increased by ρ_w gives the corresponding optimal vdW DB. For small molecules, the optimal vdW DB based on BONDI + 0.2 Å radii can yield ΔG_el estimates at least as accurate as those based on the optimal MS DB. Also, in small molecules, pairwise charge-charge interactions computed with the optimal vdW DB are virtually equal to those computed with the MS DB, suggesting that in this case the two boundaries are practically equivalent by the electrostatic energy criteria. In structures other than small molecules, the optimal vdW and MS dielectric boundaries are not equivalent: the respective pairwise electrostatic interactions in the presence of solvent can differ by up to 5 kcal/mol for individual atomic pairs in small proteins, even when the total ΔG_el are equal. For small proteins, the average decrease in pairwise electrostatic interactions resulting from the switch from optimal MS to optimal vdW DB definition can be mimicked within the MS DB definition by doubling of the solute dielectric constant. However, the use of the higher interior dielectric does not eliminate the large individual deviations between pairwise interactions computed within the two DB definitions. It is argued that while the MS based definition of the dielectric boundary is more physically correct in some types of practical calculations, the choice is not so clear in some other common scenarios.

1 Introduction

Accurate and at the same time computationally facile description of the solvent environment is essential for realistic biomolecular modeling. Replacing the discrete molecules by an infinite continuum with the dielectric and “hydrophobic” properties of water is at the heart of the so-called implicit solvent framework^1–8 which has gained popularity over the past two decades. Within the framework, approaches based on solving the Poisson-Boltzmann (PB) equation⁹ of linear response, continuum electrostatics are arguably most widely used. A variety of numerical schemes for solving the PB equation have been developed.^2,7,10–18 When speed and algorithmic simplicity are paramount, as in molecular dynamics simulations, the generalized Born (GB) model^19–42 is usually preferred. The GB model provides an approximate analytical expression for electrostatic solvation free energy, and shares the same underlying physics of linear response continuum electrostatics with the PB approach. A key step in these continuum calculations^2,12,43 is defining the solute/solvent dielectric boundary (DB) – a region of space over which the dielectric constant ε(r) changes from the value characteristic of the molecular interior (e.g. ε = 1 or 4) to that of the solvent, (e.g. 80 for water). While technically there is no notion of a dielectric boundary in the main equation of the GB model, see “Methods”, the solute/solvent boundary still enters into the model via the so-called effective Born radii – the latter are typically computed as exact or approximate integrals over the suitably chosen solute volume⁴⁴ or surface.^27,45 Schematics of three basic surface definitions that have so far most commonly been used in biomolecular computations are shown in fig. 1. Among these, the Van-der-Waals (vdW) representation of the molecule – the union of hard atomic spheres – is the simplest and most computationally facile. However, it is the Lee-Richards molecular surface⁴⁶ (MS), that has been utilized most often in numerical PB or GB calculations.^10,12,44 In analytical GB formulations considerable effort was made to approximate this type of boundary, with various degrees of success, see e.g. Ref.⁴⁷ for a review. Still, the Lee-Richards molecular surface is not the only type of DB proposed for use in the PB^14,48–51 and the GB models.^52–55 Other recent examples of DB definitions include Gaussian boundary in which a transition between the low and high dielectric regions is smooth,⁴⁸ and the skin surface^50,56 which has a similar appearance to the Lee-Richards surface, but avoids singularities associated with the latter.

Figure 1.

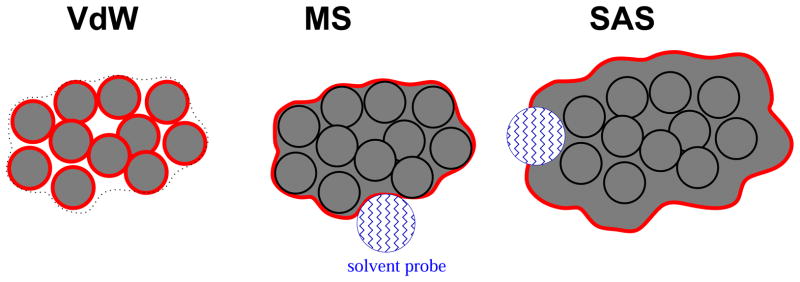
The three representations of solute–solvent dielectric boundary (thick red line) tested in this work. Left panel The van-der-Waals (vdW) boundary coincides with the surface of atomic spheres, the inter-atomic interstitial space is treated as high dielectric solvent (white). Middle panel: The Lee-Richards molecular surface (MS): all interstitial space, small voids and invaginations inside the surface are treated as low dielectric solute (Grey). (3) Right panel: The solvent accessible surface (SAS) defines the boundary: all interstitial space and small voids inside the SAS are treated as low dielectric solute.

Arguments in favor of a particular DB representation can be purely technical/computational. For example, the use of a smooth representation for DB can significantly increase convergence rate of iterative solutions of the PB equation. Likewise, representing the solute as a collection of vdW spheres simplifies the calculation of the effective Born radii in the GB model, compared to using the Lee-Richards surface to define the solute/solvent boundary. These technical considerations are very important in practical computations and weigh heavily in the accuracy/speed trade offs made in the development and use of the implicit solvent models. A more fundamental question is which of the alternative representations of the solute/solvent dielectric boundary is more physically realistic in atomistic calculations? The question is not trivial and may not have a unique answer as the very notion of dielectric boundary is a concept borrowed from classical electrostatics of macroscopic dielectric media. At the atomic level the concept is a serious approximation. For example, dielectric boundary is completely external to the current PB/GB formalism where the boundary is a purely geometric construct that does not depend on the charge distribution within the solute. In reality, water structure around a microscopic solute responds to its electric field (electrostriction), the response depends not only on the magnitude but also the sign of the solute charge (charge hydration asymmetry). Within the limitations of the current continuum electrostatics formalism, the choice of the right dielectric boundary definition is very important since the outcomes of such calculations are extremely sensitive to details of the DB.⁵⁷ The sensitivity is expected: solvation energy of a single “Born” ion is of an order of a 100 kcal/mol, and is inversely proportional to the ion radius. Thus, for an isolated surface atom, a 10 % change in the atomic radius – a mere 0.1 Å shift in the position of the dielectric boundary – can result in a 10 kcal/mol change in the energy, comparable to stability of a typical protein.

Arguably the two conceptual limiting cases of the currently used DB definitions are the MS and vdW surfaces, fig. 1. Physically, the most important difference between these two distinct treatments of the solute/solvent separation is the assignment of dielectric to the interstitial space in-between the atomic spheres: the vdW representation treats any tiny crevasse as filled with high dielectric solvent, while within the DB definition based on molecular surface the entire interior of the molecule is treated as low dielectric space (internal cavities large enough to fit a water molecule are treated as high dielectric). Other, more complex surface definitions^48,52 can typically be parametrized to approach one of these limiting cases. While it was often argued, based on individual case studies⁵⁸ and general physical considerations⁵⁹ that the DB based on molecular surface is physically more realistic than the vdW alternative, the issue is certainly not yet settled. Opposite arguments and case studies exist.⁶⁰ In fact, it is surprising that so few works address this important issue as their primary focus. Here we revisit the question of accuracy of the vdW vs. MS DB definition within the context of continuum electrostatic calculations. A fairly large and diverse set of test molecular structures is employed. While our main focus here is the accuracy of the electrostatic solvation free energies computed via the standard continuum treatment based on the Poisson equation, we will also investigate the equivalent generalized Born calculations. Three common definitions of the dielectric boundary (DB) will be explored – molecular surface (MS), van-der-Waals surface (vdW) and solvent accessible surface (SAS), fig. 1.

While more sophisticated implicit solvent approaches exist^61–66 that make fewer approximations to reality than do the PB and GB models, the latter continue to be work horses of practical continuum electrostatic calculations due to their robustness, conceptual simplicity, computational speed, and availability in many popular packages. The following study should help improve outcomes of such calculations.

2 The Approach

Biomolecular continuum electrostatic calculations, be that PB or GB, produce a range of physical quantities that can be compared either to more accurate models of solvation or directly to experiment. While comparison with experiment is the ultimate test of any theory, we argue that it is not ideal for the task at hand – evaluating the performance of various boundary definitions in PB or GB calculations. This is because to go from PB/GB to an experimental observable one has to make several different approximations unrelated to the DB definition. Limited conformational sampling and, as a consequence, inadequate structural relaxation and dielectric response, is just one such example that adds considerable uncertainty to these calculations. The absence of explicit structural relaxation in many types of continuum electrostatic calculations⁶⁷ often requires^13,68 the use of interior dielectric constants larger than 1, which is an additional approximation complicating comparisons between various DB definitions. In this work we will try to reduce such uncertainties as much as possible, which leads to the following choices. Our reference solvation model is explicit solvent (TIP3P). To avoid conformational sampling issues, conformations of all of the test molecules are fixed. We choose only net neutral compounds mainly to mitigate the uncertainties associated with the absence of charge hydration asymmetry from the conceptual basis of the PB or GB model. As was argued elsewhere,⁶⁹ the issue of the dielectric boundary placement can be treated separately from the charge hydration asymmetry effects. Also, the absence of charged compounds in the test set simplifies the explicit solvent free energy calculations significantly (no need to consider net charge corrections to the PME based calculation), likely making the corresponding computation as of ΔG_el more robust. Finally, our target “observable” is the electrostatic solvation free energy. It can be estimated in a straightforward manner in both the implicit and explicit solvent. Unless otherwise stated, we use internal dielectric of 1. Accurate computation of biomolecular solvation free energy (ΔG_solv) is central to numerous areas of fundamental, bio-medical and industrial research.^70–75

As was mentioned above, three types of solute/solvent boundaries are explored here: the Lee- Richards (MS) surface, the van-der-Walls (vdW) surface, and the solvent accessible (SAS) surface, fig. 1. We vary the solvent probe radius to transition between the boundary types in a continuous manner, which helps clarify the trends. For example, the vdW surface corresponds to setting the probe radius to zero in the Lee-Richards MS surface definition; on the other hand, using a very large probe radius approximates the convex hull of the molecule. The commonly used MS lies in-between, at probe radius of 1.4 Å for water. In addition, we vary details of the boundary by switching between three sets of atomic radii: two commonly used, “all purpose” sets of intrinsic atomic radii, BONDI,⁷⁶ PARSE,⁷⁷ plus a relatively new set ZAP9⁷⁵ developed specifically for neutral small molecules. A change of the solvent probe radius in SAS is equivalent to a uniform shift in the intrinsic atomic radii in vdW surface, an equivalence which effectively allows us to probe a range of radii as well. Key parameters that define geometry of each of the DB types shown in fig. 1 are intrinsic radii of individual atoms in the molecule, and, in the case of molecular and SAS boundary, the radius of the solvent probe. Partial atomic charges are external to the PB/GB models, we use the same set charges for the corresponding explicit solvent reference calculations, see “Methods”.

3 Methods

3.1 Molecules used as test sets

We use three test sets of neutral molecules in this work: (1) 19 small proteins. (2) A subset of 248 neutral drug-like small molecules,⁷⁸ which is becoming a de-facto standard for testing performance of various computational models.^79–82 (3) 4 conformational states of alanine decapeptide (Ala10), fig. 2

Figure 2.

Cartoon representation of the four conformational states of alanine decapeptide, Ala10, used in this work.

The structures of the 4 conformational states of Ala10 were kindly provided by Daniel Roe. A detailed description of the Ala10 structures and the methods used to compute ΔG_el for these structures can be found in Roe. et al.⁸³ Briefly, the conformations Alpha, Left, and PP2 were obtained using the LEAP module of AMBER. The Hairpin conformation was generated from the backbone of the peptide Trpzip2. The values of ΔG_el for the four conformations were then calculated by Thermodynamic Integration (TI). For our calculation, each of the 4 conformational states of fig. 2 was represented by 100 snapshots obtained from the TI protocol described in Ref.⁸³ Within each conformational state, structures of individual snapshots differ little since they were generated under strong all-atom restraints.

The data set of 19 small proteins was randomly selected from a larger data set of representative proteins structures from Feig et al.,⁸⁴ the selection criterion being that the compounds are small enough to allow for high-resolution grid computations. Their PDB IDs are 1az6, 1bh4, 1bku, 1brv, 1byy, 1cmr, 1dfs, 1dmc, 1eds, 1fct, 1fmh, 1fwo, 1g26, 1ha9, 1hzn, 1paa, 1qfd, 1qk7, and 1scy. Chain “A” or “model 1” has been chosen when appropriate. We used the H++ server⁸⁵ to assign partial charges and protonation states of ionizable aminoacids. Moreover, using specific values of pH, H++ allowed us to obtain structures with neutral net charge. The random selection resulted in a fairly representative sampling of various structural classes. The structural composition of the proteins is as follows: 6 mostly α helical, 4 mostly β sheet, 4 roughly equal mix of α/β, and 5 mostly disordered. The size of most of these proteins is about 30 amino acids. For this set only, a slightly modified version of BONDI radii (MBONDI2⁴⁰) was used for all PB and GB calculations. The difference between BONDI and MBONDI2 is in the radii of hydrogens bound to nitrogen atoms; MBONDI2 assigns a radius of 1.3 Å to those hydrogens while BONDI assigns 1.2 Å.⁴⁰

The set of rigid small molecules consists of 248 molecules selected from a larger and diverse set of 504 molecules, originally examined by Mobley et al.⁷⁸ We selected only the molecules with average RMS deviation smaller than 0.3 Å relative to the t=0 (initial) conformation of each molecule, calculated over 10ns implicit solvent molecular dynamics (MD) trajectories of the original set of 504 molecules; the trajectories were taken from Ref.^86,87 The t=0 conformations were also used to compute the solvation energies reported in this work. The coordinates, charge distribution, and the TIP3P based polar solvation energies ΔG_el were taken from Ref.⁷⁸ Merck-Frosst implementation of AM1-BCC⁸⁸ was used to assign the partial charges. The alchemical (TI) hydration free energies were computed using the Bennett acceptance ratio⁸⁹ in TIP3P water.

3.2 Poisson-Boltzmann calculations

Within the linear response continuum solvent framework, and in the absence of mobile ions, the electrostatic potential ϕ(r) produced by an arbitrary charge distribution ρ(r) is given by the Poisson equation:

$$\nabla [\epsilon (\mathbf{r})\nabla \varphi (\mathbf{r})]=-4\pi \rho (\mathbf{r}).$$ (1)

The charge density ρ(r) is given by a set of “fixed” atomic charges q_i at positions r_i inside the dielectric boundary, ρ(r) = Σ_iq_iδ(r−r_i). All three dielectric boundary definitions tested here, fig. 1, assume an abrupt dielectric boundary in which ε(r) takes only two values: ε_in inside the dielectric boundary and ε_out outside. Once the potential ϕ(r) is solved for, the electrostatic part of the solvation (transfer, if ε_in > 1) free energy is given by:⁹⁰

$$\mathrm{\Delta }{G}_{\text{el}}=\frac{1}{2}\sum _i{q}_i[\varphi ({\mathbf{r}}_i)-\varphi ({\mathbf{r}}_i){\mid }_{\mathit{vac}}]=\frac{1}{2}\sum _{ij}\mathbf{F}({\mathbf{r}}_i,{\mathbf{r}}_j)q_i{q}_j=\sum _{i\ge j}\mathrm{\Delta }{G}_{ij}^{\text{el}},$$ (2)

where ϕ(r_i)|_vac is the electrostatic potential computed for the same charge distribution in the absence of the dielectric boundary, e.g. in the uniform dielectric ε_in of molecular interior. Here, F(r_i,r_j) is the reaction field Green function of the corresponding boundary value problem and $\mathrm{\Delta }{G}_{ij}^{\text{el}}$ are the pairwise components of the electrostatic solvation free energy.

All the Poisson calculations of the total ΔG_el were performed using DELPHI version 2.0¹¹ with a grid spacing of 0.25 Å. Unless otherwise specified, the internal and external dielectrics were set to 1, and 80 respectively. The monovalent salt concentration was set to zero, making it a pure Poisson model. We use “PB” abbreviation because it is well recognized. Given a specific water probe radius ρ_w, DELPHI uses the standard molecular surface as solute/solvent dielectric interface. A vdW based solute/solvent dielectric interface is obtained by setting the input probe radius ρ_w to zero. To set up the dielectric interface as the solvent accessible surface (SAS), the atomic radii are increased uniformly by the given probe radius ρ_w. The modified atomic radii and a probe radius of zero is then used as input for DELPHI.

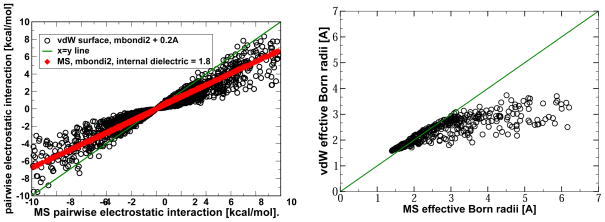
For the pairwise electrostatic interactions shown in fig. 7, the corresponding Poisson problem is handled by PEP software package originally developed by Beroza et al.,³ which computes F(r_i,r_j). The finest grid spacing used in these calculations is 0.07 Å, decreasing from 4 Å in eight steps of focusing on the atom in question. The pairwise interactions are the off-diagonal (i > j) elements of the total charge-charge interaction matrix⁹¹ $W_{ij}=\mathrm{\Delta }{G}_{ij}^{\text{el}}+q_i{q}_j/({\epsilon }_{\text{in}}{r}_{ij})$. For the analysis we have excluded all 1–2, 1–3 and 1–4 bonded interactions along the atom chain, as is the standard practice in molecular simulations.

Figure 7.

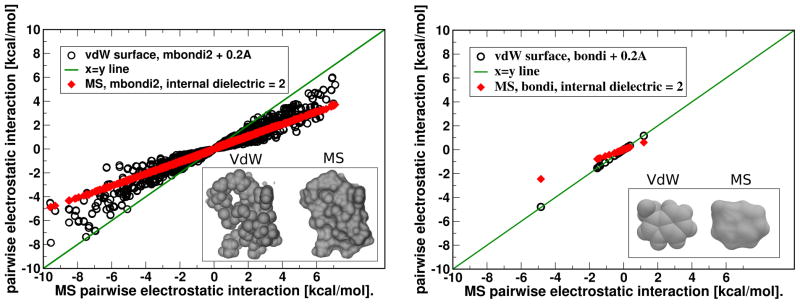
Pairwise electrostatic interactions between atoms in a small protein (PDB 1BH4, left panel) and a small molecule (3-methyl-1h-indole, right panel) computed using optimal vdW and MS based dielectric boundary definitions that yield nearly equal respective ΔG_el within the PB model. The different surfaces are shown in the insets. For visual clarity, only interactions larger than 10⁻² kcal/mol are shown for the protein.

3.3 The generalized Born Model

The polar component of the solvation energy was calculated by the ALPB model,⁹² which introduces physically correct dependence on dielectric constants into the original GB model of Still et al.,²⁰ while maintaining the efficiency of the original. The ALPB model approximates ΔG_el using the following formula:

$$\mathrm{\Delta }{G}_{\text{el}}\approx -\frac{1}{2}\left(\frac{1}{{\epsilon }_{\text{in}}}-\frac{1}{{\epsilon }_{\text{out}}}\right)\frac{1}{1+\beta \alpha }\sum _{ij}{q}_i{q}_j\left(\frac{1}{f^{\text{GB}}}+\frac{\alpha \beta }{A}\right),$$ (3)

where ε_in and ε_out are the dielectric constants of the solute and the solvent respectively, β =ε_in/ε_out, α = 0.571412, and A is the electrostatic size of the molecule, which is essentially the over-all size of the structure which can be computed analytically.⁹² We employ the most widely used functional form²⁰ of $f^{\text{GB}}:f^{\text{GB}}={\left[r_{ij}^2+R_i{R}_{j}exp(-r_{ij}^2/4R_i{R}_j)\right]}^{\frac{1}{2}}$, where R_i is the so-called effective Born radius of atom i, and r_ij is the distance between atoms i and j. Unless otherwise specified, we set ε_in = 1, and ε_out = 80 in eq. (3).

In this work, we use the so-called R6 effective Born radii

$$R_i^{-1}={\left(\frac{3}{4\pi }{\int }_{\mathit{ext}}\frac{d\mathbf{V}}{{\mid \mathbf{r}-{\mathbf{r}}_i\mid }^6}\right)}^{1/3},$$ (4)

proposed by Svrcek-Seiler⁹³ and independently by Grycuk.⁹⁴ In eq. (4) the integral (ext) is taken over the region outside the molecule’s DB. We use an equivalent formulation described in Mongan et al.:⁴⁴

$$R_i^{-1}={\left(-\frac{1}{4\pi }{\oint }_{\partial V}\frac{\mathbf{r}-{\mathbf{r}}_{\mathbf{i}}}{{\mid \mathbf{r}-{\mathbf{r}}_{\mathbf{i}}\mid }^6}·d\mathbf{S}\right)}^{1/3},$$ (5)

which, by Gauss-Ostrogradski theorem, is equivalent to eq. (4). Here, ∂V represents the DB of the molecule, and dS is the infinitesimal surface vector. eq. (5) is estimated by a numerical procedure described in Ref.⁴⁵ An empirical constant offset B is added to the computed inverse radii to obtain the best agreement with the PB ΔG_el.⁴⁴ Although B = 0 was later found to give better agreement with explicit solvent ΔG_el for small molecules,⁷⁹ here we use the same B = 0.028 Å⁻¹ for all structures for consistency between the GB and PB results.⁴⁴

To represent the DB computationally, we employ triangulation of the MS generated by MSMS⁹⁵ tool which takes the solvent probe radius ρ_w as input. The vdW based effective Born radii are approximated by using a very small probe radius, ρ_w = 0.01 Å. Note that there may exit small cavities that are completely buried in the interior of the molecules even for ρ_w =0. We found that these are not included in the MSMS output triangulated surface. Thus, the true vdW effective Born radii are slightly smaller than those estimated by our strategy, which can only increase the differences between the vdW vs. MS based radii seen in fig. 9, right panel. Our main conclusion is therefore unaffected. Given relatively small sizes of the tested proteins, any difference between the true and the approximate vdW effective Born radii is expected to be small. The pairwise interactions are the off-diagonal (i > j) elements of the total charge-charge interaction matrix⁹¹ $W_{ij}=\mathrm{\Delta }{G}_{ij}^{\text{el}}+q_i{q}_j/({\epsilon }_{\text{in}}{r}_{ij})$. For the analysis we have excluded all 1–2, 1–3 and 1–4 bonded interactions along the atom chain, as is the standard practice in molecular simulations.

Figure 9.

Left: GB pairwise electrostatic interactions between atoms in a small protein (PDB 1BH4) computed using optimal vdW and MS based solute/solvent boundary definitions. For visual clarity, only interactions larger than 10⁻² kcal/mol are shown. Right: Comparison of the vdW and MS based effective Born radii computed via eq. (5); the radii enter the generalized Born formula via eq. (3). To match the vdW and MS based total ΔG_el exactly (ε_in = 1), the solvent probe used to define the MS was increased to ρ_w = 2.0 Å.

3.4 Explicit solvent solvation free energies

Standard Thermodynamic Integration(TI) protocol was employed to compute the explicit solvent electrostatic solvation free energies used as reference. The calculations were performed in explicit (TIP3P) solvent in Amber12⁹⁶ simulation package. The electrostatic (polar) contribution was computed as the difference of the charging energy of the molecular cavity in the aqueous phase and the gas phase.⁸³ The TI integrals were approximated using a five point Gaussian weighted sum. All simulations were performed using the Langevin thermostat with a collision frequency of 2 ps⁻¹ and a time step of 2 fs. Hydrogen bonds were constrained with SHAKE⁹⁷ using a geometrical tolerance of 10⁻⁶ Å. For the TI computations in the aqueous phase, the molecules were placed in a truncated octahedral box such that the minimum distance between the solute atoms and the box edge is 12 Å. The non-bonded interaction cutoff was 10 Å, and long-range electrostatic interactions were calculated using periodic boundary conditions via the particle mesh Ewald (PME) summation.^98,99 Note that since all the structures are net neutral, no additional corrections were required. Positional restraints of 200 kcal/mol/ per Ų on all atoms were employed to hold the solute in the desired conformation. The system was gradually heated at constant volume for 50 ps, followed by a 1 ns equilibration at constant pressure of 1 atm and pressure relaxation time of 2 ps. The last 1 ns of a 2 ns constant volume simulation was used for the free energy calculations.

4 Results

In what follows we present a set of calculations that systematically explore the influence of the dielectric (solute/solvent) boundary definition on the accuracy of the standard continuum solvent treatment of electrostatic free energies. While our main focus is the Poisson type calculations, towards the end of the section we also briefly discuss the generalized Born model in the same context.

4.1 vdW vs. MS dielectric boundary in the PB model

The Poisson equation estimates of the electrostatic solvation energies for several classes of molecules are shown in fig. 3 and fig. 4.

Figure 3.

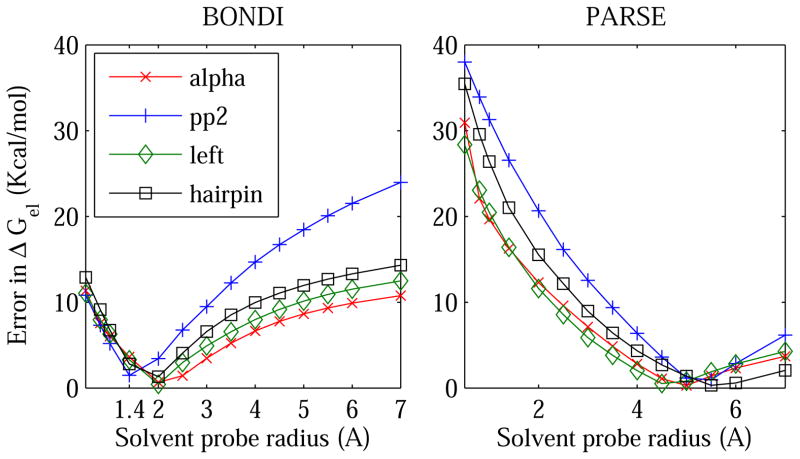
Absolute error, relative to the explicit solvent (TIP3P) reference, in the PB electrostatic solvation free energy ΔG_el of 4 conformational states of alanine decapeptide. The error is shown as a function of the solvent probe radius ρ_w used to define the dielectric boundary (solute/solvent surface). Different definitions of the boundary are accessed by varying the solvent probe radius within the Lee-Richards MS definition: the vdW surface corresponds to ρ_w = 0. The details of the boundary are also varied by switching between two sets of atomic radii: BONDI (left) and PARSE (right). The computations are performed individually for the four conformational states of Ala10 (pp2, alpha, left, and hairpin) shown in fig. 2.

Figure 4.

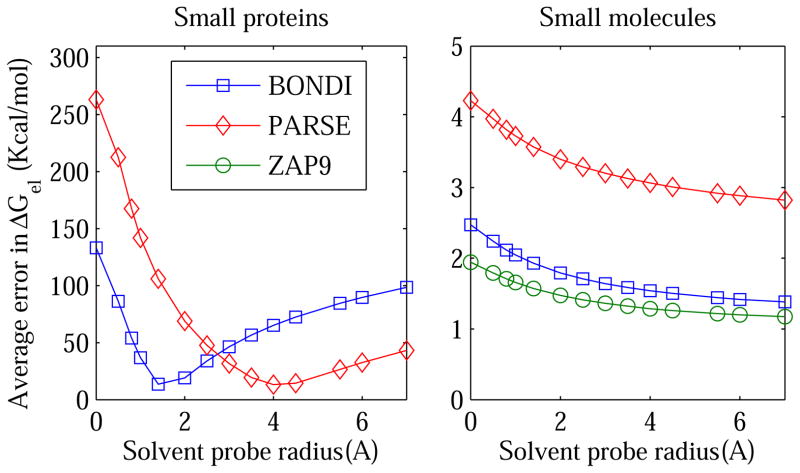
Average (RMS) error in the PB electrostatic solvation free energy ΔG_el as a function of the solvent probe radius ρ_w used to define the dielectric boundary (solute/solvent surface). The error is calculated relative to the explicit solvent (TIP3P) reference. Different definitions of the boundary are accessed by varying the solvent probe radius within the Lee-Richards MS definition: the vdW surface corresponds to ρ_w =0. The calculations are performed for 19 small proteins(Left) and 248 small molecules (Right), for three sets of atomic radii shown in the legend box.

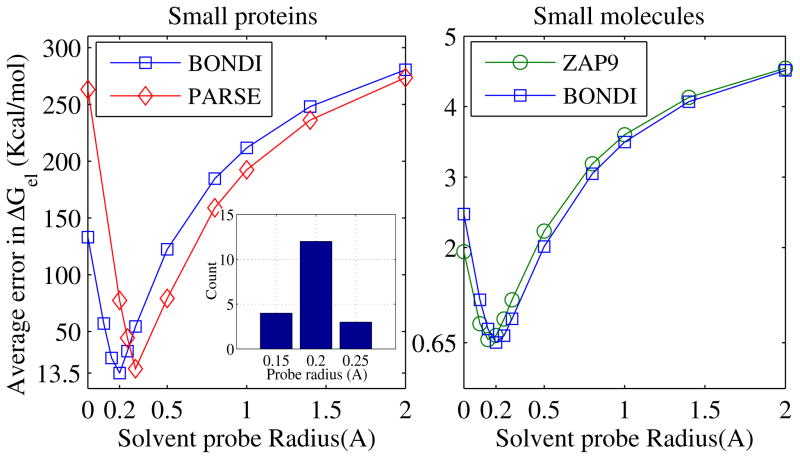
The immediate conclusion one makes by examining these figures is that the vdW surface (the 13 ρ_w = 0 point) based on all three “standard” radii sets is far from optimal for representing the dielectric boundary in PB electrostatic energy calculations. The conclusion holds true for all of the molecule types tested. In contrast, the standard Lee-Richards molecular surface based on BONDI atomic radii is close to optimal for the alanine decapeptide and small proteins. The optimal solvent probe radius ρ_w is close to that of the water molecule, ρ_w = 1.4 Å, although some variability of the optimum ρ_w in the range 1.4 to 2.0 Å is seen between the four types of secondary structures of Ala10, and also for the small proteins. The use of PARSE radii requires considerably larger probe radius, in the range of 3.5–6 Å, for the best accuracy relative to explicit solvent ΔG_el. For small molecules, the larger the probe the smaller the error in the continuum solvent ΔG^el, suggesting that in this case the optimal dielectric boundary is close to the convex hull for all three radii sets tested. Not surprisingly, ZAP9 shows lowest error among the three sets, since it was originally optimized⁷⁵ on a set of 200 neutral small molecules similar to the set of small molecules used in this work^*

4.2 SAS dielectric boundary in the PB model

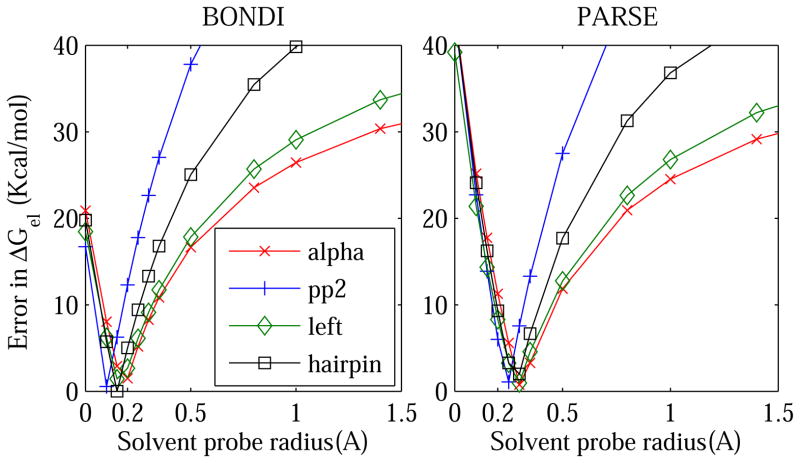
Compared to molecular surface, SAS is not as commonly used¹⁰⁰ in estimates of solvation free energies, as it is often employed in other types of continuum electrostatics calculations. For our purposes here, SAS provides a convenient way to probe variable atomic radii within the same general approach of this work. We therefore examine SAS-based DB definition here on the same footing with the other two DB definitions, fig. 1. At zero probe radius, the SAS coincides with the vdW surface, which for the three common radii sets tested so far, does not give accurate ΔG_el estimates relative to the explicit solvent. However, as the solvent probe increases, the average error in the SAS-based estimates of ΔG_el decreases until a minimum is reached between ρ_w =0.1 Å and 0.3 Å, the average optimal value being ≈ 0.2 Å, fig. 5. For small proteins, the average accuracy of the SAS-based ΔG_el at the optimum is essentially equal to that of the MS based calculation at its respective optimum. Moreover, for small molecules the SAS yields better accuracy at the optimum than the molecular surface based calculation at any probe radius from 0 to the maximum tested (ρ_w = 7 Å). We stress that the specific location of the optimum ρ_w is sensitive to the structure, see the inset in the left panel of fig. 5. The sensitivity is also evident from the range of optimum probes seen for the four conformations of Ala10, fig. 5. The fact that there is no “one-size-fits-all” optimum DB is a manifistation of the limitations of the linear response continuum theory, in particular the absence of charge hydration asymetry in its foundation.⁶⁹

Figure 5.

Absolute error in the PB electrostatic solvation free energy ΔG_el as a function of the solvent probe radius used to define the Solvent Accessible Surface (SAS) dielectric boundary. The error is calculated relative to the explicit solvent (TIP3P) reference. The computations are performed individually for four conformational states of alanine decapeptide (pp2, alpha, left, and hairpin) shown in re 2.

Note that for any probe radius ρ_w, SAS is equivalent to vdW surface computed with the same radii uniformly increased by constant ρ_w. Which means that by adding 0.2 Å to either of the common radii sets explored here, one can use the resulting vdW surface DB to match on average (for small proteins) or even exceed on average (for small neutral molecules) the accuracy of PB ΔG_el calculations performed with the standard ρ_w = 1.4 Å MS DB and the common radii. By itself, it is not news^57,101 that one can come up with a set of radii optimal for the vdW dielectric boundary definition, and that such set can yield equally accurate electrostatic solvation energies when compared to a radii set optimized for molecular surface PB calculations.¹⁰¹ The question is whether the optimal vdW and MS based dielectric boundaries are equivalent within the Poisson (and GB) continuum framework, and if so, in which sense and for which types of molecular structures? And if not, then why?

To address the question, we have selected from out test sets two small proteins and two small molecules that best represent the possible equivalence: for each pair of structures in table 2, their PB electrostatic solvation energies are closest to each other and also to their respective explicit solvent values both for the optimal vdW and MS dielectric boundary definitions considered above. The careful selection is needed here becasue the optimal MS ρ_w and vdW radii vary from structure to structure: for example, the 0.2 Å uniform shift in the BONDI radii, while optimal on average, is not necessarily optimal for every structure used to compute the RMS deviations from explicit solvent seen in fig. 6 and fig. 4. We have chosen to analyze proteins and small molecules as the two limiting cases of structure size in our test sets: large and small.

Table 2.

Examples of two proteins and two small molecules for which optimal vdW and MS based dielectric boundary definitions yield equally accurate PB estimates of ΔG_el, kcal/mol. The vdW DB calculations are based on BONDI + 0.2 Å atomic radii. For the proteins the standard value of ρ_w = 1.4 Å was used to compute the MS. Since, in the case of the small molecules and MS DB, the 3 common radii sets did no yield an optimal agreement with the explicit solvent for any solvent probe radius ρ_w < 7 Å, fig. 6, we increased all the atomic radii slightly to reach the optimum at a reasonable ρ_w. Specifically, a uniform scaling (multiplication) of all the radii in the BONDI set by 1.096 gave a clear minimum at ρ_w = 3 Å in the PB vs. explicit solvent ΔG_el average error curve (graph not shown); here we used this value of ρ_w to define MS for the PB calculations on small molecules.

Structure class	small protein	small protein	small molecule	small molecule
Name	1BH4	1BRV	3-methyl-1h-indole	1-naphthol
Number of atoms	427	265	19	19
ΔGel, PB vdW	−237.9	−210.0	−7.5	−8.0
ΔGel, PB MS	−240.9	−213.4	−7.4	−8.1
ΔGel, TIP3P	−239.7	−206.7	−7.5	−8.3

Figure 6.

Average (RMS) error of the PB ΔG_el relative to the explicit solvent (TIP3P) reference, as a function of the solvent probe radius used to define the SAS dielectric boundary. RMS deviations are computed over 248 small molecules (Right) and 19 small proteins(Left); the inset shows the distribution of the optimal probe radius for the proteins (bondi atomic radii).

If numerical equality of the electrostatic solvation energies between the two DB definitions – vdW and MS – is taken as a sole accuracy metric, then these two “opposing” definitions are indeed equivalent in the context of linear PB calculations, at least for the types of structures explored in table 2^*. However, it is well known that even though two estimates of $\mathrm{\Delta }{G}_{\text{el}}={\sum }_{ij}\mathrm{\Delta }{G}_{ij}^{\text{el}}$ may be close to each other, the individual pairwise components of the total, $\mathrm{\Delta }{G}_{ij}^{\text{el}}$, may differ substantially.^91,102 This possibility is investigated in fig. 7, where pairwise electrostatic interactions (in the presence of solvent) between individual atomic charges are compared for the two DB definitions, vdW and MS. For the small proteins, we see large – up to 5 kcal/mol – deviations between some of the charge-charge interactions computed within the two DB definitions being compared.

We also find that in this case the average effect of the switch from MS to vdW surface can be mimicked within the MS based PB calculations by increasing the internal dielectric constant from 1 to almost 2, fig. 7 (left panel). However, the near doubling of the interior dielectric still does not make the two DB definitions equivalent: it has little effect on the spread of the deviations between the pairwise interactions estimated via the two DB definition, which remain large. The deviations between the vdW and molecular surface based PB interactions are due to the differences in how the two surface definitions treat the small interstitial void space between the atoms, voids that are smaller than the solvent probe. Within the VdW DB, this interstitial space is considered to be filled with the high dielectric solvent, while the same voids and small invaginations are treated as low dielectric interior within the MS based DB definition, fig. 7 (inset of left panel). Thus, the dielectric constant averaged over the molecular interior is obviously larger in the vdW DB than in the MS DB, in agreement with the calculation shown in fig. 7 (left panel).

In contrast, small molecules do not have the interior in the same sense as larger compounds do – virtually every atom is a surface atom. Consequently, it is not surprising that in small molecules, the pairwise interactions agree very well between the two DB definitions, fig. 7 (right panel). A change in the internal dielectric is unlikely to improve the already tight agreement, fig. 7. Thus, for small proteins, the vdW and molecular surface definitions of DB are not equivalent with respect to pairwise charge-charge interactions. For small molecules, the two definitions appear equivalent by our energy-based criteria. Note that the accuracy of individual pairwise interactions in electrostatic computations is important: for example, even a single wrong charge-charge interaction may lead to significant under- or over- sampling of salt-bridges in molecular dynamics simulations, which in turn can alter the thermodynamics of the system.¹⁰³ Likewise, accuracy of individual charge-charge interactions is key for successful continuum electrostatic estimates of biomolecular pK values.^13,104–106

4.3 vdW vs. MS dielectric boundary in the generalized Born Model

While there is no notion of dielectric boundary (DB) per se in the key equation of the generalized Born (GB) model, eq. (3), the DB enters the model via the effective Born radii R_i. Theoretically, R_i can be computed directly from the solution of the PB equation, which makes the self-energy terms $\mathrm{\Delta }{G}_{ii}^{\text{el}}$ of the GB approximation exactly equal to the corresponding PB values based on the chosen DB definition. When these perfect effective radii are used, the total GB ΔG_el approximates the PB result closely.¹⁰² In practice, one tries to approximate the perfect effective radii as close as possible using approximation less computationally expensive than the PB. In this work we use the so-called R6 GB flavor, see “Methods”, which was shown to match the PB ΔG_el very closely for both the small proteins⁴⁴ and small molecules⁷⁹ used in this work. Since the GB model is an approximation to the Poisson treatment^47,94 of electrostatics, and both models are based on the same continuum electrostatics framework, it is expected that the conclusions made above for the PB will hold for the GB model as well.

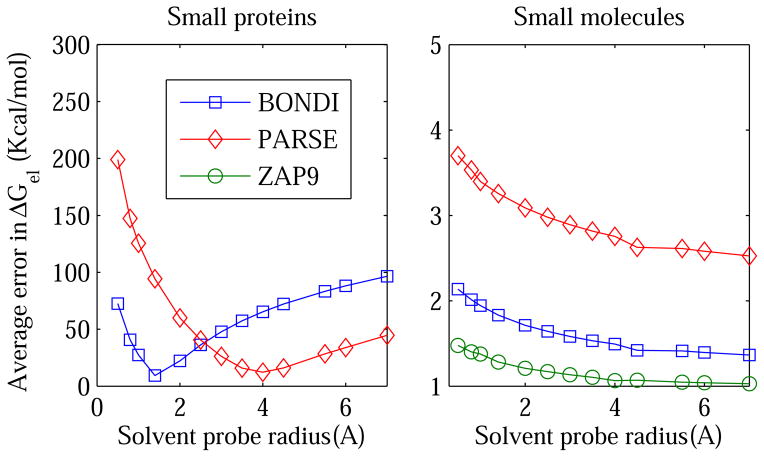
As expected for the GB model employed here, fig. 8 is very similar to its PB counterpart, fig. 4. As in the PB case, the vdW surface based on all three “standard” radii sets is far from optimal for representing the dielectric boundary in GB electrostatic energy calculations. The conclusion holds true for the small proteins and small molecules alike (we did not test the alanine decapeptide explicitly since we do not expect qualitatively different conclusions). The standard molecular surface based on the three common atomic radii sets is close to optimal for the small proteins; for each radii set tested, the optimal solvent probe radius is close the corresponding optimal for the PB case discussed above. For the small molecules, just like in the PB estimates, the larger the probe the smaller the error in the continuum solvent ΔG_el relative to explicit solvent, suggesting that in the GB case the optimal dielectric boundary is also close to the convex hull for all three common radii sets tested.

Figure 8.

Average (RMS) error the GB ΔG_el relative to the explicit solvent (TIP3P) reference, as a function of the solvent probe radius. The Molecular Surface is used as the solvent/solute boundary employed in the estimates the effective Born radii via the “R6” surface integral eq. (5); the radii enter into the generalized Born formula eq. (3) for ΔG_el. RMS error is computed over 19 small proteins (Left) and 248 small molecules (Right).

It is known that for small molecules one can adjust atomic radii to approximate MS based PB ΔG_el values via the GB approximation based on effective radii computed over vdW surface.⁵⁴ The question is whether in the GB model, the vdW and MS representations of the dielectric boundary are also equivalent for small molecules in the same sense as discussed above in the context of PB calculations? That is with respect to pairwise charge-charge interactions. Not surprisingly, the answer is also positive for the GB, based on an analysis of the same small molecules in table 2 that were used to address this question within the PB. For these two small molecules (results not shown), not only the total ΔG_els, but also the corresponding pairwise interactions agree very well between the vdW and molecular surface definitions of the DB. For the small proteins, just like in the PB case, there is no equivalence between the two DB definitions, fig. 9 (left panel). As in the PB case, the GB vdW based pairwise interactions in small proteins can be mimicked by increasing the internal dielectric constant, but again only in an average sense: large deviations between individual charge-charge interactions persist. We did not test the small molecules explicitly in the GB context, as the outcome is not expected to be different from the PB case discussed above.

The closed form of the GB model allows one to explore the origin of the vdW vs. MS differences further. Here, and in contrast to the PB model, solvation self energies $\mathrm{\Delta }{G}_{ii}^{\text{el}}$, or the effective Born radii, uniquely determine all pairwise interactions within the GB approximation.⁴⁷ For the small proteins, the optimal vdW based DB leads to a pronounced underestimation of the effective radii for atoms buried within the protein interior relative to the optimal MS based estimate, fig. 9; this underestimation is compensated by a slight overestimation of the relatively small effective radii of the surface atoms, which nevertheless contribute substantially to the total $\mathrm{\Delta }{G}_{\text{el}}(\mathrm{\Delta }{G}_{ii}^{\text{el}}~1/R_i)$. The overestimation of the small effective radii is a direct consequence of using the slightly larger (by 0.2 Å in our example) atomic radii in the optimal vdW DB. Combined with the pronounced underestimation of the large effective radii, fig. 9, the net result is a total vdW ΔG_el that is deceptively equal to that of the MS based ΔG_el. The underestimation of the large effective radii occurs because small invaginations and interstitial voids between the atom spheres are treated as solvent in the vdW based integral approaches to the estimation of the effective radii,¹⁰² that is the corresponding volume is missing from the integrals such as eq. (4). The net result is similar to filling the voids and small invaginations with high dielectric solvent in the PB calculations based on vdW dielectric boundary. Note that the small, ~ 0.2 Å, increase in the atomic radii required to make the vdW DB optimal, is not going to close many of these voids in structures with pronounced interior regions, fig. 7 (insets). The above argument applies only to molecules that posses pronounced interior, such as proteins. In contrast, small molecules do not have an interior – virtually every atom is a surface atom – and so the “missing volume” problem does not arise.

5 Discussion

In this work we have investigated how the use of three common dielectric boundary definitions – van-der-Waals (vdW), molecular (MS) and solvent accessible surface (SAS) – affects the accuracy of computing the electrostatic component of solvation free energy (ΔG_el) within the Poisson (PB) and the generalized Born (GB) continuum solvent models. The following conclusions were essentially the same for both models, although we have tested fewer options within the GB which is an approximation to PB.

The energies were computed for a set of neutral compounds representing several molecular classes: small proteins, peptides, and small rigid molecules. We have started with two general purpose atomic radii sets, BONDI and PARSE, and a newer set ZAP9 optimized for small molecules. When any of these radii were used to set the dielectric boundary (DB) in the PB calculations, the MS dielectric boundary emerged as a clear winner, judging by the accuracy of ΔG_el estimates relative to explicit solvent free energy calculation taken as reference. As a testament to limitations of the continuum electrostatics approach, the optimal value of the solvent probe radius ρ_w varies appreciably between structure types and atomic radii sets. For example, the use of the typical water radius of 1.4 Å leads to smallest errors for proteins and BONDI radii, while PARSE radii and small molecules required much larger ρ_w to minimize the average deviation from the explicit solvent. Variations of the optimal probe radius were also seen within individual structural classes. The SAS boundary definition, computed with an optimal probe, proved to be competitive, on average, with the MS based definition. Namely, for a very small ρ_w ~ 0.2 Å, optimal ΔG_el values computed with the SAS boundary were nearly identical to the optimal ΔG_els based on the MS boundary. The exact optimum was extremely sensitive to the probe size and the specific radii set, and varied somewhat from structure to structure. Since SAS is geometrically equivalent to the vdW surface derived from atomic radii shifted by the solvent probe value, we have further investigated the possibility of equivalence of optimal MS and vdW surface based dielectric boundaries. Our main finding is that while the total ΔG_el computed within these two definitions may nearly equal each other for their respective optimal boundary parameters (atomic and probe radii), the individual charge-charge interaction energies can differ substantially between the vdW and MS based computations. The differences were found to be large, up to several kcal/mol for some pairs of atoms, in a carefully selected representative sample of small proteins. The observation makes the two boundary representations not equivalent for this structure type. On the other hand, pairwise charge-charge interactions in sample small molecules were nearly unaffected by a switch between optimal MS and vdW boundaries, suggesting that at least for small rigid molecules the two DB definitions may be interchangeable in practical PB or GB calculations. We have attributed this difference between proteins and small molecules to the fact that proteins have well defined interior regions, while small molecules do not have interior regions – essentially every atom is at the surface. Thus, for small molecules, differences between MS and vdW boundary definitions with respect to the interior regions are almost irrelevant, while for structures with well defined interiors these differences play a larger role. Within the vdW DB, the interstitial void space between the atoms and small internal cavities is considered to be filled with the high dielectric solvent, while the same voids (smaller than the solvent probe size) are treated as low dielectric interior within the MS based DB definition. We have also found that, for the small proteins, one can mimic the average decrease in pairwise atom-atom electrostatic interactions due to the switch from MS to vdW DB by simply doubling the interior dielectric value in the MS based calculations. The observation is consistent with the above picture: once the solvent filled voids are taken into account, the dielectric constant averaged over the molecular interior is obviously larger for the vdW DB then for MS DB. For structures with no interior, there should be no difference, which is exactly what we see for the small molecule examples.

Since the two limiting cases of the dielectric boundary definitions (vdW and MS) are not expected to be equivalent for biomolecular structures other than small molecules with virtually no interior region, it is natural to ask which of the two definitions is physically more correct? The issue is especially important since novel approaches to define and compute dielectric boundary are being developed, which can be parametrized to mimic one or the other limiting definition of the DB. We believe that the answer depends on which other approximations – on top of the linear response continuum – are used in each particular application of the PB or GB model. First, consider a scenario in which adequate conformation dynamics and sampling is expected to reproduce correct structural reorganization that leads to proper dielectric response. For example, if a continuum model is used to estimate electrostatics in all-atom molecular dynamics, then a dielectric of 1 is appropriate for molecular interior¹, which is better reproduced by MS based DB, not vdW. In this scenario, physical phenomena that give rise to higher than 1 interior dielectric, e.g. transient water penetration and reorganization of molecular dipoles, are supposed to be accounted for by the correct dynamics, not by an artificial increase of the internal dielectric constant. For instance, native proteins transiently unfold at room temperature, exposing some of their interior to the high dielectric solvent for short periods of time. At these brief moments, the interactions between some of the protein charges are reduced substantially, leading to somewhat lower mean interactions when averaged over a long time. The resulting effective dielectric constant will be larger than 1, but this does not mean that the constant internal dielectric used in the equations of motions that govern the dynamics of the molecule, e.g. those based on the GB model eq. (3), should be different from unity.

Consider now a very different scenario of continuum electrostatics usage, one in which atomic level structural relaxation is not part of the computational model. A good example is estimation of pK and ionization states of protein titratable groups based on single conformational state¹³ of the molecule. In this case, polarization of protein dipoles, water penetration, etc. does not come in naturally via dynamics, but is instead accounted for, albeit in some average sense, by using a higher than 1 interior dielectric, typically in the range of 4 to 20.^85,107 As we have seen above, increased interior dielectric can be mimicked, at least on average, by employing the vdW DB definition. This correspondence may justify the use of vdW DB in scenarios where ε_in > 1 is called for by limitations of the underlying model; such scenarios are not limited to pK estimation.⁶⁰ We can still argue that a smoothly varying representation of higher dielectric interior¹⁰⁸ afforded by a uniform dielectric model (and MS boundary) is more physical than the very granular representation that would result from filling a myriad of inter-atomic voids with high dielectric of the solvent (vdW boundary), thus creating a great number of tiny sharp dielectric boundaries within the protein interior. It is unlikely that the correct spatial variation of the internal dielectric, which stems from several physical effects including variation in charge and mobility of structural components, can be accurately reproduced by a distribution of high dielectric pockets resulting from purely geometric voids in the vdW representation. However, most of the current PB-based pK estimates, as well as many other continuum electrostatics calculations, still use the simplest two-dielectric model, in which the entire protein interior is assigned a single dielectric value – a drastic approximation to reality in which the dielectric response varies considerably within the protein.^108,109 Moreover, the very notion of intramolecular dielectric constant is problematic,¹¹⁰ the specific values may depend on the model being employed.^67,111 Therefore, it is still unclear whether the simplified two-dielectric MS based DB can always be expected to provide more accurate charge-charge interactions than the alternative vdW based treatment in which one can attempt to mimic locally averaged variable dielectric by appropriately adjusting the atomic radii throughout the protein – a relatively inexpensive proposition, computationally. In particular, the latter approach can be useful in situations where the key charge-charge interactions within the protein are spatially separated from the region of variable dielectric, for example when the vdW DB was used to mimic variable dielectric across a membrane¹¹² that surrounds the protein in question. Successful use of vdW based DB was also reported in several PB studies unrelated to pK calculations, see e.g. Ref.⁶⁰ for a recent review.

A comparison of the accuracy of continuum electrostatic calculations based on vdW vs. MS based dielectric boundary definitions can be made by comparing a set of computed observables directly against experiment. However, such comparisons may not always be straightforward, as many other approximations are involved. Conclusions from such comparisons also depend on the specific atomic radii set used; ideally one wants to compare between sets optimized for each specific type of the DB in the context of the specific problem, which may be computationally very demanding for large structures. The use of variable internal dielectric to account for missing conformational rearrangements complicates such comparison even further, as its effects on charge-charge interactions is similar to that of changing the dielectric boundary definition. In the present work we have attempted to avoid many such complications and make a more direct comparison between the two common dielectric boundary definitions by focusing on a fairly representative test of small rigid structures and explicit solvent solvation energies as reference.

Table 1.

Radii sets used in this work. For the small proteins we used a modification of BONDI (MBONDI2) in which the radius of a hydrogen atom bound to nitrogen is increased to 1.3 Å versus 1.2 Å in the original BONDI set.

	Atomic Radii (Å)
	C	H	N	O	S	P	F	Cl	Br	I
BONDI	1.7	1.2	1.55	1.5	1.8	1.8	1.47	1.75	1.85	1.98
PARSE	1.7	1.0	1.5	1.4	1.85	1.8	1.47	1.75	1.85	1.98
ZAP9	1.87	1.1	1.55a	1.52b	2.15	1.8	2.4	1.82	1.85	2.65

^a1.4 Å for Secondary and Tertiary N

^b1.76 Å for carbonyl O