Prediction of Longitudinal Development of Infant Cortical Surface Shape Using a 4D Current-based Learning Framework

Abstract

Understanding the early dynamics of the highly folded human cerebral cortex is still an actively evolving research field teeming with unanswered questions. Longitudinal neuroimaging analysis and modeling have become the new trend to advance research in this field. However, this is challenged by a limited number of acquisition timepoints and the absence of inter-subject matching between timepoints. In this paper, we propose a novel framework that unprecedentedly solves the problem of predicting the dynamic evolution of infant cortical surface shape solely from a single baseline shape based on a spatiotemporal (4D) current-based learning approach. Specifically, our method learns from longitudinal data both the geometric (vertices positions) and dynamic (temporal evolution trajectories) features of the infant cortical surface, comprising a training stage and a prediction stage. In the training stage, we first use the current-based shape regression model to set up the inter-subject cortical surface correspondences at baseline of all training subjects. We then estimate for each training subject the diffeomorphic temporal evolution trajectories of the cortical surface shape and build an empirical mean spatiotemporal surface atlas. In the prediction stage, given an infant, we first warp all training subjects onto its baseline cortical surface. Second, we select the most appropriate learnt features from training subjects to simultaneously predict the cortical surface shapes at all later timepoints from its baseline cortical surface, based on closeness metrics between this baseline surface and the learnt baseline population average surface atlas. We used the proposed framework to predict the inner cortical surface shape at 3, 6 and 9 months from the cortical shape at birth in 9 healthy infants. Our method predicted with good accuracy the spatiotemporal dynamic change of the highly folded cortex.

1 Introduction

The highly folded human cerebral cortex nests vital cognitive and decision-making functions that control our behavior. Analyzing cortical morphometrics from neuroimages opens a wide widow to pinpoint population and individual based cortical growth patterns [1]. In particular, characterizing the morphological dynamics of the cerebral cortex as it matures will enable us to examine their relationship with functional dynamics and thereby advance our understanding of how the cerebral cortex grows and what modulates its development [2]. Besides, quantifying cortical morphological dynamics at an early stage of cortical growth will help unravel early developing brain disorders [3]. More importantly, the possibility of predicting cortical morphological changes will eventually help improve prognosis for infants with neurodevelopmental brain disorders.

However, despite their importance, modeling approaches for examining the early postnatal human brain morphometrics and dynamics using longitudinal neuroimaging data are scarce. In [4], a computational mechanical cortical growth model was developed to simulate the dynamics of cortical folding from longitudinal data in the first year of life, during which the cortical surface area increase by 76% [3]. Although promising, this method requires the use of cortical surfaces at all later timepoints of the same infant to guide the growth model and also will gradually lose its accuracy and informative potential as the number of data acquisition timepoints decreases. Ideally, a cortical growth model should be able to accurately and dynamically predict the highly convoluted shape of the cortical surface from one or a very limited number of input surfaces. By cortical dynamic prediction, we imply the estimation of the spatiotemporal cortex shape deformation in the future (i.e. the evolution trajectories of the shape) using a set of existing observations and measurements. Recently developed methods [5–8] proposed various geodesic shape regression models to estimate smooth diffeomeorphic evolution trajectories; however, they were implemented for image time-series change tracking. A non-linear mixed effect dynamic prediction model was proposed in [9] to estimate temporal change trajectories of radial diffusivity images derived from diffusion tensor imaging (DTI) of early brain development. However, its application was only limited to estimate region-level changes in the image space, and also it required a predefined complex parametric form of the development trajectory.

This paper proposes a learning-based framework that predicts the dynamic postnatal cortical shape from a single baseline cortical surface at birth using a recently developed spatiotemporal (4D) diffeomorphic surface growth model based on the theory of ‘measuring’ a surface as a current [10, 11]. The theory of currents elegantly and generically represents a shape as a current without the need to establish the point-to-point surface landmark correspondence on the longitudinal and cross-sectional shapes. Furthermore, piece-wise geodesic current deformation trajectories can be estimated from disparately spaced-out measurements in time for 0-currents (set of points), 1-currents (curves), 2-currents (surfaces) and 3-currents (volumes) using a robust converging numerical scheme developed in [10]; thereby facilitating the integration of multidimensional shapes from multimodal images in a unified statistical framework for data analysis. Specifically, our approach is composed of a training stage and a prediction stage. In the training stage, the proposed framework learns both geometric (vertices positions) and dynamic (smooth and invertible evolution trajectories) features of cortical surface growth for each infant using the available acquisition timepoints. We then estimate the mean empirical spatiotemporal atlas at the most commonly shared timepoints among the training subjects to simultaneously initialize the cortical surface shapes at all later timepoints for prediction. In the prediction stage, for each new subject, we refine this initialization by jointly moving some vertices based on different closeness metrics between the baseline cortical shape and the baseline cortical atlas. Once the baseline vertices positions are updated, they form together a virtual baseline shape, which is proximal to the ground truth baseline cortical shape. Finally, retrieving the corresponding learnt smooth deformation trajectory for every vertex belonging to the constructed virtual shape predicts the cortical shape up to the last timepoint in the training dataset. Of note, the proposed method requires neither predefined prarametric forms of the cortical developmental trajectories nor the guidance from the later time points of the same subject.

2 Current-based Learning of Shape Growth Model

2.1 Spatiotemporal current-based atlas building (training stage)

We first present the key mathematical ingredients for ‘measuring’ a surface as a current. In this context, the current metric is used for building a diffeomorphic regression model that matches a set of shapes 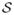= {S₀, . . . , S_N} with high accuracy as demonstrated in [11]. More details can be found in [10, 11].

Cortical surface representation using currents

The concept of representing a surface as a current derives from Faraday’s law of induction in physics, which states that the variation of any magnetic vector field W through a surface S induces a current in the space W^* within a wire loop delimiting S [10]. The intensity of the current is proportional to the variation of the flux of this magnetic field, which mathematically translates as an integration of the vector field elements ω ∈ W along the shape unit normal vectors n: S = ∫ ω(x)^tn(x)dλ(x), where dλ denotes Lebesgue measure on the surface. Hence, a surface can be geometrically defined as the collection of local fluxes for all possible vector fields traversing it. In this regard, W is defined as a Reproducing Kernel of Hilbert Space (RKHS) spanned by convolutions between a square integrable vector field and a Gaussian smooth kernel $K(x,y)=\mathit{exp}(-{\mid x-y\mid }^2/{\sigma }_W^2)$. The rate of decay of the kernel σ_w denotes the scale under which the geometric details of the surface –when converted into a current– are overlooked.

A vector ω ∈ W can be measured at a location x for any fixed points y and vectors α as a convolution between the kernel K^W and vectors α: ω(x) = K^W(x, y)α(y), where the couple (x, α) is called a momentum. On the other hand, the space of currents W^* is defined as a vector space containing the set of all continuous linear maps from W to ℝ (i.e. the dual space of W). Any current in W^* is then defined as: $\omega \mapsto {\delta }_x^n(\omega )=n^t\omega (x)$, where ${\delta }_x^n$ defines a Dirac delta current. Although it is scale-dependent, W enables to densely ‘convert’ the surface S into a current by locally measuring these localized Dirac delta currents and summing them up: $S={\sum }_k{\delta }_{x_k}^{{\alpha }_k}$; thus S becomes fully parameterized by its meshes (triangles) k and normals n_k located at each center of these meshes and approximated using the Dirac delta currents located at the center of each of its meshes k (Figure 1). Hence, any surface can be decomposed into an infinite sum of Dirac delta currents which act as basis vectors in the space of currents W^*. More importantly, the current space W^* is endowed with a metric that enables us to measure the distance between two shapes (i.e. two currents): $<S,S^{\prime }{>}_W^{\ast }={\sum }_i{\sum }_j{\alpha }_i^t{K}^W(x_i,x_j){\beta }_j$ where $S={\sum }_i{\delta }_{x_i}^{{\alpha }_i}$ and $S^{\prime }={\sum }_j{\delta }_{x_j}^{{\beta }_j}$, thereby elegantly paving the way to formulate and solve geodesic surface matching problems.

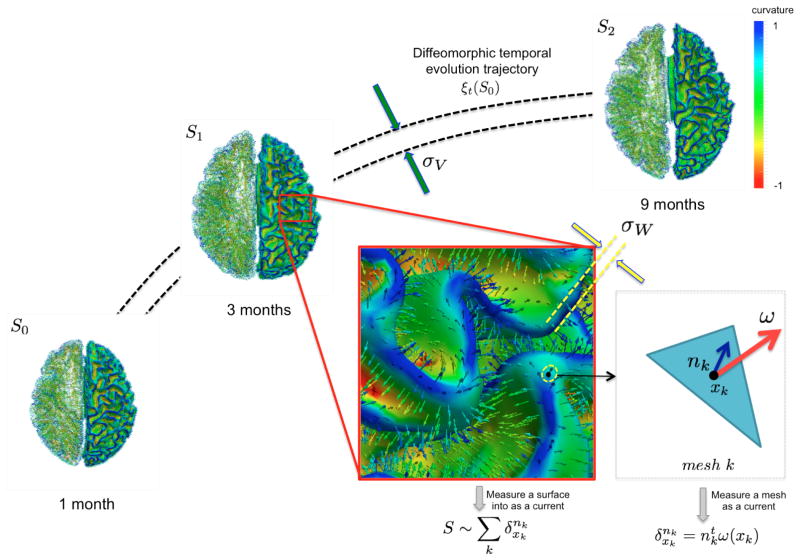
Fig. 1. Geodesic longitudinal shape regression using currents.

Each cortical surface S_i is represented by the sum of the Dirac delta currents ${\delta }_{x_k}^{n_k}$ with x_k being the center of the mesh k (triangle) and n_k as its normal (illustrated in the left hemispheres).

Spatiotemporal diffeomorphic current-based surface regression model

Considering a set of longitudinal cortical surfaces 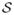= {S₀, . . . , S_N} acquired at different timepoints t_i, i ∈ [0,N], we estimate a spatiotemporal surface growth model that successively deforms the baseline shape S₀ onto the consecutive shapes: S(t) = ξ_t(S₀). This deformation process is guided by the diffeomorphic mapping ξ_t, which identifies for each mesh the optimal evolution trajectory as a solution of the following flow equation:

$$\{\begin{array}{ll}\frac{d{\xi }_t(x)}{dt}=v_t({\xi }_t(x)),\hfill & t\in [0,T]\hfill \\ {\xi }_0=Id.\hfill & \hfill \end{array}$$

Here v_t ∈ V denotes the time-dependent deformation velocity. To guarantee the smoothness and the invertibility of the estimated deformation trajectory ξ_t, the velocity field V is defined as a RKHS with a Gaussian kernel K^V . The deformation kernel decays at a rate σ_V denoting the scale under which deformations are locally similar to the identity map (no deformation). The time-dependent velocity writes as $v_t(x)={\sum }_{k=1}^M{K}^V(x_k(t),x){\alpha }_k(t)$, with M the number of meshes in the baseline shape S₀ [10]. For a static shape S₀, the vector field W associated with it is closely spanned by the the momenta (x, n). To cause S₀ to become dynamic and warp it onto different shapes, an external momentum (x_k, α_k) of the deformation field locally acts on its Dirac delta currents ${\delta }_{x_k}^{n_k}$ to geodesically deform it into the consecutive observed shapes. The estimation of the momenta (x_k(t), α_k(t)) fully defines the surface deformation process from t = 0 to t = T. This is achieved through conjugate gradient descent algorithm minimizing the following energy:

$$E={\int }_0^1{\Vert v_t\Vert }_V^{2}dt+\frac{1}{\gamma }{\sum }_{j\in \{1,\dots ,N\}}{\Vert {\xi }_{t_j}^v·S_0-S_j\Vert }_{W^{\ast }}^2$$

Where γ denotes a trade-off parameter between the total kinetic energy of the deformation (first term) and the similarity measure between the deformed baseline shape and the consecutive ground truth observations (second term).

Current-based geometric and dynamic features learning

In the training stage, we estimate a cortical surface growth scenario for each infant in our training dataset using the available MR acquisition timepoints. We first register all the baseline surfaces of the training subjects into a common space. Then, for each warped baseline shape in this space, we estimate its temporal evolution trajectory. Both of these steps are achieved using the current-based deformation model, thereby providing a normalized current space, where all subjects’ longitudinal shapes become ‘linked’ in space and time. This facilitates inter-subject comparison of deformation features estimated at any timpoint falling in the in-between obervations interval ]t_i, t_i+1[. At this point, we introduce the notion of a cloud 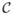, which is composed of points c(x, t) = (x, ξ(x, t)) with x a vertex belonging to any baseline shape S₀ in the training data and ξ(x, t) as its corresponding temporal deformation trajectory. In other words, a point c(x, t) in the cloud locates the new position ξ(x, t) of any baseline vertex x at a specific timepoint t. Here, the 3D position of any baseline vertex x defines the geometric feature and its evolution trajectory c(x, t)_{t∈[0,T ]} defines the dynamic feature of the learnt model. We will exploit both of these features to predict the evolution trajectory for a new baseline shape.

Cortical spatiotemporal atlas estimation

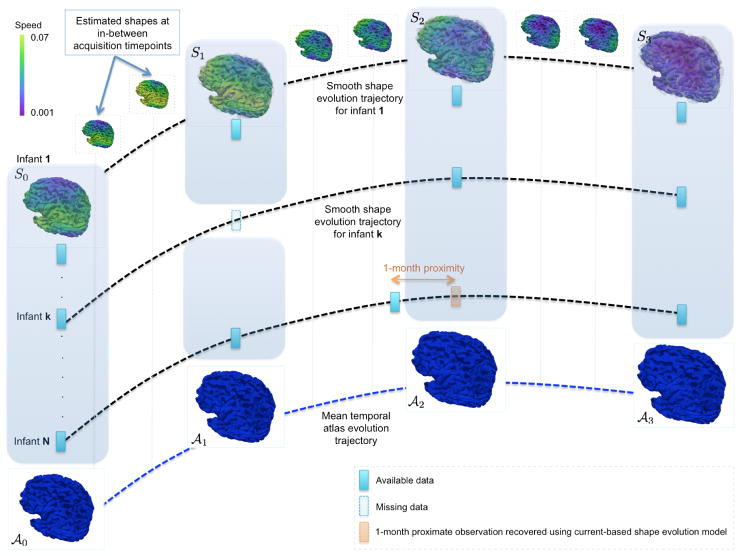
For each of the most commonly shared acquisition timepoints t_{i{i∈0,...,N}}, we build an empirical mean atlas 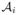by computing the mean 3D position of the spatiotemporally aligned training subjects. We also include the estimated shapes using the current-based surface growth model for the atlas building if these shapes were acquired at ±1–month gap from the ground-truth shape (Figure 2). Indeed, at ±1–month gap, the current-model recovers neighboring information with high accuracy (mean ± std = 1.05 ± 0.16mm). One could intuitively explain this by recalling the principle of the least action in a classical mechanical Lagrangian framework, which grounds the diffeomorphic geodesic surface deformation framework. This strategy allows us to include more data into building the temporal atlas {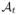} with t ∈ {t₀, . . . , t_N} and to better capture inter-subject variability.

Fig. 2. An overview of the proposed framework for learning dynamic cortical surface growth (training stage).

We estimate a smooth temporal trajectory for each of the baseline cortical shapes in the training dataset. Here we overlay the ground truth shapes (transparent gray) with the estimated ones. A spatiotemporal atlas is built at the most commonly shared acquisition timepoints in the training subjects. We also include the estimated cortical surface if it is ±1–month distant from the ground truth in the atlas building process.

2.2 Prediction using the learnt geometric and dynamic features

To predict the evolution of the cortical surface for a new infant, the only information we need is the shape of the baseline cortical surface S₀ (at the first acquisition timepoint). Here we propose two different methods that exploit S₀ to select geometric and dynamic features from the cloud. The extracted features will define the temporal evolution of the cortical surface up to the last common acquisition timepoint in the training dataset. Both methods are based on the intuitive idea that vertices in the baseline ground truth shape dynamically behave in a way that is similar to their nearest neighboring vertices in the cloud. Subsequently, we introduce the concept of a virtual shape that explores the learnt shape features to find the closest shape in the cloud to the baseline shape S₀. The prediction framework for the spatiotemporal evolution of the ground truth surface S₀ is composed of two main steps:

• Step 1: Virtual shape construction for simultaneous shape prediction at all late timepoints. First, we define a virtual shape S_virtual as the ensemble of baseline vertices from the cloud 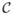that are close to the ground truth baseline shape S₀ (Figure 3). We initialize the virtual shape as the baseline atlas shape 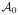and also the shapes to predict {S̃_i} as the mean atlases 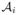at the timepoint t_i. If the error distance between any vertex in the mean atlas shape 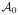and its corresponding baseline vertex in S₀ is smaller than, then we keep this vertex unmoved. Otherwise, we seek the closest vertex from the cloud that is within an -neighborhood of the current vertex. If the -closest vertex exists, then the position of the current vertex in S_virtual is updated accordingly. Otherwise, for vertices in S_virtual having no closest vertex in the –range in the baseline shape, we propose two closeness metrics to construct the virtual shape S_virtual:

  1. The Mahalanobis distance from the cloud (Metric 1): We use the Mahalanobis metric to update vertices in S_virtual that are > ε–further from the baseline shape S₀. More specifically, we select vertices from the cloud C that are closer to S₀ and fall within the –neighborhood.

     $$S_{\mathit{virtual}}={\{v_i\}}_{\{i=1,\dots ,M\}}={\mathit{argmin}}_{v_k\in {\mathcal{C}}_j;j\in \{0,\dots ,N\}}{(v_i-v_k)}^t{\mathit{\sum }}_j^{-1}(v_i-v_k)$$

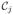     is the points of the cloud C that belong to the j^th subject in the training dataset. Σ_j is the covariance matrix of the vertices in the cloud 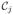. Finally, for each vertex in the virtual shape, we retrieve its dynamic feature c(x, t)_{t∈[0,T ]} from the cloud. This ultimately defines the smooth temporal trajectory for every vertex in the constructed virtual shape and predicts its shape at any later timepoint.

  2. The k–closest neighbors from the cloud (Metric 2): We update the position of a virtual vertex x that is > –far from S₀ by computing the mean position of the k-closest vertices in the cloud to x using Euclidean distance. We compute the mean evolution trajectory ξ̄ over the k retrieved trajectories. This mean spatially smoothed trajectory predicts the growth of the input baseline surface S₀.

     These key steps are briefly stated in Algorithm 1.

     Algorithm 1.

     Prediction of cortical surface shape evolution from a baseline shape

     1: INPUTS:

     The learnt mean atlases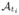

     The learnt cloud C

     The baseline ground truth shape S0

     2: Initialize Svirtual ←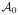0.

     3: Initialize S̃i ←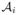i for i ∈ {1, . . . , N}

     4: Initialize ε as the mean distance between S0 and 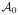0 plus its standard deviation

     5: for every vertex x in the virtual shape Svirtual that is located outside the ε–neighborhood from S0 do

     Update its position using the closeness metric (1 or 2)

     Retrieve (or update if using Metric 2) its dynamic feature (evolution trajectory) c(x, t)t∈[0,T]

     $${\stackrel{\sim }{S}}_i(x)=c(x,t_i)$$

     6: end for

     7: Estimate the geodesic current-based baseline shape evolution using {S0, {S̃i}} by minimizing: $$\stackrel{\sim }{E}={\int }_0^1{\Vert v_t\Vert }_V^{2}dt+\frac{1}{\gamma }{\sum }_i{\Vert {\stackrel{\sim }{S}}_i-{\varphi }_{t_i}^v·S_0\Vert }_{W^{\ast }}$$

     8: OUTPUT:

     Set of predicted surfaces { S̃i} at timepoints ti with i ∈ {0, . . . , N}

     Set of smooth temporal evolution trajectories for vertices in S0 for t ∈ [0, tN]

• Step 2: Estimation of a geodesic evolution of the cortical shape for a new subject. Once the set of shapes {S̃_i} are predicted at later timepoints, we minimize the energy Ẽ (Algorithm 1) to estimate the spatiotemporal deformation trajectory of the baseline shape S₀.

Fig. 3. Illustration of the concept of the cloud 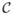and the virtual shape S_virtual used in the prediction stage.

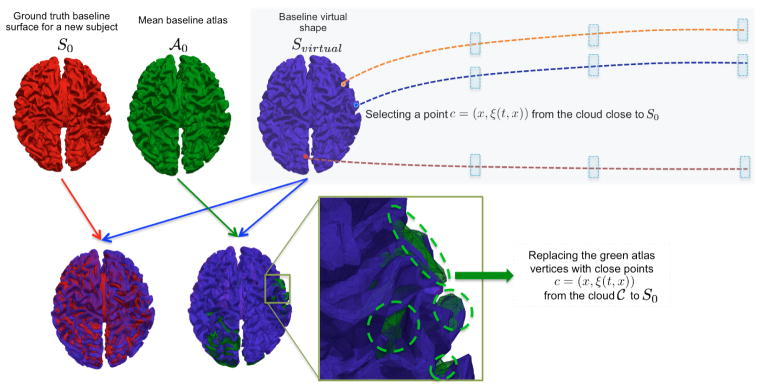
The green vertices visible in the overlap between the baseline atlas 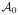and the virtual shape S_virtual were updated using better candidates from the cloud C. Notice that we have a good overlap between the baseline atlas shape and the baseline input shape S₀. Orange, blue and red vertices belong to the cloud where their learnt trajectories can be easily retrieved to track forth their spatiotemporal deformation. The blue rectangles represent the later timepoints where the spatiotemporal atlas was estimated.

3 Results

3.1 Data and parameters setting

We evaluated the proposed framework on longitudinal inner cortical surfaces of 9 infants randomly selected from 17 healthy infants, each with 4 serial MRI scans acquired at around birth, 3 months, 6 months and 9 months of age. After rigid alignment of longitudinal and cross-sectional infant MR images and brain tissue segmentation, we reconstructed the cortical surfaces with correct topology and geometry using the method proposed in [12]. We used the current-based geodesic shape regression model with parameters γ = 10⁻⁵, σ_W = 5, and set σ_V as half size the bounding box confining the surface at the last acqusition timepoint [10, 11].

3.2 Cortical shape prediction evaluation

We built three spatiotemporal atlases using alternatively selected 14 different training subjects from the dataset, while leaving 3 subjects for testing to predict the inner cortical surface shape at 3, 6 and 9 months from the cortical surface shape at birth.

Spatiotemporal mean population atlas building

We set the inter- and intra-subject cortical correspondences using the current-based shape regression model, so we can easily navigate from any subject at any timepoint to a different subject at a different timepoint. We then built spatiotemporal mean atlases at 0, 3, 6 and 9 months. Each spatiotemporal atlas {,,,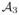} was estimated using 14 infants, while leaving 3 infants out for testing.

Cortical shape prediction from the baseline cortical surface S₀

We implemented Algorithm 1 using the two proposed closeness metrics to construct the virtual shape for each of the 9 testing infants. The parameter ε was fixed as the mean distance between S₀ and 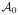plus its standard deviation. We chose k = 4 closest neighbors for the second metric. We display in Table 1 a comparison between the prediction surface distance error for the two different metrics. Clearly, the prediction method based on Metric 2 shows a more promising performance in decreasing the prediction errors at later timepoints, compared with Metric 1 (Table 1). One could intuitively explain this observation as a result of including more vertices (here k = 4 closest neighbors) from the cloud to contribute into building more robust baseline virtual shape S_virtual. This in turn allows to stretch the neighborhood of vertices formed when shooting S_virtual to the next missing timepoint by tracking their temporal evolution trajectories. In other words, this leads to better capture inter-subject spatial variability at later timepoints. Therefore, Metric 2 was used to build the spatiotemporal evolution of the baseline shape S₀.

Table 1. Shape prediction errors (mm) from a single baseline cortical surface for 9 infants.

Mean ± standard deviation and median distance between the predicted shape and the ground truth shape were computed using metrics 1 (Mahalanobis distance) and 2 (k-closest vertices, k = 4).

Timepoint	Mean Error 1	Median Error 1	Mean Error 2	Median Error 2
3 months	1.279 ± 1.692	0.912	1.235 ± 1.604	0.865
6 months	1.324 ± 1.551	0.967	1.296 ± 1.615	0.925
9 months	3.347 ± 8.313	1.414	1.695 ± 3.205	1.147

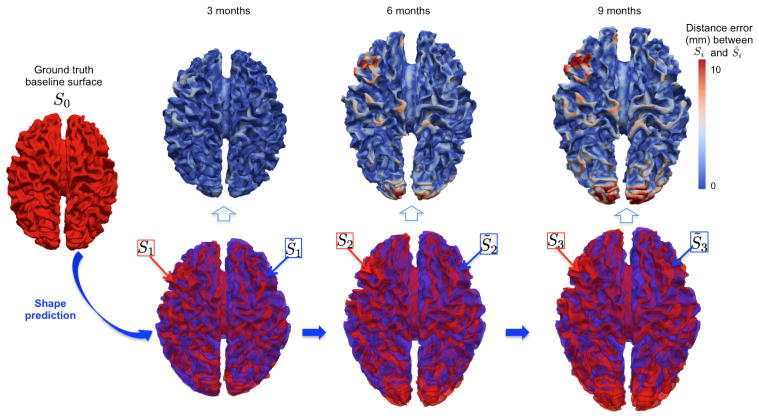
We show in Figure 4 the vertex-wise distance error map between the predicted {S̃_i} and the ground truth shapes {S_i} at 3, 6 and 9 months (top row) and their spatial overlap (bottom row) for one representative testing infant. The prediction error gradually increases as the shape to predict becomes very distant in time from S₀.

Fig. 4. Spatiotemporal shape prediction in one representative infant.

(Top row) The 3D surface distance error map between the ground truth shape (in red) and the predicted shape (in blue) from the baseline shape S₀.

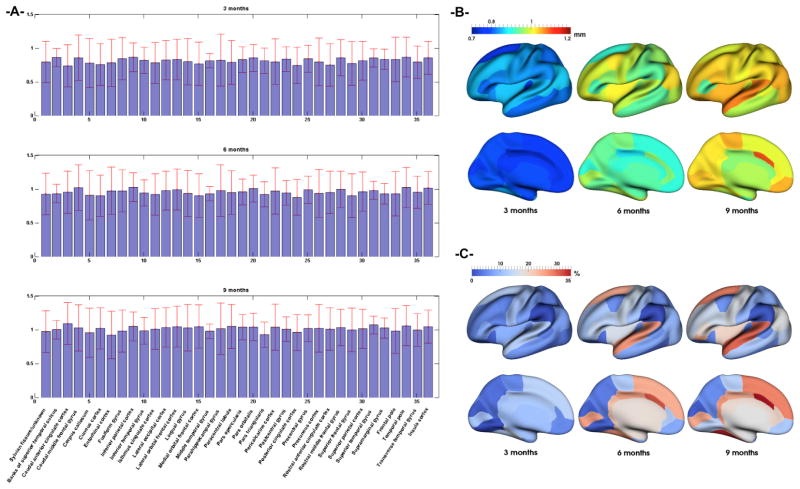
Figure 5 (a) and (b) shows the mean value and standard deviation prediction errors over the 9 testing infants in each cortical region defined in [13] at 3, 6 and 9 months. The average distance errors over two hemispheres and across all 36 ROIs are 0.811mm, 0.953mm and 1.011mm at 3, 6, and 9 months, respectively. As we can see, the distance errors are quite small, although they gradually increase from 3 to 9 months. Besides, the mean prediction error across the 9 subjects peaks at 0.86mm (in the right and left temporal poles), 1.11mm (in the right and left superior temporal gyri) and 1.05mm (in the right and left superior temporal gyri) successively for 3, 6 and 9 months. We also observe regionally non-uniform error maps, which is most likely caused by the spatially variable inter-subject variations in terms of cortical folding and its development. We also report the percentage of surface area difference in each ROI between the ground truth and the predicted cortical surfaces in Figure 5 (c). The average surface area difference across all ROIs are 7.8%, 12.9% and 15.4% at 3, 6, and 9 months, respectively, further demonstrating the good performance of the proposed method.

Fig. 5.

(A) Mean prediction error and its standard deviation (red bars) in mm across 9 testing infants in 36 cortical regions of interest (ROI). (B) Mean prediction error distance (in mm) of each ROI mapped onto inflated cortical surface. (C) Absolute surface area difference in each ROI (in %) between predicted and ground truth surfaces.

4 Discussion and conclusion

We presented the first prediction model for dynamic cortical surface evolution in infants during the first year based solely on a single baseline cortical shape. We used the diffeomeorphic 4D current-based shape regression model to learn both geometric and dynamic features of cortical surface shape growth for shape prediction at later timepoints. Although the infant cortical shape is very challenging to model due to its highly convoluted foldings and dynamic growth, the proposed framework showed promising prediction results. We would like to note that the proposed learning framework is generic and can also be applied to a new infant that has a limited set of measurements. In our future work, we would further boost up its performance by including more than one input shape and also additional morphological features (e.g. surface thickness or gyrification index) for predicting the shape evolution in space, time and morphology. Furthermore, exploring the recently developed unbiased approaches for 3D shape atlas building may also increase the prediction accuracy [14].