Methods for analysis of size-exclusion chromatography–small-angle X-ray scattering and reconstruction of protein scattering

Methods were developed to facilitate analysis of size-exclusion chromatography–small-angle X-ray scattering experiments by singular value decomposition and improve reconstruction of protein scattering by Guinier-optimized linear combination with or without buffer subtraction.

Abstract

Size-exclusion chromatography in line with small-angle X-ray scattering (SEC–SAXS) has emerged as an important method for investigation of heterogeneous and self-associating systems, but presents specific challenges for data processing including buffer subtraction and analysis of overlapping peaks. This paper presents novel methods based on singular value decomposition (SVD) and Guinier-optimized linear combination (LC) to facilitate analysis of SEC–SAXS data sets and high-quality reconstruction of protein scattering directly from peak regions. It is shown that Guinier-optimized buffer subtraction can reduce common subtraction artifacts and that Guinier-optimized linear combination of significant SVD basis components improves signal-to-noise and allows reconstruction of protein scattering, even in the absence of matching buffer regions. In test cases with conventional SAXS data sets for cytochrome c and SEC–SAXS data sets for the small GTPase Arf6 and the Arf GTPase exchange factors Grp1 and cytohesin-1, SVD–LC consistently provided higher quality reconstruction of protein scattering than either direct or Guinier-optimized buffer subtraction. These methods have been implemented in the context of a Python-extensible Mac OS X application known as Data Evaluation and Likelihood Analysis (DELA), which provides convenient tools for data-set selection, beam intensity normalization, SVD, and other relevant processing and analytical procedures, as well as automated Python scripts for common SAXS analyses and Guinier-optimized reconstruction of protein scattering.

1. Introduction  

Small-angle X-ray scattering (SAXS) can be used to obtain native-like structural information on a wide variety of biological systems (Petoukhov & Svergun, 2013 ▸; Putnam et al., 2007 ▸; Lipfert et al., 2007 ▸; Lipfert & Doniach, 2007 ▸). In synchrotron SAXS experiments, buffer and protein solutions are briefly (ms to s) exposed to high-flux X-rays, typically under flow to minimize radiation damage. The measured intensities over a range of scattering angles (2θ) are radially averaged to obtain a one-dimensional intensity profile as a function of the momentum transfer vector q (herein |q| = 4π sin θ/λ, with the wavelength λ in Å). The protein contribution is extracted by subtraction of matched buffer scattering after normalization by the incident (I ₀) or transmitted (I ₁) beam intensity. Because of errors associated with extrinsic factors such as imperfect beam intensity measurement, beam path drift and differences in parasitic scattering, the buffer scattering may need to be scaled by a constant prior to subtraction. If the extrinsic errors are negligible, a scaling constant taking into account the volume occupied by the protein can in principle be estimated from the known protein concentration and average partial specific volume of standard proteins (Mylonas & Svergun, 2007 ▸). In practice, complete elimination of extrinsic sources of error is rarely achieved, and experimental approaches for estimating a scaling constant have been developed, including water calibration using wide-angle X-ray scattering (WAXS) (Chen et al., 2012 ▸; Davies et al., 2005 ▸; Hammel et al., 2005 ▸; Wang et al., 2009 ▸). In the absence of aggregation, subtracted scattering data are expected to scale linearly with macromolecular concentration (Putnam et al., 2007 ▸) and, if necessary, can be extrapolated to infinite dilution to correct for ‘interparticle repulsion’ (Konarev et al., 2003 ▸). The resulting scattering curves are used for subsequent analyses including comparison with theoretical scattering from atomic resolution coordinates, rigid-body modeling and determination of ab initio shape envelopes (Petoukhov & Svergun, 2013 ▸; Putnam et al., 2007 ▸).

Given the sensitivity of SAXS to trace high-molecular-mass species, sample purity and monodispersity are essential for many structural and computational analyses as well as ab initio shape determination (Putnam et al., 2007 ▸; Lipfert & Doniach, 2007 ▸). However, because of the inherent properties of biological macromolecules, in particular reversible oligomerization and aggregation, it is often difficult to satisfy these requirements. Size-exclusion chromatography in line with SAXS (SEC–SAXS) was originally implemented at the Advanced Photon Source (APS) BioCAT beamline (Mathew et al., 2004 ▸) and is increasingly used to address these and related issues (Pérez & Nishino, 2012 ▸; David & Pérez, 2009 ▸; Watanabe & Inoko, 2009 ▸; Gunn et al., 2011 ▸). Partial or complete resolution of sample components by SEC–SAXS has facilitated investigation of challenging structural targets. Subtraction of buffer scattering acquired separately or from an average of pre-void volume and/or post-included volume data sets yields scattering profiles approximating the protein scattering during elution. Estimation of the scaling constant for the buffer and/or extrapolation to zero concentration is nontrivial, since determination of the protein concentration requires alignment with a high-quality UV chromatogram and, in the case of overlapping peaks, deconvolution of the component species. Measurement of peak and buffer scattering at substantially different times and capillary fouling also contribute to buffer mismatching in SEC–SAXS. Moreover, analyses restricted to peak data sets neglect useful redundant as well as concentration-dependent information. A more sophisticated approach for SEC–SAXS data analysis after buffer subtraction involves iterative integral baseline correction and modeling of the entire SAXS elution profile with Gaussian or exponentially modified Gaussian functions (Brookes et al., 2013 ▸).

Regardless of the data collection strategy, sample quality is difficult to quantify, and the presence of impurities or other problematic artifacts may not be obvious. Thus, objective assessment of data quality, and in particular the number of significant species, is essential for analysis of mixtures by SEC–SAXS. Singular value decomposition (SVD) has been used to diagnose uniqueness and increase signal-to-noise in complex biophysical and biochemical data sets (Haldrup, 2014 ▸; Sadygov, 2014 ▸; Man et al., 2014 ▸; Pérez et al., 2001 ▸; Fetler et al., 1995 ▸; Lambright et al., 1991 ▸), and has found a number of uses for analysis of SAXS data (Kathuria et al., 2014 ▸; Brookes et al., 2013 ▸; Williamson et al., 2008 ▸; Pérez et al., 2001 ▸; Fetler et al., 1995 ▸). SVD is a matrix algebra method that is particularly useful for determining the minimum number of components required to accurately represent data sets with a high redundancy. As applied here, SAXS data sets are represented as an M × N matrix A, with N columns corresponding to individual scattering curves sampled at M q values. A is decomposed (Golub & Reinsch, 1970 ▸) as a product of orthonormal basis vectors (columns of an M × N matrix U), singular values (elements of an N × N diagonal matrix S) and orthonormal coefficients (columns of a transposed N × N matrix V):

The singular values applied to the coefficients in V ^T(S V ^T) specify the linear combination of basis components in U required to exactly reconstruct both the signal and noise in each scattering curve in A. A particularly useful property of SVD derives from the rotation of the matrices so as to generate a rank-ordered series of vectors that successively maximize the contribution of each column of U. Thus, the singular values indicate the relative contribution of each column of U, with the most significant columns having reduced contributions from random noise or small systematic artifacts, which are filtered into the remaining columns.

Here we describe widely applicable, novel approaches for SAXS and SEC–SAXS data processing and analysis using data from samples with known atomic resolution structures and the recently developed software package Data Evaluation and Likelihood Analysis (DELA), which combines embedded Python scripting with built-in tools including SVD to intuitively perform semi-automated SAXS analyses (Lambright et al., 2013 ▸). We show that an accurate approximation of the protein scattering can be reliably reconstructed by linear combination of SVD basis components using optimized coefficients automatically determined from a systematic analysis of linearity in the Guinier region. Notably, the approach does not require buffer subtraction or separate determination of a buffer scaling constant, and can be applied even in cases where matched buffer scattering is not available. The approach also leverages the noise-filtering and diagnostic benefits of SVD to improve the quality of the reconstructed SAXS data for dilute protein samples. Conventional SAXS experiments with cytochrome c (cyt c) indicate that this method can recapitulate buffer subtraction while simultaneously correcting for over- or under-subtraction artifacts. Linear combination of SVD components from SEC–SAXS data for the monodisperse GTPase Arf6 illustrates application of the method to the entire elution profile under nearly ideal conditions. Finally, this approach allowed reconstruction of both monomer and dimer species for the Arf GTPase guanine nucleotide exchange factor (GEF) Grp1 under suboptimal conditions at peak protein concentrations near or below 2 mg ml⁻¹ in the absence of a matching buffer region. In each case, the reconstructed protein scattering was well described by the theoretical scattering calculated from the corresponding crystal structures. Collectively, the new methods have the potential to facilitate SEC–SAXS analyses, enhance reconstruction of protein scattering and extend the range of SEC–SAXS to low-abundance mixtures of macromolecular species.

2. Experimental procedures and analyses  

2.1. Constructs, expression and protein purification  

Arf6, Grp1 and cytohesin-1 constructs were amplified with Vent polymerase, digested with BamHI and SalI or XhoI, and ligated into a modified pET15b vector that incorporated an N-terminal MGHHHHHHGS tag. Mutants were generated using whole-plasmid polymerase chain reaction supplemented with QuikSolution (Stratagene) followed by DpnI digestion (NEB). BL21(DE3) cells (Novagen) were transformed with plasmids, grown in 2×YT with 100 mg l⁻¹ ampicillin to an OD₆₀₀ = 1.0–1.2 or 0.2–0.4, and protein expression induced with 1 mM or 50 µM isopropyl β-d-1-thiogalactopyranoside at 310 or 291 K, respectively. Harvested cells were resuspended in buffer (50 mM Tris pH 8.0, 150 mM NaCl, 2 mM MgCl₂, 0.05% 2-mercaptoethanol) and incubated with 0.1 mM phenylmethylsulfonyl fluoride, 0.2 mg ml⁻¹ lysozyme and 0.01 mg ml⁻¹ protease-free DNAse I (Worthington). Lysates were sonicated, centrifuged at 30 000g for 1 h with 0.5% Triton X-100 and purified by batch elution from Ni–NTA beads, ion exchange over HiTrap SP or Q columns, and gel filtration on Superdex-75 or 200 (GE Healthcare).

2.2. SAXS and SEC–SAXS data collection  

SAXS experiments were performed at the BioCAT beamline at Sector 18-ID of the APS of Argonne National Laboratory. Horse heart cytochrome c was prepared at 4 mg ml⁻¹ in buffer containing 200 mM potassium phosphate, 200 mM imidazole pH 7.0. For conventional SAXS experiments, buffer and protein solutions were delivered using an autosampler and 1 s exposures recorded during continuous unidirectional flow. The incident X-ray flux was ∼1 × 10¹³ photons s⁻¹ at 12 keV and scattering patterns were detected using a MAR 165 CCD detector (Rayonix Inc., Evanston, IL, USA) for in-line SEC–SAXS or Pilatus 100k and Pilatus 3 1M pixel array detectors (Dectris Inc., Baden, Switzerland) for conventional SAXS. For in-line SEC–SAXS, 0.1–0.5 ml protein samples at 10–20 mg ml⁻¹ were loaded onto a 24 ml Superdex-200 column (GE Healthcare) equilibrated with buffer containing 20 mM Tris pH 8.0, 150 mM NaCl, 2 mM MgCl₂, 1 µM inositol(1,3,4,5)tetrakisphosphate (IP₄). Columns were connected in-line with the flow cell for SAXS data collection and 1 s exposures taken at 5 s intervals during elution. Samples containing Grp1 or cytohesin-1 were incubated with a 1.2 molar excess of IP₄ for 1–5 h prior to injection. The UV absorbance at 280 nm was monitored during chromatography and showed consistent separation of monomeric and dimeric species. For conventional SAXS experiments with Arf6, Grp1 and cytohesin-1, data were acquired within 20 min after SEC on a 3 ml Superdex-200 Increase column.

2.3. Data processing and normalization  

Raw data images were radially averaged over the q range 8.25 × 10⁻³–3.36 × 10⁻¹ Å⁻¹ using Igor Pro with BioCAT beamline extensions (cyt c and SEC–SAXS) or the ATSAS package. The resulting text files containing the q values, intensities and errors were imported into DELA (see §2.6 below) for further processing and analysis. Total scattering profiles generated by summing the intensities over the entire q range of each data set were plotted against the data-set index for data processing and subsequently converted to elution volume for presentation. Radially averaged data were normalized using a weighted average of the incident (I ₀) and transmitted (I ₁) beam intensities as

where

〈C _norm〉 is the average value of the normalization constant C _norm and k is a constant that compensates for the reduced individual contributions of I ₀ and I ₁ in the weighted average. Values for w ₀, w ₁ and k were determined by inspecting the effect of normalization on the total scattering profile and, in particular, the reduction of beam intensity fluctuations and drift. Simpler sequential normalization with C _norm = 1/I ₀/I ₁ was applied in situations where time was limited (e.g. online processing during data collection). Sequential normalization, though not as effective for reducing beam intensity related artifacts as normalization using a weighted average, was consistently superior to normalization by either I ₀ or I ₁ alone.

2.4. Guinier optimization and reconstruction of protein scattering  

For buffer subtraction, data sets from sample and buffer under continuous flow (conventional SAXS) or from peak and buffer regions (SEC–SAXS) were averaged prior to direct subtraction or Guinier optimization of the buffer scaling constant. Optimal coefficients or buffer scaling constants were determined using an automated grid search algorithm with three main calculations at each grid point: (i) reconstruction of a protein scattering curve by linear combination or scaled buffer subtraction; (ii) Guinier transformation of q and I(q) as log q and q ² I(q), respectively; and (iii) calculation of the unweighted merit statistic R ² after linear least-squares fitting of the Guinier region subject to q R _G < 1.0–1.3. The overall algorithm involved an initial broad search on a coarse grid without restriction on the number of points in each fit, a subsequent search with a finer grid spacing and uniform number of points for each fit (taken as the number of points satisfying q R _G < 1.0–1.3 in the curve with the highest R ² from the initial coarse search), and a final refinement search around the R ² maximum to determine the optimal linear coefficient or scaling constant within a specified fractional tolerance. The Guinier optimization algorithm was implemented as a Python script, with user-modifiable control parameters.

2.5. Post-processing  

For normalization as well as direct and Guinier-optimized buffer subtraction, errors were propagated. For SVD with Guinier-optimized linear combination (SVD–LC) reconstructions, the relationship with the original error estimates is complicated by the noise-filtering characteristics of SVD and consequently errors were re-estimated at each q value by Savitzky–Golay smoothing using a second-order polynomial with a window size of 11 points (Savitzky & Golay, 1964 ▸). A constant was subtracted from the data to obtain a Porod volume with a theoretical molecular weight within 10% of the corresponding solvent-free protein. Porod and Guinier plots and fits were calculated in DELA. For the general linear least-squares fitting in Fig. 6 in §3.4, CRYSOL models were calculated with 5000 points, resampled with linear interpolation to match the q grid of the data, and scaled such that I(0) was proportional to the molecular mass of the relevant oligomeric species.

2.6. Data evaluation and likelihood analysis (DELA)  

DELA is a native 64-bit Intel Mac OS X application written in Objective C using the Cocoa and Quartz frameworks for the graphical user interface. The application is extensible through an embedded Python interpreter with an extensive application programming interface (API) consisting of Python modules for data transfer between the application’s intuitive graphical user interface and the Python interpreter as well as control of core application functionality via Python scripts. The application includes built-in tools for global and local maximum-likelihood fitting to SEC–SAXS elution profiles (Gaussian, exponentially modified Gaussian and higher-order Gaussian functions), calculation of maximum entropy method (MEM) pair-distribution functions from SAXS data, SVD, matrix transposition, least-squares scaling/constant subtraction, normalization, error estimation, integration, differentiation, data editing, masking, processing, and transformation. Python scripts executed from within the application were developed to support SEC–SAXS data processing and post-processing analyses including Guinier, Kratky and Porod plots. The application also includes undo functionality, archival storage of data and results as a document file, and export of publication-quality plots in standard image formats. All processing, averaging, matrix methods, transformations, graphical analyses, error estimation and generation of plots for the figures in this paper were done with DELA. The program, including SAXS-specific Python scripts, example data sets, and a tutorial are available on request.

3. Results  

3.1. SAXS data processing using singular value decomposition and Guinier-optimized linear combination  

An initial goal was to develop an objective means of assessing data quality and reliably extract the protein scattering contribution for a wide range of experimental setups and sample compositions. To expedite exploration, testing, implementation and improvement of new approaches, the document-based Mac OS X application DELA was extended to include a suite of Python scripts for SAXS data processing and analysis. Radially averaged one-dimensional SAXS data sets in a variety of input formats can be imported, organized, annotated, edited, graphically visualized, processed and analyzed using built-in tools and Python scripts executed within the application. Documents can be saved/opened, and processed data sets exported as text files compatible with common SAXS software including the ATSAS suite (Konarev et al., 2006 ▸). Axes for plots can be switched between multiple scaling options (e.g. linear, log, squared etc.) to facilitate analysis of data and results. SAXS-specific Python scripts are selected from a menu in the application and typically present options that can be modified before execution. Data and results are transferred directly between the application and Python interpreter. Target data are selected from a list of objects in the application’s contents browser. Additional information about the application and Python scripts is provided in §2.6.

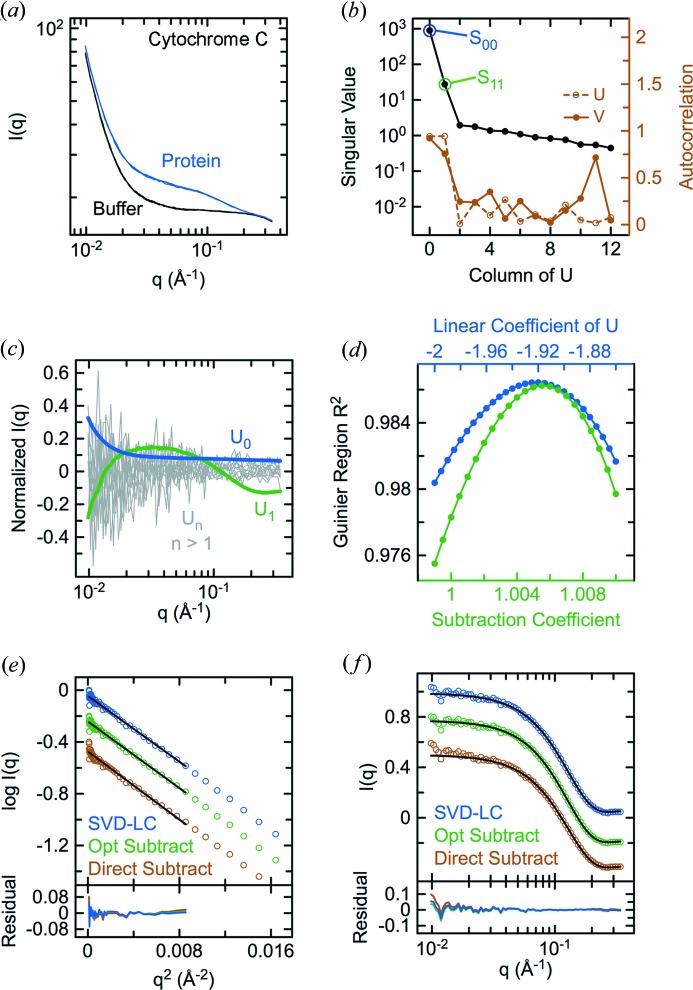
Cyt c, which is monodisperse and has a known crystal structure, was used during initial method development and validation. SAXS data sets interleaving buffer (seven data sets) with 4 mg ml⁻¹ protein (six data sets) were collected and radially averaged (Fig. 1 ▸ a), producing scattering curves with little evidence of aggregation or interparticle repulsion in Guinier plots after direct buffer subtraction (see Fig. 1 ▸ e). SVD of a matrix containing the sample and buffer scattering data normalized by the incident beam intensity revealed two significant components as judged by the magnitude of the singular values, autocorrelation of the columns of U and V (Fig. 1 ▸ b), and plots of the columns of U (Fig. 1 ▸ c). Whereas U ₀ and U ₁ exhibited high signal-to-noise and resembled combinations of protein and buffer scattering, the remaining columns consisted of noise without substantial signal content. Indeed, U ₀ and U ₁ were sufficient to reconstruct an accurate approximation of the original matrix with improved signal-to-noise. Reconstruction using U ₂ − U ₁₂ confirmed that the remaining columns represented noise without significant signal (not shown). Thus, within the noise level of the experiment, the data matrix contains signal contributions from only two distinguishable components corresponding to protein and buffer scattering.

Figure 1.

Guinier optimization of buffer subtraction for cyt c. (a) Raw scattering data sets with buffer or 4 mg ml⁻¹ horse heart cyt c. (b) Singular values and autocorrelation of the columns of U and V after SVD of the data in (a). (c) Columns of the orthonormal U matrix corresponding to the rank-ordered singular values in (b). (d) R ² values from automated Guinier optimization of the U ₀ coefficient for linear combination of the two most significant SVD basis components or the scaling constant for buffer subtraction. Guinier (e) and CRYSOL (f) fits of the theoretical scattering for the crystal structure (PDB entry 1hrc; Bushnell et al., 1990 ▸) to the protein scattering curves obtained by SVD–LC, optimized buffer subtraction or direct subtraction.

Given that the significant columns of U comprise an orthonormal basis set spanning the two-dimensional signal space of the original matrix, it follows that any vector in that space, including the protein scattering curve of interest, can be accurately represented as a linear combination of U ₀ and U ₁ with coefficients c ₀ and c ₁:

or

where c = c ₀/c ₁. The latter rearrangement indicates that, apart from a scaling constant (1/c ₁), the protein scattering curve can be directly reconstructed from U ₀ and U ₁, provided the value of the single coefficient can be reliably determined with sufficient accuracy. Moreover, the linear combination of U ₀ and U ₁ also applies to SAXS data consisting of scattering from protein solutions at different concentrations in the absence of scattering from buffer alone.

A potential solution to the problem of finding c, and by logical extension the scaling constant for buffer subtraction, is suggested by the generally accepted criteria for evaluating the quality of buffer-subtracted scattering data, in particular the linearity of the low-q region following Guinier transformation. After buffer subtraction, positive and negative deviations from linearity in the low-q region of a Guinier plot are used to diagnose aggregation or interparticle repulsion, respectively, but may also result from under- and over-estimation of the scaling constant for the buffer. For data collected at a single concentration, it is difficult to distinguish interparticle interactions from incorrect estimation of the scaling constant. In the case of a highly monodisperse protein such as cyt c at a dilute concentration, however, deviations from linearity are expected to reflect buffer scaling rather than interparticle effects. We therefore used the cyt c data as a test case to explore the possibility of determining an optimal coefficient for linear combination or equivalent scaling constant for buffer subtraction by systematically analyzing the linearity of the Guinier region over a range of coefficients/scaling constants using the unweighted merit statistic R ² from a linear least-squares fit of the data satisfying q R _G ≤ 1.3.

As shown in Fig. 1 ▸(d), R ² varies smoothly as a function of the coefficient/scaling constant and has a well defined maximum, provided a consistent number of points are used in all of the fits (see §2). Apart from an overall scale factor, nearly identical protein scattering curves were obtained after SVD with Guinier-optimized linear combination (c U ₀ + U ₁; SVD–LC) and buffer subtraction with a Guinier-optimized scaling constant (I _sample − k I _buffer). As expected, the Guinier plots after SVD–LC or optimized buffer subtraction have improved linearity in the Guinier region with higher R ² values in weighted as well as unweighted fits compared with direct buffer subtraction (Fig. 1 ▸ e and Table 1 ▸). The small positive deviation from linearity at low q after direct buffer subtraction could in principle reflect minor aggregation, buffer mismatching or, more likely in this case, imperfect beam normalization. Notably, the SVD–LC and optimized buffer subtraction scattering curves also exhibited substantially lower root-mean-squared deviations (RMSDs) from the theoretical scattering (Fig. 1 ▸ f and Table 1 ▸) calculated from the crystallographic coordinates using CRYSOL (Svergun et al., 1995 ▸).

Table 1. R ² and RMSD for Guinier and CRYSOL fits to protein scattering from direct buffer subtraction and Guinier-optimized buffer subtraction or linear combination of SVD components.

Bold font indicates best, roman font intermediate, and italic font worst agreement with the data (R ²) or theoretical model (RMSD).

Protein	Direct subtraction		Optimized subtraction		SVDLC
	Guinier R 2	CRYSOL RMSD	Guinier R 2	CRYSOL RMSD	Guinier R 2	CRYSOL RMSD
Cytochrome C	0.978	0.020	0.986	0.014	0.986	0.014
Arf6N13 Q67L	0.978	0.024	0.987	0.012	0.993	0.008
Grp163399 (monomer)	0.741	0.108	0.967	0.036	0.990	0.010
Grp163399 (dimer)	0.322	0.320	0.917	0.043	0.943	0.020
Cyth158400 (monomer)	0.993	0.008	0.993	0.008	0.998	0.005
Cyth158400 (dimer)	0.937	0.022	0.973	0.018	0.976	0.013

3.2. SVD–LC applied to SEC–SAXS  

SEC–SAXS data sets typically comprise in excess of 100 scattering curves acquired over 10–40 min with potentially overlapping and/or interacting species spanning a wide concentration range. In any given experiment, data sets corresponding to candidate buffer regions (e.g. pre-void volume and/or post-included volume) are collected well before or after peaks of interest and may not be optimally matched even after normalization for beam intensity fluctuations and drift. Moreover, buffer subtraction using only peak and buffer data sets neglects useful diagnostic information as well as redundant signal content embedded in the concentration variation over the SAXS elution profile. SVD is a powerful tool for analyzing the number of independent components contributing to the scattering for all or a subset of the complete data matrix, and thereby identifying regions suitable for reconstruction of the protein scattering by Guinier-optimized linear combination.

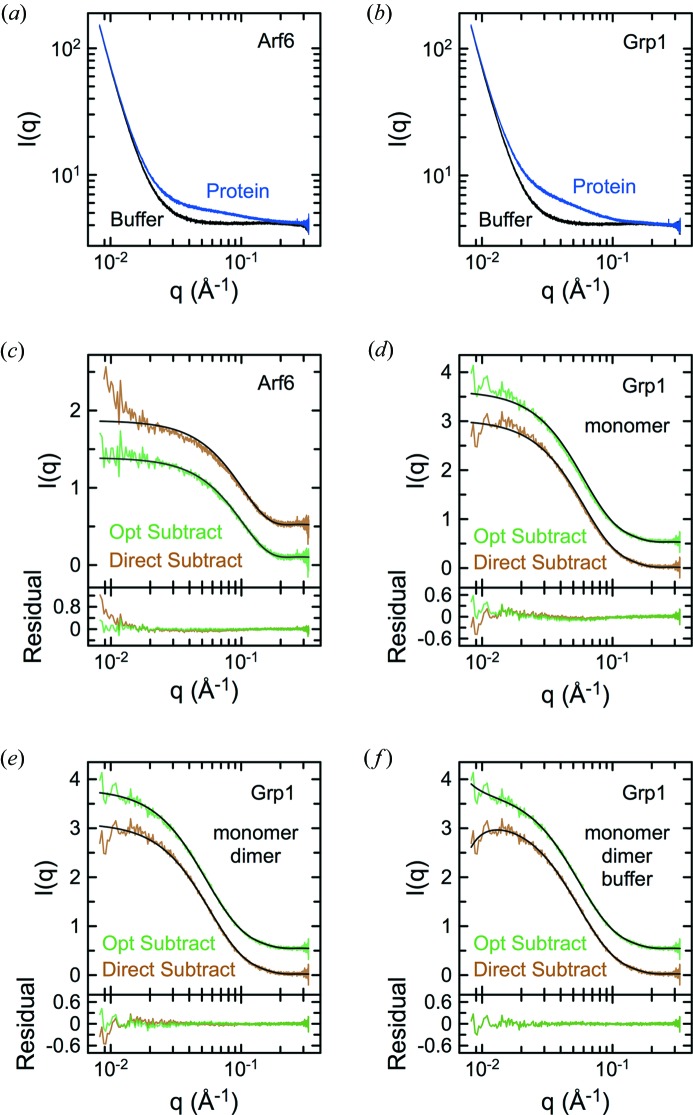
To explore the applicability of SVD–LC to SEC–SAXS, a truncated form of the Arf6 GTPase (Arf6NΔ13Q67L), which has been analyzed previously by SEC–SAXS (Biou et al., 2010 ▸), was used as a nearly ideal test case. Like cyt c, Arf6NΔ13Q67L is monodisperse and atomic resolution coordinates are available. Summation of individual scattering curves (Fig. 2 ▸ a) to generate a total intensity profile as a function of elution volume (Fig. 2 ▸ b) showed a single peak. The data were normalized as a weighted average of incident and transmitted beam intensities to account for beam intensity fluctuations, which are best represented by I ₀, and long-term drift, which is best reflected in I ₁ (Fig. 2 ▸ b). In general, normalization by both I ₀ and I ₁ appeared to be more effective than normalization by either one alone and aided in interpretation of the elution profile by reducing or eliminating otherwise misleading artifacts. For direct and Guinier-optimized buffer subtraction, evaluation of potential buffer regions was aided by graphical selection tools in DELA (Fig. S1A in the supporting information). Direct subtraction of different buffer regions produced arbitrary positive or negative trends in the low-q region, despite yielding R _G values from weighted Guinier fits that were similar to theoretical values calculated from the crystal structure with CRYSOL (16.4–16.7 versus 16.1 Å, Fig. S1B).

Figure 2.

SVD analysis and reconstruction of protein scattering from an SEC–SAXS experiment for Arf6. (a) Raw scattering data sets for Arf6NΔ13Q67L acquired in-line with chromatography on a 24 ml Superdex-200 column. (b) Raw and normalized total intensity elution profiles calculated by summing the intensities for each data set in (a) over the entire q range. Also shown are the incident (I ₀) and transmitted (I ₁) beam intensity profiles. (c) Singular values and autocorrelation of the columns of U and V after SVD of the data in (a). (d) Columns of the orthonormal U matrix corresponding to the rank-ordered singular values in (c). (e) Columns of the orthonormal V matrix multiplied by the corresponding rank-ordered singular values in (c). (f) CRYSOL fits of the theoretical scattering for the Arf6NΔ13Q67L-GTPγS crystal structure [PDB entry 2j5x (Pasqualato et al., 2001 ▸), with or without addition of a His₆ tag from chain A in 2r09] to the protein scattering reconstructed by SVD–LC, Guinier-optimized subtraction or direct subtraction.

SVD of the entire data matrix revealed two significant basis components as indicated by the singular values, autocorrelations, and comparison of the columns of U and V (Figs. 2 ▸ c–2 ▸ e). To assess contributions of each component to the scattering profile, singular value weighted columns of V (S_nn V_n) were plotted as a function of the column index (Fig. 2 ▸ e). The total intensity elution profiles could be accurately reconstructed using S ₀₀ V ₀ and S ₁₁ V ₁, whereas the remaining components represented noise. Homogeneity across the elution peak was independently confirmed by analyzing R _G values from weighted Guinier fits for each scattering curve in the peak region after direct buffer subtraction (Fig. S1A). The protein scattering reconstructed by SVD–LC was characterized by high linearity in the low-q region following Guinier transformation (Figs. S1D and S1E) and was well described by the fitted CRYSOL model for the crystal structure (Fig. 2 ▸ f), provided the model included a His₆ tag present in the construct used for the SEC–SAXS experiments but not in the crystal structure (Fig. S1F). With respect to both weighted Guinier and CRYSOL fits (Fig. 2 ▸ f, Fig. S1B versus S1E, and Table 1 ▸), the SVD–LC reconstruction (Guinier R ² 0.993; CRYSOL RMSD 0.008) was superior to direct buffer subtraction (Guinier R ² 0.978; CRYSOL RMSD 0.024) and also better than Guinier-optimized buffer subtraction (Guinier R ² 0.987; CRYSOL RMSD 0.012). The latter result is not unexpected, since SVD–LC benefited from signal averaging over the entire data matrix, whereas the Guinier-optimized buffer subtraction was necessarily restricted to peak and buffer regions. The accuracy of the reconstruction is also expected to improve with increasing signal-to-noise.

3.3. Analysis of overlapping oligomeric species by SVD–LC without distinct buffer regions  

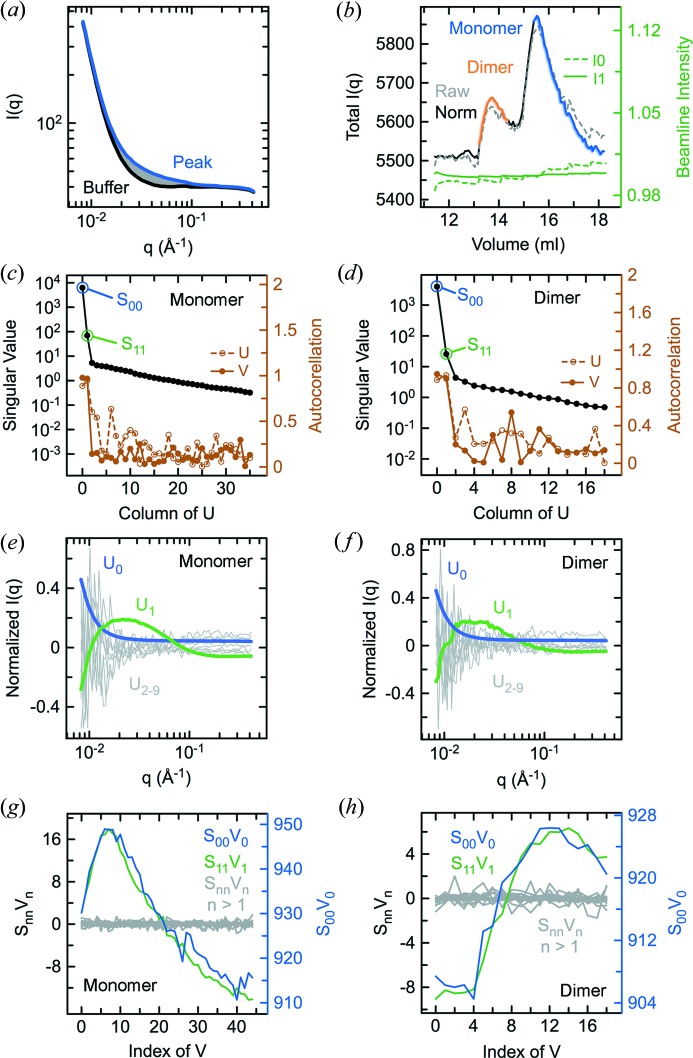
To investigate the application of SVD–LC to a more challenging case, we examined an SEC–SAXS data set (Fig. 3 ▸ a) for an autoinhibited construct of the Arf exchange factor Grp1 (Grp1_63–399). Crystallographic coordinates are available for two molecules in the asymmetric unit, which have slightly different orientations of the catalytic Sec7 domain and phosphoinositide-binding PH domain (PDB entry 2r09; DiNitto et al., 2007 ▸). Although this construct is predominantly monomeric in the low micromolar range (DiNitto et al., 2007 ▸), weakly populated oligomeric species were observed in SEC–SAXS (Fig. 3 ▸ b), probably related to the high injection concentration of 325 µM. As with Arf6, normalization by both incident and transmitted beam intensities appeared to be more effective than either alone (Fig. 3 ▸ b). Direct subtraction using the most suitable candidate buffer regions proximal to peaks in the total scattering profile produced unsatisfactory results (Figs. S2A–S2B). SVD of the entire data matrix revealed three significant components (Figs. S2C–S2E), which represent linear combinations of scattering from the expected monomer, a putative dimer and buffer. An apparent minor peak near the beginning of the total scattering profile may represent a low-abundance oligomeric species. The R _G profile over the main peaks is consistent with two partially overlapping species (Fig. S2A). To resolve the scattering contributions from each species, SVD was performed on data matrices corresponding to selected regions of the total scattering profile and the boundaries of each region adjusted until two significant components were detected (Figs. 3 ▸ b–3 ▸ h). Analysis on the region corresponding to the minor peak also revealed two significant components, albeit of inadequate signal-to-noise for reconstruction (Fig. S2F).

Figure 3.

SVD analysis of an SEC–SAXS experiment for Grp1_63–399. (a) Raw scattering data sets for Grp1_63–399 acquired in-line with chromatography on a 24 ml Superdex-200 column. (b) Raw and normalized total intensity elution profiles calculated by summing the intensities for each data set in (a) over the entire q range. Also shown are the incident (I ₀) and transmitted (I ₁) beam intensity profiles. Singular values and autocorrelations of the columns of U and V after SVD of the monomer (c) and dimer (d) data sets corresponding to the peak regions indicated in (b). Columns of U corresponding to the rank-ordered singular values in (c) and (d) for the monomer (e) and dimer (f) regions. Columns of V multiplied by the corresponding rank-ordered singular values in (c) and (d) for the monomer (g) and dimer (h) regions.

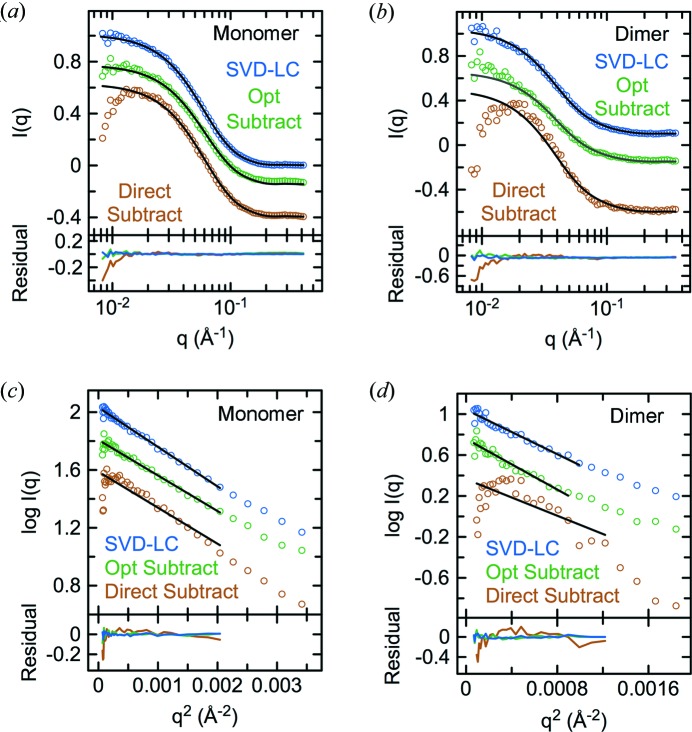
Protein scattering curves were reconstructed by SVD–LC (Figs. 4 ▸ a–4 ▸ b) using data sets from the regions indicated in Fig. 3 ▸(b) or by Guinier optimization of the scaling constant for buffer subtraction (Figs. 4 ▸ c–4 ▸ d) using data from the peak and buffer regions indicated in Fig. S2A. For the main monomer peak, both the linearity of the Guinier region and CRYSOL fits with either molecule in the asymmetric unit (Figs. 4 ▸ a and 4 ▸ c, and Fig. S4) were substantially better for the SVD–LC reconstruction (Guinier R ² 0.990; CRYSOL RMSD 0.010) than Guinier-optimized buffer subtraction (Guinier R ² 0.967; CRYSOL RMSD 0.036), which was substantially better than direct buffer subtraction (Guinier R ² 0.741; CRYSOL RMSD 0.108). The CRYSOL fit is better for chain A than chain B (Fig. S4), probably reflecting extensive crystal contacts between chain B and the His₆ tag of chain A, which appears to influence the relative orientation of the Sec7 and PH domains in chain B. As with Arf6, the fits are improved by inclusion of the His₆ tag present in the crystallographic models of both molecules. For the dimer peak, the linearity of the Guinier region (Fig. 4 ▸ d and Table 1 ▸) was substantially higher for the SVD–LC reconstruction (Guinier R ² 0.943) than Guinier-optimized buffer subtraction (Guinier R ² 0.917), which was substantially higher than direct subtraction (Guinier R ² 0.322). CRYSOL fits to the SVD–LC reconstruction suggest that the dimer species may be related to the dimer in the asymmetric unit (Fig. 4 ▸ b). For both the monomer and dimer peaks, the SVD–LC reconstructions were better than buffer subtraction with an optimized scaling constant (Fig. 4 ▸, Figs. S3 and S4), presumably because of the higher signal-to-noise for the SVD–LC reconstruction. Similar results were obtained for the corresponding construct of the Grp1 paralog cytohesin-1 (Figs. S5 and S6).

Figure 4.

Evaluation of methods for reconstructing the monomer and dimer scattering for the Grp1_63–399 SEC–SAXS experiment. CRYSOL fits of the monomer (a) and dimer (b) scattering reconstructed by SVD–LC, Guinier-optimized subtraction or direct subtraction with the theoretical scattering for either chain A or chains A and B (alternative definition of asymmetric unit) of the His₆-Grp1_63–399 crystal structure (PDB entry 2r09). Guinier fits of the monomer (c) or dimer (d) scattering reconstructed by SVD–LC, Guinier-optimized subtraction, or direct subtraction.

As an alternative approach, the entire data matrix was transposed and fitted with a sum of three exponentially modified Gaussians:

where λ is the exponential ‘rate’ parameter, μ is the mean, σ is the standard deviation and erfc is the complementary error function. This approach is analogous to that described for US-SOMO (Brookes et al., 2013 ▸), with the exception that the data were analyzed without buffer subtraction or integral baseline correction. Although the exponentially modified Gaussian model fits the data reasonably well (Figs. 5 ▸ a and 5 ▸ b), the amplitudes a_i(q) provided a poor reconstruction of the protein scattering and resembled the curves obtained by direct subtraction. The problem may be due to the tails of the exponentially modified Gaussians, which appear to overestimate the overlap between the peaks. Nevertheless, the constant b(q) appeared to provide a remarkably accurate reconstruction of the expected buffer scattering (Figs. 5 ▸ d–5 ▸ f). Indeed, using b(q) for direct buffer subtraction resulted in a protein scattering curve with a minor negative deviation in the low-q region (Fig. 5 ▸ e). Guinier optimization of the constant for buffer subtraction using b(q) yielded a scattering curve that was nearly identical to the SVD–LC reconstruction (Figs. 5 ▸ e and 5 ▸ f).

Figure 5.

Alternative analysis of the Grp1_63–399 SEC–SAXS data. (a) Transposed scattering data fitted with a sum of exponentially modified Gaussians as described in the text. (b) Individual components from a fit of the total scattering profile [equivalent to a summation of the transposed data in (a)] with a sum of exponentially modified Gaussians, where b is a baseline constant and eg1, eg2 and eg3 are the individual amplitude-weighted exponential Gaussian terms. (c) Comparison of the fitted baseline constant b(q) and the raw scattering data. Note that b(q) strongly resembles the expected buffer scattering. (d) R ² values for Guinier optimization of the scaling constant for buffer subtraction using b(q) as the buffer. Comparison of protein scattering curves (e) and weighted Guinier fits (f) for direct and Guinier-optimized buffer subtraction using b(q) as buffer with the protein scattering curves and Guinier fits for Guinier-optimized reconstruction following SVD. For comparison, the curves were scaled by linear least squares.

Linearity in the Guinier region is relatively insensitive to the addition or subtraction of a small constant and, consequently, scattering curves reconstructed by Guinier optimization may differ from the actual curves by a small constant expected to be of the order of the noise level in the experiments. In the case of the main peak in the Grp1 SEC–SAXS data, for example, the highest q data points were negative; however, addition of a small constant (approximately 1% of the maximum) was sufficient to place the high-q region in the positive range required for plotting on a log scale. In the case of slight buffer mismatching, the initial terms in a series expansion are linear and thus Guinier optimization may provide an implicit first-order correction for buffer mismatching in addition to correcting for imperfect normalization. In test cases (not shown), we have found that systematic first-order buffer mismatching, while affecting the shape of the scattering curve over the entire q range for direct buffer subtraction, results in zero-order deviations for Guinier-optimized reconstructions. Indeed, deviation of experimental and theoretical scattering curves by a constant is not uncommon, and many programs for analysis of SAXS scattering curves allow bulk solvent subtraction, often implemented by default using automated algorithms for determination of an optimal constant as described in the documentation for the ATSAS programs (Konarev et al., 2006 ▸).

3.4. Comparison of in-line SEC–SAXS with conventional SAXS after SEC  

For comparison with in-line SEC–SAXS, conventional SAXS experiments were performed with Arf6 and Grp1 fractions from the main peak after SEC (Figs. 6 ▸ a and 6 ▸ b). Direct subtraction using buffer fractions from a blank run yielded scattering curves with artifacts in the low-q region that were qualitatively similar to those in the in-line SEC–SAXS experiments (Figs. 6 ▸ c and 6 ▸ d). These artifacts were effectively minimized in the Guinier-optimized subtractions. For Arf6, the RMSD of the residuals after fitting with the CRYSOL model was substantially lower for Guinier-optimized versus direct subtraction (0.0012 versus 0.0059). Indistinguishable residuals with little or no systematic deviation and an RMSD of 0.0011 were observed for both subtraction methods when buffer scattering was included as a second component (not shown). For Grp1, systematic deviations in the residuals for direct versus Guinier-optimized subtraction (RMSD 0.0023 versus 0.0030) were observed for fits with the monomer CRYSOL model (Fig. 6 ▸ d) and even larger systematic deviations (RMSD 0.025 versus 0.019) for fits with the dimer CRYSOL model (not shown). The systematic deviations were substantially reduced when both monomer and dimer CRYSOL models were included in the fits (Fig. 6 ▸ e), although the improvement was less substantial for direct versus Guinier-optimized subtraction (RMSD 0.0019 versus 0.0013). Consistent with these observations, the fraction of dimer species derived from the fitted linear coefficients was 16% for Guinier-optimized subtraction compared to 7% for direct subtraction. Inclusion of the buffer scattering as a third component eliminated the systematic deviations (Fig. 6 ▸ f) and resulted in indistinguishable residuals for both subtraction methods, with an RMSD of 0.0012 and dimer fraction of 13%. Moreover, the magnitude of the buffer scattering component for Guinier-optimized subtraction was half that for direct subtraction. Although it is formally possible that an apparent under-subtraction artifact might reflect the presence of higher-order oligomeric species with scattering similar to the buffer scattering, the simplest interpretation is that Guinier optimization changes the sign and substantially reduces the magnitude of the buffer subtraction artifact but does not entirely eliminate it, probably because of the effect of noise in the low-q region on the Guinier analysis. Notably, equivalent results were obtained for two (Arf6) or three (Grp1) component fits to the unsubtracted data (not shown), suggesting the buffer subtraction or alternative reconstruction of protein scattering may not be essential for analyses in which buffer scattering can be included as a component in fits with macromolecular scattering components.

Figure 6.

Conventional SAXS experiments for Arf6 and Grp1 after SEC. SAXS data sets for Arf6NΔ13Q67L (a) and Grp1_63–399 (b) acquired after chromatography on a 3 ml Superdex-200 Increase column. Individual curves are from consecutive acquisitions under flow. (c) Fit of the His₆-Arf6NΔ13Q67L CRYSOL model to the direct and Guinier-optimized buffer subtractions after averaging the data in (a). (d) Fit of the His₆-Grp1_63–399 chain A monomer CRYSOL model to the direct and Guinier-optimized buffer subtractions after averaging the data in (b). Fits of the subtractions in (d) to a linear combination of CRYSOL models for the His₆-Grp1_63–399 chain A monomer and chain A/B dimer either without (e) or including (f) a buffer scattering component. Black lines represent fitted models. All fits were performed by general linear least squares in DELA using theoretical models from CRYSOL.

4. Discussion  

The approaches presented here were developed to supplement currently available methods and, in particular, to improve the reliability, objectivity and ease of SEC–SAXS data processing and analysis. Direct buffer subtraction was reasonably effective in the case of cyt c, for which interleaved data sets for the protein solution and a well matched buffer were collected. Nevertheless, determination of an optimal scaling constant for buffer subtraction using a novel method that maximizes the linearity of the low-q region following Guinier transformation improved the overall data quality as indicated by the weighted Guinier fit as well as the CRYSOL fit with the theoretical scattering calculated from the crystallographic model. Identical results were obtained when the data were decomposed by SVD, and the protein scattering was reconstructed by linear combination of the two most significant basis components. The same general approach was applicable to SEC–SAXS data sets for a nearly ideal case as well as a highly problematic case involving overlapping oligomeric species with no appropriate buffer region to use for subtraction. In all of the test cases examined here, SVD–LC provided the best reconstruction with respect to linearity of the low-q region in Guinier plots and CRYSOL fits with the theoretical scattering calculated from atomic resolution coordinates. For the SEC–SAXS data sets, normalization by both incident and transmitted beam intensities, either successively or as a weighted average, reduced beam-related artifacts to a greater extent than normalization by either alone, allowing features in the total scattering profile to be more clearly visualized. However, normalization involves division by a constant and therefore has no net effect on the protein scattering curves reconstructed by Guinier optimization (only the value of the subtraction constant or linear coefficient are changed) even though the effect can be substantial for direct buffer subtraction. Moreover, the over-subtraction artifacts for direct buffer subtraction in the SEC–SAXS experiments depend strongly on the regions selected for the buffer and only weakly on the normalization scheme.

Many potentially interesting studies of biological samples by SAXS are frustrated by buffer mismatching, inhomogeneity, aggregation and the requirement for large quantities of the relevant macromolecules at relatively high concentrations (Putnam et al., 2007 ▸). A major advantage of SEC–SAXS is the ability to resolve or partially resolve oligomeric or contaminating species that differ with respect to size and/or shape, and to continuously sample the scattering during elution (Mathew et al., 2004 ▸; Pérez & Nishino, 2012 ▸; David & Pérez, 2009 ▸; Watanabe & Inoko, 2009 ▸; Gunn et al., 2011 ▸). Problems inherent in SEC–SAXS include measurement of buffer and macromolecular scattering at substantially different times as well as sample dilution and potential changes in buffer composition during elution. In addition, the concentration of macromolecular species at each point is not known, although it can, in principle, be recovered from the aligned absorbance chromatogram. UV chromatograms, however, are subject to baseline drift and interference by commonly used reducing agents and may not provide sufficiently accurate concentration estimates, particularly at low protein concentrations.

SVD has been widely used to identify the number of unique components in data sets that can be represented in matrix form, including SAXS and SEC–SAXS (Haldrup, 2014 ▸; Sadygov, 2014 ▸; Man et al., 2014 ▸; Fetler et al., 1995 ▸; Pérez & Nishino, 2012 ▸; Gunn et al., 2011 ▸; David & Pérez, 2009 ▸; Watanabe & Inoko, 2009 ▸; Pérez et al., 2001 ▸; Lambright et al., 1991 ▸). In the present application, SVD is applied directly to the normalized data sets without buffer subtraction and used initially to identify a contiguous or even non-contiguous range of data sets with only two significant components corresponding to buffer and protein scattering. The number of significant components can be reliably determined by comparing both the singular values and autocorrelations of the columns of U and V. The significant basis components of U are subsequently used to reconstruct the protein scattering by linear combination using a Guinier optimization procedure that is automated, is robust and can use (but does not require) scattering from matching buffer data sets. As illustrated by the autoinhibited Grp1 test case, high-quality protein scattering can be reconstructed in the absence of matching buffer scattering, provided there is sufficient concentration variation to define the protein–buffer scattering space.

Although Guinier-optimized reconstruction appears to consistently yield scattering curves with superior quality compared to direct buffer subtraction, there are nevertheless predictable sources of error. The first relates to the linearity of the Guinier region, which is an approximation that improves as the high-q cutoff for linear regression is decreased. In most cases a cutoff of q R _G < 1.0 appears to provide satisfactory results; however, larger values (e.g. 1.3) may be required in cases where the signal-to-noise is low, whereas smaller values may be required for elongated proteins and may also provide more accurate reconstructions for data sets with high signal-to-noise. A portion of the low-q region may also need to be omitted owing to the poor quality, excessive noise and/or the presence of high-molecular-weight aggregates; however, some caution is warranted with respect to more restrictive than necessary cutoffs, since the accuracy of Guinier analyses also depends on the number of samples in the Guinier region. Low-q truncation in particular can introduce uncertainty since the deviations from linearity are largest in the low-q region. Likewise, owing to the typically larger error at low q, a weighted R ² statistic should probably be avoided for Guinier optimization, even though it may improve the quality of post-reconstruction Guinier analyses. A second source of error discussed above relates to the relative insensitivity of the Guinier region to subtraction of a small constant. As a result of noise or systematic deviations (e.g. minor buffer mismatching), the reconstructed scattering curves are expected to differ from theoretical scattering curves by a small constant. Thus, automated or manual subtraction of a bulk constant may be required for subsequent modeling. Larger than expected or systematic deviations in the Guinier region would be indicative of more serious problems (e.g. aggregation) that cannot be ignored (Putnam et al., 2007 ▸). Although post-column aggregation, capillary fouling, radiation damage and related phenomena may affect the linearity of the Guinier region, the presence of these artifacts is expected to alter the shape of the scattering profiles in a protein concentration dependent manner and should be detectable by SVD, which is sensitive to even minor differences in scattering profiles. As with direct buffer subtraction, it remains important to minimize these effects to the greatest extent possible. Indeed, even when optimized, the quality of the Guinier analysis remains an important indicator of the quality of the reconstructed protein scattering curves.

Finally, a fundamental limitation of the SVD–LC approach relates to the distinction between the shape of the protein and buffer scattering as well as the camera geometry and sampling in the Guinier region. Since the method involves a Guinier analysis, the same experimental requirements and limitations apply. At the BioCAT beamline with the standard camera geometry and experimental conditions, we have obtained high-quality reconstructions for proteins and oligomeric complexes with R _G values up to approximately 56 Å. The applicability of SVD–LC with data collected at other beamlines remains to be explored.

5. Conclusions  

Initial applications of SEC–SAXS were focused on obtaining structural information on samples that are hard to characterize owing to poor stability or aggregation. Nevertheless, the advantages of SEC–SAXS are more generally relevant, since many homogeneous biological samples exhibit some tendency to form oligomers or aggregate at concentrations required for SAXS experiments. The approach described here represents an alternative to traditional buffer subtraction, allowing objective identification of data sets for reconstruction of protein scattering by Guinier-optimized linear combination. The quality of reconstructed scattering curves is further improved by exploiting the signal-filtering power of SVD and implicitly providing first-order correction for subtraction-related issues including imperfect beam intensity normalization, beam path drift and minor buffer mismatching. Since SVD–LC assumes only that the Guinier region should be approximately linear but does not otherwise impose a specific model to represent either protein scattering or the shape of the peak in the elution profiles, it is effectively a ‘model-free’ method for analysis of SEC–SAXS data sets. Finally, we note that inclusion of buffer scattering as an additional component in fits with calculated macromolecular scattering compensates for buffer subtraction artifacts and might eliminate the need for buffer subtraction altogether. We provide the DELA application and associated Python scripts, which can be used to compare different approaches for buffer subtraction and reconstruction of protein scattering, and encourage feedback from the SAXS community to better understand the applicability and limitations of the methods and to inform future development.