The Mechanics of Human Achievement

Abstract

Countless studies have addressed why some individuals achieve more than others. Nevertheless, the psychology of achievement lacks a unifying conceptual framework for synthesizing these empirical insights. We propose organizing achievement-related traits by two possible mechanisms of action: Traits that determine the rate at which an individual learns a skill are talent variables and can be distinguished conceptually from traits that determine the effort an individual puts forth. This approach takes inspiration from Newtonian mechanics: achievement is akin to distance traveled, effort to time, skill to speed, and talent to acceleration. A novel prediction from this model is that individual differences in effort (but not talent) influence achievement (but not skill) more substantially over longer (rather than shorter) time intervals. Conceptualizing skill as the multiplicative product of talent and effort, and achievement as the multiplicative product of skill and effort, advances similar, but less formal, propositions by several important earlier thinkers.

Distance equals speed times time. Acceleration equals the rate of change in speed per unit time. These simple equations are among Isaac Newton's great contributions to science, laying the foundations of modern physics and making possible for the first time in history the precise prediction of the motion of objects through time and space. So intuitive are Newton's laws that it is difficult to appreciate Newton's epitaph, courtesy of his contemporary, the great poet Alexander Pope: “Nature and Nature's Laws lay hid in Night: God said, ‘Let Newton be!’ and all was light.”

In this essay, we propose a model for understanding human achievement inspired by Newtonian classical mechanics. We suggest distance traveled as a metaphor for human achievement, reasoning that achievement in any endeavor (science, art, industry) connotes progress from a starting point toward some valued end. Moreover, just as distance is the multiplicative product of speed and time, achievement is the multiplicative product of skill and effort. And, finally, with effort, not only does achievement increase, so, too, does skill, since skill is the multiplicative product of talent and effort.

Our model for achievement identifies just two classes of individual difference variables: effort and talent. We suggest that traits that have been shown to predict achievement operate by one of these two mechanisms. The constructs we define in the context of this framework (i.e., achievement, skill, talent, effort) correspond to intuitive and widely used terms but, crucially, are sharply defined based on their functional interrelations rather than their covariance, ontology (e.g., genetic vs. environment), or cognitive (vs. non-cognitive) nature. Next, making a few weak assumptions, we show that variables that determine effort are predicted to influence achievement in the long run more substantially than variables that determine talent. Finally, in the spirit of “standing on the shoulder of giants,” (Newton, 1676) we highlight historical precedents for our model.

A Newtonian Model of Achievement

Because we have taken inspiration from the motion of objects, we begin with a very brief review of Newtonian mechanics. With objects traveling through space, speed is the derivative (i.e., the rate of change) of distance per unit time, and acceleration is the derivative of speed per unit time. When acceleration is zero, speed is constant, and distance is a linear function of time. However, when acceleration is positive, as in the case of an object free falling towards earth, for example, speed increases, and distance traveled increases at faster and faster rates.

By analogy, we define skill as the rate of change of achievement per unit effort. We use effort in our model rather than time because, as we all know from experience, the quality of time on task can vary widely, from full concentration to mindless going through the motions (Kahneman, 1973). At higher skill levels, more gets accomplished per unit effort than at lower skill levels. In the notation of calculus, just as

$$\begin{array}{cc}\hfill speed={\left(distance\right)}^{\prime }=& \frac{d\left(distance\right)}{d\left(time\right)}\hfill \\ \hfill skill={\left(achievement\right)}^{\prime }=& \frac{d\left(achievement\right)}{d\left(effort\right)}\hfill \end{array}$$

where (achievement)’ simply indicates the derivative of that variable with respect to effort.

Conversely, the integral of speed over time is distance, and given by the area under the speed curve:

$$distance=\int speeddt$$

Similarly, the integral of skill over effort is achievement.

$$achievement=\int skilld\left(effort\right)$$

In turn, talent describes the rate of change in skill (per unit effort). Put another way, talent is the derivative of skill (the instantaneous rate of change in skill) with respect to effort. With effort, almost any skill increases, but more talented individuals improve faster than others. So, most simply put, we argue that:

$$talent=\left(skill\right)’$$

This formulation of talent as the rate of change of skill, if inverted, gives us the following integral formulation for skill, assuming talent to be a constant:

$$skill=\int talentd\left(effort\right)=talent\cdot effort$$

This is analogous, of course, to

$$speed=\int accelerationd\left(time\right)=a\cdot \mathrm{t}$$

in the case of Newtonian mechanics for a constant acceleration.

Given that skill = talent · effort, it is possible to be highly talented and yet, for lack of applied effort, unskilled. It is also possible to be modestly talented yet, through cumulative effort, highly skilled. Likewise, the individuals with the highest achievement in society will be those who are exceptional in both talent and effort. Since these variables multiply rather than add in their influence, such outliers in achievement are expected to be not just a bit better, but dramatically better—excelling “the rest of us” more than would be expected in a normal curve distribution (Shockley, 1957).

When we now integrate the skill equation, we obtain:

$$achievement=\frac{1}{2}\cdot talent\cdot effor{t}^2$$

In the popular vernacular, the term talent is sometimes used to describe the latent potential of an individual to achieve some level of skill (thus the expression “wasted talent”). Other times, talent is used to describe manifest skill (as in the frequent refrain of sportscasters: “what a marvelous display of talent there is tonight on the field”), which is also latent in the sense that individuals may or may not display skill at a given point in time. In our model, talent corresponds exclusively to the former intuition and skill exclusively to the latter. Similarly, in our model, skill is distinguished from achievement. A very skilled academic may not get anything done for lack of effort. A very productive academic, on the other hand, is without doubt applying effort in his or her domain of expertise.

Now that we have specified our model, we have a clear view of functionally distinct individual differences that determine achievement in any domain. Certain traits determine talent, defined as the rate at which skill is acquired with effort. Other traits determine how much effort an individual invests in a given domain. See Table 1 for incomplete lists of both types of traits. Notably, the list of well-studied constructs classifiable as influencing achievement via talent (i.e., determining the rate at which individuals acquire skill) is quite narrow in range, suggesting that individuals differ in many more talents than those few that psychologists have bothered to measure (Gardner, 2004; Sternberg, 2006).

Table 1.

An Incomplete List of Traits That Influence Achievement, Organized by Mechanism of Action

Talent traits that influence rate of skill acquisition	Effort traits that influence cumulative effort
creativity	Big Five conscientiousness
emotional intelligence	core self-evaluation
fluid intelligence	curiosity
general cognitive ability	distress tolerance
long-term memory	goal commitment
processing speed	grit
rationality	growth mindset
spatial intelligence	interests
verbal intelligence	internal locus of control
working memory	mental energy
	need for achievement
	optimistic explanatory style
	industriousness
	physical energy
	self-control
	self-efficacy
	typical intellectual engagement
	zest

Predicting Achievement in the Long Run

Let us now turn to a surprising prediction from the proposed model. Our equation specifies a quadratic dependence of achievement on effort—it appears raised to the second power (achievement = ½ · time · effort²). Over the long haul, then, individual differences in effort should trump individual differences in talent as a predictor of achievement. To illustrate, we have taken data on skill from William and Harter (1899) and in Figure 1 and calculated talent and achievement. Specifically, we show how the rate at which men can receive telegrams increases approximately linearly over time and, by derivation, how talent is in this sample reasonably stable over time and, when integrated over time, how achievement increases non-linearly (quadratically).

Figure 1.

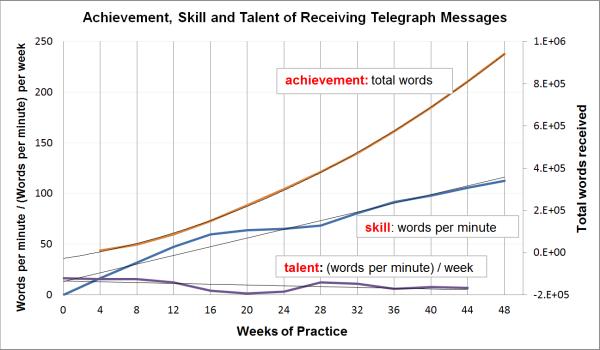
An illustration of achievement, skill, and talent based on published data on the acquisition of telegraphy receiving skill averaged across seven operators (William & Harter, 1899). Skill was originally reported as the number of words per minute that could successfully be received in Morse code and then translated into English. Achievement in this graph is calculated as the total number of words received (assuming 20 hours of work a week), and talent is calculated as the rate of change in skill. Lines of best fit are superimposed (linear for skill and talent, and a parabola for achievement), suggesting talent can be approximated as a constant, skill as a linearly increasing function, and achievement as a quadratic function, as stipulated by our framework.

Thus, choosing a graduate student, with whom one expects to work for four or five years, one might favor a student with slightly less talent but capacity for sustained effort. In hiring a summer intern, with whom one expects to work for just one or two months, the capacity for sustained effort should matter less, and instead their baseline skill when they come in should be considered with priority.

This superlinear (quadratic) dependence of achievement on effort is one of the most explicit and testable predictions of our model. In traditional statistical analysis, it should translate into variables in the effort class accounting for more of the variance in achievement class variables than variables in the talent class. This follows intuitively from our model: because the talent equation includes effort raised to the second power, any small variation (“wiggle”) in effort will be amplified in its effect on achievement.

When it comes to the acquisition of skill, talent and effort are equally important (skill = time · effort) but not equally important to cumulative achievement, at least not in the long run. Of course, in some fields, skill may be of greater interest than accomplishment. For instance, many athletes such as runners are most concerned with their “PR” (personal record)—their peak skill level—rather than the total number of races they have won. Nevertheless, in most domains, it is cumulative achievement that matters more, or at least, equally. Speaking for ourselves, we hope to be judged at the ends of our respective careers by the number of important scientific insights we have contributed, not the rate at which we did so.

Situational Influences

Our model speaks to individual differences in talent and effort but is silent about situational influences that surely influence success. In this first presentation of our theory, the omission is intentional; we have deliberately chosen simplicity over completeness. In this respect, our approach shares the strengths and limitations of most work on individual differences: by holding situational influences constant, we can better appreciate what contribution an individual's own actions make to his life outcomes. However, no two individuals have ever lived out their lives under the exact same circumstances. It is thus worth considering, even cursorily, how situational influences might enter our model.

In the most parsimonious expansion, situational factors influence the rate at which individuals acquire skill (talent) or the effort they expend toward skill building and achievement. In other words, the dichotomy between talent and effort variables may also apply to diverse situational factors. Of course, when discussing individual differences, the term talent is apt for describing the speed with which skills improve with effort, but it seems decidedly less appropriate for corresponding situational factors. Likewise, situational influences on the cumulative effort individuals invest in achieving their goals may call for another term than effort. Howsoever named, examples abound for situational influences that fall into one category or the other, though many may influence achievement via both mechanisms. One way to express such exogenous influences formally in our model would be through inclusion of coefficients that modify the endogenous effort or talent variables.

For example, there is considerable empirical evidence that some teachers are more effective at facilitating learning in their students than others (Rivkin, Hanushek, & Kain, 2005). Extending the logic of our individual differences model, we posit that more effective teachers might increase the rate at which pupils learn (e.g., by superior pedagogical technique) or, alternatively, by increasing the effort students voluntarily devote to their studies (e.g., by inspiring them to strive harder, by helping them manage their time better, by teaching them self-control strategies). Relatedly, group differences in achievement (e.g., the academic achievement gap separating rich and poor students, the income gap separating male and female workers) may reflect, at least in part, differences in situational affordances to improve skills or differences in situational incentives to try hard—or both.

There are also historical changes that influence how quickly individuals learn. For instance, the fastest time in the 1897 Boston Marathon was just over 2 hours and 55 minutes, whereas the current course record, set in 2011, stands at just over 2 hours and 3 minutes (“Boston Marathon history,” 2015; Martin, Benario, & Gynn, 1977). Elite runners today may log more hours of training than their historical counterparts, but advances in nutrition, exercise physiology, and running technique have also improved how much runners improve per unit effort (McArdle, Katch, & Katch 2010; McNitt-Gray et al., 2015). Similarly, in the domain of chess, it has been suggested that computerized chess programs have increased the rate at which new players are able to improve their game (Grossekathöfer, 2010). Likewise, raw scores on tests of fluid intelligence and analogical thinking have been steadily rising worldwide for the last five decades (Flynn, 2012). One explanation for this secular trend is that children grow up today with affordances and incentives to think analytically that simply did not exist a generation ago. Moreover, as each child gets “smarter,” he or she enriches the overall intellectual environment for other children (Dickens & Flynn, 2001). One can imagine that in such an enriched environment, both the effort devoted to developing analytic skills, and the rate at which they are developed, improve.

Expanding the current model to accommodate situational influences is a promising direction for future work. However, the above examples suggest that many situational factors may simultaneously modify both talent and effort. To the extent that is generally true, our dichotomous talent vs. effort taxonomy may prove less illuminating for classifying situational influences.

Historical Precedents

In homage to Newton's acknowledgement that seeing further is possible when “standing on the shoulders of giants,” we devote the remainder of this paper to a historical review of ideas and observations that led to the proposed integrative framework for understanding achievement.

Francis Galton was among the first to recognize that talent alone is no guarantee for success. Reviewing biographical information on eminent nineteenth century British judges, statesmen, scientists, poets, musicians, painters, athletes, and others, Galton (1869) concluded that high achievers were triply blessed by “ability combined with zeal and with capacity for hard labour” (p. 33). Charles Darwin, Galton's half-cousin, wrote in response to Galton's treatise on genius: “I have always maintained that, excepting fools, men did not differ much in intellect, only in zeal and hard work; and I still think this is an eminently important difference” (December 23, year unknown, published in Darwin, Darwin, & Seward, 1903).

Four decades later, William James (1907) also drew attention to the difference between ability and the capacity to realize such potential. James urged his fellow psychologists to undertake two broad lines of inquiry: First, to explore the variety of human talents and, second, to understand the diverse means by which individuals unleash these abilities. Across the Atlantic, architect of the first modern intelligence test, Alfred Binet (1916), noted that performance in school “admits of other things than intelligence; to succeed in his studies, one must have qualities which depend on attention, will, and character; for example a certain docility, a regularity of habits, and especially continuity of effort. A child, even if intelligent, will learn little in class if he never listens, if he spends his time in playing tricks, in giggling, in playing truant” (p. 254, italics added).

Similarly, Clark Hull (1928) observed, “One of the most significant contrasts among the factors residing within the individual is that between capacity and industry” (p. 184). Hull recognized that talent, effort, and circumstance are likely interrelated in complex ways but maintained that, nevertheless, one could disentangle their separate effects on success. Reviewing the available evidence, Hull guessed that individual differences in capacity accounted for 50% of the variance in success outcomes, differences in industry explained 35%, and chance or accident explained 15%.

In 1940, David Wechsler, author of the Wechsler Adult Intelligence Scale and the Wechsler Intelligence Scale for Children, argued that nonintellective factors, including drive, energy, persistence and impulsiveness, contributed dramatically to intelligent behavior:

As soon as one attempts to appraise intelligence-test ratings in terms of global capacity, that is, the ability or abilities to deal effectively with any and all rather than specific situations, it becomes strikingly evident that even our best tests of intelligence give only incomplete measures of the individual's capacity for intelligent behavior...our intelligence tests as now constituted measure effectively only a portion of and not all of the capacities entering into intelligent behavior. (p. 101)

Wechsler argued from two lines of evidence. First, he observed that individuals of identical IQ often differed dramatically in their level of global functioning. Second, he noted that factorial analyses of IQ tests showed that as much as 40 to 60% of the shared variance among IQ subtests could not be explained by “g” or any of the more specific mental abilities. He called for the construction of scales that would measure non-intellective as well as intellectual factors: “Under these circumstances, (our scales) might not be so efficient in selecting individuals likely to succeed in Latin and geometry, but they should do a much better job in selecting those destined to succeed in life” (p. 103).

About 30 years later, Raymond Cattell undertook several investigations of achievement as it related to ability and non-ability variables. “Abilities form the most important group of predictors of school achievement,” Cattell and Butcher (1968) wrote, “but even in this context, personality and motivation must not be forgotten. In achievement after school, the last two are probably of equal importance with abilities” (p. 30). Cattell's distinction between fluid intelligence and crystallized intelligence parallels our distinction between talent and skill, though the clarity of this conceptual distinction belies, in our view, considerable confusion in measurement. Whether conventional measures of intelligence successfully parse the rate at which individuals can learn new things (talent) from what they have already learned (skill) seems debatable (Grigorenko & Sternberg, 1998; Kelley, 1927; McClelland, 1973).

In the same era as Cattell, major figures in industrial psychology, Vroom (1964) and Maier (1965) both proposed that achievement was a multiplicative function of ability and motivation. More recently, Lubinski and Benbow (2006) alluded to a multiplicative model whereby achievement is the product of talent and effort: “To understand the possible impact of this factor, one need only imagine the differences in research achievement likely to accrue over a 5- to 10-year interval between faculty members, research scientists, or lawyers who work 45-hr weeks and those who work 65-hr weeks (other things being equal)” (p. 333). Similarly, Lykken (2005) proposed a multiplicative model for achievement similar to ours: “Mental energy (e)—the ability to persist for long periods thinking productively about a problem, the ability to focus attention, to shut out distractions, to persist in search of a solution—is perhaps as important as general intelligence (g) in determining both successful performance and constructive achievement and the product of these two variables, g*e, provides the most valid predictor of success and achievement” (p. 331). In the only published exposition of his theory, Lykken suggests that the multiplicative function of talent and energy was always, to him, blindingly obvious, a claim he substantiates by summarizing the anecdotal data on a dozen great figures in history, all of whom were known for prodigious effort sustained over long periods of time.

Future Directions

We have argued that talent, effort, skill and achievement are separate constructs, and that effort has a superlinear impact on achievement. Specifically, effort improves skill at a rate proportional to talent and achievement at a rate proportional to skill. For example, as an academic puts more effort into writing, she becomes a faster and better writer, and in tandem produces more, higher-quality papers. Many scholars have made similar observations, but we have formulated this model in more formal terms and suggested that diverse individual differences relevant to achievement can be parsimoniously characterized as either talent or effort variables. Further, our formulation predicts that effort is more important to achievement than talent the longer the time period being considered. In the short run, effort has no advantage. In the very long run, however, bet on the tortoise not the hare. Unless, of course, you can bet on a hare that works as hard as the tortoise.

Our model is clearly an extreme oversimplification, raising many questions we have not attempted to address in this introductory exposition. A complete treatment of situational influences is one priority. Another is the exploration of boundary conditions. For instance, do the most accomplished novelists, entrepreneurs, chefs, film directors, CEOs, painters, and academics invariably exemplify both talent and effort—or, are there exceptions that suggest amendments to our proposed rule? We have assumed throughout our exposition that skills can continually improve; we have failed to mention asymptotic limits to what human beings can do. But structural limitations, anatomical or otherwise, most certainly put a ceiling on skill development. You can't train height, as they say, and there may well be other aspects of skill that are similarly immutable. In addition, beyond the exogenous influence we've alluded to, we omitted any discussion of the frictional (vs. enabling) forces which influence the individual, but should we expand our model to account for individual differences that reliably elicit or discourage the occurrence of such forces? Do some qualities attract effective mentors and others deter them? What about the direction in which individuals choose to proceed? Can any complete model of achievement remain silent on the individual differences related to taste, values, and judgment?

Finally, the logic of our model is straightforward, but how testable is it? Some longitudinal studies have found that talent variables interact with effort variables (O'Reilly & Chatman, 1994) but others have not (Mount, Barrick, & Strauss, 1999). Fortunately, a simple log transformation makes our model testable even within the ordinary least squares regression paradigm: we propose that if skill really equals the product of talent and effort, then log(skill) = β₁ log(talent) + β₂ log(effort), with beta coefficients of similar size, with their deviation from unity determined by the reliability of measurement. Similarly, we predict that log(achievement) = β₁ log(skill) + β₂ log(effort), again with beta coefficients of similar size. In addition, following from achievement = ½ talent · effort², we predict that log(achievement) = β₁ log(talent) + β₂ log(effort) + α, where we predict β₂ to be approximately twice β₁, but at minimum significantly larger than β₁ (reflecting the superlinear dependence on Effort), and α to a constant smaller than 0 (as the logarithm of numbers smaller than unity are negative). Ideally, to test the fit of such models to real data, absolute measures or ratio scales of talent, effort and achievement should be used, for which there is a meaningful and definite zero point and an indefinite range of values; such measures are rare in psychology (Walberg, Strykowski, Rovai, & Hung, 1984). However, depending on the case and measure chosen it may be possible to meaningfully rescale the measure accordingly (Taagepera, 2005). Moreover, to avoid conflation of talent and skill, a direct test of our model would use measures of talent that gauge the rate at which individuals acquire a novel skill, given a structured opportunity to do so, an approach to assessment that requires substantially more investment on the part of researchers than is required for administering conventional intelligence tests (Caffrey, Fuchs, & Fuchs, 2008; Kalyuga & Sweller, 2005).

It is worth noting how our proposed empirical next steps differ from business as usual in psychology: given this multiplicative framework, we have made testable predictions about the magnitude of regression coefficients, not that they merely be significant at some conventional threshold value. With the above model, we have committed ourselves to a testable equation with no parameter that is free to vary arbitrarily, merely fulfilling some weaker requirement of statistical significance. We are not just claiming that Achievement and Skill depend on Effort and Talent—rather we are specifying how they depend, and we sketch how our prediction can be empirically tested. In this we hold ourselves accountable to the style of theory building familiar to the physical sciences: our stronger and specific claims are eminently falsifiable. We do not expect our model to fit the data significantly better than a linear regression as usual (in terms of variance accounted for, or R²), as most curved relationships can be approximated linearly within in reason (Taagespera, 2005). Instead, the magnitudes of our coefficients (not just their significances) have become part of our theory, and are, if confirmed, transferable as part of a generalized explanatory structure to new contexts and datasets, in which we would also expect them to obtain with comparable standardized magnitudes.

Conclusion

In this essay, we have argued for organizing achievement-related traits based on their mechanism of action. Taking inspiration from Newtonian mechanics, we posit that some traits influence the rate at which individuals grow in skill—such talent variables determine which of us are, given the same situational affordances, “quick studies” and others of us “slow learners.” Other traits influence the cumulative effort individuals invest in improving skill and, concurrently, increasing productive output. Thus, as so many great thinkers have intuited, the diverse universe of human traits that bear on achievement can indeed be divided in two. Crucially, talent and effort are functionally distinct categories that are, in our view, more useful than other groupings, including nature vs. nurture and cognitive vs. non-cognitive. Moreover, the formalization we offer here makes the novel prediction that achievement in the long run depends more on effort than talent. In closing, we remark that there is nothing in our model requiring talent variables to be less mutable than effort variables—folk wisdom to the contrary, it would seem that we can, in fact, change the rate at which we can learn and improve (Bryck & Fischer, 2012). In fact, it would seem that all traits exhibit mean-level, rank-order, and within-person variability, and that thoughtful consideration about the sources of such variability could lead to interventions that could improve levels of both talent and effort.