Incorporating temporal EHR data in predictive models for risk stratification of renal function deterioration

Abstract

Predictive models built using temporal data in electronic health records (EHRs) can potentially play a major role in improving management of chronic diseases. However, these data present a multitude of technical challenges, including irregular sampling of data and varying length of available patient history. In this paper, we describe and evaluate three different approaches that use machine learning to build predictive models using temporal EHR data of a patient.

The first approach is a commonly used non-temporal approach that aggregates values of the predictors in the patient’s medical history. The other two approaches exploit the temporal dynamics of the data. The two temporal approaches vary in how they model temporal information and handle missing data. Using data from the EHR of Mount Sinai Medical Center, we learned and evaluated the models in the context of predicting loss of estimated glomerular filtration rate (eGFR), the most common assessment of kidney function.

Our results show that incorporating temporal information in patient’s medical history can lead to better prediction of loss of kidney function. They also demonstrate that exactly how this information is incorporated is important. In particular, our results demonstrate that the relative importance of different predictors varies over time, and that using multi-task learning to account for this is an appropriate way to robustly capture the temporal dynamics in EHR data. Using a case study, we also demonstrate how the multi-task learning based model can yield predictive models with better performance for identifying patients at high risk of short-term loss of kidney function.

1. Introduction

By keeping track of repeated measurements of a patient’s state over time, EHR data contain important information about the evolution of disease. In principle, this information can be used to build models that can potentially help predict disease progression.

Medical data stored in EHRs present a multitude of technical challenges for building predictive models. Patient data are recorded only during a healthcare episode or when a patient visits the hospital for routine medical care. This leads to irregular sampling of data, i.e. the time between measurements vary within a patient and across patients. Another characteristic of EHR data is that patients are tracked for different periods of time.

In this paper, we describe three different approaches to using temporal EHR data to build predictive models for risk stratification. A predictive model that can use historical patient information up to and including the present to predict an adverse outcome is clinically useful. The goal of our study is to investigate how to represent the temporal information in the medical history and how to use the representation to learn a predictive model. We develop and evaluate our methods for risk stratification of patients with compromised kidney function.

Chronic kidney disease (CKD) affects an estimated 10–15% of adults in the United States, with similar estimates reported globally [1]. CKD is typically defined by loss of kidney function as shown by estimated by glomerular filtration rate (eGFR), which is calculated from serum creatinine. CKD is not only associated with decreased quality of life and increased health care expenditure, but is also an independent risk factor for both all-cause and cardiovascular mortality [2].

CKD is divided into five stages. Stage 3 is defined as eGFR in the range of 30–60 ml/min/1.73 m², with eGFR ≤ 45 ml/min/1.73 m² classified as Stage 3b. Recent studies demonstrate that Stage 3b is the inflection point for adverse outcomes including progression to end-stage renal disease (ESRD) and adverse cardiovascular outcomes [3,4]. To help guide clinical decision-making, it is important to accurately risk stratify patients before they progress to Stage 3b.

In our study, we consider patients with mildly to moderately compromised kidney function, which we define to be eGFR between 45 and 90 ml/min/1.73 m². For this patient population, we focus on developing risk stratification models to predict progression of loss of kidney function over the next year.

To the best of our knowledge, the task of predicting short-term progression in patients with compromised kidney function has not been addressed in the literature. Previous studies have aimed at developing predictive models for progression to ESRD or death [5–8]. Many of the past studies performed to predict progression use data from carefully controlled prospective studies [6,7,9]. In contrast, we focus on developing models using longitudinal patient history that is already available in the EHR. Tangri et al. developed a predictive model for progression to ESRD using EHR data [5]. However, they only use data from the initial nephrology visit.

The use of temporal information in patient data has been studied in other clinical applications. Liu et al. use Gaussian processes to model longitudinal time series of numerical variables of post-surgical cardiac patients [10]. Luo et al. explored sequential data modeling techniques such as Markov processes to estimate kidney disease stage transition probabilities using longitudinal eGFR measurements [11]. In [12], Toma et al. extract temporal patterns in daily Sequential Organ Failure Assessment (SOFA) scores during an ICU stay. All of these studies assume that the longitudinal measurements of only a single predictor are present. In contrast, in our work we focus on developing methods that can exploit longitudinal measurements for multiple predictors including both numerical and categorical predictors.

Some of the previous methods have been extended to learn models that can incorporate multiple predictors. In [13], Toma et al. extract temporal patterns of severity scores of six different organ systems in the past to predict mortality at day d. The authors learn separate models, one for the first D days in the ICU using the temporal patterns as features. A model for day d ≤ D only uses data from patients who stayed at least d days in the ICU. As d increases, the number of patients with at least d days in the ICU decreases, while the length of the patterns, and consequently the feature dimensionality, increases. This makes the approach susceptible to overfitting. In contrast, our work presents a multi-task learning based approach that can handle patient data with different lengths of patient history. In addition, we use a temporal smoothness constraint to reduce overfitting for tasks with fewer patients.

We use data from the EHR of Mount Sinai Medical Center in New York City to develop and evaluate three risk stratification models to predict loss of kidney function over the next year.

Our results show that exploiting temporal dynamics when using longitudinal EHR data can improve performance of predictive models. They also demonstrate that exactly how one incorporates this information is important. In particular, our results show that the relative importance of different predictors varies over time, and that multi-task learning is an appropriate way to capture this information.

2. Materials

Our data comes from a de-identified version of the Mount Sinai Data Warehouse that contains electronic health records of patients in the Mount Sinai Hospital and Mount Sinai Faculty Practice Associates in New York City. We extracted data from patients with compromised renal function who were also diagnosed with hypertension, diabetes, or both. We focus on this population because approximately two thirds of cases with compromised renal function are attributable to diabetes or hypertension [14].

The electronic health records contain comprehensive patient information from each medical encounter. The information includes diagnoses, lab measurements, vital signs, procedures and prescribed medications, along with patient demographics. We compute eGFR from serum creatinine measurement using the CKD-EPI formula [15].

In our study, we only consider patients from the study population who satisfy the following inclusion criteria:

1. Patients who have at least a 2-year medical history on record.

2. Patients whose median estimated glomerular filtration rate (eGFR) in the first year in the database is between 45 and 90 ml/min/1.73 m². As discussed in Section 1, we focus on this patient population since it is important to accurately risk stratify patients before they progress to Stage 3b – the inflection point for outcomes such as ESRD and adverse cardiovascular events.

There are 6435 patients in the database that satisfy our inclusion criteria. Approximately 28% of the patient population has eGFR in the range of 45–60 and the rest of the patients have eGFR in between 60 and 90.

3. Problem formulation

We consider the clinical task of predicting loss of kidney function for a patient over the next year using longitudinal EHR data.

Given a sequence of time-stamped outpatient eGFR values for a patient, we generate multiple examples per patient. More specifically, we consider each outpatient eGFR measurement of a patient as an example. Hence, an example is associated with a tuple of a patient P, a time-stamp t₀, and an eGFR measurement. In our study, given a patient, we only consider examples that satisfy the following inclusion criteria:

1. Patient P has at least two outpatient eGFR measurements in the 1-year window following t₀, and the 1-year window preceding t₀. This is done to ensure a robust measure of short-term progression.

2. The previous example from patient P is at least 1-year earlier than from the current example. This is done to avoid bias towards sicker patients who tend to have more outpatient eGFR measurements that those who are stable.

From 6435 patients, we extract 12,337 examples.

We represent each example by extracting the predictors from the patient’s medical history before time t₀. Table 1 lists the predictors that we include in our predictive model. For numerical predictors such as vital signs and lab values, we compute the mean, median, min, max and standard deviation each of the predictors over a specified time-window. In addition, we also compute the linear slope of the numerical predictors in a time-window. More specifically, we fit a line that fits the data using least squares and used the slope of the fit as a feature.

Table 1.

Predictors extracted from the past medical history of a patient for predicting progression of kidney function loss. The numbers in parenthesis for each predictor group is the number of binary variables associated with the given set of predictors. For demographics and numerical predictors, the table also shows the statistics for the patients in the most recent EHR data.

Predictors
Demographics (6)
Age (Mean ± SD)	67.7 ± 11.5 years
Gender	Male: 40%
Race	African American: 27%
Vital signs (56)
Systolic blood pressure (Mean ± SD)	132.8 ± 16.1 mmHg
Diastolic blood pressure (Mean ± SD)	73.3 ± 12.4 mmHg
Lab values (60)
eGFR (Mean ± SD)	66.8 ± 12.1 ml/min/1.73 m2
HbA1c (Mean ± SD)	7.21 ± 1.08%
Diagnoses and procedures (8174)
ICD-9 codes
Medications (180)
Anti-hypertensives, medications for Type-2 Diabetes, Insulin, Nephrotoxic medications

All predictors are represented using binary variables. We represent diagnoses, procedures and medications as a binary variable indicating whether or not the patient associated with the example was assigned an ICD-9 code or prescribed a medication during a specified time-window in the past. We discretize the numerical predictors into four bins based on the quartiles of the corresponding predictor and then map them into binary variables. For example, we map the mean systolic blood pressure for the most recent time window, into four bins: SBP ≤ 120, 120 < SBP ≤ 130, 130 < SBP ≤ 140 and SBP > 140, each corresponding to a binary variable. For a patient with SBP of 125 mmHg, we set the binary variable corresponding to 120 < SBP ≤ 130 to 1 and others to 0.

We measure short-term progression based on the drop of eGFR 1-year in the future. To handle fluctuations in the eGFR values, we compute the median eGFR in the most recent 1-year history (eGFR-past) and 1-year in the future (eGFRfuture). Next, we compute the percentage drop as follows:

$$\%\mathrm{\Delta }=\frac{\mathit{eGFRpast}-\mathit{eGFRfuture}}{\mathit{eGFRpast}}\times 100$$ (1)

We formulate the task of predicting progression as a binary classification task where the example is assigned a positive label if %Δ ≥ threshold, and a negative label if the %Δ < threshold. Since there is not a well-established threshold in the literature, we build models using two values of threshold (10% and 20%).

Using EHR data from M patients, we obtain dataset D

$$D={\{({\mathit{x}}_{\mathit{i}},y_i)\mid {\mathit{x}}_{\mathit{i}}\in {ℝ}^F,y_i\in \{-1,1\}\}}_{i=1}^N$$ (2)

where x_i represents the ith example, F = dimensionality of the feature space and N = number of examples. In total, we extract around 8500 binary variables from a patient’s medical history. Because of the large number of variables, each variable is sparsely represented in the data. To reduce overfitting, we only consider variables that have a statistically significant (p < 0.05) univariate correlation with y. Section 4 discusses this in more detail.

4. Methods

We describe three different approaches we use to incorporate longitudinal data in predictive models. We also discuss how the approaches handle various challenges associated with using EHR data.

One of the key modeling decisions that has to be made is picking a level of granularity based on time to define a time-window. Choosing a fine granularity such as a day may not be relevant for analysis of chronic conditions. On the other hand, choosing a coarse granularity may result in loss of useful temporal relationships. A complication in choosing a window size is that patient data are recorded only during a healthcare episode or a when a patient visits the clinic for routine medical care. This leads to irregular sampling of data, i.e. the times between measurements vary within a patient and across patients.

Given a granularity level L, we divide the medical history of a patient into T non-overlapping time-windows, and then construct a logistic regression model f : ℝ^F → ℝ using the most recent T time windows.

$$f(\mathit{x})=\frac{1}{1+exp(-({\mathit{w}}^{\mathit{T}}\mathit{x}+c))}$$ (3)

where w ∈ ℝ^F are the feature weights and c is the intercept. Specifically, we use an L2-regularized logistic regression model that solves the following optimization problem:

$$\underset{w}{min}\sum _{i=1}^{N}log(1+exp(-y_i({\mathit{w}}^{\mathit{T}}{\mathit{x}}_{{\mathit{i}}_{\mathit{t}}}+c)))+{\lambda }_1{\Vert \mathit{w}\Vert }_2^2$$ (4)

where λ₁ is a tuning parameter. The L2-regularization reduces overfitting. This is important for our application since the feature vectors are sparse.

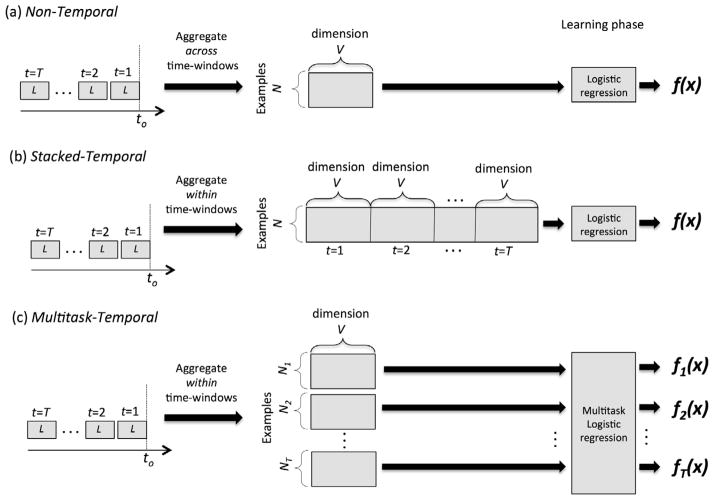
Fig. 1 depicts the three different approaches we use to build the models. Each approach is described in Sections 4.1 and 4.2.

Fig. 1.

Schematics illustrating how the risk stratification models were learned using (a) Non-temporal approach, (b) Stacked-Temporal approach and (c) Multitask-Temporal approach. V is the number of variables.

4.1. Non-Temporal approach

In this approach, when extracting variables for example x_i we aggregate the information across all T time-windows. E.g. a binary variable representing a diagnosis is set to 1 if a patient is assigned that diagnosis during a medical encounter in any of the T time-windows. When computing the mean, median and other statistics for numerical predictors, we aggregate the measurements taken during all of the medical encounters in the T time-windows. This approach represents an example x_i by an F dimensional vector, where F is the number of variables.

The Non-Temporal approach handles the challenge of irregular sampling and missing data by aggregating patient data over the windows for which data is available.

While the Non-temporal approach uses the longitudinal information, it does not capture any temporal information in the data. E.g. a binary variable representing a diagnosis is set to 1 regardless of whether the patient was given the diagnosis on the first time-window (t = 1) or the tth time-window.

Once the variables shown in Table 1 are extracted, we only consider variables that have a statistically significant (p < 0.05) univariate correlation with y in the training set. Next, we learn a logistic regression model using Eq. (4).

4.2. Temporal approaches

We present two approaches to model the temporal information in the longitudinal data. For both methods, we first extract variables for each of the T time-windows separately by aggregating the irregularly sampled patient information within the time-window. This allows us to retain the temporal information between the time windows. E.g., this representation can capture when (in which time-windows) a patient was assigned a certain diagnosis. After extracting variables, we only keep variables that have a statistically significant (p < 0.05) univariate correlation with y in at least one of the T windows in the training set.

4.2.1. Stacked-Temporal

Given the variables for all T time-windows, the Stacked-Temporal approach stacks/concatenates the variables from all windows to represent example x_i using an F dimensional vector, where F = number of variables × T. Next, we learn a linear predictive model f(x_i) solving Eq. (4).

When extracting the variables, we handle missing data using a simple imputation approach. For categorical variables such as diagnoses, procedures and medications, we set the value of the predictor to 0. For numerical predictors, we use the value of the closest time-window for which measurements are available.

One of the disadvantages of Stacked-Temporal is that the feature dimensionality F increases proportionally to T. Therefore, as we increase the number of time-windows, the Stacked-Temporal approach is likely to suffer from overfitting.

4.2.2. Multitask-Temporal

In this approach, we formulate the problem as a multi-task learning problem. Specifically, we consider the task of predicting the outcome using each tth window as a separate task, where t = 1, …, T. For each task t, the data set D_t is

$$D_t={\{({\mathit{x}}_{{\mathit{i}}_{\mathit{t}}},y_i)\mid {\mathit{x}}_{{\mathit{i}}_{\mathit{t}}}\in {ℝ}^F,y_i\in \{-1,1\}\}}_{i=1}^{N_t}$$ (5)

where x_it represents the variables extracted from the tth window, F = the number of variables, and N_t is the number of examples for task t.

We learn all T tasks jointly using the following multi-task formulation:

$$\underset{w_1,\dots ,w_T}{min}\sum _{t=1}^T\left[\sum _{i=1}^{N_t}log(1+exp(-y_i({\mathit{w}}_{\mathit{t}}^{\mathit{T}}{\mathit{x}}_{i_t}+c_t)))+{\lambda }_1{\Vert {\mathit{w}}_{\mathit{t}}\Vert }_2^2\right]+{\lambda }_2\sum _{t=1}^{T-1}{\Vert {\mathit{w}}_{\mathit{t}}-{\mathit{w}}_{\mathit{t}-\mathit{1}}\Vert }_2^2$$ (6)

where w_t are the weights for tth task, and λ₁ and λ₂ are the tuning parameters.

Although we learn separate f _t(x_it ) or t = 1, …, T, the joint learning in Eq. (6) enforces a temporal smoothness constraint on the weights from adjacent time-windows. Specifically, the last term in Eq. (6) encourages the weights of the neighboring windows to be similar, unless the data strongly suggests that the weights be different. Therefore, this constraint helps reduce overfitting of the tasks for which N_t is small.

Once we learn the models, to generate a prediction for a new example x_i, we first obtain the intermediate predictions [ŷ_i1, …, ŷ_iT] from each f_t(x_it). Next, we generate a single prediction ŷ_t by averaging the prediction from the T time-windows (Fig. 1). (In our preliminary analysis, we also considered other aggregation techniques, including weighted average where the weights were learned. However, these more complex approaches did not lead to significant changes in performance.)

The Multitask approach does not perform any imputation for time-windows during which little information is available about the patient. We use the number of encounters within a time-window as a proxy for the amount of patient information within a window. Since we learn separate f_t for each time-window, this formulation allows the number of examples N_t for each task to be different. When learning f_t, only use examples for which there are at least five medical encounters within the time-window t. When generating a prediction for a new example, we use the time-windows with at least five medical encounters and then take the average to yield the single prediction.

Unlike Stacked-Temporal, the feature dimensionality does not increase proportionally with the number of time-windows considered. On the other hand, the number of tasks increases proportionally with the number of time-windows considered. The number of examples declines as the value of t increases, because not every patient will have t windows of medical history. The temporal smoothness constraint in Eq. (6) reduces overfitting for tasks with fewer examples.

5. Experiments and results

5.1. Experimental setup

We evaluate the different methods in the context of predicting short-term progression of loss of kidney function. For all our experiments, we set the granularity of the time-window to 6 months since on average the patients in our dataset have about one medical encounter with an eGFR measurement every 6 months. We consider models that incorporate longitudinal data from up to 10 time-windows, i.e. 5 years, in the past.

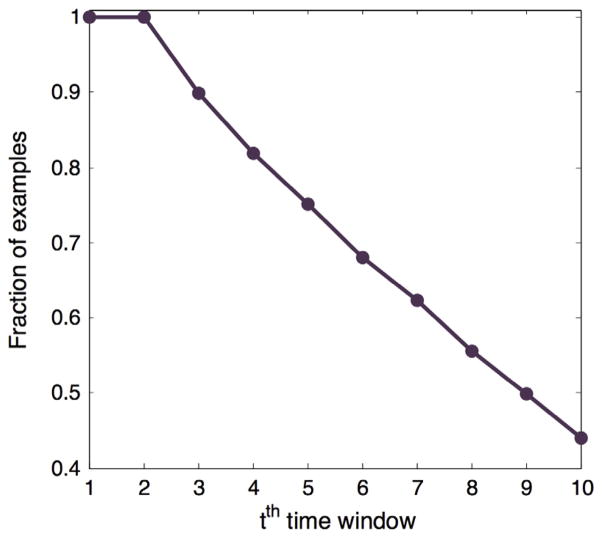
Fig. 2 shows the fraction of examples in our dataset for which a given time-window t has at least one medical encounter.

Fig. 2.

The fraction of examples in our dataset with the different number of time-windows for which at least one medical encounter is available in the EHR.

We formulate the task of predicting progression as a binary classification task where the example is assigned a positive label if %Δ ≥ threshold, and a negative label if the %Δ < threshold. In our experiments, we considered models using 10% and 20% as threshold.

To learn the risk stratification models, we first divide the 6435 patients into training and holdout patients with an 80/20 split. We learn the models using the examples from the patients in the training set. We select the tuning parameters λ₁ and λ₂ using 5-fold cross-validation on the training set. Finally, we evaluate the performance of the trained models on the examples from the holdout patients using the area under the receiver-operating characteristic (AUROC). For each approach, we generate 100 different training and holdout splits and repeat the experiments on each of the 100 splits.

Table 2 shows the average number of positive examples in the holdout set across the 100 splits for the two thresholds.

Table 2.

The average number of positive examples for different thresholds in the holdout sets. The value in the parenthesis shows what fraction of the total number of examples is positive.

Threshold (%)	Number of positive examples
10	1151 (0.315)
20	422 (0.116)

As described in Section 4, for both non-temporal and temporal approaches we only consider variables that have a statistically significant (p < 0.05) univariate correlation with y in the training set. For Stacked-Temporal and Multitask-Temporal, we keep variables that have a statistically significant (p < 0.05) univariate correlation with y in at least one of the T windows in the training set. Table 3 shows the number of variable per time window for each approach for the different years of patient history.

Table 3.

The mean number of variables considered per time window for non-temporal and temporal approaches across 100 splits. The number in the parenthesis is the standard deviation across the splits.

Years of patient history	Threshold 10%		Threshold 20%
	Non-Temporal	Temporal	Non-Temporal	Temporal
1	740 (25)	950 (30)	1084 (34)	1482 (43)
2	792 (33)	1268 (33)	1170 (40)	2022 (51)
3	765 (31)	1465 (36)	1074 (39)	2358 (54)
4	730 (32)	1619 (35)	1046 (40)	2611 (58)
5	732 (31)	1727 (37)	1042 (41)	2835 (63)

5.2. Results

5.2.1. Performance evaluation

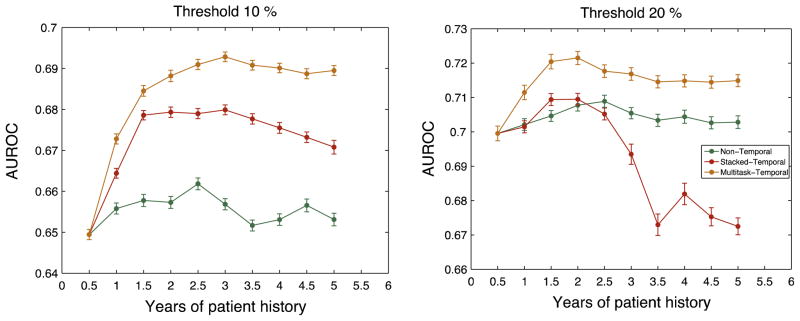
Fig. 3 shows the results for our experiments. The x-axis represent the length of patient history considered in terms of years. For 0.5 years (or T = 1) all three methods have equivalent performance. Since T = 1, there is only a single time-window and there is no temporal information to exploit.

Fig. 3.

Average performance of the different methods for threshold 10% and 20%. The x-axis shows the years of patient history that is considered for the model. The error bars show the standard error in the 100 splits.

Overall, the results in Fig. 3 suggest that incorporating longitudinal information for risk stratification of short-term loss of kidney function improves prediction, although the amount of improvement varies across different methods, different thresholds and the length of patient history considered.

Multitask-Temporal performs at least as well as Stacked-Temporal for all the different lengths of patient history considered, across both the thresholds, and consistently dominates the Non-temporal approach. Fig. 3 shows that as we increase the length of patient history considered, the performance of Stacked-Temporal eventually dips. On the other hand, the performance of Multitask-Temporal improves and eventually plateaus.

Since Multitask-Temporal clearly dominates Stacked-Temporal, we henceforth consider Multitask-Temporal as the only temporal approach.

For each threshold, the AUROC of Multitask-Temporal is significantly (statistically) higher than that of the Non-Temporal approach. These results highlight the importance of exploiting temporal information.

To further illustrate how exploiting longitudinal data and its temporal information can improve performance, Table 4 compares the performance of the best Multitask-Temporal models (models using 3 and 2 years of patient history for threshold 10% and 20% respectively) with the model that uses only the most recent time-window, i.e. T = 1.

Table 4.

Performance comparison of Multitask-Temporal approach with the models that use the most recent time-window. The * and ^# indicates that the average is significantly (p < 0.001) different from the average performance of Non-temporal and GLMM respectively, when evaluated using the matched t-test.

Threshold	Average sensitivity			Average true positive			Average positive predictive value
	Non-Temporal	GLMM	Multitask-Temporal	Non-Temporal	GLMM	Multitask-Temporal	Non-Temporal	GLMM	Multitask-Temporal
Threshold	Average Specificity			Average True Negative			Average Negative Predictive Value
10%	0.375	0.391	0.412*#	383	392	421*#	0.487	0.508	0.536*#
20%	0.501	0.433	0.522*#	176	157	183*#	0.236	0.203	0.244*#
Threshold	Average Specificity			Average True Negative			Average Negative Predictive Value
	Non-Temporal	GLMM	Multitask-Temporal	Non-Temporal	GLMM	Multitask-Temporal	Non-Temporal	GLMM	Multitask-Temporal
10%	0.810	0.812	0.828*#	1698	1705	1736*#	0.729	0.736	0.745*
20%	0.784	0.774	0.786#	2168	2113	2174#	0.923	0.911	0.925#

We consider two different approaches that only use the most recent time-window: Non-Temporal approach and Generalized Linear Mixed Models (GLMM) with time-dependent covariates [16]. For GLMM, we consider random intercept linear mixed model to account for correlations between multiple examples generated from the same training patient. To capture the information that the examples for a patient were extracted at different time points, we also include time (in days, relative to the time of the first example for the patient) as a covariate along with other predictors.

To compute the performance measures shown in Table 4, we consider the test examples with predicted probability of outcome in the top quartile as positive.

Among the methods that use only the most recent time window, GLMM outperforms the Non-Temporal approach for 10% threshold (although not statistically significant). However, for 20% threshold, GLMM significantly underperforms the Non-Temporal approach. A potential reason for this could be overfitting because of a larger class imbalance in the data.

Next, we compare the performance of Multitask-Temporal with Non-Temporal and GLMM. For 10% threshold, Multitask-Temporal correctly identifies 38 and 29 more examples as high risk than Non-Temporal approach and GLMM respectively. Moreover, the boost in sensitivity is achieved by simultaneously improving the positive predictive value from 48.7% in Non-Temporal and 50.8% in GLMM to 53.6% in Multitask-Temporal. For 20% threshold, Multitask-Temporal also outperformed both GLMM and Non-Temporal, although the magnitude of improvement was smaller. For each threshold, the increase in sensitivity and positive predictive value were found to be statistically significant relative to both GLMM and the Non-Temporal approach.

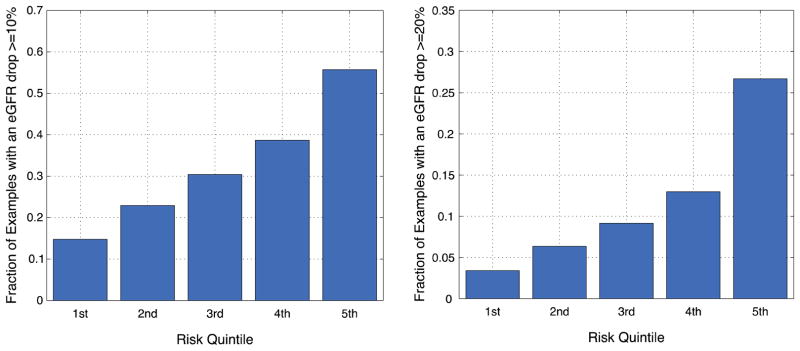
To further convey the ability of our models to risk stratify patients, we divide the test patients into quintiles (as often done in clinical studies) based on the predicted probability of outcome. Next, for each quintile, we compute the observed probability of a positive outcome. Fig. 4 shows that the observed probability of the outcome increases with each quintile for both thresholds. For thresholds of 10% and 20%, patients in the 5th quintile are at 3.7-fold and 7.7-fold greater risk of progression than patients in the 1st quintile.

Fig. 4.

Fraction of examples with a positive outcome in each predicted risk quintile for threshold 10% and 20%.

5.2.2. Visualization of temporal dynamics of variables

Our results demonstrate that the Multitask-Temporal approach is able to capture the temporal dynamics of the variables in longitudinal EHR data to achieve a risk stratification model that is statistically more accurate than models that ignore temporal structure for predicting short-term progression of kidney function loss. In this subsection we examine one aspect of the temporal dynamics: how the relative contributions of individual variables change across windows.

The analysis of the weights assigned by a logistic regression model sheds light on the relative contributions of each variable to the regression equation after accounting for the contributions of other variables in the model [16]. Because some variables may be highly correlated with others, the weights do not perfectly capture the independent association of each variable with the outcome. A positive weight means that the presence of the variable increases the likelihood of a positive outcome. A negative weight suggests that the presence of the variable decreases the likelihood of the outcome. If a weight is close to 0, this suggests that the model does not consider the variable useful for estimating the likelihood.

To analyze the temporal patterns in variable weights, we first compute the normalized weight assigned by the model for a given variable. Given the model associated with a time-window t, we compute the normalized weight for variable ν by:

$${\mathit{normWeight}}_v=\frac{{\mathit{weight}}_v}{{\sum }_i\left|{\mathit{weight}}_i\right|}$$ (7)

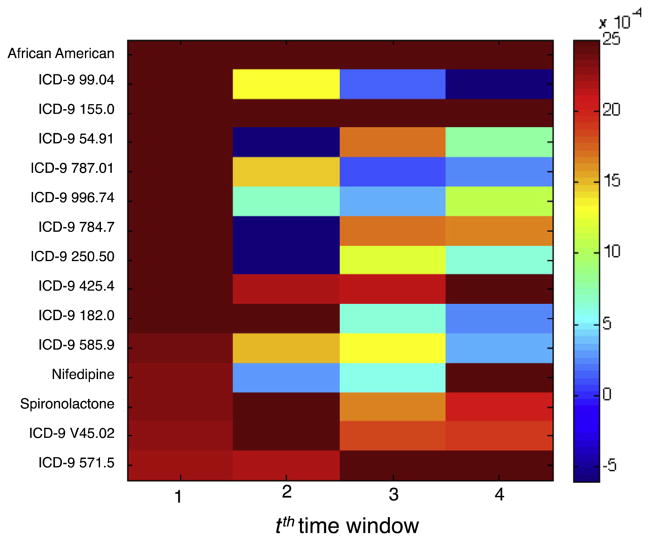
Next, we compute the mean and the variance of the normalized weights across the 100 splits. Fig. 5 shows the mean normalized weights of variables for each of the 4 time-windows obtained from the Multitask-Temporal model learned using 2 years of patient history for a threshold of 20%. The variables shown are the 15 variables, which are not derived from a patient’s eGFR, that most significant positive weights for time-window t = 1.

Fig. 5.

Temporal patterns in normalized variable weights of the 15 variables of the Multitask-Temporal model for threshold = 20%.

In Fig. 5, we observe that the normalized weights for a variable can vary across time-windows. In other words, the relative importance of variables can change over time. For example, the normalized weight of ICD-9 585.9 declines over time whereas that of ICD-9 571.5 increases. This variation could explain why the Non-Temporal approach that allows only a single weight for a variable over multiple windows does not perform as well as Multitask-Temporal.

5.2.3. A case study

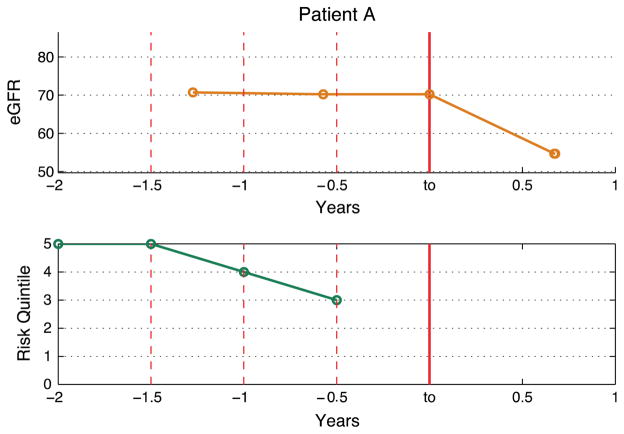
To demonstrate the potential utility of our models we present a case study from a patient in our test set. Fig. 6(a) shows the eGFR trend of Patient A. At t_o, Patient A experiences an eGFR drop of ≥ 20% despite having had a stable eGFR in the most recent year. Fig. 6(b) shows the predicted risk quintile by the Multitask-Temporal models learned using data from varying number of years in the patient history relative to t_o.

Fig. 6.

(a) eGFR Trend for Patient A. (b) Predicted risk quintile by the Multitask-Temporal approach for varying number of patient history. The x-axis represent the number of years where Years < 0 refers to the past and Years > 0 refers to the future, relative to the baseline at t_o.

For Patient A, the predicted risk quintile increases from the 3rd to the 5th as we increase the number of years of patient history. This illustrates that by including the longitudinal data the model correctly predicted a much higher risk of progression.

6. Discussion

In this paper, we have demonstrated that incorporating temporal information in longitudinal data that already exists in EHR can improve the predictive performance. In the application to patients with mildly or moderately compromised kidney function, our results showed that Multitask-Temporal is able to exploit the temporal dynamics in the data to improve prediction of short-term loss in kidney function.

6.1. Predictive performance

6.1.1. Performance comparison of the three proposed methods

In Fig. 3, the Multitask-Temporal approach dominates Stacked-Temporal and Non-Temporal approach for both thresholds for all lengths of patient history considered. The performance of Stacked-Temporal initially improves but eventually dips as we increase the number of years included in the predictive model.

For Stacked-Temporal, as we add more patient history, there exist two competing factors: the predictive information in the additional time-windows is offset by the increased dimensionality, which increases the potential overfitting. For both thresholds of 10% and 20%, the performance of Stacked-Temporal initially improves. However, the overfitting becomes dominant with the 7th (3.5 years) or the 5th window (2.5 years) causing the performance to dip.

We observe that the rate of drop in performance is different for 10% and 20% threshold. For 10% threshold, while the performance starts to dip, Stacked-Temporal still outperforms Non-Temporal. On the other hand, for 20% threshold, Stacked-Temporal underperforms relative to Non-Temporal after 2.5 years. One possible reason for the difference is the fraction of positive examples for each threshold. The ratio of positive examples for 10% and 20% threshold is approximately 30% and 10% respectively. The larger class imbalance for 20% threshold makes it more susceptible to overfitting.

Another reason could be the difference in the number of features that has a significant correlation with y. E.g. For 1 years of patient history, there were approximately 1000 features and 1500 features with a significant correlation (p < 0.05) with y for 10% and 20% threshold respectively (Table 3). As we increase the years of patient history considered in our model, the higher feature dimensionality coupled with higher class imbalance make Stacked-Temporal more likely to overfit for 20% threshold.

Our Multitask-Temporal method yielded statistically better sensitivity and positive predictive value than the baseline approaches that do not use temporal information. Although the magnitude of improvement is not large, our method can easily be automated to improve care by exploiting already available EHR data.

6.1.2. Comparison with existing models in the literature

Prior research in developing models to predict the trajectory of kidney dysfunction has focused primarily on progression to ESRD or death [5–8], and has relied on albuminuria (proteinuria) as a predictor. However, albuminuria is rarely measured in the early stages of reduced kidney function [17]. In contrast, our work focuses on predicting short-term progression for patients at early stages of the disease, and use only predictors found in standard-of-care clinical records.

Many existing work on predicting CKD progression use data from prospective studies [6,7,9]. In contrast, we focus on developing models using patient data available in the EHR. Unlike the data collected from prospective cohort studies where patients are tracked at regular intervals, EHR data is irregularly sampled and noisy.

Because of these differences in the task definition of progression, the predictors and the quality of data used in the models, a side-by-side comparison of our models to the existing models is not possible.

6.2. Important predictors

Fig. 5 shows the temporal dynamics of 15 variables with most significant positive weights for predicting patients who will experience an eGFR drop of 20% or more in the next year. Many of these variables shown in the figure are known risk factors of kidney function.

Past studies have shown that African Americans are reported to have a faster progression rate than non-African Americans [18]. Diabetics (indicated by ICD-9 250.50 Diabetes with ophthalmic manifestations) is also a leading risk factor that for kidney dysfunction [18]. Liver damage (indicated by ICD-9 571.5 Cirrhosis of liver without mention of alcohol) and cancer (indicated by ICD-9 155.0 Malignant neoplasm of liver) has also been linked with renal dysfunction [19,20].

7. Limitations

Our study focuses on how to represent and use temporal information in EHR data to learn predictive models. In this paper, we assume that all the examples are independent of each other. However, this is not true since multiple examples were extracted from a single patient. The generalized linear mixed-effects models (GLMM) focus on capturing correlations between examples from the same patient when learning model parameters. In future work, it would be interesting to explore how multi-task learning based approach could be adapted to learn fixed-effect (or population-wide) and random-effect (patient specific) parameters to account for such correlations.

We represent all numerical predictors as binary variables using quartile-based discretization method. While this allows us to capture non-linear relationships between the predictor and log-odds of outcome, discretization usually leads to loss of information. Using alternative methods such as splines can potentially improve performance.

In this paper, we use a linear model that assumes linear relationships between the variables and the outcome. We did not consider interaction variables and therefore, we do not account for combination of different predictors that can potentially affect the outcome.

8. Summary and conclusions

In this study we presented three different methods to leverage longitudinal data: one that does not use temporal information and two methods that capture temporal information. These methods address some of the challenges faced in using EHR data, rather than data from controlled studies, in building models. These challenges include irregularly sampled data and varying lengths of patient history.

Our results show that exploiting temporal information can yield improvements in predicting deterioration of kidney function. Our results also demonstrate that the choice of approach is crucial in successfully learning temporal models that generalize well. In particular, we showed that a model based on multi-task machine learning can capture temporal dynamics in EHR data without over-fitting compared to other models we evaluated.

Using a case study, we demonstrate the potential clinical utility of the proposed multi-task learning based temporal model for predicting renal deterioration for patients with compromised kidney function.