Abstract
The growing emphasis on patient-centered care has accelerated the demand for high-quality data from patient-reported outcome (PRO) measures. Traditionally, the development and validation of these measures has been guided by classical test theory. However, item response theory (IRT), an alternate measurement framework, offers promise for addressing practical measurement problems found in health-related research that have been difficult to solve through classical methods. This paper introduces foundational concepts in IRT, as well as commonly used models and their assumptions. Existing data on a combined sample (n = 636) of Korean American and Vietnamese American adults who responded to the High Blood Pressure Health Literacy Scale and the Patient Health Questionnaire-9 are used to exemplify typical applications of IRT. These examples illustrate how IRT can be used to improve the development, refinement, and evaluation of PRO measures. Greater use of methods based on this framework can increase the accuracy and efficiency with which PROs are measured.
1 Introduction
Patient-reported outcomes (PROs) have long been a staple of clinical research [1, 2]. For many years, funding agencies and regulatory bodies such as the US Federal Drug Administration, Centers for Medicare & Medicaid Services, the British National Health Services, and more recently, the Patient Centered Outcomes Research Initiative, have pushed for a greater focus on outcomes that matter to patients as part of product testing, intervention trials, and evaluation of quality of care [3–5]. In recent years, the growing prominence of patient-centered care and value purchasing based on improving population health has accelerated the demand for high-quality data from PRO measures. PROs emphasize concepts such as quality of life, fatigue, and depression, which are best reported by patients themselves. Traditionally, the construction, scoring, refinement, and validation of PRO measures have been guided by classical test theory [6–8]. However, an alternative model-based theory called item response theory (IRT) offers promise for addressing practical measurement problems found in health-related research that have been difficult to solve through classical methods [9–11]. Used extensively in educational testing applications [12], this measurement framework has garnered great interest among health researchers. However, the key assumptions, properties, and potential applications of IRT for health-related research are not broadly known.
This paper aims to (i) provide an overview of IRT, and (ii) demonstrate its applications to PRO measures for readers unfamiliar with IRT. The overview will introduce the reader to foundational concepts in IRT, as well as commonly used IRT models and their assumptions. IRT applications for PRO measure development, refinement, and the evaluation of metric equivalence will be illustrated using existing data on 636 adults who responded to the Patient Health Questionnaire-9 (PHQ-9) Depression Scale and the 43-item High Blood Pressure related Health Literacy Scale (HBP-HL). For researchers and clinicians already familiar with IRT who wish to gain technical skills sufficient to conduct IRT analysis or address advanced analytic topics, more comprehensive texts are available [11, 13, 14].
2 Overview of Item Response Theory (IRT)
2.1 What IRT Offers Patient-Reported Outcome (PRO) Measures
The advantages that IRT confers over classical test theory are well documented [9, 10, 15]. First, by modeling the relationship of individual items to the construct being measured, IRT provides a much richer description of the performance of each item, which is useful during PRO measure development or refinement to ensure that the best items are selected. Second, IRT can provide greater detail on a measure’s precision than classical test theory, where a single estimate, such as a Cronbach’s α, is used to describe a measure’s reliability. In contrast, information functions provided through IRT describe how precision may vary across different levels of the construct at the item or scale level. Third, scores estimated using IRT methods are independent of the items used as compared with observed scores from classical methods, which are dependent on a specific set of items. For example, under classical test theory, if an individual answers items on an ‘easy’ diabetes-related knowledge measure, their observed score will likely be higher than if they were administered a measure with ‘harder’ items, even though that individual’s underlying diabetes knowledge remains constant. In contrast, the IRT estimate of the individual’s underlying diabetes knowledge should be very similar regardless of the measure used because the difficulty of the items on each measure is factored in during scoring. This property is called invariance in ability. Lastly, when key assumptions are met, IRT offers the property of item invariance, in which item parameters are constant even if estimated in different samples. In contrast, a measure’s properties under classical test theory can differ by sample, requiring new evaluations of measure performance, such as reliability testing, when the scale is used in a new population. Used appropriately, IRT can greatly improve the efficiency and accuracy of measuring PROs. A glossary is provided in Table 1 to help the reader navigate new terminology.
Table 1.
Glossary of item response theory-related terms
| Term | Description |
|---|---|
| Computerized adaptive testing (CAT) | A form of computer-based testing that selects specific items for each individual based on their prior response to an item with the goal of maximizing precision (e.g. MCAT, GRE, NCLEX) |
| Ability invariance | Property in IRT in which ability scores remain constant, despite the administration of different items; driving force behind CAT |
| Item invariance | Property in IRT in which estimated item parameters are constant across different samples (i.e. measure equivalence) |
| Differential item functioning (DIF) | Measurement bias that occurs when individuals from different groups respond differently to an item, resulting in estimated parameter(s) that vary even after controlling for the underlying trait level |
| Item characteristic curve (ICC) | A probability curve that is monotonic, or continuously increasing, in nature that describes the relationship between an individual’s underlying trait and how they respond to a dichotomous item |
| Categorical response curves (CRC) | A set of probability curves that describes the relationship between an individual’s underlying trait and how they respond to a polytomous item (i.e. plots out the most likely categorical response across trait levels) |
| Polytomous item | An item with more than two response options (e.g. Likert-type) |
| Theta (θ) | A variable used to express an individual’s underlying trait or ability level (e.g. health literacy knowledge, quality of life, depression) |
| Trait score | A value that identifies an individual’s trait level along the Θ scale based on their response to a set of items |
| Item location parameter (b) | Point on the trait scale, Θ, where the probability of endorsing an item is 50 %; also referred to as item difficulty |
| Item discrimination parameter (a) | The slope of the ICC at b; describes how well an item can differentiate between individuals at different trait levels |
| Item guessing parameter (c) | The probability of correctly endorsing an item due to guessing |
| Information function curve | A plotted curve that characterizes the precision of an item across different levels of the latent trait |
| Test information function curve | A plotted curve that sums the information functions of all the items on a scale, and describes the precision of the scale across different levels of the latent trait |
| Test calibration | A process in which an IRT model is used to estimate item parameters and individuals’ trait score |
| Unidimensionality assumption | A requisite that items within a scale measure a single latent trait |
| Local independence assumption | A requisite that the response to an item is independent of responses to other items (i.e. items within a scale are not related) except for the fact that they measure the same underlying trait |
| Monotonicity | Phenomenon where the probability of endorsing an item continuously increases as trait level increases |
IRT item response theory
2.2 IRT: The Basics
2.2.1 The Item Characteristic Curve (ICC)
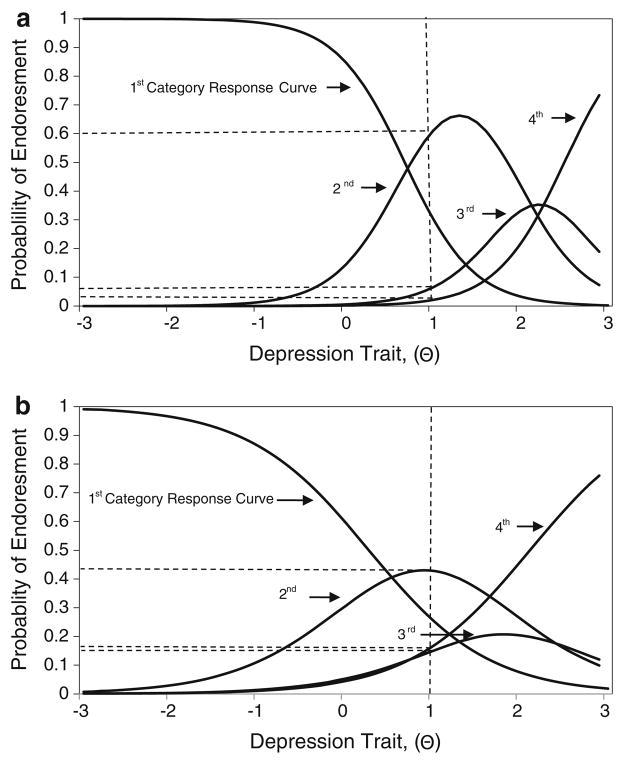
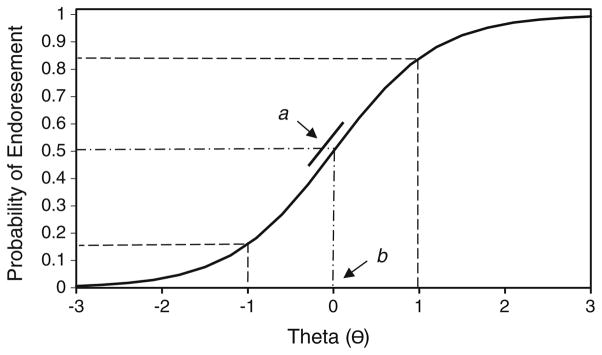
In essence, IRT is a set of mathematical models that describe the relationship between an individual’s ‘ability’ or ‘trait’ and how they respond to items on a scale. This relationship is depicted by an item characteristic curve (ICC). The ICC is a probability curve that is monotonic, or continuously increasing, in nature. As an individual’s trait level increases, the probability of endorsing an item also increases. An ICC for a dichotomous item is shown in Fig. 1. Theta (θ), a variable used to express an individual’s underlying trait level, is measured along the x-axis. Higher values of θ are associated with greater levels of the underlying trait. The y axis indicates the probability of endorsing an item and is scaled from 0.0 to 1.0. In Fig. 1, an individual with a trait level of −1 has a lower probability, 16 %, of endorsing an item than an individual with a trait level of 1, 84 %. When an item has polytomous (i.e. >2) response options, the interpretation of ICCs is slightly different in that the ICC plots the expected item score over the range of the trait. To depict the probability of endorsing each response category for a polytomous item, categorical response curves (CRCs) can be plotted, one curve for each response category. Figure 2a, b illustrates the CRCs for items #2 and #3 on the PHQ-9 Depression Scale, both of which have four response categories. Based on the ideal that CRCs should have distinct peaks, item #2 generally performs better than item #3. This is because, for the most part, item #2 is able to more precisely predict which response category an individual of a certain trait level will endorse. For example, at a trait level of 1.0 on item #2, Fig. 2a, the probability of endorsing the second response category is relatively high, 60 %, whereas the probability of endorsing the third or fourth response category is relatively low, 6 and 2 %, respectively. In comparison, at a trait level of 1.0, the probability of endorsing the second, third, or fourth response categories are 41, 17, and 18 %, respectively, for item #3, Fig. 2b.
Fig. 1.
Item characteristic curve
Fig. 2.
a Category response curve for PHQ-9, Item #2. b Category response curve for PHQ-9, Item #3. PHQ-9 Patient Health Questionnaire-9 Depression Scale
2.2.2 IRT Parameters
The key parameters under IRT are item location, discrimination, guessing, and trait score. Item location, or difficulty, typically denoted b, describes where the item functions best along the trait scale. In the simplest binary case, b is defined as the location on the latent trait where the probability of endorsing an item is 50 % (Fig. 1). This definition can be derived from the mathematical equation associated with several IRT models, including the Rasch model. Items with lower b values are considered to be ‘easier’ and expected to be endorsed at lower trait levels. Item discrimination, denoted a, describes how well an item can differentiate between examinees at different trait levels. In the simplest binary case, it is defined as the slope of the ICC at b, Fig. 1. The steeper the curve, the better the item can discriminate between individuals with different levels of the trait. If the response to an item involves guessing, as possible in health knowledge tests, a guessing parameter may be modeled. This parameter, typically denoted c, describes the probability that the response to an item is due to guessing, and can range from 0.0 to 1.0 along the y axis. Items with c > 0.35 are traditionally viewed as unacceptable [16]. For most PRO measures, such as those for quality of life or physical functioning, guessing is assumed not to be applicable and is typically not modeled. After an individual responds to a number of items, their response set is used to calculate a trait score or theta (θ), which estimates their position along the underlying trait.
2.2.3 Information Function and Standard Error of the Estimate
The concept of information is used in IRT to reflect how precisely an item or scale can measure the underlying trait. Greater information is associated with greater measurement precision. Information is inversely related to the standard error of the estimate, so, at any theta (θ), greater information will result in a smaller standard error associated with the estimated θ score. Over the range of the underlying trait, an information function curve can be derived for each item to reveal how measurement precision can vary across different levels of the trait. Item information is typically highest in the region of the trait near the location parameter, b; items with greater discrimination contribute more information. At the scale level, individual information function curves of all the items on a PRO measure can be summed to create a test information function curve. These curves can be used to compare measure precision offered by different versions of a scale. Generally, a scale with more items will have more information. However, depending on the location and discrimination of the included items, different measures will have distinct test information function curves. A test information curve with a horizontal line at a relatively high information value would indicate that all ability levels would be estimated accurately and with the same level of precision.
2.2.4 IRT Models
A variety of IRT models are available to accommodate different measurement situations. The most commonly used models are summarized here and in Table 2. The decision to use one model over another depends on several factors, including the items’ response format, whether the discrimination parameter can be held constant across items, whether guessing is plausible, and whether different category response parameters must be estimated for each item on a scale. Examining the format of item response categories is an important first step.
Table 2.
Common item response theory (IRT) models
| IRT model | Item response format | Model characteristicsa |
|---|---|---|
| Rasch model | Dichotomous | Equal discrimination across all items; location parameter estimated for each item |
| Two parameter logistic (2PL) | Dichotomous | Discrimination and location parameters estimated for each item |
| Three parameter logistic (3PL) | Dichotomous | Discrimination, location, and guessing parameters estimated for each item |
| Graded response model | Polytomous | Used for ordered responses. Discrimination varies across items |
| Generalized partial credit model | Polytomous | Used for ordered responses. Discrimination varies across items. Can be used as an alternative to graded response model |
| Partial credit model | Polytomous | Equal discrimination across all items. Separate category location parameters estimated for each item |
| Rating scale model | Polytomous | Equal discrimination across all items. A single set of categorical location parameters estimated for all items |
| Bock’s nominal model | Polytomous | Used for unordered responses. Discrimination allowed to vary across items |
For items with dichotomous response options, the Rasch, 2 parameter logistic (2PL), or 3 parameter logistic (3PL) models can be used [17, 18]. The Rasch model only estimates a location parameter for each item and assumes that the discrimination parameter is constant across all items [19]. If the assumption of equal discrimination does not hold, the 2PL model can be used to estimate (i) a location and (ii) a discrimination parameter for each item. When guessing is plausible, the 3PL model can be used to estimate the (i) location, (ii) discrimination, and (iii) guessing parameters. There are advantages to each of these types of IRT models. The main advantage of the Rasch model is its parsimony, allowing models to be fit with smaller samples sizes. In addition, the location parameters of any two items can be compared regardless of the group of subjects involved, and any two individuals’ trait score can be compared irrespective of the set of items being used [20]. However, these properties are true only if the model fits the data. In many situations, the assumptions of the Rasch model do not hold, and more complex models, such as the 2PL, which estimates separate discrimination parameters, would be appropriate [21]. The 3PL model is most useful for item content that tests ability, such as health knowledge, as it is plausible that one could correctly endorse an item by guessing.
For items with polytomous response options (e.g. Likert scales), a format typical of many PRO measures, several widely used models include the graded response, generalized partial credit, partial credit, rating scale, and Bock’s nominal models [20, 22–26]. The graded response and generalized partial credit models are the most flexible polytomous IRT models because they have fewer assumptions, which allow for separate discrimination parameters and separate category response parameters to be estimated for each item. As a result of this flexibility, these models are more likely to fit data generated from PROs. However, with more parameters that need to be estimated, the sample size requirements are typically larger than for simpler models. The partial credit and rating scale models estimate fewer parameters than the previous two models because they make the assumption that the discrimination parameter is equal across all items (for this reason, the partial credit and rating scale models belong to the ‘Rasch family’). The difference between the two models is that the partial credit model estimates separate category response parameters for each item, while the rating scale model further assumes that the thresholds for category response are also equal across items. The assumptions of equal discrimination and equal thresholds make the rating scale model among the more restrictive IRT models. Therefore, careful consideration of its appropriateness to the data under consideration is needed. For measures with items that have different category labels or scale anchors, the rating scale model may be less appropriate. For items with unordered response categories, Bock’s nominal model may be used, but these types of items are rarely used in PRO measures. Consequently, the application of the nominal model to PROs has been limited [26]. More complete description of available IRT models can be found in Hambleton et al. [11], van der Linden and Hambleton [13], Embretson and Reise [21].
2.2.5 Assessing Model and Item Fit
Once a model that is determined to be appropriate for the data has been selected, tests of model and item fit are necessary. There is currently no consensus on how to assess model and item fit. However, a number of methods have been suggested [11]. To assess model fit, techniques such as (i) comparing nested models, (ii) providing evidence that the model assumptions are met to a reasonable degree by the test data, (iii) determining if model properties such as trait and item invariance are obtained by the test data, and (iv) assessing the accuracy of model predictions using the test data, have been used [11, 27–30]. When comparing nested models (e.g. 2PL vs. 3PL), the null hypothesis is that the more parsimonious model fits well. This is tested by examining the difference in −2*log-liklihood (−2*LL) of the two model calibrations, which is distributed as a Chi-square with degrees of freedom equal to the difference in the number of estimated parameters between the two models [11]. Significant differences indicate that the additional parameters provide better fit to the data than the more parsimonious model. Techniques to check specific model assumptions are discussed in the next section. To test for invariance in trait scores, one can compare individuals’ estimated trait scores using different items within a calibrated item set, preferably with items that vary widely in difficulty. If the model fits, a plot of the pairs of trait estimates should support a strong linear relationship. To test for item invariance, the estimated item parameters can be compared using two different groups (e.g. high-trait vs. low-trait groups or by gender). If the model fits, item calibrations using different groups should yield similar parameter estimates.
To assess fit at the item level, a variety of fit statistics that measure deviations between predicted and observed responses have been developed [20, 31]. For the Rasch family of models, mean square fit statistics can be used to describe the fit of the item to the model. Two commonly used mean square fit statistics include the infit (weighted) and outfit (un-weighted) statistic. The infit and outfit statistics are often converted into an approximately normalized t statistic, with an expected value of 0 and standard deviation of 1. Values greater than ±2 are interpreted as demonstrating more variation than predicted by the Rasch model, in which case the item is considered not to conform to the unidimensionality requirement [32]. The following citations provide additional fit statistics that have been developed for the Rasch family of models [33–35]. For non-Rasch models, alternative fit indices such as the S−χ2 statistic have been developed [36]. When interpreting these fit statistics, the null hypothesis is that the item fits well, therefore, a significant result would indicate poor item fit. However, these ‘goodness-of-fit’ indices are sensitive to sample size [11]. If a sample is sufficiently large, even negligible differences will produce a result indicating poor fit. Additional details on approaches to assess model and item fit may be found in Hambleton et al. [11], van der Linden and Hambleton [13], Embretson and Reise [21], and Orlando and Thissen [36].
2.2.6 Key IRT Assumptions
Several key assumptions underlie the IRT framework, including (i) unidimensionality of the measured trait, (ii) local independence, (iii) monotonicity, and (iv) item invariance. Unidimensionality assumes that a set of items on a scale measure just one thing in common. Evaluation of unidimensionality may be done in different ways. Some researchers suggest using factor analysis, a widely used data reduction method that draws upon correlation among items to derive a smaller set of factors or domains. Under IRT, the factor analysis should ideally result in a 1-factor solution [20, 27, 28]. If multiple factors emerge, evidence of a ‘dominant’ factor (i.e. demonstrating that the first factor accounts for at least 20 % of the variance) is needed [11, 21, 27, 37]. Others recommend conducting tests of model fit to determine unidimensionality [29, 30, 38]. If misfit is detected in any item, it may indicate that the item is not closely related to the overall latent trait or that there is lack of clarity in the item, causing respondents to interpret it differently.
Local independence means that each and every item on a PRO measure is statistically independent of responses to all other items on the measure, conditional upon the latent trait. In other words, items within a measure should not be related except for the fact that they measure the same underlying trait [11]. Therefore, controlling for the trait level, any two items should be uncorrelated. Violations can occur when a set of items have a similar stem (e.g. a series of questions referring to the same graph on a mathematical ability test), rely on similar content, or are presented sequentially [39]. One way to test this assumption is to examine the discrimination parameter, a. If items display excess covariation, or dependence, they may have very high slopes (e.g. >4) relative to other items in the measure [11, 39]. Residual correlation matrices may also be examined to identify item clusters with excessive co-variation that may indicate violation of this assumption [20]. Several software programs also offer test statistics to identify violations to the local independence assumption.
Monotonicity, as described earlier, refers to the phenomenon in which the probability of endorsing an item will continuously increase as an individual’s trait level increases. For example, an individual with a trait score of 1.9 will have a higher probability of endorsing an item than an individual with a trait score of 1.7, and in turn that individual with a trait score of 1.7 will have a higher probability of endorsing the same item than an individual with a trait score of 1.5.
Item invariance is another underlying assumption of IRT. It can be described as the phenomenon in which estimated item parameters are constant across different populations. This allows for unbiased estimates of item parameters to be obtained from unrepresentative samples (e.g. low-trait groups vs. high-trait groups), so long as the data fit the model [9]. While the assumption of item invariance should theoretically hold in all cases, in real life, the data do not always support this. This may be due to poorly written items or items that are interpreted differently by different samples. When item parameters behave differently in subgroups after controlling for ability, an item is considered to have differential item functioning (DIF) [11]. DIF can occur in item location or discrimination. Items with DIF will reveal distinct ICCs or sets of CRCs for different subgroups. For items without DIF, only one ICC or one set of CRCs would be observed for both subgroups. To test for DIF’, it is important to first identify anchor items, which serve to ‘bridge’ or equate the underlying scale in the two groups. Using the anchor items, the remaining items on a measure can be tested for DIF. It is critical that these anchor items, show no DIF in the a and b parameters between two groups, as the ability estimates can be biased if the anchor items are affected by DIF [14, 40]. Anchor items can be identified using an iterative item purification process available from the IRTLRDIF® software program.
2.2.7 Sample Size Requirements
There is currently little consensus around the sample size requirements for IRT parameter estimations, but general guidelines have been published [39]. First, larger sample sizes are needed for more complex models. For simple Rasch models, sample sizes as small as 100 have been shown to be adequate [41], but there is debate about sample size requirements for more complex models, with estimates ranging from 200 to 500 [42–44]. Second, sample size requirements may vary with regard to the underlying purpose, since different levels of precision may be acceptable for different applications. For example, if item parameters will be used for high-stakes applications like large-scale accountability or pay-for-performance programs, large sample sizes are needed to ensure accurate estimates with low standard errors. However, smaller sample sizes may be adequate in preliminary evaluations of questionnaire properties [39]. Lastly, sample distribution can impact sample size requirements. A smaller sample distributed evenly across the trait levels of interest can produce more robust parameter estimates than a larger sample with narrower trait coverage, as regions of the trait with few individuals have limited information to generate estimates and will produce higher standard errors [20].
3 Applications of IRT to PRO Measures
To demonstrate how IRT can be used for PRO measures, existing data on 636 Korean and Vietnamese American adults who responded to the HBP-HL and the PHQ-9 were used. From these data, we illustrate two major applications of IRT: (i) how to use parameter estimates, ICCs, and information function curves for scale development or refinement, and (ii) how item invariance can be examined across different samples by testing for DIF. We also describe major initiatives that have applied IRT to PROs.
Briefly, the HBP-HLS is a 43-item measure that assesses health literacy (HL) in the context of high blood pressure, targeting those with limited English proficiency [45]. Each item is scored as correct or incorrect. Total scores can range from 0 to 43, with higher scores associated with higher HL. Initial psychometric evaluation using classical testing methods demonstrated high reliability (α = 0.98). The PHQ-9 is a 9-item depression scale [46]. Each item on the questionnaire asks “Over the last two weeks, how often have you been bothered with the following problems,” and is scored ‘0’ (not at all), ‘1’ (several days), ‘2’ (at least half of the days), or ‘3’ (nearly every day). The reported reliability of the PHQ-9 was also strong (Cronbach’s α = 0.89–0.86) [46, 47]. Total PHQ scores can range from 0 to 27, with scores >5 corresponding to mild depression. These measures illustrate two response formats, binary (HBP-HLS) and ordered Likert (PHQ-9), typically used in PRO measures. The 2PL model was used to calibrate the item parameter estimates for the HBP-HLS given its dichotomous response format. The graded response model was used to calibrate item parameter estimates for the PHQ-9 given its ordered polytomous response format.
Model fit and model assumption testing were conducted for both measures. However, for brevity, we report results only for the PHQ-9. The fit of the PHQ-9 to the graded response model versus the generalized partial credit model was tested based on item level fit results. The graded response model demonstrated better fit. Using the polytomous extension of the S−χ2 statistic [36], none of the items were identified as misfitting at p < 0.05 for the graded response model after controlling for type 1 error rates with the Benjamini–Hochberg adjustment [48], while one of the nine items demonstrated misfit with the generalized partial credit model. To test the assumption of unidimensionality, the eigenvalues from a principal components exploratory factor analysis on the PHQ-9 supported a 1-factor solution. To assess potential violations to the local independence assumption, the discrimination parameter, a, was evaluated to see if items displayed high slopes (e.g. >4.0) relative to other items on the measure. Based on a calibration of the PHQ-9 with the graded response model, none of the discrimination parameters exceeded 4.0 (Table 4). In addition, the standardized local dependence chi-square (LD χ2) statistic provided by IRT-PRO® was evaluated to further assess for local independence [49]. LD χ2 values that exceeded 10.0 are highly suggestive of excess dependence between items. Based on the analysis, no item pairs had LD χ2 that exceeded 10.0, which further supports the assumption of local independence among items on the PHQ-9. Therefore, it was concluded that the calibration of the PHQ-9 using a graded response model had good fit, was sufficiently unidimensional, and robust to possible violations to the local independence assumption.
Table 4.
Patient Health Questionnaire-9 parameter estimates using a graded response model
| Item # | Item description | a | b1 | b2 | b3 | S − χ2 | p value |
|---|---|---|---|---|---|---|---|
| 1 | Little interest or pleasure in doing things | 1.87 | 0.73 | 2.04 | 2.51 | 49.65 | 0.04 |
| 2 | Feeling down, depressed, or hopeless | 2.55 | 0.67 | 1.92 | 2.50 | 19.90 | 0.90 |
| 3 | Trouble falling or staying asleep | 1.45 | 0.26 | 1.53 | 2.11 | 29.34 | 0.55 |
| 4 | Feeling tired or having little energy | 1.50 | 0.28 | 1.98 | 2.48 | 32.09 | 0.51 |
| 5 | Poor appetite or overeating | 1.38 | 1.35 | 2.95 | 3.28 | 27.96 | 0.41 |
| 6 | Feeling bad about yourself | 2.02 | 1.25 | 2.56 | 3.09 | 28.40 | 0.20 |
| 7 | Trouble concentrating on things | 1.70 | 1.49 | 2.66 | 2.94 | 29.45 | 0.34 |
| 8 | Moving slowly or being so fidgety | 2.03 | 1.65 | 2.84 | 3.17 | 37.86 | 0.02 |
| 9 | Thoughts that you would be better off dead | 2.35 | 1.63 | 2.79 | 3.16 | 22.91 | 0.41 |
| Value ranges | [1.38–2.55] | [0.73–1.65] | [1.53–2.95] | [2.11–3.28] |
3.1 How to Use Parameter Estimates, ICCs/Categorical Response Curves (CRCs), and Information Function Curves for Scale Development or Refinement
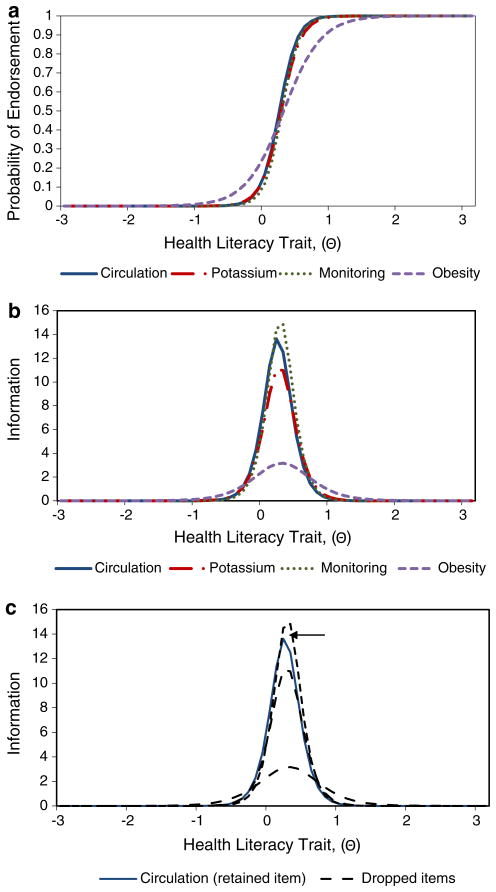
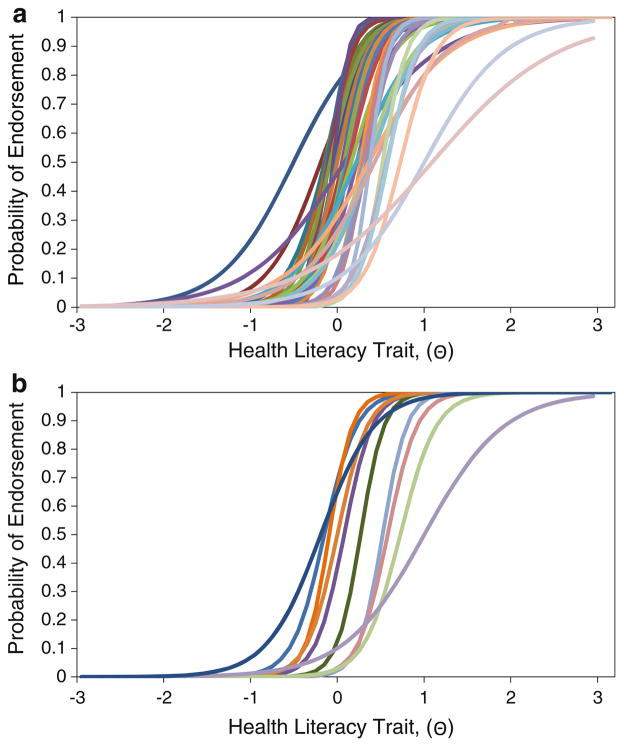
During scale development and refinement, item selection is generally guided by the underlying goal. If the goal is to create a scale that can be used to make meaningful interpretations in group differences or change over time, items should be selected such that there is an even distribution of items across a range of locations on the Θ scale. Having even item density ensures that changes in scores can be interpreted fairly, particularly if summed scores are used over IRT scores, as score gains among some individuals may be inflated if there are high concentrations of items in certain regions of the underlying trait [50]. For example, Table 3 displays the parameter estimates of select items on the HBP-HLS, sorted by their b values. The location estimates of the items shown in the table range from −0.66 to 1.04, indicating modest variation in item location, with the ‘easiest’ item listed first (“Is this Normal BP?”) and ‘hardest’ item listed last (“Time for 2nd Tablet”). We also observe a cluster of four items in a narrow region of the HL trait (b = 0.22–0.28). Given our measurement goal, we would want to retain the best performing item within this region (i.e. item with the highest a value or best discrimination). Based on this criterion, item #27 ‘Monitoring’ is the best candidate because it is most discriminating. However, other factors, including the importance of item content, may be considered during item selection. For example, if ‘monitoring’ blood pressure is conceptually covered by other items within the HBP-HLS, the developers may choose to retain item #24 ‘Circulation’ instead, which may not be covered by any other item. Examining the ICC and information function curves can further aid item selection. Based on Fig. 3a, the ICCs for ‘Circulation,’ ‘Potassium,’ and ‘Monitoring’ overlap, indicating redundancy. Furthermore, ‘Obesity’ displays the lowest level of discrimination (i.e. flattest slope). The information function curves of these four items, Fig. 3b, also indicates that ‘Monitoring’ provides the most information and ‘Obesity’ provides the least. It is worth noting that if ‘Circulation’ was retained rather than ‘Monitoring,’ as proposed above, the loss of information (i.e. area under the curve where no other item covers) would be minimal, Fig. 3c. Applying this strategy across all 43 items on the HBP-HLS (Fig. 4a), a ten-item shortened scale similar to Fig. 4b can be obtained that maximizes content coverage, minimizes loss of precision, and ensures that changes or differences in scores can be interpreted fairly.
Table 3.
HBP-HLS parameter estimates using the 2PL model, selected items
| Item # | Item description | a | b | S − χ2 | p value |
|---|---|---|---|---|---|
| 35 | Is this normal BP? | 2.43 | −0.66 | 24.46 | 0.06 |
| 36 | Appointment Date | 3.91 | −0.32 | 18.64 | 0.23 |
| · | · | · | · | ||
| · | · | · | · | ||
| 24 | Circulation | 7.4 | 0.22 | 13.83 | 0.39 |
| 28 | Potassium | 6.74 | 0.25 | 16.85 | 0.26 |
| 27 | Monitoring | 7.81 | 0.26 | 9.55 | 0.66 |
| 17 | Obesity | 3.56 | 0.28 | 20.08 | 0.58 |
| · | · | · | · | ||
| · | · | · | · | ||
| 21 | Angioplasty | 4.82 | 0.68 | 10.48 | 0.58 |
| 40 | Saturated fat in Ramen | 2.18 | 0.95 | 19.00 | 0.43 |
| 31 | Time for 2nd tablet | 1.37 | 1.04 | 31.17 | 0.18 |
BP blood pressure, HBP-HLS High Blood Pressure related Health Literacy Scale, 2PL Two parameter logistic
Fig. 3.
a Item characteristic curves of four items on the HBP-HLS. b Information function curves of four items on the HBP-HLS. c Information loss from retaining ‘Circulation’ vs. ‘Monitoring’. HBP-HLS High Blood Pressure related Health Literacy Scale
Fig. 4.
a ICCs of all 43 items on the HBP-HLS. b ICCs of a shortened ten-item HBP-HLS. HBP-HLS High Blood Pressure related Health Literacy Scale, ICC item characteristic curve
If two studies intend to target groups at different ranges of the trait, item selection should be made to ensure that measurement precision is maximized in the specific trait ranges for each group. Let us hypothetically propose to shorten the PHQ-9 for a mild depression group (Θ = −1 to 1) versus a moderate to severe depression group (Θ = 1–3) for two different studies. Table 4 displays the parameter estimates and the associated standard errors of all the items on the PHQ-9. Since the graded response model was used for the PHQ-9, (i) a discrimination and (ii) three location parameters (four response categories−1) were estimated for each item. Based on Table 4, the slope estimates range from 1.38 to 2.55, indicating modest variation in item discrimination. As expected, higher categories have higher item locations, indicating endorsement of more severe depression, b1 = (0.73–1.65), b2 = (1.53–2.95), and b3 = (2.11–3.28).
To help identify which items to select to optimize measurement precision between the two depression groups, let us compare items #3 (“Trouble falling or staying asleep”) and item #9 (“Thoughts that you would be better off dead”). Based on Table 4, the first category is endorsed at lower trait levels for item #3 than item #9 (b1 = 0.26 vs. 1.63, respectively), and this trend is consistent across all the response categories (b2 = 1.53 vs. 2.79; b3 = 2.11 vs. 3.16). This suggests that item #9 targets higher trait levels of depression than item #3. The information function curves on Fig. 5 demonstrate that item #9 provides more information at higher trait levels of depression, and item #3 provides more information at lower trait levels of depression. Therefore, item #9 should be selected when the goal is to optimize a scale to measure moderate to severe depression (Θ = 1–3), while item #3 should be selected when the goal is to optimize a scale to measure mild depression (Θ = −1 to 1).
Fig. 5.
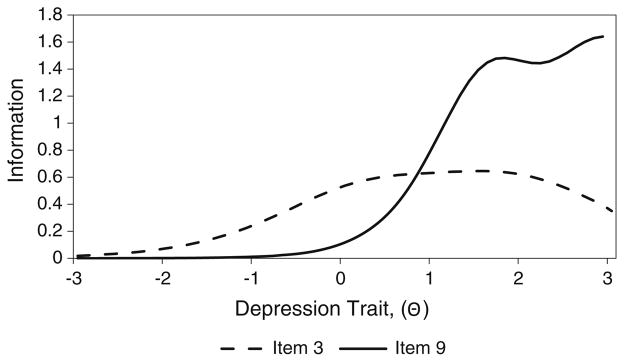
Information function curves, PHQ-9 item 3 vs. item 9. PHQ-9 Patient Health Questionnaire-9 Depression Scale
When the information function curves of all the items across a scale are summed, a total test information function curve can be computed and plotted. The test information function curves of two different versions of a shortened PHQ-9 scale are displayed in Fig. 6. The solid curve represents a shortened scale that includes items #1–4, while the dotted curve represents a shortened scale that includes items #5–9. Based on the solid curve, high levels of information can be gained along the trait region associated with Θ = 1.0–3.0, while less information can be gained in regions below Θ = 0.0. This suggests that a shortened scale with items #5–9 is good at assessing individuals with moderate to high levels of depression, and is not as good in assessing those with lower levels of depression. On the other hand, a shortened scale that includes items #1–4 provides more information in lower trait regions, and is more appropriate when the goal is to optimally measure trait levels at the Θ = −1 to 1 range versus the Θ = 0–3 range. Computing and comparing test information function curves of scales with different items can be helpful when developing and refining PRO measures to ensure that precision is optimized in the desired trait regions.
Fig. 6.
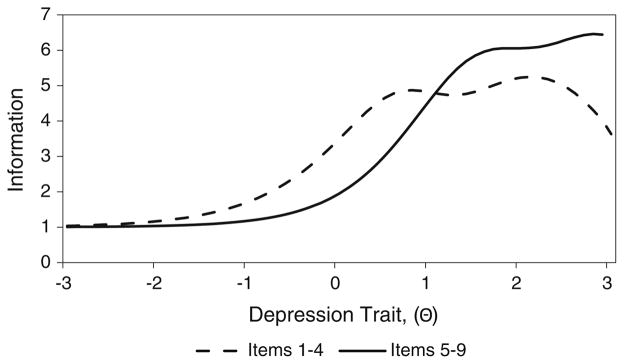
Test information function curves, PHQ-9 items (1–4) vs. (5–9). PHQ-9 Patient Health Questionnaire-9 Depression Scale
3.2 How to Use Differential Item Functions to Test for Item Invariance
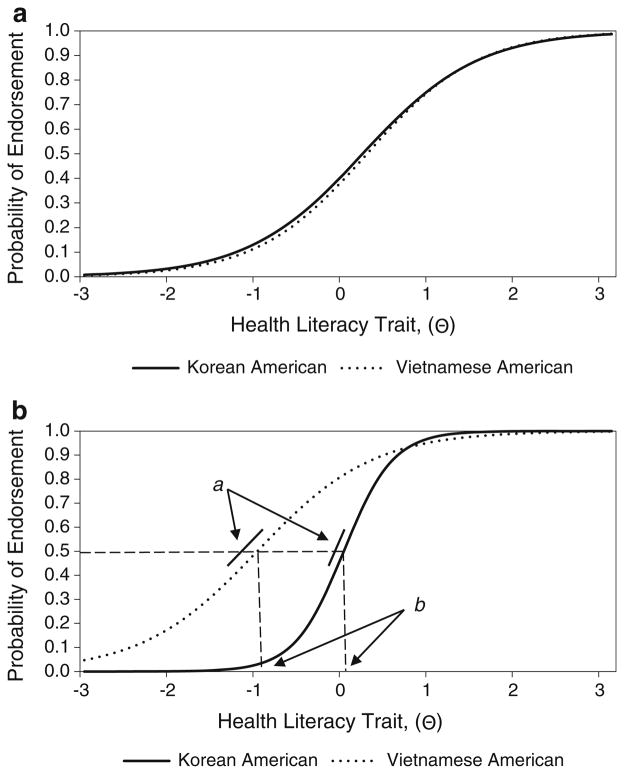
Measure invariance (i.e. item invariance), where all items have the same measurement properties across different samples, is an important property of good scales. When item parameters behave differently in subgroups after controlling for ability, an item is considered to have DIF. As noted earlier, DIF can occur due to differential interpretation, group norms in response style (e.g., avoidance of extreme categories), or other factors (how items are administered). Therefore, assessing for DIF can be particularly useful in detecting items that display cultural bias, and can be targeted for revision or removal. The 43-item HBP-HLS will be used to demonstrate how to test for DIF. As noted earlier, it is important to first identify anchor items, which serve to ‘bridge’ or equate the underlying scale in the two groups. Using IRTLRDIFF®, four non-DIF items were identified. The four non-DIF ‘bridge’ items were then used to test all other items on the scale for DIF. The results of that test revealed that eight of the 43 HBP-HLS items demonstrated significant DIF by ethnic group (Korean American vs. Vietnamese American). As an example, Fig. 7a displays item #24 (‘Circulation’) which does not demonstrate DIF, and Fig. 7b displays item #35 (“Is this Normal BP?”), which demonstrated DIF in location and discrimination. Specifically, Fig. 7b shows that item #35 is less discriminating (flatter slope) for Vietnamese Americans than for Korean Americans. In addition, the location of item #35 is lower for Vietnamese than Korean Americans. This suggests that the item was harder for Korean Americans, since many Vietnamese American respondents with lower HL can get this item correct. A possible reason for observing DIF in this item was how the item was administered. Within the Vietnamese American sample, the HBP-HLS was administered after taking respondents’ blood pressure; and many of the respondents inquired about normal blood pressure values upon receiving their readings. On the other hand, this scale was administered before taking blood pressure measurements in the Korean American sample. Therefore, correctly responding to #35 (“Is this normal PB?”) may have been easier for individuals in the Vietnamese American subgroup. While it is ideal to only retain non-DIF items, DIF can be accounted for and modeled if items with DIF are absolutely necessary.
Fig. 7.
a HBP-HLS item #24, No DIF. b HBP-HLS item #35, DIF in the location and discrimination parameters. DIF differential item functioning, HBP-HLS High Blood Pressure related Health Literacy Scale
3.3 CAT
More recently, there has been significant interest in utilizing IRT to support CAT for PRO domains. IRT makes CAT possible by calibrating all items for a particular domain (e.g., physical function) along a common scale. Once calibrated, an algorithm may be applied to this set of items, also known as an item bank, so that items can be adaptively administered to target the estimated trait level of the respondent. For example, if an individual endorses an item on a CAT that indicates a moderate level of physical functioning, the next administered item would assess a higher level of physical functioning than the prior item. If the individual did not endorse the original item, an item indicating a lower level of functioning would be administered. This process is repeated until a specified number of items or specific standard error for the individual’s score is attained. This approach is appealing, as it allows for greater measurement precision while reducing respondent burden, as less informative or less relevant questions are not asked [51]. Moreover, since items are aligned on a common scale, IRT scores across different individuals can be compared even though individuals may be administered a different subset of items.
Efforts to implement PRO measures on CAT platforms have already begun. For example, the National Institutes of Health (NIH) has engaged in ambitious multi-institute roadmap initiatives to re-engineer the clinical infrastructure [52, 53]. The Patient Reported Outcome Measurement Information System (PROMIS) and Neurology Quality of Life (Neuro-QoL) initiatives aim to build and validate item banks and CATs that measure important symptoms and health concepts such as physical functioning, pain, depression, and quality of life. Many of the item banks and CATs are available in multiple languages, including English, Spanish, Portuguese, and Chinese. The results from the first set of validated item banks have been promising, supporting the ability to field fewer questions to participants without loss of scale precision, and the possibility for data comparison across studies [54, 55].
3.4 IRT Software Programs
Existing software programs are available to conduct IRT analysis. Some of the most commonly used programs include PARSCALE®, Multilog®, IRTPRO®, BILOG®, M-PLUS®, flexMIRT®, RUMM2030®, and Winsteps® [56–63]. STATA® may be used to run some IRT models [64]. There are also two free statistical packages for R® that conduct IRT analyses, they include ‘ltm’ for IRT models and ‘eRm’ for Rasch models [65, 66]. A thorough discussion of these programs is beyond the scope of this paper, but more information may be offered by the software vendors and a few publications with more details on these programs exist [67, 68].
4 Conclusions
IRT offers great potential for addressing important measurement problems found in health-related research. We have highlighted important applications of IRT, including how it may be used in item selection during the development and refinement of PRO measures, as well as how it may be used to identify items that do not perform comparably in different groups. Finally, IRT provides the theoretical and computational underpinning that drives CAT applications, such as for PROMIS and Neuro-QoL, which can increase the precision and standardization of PRO measures while limiting respondent burden. With broader understanding of IRT and its applications, we expect that the tools and methods based on this framework can significantly improve the measurement of PROs.
Key Points for Decision Makers.
Using item response theory as compared with traditional classical test theory provides much richer and more accurate descriptions of item- and scale-level performance.
Item response theory is a useful tool because it can help identify (i) the best items to use based on the purpose of a measure, (ii) where along the underlying trait continuum an item, as well as the overall measure, performs best, and (iii) measure equivalence across different subgroups.
Item response theory provides the theoretical and computational underpinning that drives computerized adaptive testing (CAT) applications (e.g. Graduate Record Examinations [GRE]); and has recently been used to develop computerized adaptive tests for patient-reported outcome domains. This technology allows for the ability to field fewer questions to participants without loss of measurement precision, and the possibility for data comparison across studies.
Broader understanding of item response theory and its applications can lead to increased utilization of this measurement framework, and ultimately improve the quality of patient-reported outcome measures.
Acknowledgments
This work was not externally funded.
Footnotes
None of the authors have any conflicts of interest, perceived or real, relevant to this paper.
Contributor Information
Tam H. Nguyen, Boston College, Connell School of Nursing, 140 Commonwealth Avenue Cushing Hall, #336C, Chestnut Hill, MA 02467, USA
Hae-Ra Han, School of Nursing, Johns Hopkins University, 525 North Wolfe Street, #526, Baltimore, MD 21205, USA.
Miyong T. Kim, School of Nursing, The University of Texas at Austin, 1710 Red River, NUR 5.141, Austin, TX 78701, USA
Kitty S. Chan, Email: kchan@jhsph.edu, Department of Health Policy and Management, Bloomberg School of Public Health, Johns Hopkins University, 624 N. Broadway, #633, Baltimore, MD 21205, USA
References
- 1.Brook RH, Ware JE, Jr, Davies-Avery A, Stewart AL, Donald CA, Rogers WH, et al. Overview of adult health measures fielded in Rand’s health insurance study. Med Care. 1979;17(7 Suppl):iii–x. 1–131. [PubMed] [Google Scholar]
- 2.Willke RJ, Burke LB, Erickson P. Measuring treatment impact: a review of patient-reported outcomes and other efficacy endpoints in approved product labels. Control Clin Trials. 2004;25(6):535–52. doi: 10.1016/j.cct.2004.09.003. [DOI] [PubMed] [Google Scholar]
- 3.Darzi L. High quality care for all: NHS Next Stage Review final report. 2008. Contract No. [Google Scholar]
- 4.Selby JV. The patient-centered outcomes research institute: a 2013 agenda for “research done differently”. Popul Health Manag. 2013;16(2):69–70. doi: 10.1089/pop.2013.1621. [DOI] [PubMed] [Google Scholar]
- 5.Speight J, Barendse SM. FDA guidance on patient reported outcomes. BMJ. 2010;340:c2921. doi: 10.1136/bmj.c2921bmj.c2921. [DOI] [PubMed] [Google Scholar]
- 6.Gulliksen H. Theory of mental tests. New York: Wiley; 1950. [Google Scholar]
- 7.Hambleton RK. Emergence of item response modeling in instrument development and data analysis. Med Care. 2000;38(9 Suppl):II60–5. doi: 10.1097/00005650-200009002-00009. [DOI] [PubMed] [Google Scholar]
- 8.Nunnally JC. Psychometric theory. New York: McGraw Hill; 1967. [Google Scholar]
- 9.Embretson SE. The new rules of measurement. Psychol Assess. 1996;8(4):341–9. [Google Scholar]
- 10.Hambleton RK, Jones RW. Comparison of classical test theory and item response theory and their applications to test development. Instructional Topics in Educational Measurement. 1993:38–47. [Google Scholar]
- 11.Hambleton RK, Swaminathan H, Rogers WH. Fundamentals of item response theory. Newbury Park: Sage Publications; 1991. [Google Scholar]
- 12.Brennan RL, editor. Educational measurement. 4. Westport: Praeger Publishers; 2006. [Google Scholar]
- 13.van der Linden WJ, Hambleton RK. Handbook of modern item response theory. New York: Springer; 1997. [Google Scholar]
- 14.Holland PW, Wainer H. Differential item functioning. Hillsdale: Lawrence Erlbaum Associates; 1993. [Google Scholar]
- 15.Reeve BB. An introduction to modern measurement theory. National Cancer Institute; 2002. [Google Scholar]
- 16.Baker F. The basis of item response theory. 2. College Park: ERIC Clearinghouse on Assessment and Evaluation; 2001. [Google Scholar]
- 17.Lord FM. The relation of test score to the trait underlying the test. Educ Psychol Meas. 1953;13:517–48. [Google Scholar]
- 18.Birnbaum A. Part 5: some latent trait models and their use in inferring an examinee’s ability. In: Lord FM, Novick MR, editors. Statistical theories of mental test scores. Reading: Addison-Wesley; 1968. [Google Scholar]
- 19.Rasch G. Probabilistic models for some intelligence and attainment tests. Chicago: MESA; 1960. [Google Scholar]
- 20.Reeve BB, Fayers P. Applying item response theory modeling for evaluating questionnaire item and scale properties. In: Fayers P, Hays RD, editors. Assessing quality of life in clinical trials: methods of practice. 2. Oxford: Oxford University Press; 2005. pp. 55–73. [Google Scholar]
- 21.Embretson SE, Reise SP. Item response theory for psychologists. Mahwah: Lawrence Erlbaum Associates; 2000. [Google Scholar]
- 22.Samejima F. Estimation of latent ability using a response pattern of graded scores. Psychom Monogr. 1969;34(17 Suppl):386–415. [Google Scholar]
- 23.Andrich D. A rating formulation for ordered response categories. Psychometrika. 1978;43:561–73. [Google Scholar]
- 24.Masters GN. A Rasch model for partial credit scoring. Psychometrika. 1982;47:149–74. [Google Scholar]
- 25.Muraki E. A generalized partial credit model: application of an EM algorithm. Appl Psychol Meas. 1992;17:159–76. [Google Scholar]
- 26.Bock RD. Estimating item parameters and latent ability when responses are scored in two or more nominal categories. Psychometrika. 1972;37:29–51. [Google Scholar]
- 27.Reckase M. Unifactor latent trait models applied to multifactor tests: results and implications. J Educ Stat. 1979;4:207–30. [Google Scholar]
- 28.Hattie J. Methodology review: assessing unidimensionality of tests and items. Appl Psychol Meas. 1985;9:139–64. [Google Scholar]
- 29.Stout W. A nonparametric approach for assessing latent trait unidimensionality. Psychometrika. 1987;52:589–617. [Google Scholar]
- 30.Gessaroli M, DeChamplain A. Using an approximate Chi-square statistic to test the number of dimensions underlying the responses to a set of items. J Educ Meas. 1996;33:157–79. [Google Scholar]
- 31.Reise SP. Item response theory and its applications for cancer outcomes measurement. In: Lipscomb J, Gotay CC, Snyder C, editors. Outcomes assessment in cancer: measures, methods, and applications. Cambridge: Cambridge University Press; 2004. pp. 425–44. [Google Scholar]
- 32.Smith AB, Rush R, Fallowfield LJ, Velikova G, Sharpe M. Rasch fit statistics and sample size considerations for polytomous data. BMC Med Res Methodol. 2008;8:33. doi: 10.1186/1471-2288-8-33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Smith RM, Plackner C. The family approach to assessing fit in Rasch measurement. J Appl Meas. 2009;10(4):424–37. [PubMed] [Google Scholar]
- 34.Bond TG, Fox CM. Applying the Rasch model: fundamental measurement in the human sciences. Hillsdale: Lawrence Erlbaum Baum Associates; 2001. [Google Scholar]
- 35.Wright BD, Mead J. Research Memorandum No. 23. Chicago: University of Chicago, Department of Education, Statistical Laboratory; 1977. BICAL: calibrating items and scales with the Rasch model. [Google Scholar]
- 36.Orlando M, Thissen D. Likelihood-based item-fit indices for dichotomous item response theory models. Appl Psychol Meas. 2000;24(1):50–64. [Google Scholar]
- 37.McLeod LD, Swygert KA, Thissen D. Factor analysis for items scored in two categories. In: Thissen D, Wainer H, editors. Test scoring. Mahwah: Lawrence Earlbaum & Associates; 2001. [Google Scholar]
- 38.Haley SM, McHorney CA, Ware JE., Jr Evaluation of the MOS SF-36 physical functioning scale (PF-10): I. Unidimensionality and reproducibility of the Rasch item scale. J Clin Epidemiol. 1994;47(6):671–84. doi: 10.1016/0895-4356(94)90215-1. (pii: 0895-4356(94)90215-1) [DOI] [PubMed] [Google Scholar]
- 39.Edelen MO, Reeve BB. Applying item response theory (IRT) modeling to questionnaire development, evaluation, and refinement. Qual Life Res. 2007;16(Suppl 1):5–18. doi: 10.1007/s11136-007-9198-0. [DOI] [PubMed] [Google Scholar]
- 40.Looveer J, Mulligan J. The efficacy of link items in the construction of a numeracy achievement scale—from kindergarten to year 6. J Appl Meas. 2009;10:247–65. [PubMed] [Google Scholar]
- 41.Linacre JM. Sample size and item calibration stability. Rasch Meas Trans. 1994;7(4):328. [Google Scholar]
- 42.Tsutakawa RK, Johnson JC. The effect of uncertainty of item parameter estimation on ability estimates. Psychometrika. 1990;55:371–90. [Google Scholar]
- 43.Orlando M, Marshall GN. Differential item functioning in a Spanish translation of the PTSD checklist: detection and evaluation of impact. Psychol Assess. 2002;14(1):50–9. doi: 10.1037//1040-3590.14.1.50. [DOI] [PubMed] [Google Scholar]
- 44.Thissen D, Steinberg L, Gerrard M. Beyond group mean differences: the concept of item bias. Psychol Bull. 1986;99(1):118–28. [Google Scholar]
- 45.Kim MT, Song HJ, Han HR, Song Y, Nam S, Nguyen TH, et al. Development and validation of the high blood pressure-focused health literacy scale. Patient Educ Couns. 2012;87(2):165–70. doi: 10.1016/j.pec.2011.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Spitzer RL, Kroenke K, Williams JB. Validation and utility of a self-report version of PRIME-MD: the PHQ primary care study. Primary Care Evaluation of Mental Disorders. Patient Health Questionnaire. JAMA. 1999;282(18):1737–44. doi: 10.1001/jama.282.18.1737. (pii: joc90770) [DOI] [PubMed] [Google Scholar]
- 47.Kroenke K, Spitzer RL, Williams JB. The PHQ-9: validity of a brief depression severity measure. J Gen Intern Med. 2001;16(9):606–13. doi: 10.1046/j.1525-1497.2001.016009606.x. (pii: jgi01114) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc. 1995;57:289–300. [Google Scholar]
- 49.Chen WH, Thissen D. Local dependance indices for item pairs using item response theory. J Educ Behav Stat. 1997;22:265–89. [Google Scholar]
- 50.Stucki G, Daltroy L, Katz JN, Johannesson M, Liang MH. Interpretation of change scores in ordinal clinical scales and health status measures: the whole may not equal the sum of the parts. J Clin Epidemiol. 1996;49(7):711–7. doi: 10.1016/0895-4356(96)00016-9. (pii: 0895-4356(96) 00016-9) [DOI] [PubMed] [Google Scholar]
- 51.Ware JE, Bjorner JB, Kosinski M. Practical implications of item response theory and computerized adaptive testing: a brief summary of ongoing studies of widely used headache impact scales. Med Care. 2000;38(9 Suppl):II73–82. [PubMed] [Google Scholar]
- 52.Cella D, Nowinski C, Peterman A, Victorson D, Miller D, Lai JS, et al. The neurology quality-of-life measurement initiative. Arch Phys Med Rehabil. 2011;92(10 Suppl):S28–36. doi: 10.1016/j.apmr.2011.01.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Cella D, Yount S, Rothrock N, Gershon R, Cook K, Reeve B, et al. The Patient-Reported Outcomes Measurement Information System (PROMIS): progress of an NIH Roadmap cooperative group during its first two years. Med Care. 2007;45(5 Suppl 1):S3–11. doi: 10.1097/01.mlr.0000258615.42478.55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Cella D, Riley W, Stone A, Rothrock N, Reeve B, Yount S, et al. The Patient-Reported Outcomes Measurement Information System (PROMIS) developed and tested its first wave of adult self-reported health outcome item banks: 2005–2008. J Clin Epidemiol. 2010;63(11):1179–94. doi: 10.1016/j.jclinepi.2010.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Salsman JM, Victorson D, Choi SW, Peterman AH, Heinemann AW, Nowinski C, et al. Development and validation of the positive affect and well-being scale for the neurology quality of life (Neuro-QOL) measurement system. Qual Life Res. 2013 doi: 10.1007/s11136-013-0382-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Muraki E, Bock RD. PARSCALE 4 for windows: IRT based test scoring and item analysis for graded items and rating scales [Computer software] Skokie: Scientific Software International, Inc; 2003. [Google Scholar]
- 57.Thissen D, Chen WH, Bock RD. MULTILOG 7 for windows: multiple-category item analysis and test scoring using item response theory [Computer software] Skokie: Scientific Software International, Inc; 2003. [Google Scholar]
- 58.Muthén LK, Muthén BO. Mplus user’s guide. Los Angeles: Muthén & Muthén; 2011. [Google Scholar]
- 59.Cai L, Thissen D, du Toit S. IRTPRO 2.1 for Windows: Item response theory for patient-reported outcomes [Computer software] Lincolnwood: Scientific Software International, Inc; 2011. [Google Scholar]
- 60.Zimowski MF, Muraki E, Mislevy RJ, Bock RD. BILOG-MG 3 for windows: multiple-group IRT analysis and test maintenance for binary items [Computer software] Skokie: Scientific Software International, Inc; 2003. [Google Scholar]
- 61.Houts CR, Cai L. flexMIRT version 1.88: a numerical engine for multilevel item factor analysis and test scoring [Computer software] Seattle: Vector Psychometric Group; 2012. [Google Scholar]
- 62.RUMM Laboratory Pty Ltd. RUMM2030 [Computer software] Perth: RUMM Laboratory Pty Ltd; 2012. [Google Scholar]
- 63.Linacre JM. Winsteps version 3.80.0 [Computer Software] Beaverton: Winsteps.com; 2013. [Google Scholar]
- 64.StataCorp. Stata Statistical Software: Release 13. College Station: StataCorp LP; 2013. [Google Scholar]
- 65.Rizopoulos D. ltm: an R package for latent variable modelling and item response theory analyses. J Stat Softw. 2006;17:1–25. [Google Scholar]
- 66.Mair P, Hatzinger R, Maier MJ. eRm: extended rasch modeling. R package version 0.15-1. 2012 http://CRAN.R-project.org/package=eRm.
- 67.Childs RA, Chen WH. Obtaining comparable item parameter estimates in MULTILOG and PARSCALE for two polytomous IRT models. Appl Psychol Meas. 1999;23:371–9. [Google Scholar]
- 68.Paek I, Han KT. IRTPRO 2.1 for windows (item response theory for patient-reported outcomes) Appl Psychol Meas. 2013;37(3):242–52. [Google Scholar]