Abstract
Purpose
To investigate the feasibility and potential clinical benefit of linear energy transfer (LET) guided plan optimization in intensity-modulated proton therapy (IMPT).
Methods and Materials
A multi-criteria optimization (MCO) module was utilized to generate series of Pareto-optimal IMPT base plans (BPs), corresponding to defined objectives, for 5 headand- neck and 2 pancreatic cancer cases. A Monte Carlo platform was used to calculate dose and LET distributions for each BP. A custom-designed MCO navigation module allowed the user to interpolate between BPs to produce deliverable Pareto-optimal solutions. Differences among the BPs, were evaluated for each patient, based on dose- and LET-volume histograms and 3D distributions. An LET-based RBE (relative biological effectiveness) model was employed to evaluate the potential clinical benefit when navigating the space of Pareto-optimal BPs.
Results
Mean LET values for the target varied up to 30% among the BPs for the head-and-neck cases, and up to 14% for the pancreatic cancer cases. Variations were more prominent in organs-atrisk (OARs), where mean LET values differed by up to a factor of 2 among the BPs for the same patient. An inverse relation between dose and LET distributions for the OARs was typically observed. Accounting for LET-dependent variable RBE values, a potential improvement on RBE weighted dose of up to 40%, averaged over several structures under study, was noticed during MCO navigation.
Conclusions
We present a novel strategy for optimizing proton therapy to maximize doseaveraged LET in tumor targets while simultaneously minimizing dose-averaged LET in normal tissue structures. MCO BPs show substantial LET variations, leading to potentially significant differences in RBE-weighted doses. Pareto-surface navigation, utilizing both dose and LET distributions for guidance, provides the means for evaluating a large variety of deliverable plans, and aids in identifying the clinically optimum solution.
Keywords: Linear energy transfer, radiobiological optimization, intensity modulated proton therapy
Introduction
The relative biological effectiveness (RBE) of proton beams relative to photon beams is currently approximated clinically with a constant value of 1.1[1]. The use of variable RBE as a function of dose, endpoint, and linear energy transfer (LET) is hindered due to considerable model uncertainties for clinically relevant tissues, mostly due to the lack of data to extract accurate α/β values, included in RBE models. Reported α/β values for many tissue types are often accompanied by more than 50% uncertainty[2], rendering biological optimization for intensity modulated proton therapy (IMPT) based on RBE modeling subject to similar inaccuracies. However, several in vivo and in vitro studies demonstrated that for a given endpoint and for dose and energy ranges used clinically, the RBE values in proton therapy show a linear dependence on LET[1, 2]. Unlike biological parameters, physical quantities, such as LET, can be predicted with high accuracy. Calculation of threedimensional (3D) LET distributions in patients is possible through Monte Carlo simulation for any patient geometry and delivery technique (e.g., passive scattering, pencil beam scanning). Previous work by Grassberger et al[3] has shown that different IMPT planning techniques may yield equivalent dose distributions, yet distinctly different LET distributions.
Following these considerations, in our current work we investigate the differences in LET distributions among various treatment plans for the same planning technique (3D-IMPT). We examine the feasibility of LET-guided optimization, as an indirect RBE optimization, by influencing the LET distributions. Our basic hypothesis is that, in addition to the physical dose considerations, minimizing LET in the organs-at-risk (OARs), can lead to a potential clinical benefit. This technique may be especially substantial for organs with low α/β values, for which radiobiological effectiveness shows a higher dependence on the LET of the radiation used[2]. We demonstrate how this strategy can be incorporated in optimizing treatment plans for proton therapy patients.
Materials and Methods
Patient selection and treatment planning
Seven patients, previously treated with 3D-conformal proton therapy, were selected: five headand- neck (H&N) cases and two pancreatic cancer (PC) cases. Prescriptions varied between 50.4 and 59.4 Gy(RBE) (1.8 Gy/fraction) for brain and H&N, and 25 Gy(RBE) (5 Gy/fraction) for PC, where Gy(RBE) is the unit for the relative biological effective dose. A RBE value of 1.1 is used for the clinical prescription doses reported in this sub-section. A multi-criteria optimization (MCO)[4] inhouse treatment planning system (TPS), Astroid, generated a series of base plans (BPs) for IMPT, using the same beam configuration as the clinical plans. Each of BPs emphasized a specific planning objective. By design, MCO BPs are Pareto-optimal, meaning that if a plan could be improved by one measure, it would get worse by others. Typically 12–23 BPs are pre-calculated. During the planning process, intermediate solutions are created by interpolation. The MCO environment allows the user to navigate the multi-dimensional Pareto-space defined by the BPs, in order to find the most suitable solution.
Optimized plans were generated for two different beam spot sizes (σ-sigma at the isocenter in air of ~12 and ~3mm - σ is the standard deviation of the Gaussian distribution representing beam’s spot shape), being the two extremes currently used at scanning centers. Spot spacing was equal to one σ for all proton energies and spot sizes. Hard constraints for the target used in the optimization process limited the dose deviation in every voxel to no more than 10% of the prescription dose. Optimization objectives included: minimize maximum, maximize minimum and mean dose to the target, minimize mean dose to the OARs.
Multi-objective LET optimization
The proton fluence files from Pareto-optimal BPs were imported into TOPAS (Tool for PArticle Simulation)[5] Monte Carlo system, which calculated both dose and LET distributions for each plan. Monte Carlo parameters, cross-sections for physics processes used and associated uncertainties in this Geant4-based platform can be found in the papers by Perl et al[5] and Zacharatou et al[6]. Detailed description of the LET scoring method is included in the work by Grassberger et al[3]. The difference in the present study is that reported doses were scored as dose-to-water [7]. LET values were scored as LET per tissue density in each voxel, having a unit of keV/μm/(g/cm3), equal to keV m2/g. Less than 2% statistical uncertainty is associated with dose and LET calculation throughout this study. A CERR (computational environment for radiotherapy research) -based in-house module[8] was developed allowing the user to navigate the Pareto-space defined by the BPs, by modifying the relative weights for each objective, through objective-specific sliders. Dose and LET distributions and volume histograms are displayed for each navigated location, to facilitate the decision making process. For navigated plans, the dose distributions are given as a weighted linear combination of several BPs, and the LET distribution is calculated as a dose-weighted average:
| (1) |
where LETd is the dose-weighted LET distribution for the current navigated plan, Di, LETd,i and wi are the 3D dose distribution, LET distribution and relative weight, respectively, for the ith BP used in the current navigated plan. Differences between individual plans were evaluated by comparing dose-volume and LET-volume histogram (DVHs and LET-VHs) parameters:
V100: Target volume covered by the prescription dose.
Dmean: Mean dose to a structure.
LETmean: Mean LET value to a structure.
LETmedian: Median LET value to a structure (LET value recorded by 50% of the voxels of the structure).
The relative variation of each dose-volume index among the BPs was estimated by
| (2) |
where MaxIndex, MinIndex and MeanIndex are the maximum, minimum and mean values for a specific index, among the BPs. Relative variations in LET and dose-volume parameters were evaluated in order to estimate the potential benefit when navigating the Pareto-surface.
RBE model
While our main goal is to incorporate LET as a physical surrogate of biological effect in treatment planning independent of RBE, an LET-based RBE model[2] was used to evaluate the potential clinical impact of LET variations. Although other OARs were considered in the plan optimization process, due to the scarcity of accurate values for the α/β ratio in the literature, the OARs included in the RBE-based evaluation for the H&N patients (H&N 1–5) were the brainstem and chiasm, and for the pancreatic cases (PC 1–2) were the liver, left and right kidneys and stomach. RBE values were calculated for every voxel in the specified dose grid, using the LET-based RBE model by Carabe et al[2]. Accordingly, the RBE-weighted dose (DRBE) was obtained as a voxel-based multiplication of RBE and physical dose. The mean RBE and DRBE values for each structure were obtained as an average over the voxels inside the structure’s contour.
Results
Plan interpolation
The accuracy of dose-weighted interpolation of LET distributions, when navigating between BPs, was tested by comparing the results of two methods of LET calculation for the same combination of BPs. In the first method, the fluence maps of the navigated combination plan were exported directly from the TPS, and the LET distribution was calculated via TOPAS. In the second method, the LET distributions were calculated separately for each BP and scaled according to their contribution to the navigated plan; the LET distribution of the navigated plan was then calculated as their dose130 weighted average (Eq. 1). The difference between the two obtained LET distributions was examined using a voxel-by-voxel analysis. Accounting for all voxels receiving at least 1% of the prescription dose, an average LET difference of 0.03 keV m2/g (standard deviation of 0.05 keV m2/g) was noticed, corresponding to 1.7% of the average LET value (1.6 keV m2/g ±1.4 keV m2/g).
After verifying the accuracy of our interpolation method for the LET distributions, in the following sections we examine the range of values for dosimetric and radiobiological indexes while navigating among the extreme points in the Pareto-space, the BPs.
LET based MCO
Shown in figure 1 are the dose and LET distributions for a pediatric chordoma case. Due to its irregularly shaped tumor, and proximity to the OARs, this case is considered a good candidate where the LET distribution at the edges of the tumor could have a clinical impact, and plan optimization considering the combination of dose and LET for the OARs may be clinically useful. All BPs delivered the prescription dose to more than 90% of the target, resulting in mean target dose above the prescription, which differed by less than 2Gy between different BPs due to various degree of homogeneity. However, significant differences between corresponding LET distributions were noticed, as marked in the figure (brainstem median LET 3.1 versus 4.2keV m2/g).
Figure 1.
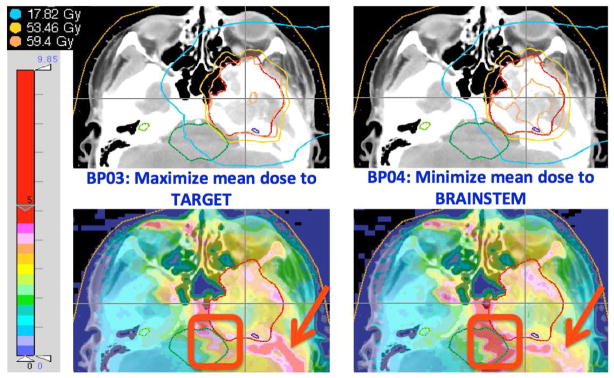
Dose (upper) and LET (lower) distributions for two different BPs for a pediatric chordoma case. The red squares and arrows emphasize differences in LET distributions between the two plans that both provide adequate dose coverage. The colorbar on the left represents the scale for LET values.
Figure 2a shows the variation of LET volume histograms among different BPs for patient H&N4 and large spot size. LETmean values, calculated for a variety of structures, BPs and both beam spot sizes for the H&N patients, are presented in Figure 2b. The height of the individual bars correspond to the LETmean value of a specific structure, averaged over the various BPs, and the error-bars demonstrate its minimum and maximum values over the variety of BPs. Substantial variations in LETmean values were observed especially for structures having lower α/β values, like the brainstem and chiasm for the H&N cases under study (brainstem LETmean values for H&N2 case, for the 3mm beam spot, varied from 1.9 to 8.1keV m2/g among the BPs).
Figure 2.
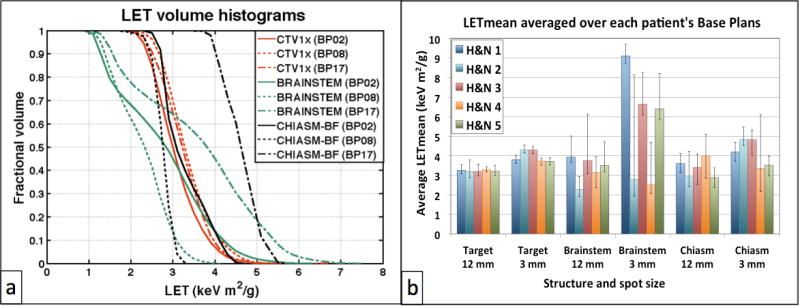
(a) Variation of LET distributions for different base plans (BP) and structures for patient H&N4. BP02: Maximize minimum dose to Target; BP08: Minimize mean dose to left Cochlea; BP17: Mixed balanced base plan. (b) Variation of LETmean values for all H&N cases: bars represent LETmean values averaged over the BPs for each structure, patient and spot size; error bars demostrate minimum and maximum values among BPs.
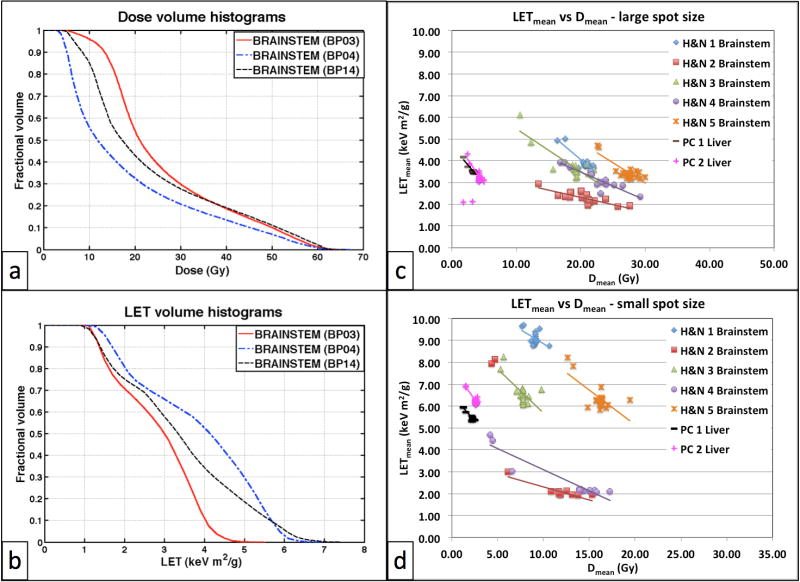
It was observed that BPs giving on average the lowest dose to a structure resulted in its highest LET-VH, and vice versa, as shown in figure 3 (a–b). Consider BP04, which was generated with the objective to minimize the mean dose to the brainstem. While resulting in the lowest DVH (blue line – Figure 3a) compared to BPs optimized for other objectives, as expected, this plan gives rise to the highest LET-VH. This inverse relation between dose and LET distributions holds for all structures under study, and for both spot sizes considered, as shown in figure 3 (c–d) where the LETmean is plotted versus the mean dose for all BPs, spot sizes and patients, for the two structures where this effect was most significant, the brainstem and liver.
Figure 3.
(a) DVH and (b) LET-VH in the brainstem for a representative head-and-neck patient case (H&N4 – spot size of 12 mm) from various base plans: BP03 (maximize mean dose to target), BP04 (minimize mean brainstem dose), BP14 (minimize mean dose to chiasm - balanced). Each data point in figures (c) and (d) corresponds to a base plan of the referenced patient. The lines in figures (c) and (d) are showing the trend. BP: Base Plan, LET: Linear Energy Transfer, H&N: Head & Neck patient, PC: Pancreatic Cancer patient.
Thus, in IMPT, optimizing to OAR dosimetric constraints is achieved by using the distal edge to conform the beam, yielding higher LET values, a fact currently not considered in treatment planning. The question becomes whether a decrease in (mean) dose to an OAR may be negated by an increase in (mean) LET and the associated expected increase in biological effect. In order to answer this question we analyzed the RBE-weighted dose in correlation with the LET and physical dose for each structure.
Consideration of RBE-weighted dose
Variations in LETmean and RBEmean values among the BPs were calculated for all structures and spot sizes based on equation 2. LETmean and RBEmean values were associated with less than 0.1% statistical uncertainty. Since we study relative differences among BPs, uncertainties associated with patient tissue composition do not impact our results and are therefore not reported in the tables.
Utilizing the large beam spot, up to 81% variations (as calculated from equation 2) on LETmean values were observed for the brainstem (range from 3.08 to 6.12 keV m2/g), with reference to the average LETmean (3.75 keV m2/g) value calculated over the set of BPs for the corresponding patient. Accordingly, up to 38% variations on RBEmean values (average of 1.42, ranging from 1.32 to 1.85) for the same structure (Table 1) were observed. Higher variations were noticed for some patient cases for the small beam spot: up to 222% (average of 2.78 keV m2/g, ranging from 1.94 to 8.13 keV m2/g) on LETmean, associated with 75% variations on RBEmean values (average of 1.31, ranging from 1.18 to 2.17) for the brainstem structure. Smaller variations overall were observed for the PC cases, where the liver showed the highest variation in RBEmean values among BPs (32%, average value of 1.71, ranging from 1.36 to 1.92). Note, however, that RBE values, calculated according to the model by Carabe et al.[2], depend on both LET and dose values for each voxel.
Table 1.
Variations of mean LET and mean RBE values among BPs for head-and-neck (H&N) and pancreatic cancer (PC) patients, as calculated by Equation 2.
| patient | Spot Size | Target (α/β = 12 Gy) | Brainstem (α/β = 2.1 Gy) | Chiasm (α/β = 2.9 Gy) | |||
|---|---|---|---|---|---|---|---|
|
| |||||||
| LETmean variation | RBEmean variation | LETmean variation | RBEmean variation | LETmean variation | RBEmean variation | ||
| H&N1 | Large | 15.0% | 1.3% | 34.5% | 18.3% | 27.2% | 4.9% |
| Small | 11.5% | 1.2% | 10.5% | 8.3% | 22.8% | 4.9% | |
| H&N2 | Large | 28.5% | 2.5% | 45.5% | 13.9% | 61.9% | 9.7% |
| Small | 9.5% | 1.1% | 221.6% | 74.9% | 19.5% | 4.7% | |
| H&N3 | Large | 18.6% | 1.7% | 80.9% | 37.8% | 45.8% | 8.2% |
| Small | 8.9% | 1.0% | 32.8% | 20.7% | 27.0% | 6.5% | |
| H&N4 | Large | 8.3% | 0.8% | 50.0% | 16.4% | 56.3% | 13.1% |
| Small | 9.8% | 1.0% | 103.0% | 37.3% | 117.2% | 31.2% | |
| H&N5 | Large | 16.4% | 1.4% | 43.9% | 16.3% | 35.0% | 6.0% |
| Small | 10.3% | 1.0% | 37.3% | 19.6% | 28.9% | 5.3% | |
| PTV (α/β = 9.8 Gy) | Liver (α/β = 1.5 Gy) | Lt Kidney (α/β = 3.0 Gy) | Rt Kidney (α/β = 3.0 Gy) | Stomach (α/β = 8.5 Gy) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||
| LETmean variation | RBEmean variation | LETmean variation | RBEmean variation | LETmean variation | RBEmean variation | LETmean variation | RBEmean variation | LETmean variation | RBEmean variation | ||
| PC1 | Large | 7.9% | 0.5% | 61.3% | 32.4% | 25.0% | 2.9% | 36.3% | 5.8% | 26.2% | 2.6% |
| Small | 1.2% | 0.3% | 11.7% | 7.5% | 14.4% | 3.6% | 23.4% | 7.7% | 7.3% | 1.0% | |
| PC2 | Large | 14.3% | 0.8% | 38.1% | 16.2% | 35.3% | 4.2% | 60.5% | 9.3% | 58.0% | 7.1% |
| Small | 5.1% | 0.5% | 13.9% | 8.3% | 22.2% | 6.1% | 54.1% | 17.4% | 19.0% | 4.2% | |
Case H&N4 (Figure 1) may illustrate the potential clinical significance of utilizing LET-guided navigation. Navigating from BP03 (maximize minimum target dose) to BP04 (minimize brainstem dose) for this patient (large beam spot) the brainstem Dmean decreased by 35%, while LET increased by 30%, moderating the decrease in the mean DRBE to 24%. Assuming constant RBE value, instead of the variable LET-dependent value, the decrease in mean RBE-weighted dose would equal the decrease in physical dose. That would be a misleading overestimation of the sparing of this OAR.
Relationship between variations in mean LET and RBE-weighted dose
Due to the variety of patient geometries and prescription doses, it is not possible to obtain a single direct correlation between the absolute values of DRBE,mean and LETmean (Figure 3c and d) that would be independent of patient cases. However it appears feasible to predict the relative change in mean DRBE between two BPs for a specific structure and beam spot size, based on their respective difference in mean LET and physical dose D. Figure 4 displays relative differences, between all pairs of consecutively numbered BPs, in the LETmean and Dmean versus DRBE,mean values, for all patients. The differences are normalized to the respective average LETmean, Dmean, DRBE,mean for all BPs for each patient. The data (plotted in figure 4) was analyzed separately for each spot size and structure, since RBE strongly depends on the (α/β)X value[2]. A linear regression analysis was applied to obtain a relation represented by
Figure 4.
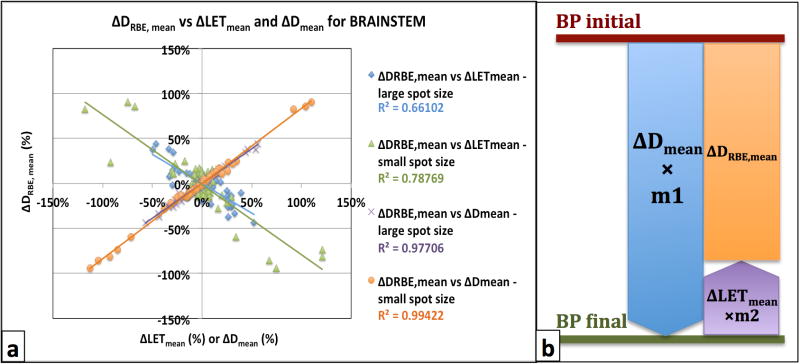
(a) Plot showing how differences in mean RBE-weighted doses (ΔDRBE, mean) correlate with differences in mean LET (ΔLETmean) and mean Dose (ΔDmean) values for both beam spot sizes (large: 12mm on average, small: 3mm on average). The R2 values on the legend represent the coefficient of determination for each set of data. (b) Schematic diagram of equation 3 accounting for the inverse correlation between ΔDmean and ΔLETmean.
| (3) |
Figure 4b demonstrate the physical meaning of equation 3, accounting for the inverse relation between ΔDmean and ΔLETmean: the LETmean difference between two plans is weighted by m2 and subtracted from the Dmean difference to result in the final DRBE,mean gain. The values for all parameters in equation 3, for each structure and spot size, are shown in Table 2. The normalized values for m2 are with reference to m1 and represent the contribution of the ΔLETmean to the final ΔDRBE,mean, as a measure of potential error associated with the assumption of constant RBE. Table 2 also shows the coefficient of determination R2, indicating how well the equation resulting from the regression analysis explains the relationship among the variables, ranging from 0 (poor correlation) to 1 (excellent correlation).
Table 2.
Parameters derived from the linear regression analysis on the correlation among ΔDmean, ΔLETmean and ΔDRBE, mean values among the BPs for all patients and for the two beam spot sizes (see Equation 5).
| Spot Size | Structure | m1 | m2 | Normalized values | R2 | (α/β)Χ [Gy] | |
|---|---|---|---|---|---|---|---|
| m1 | m2 | ||||||
| 12 mm | H&N Target | 1.024± 0.001 | (9.11± 0.04)×10−2 | 1.00 | 0.09 | 1.000 | 12.0 |
| PC Target | 1.035± 0.001 | (5.49± 0.04)×10−2 | 1.00 | 0.05 | 1.000 | 9.8 | |
| Stomach | 0.975± 0.008 | 0.047± 0.005 | 1.00 | 0.05 | 0.999 | 8.5 | |
| Kidneys | 1.030± 0.005 | 0.17± 0.01 | 1.00 | 0.17 | 1.000 | 3.0 | |
| Chiasm | 0.958± 0.008 | 0.178± 0.002 | 1.00 | 0.19 | 0.995 | 2.9 | |
| Brainstem | 0.95± 0.02 | 0.21± 0.02 | 1.00 | 0.22 | 0.992 | 2.1 | |
| Liver | 0.914± 0.005 | 0.024± 0.007 | 1.00 | 0.02 | 0.999 | 1.5 | |
|
| |||||||
| 3 mm | H&N Target | 1.018± 0.001 | 0.109± 0.001 | 1.00 | 0.11 | 1.000 | 12.0 |
| PC Target | 1.032± 0.000 | (6.31± 0.08)×10−2 | 1.00 | 0.06 | 1.000 | 9.8 | |
| Stomach | 0.97± 0.01 | 0.04± 0.02 | 1.00 | 0.04 | 0.998 | 8.5 | |
| Kidneys | 0.994± 0.005 | 0.08± 0.02 | 1.00 | 0.08 | 1.000 | 3.0 | |
| Chiasm | 0.896± 0.005 | 0.202± 0.004 | 1.00 | 0.22 | 0.999 | 2.9 | |
| Brainstem | 0.82± 0.02 | −0.02± 0.02 | 1.00 | −0.02 | 0.996 | 2.1 | |
| Liver | 0.972± 0.009 | 0.10± 0.04 | 1.00 | 0.10 | 1.000 | 1.5 | |
According to literature on RBE models[2, 9], higher dependence on LET variations is expected for lower (α/β)X values. This inverse relation should be demonstrated by increased m2 values (normalized) for structures with lower (α/β)X values, within the same treatment site and spot size. Results on H&N plans and large beam spot agree with this observation, as shown by the m2 and (α/β)X values for the H&N target, chiasm and brainstem structures (Table 2). Exceptions from this rule were noticed for the H&N plans and small beam spot, where the normalized m2 value for the brainstem (−0.02) was found to be much smaller than the one for chiasm (0.22).
Discussion
We present a novel strategy for optimizing proton therapy using dose-weighted-LET as surrogate for RBE. Utilizing calculated LET-distributions, after dose-based MCO optimization, we demonstrated that treatment plans having equivalent dose distributions, in terms of target coverage, could show substantial difference in the underlying LET distributions in proton therapy. Thus, taking the LET into consideration has the potential to enhance treatment plan optimization. In MCO the user is able to select a point in the Pareto-space, utilizing both dose and LET distributions for guidance.
When comparing LETmean values for the same structure and patient case between plans using different beam spot size, higher LET values were noticed when a smaller spot size (3 mm) was used. This can be observed by comparing the figures 3c and 3d, where the LETmean values are higher in the case of the smaller spot size, corresponding to narrower penumbra and lower Dmean in OARs. The smaller the spot size is, the higher is the number of beam spots utilized per volume, and the higher is the dose conformity achievable due to increased degrees of freedom (weights for the beam spots) in the optimization. This leads to a larger share of protons stopping closer to the outer surface of the target, and inside the sensitive structures such as the brainstem, optic chiasm and liver, in our study, having a higher contribution in LET values in these regions.
Navigating the dose-optimized Pareto space, a trade-off between low doses and low LET values for the OARs was observed indicating the need for a method to gauge the relative importance of dose and LET to the clinical outcome of the patient. Substantial RBE variations among BPs for all patients considered in this study were associated with substantial variations in LETmean values, along with variations in dose. Higher dependence of RBE on LET values was noticed for structures having lower values of (α/β)X, indicating the potentially higher relevance of LET-guided optimization in these cases. This observation is in agreement with other studies[1, 9] and is implied by the RBE model used for the calculations in our study[2]. A linear relationship was established, through linear regression analysis, that allows estimating the effect on mean RBE-weighted dose, DRBE,mean, based on the known Dmean and LETmean for a specific structure. Differences in LETmean values translate in proportion of up to 20% to the difference in DRBE,mean between two plans, as shown by the normalized m1 and m2 values in Table 2. With figure 4b as reference, since a decrease in Dmean is correlated with an increase in LETmean, ignoring the LET distribution in optimization may lead to an overestimation of dose decrease in the OARs by up to 22%.
In this study, the beam directions used in clinical 3D-conformal treatments were used. LET distribution could be further influenced by optimizing the beam angles in order to minimize the number of protons stopping inside a sensitive structure, and moderate the high LET associated with the end of range. Future studies can also include an a-priori hybrid optimization, including both dose and LET-based objectives, to study the method’s feasibility and examine if a trade-off between low doses and low LET values would still exist.
Summary.
A novel multi-criteria optimization strategy for intensity modulated proton therapy (IMPT) is suggested, utilizing both dose and linear energy transfer (LET) distributions for guidance. We demonstrate how this technique incorporates biological effect considerations, independently of any biological model subject to α/β value uncertainties. Observed inverse correlation between dose and LET distributions could be considered in treatment planning for IMPT in order to avoid overestimating the dose sparing for the organs at risk.
Acknowledgments
This work has been supported by the Federal Share of program income earned by Massachusetts General Hospital on C06 CA059267, Proton Therapy Research and Treatment Center.
Footnotes
Parts of this work have been presented at the 54th Annual AAPM meeting in Charlotte, NC (2012), and the 54th Annual ASTRO meeting in Boston, MA (2012)
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errorsmaybe discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Paganetti H, Niemierko A, Ancukiewicz M, et al. Relative biological effectiveness (RBE) values for proton beam therapy. Int J Radiat Oncol Biol Phys. 2002;53(2):407–21. doi: 10.1016/s0360-3016(02)02754-2. [DOI] [PubMed] [Google Scholar]
- 2.Carabe A, Moteabbed M, Depauw N, et al. Range uncertainty in proton therapy due to variable biological effectiveness. Phys Med Biol. 2012;57:1159–72. doi: 10.1088/0031-9155/57/5/1159. [DOI] [PubMed] [Google Scholar]
- 3.Grassberger C, Trofimov A, Lomax A, et al. Variations in linear energy transfer within clinical proton therapy fields and the potential for biological treatment planning. Int J Rad Onc Biol Phys. 2011;80(5):1559–1566. doi: 10.1016/j.ijrobp.2010.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Craft D, Halabi T, Shih HA, et al. An approach for practical multiobjective IMRT treatment planning. Int J Radiat Oncol Biol Phys. 2012;69(5):1600–7. doi: 10.1016/j.ijrobp.2007.08.019. [DOI] [PubMed] [Google Scholar]
- 5.Perl J, Shin J, Schuemann J, et al. TOPAS – An innovative proton Monte Carlo platform for research and clinical applications. Med Phys. 2012 doi: 10.1118/1.4758060. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zacharatou-Jarlskog C, Paganetti H. Physics Settings for Using the Geant4 Toolkit in Proton Therapy. IEEE Trans Nucl Sci. 2008;55(3):1018–24. [Google Scholar]
- 7.Paganetti H. Dose to water versus dose to medium in proton beam therapy. Phys Med Biol. 2009;50:4399–4421. doi: 10.1088/0031-9155/54/14/004. [DOI] [PubMed] [Google Scholar]
- 8.Deasy JO, Blanco AI, Clark VH. CERR: a computational environment for radiotherapy research. Med Phys. 2003;30(5):979–85. doi: 10.1118/1.1568978. [DOI] [PubMed] [Google Scholar]
- 9.Wedenberg M, Lind BK, Hardemark B. A model for the relative biological effectiveness of protons: The tissue specific parameter α/β of photons is a predictor for the sensitivity to LET changes. Acta Oncol. 2012 doi: 10.3109/0284186X.2012.705892. (in press) [DOI] [PubMed] [Google Scholar]