Trends of HIV-1 incidence with credible intervals in Sweden 2002–09 reconstructed using a dynamic model of within-patient IgG growth

Abstract

Background: HIV-1 is a lifelong disease, often without serious symptoms for years after infection, and thus many infected persons go undetected for a long time. This makes it difficult to track incidence, and thus epidemics may go through dramatic changes largely unnoticed, only to be detected years later. Because direct measurement of incidence is expensive and difficult, several biomarker-based tests and algorithms have been developed to distinguish between recent and long-term infections. However, current methods have been criticized and demands for novel methods have been raised.

Methods: We developed and applied a biomarker-based incidence model, joining a time-continuous model of immunoglobulin G (IgG) growth (measured by the IgG-capture BED-enzyme immunoassay) with statistical corrections for both sample size and unobserved diagnoses. Our method uses measurements of IgG concentration in newly diagnosed people to calculate the posterior distribution of infection times. Time from infection to diagnosis is modelled for all individuals in a given period and is used to calculate a sample weight to correct for undiagnosed individuals. We then used a bootstrapping method to reconstruct point estimates and credible intervals of the incidence of HIV-1 in Sweden based on a sample of newly diagnosed people.

Results: We found evidence for: (i) a slowly but steadily increasing trend in both the incidence and incidence rate in Sweden; and (ii) an increasing but well-controlled epidemic in gay men in Stockholm. Sensitivity analyses showed that our method was robust to realistic levels (up to 15%) of BED misclassification of non-recently infected persons as early infections.

Conclusions: We developed a novel incidence estimator based on previously published theoretical work that has the potential to provide rapid, up-to-date estimates of HIV-1 incidence in populations where BED test data are available.

Key Messages.

• Incidences in Sweden as a whole and in MSM in Stockholm show a complex but generally increasing trend over the period 2002–09.

• Treating IgG measures continuously and accounting for biological variance in IgG response improves incidence estimation.

• Credibility intervals accounting for variance from data imputation and uncertainty in time of infection given IgG levels suggested that observed trends were real.

• Differential misclassification of BED results lead to overestimation of the incidence; however, the magnitude of the bias was small and did not affect trends.

Introduction

Knowing the incidence of HIV is essential for determining the effectiveness of public health campaigns and for tracking the epidemic as it spreads through populations. Estimating the incidence for any infectious disease is difficult, but the long potential delay from infection to characteristic symptoms complicates incidence inference for HIV. HIV surveillance and detection have improved, but still a large proportion of newly diagnosed individuals are diagnosed with CD4 counts below 350 suggesting that many of these individuals remain undiagnosed for years following infection.^1–4

The need for a better understanding of HIV epidemiology has led to the development of a class of HIV-1 incidence estimators based on determining whether or not a person was recently infected,⁵ such as the widely used immunoglobulin G (IgG)-capture BED-enzyme immunoassay (BED assay).⁶ The most common approach considers people with a clinical marker below a given threshold to be recently infected, where the meaning of ‘recent’ is determined from the biological dynamics of the marker.^6–9 In that implementation, sample weights are calculated to estimate HIV-1 incidence based on the subset of people with below-threshold clinical markers. The BED assay has been used in many countries in both surveillance and research contexts, but in 2006 a Joint United Nations Programme on HIV/AIDS (UNAIDS) Reference Group on Estimates, Modelling and Projections claimed that the current BED-based methods overestimates incidence¹⁰ because of misclassification of late-stage HIV infection, impact of sample storage conditions, viral loads and variation due to HIV-1 subtype.^10,11 The Reference Group called for more research on the validity of the BED assay, as well as alternative assays and modelling methods. Recently, Guy et al. compared 13 different assays and found that serological assays, including BED, have reasonable sensitivity for the detection of recent infection, but are vulnerable to misclassifying established infections as recent.¹² This misclassification has been directly observed in several African populations,^13,14 and modelling studies have shown that if misclassification increases with time since infection, the overall incidence estimates could vary by place, time and age group.¹⁵ Furthermore, the dichotomization of the continuous optical density reading implies an information loss, which may lead to statistical inefficiency.⁵ Thus, although adding valuable information,^12,16,17 there is a consensus that current serological tests and modelling algorithms urgently need to be improved.^12,15,18

To address these issues and propose an alternative algorithm, in this paper we combine a recently published model of within-host time-continuous IgG dynamics¹⁹ with a Bayesian incidence estimator developed by Sommen et al.²⁰ to estimate the incidence of HIV-1 in Sweden based on available BED test results. We reduce critical late-stage infection misclassification by removing recently diagnosed individuals with low CD4 counts, and in addition model increasing levels of remaining misclassifications.

Methods

Statistical model of IgG concentration as a function of time from seroconversion

We modelled the time of HIV-1 seroconversion assuming logistic growth of within-patient IgG concentration as developed in Skar et al.¹⁹ IgG was measured by the log-scale optical density as:

$$Y\left(t\right)= K+\left(Y\left(0\right)-K\right)\exp [\left(-e^r\right)t]$$

where Y(t) is the optical density at time t from infection, Y(0) is the optical density in a susceptible person, K is the maximum optical density and r is the log-scale growth rate. Skar et al. fit this model to cohort data using a mixed effects model where both the slope and the asymptote had random effects to account for inter-patient differences. We will refer to this model as the OD model. The OD model was trained using meta-cohort data described in Parekh et al.⁷ containing BED results from different human populations as well as humans infected with different HIV-1 subtypes that show different rates of development of BED-specific IgG in response to HIV-1 infection. As described below, our Swedish data also consisted of patients of different genetic backgrounds as well as infections with different HIV-1 subtypes.^21,22 In the fixed effects model, the maximum OD value is 1.84, which corresponds to seroconversion having occurred 711 days from the time of diagnosis.¹⁹ Both the fixed and random effects estimated by Skar et al. were used to calculate the posterior probability of the time of seroconversion for individuals in the Swedish surveillance dataset.

Study subjects

The study subjects were recruited between mid- 2002 and mid 2010 as part of a national study on transmitted drug resistance (TDR) in Sweden, which enrolled 1463 cases from 2003–10.²² In our expanded set, 660 cases (45%) were infected while living in Sweden, with the remainder being infected before immigrating to Sweden.²² Although persons infected before immigrating to Sweden were not included directly into the data, secondary infections generated by these persons are included. Of the cases who were infected while living in Sweden, 558 (85%) were male, 107 (16%) reported a heterosexual transmission route, 378 (57%) were men who have sex with men (MSM), 130 (20%) were injection drug users, 609 (92%) had a BED test result and 392 (59%) had a BED test result OD ≤ 1.84 that suggested a high probability of infection within the previous 711 days.¹⁹

The five clinical centres for HIV care in the three largest Swedish cities (Stockholm, Gothenburg and Malmö) took part in the study from the start. Fifteen additional HIV centres were added from 2005 so that 20 of the 29 centres in Sweden eventually took part in the study. Due to partially incomplete data, we only estimated Swedish incidence in the period 2003–09, and likewise for MSM in Stockholm 2003–09.

Because late-stage HIV infection is well known to potentially lower the BED-OD value,^6,11,23,24 causing ‘false-recent’ classification, we removed recently diagnosed patients with AIDS defining or late-stage symptoms from the BED incidence modelling [Centers for Disease Control and Prevention (CDC) category C or an AIDS-defining illness). However, these cases still contain the information that they are long-term infections, with a known distribution of time to AIDS,²⁵ and were thus included in the overall incidence estimation as described below.

HIV-1 subtype determination

Genetic subtype was determined based on pol sequences derived by direct population sequencing of patient plasma within the TDR study.^22,26,27 A phylogenetic tree, including HIV-1 subtype reference sequences,²⁸ classified each patient’s HIV-1 sequence into its subtype.

Data imputation

Missing BED-OD values (n = 51, 7.7%) were imputed using the multiple imputation method in the library mi-0.09-18^{2 9} for the R programming language.³⁰ The imputation model used age, gender, transmission route, viral load, CD4 count, viral subtype, indication of primary HIV infection and time from previous negative test to impute missing OD values. To again avoid errors related to low BED-OD values in late-stage HIV infection, the BED results of people with an AIDS-defining illness at the time of diagnosis were not used to impute the missing data. All semi-continuous variables were log-transformed to prevent imputation of negative OD values. The imputation method was run until convergence five times, to generate independently imputed datasets.

Incidence estimator

The incidence estimator we developed is based on the estimator described in Sommen et al.²⁰ and contains three components: (i) the posterior density of infection times given an observed or imputed OD value; (ii) the probability of being diagnosed in a specified interval conditional on infection having occurred in the same interval; and (iii) inference to the target population. The posterior density of infection times determines the probability that a person in the study was infected in a specific interval. The conditional probability of being diagnosed determines a set of sampling weights to account for infections that occurred in a specific interval but were not diagnosed until later.

To obtain the posterior density of infection times, we first integrated out the random effects of the OD model to get the conditional density of the OD measurement:

$$f_{\left(y\text{|}r,l,u\right)}=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}\frac{1}{2\pi {\sigma }_{\epsilon }^2}\exp \left(-\frac{\left(y-g{\left(r-u,\mathit{a}\right)}^2\right)}{2{\sigma }_{\epsilon }^2}\right)f_{\mathit{a}} \text{d}\mathit{a}$$

where y is the OD measurement, u is the time of infection, r is the time at diagnosis, l is the time of the previous negative test, $g(t,\mathit{a})$ is the mean dynamics of IgG measurements according to the OD model at time t given random effects ${\sigma }_{\epsilon }^2$ is the variance of the normally distributed error in the OD model, and $f_{\mathit{a}}$ is the density of the random effects also obtained from the OD model. If no known negative test existed, the person was assumed to have ‘tested’ negative 12 years before they were diagnosed. The posterior density of infection times is obtained from Bayes rule:

$$f_{\left(u\text{|}r,l,y\right)}=\frac{f_{y|r,l,u}{f}_{r|u}}{{{\displaystyle \int }}_l^r{f}_{y|r,l,u }{f}_{r|u} \text{d}u}$$

The prior probability of diagnosis given infection $f_{r|u}$ was assumed to be a Gamma distributed random variable fit to times from infection to diagnosis based on the fixed effects OD model for individuals with observed OD values.

Many persons who are infected in a given year are unlikely to be diagnosed in that same year. To account for this, we developed a weighting method that models the number of infected persons in a given interval based on the probability that that a person would be infected and diagnosed in the same interval. Each person diagnosed in the specific interval is weighted by the inverse probability of having been infected in that interval. That probability was determined by the time from infection to diagnosis for all persons diagnosed in the specific interval. With respect to infection times, there are three types of diagnosed people: (i) people with OD ≤ 1.84 without AIDS; (ii) people with OD > 1.84 without AIDS; and (iii) people with AIDS regardless of OD value. For type 1 people, we drew a random infection time from the posterior distribution of infection times as an estimate of time from infection to diagnosis, and for types 2 and 3 people we drew a random infection time from the previously published Gamma distributed estimates of time from infection to AIDS.²⁵ The scale parameter for each type 2 person was found numerically such that 99% of the probability density was between the last negative test and diagnosis dates. The motivation for partitioning persons into these groupings is that between; (i) individuals that have BED results without AIDS; (ii)people with AIDS at diagnosis; and (iii) people with previous negative tests, most of the sampled cases have useful information about the time they were infected, which allowed us to estimate the probability that an infected person would be diagnosed in given interval.

We estimated the yearly incidence and the 95% credible intervals by generating a bootstrap sample that accounted for variance from: (i) the data imputation method; (ii) the time of infection; (iii) the conditional probability of being diagnosed; and (iv) the sample size. An explicit specification of the full algorithm that we used to get the point estimates and credible intervals is given in the online supplementary materials, available as Supplementary data at IJE online.

Sensitivity analysis

A concern with the BED test is that people deemed by the BED assay to have been recently infected could have, in fact, been infected for a long time.¹⁰ To test if our method was robust to this violation, we changed the time from infection to diagnosis for a random subset of recently infected persons. In each of 10 000 bootstrap samples, 5–20% of recently infected persons were selected and had their estimated time from infection to diagnosis switched with a randomly selected non-recently infected person (OD > 1.84 or AIDS). Their BED value was unchanged. Thus, this method produced random datasets where we could examine the conclusion our analysis would have come to if this kind of misclassification had been present. We also tested the assumption that persons who were not found to be recently infected and did not have AIDS at the time of diagnoses were infected no more than 12 years from the time of diagnosis, by changing that parameter to 25 years.

Results

Increased HIV-1 incidence in Sweden

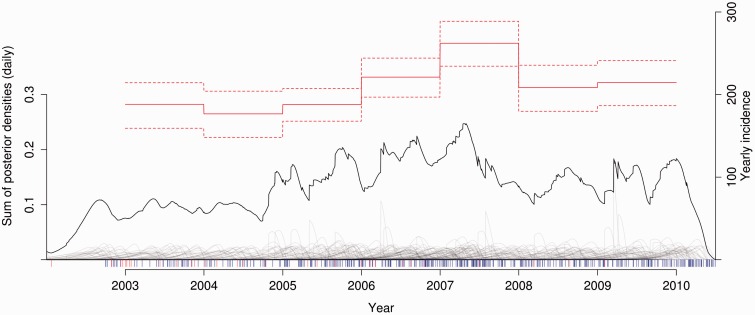
Figure 1 shows the relationship between the estimated incidence, the sum of posterior probabilities of infection times in the study, and the individual posterior distributions of infection times for diagnosed persons. The overall trend in HIV-1 incidence from 2003 was slightly increasing, with a clear spike consistent with an outbreak beginning in 2006 and peaking in 2007 (Table 1). The per capita incidence rates also showed a slightly increasing trend, with the exception of the 2006–07 elevated incidence. The total number of estimated new infections (n = 1459) was greater than the number of actual diagnoses (n = 1190). The difference is due to cases that were infected in 2003–09, but not diagnosed during the study period.

Figure 1.

Incidence of HIV-1 in Sweden 2003–09. This shows the yearly incidence of HIV-1 infections adjusted for the probability of being diagnosed (estimate, solid red line; 95% credible intervals, dashed red lines; right scale), the posterior density of infection times for all diagnosed persons with a usable BED test (grey lines, not shown to scale), the incidence rate per day unadjusted for unknown cases and the probability of being diagnosed (solid black line; left scale), and the time of diagnosis for each individual with a measured BED test below 1.84 (blue rug), and imputed BED results below 1.84 (red rug).

Table 1.

Swedish incidence estimation and model sensitivity analyses

Sample characteristics	2003	2004	2005	2006	2007	2008	2009
Enrolleda	52	64	79	84	124	94	87
Diagnosed (%)a	152 (0.25)	144 (0.24)	140 (0.40)	168 (0.41)	230 (0.51)	176 (0.43)	180 (0.39)
BED (<1.84)a	39 (24)	55 (30)	73 (55)	75 (57)	120 (73)	91 (51)	86 (53)
AIDSa	2	2	6	8	7	9	7
Incidence estimateb
Count	188 (159,214)	177 (148,204)	188 (168,207)	221 (197,244)	262 (234,289)	208 (180,236)	215 (187,241)
Rate	2.10	1.96	2.08	2.43	2.86	2.25	2.30
Sensitivity analysisb
25 yearsc	194 (164,222)	183 (153,211)	191 (170,210)	228 (203,252)	271 (242,300)	216 (186,244)	223 (194,251)
5% misclass.d	198 (165,235)	185 (152,220)	197 (174,223)	232 (204,262)	275 (243,308)	220 (187,256)	225 (194,258)
10% misclass.d	208 (172,253)	196 (159,239)	208 (181,239)	244 (212,281)	290 (253,330)	233 (196,277)	238 (202,279)
15% misclass.d	220 (175,278)	207 (166,262)	219 (187,257)	258 (220,302)	305 (264,355)	248 (204,302)	251 (210,302)
20% misclass.d	234 (183,309)	221 (174,287)	232 (195,279)	274 (230,327)	324 (276,382)	265 (214,332)	267 (219,328)

Individuals who had no reported location of infection were assumed to have been infected in Sweden with the marginal probability of being infected in Sweden for each year.

^aThe rows ‘Enrolled’, ‘Diagnosed’, ‘BED’ and ‘AIDS’ refer to the number of people in the study, the proportion of all diagnosed cases (infected in Sweden) in the sample, the number of people with a BED assay result, and the number of people with AIDS at the time of diagnosis, respectively.

^bThe incidence rate is expressed per 100 000 person years. For the incidence estimates and sensitivity analysis, values in parentheses are 95% credible intervals.

^cThe row ‘25 years’ shows the incidence estimate under the assumption that non-recent, non-AIDS cases could have been infected up to 25 years ago (rather than the 12 we assumed).

^dThe rows ‘% misclass.’ give the incidence estimates for a given degree of misclassification of recently infected persons.

There was no significant trend of changing viral loads (VL) in diagnosed persons over time (overall linear regression slope = 92 VL units/year, R²= 0.0006, P = 0.16; fraction VL < 10 000 in 2002–04 and in 2009–10 both at 20%; and loess and moving average showing no trends), and thus potential problems relating to VL trends misleading incidence did not occur.¹⁵ However, 14% of cases were diagnosed with an AIDS-defining illness, meaning that they could have been infected for a decade or longer when diagnosed. Likewise, the long time from infection to diagnosis means that in a given year a large proportion of incident cases are unlikely to be diagnosed. The overall median time from infection (seroconversion) to diagnosis was 2.5 years, which is consistent with previous estimates.³¹ Interestingly, these trends were robust to altering by simulation the rate of misclassified recent infections at diagnosis. Misclassifying recently infected persons as, in fact long-term infections but with OD < 1.84 of up to 15%, had minor effects on the incidence trends, not changing the overall pattern of slowly increasing incidence from 2003 onwards, with a clear spike in 2006–07 (Table 1). Higher rates of misclassification led to a higher degree of bias, but the qualitative features of the trends were unaffected. This suggests that our novel incidence algorithm likely could be used in other populations with different diagnosis response times from those in Sweden.

Increased HIV-1 incidence in gay men in Stockholm

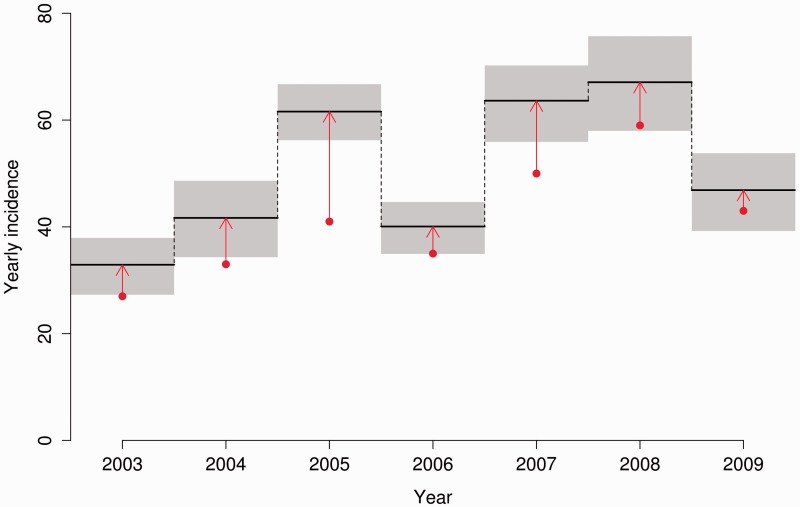
Figure 2 shows the estimated incidence in gay men in Stockholm 2003–10, with grey envelopes indicating 95% credible intervals and red dots indicating the number diagnosed (numbers in Table 2). The trend is generally increasing although, given lower numbers of incident cases in 2006 and 2009 and the generally low number of incident cases, it is not possible to rule out random year-to-year variation as the cause of the apparent pattern. In general the number of diagnosed cases was not greatly lower than the estimated number of incident cases, which is consistent with the low average time from infection to diagnosis (2.1 years) in this subpopulation. The main exception is 2005, where the estimated incidence was 44% higher than the number diagnosed. The cause of this effect was the large number of recently infected persons diagnosed later in the year who, by definition, have a high probability of being infected in that year. Given that we assume a constant probability within a given interval, the only way to observe this pattern is with a large number of new infections occurring in 2005. An alternative explanation for this pattern that cannot be ruled out with the available data is an increasing probability of diagnosis from the beginning to the end of 2005.

Figure 2.

Incidence of HIV-1 in MSM in Stockholm. Red dots show number of diagnosed cases per year. Black lines, with grey 95% credible intervals, show our yearly incidence estimates. Red arrows indicate the increase over the number of diagnosed cased that our novel method infers based on BED results and corrections for number of unknown cases.

Table 2.

Stockholm MSM incidence estimation

	2003	2004	2005	2006	2007	2008	2009
Incidencea	33(27,38)	42(34,49)	62(56,67)	40(35,45)	64(56,70)	67(58,76)	47(39,54)
Enrolledb	25	30	43	34	46	54	38
Diagnosedc	27	33	43	35	50	59	43
BED (<1.84)d	24(17)	30(18)	42(35)	32(26)	46(35)	52(30)	38(30)
AIDSe	1	1	2	1	3	4	3

^aEstimated number of new infections (95%CI).

^bNumber of persons enrolled in the study.

^cNumber of persons reported to have been diagnosed.

^dNumber of persons with BED results (number below 1.84).

^eNumber of persons with AIDS at the time of diagnosis.

Differential misclassification of BED results

To study the role of differential misclassification of BED results, we generated a dataset with different proportions of persons misclassified as being recently infected. The results show a clear trend that this kind of misclassification would lead to an overestimation of the incidence compared with the actual analysis (Table 1). This overestimation is caused by the fact that in the misclassified dataset, the average time from infection to diagnosis is longer and therefore the sample weights are higher. Recently infected individuals who are likely to have been infected in the interval of interest will have a disproportionate contribution to the incidence from the increased sample weights.

Although the estimator is sensitive to this kind of misclassification, the magnitude is relatively small even at 15% misclassification. With 15% misclassification, the average overestimation was 36 cases per year, i.e. less than 17% overestimation. The qualitative features of the trend (increasing with a drop in 2008) are robust to this kind of misclassification. Given these facts we believe that, whereas our estimator might slightly overestimate the number of infected cases, our results are robust to this kind of misclassification at realistic levels. Note also that in the Swedish data we removed persons with low CD4 counts from the BED results, so the actual misclassification level is likely well below 15%.

Table 1 also shows that our algorithm is robust to the assumption that persons who were not found to be recently infected and did not have AIDS at the time of diagnosis were infected no more than 12 years from the time of diagnosis. Relaxing this assumption to 25 years only increased the estimated incidence slightly.

Discussion

Because HIV-1 infection often goes undetected, it is common that positive diagnosis occurs with a considerable delay relative to the time of infection. Therefore, number of diagnoses per unit time, e.g. per year, is a poor estimator of the spread dynamics in a population. Here we present an incidence estimator based a time-continuous growth model of a biomarker (BED) with corrections for undiagnosed cases and sample size. We show that the incidence in Sweden in general and in gay men in Stockholm in particular has increased over the past decade, although to a modest degree.

Previous studies have shown that false-recent misclassification may occur at 1.7–15.1%,^11,32 and in African settings it has been shown that the traditional recent/long-term cut-off interpretation of BED results may overestimate incidence by as much as 360%.³³ Our incidence estimation, based on a time-continuous BED growth model, only overestimates incidence by 17% when false-recent misclassifications occur at 15%. Furthermore, in our analysis of the Swedish HIV-1 epidemic, we avoided known problems associated with ‘false-recent’ classification^5,6,11,23,24 by removing individuals with clinical symptoms (low CD4 counts or AIDS-defining illness) from the posterior OD model-based incidence estimation. Thus, using additional data to reduce the false-recent rate improves BED-based incidence estimations, but even if misclassifications should remain at up to 15%, we show by simulation that our new method robustly infers incidence trends in Sweden.

Arneborn and Blaxhult reported that there had been a dramatic increase of reported diagnoses in 2007.³⁴ They noticed that the increase was primarily among MSM and injecting drug users (IDU). Our estimates of the overall incidence of HIV in Sweden are consistent with this observation as we find elevated incidence in both 2006 and 2007. The increase in 2006–07 is possibly explained by an outbreak among IDU infected with HIV-1 CRF01 in 2006, linked to a Finnish IDU outbreak around 2003.³⁵ Our analysis also found some evidence for increasing HIV incidence in gay men in Stockholm. These results are surprising, as most diagnosed cases in Sweden have successful therapy (in 2012, 87% of diagnosed patients were on antiretroviral therapy (ART) and 92% of these had <50 RNA copies/ml³⁶), essentially making them non-infectious.³⁷ Factors such as spread from undiagnosed, and therefore untreated, individuals as well as episodic high viral loads in treated individuals probably contribute disproportionally to the epidemic. Overall, the peak of reported cases in 2007^{3 4} was preceded by elevated incidence in 2006.

Our estimator is different from both the method proposed in Sommen et al.²⁰ and the method also based on BED measurements detailed in Karon et al.³⁸ Both the Sommen et al. and Karon et al. methods divide the population into a group of regular and non-regular testers, based on the existence of a previous negative test. In regular testers (individuals with a previous negative test), the conditional density of the time of testing, given infection, is derived from the assumption that testing is a Poisson process with intensity determined by the time from the previous negative test to diagnosis. For the non-regular testers, the hazard of infection is assumed to be constant and estimated from other data such as proportion of AIDS diagnoses. We believe that the assumptions of (i) stable testing rates in all individuals with a previous negative test and (ii) a constant hazard of testing in individuals without a negative test are not realistic.¹⁹ Our method exploits the fact that in a given interval, most infected persons have some information about the time from infection to diagnosis for that interval. Even for individuals with OD > 1.84 and no indication of an AIDS-defining illness, we know that they were likely to have been infected between their last negative test (if it exists) and diagnosis. There is no optimal a priori distribution of times to diagnosis for this group of people; however, the uncertainty of infection times for these individuals is incorporated into the credible intervals.

The credible intervals around our point estimates include variance from the data imputation method, probability of the infection time, and the distribution of time from infection to test. Additional sources of variance should be included in future work, to gain potentially more accurate credible intervals such as uncertainty in the BED measurement, uncertainty in the number of diagnosed cases due to reporting delays and uncertainty in time of previous negative test. Increasing the number of random quantities in the estimator increases the necessary size of the bootstrap sample to obtain good point estimates increasing the computational requirements. The ability to explicitly model uncertainty in both the data and the posterior distribution of infection times in a Bayesian context is a strength of our method.

Because we allow the probability of being diagnosed to vary between time intervals, we mitigated some of the possible effects of changing patterns of testing and diagnosis. Although we assume that the probability of being diagnosed is constant within a time interval, time units can be subdivided further to reduce the strength of this assumption. However, the trade off in subdividing time intervals is that small sample numbers may lead to poor estimates of the sample weights and therefore unreliable point estimates.

Parekh et al. have shown that the BED test may perform differently in different human populations as well as in humans infected with different HIV-1 subtypes.⁷ The parameter values of our logistic model were informed by the same data (provided by Dr Parekh) and thus, as in Skar et al.,¹⁹ both the model calibration and the Swedish data reflect human and HIV-1 variation, because the HIV-1 epidemic in Sweden is small but diverse, involving most HIV-1 subtypes.²¹ We note that adjusting for human and HIV genetic variation would be difficult because such a model would require massive and typically unavailable data, and differences within HIV-1 subtypes appear to affect BED results as much as between subtypes.⁷ Nevertheless, it is possible that future biomarkers will be less sensitive to human and HIV genetic variation. Our model was based on BED assay results because it is currently the most used biomarker for recency estimation. However, our model could be adjusted to other available and future serological biomarkers as well as be included in multi-assay approaches.^16,39,40 Motivated by the fact that all natural systems have limited resources, we model the HIV-specific biomarker growth within a patient by logistic growth up to a carrying capacity.¹⁹ Other researchers have tested alternatives based on statistical arguments, reaching similar descriptions of biomarker development.^20,31

Incidence estimation using time-continuous biomarker data makes a fast and powerful combination to monitor spread dynamics. Further development of the methods presented here could allow for rapid and up-to-date estimates of HIV incidence in a broad variety of settings.

Funding

E.O.R.S. and T.L. were supported by NIH grant AI087520. C.L.P. was supported in part by the U.S. Department of Energy, Office of Science, Office of Workforce Development for Teachers and Scientists (WDTS) under the Science Undergraduate Laboratory Internship (SULI) programme. J.A. was supported by Swedish Research Council grant K2008-56X-09935-17-3 and the EU projects: SPREAD (QLK2-CT-2001-01344) and CHAIN (FP7/2007–2013) ‘Collaborative HIV and Anti-HIV Drug Resistance Network’ grant agreement no. 223131.

Conflict of interest: None declared.