Numerical Study on the Partitioning of the Molecular Polarizability into Fluctuating Charge and Induced Atomic Dipole Contributions

Abstract

In order to carry out a detailed analysis of the molecular static polarizability, which is the response of the molecule to a uniform external electric field, the molecular polarizability was computed using the finite-difference method for 21 small molecules, using density functional theory. Within nine charge population schemes (Löwdin, Mulliken, Becke, Hirshfeld, CM5, Hirshfeld-I, NPA, CHELPG, MK-ESP) in common use, the charge fluctuation contribution is found to dominate the molecular polarizability, with its ratio ranging from 59.9% with the Hirshfeld or CM5 scheme to 96.2% with the Mulliken scheme. The Hirshfeld-I scheme is also used to compute the other contribution to the molecular polarizability coming from the induced atomic dipoles, and the atomic polarizabilities in 8 small molecules and water pentamer are found to be highly anisotropic for most atoms. Overall, the results suggest that (a) more emphasis probably should be placed on the charge fluctuation terms in future polarizable force field development; (b) an anisotropic polarizability might be more suitable than an isotropic one in polarizable force fields based entirely or partially on the induced atomic dipoles.

Introduction

Molecular dynamics (MD) simulations are now routinely utilized in the study of proteins and other biological molecules,¹ with the accuracy controlled by the underlying energy functions and sampling algorithms. Contemporary nonpolarizable force fields, i.e., in which fixed partial charges are used for all of the atoms in the system, are the predominant methods of choice for energy functions in classical MD simulations. In addition, these methods are also widely used in hybrid quantum mechanics/molecular mechanics (QM/MM) calculations to provide electrostatic embedding potentials for the quantum mechanical (QM) atoms. Despite their popularity and success in numerous applications, nonpolarizable force fields lack an explicit description of electron response to the specific chemical environment. Thus, they have limited ability in describing the kinetics and dielectric properties of polar solvents,^2,3 charge transfer between diverse dielectric media, and the interactions between ions and π-orbitals, where this polarization effect can be rather significant.⁴ This limitation also impacts QM/MM calculations in cases where mutual polarization between the QM and MM regions are required.^5–7

To overcome this limitation, several methodologies have been proposed to explicitly account for such polarization effects in classical force fields,^8–12 and include the fluctuating charge model,^13–18 the induced multipole model,^19–27 and Drude oscillator schemes.^28–34 In addition, a hybrid scheme that combines the fluctuating charge and induced dipole models has also been developed.^35,36 Some of these polarizable force fields have been implemented in various MD simulation packages, such as AMBER,³⁷ CHARMM,³⁸ NAMD,³⁹ and Gromacs.⁴⁰

In the fluctuating charge model, a molecule responds to an external electrostatic environment through charge flow between its constituent atoms. This charge redistribution restores electronegativity equality and lowers the total potential energy of the molecule. Conceptually speaking, the fluctuating charge model is simple, but unless extra “off-atom” sites are employed, this model cannot accurately describe the anisotropic response of the electron density around each atomic nucleus to an external perturbation. A notable and important example of this shortcoming is the out-of-plane distortion of the electron density associated with an aromatic ring involved in an ion-π interaction.

In the induced multipole model, a series of extra multipoles are placed on each atom that vary in response to the local electrostatic field, the extent to which is governed by pre-assigned atomic polarizabilities.²⁴ For example, the AMOEBA force field utilizes atomic polarizabilities that were originally proposed by Thole⁴¹ and have been reoptimized using high-level quantum chemical calculations.⁴² In the AMBER force field, the atomic polarizabilities are mainly derived from numerical fitting to the experimental molecular polarizabilities of 420 molecules obtained from the molecular refraction measurements.²⁴

In the Drude oscillator model (also known as the shell model^43,44 or charge-on-a-spring model⁴⁵), a fictitious charged particle is attached to each polarizable (parent) atom through a spring, and, together with the parent atom, forms an instantaneous local dipole which describes the local polarization. In the CHARMM implementation of the Drude oscillator model, the atomic polarizabilities are fit to high-level quantum chemical calculations in the gas phase, but are scaled for use in condensed-phase simulations.⁴⁶ In the early (massless) implementations,²⁸ the position of the Drude particles (and thus the orientation and magnitude of the local dipoles) were solved for self-consistently at each confguration along a MD trajectory. More recently, the Drude particles acquired a small (fictitious) mass and thus became pseudoatoms,³² which allows their associated positions and velocities to be updated along with other normal atoms. However, shorter MD time steps are now required to accurately integrate the corresponding equations of motion because of the relatively fast motion of the lighter Drude particles. Nonetheless, implementation of the Drude oscillator model into existing MD packages is straightforward, in which the fictitious particles are treated in essentially the same manner as standard atoms. Recently, the Drude model has also been utilized in QM/MM simulations to improve the description of the interface between the QM and MM regions.^5,47,48

To further improve upon the accuracy and applicability of polarizable force fields, it is desirable to gain a clearer picture of the electrostatics and polarization interactions present in macromolecular systems. However, such a task can be challenging for the following reasons:

1. The electrostatics/polarization interactions are strongly coupled to bonded interactions. In this regard, bond stretching, angle bending, and/or torsional motion alter the electronic structure of a molecule, and thus its atomic multipoles; however, the related changes in the electrostatic energy are already folded into the bonded terms. As such, the 1-2 and 1-3 nonbonded (electrostatics and van der Waals) interactions are completely omitted while the 1-4 nonbonded interactions may be scaled down in most widely used force fields.

2. The distinction between permanent electrostatics and instantaneous polarization is equally, if not more, vague in this context, because such a distinction heavily depends on the reference structure(s) from which the parameters describing the permanent electrostatics are derived. To the extent that the atomic partial charges are often fitted from condensed-phase calculations and/or averaged over multiple conformations,^49–58 most nonpolarizable force fields in widespread use today actually utilize “prepolarized” parameters for the permanent electrostatics.⁵⁹ In some MD simulations, one uses a “polarized” force field with atomic partial charges that are periodically refitted or updated on the fly.^54,60

3. As Söderhjelm et al.⁶¹ discussed, the external electrostatic potential and field at the molecular fragment under consideration can also be highly non-uniform. This in turn will affect the accuracy of some polarizable force fields, as current implementations of the fluctuating charge model only utilize the local electrostatic potential at the nuclear positions while the induced multipole model only uses the local electrostatic field at these positions in space.

4. In a molecule, the atomic partial charges, dipole moments, higher-order multipole moments, and polarizabilities, all of which are central to current nonpolarizable and polarizable force fields, are not physical observables. While these quantities can be parameterized through extensive simulations to reproduce condensed-phase experimental data,⁶² the dominant approach is still to fit them to ab initio QM calculations. There, in addition to the obvious dependence on the QM method and the chosen basis set, the parameterization of these “atomic” quantities also varies with the decomposition/localization scheme employed for dividing molecular properties (densities, polarizabilities, etc.) into atomic contributions.^63–65

In view of these challenges, we seek to gain a deeper understanding of polarization effects in this work by analyzing the static polarizabilities of 21 representative molecular systems using a finite-difference approach. In this work, all of the molecules were studied at their equilibrium geometries, so the aforementioned bonded terms will not affect the electronic structure at all. In this regard, it is convenient to use the electronic structure of a given molecule in the absence of an external electrostatic field as the reference, which allows for a clear separation between the permanent electrostatics and the instantaneous polarization. In a finite-difference calculation, a uniform external electrostatic field is applied in six different directions (±x, ±y, ±z) — this partially addresses the third issue above (non-uniform external electrostatic potential and field), but admittedly the effective electrostatic potential and field at and around the atoms can still be somewhat non-uniform. (In a related work, the polarization effects on the molecular electronic structure within the external non-uniform electrostatic potential due to solvent molecules or a protein were studied numerically.⁶⁶)

This approach will allow us to focus on the last issue above, i.e., the partitioning of molecular polarizabilities into atomic polarizabilities, with the goal of improving the parameterization of advanced classical force fields. More specifically, nine charge population schemes (Mulliken, Löwdin, natural population analysis (NPA), electrostatic potential based charge (ESP), CHELPG, Hirshfeld, iterative Hirshfeld (abbreviated as Hirshfeld-I hereafter), charge model 5 (CM5), and Becke) were used to compute the fluctuating charge contributions to the static molecular polarizabilities. With four schemes (Mulliken, Hirshfeld, Hirshfeld-I, and Becke), for which atom-in-molecule densities are clearly defined, the induced atomic dipoles and thus the atomic polarizabilities were also computed, and the transferability of these approaches between different molecules was examined. Furthermore, the dependence on the specific density functional approximations and the underlying one-particle basis sets was also analyzed herein.

Theory and Computational Details

Charge Definitions

Despite their widespread use in molecular modeling, atomic charges are not physical observables and thus do not have a unique definition that can be rigorously derived from quantum mechanics. As a result, numerous models have been developed over the past several decades for computing atomic charges. According to Truhlar and coworkers,^67,68 these models fall into the following four general categories:

Class I charge models

These models do not have a solid quantum mechanical foundation. Instead, they are derived from classical mechanical models such as classical electronegativity equalization^14,69,70 or from experimental measurements, for instance, of the electron density from X-ray diffraction.⁷¹

Class II charge models

These models are based on charge partition schemes, in which the electron density obtained from a quantum mechanical calculation is allotted to the atoms in the molecule. Several partition schemes have been proposed, and include Mulliken population analysis,^72,73 Löwdin population analysis,^74,75 atom-in-molecule (AIM) population analysis,⁷⁶ natural population analysis (NPA),^77,78 Hirshfeld population analysis,⁷⁹ Hirshfeld-I population analysis,⁸⁰ and Becke population analysis.⁸¹

The Mulliken population analysis method was proposed by Mulliken in 1955, and is based on the linear combination of atomic orbitals-molecular orbital (LCAO-MO) method.^72,73 In this method, the Mulliken charge is calculated as

$$Q_A^{\text{Mulliken}}=Z_A-\sum _{\mu \in A}{\left(\mathbf{PS}\right)}_{\mu \mu },$$ (1)

where Z_A is the nuclear charge, P is the density matrix which depends on the occupied molecular orbital coefficients (C_μi), i.e.,

$$P_{\mu \nu }=\sum _{i\in \mathit{occ}}{C}_{\mu i}{C}_{\nu i}$$ (2)

and S is the overlap matrix between atomic orbitals (μ, ν), and i refer to occupied molecular orbitals.

The Löwdin charge is defined as

$$Q_A^{\mathrm{L}\ddot{\mathrm{o}}\mathrm{wdin}}=Z_A-\sum _{\mu \in A}{\left({\mathbf{S}}^{1∕2}{\mathbf{PS}}^{1∕2}\right)}_{\mu \mu },$$ (3)

which is based on a symmetric matrix, S^1/2PS^1/2 (as opposed to the nonsymmetric PS for the Mulliken charge in Eq. 1).

NPA charge, the natural charge for an atom, is the sum of the natural populations from the natural bond orbital (NBO) analysis.⁷⁷ NBO analysis localizes and classifies the orbitals into bonding, antibonding, nonbonding, and Rydberg types. Only the bonding orbitals are shared between atoms and are partitioned in a similar way as the Mulliken population analysis above.

In the Hirshfeld partition scheme,⁷⁹ the molecular electron density ${\rho }_{\mathit{mol}}\left(\overrightarrow{\mathbf{r}}\right)$ is partitioned into a sum of atomic densities, ${\rho }_A\left(\overrightarrow{\mathbf{r}}\right)$, via the following weight functions, ${\omega }_A\left(\overrightarrow{\mathbf{r}}\right)$:

$$\begin{array}{cc}\hfill {\rho }_A\left(\overrightarrow{\mathbf{r}}\right)=& {\omega }_A\left(\overrightarrow{\mathbf{r}}\right){\rho }_{\mathit{mol}}\left(\overrightarrow{\mathbf{r}}\right)\hfill \\ \hfill =& \frac{{\rho }_A^0\left(\overrightarrow{\mathbf{r}}\right)}{{\sum }_B{\rho }_B^0\left(\overrightarrow{\mathbf{r}}\right)}{\rho }_{\mathit{mol}}\left(\overrightarrow{\mathbf{r}}\right),\hfill \end{array}$$ (4)

in which ${\rho }_X^0\left(\overrightarrow{\mathbf{r}}\right)$ is the electron density of an isolated atom X in vacuum. The Hirshfeld atomic charges are thus defined as

$$Q_A^{\text{Hirshfeld}}=Z_A-\int d\overrightarrow{\mathbf{r}}{\rho }_A\left(\overrightarrow{\mathbf{r}}\right),$$ (5)

and tend to be quite small.⁸⁰ Hence, this scheme significantly underestimates the molecular dipole moment if only atomic charges are used (in other words, the atomic dipoles that are defined later as the second term in Eq. 13 are significant). Besides, the selection of the promolecular density, ${\sum }_B{\rho }_B^0\left(\overrightarrow{\mathbf{r}}\right)$, is somewhat arbitrary and it has been shown that the computed Hirshfeld charges can depend substantially on the definition of the promolecular density.⁸²

In order to increase the molecular dipole moments as predicted from atomic charges (i.e., to enhance the charge separation), several variations/extensions of the Hirshfeld population analysis have been proposed, including Hirshfeld-I,⁸⁰ Fractional Occupation Hirshfeld-I method (FOHI),^83,84 Iterative Stockholder Analysis (ISA)^85,86 and its Gaussian variant⁸⁷ as well as density-derived electrostatic and chemical (DDEC) charge,^88–90 which is a combination of Hirshfeld-I and ISA. The main strategy in all of these methods is to generate atomic densities with a fractional number of electrons for each atom in a self-consistent manner. For instance, in the Hirshfeld-I scheme, for an atom with N_A + Δ_A electrons and Δ_A ∈ [0, 1] (and thus a net charge of Z_A − N_A − Δ_A), its atomic density is defined as an interpolation between the atomic charge densities with N_A (floor) and N_A + 1 (ceiling) number of electrons,

$${\rho }_A={\rho }_A^{\left(N_A\right)}+{\Delta }_A\left[{\rho }_A^{(N_A+1)}-{\rho }_A^{\left(N_A\right)}\right].$$ (6)

These interpolated atomic densities are then utilized to compute atomic charges in the next iteration, and this procedure continues until convergence is reached. However, a recent study showed that the Hirshfeld-I scheme sometimes overshoots the deficiency of the Hirshfeld population analysis and leads to overestimated molecular dipole moments.⁹¹

Originally, Becke weights⁸¹ were proposed for dividing integrals over the entire molecular volume into atomic sums, making the integration more convenient to compute. The Becke weights, ${\omega }_A\left(\overrightarrow{\mathbf{r}}\right)$, are constructed from cell functions, P_A, which are simple polynomials in the distance between nuclei (A) and grid points (r),

$${\omega }_A\left(\overrightarrow{\mathbf{r}}\right)=\frac{P_A\left(\overrightarrow{\mathbf{r}}\right)}{{\sum }_B{P}_B\left(\overrightarrow{\mathbf{r}}\right)},$$ (7)

and satisfy the normalization condition, ∑_A ω_A = 1. Then the Becke charges can be calculated as

$$Q_A^{\text{Becke}}=Z_A-\int d\overrightarrow{\mathbf{r}}{\omega }_A\left(\overrightarrow{\mathbf{r}}\right){\rho }_{\mathit{mol}}\left(\overrightarrow{\mathbf{r}}\right).$$ (8)

Becke charges are sometimes used in constrained density functional theory (CDFT) calculations⁹² for the study of charge-transfer processes. In the work, we adopt the atom size adjustment⁸¹ and the corresponding Bragg radii are 0.25 Å for H, 0.70 Å for C, 0.65 Å for N, and 0.60 Å for O atoms.

Class III charge models

Within these models, atomic charges are fitted to certain physical quantities obtained from quantum mechanical calculations, especially the electrostatic potential (ESP).^93–98 However, ESP-based charges, such as Merz-Kollman (MK-ESP) charges⁹⁶ and CHELPG charges,⁹⁸ are not strictly rotationally invariant and can suffer from numerical instabilities, which leads to difficulties in determining partial charges for buried atoms.^99,100 Accordingly, several amendments were proposed to mitigate these numerical difficulties by implementing regularization techniques,¹⁰¹ appending the electronegativity equalization to the ESP fit,¹⁰² adding more grid points and using a smooth cutoff method,¹⁰³ or by splitting atomic charges into a mean-field charge and a small perturbation.¹⁰⁴

We note that another numerical issue with ESP charges comes from the appearance (or disappearance) of some grid points, even with a relatively small change in the molecular geometry/conformation. This can cause the ESP charges to have a non-smooth dependence on the molecular geometry, thereby causing difficulties during the computation of analytical derivatives of these charges with respect to the nuclear coordinates,¹⁰⁵ which might be required if one updates the ESP charges on the fly (like the CHELPG charges used to represent the QM electronic density in a QM/MM Ewald calculation). However, this latter issue has recently been addressed.^106,107

Class IV charge models

With these models, atomic charges are parameterized to reproduce some observables from either experiments or high-level QM calculations.^{67,68,108–110} For example, the Charge Model 5 (CM5)⁶⁸ builds upon the Hirshfeld charges via

$$Q_A^{\mathrm{CM}5}=Q_A^{\text{Hirshfeld}}+\sum _{k^{\prime }\ne k}{T}_{{\mathit{kk}}^{\prime }}{B}_{{\mathit{kk}}^{\prime }},$$ (9)

where the Pauling bond order, B_kk′, is a function that approximately describes the electron density overlap between two atoms and is defined as

$$B_{{\mathit{kk}}^{\prime }}=\exp [-\alpha (r_{{\mathit{kk}}^{\prime }}-R_{Z_k}-R_{Z_{k^{\prime }}}\left)\right].$$ (10)

The α parameter in Eq. 10 and the T_kk′ parameters were optimized by Marenich et al..⁶⁸ It is worth noting here that the second term on the right hand side of Eq. 9 is independent of the molecular electronic structure. Therefore, CM5 and Hirshfeld charges have the same basis-set and functional dependence, and the molecular responses to the external perturbation also remains the same for these two schemes. Scaled CM5 charges have recently been used in condensed-phase modeling for computing hydration free energies.¹¹¹

Decomposition of the Molecular Dipole Moment and Static Polarizability

With four charge models (Mulliken, Hirshfeld, Hirshfeld-I, and Becke) in use in this numerical study, the electron density of a molecule, $\rho \left(\overrightarrow{\mathbf{r}}\right)$, can be decomposed into atomic densities, ${\rho }_A\left(\overrightarrow{\mathbf{r}}\right)$, at every point in real space,

$$\rho \left(\overrightarrow{\mathbf{r}}\right)=\sum _A{\rho }_A\left(\overrightarrow{\mathbf{r}}\right),$$ (11)

and then the partial atomic charges can be computed according to Eq. 5. The electronic portion of the molecular dipole moment is

$$\overrightarrow{\mu }=\int d\overrightarrow{\mathbf{r}}\overrightarrow{\mathbf{r}}\rho \left(\overrightarrow{\mathbf{r}}\right)=\sum _A\int d\overrightarrow{\mathbf{r}}\overrightarrow{\mathbf{r}}{\rho }_A\left(\overrightarrow{\mathbf{r}}\right).$$ (12)

Therefore, the molecular dipole moment (including both electronic and nuclear contributions) can be written as follows:

$$\begin{array}{cc}\hfill \overrightarrow{\mu }=& \sum _A{Q}_A{\overrightarrow{\mathbf{R}}}_A+\sum _A\int d\overrightarrow{\mathbf{r}}(\overrightarrow{\mathbf{r}}-{\overrightarrow{\mathbf{R}}}_A){\rho }_A\left(\overrightarrow{\mathbf{r}}\right)\hfill \\ \hfill =& \sum _A{Q}_A{\overrightarrow{\mathbf{R}}}_A+\sum _A{\overrightarrow{\mu }}_A,\hfill \end{array}$$ (13)

with the first term on the right hand side corresponding to the dipole formed by atomic partial charges and the second term corresponding to local atomic dipoles.

In the computation of the static molecular polarizability tensor, which is the response of the molecular dipole moment with respect to the applied external electrostatic field,

$$\begin{array}{cc}\hfill {\alpha }_{\mathit{ij}}=& {\left(\frac{\partial {\mu }_i}{\partial E_j}\right)}_{E=0}\hfill \\ \hfill =& \underset{E_j\to 0}{\lim }\frac{{\mu }_i\left(E_j\right)-{\mu }_i(-E_j)}{2E_j},\hfill \end{array}$$ (14)

where i, j ∈ x, y, z, while μ_i refers to the x, or y, or z component of the molecular dipole moment, E_j is the strength of the electrostatic field along direction j. Just like the molecular dipole moment in Eq. 13, the dipole moment difference, given in the numerator in Eq. 14, also has two contributions:

$$\begin{array}{cc}\hfill \Delta \overrightarrow{\mu }=& \sum _A\Delta Q_A{\overrightarrow{\mathbf{R}}}_A+\sum _A\int d\overrightarrow{\mathbf{r}}(\overrightarrow{\mathbf{r}}-{\overrightarrow{\mathbf{R}}}_A)\Delta {\rho }_A\left(\overrightarrow{\mathbf{r}}\right)\hfill \\ \hfill =& \sum _A\Delta Q_A{\overrightarrow{\mathbf{R}}}_A+\sum _A\Delta {\overrightarrow{\mu }}_A,\hfill \end{array}$$ (15)

where the first term corresponds to the charge fluctuation (migration) in the molecule, and the second term corresponds to the change in the local atomic dipoles. Accordingly, the static polarizability tensor in Eq. 14 also has the fluctuating charge (FC) and induced atomic dipole (IAD) contributions, i.e.,

$${\alpha }_{\mathit{ij}}={\alpha }_{\mathit{ij}}^{\mathit{FC}}+{\alpha }_{\mathit{ij}}^{\mathit{IAD}},$$ (16)

wherein

$${\alpha }_{\mathit{ij}}^{\mathit{FC}}=\underset{E_j\to 0}{\lim }\sum _A=\frac{\left[Q_A\right(E_j)-Q_A(-E_j\left)\right]R_{A,i}}{2E_j},$$ (17)

$${\alpha }_{\mathit{ij}}^{\mathit{IAD}}=\underset{E_j\to 0}{\lim }\sum _A\frac{{\mu }_{A,i}\left(E_j\right)-{\mu }_{A,i}(-E_j)}{2E_j}.$$ (18)

where R_A,i in Eq. 17 refer to the i-th (x, or y, or z) coordinate of atom A.

To compute the static polarizabilities in Eq. 14, we used a finite difference approach, wherein an external electrostatic field of 10⁻³ a.u. was applied in the ±x, ±y, ±z directions. In Eq. 14, one cancels out all even-order (0, 2, 4, …) responses in the molecular dipole moments, leaving only the odd-order (1, 3, 5, …) responses. Increasing the field strength by 1 order of magnitude (i.e., to 10⁻² a.u.) was found to yield insignificant changes to the results, suggesting that the third and higher order responses are negligible and that the molecules are in the linear response region. Alternatively, one can explicitly cancel the third-order contributions by carrying out extra single-point calculations within external electrostatic fields of doubled strength through¹¹²

$${\alpha }_{\mathit{ij}}=\underset{E_j\to 0}{\lim }\frac{8\left[{\mu }_i\right(E_j)-{\mu }_i(-E_j\left)\right]-\left[{\mu }_i\right(2E_j)-{\mu }_i(-2E_j\left)\right]}{12E_j},$$ (19)

which, as expected, was also found to have a negligible effect on the results.

Molecular Systems Studied

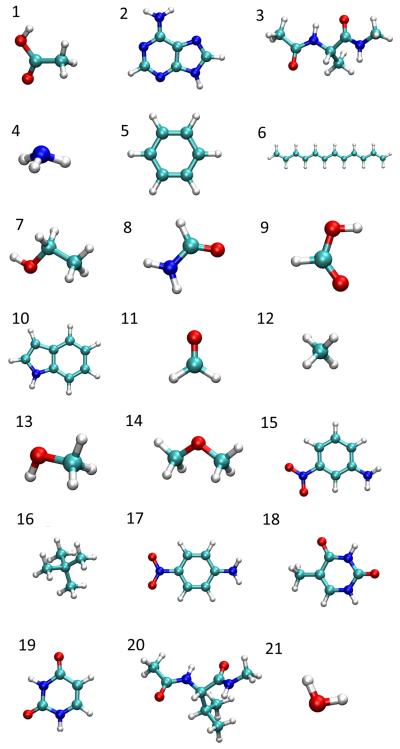
Altogether, 21 molecules were studied in this work, which are shown in Fig. 1, using a development version of Q-Chem 4.2.¹¹³ For these molecules, we will begin by examining the atomic charges and the molecular dipole moments (as computed from these charges) as predicted by nine charge schemes (Mulliken, Löwdin, Becke, Hirshfeld, Hirshfeld-I, CM5, NPA, ESP, and CHELPG). When an external electrostatic field is applied (in any of the aforementioned 6 directions), one can compute the perturbed molecular dipole and atomic charges using any charge scheme, leading to the total molecular polarizability and its charge-fluctuating contribution (Eq. 13). With four charge schemes (Mulliken, Hirshfeld, Hirshfeld-I, and Becke), the induced-atomic-dipole contributions are also computed according to Eq. 18. There, Hirshfeld and Hirshfeld-I atomic dipoles are always computed using field-free atomic densities.

Fig. 1.

Monomers studied in this work. 1. Acetic acid. 2. Adenine. 3. Alanine dipeptide. 4. Ammonia. 5. Benzene. 6. Dodecahexene. 7. Ethanol. 8. Formamide. 9. Formic acid. 10. Indole. 11. Methanal. 12. Methane. 13. Methanol. 14. Methyl ether. 15. m-Nitroaniline (mNA). 16. Neopentane. 17. p-Nitroaniline (pNA). 18. Thymine. 19. Uracil. 20. Valine dipeptide. 21. Water.

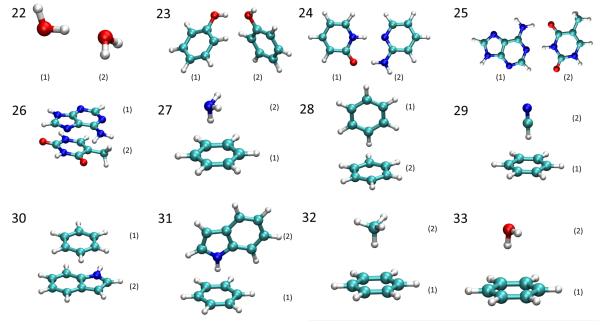
In addition, 12 dimers from the S22 database¹¹⁴ were also studied, which are shown in Fig. 2. In these complexes, the monomers are interacting with each other through either hydrogen bonding or (parallel or T-shaped) π-π stacking. By calculating the amount of charge transferred between the monomers in each complex under the partition schemes, we investigated the significance of intermolecular charge transfer (CT), which might be useful guidance as to whether or not intermolecular CT can be neglected in the development of polarizable force fields.

Fig. 2.

Dimers chosen from the S22 database. 22. water dimer. 23. phenol dimer. 24. 2-pyridoxine/2-aminopyridine complex. 25. Hydrogen-bonded adenine/thymine complex. 26. Stacked adenine/thymine complex. 27. Benzene/ammonia complex. 28. T-shaped benzene dimer. 29. Benzene/HCN complex. 30. Stacked benzene/indole. 31. T-shaped benzene/indole complex. 32. Benzene/methane complex. 33. Benzene/water complex. Numbers in the parentheses are the sequences of the monomers in each dimer.

In order to study the environment effect on the polarizability, a water pentamer, as shown in Fig. 3, was also considered. In this complex, a central water molecule is hydrogen bonded to four water molecules in a tetrahedral arrangement.

Fig. 3.

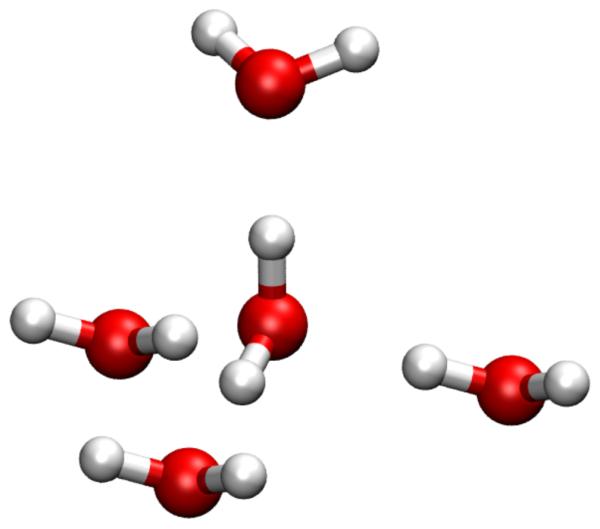
A water pentamer extracted from ice Ih,¹²⁵ in which the central water molecule interacts with the other four water molecules through hydrogen bonds.

Results and Discussion

Atomic Charges and Molecular Dipoles

Basis Set and Functional Dependence of the charge definitions

The basis set dependence of the atomic multipoles (especially the monopoles) can be an important issue in force field development. To investigate this dependence, 9 atomic orbital basis sets were utilized in the calculation of the electronic structures of the model systems at the B3LYP¹¹⁵ level of theory, including 7 Pople-style basis sets (6-31G(d), 6-31+G(d), 6-31+G(d,p), 6-311+G(d), 6-311+G(d,p), 6-311++G(d,p), 6-311++G(3df,3pd)) and 2 Dunning-style basis sets (cc-pVDZ and cc-pVTZ). The basis set dependence of the fitted charge for each definition was measured by

$$\chi =\sqrt{\frac{{\sum }_i{\sum }_j{(Q_{\mathit{ij}}-\langle Q_i\rangle )}^2}{{\sum }_i{\sum }_{j}1}},$$ (20)

where index i is for the atoms in all the molecules studied in this work and index j is for the basis sets. ⟨Q_i⟩ is the atomic charge for atom i averaged over all the basis sets. The results are shown in Table 1. Löwdin (χ = 0.1617 e) and Mulliken (χ = 0.1790 e) charges show the strongest basis set dependence, which is well-known in the community. Hirshfeld-I (χ = 0.0295 e), NPA (χ = 0.0234 e), and two ESP based charges, CHELPG (χ = 0.0253 e) and MK-ESP (χ = 0.0302 e), display basis set dependencies that are comparable among themselves, but are about one order of magnitude smaller than those of the Löwdin and Mulliken schemes and one order of magnitude larger than those of Becke (χ = 0.0031 e) and Hirshfeld/CM5 (χ = 0.0039 e) charges. Therefore, as far as basis set dependence is concerned, Löwdin and Mulliken charges are generally not ideal choices for the parameterization of force fields. Hirshfeld-I, NPA, CHELPG and MK-ESP are acceptable, while the best choices are Becke, Hirshfeld, and CM5 charges.

Table 1.

Atomic charge fluctuation (a.u.) among different basis sets and density functionals measured by Eq. 20.

charge definition	Löwdin	Mulliken	Becke	Hirshfeld (CM5)	Hirshfeld-I	NPA	CHELPG	MK-ESP
χ basis	0.1617	0.1790	0.0031	0.0039	0.0295	0.0234	0.0253	0.0302
χ functional	0.0016	0.0050	0.0014	0.0014	0.0067	0.0019	0.0039	0.0039

The density functional dependence (χ_functional in Table 1) is also calculated with Eq. 20 by comparing the fitted atomic charges from three density functional approximations, namely, B3LYP,¹¹⁵ M06-2X,¹¹⁶ and ωB97X-D,¹¹⁷ with the 6-31G(d) basis set. Here j is the index for the functionals and ⟨Q_i⟩ is averaged over these three density functionals for atom i. The functional dependence is very weak with a root-mean-square-fluctuation (RMSF) of the atomic charges ranging from 0.0014 e for Becke and Hirshfeld/CM5 charges to 0.0067 e for Hirshfeld-I charges.

Molecular Dipoles

Molecular dipole moments, as computed from atomic charges (i.e., the first term in Eq. 13), are shown in Table 2, where they are compared against the QM dipole moments computed from the electron density. We shall not attempt to compare them against experimental dipole moments because: (a) experimental dipole moments are not available for some molecules in our study; and (b) we have no reason to expect that the dipole moments from atomic charges are more accurate than the underlying QM level of theory. Here are some observations from Table 2:

• The dipole moments from NPA charges show the largest positive deviation from the QM dipoles, with dipoles overestimated by 1.14 D in terms of the root-mean-square-deviation (RMSD^b, which only accounts for the scalar value of the dipole moments), and 35.6% in terms of the mean relative difference (MRD). This overestimation is more pronounced for molecules with small dipole moments, such as methyl ether, ethanol, methanol, and methanal.

• On the opposite end, due to the small charge values, the dipole moments from Hirshfeld charges are significantly lower than the QM values by 0.90 D in terms of the RMSD^b and −31% in terms of the MRD.

• Mulliken (RMSD^b = 0.69 D; MRD = 8.9%), Becke (RMSD^b = 0.47 D; MRD = −6.5%), and Löwdin (RMSD^b = 0.30 D; MRD = −3.9%) show increasingly improved dipole moments over NPA and Hirshfeld charges.

• With a correction to the systematic deviation in Hirshfeld charges, CM5 offers much improved dipole moments (RMSD^b = 0.22 D; MRD = −6.2%).

• Hirshfeld-I, another scheme to improve upon Hirshfeld charges, also offers more accurate dipoles with a slightly lower RMSD^b value of 0.18 D and a much better MRD value of −1.4%. This result is somewhat surprising because previous studies by other groups showed that the Hirshfeld-I scheme overestimates the atomic charges.^91,118

• Out of all of the charge models, CHELPG and MK-ESP charges best reproduce the molecular dipole moments with a RMSD^b value as small as 0.04 D and a MRD value of 1.1%. This is not surprising because these charges are fitted from the electrostatic potential on grid points around the molecules, which arise mainly from the molecular dipole moments (with smaller contributions from higher-order moments) for the 21 neutral molecules in this study.

Table 2.

QM molecular dipole moments (in debye) from B3LYP/6-31G(d) calculations and those computed from atomic charges within various charge models (first term in Eq. 13). Molecules with zero dipole moments (benzene, dodecahexene, methane and neopentane) are excluded. Relative differences in the dipole moments are shown in parentheses, with the mean relative difference (MRD) listed in the last row.

	QM	Löwdin	Mulliken	Becke	Hirshfeld	Hirshfeld-I	CM5	NPA	CHELPG	MK-ESP
acetic acid	4.40	4.09	5.01	4.08	2.87	4.38	4.22	6.02	4.43	4.41
		(−7.0%)	(13.9%)	(−7.3%)	(−34.8%)	(−0.5%)	(−4.1%)	(36.8%)	( 0.7%)	( 0.2%)
adenine	2.66	2.11	2.38	2.24	1.84	2.67	2.42	2.85	2.69	2.71
		(−20.7%)	(−10.5%)	(−15.8%)	(−30.8%)	( 0.4%)	(−9.0%)	( 7.1%)	( 1.1%)	( 1.9%)
alanine	3.11	3.31	2.87	3.46	2.81	3.04	3.02	3.60	3.11	3.13
		( 6.4%)	(−7.7%)	(11.3%)	(−9.6%)	(−2.3%)	(−2.9%)	(15.8%)	( 0.0%)	( 0.6%)
ammonia	1.70	1.26	1.45	1.17	0.48	1.80	1.39	1.78	1.75	1.77
		(−25.9%)	(−14.7%)	(−31.2%)	(−71.8%)	( 5.9%)	(−18.2%)	( 4.7%)	( 2.9%)	( 4.1%)
ethanol	1.56	1.67	2.14	1.17	0.70	1.73	1.48	2.99	1.56	1.56
		( 7.1%)	(37.2%)	(−25.0%)	(−55.1%)	(10.9%)	(−5.1%)	(91.7%)	( 0.0%)	( 0.0%)
formamide	3.82	3.47	3.83	3.44	2.84	3.69	3.53	4.94	3.83	3.82
		(−9.2%)	( 0.3%)	(−9.9%)	(−25.7%)	(−3.4%)	(−7.6%)	(29.3%)	( 0.3%)	( 0.0%)
formic acid	1.75	1.57	1.54	2.00	1.62	1.70	1.68	1.88	1.76	1.76
		(−10.3%)	(−12.0%)	(14.3%)	(−7.4%)	(−2.9%)	(−4.0%)	( 7.4%)	( 0.6%)	( 0.6%)
indole	2.19	2.04	0.98	2.30	1.89	2.27	1.85	1.78	2.18	2.19
		(−6.8%)	(−55.3%)	( 5.0%)	(−13.7%)	( 3.7%)	(−15.5%)	(−18.7%)	(−0.5%)	( 0.0%)
methanal	2.19	1.82	2.56	1.47	1.42	2.05	2.10	3.63	2.22	2.21
		(−16.9%)	(16.9%)	(−32.9%)	(−35.2%)	(−6.4%)	(−4.1%)	(65.8%)	( 1.4%)	( 0.9%)
methanol	1.69	1.79	2.27	1.46	0.77	1.69	1.59	2.96	1.70	1.70
		( 5.9%)	(34.3%)	(−13.6%)	(−54.4%)	( 0.0%)	(−5.9%)	(75.1%)	( 0.6%)	( 0.6%)
methyl ether	1.27	1.60	2.21	1.33	0.64	0.91	1.38	2.99	1.33	1.32
		(26.0%)	(74.0%)	( 4.7%)	(−49.6%)	(−28.3%)	( 8.7%)	(135.4%)	( 4.7%)	( 3.9%)
mNA	5.65	5.67	7.10	6.07	4.59	5.37	5.39	6.94	5.74	5.72
		( 0.4%)	(25.7%)	( 7.4%)	(−18.8%)	(−5.0%)	(−4.6%)	(22.8%)	( 1.6%)	( 1.2%)
pNA	7.12	7.17	8.22	7.65	6.00	6.80	6.83	8.32	7.19	7.18
		( 0.7%)	(15.4%)	( 7.4%)	(−15.7%)	(−4.5%)	(−4.1%)	(16.9%)	( 1.0%)	( 0.8%)
thymine	4.29	3.89	5.00	3.65	3.39	4.11	4.01	5.96	4.29	4.26
		(−9.3%)	(16.6%)	(−14.9%)	(−21.0%)	(−4.2%)	(−6.5%)	(38.9%)	( 0.0%)	(−0.7%)
uracil	4.32	3.89	5.07	3.47	3.45	4.31	4.03	5.95	4.37	4.36
		(−10.0%)	(17.4%)	(−19.7%)	(−20.1%)	(−0.2%)	(−6.7%)	(37.7%)	( 1.2%)	( 0.9%)
valine	2.88	3.15	2.69	3.51	2.71	2.79	2.80	3.19	2.91	2.90
		( 9.4%)	(−6.6%)	(21.9%)	(−5.9%)	(−3.1%)	(−2.8%)	(10.8%)	( 1.0%)	( 0.7%)
water	2.08	1.94	2.20	1.82	0.89	2.41	1.83	2.64	2.14	2.14
		(−6.7%)	( 5.8%)	(−12.5%)	(−57.2%)	(15.9%)	(−12.0%)	(26.9%)	( 2.9%)	( 2.9%)
RMSD1		0.36	0.87	0.66	0.94	0.25	0.24	1.24	0.06	0.06
RMSD2		0.30	0.69	0.47	0.90	0.18	0.22	1.14	0.04	0.04
MRD		(−3.9%)	( 8.9%)	(−6.5%)	(−31.0%)	(−1.4%)	(−6.2%)	(35.6%)	( 1.1%)	( 1.1%)

The RMSD^a values in Table 2, which are the RMSD of the vector difference between the computed and QM dipoles, can arise not only from a change in the magnitudes of the dipole moments but also from a change in their directions. Overall, RMSD^a values correlate well with RMSD^b values in this Table. For example, the RMSD^a values are also small for the CHELPG and MK-ESP models, suggesting that these two models produce dipole moments with accurate values and To more clearly directions.

To more clearly measure the directionality, we collected the angles between the computed dipoles using various charge schemes and the QM dipoles in Table 3. The CHELPG and MK-ESP dipole moments align very well with the QM dipole moments, with an average angular deviation of 0.65°and 0.57°. Mulliken, Becke and NPA schemes change the orientation of the dipole moments the most, with an average angular deviation of 7.55°, 7.14°, and 6.78°, respectively. In between, four other schemes have moderate errors in the dipole angles: 4.24°(Hirshfeld), 3.43° (Löwdin), 2.87° (Hirshfeld-I), and 1.42° (CM5).

Table 3.

Angles (in degree) between the QM dipole and the dipoles computed from atomic charges.

	Löwdin	Mulliken	Becke	Hirshfeld	Hirshfeld-I	CM5	NPA	CHELPG	MK-ESP
acetic acid	2.74	7.49	2.29	2.74	2.48	0.35	4.62	0.29	0.16
adenine	12.06	10.23	20.96	18.58	5.28	4.98	7.77	1.81	2.30
alanine	1.50	2.33	9.29	2.40	5.22	2.03	1.89	1.14	0.75
ammonia	0.32	0.00	0.00	0.00	0.00	0.00	0.00	0.01	0.14
ethanol	11.96	17.19	6.13	9.27	8.22	2.68	20.75	1.49	1.08
formamide	1.53	7.47	6.32	1.37	2.89	2.05	10.31	0.38	0.55
formic acid	7.19	13.69	19.24	7.30	2.16	1.13	25.06	1.15	1.09
indole	2.44	17.49	6.30	3.80	0.94	3.44	3.58	0.08	0.03
methanal	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.05	0.00
methanol	9.22	16.00	10.94	5.05	6.28	1.26	19.06	1.33	1.04
methyl ether	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.08	0.00
mNA	2.12	9.10	4.94	6.71	2.08	0.32	6.78	0.82	0.98
pNA	1.36	0.85	1.56	4.28	1.41	0.18	0.24	0.64	0.74
thymine	1.67	12.35	4.78	1.60	1.79	2.13	4.11	0.69	0.33
uracil	2.56	10.94	9.15	2.32	2.76	1.20	6.63	0.40	0.27
valine	1.54	3.22	18.98	6.30	7.19	2.44	4.23	0.67	0.19
water	0.10	0.08	0.48	0.40	0.03	0.03	0.22	0.02	0.12
Average	3.43	7.55	7.14	4.24	2.87	1.42	6.78	0.65	0.57

Therefore, as far as the dipole moment is concerned, CHELPG and MK-ESP charges appear to be good choices for developing force fields, while the Hirshfeld-I and CM5 charges might also be acceptable. Löwdin charges can be considered if one has to use a more conventional charge scheme.

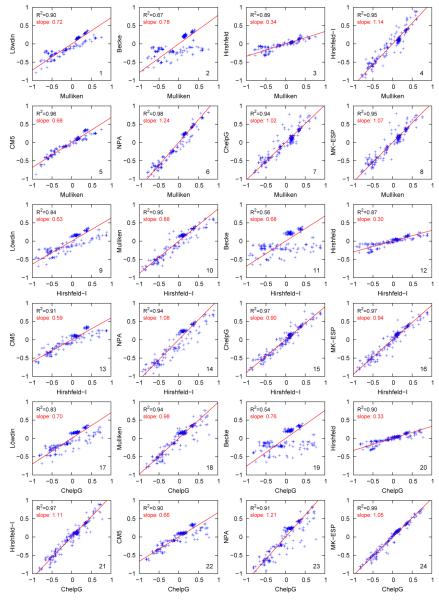
Cross-Correlation among Charge Schemes

To further understand the various trends observed above for the computed molecular dipole moments, we plot the atomic charges derived from one scheme against those from another scheme in Fig. S1 and partially in Fig. 4. For each pair of schemes, the slope is calculated by minimizing a symmetric objective function ${\chi }^2={\sum }_i{(q_2^i∕\sqrt{s}-\sqrt{s}{q}_1^i)}^2$, which leads to $s=\sqrt{{\sum }_i{\left(q_2^i\right)}^2∕{\sum }_i{\left(q_1^i\right)}^2}$. The slope values and correlations R² are listed in each panel in Fig. S1 and are also collected in Table 4. It is clear from these data that:

• The Löwdin charges correlate well with Mulliken charges (R² = 0.90), but a slope of 0.72 shows that Löwdin charges are smaller in many cases. In general, these two sets of charges correlate well with charges from other schemes, but the Mulliken charges tend to correlate much better with the ESP charges (CHELPG and MK-ESP) in terms of both R² values (0.94 and 0.95 versus 0.83 and 0.86) and slope values (1.02 and 1.07 versus 1.43 and 1.50).

• In general, the Becke charges do not correlate well with other charges, with R² values ranging from 0.54 with CHELPG charges to 0.75 with NPA charges. The only exception is the correlation between Becke charges and Löwdin charges (R²=0.91 and slope=0.92).

• The Hirshfeld charges correlate reasonably well with those from other schemes (R² ranges from 0.84 with Löwdin to 0.90 with CHELPG), with the exception of Becke charges (R² = 0.60). On the other hand, Hirshfeld charges are consistently smaller than other charges, with a slope ranging from 0.27 against NPA charges and 0.50 against CM5 charges. This qualitatively explains the small dipole moments from Hirshfeld charges, which were shown above to have a −31.0% mean relative error.

• Both improvements to Hirshfeld charges, Hirshfeld-I and CM5, in general correlate well with other charges (again with the exception of Becke charges). Of the two, Hirshfeld-I correlates better with ESP charges in terms of the R² values (0.94 and 0.97 versus 0.90 and 0.90) and the slopes (0.90 and 0.94 versus 1.51 and 1.58).

• The NPA charges correlate reasonably well with most other schemes (R² values ranges from 0.89 with Hirshfeld to 0.98 with Mulliken charges), with the exception of Becke charges (R²=0.75). NPA charges in general tend to be larger than other charges, with a slope of 1.15 against MK-ESP charges to 1.82 against CM5 charges. This is in qualitative agreement with the above observation that NPA dipole moments are on average 35.6% too large. Surprisingly, though, while NPA charges correlate well with Hirshfeld-I charges with R²=0.94 and a slope of 1.08, the latter tend to better reproduce QM dipole moments.

• The best correlation occurs between two sets of ESP charges: CHELPG and MK-ESP. The R² value is 0.99 and the slope of CHELPG charges against MK-ESP charge is 0.95.

Fig. 4.

Correlation among various charge definitions for the monomers calculated at the B3LYP/6-31G(d) level of theory.

Table 4.

Slope and R² values (in parentheses) for the correlation among atomic charges from different charge schemes.

		Löwdin	Mulliken	Becke	Hirshfeld	Hirshfeld-I	CM5	NPA	CHELPG	MK-ESP
Löwdin	slope		0.72	0.92	2.12	0.63	1.06	0.58	0.70	0.67
	R 2		(0.90)	(0.91)	(0.84)	(0.84)	(0.91)	(0.95)	(0.83)	(0.86)
Mulliken	slope	1.40		1.28	2.97	0.88	1.48	0.81	0.98	0.93
	R 2	(0.90)		(0.67)	(0.89)	(0.95)	(0.96)	(0.98)	(0.94)	(0.95)
Becke	slope	1.09	0.78		2.31	0.68	1.15	0.63	0.76	0.73
	R 2	(0.91)	(0.67)		(0.60)	(0.56)	(0.72)	(0.75)	(0.54)	(0.60)
Hirshfeld	slope	0.47	0.34	0.43		0.30	0.50	0.27	0.33	0.31
	R 2	(0.84)	(0.89)	(0.60)		(0.87)	(0.89)	(0.89)	(0.90)	(0.80)
Hirshfeld-I	slope	1.59	1.14	1.46	3.38		1.68	0.92	1.11	1.06
	R 2	(0.84)	(0.95)	(0.56)	(0.87)		(0.91)	(0.94)	(0.94)	(0.97)
CM5	slope	0.95	0.68	0.87	2.01	0.59		0.55	0.66	0.63
	R 2	(0.91)	(0.96)	(0.72)	(0.89)	(0.91)		(0.95)	(0.90)	(0.90)
NPA	slope	1.73	1.24	1.59	3.67	1.08	1.82		1.21	1.15
	R 2	(0.95)	(0.98)	(0.75)	(0.89)	(0.94)	(0.95)		(0.91)	(0.94)
CHELPG	slope	1.43	1.02	1.31	3.04	0.90	1.51	0.83		0.95
	R 2	(0.83)	(0.94)	(0.54)	(0.90)	(0.97)	(0.90)	(0.91)		(0.99)
MK-ESP	slope	1.50	1.07	1.38	3.18	0.94	1.58	0.87	1.05
	R 2	(0.86)	(0.95)	(0.60)	(0.88)	(0.97)	(0.90)	(0.94)	(0.99)

Intermolecular Charge Transfer

Charge transfer occurs naturally when there is a significant overlap of the electron density between two molecules. The amount of charge transferred from one monomer to another depends on the charge decomposition scheme, the basis set in use, and the underlying theoretical method. Table 5 lists the RMSF of the charge transferred as calculated at the B3LYP level of theory with the same basis sets used above. As in the case of individual monomers, the Löwdin decomposition scheme exhibits a significant basis set dependence (RMSF = 0.0187 e) and the Mulliken scheme displays an even more significant dependence (RMSF = 0.0418 e). On the other hand, other charge schemes display much weaker basis set dependence — RMSF ranges from 0.0023 e with Becke or NPA charges to 0.0069 e with MK-ESP charges, all below one hundredth of an electron.

Table 5.

Root-mean-square-fluctuations (RMSF) of the amount of charge transfer between monomers calculated at the B3LYP level of theory with 9 basis sets

charge definition	Löwdin	Mulliken	Becke	Hirshfeld	Hirshfeld-I	CM5	NPA	CHELPG	MK-ESP
RMSF	0.0187	0.0418	0.0023	0.0041	0.0062	0.0041	0.0023	0.0050	0.0069

B3LYP/6-31G(d) calculations were performed for the 12 dimers in Fig. 2, and the amount of charge transfer between the monomers is listed in Table 6. In general, less than 0.1 electron gets transferred between the monomers, with the only exception being the hydrogen bonded 2-pyridoxine/2-aminopyridine dimer for which MK-ESP scheme predicts a net transfer of 0.144 electron. Here are some observations:

• Despite its tendency to underestimate atomic charges (and thus molecular dipole moments), the Hirshfeld scheme produces the most significant charge transfer in 4 out of 12 complexes (benzene/water, T-shaped benzene/indole, phenol dimer, and water dimer; see boldfaced numbers in Table 6). As a result, the Hirshfeld scheme yields the most significant charge transfer (0.056 e) in terms of the mean unsigned average (MUA).

• Despite its tendency to overestimate atomic charges, the NPA scheme produces the least significant charge transfer in 9 out 12 complexes (see underlined numbers in Table 6). This is consistent with the localized picture in the NPA scheme. Consequently, its MUA is also the lowest (0.012 e).

• Except for 2-pyridoxine/2-aminopyridine and the hydrogen bonded adenine/thymine complex, the Becke scheme predicts an opposite direction for the charge transfer when compared against other schemes. It also leads to the most significant mean signed average (MSA) of charge transfer (−0.011 e) among all of the charge schemes.

• In most of the dimers containing benzene (benzene/ammonia, T-shaped benzene dimer, benzene/HCN, benzene/methane, benzene/water, T-shaped benzene/indole), in which benzene interacts with the other monomer through its delocalized π-electrons, the benzene plays the role of electron donor. The only exception is the stacked benzene/indole complex. With the Hirshfeld-I scheme, the amount of electron charges transferred out of benzene depends on the electronegativity of the other monomer. HCN attracts the largest amount of electron density from benzene, followed by benzene and water.

• Similar amounts of charge transfer can also be observed for the phenol dimer and water dimer. With most charge schemes, the amount of charge transfer becomes significantly lower in the 2-pyridoxine/2-aminopyridine complex and the hydrogen bonded adenine/thymine dimer, where each monomer functions as both a hydrogen bond donor and an acceptor. For these two complexes, we note that the ESP schemes (CHELPG and MK-ESP) predict quite significant charge transfers, which likely only reflects the deficiencies of these ESP-based schemes on systems with buried atoms.

Table 6.

Charge transfer from the 2nd molecule to the 1st molecule at the B3LYP/6-31G(d) level of theory for the dimers in Fig. 2 (units: a.u.). For each molecule (and the averages), the underlined values correspond to the smallest amount of charge transfer, while the bold-faced values highlight the largest amount of charge transfer.

	Löwdin	Mulliken	Becke	Hirshfeld	Hirshfeld-I	CM5	NPA	CHELPG	MK-ESP
water dimer	−0.055	−0.053	0.005	−0.100	−0.054	−0.086	−0.027	−0.038	−0.040
phenol dimer	−0.047	−0.040	0.020	−0.097	−0.057	−0.081	−0.023	−0.027	−0.041
2-pyridoxine/2-aminopyridine	−0.031	−0.022	−0.025	−0.038	−0.033	−0.032	−0.016	−0.086	−0.144
Adenine/Thymine H-bonded	0.035	0.021	0.047	0.041	0.026	0.032	0.026	0.054	0.078
Adenine/Thymine stacked	0.016	0.015	−0.018	0.030	0.022	0.024	0.012	0.043	0.048
benzene/ammonia	0.007	0.013	−0.054	0.043	0.029	0.041	0.003	0.016	0.025
benzene/benzene T-Shaped	−0.009	−0.017	0.053	−0.048	−0.040	−0.043	−0.005	−0.017	−0.041
benzene/HCN	0.021	0.032	−0.033	0.072	0.057	0.067	0.010	0.058	0.084
benzene/indole stacked	−0.011	−0.012	0.025	−0.021	−0.020	−0.018	−0.009	−0.011	−0.011
benzene/indole T-Shaped	0.021	0.034	−0.037	0.089	0.066	0.085	0.009	0.046	0.076
benzene/methane	0.004	0.010	−0.068	0.032	0.026	0.029	0.003	0.006	0.013
benzene/water	0.014	0.021	−0.041	0.061	0.037	0.058	0.005	0.038	0.046
mean signed average	−0.003	0.000	−0.011	0.005	0.005	0.006	−0.001	0.007	0.008
mean unsigned average	0.023	0.024	0.036	0.056	0.039	0.050	0.012	0.037	0.054

Decomposition of Static Molecular Polarizabilities

Molecular Polarizability

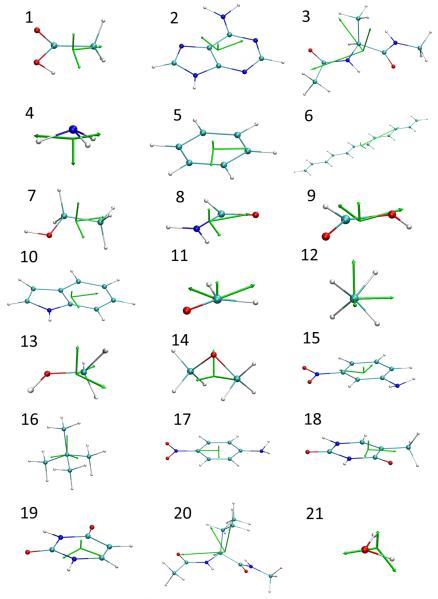
After diagonalizing the static molecular polarizability tensor (computed via finite differences), the anisotropy of the polarizability can be measured by¹¹⁹

$$\Delta \alpha =\frac{\sqrt{\frac{1}{2}[{({\tilde{\alpha }}_{\mathit{xx}}-{\tilde{\alpha }}_{\mathit{yy}})}^2+{({\tilde{\alpha }}_{\mathit{yy}}-{\tilde{\alpha }}_{\mathit{zz}})}^2+{({\tilde{\alpha }}_{\mathit{zz}}-{\tilde{\alpha }}_{\mathit{xx}})}^2]}}{\frac{1}{3}({\tilde{\alpha }}_{\mathit{xx}}+{\tilde{\alpha }}_{\mathit{yy}}+{\tilde{\alpha }}_{\mathit{zz}})},$$ (21)

where ${\tilde{\alpha }}_{\mathit{xx}},{\tilde{\alpha }}_{\mathit{yy}}$ and ${\tilde{\alpha }}_{\mathit{zz}}$ are the real part of the three components of the diagonalized polarizability tensor $\tilde{\alpha }$. The results calculated at the B3LYP/6-31G(d) level of theory are depicted in Fig. 5 and are also listed in Table 7. Clearly, the anisotropies are quite different among these molecules. Due to their high point group symmetry (T_d), the anisotropies for neopentane and methane are exactly zero. On the other hand, planar molecules can have large anisotropies, because the in-plane polarizability is much larger than the out-of-plane polarizability. In fact, adenine, benzene, formamide, indole, methanal, pNA, mNA, thymine, uracil, and water all have high levels of anisotropy between 0.698 (formic acid) and 1.020 (indole). Dodecahexene, whose polarizability aligns mainly along the molecular axis, has an even larger anisotropy of 2.061.

Fig. 5.

Molecular polarizability tensor shown as green arrows. The atoms and covalent bonds have been shrunk to make the tensors presented more clearly.

Table 7.

Molecular polarizability (a.u.) and anisotropy computed at the B3LYP/6-31G(d) level of theory.

	polarizability			anisotropy		polarizability			anisotropy
acetic acid	18.29	28.18	33.57	0.503	adenine	31.02	92.38	108.07	0.914
alanine	107.20	78.59	59.83	0.505	ammonia	5.12	9.10	9.10	0.511
benzene	20.99	75.11	75.11	0.948	dodecahexene	552.60	105.61	42.69	2.061
ethanol	29.70	25.72	23.80	0.198	formamide	28.46	21.70	9.67	0.826
formic acid	19.21	21.12	8.84	0.698	indole	125.88	95.55	29.54	1.020
methanal	14.13	18.35	6.76	0.777	methane	12.36	12.36	12.36	0.000
methanol	17.71	15.41	14.00	0.207	methyl ether	30.96	24.49	24.17	0.250
mNA	115.13	98.80	29.64	0.968	neopentane	53.44	53.43	53.44	0.000
pNA	138.87	29.45	95.64	1.085	thymine	94.29	72.01	32.72	0.814
uracil	23.68	61.98	79.26	0.896	valine	120.57	98.17	87.43	0.287
water	7.25	5.31	2.84	0.746

Contribution from Fluctuating Charges

The ratio of the charge fluctuation contributions to the total static molecular polarizability can be calculated as

$$s=\frac{\mathbf{Tr}\left({\alpha }^{\mathit{FC}}\right)}{\mathbf{Tr}\left(\alpha \right)},$$ (22)

where Tr is the trace operator and the values of s are shown in Table 8. From this table, it is clear that charge fluctuations contribute substantially to the molecular polarization, with its ratio ranging from 59.94% with the Hirshfeld scheme to 96.25% with the Mulliken scheme. Sometimes, especially with the Mulliken scheme, the ratio of the FC contribution can be over 100%, which simply means that the sum of induced atomic dipoles (i.e., the second term in Eq. 15) has the opposite direction to the FC contribution (i.e., the first term in Eq. 15), making the net induced dipole smaller than the FC contribution. The Hirshfeld-I charge model has very large FC contributions, with the smallest being for methanal (69.44%). This result indicates that it might be problematic to neglect charge transfer effects in polarizable force fields, which would require rather large atomic polarizabilities (and thus induced atomic dipoles) to mimic the significant amount of charge migration under an external perturbation.

Table 8.

The percentage of charge fluctuation contributions to the total molecular polarizability of 21 molecules, as defined in Eq. 22 using different charge schemes.

	Löwdin	Mulliken	Becke	Hirshfeld (CM5)	Hirshfeld-I	NPA	CHELPG	MK-ESP
acetic acid	62.41	93.27	59.33	56.90	74.84	63.97	93.99	94.52
adenine	72.20	90.30	70.28	69.59	80.90	71.38	91.33	92.08
alanine	70.48	106.17	67.69	66.45	80.94	68.36	98.68	99.19
ammonia	47.11	83.87	44.13	39.16	76.69	55.01	94.84	95.73
benzene	73.32	104.17	69.36	68.07	82.13	73.92	86.53	87.29
dodecahexene	86.66	101.49	84.80	84.17	91.35	86.64	93.24	93.65
ethanol	62.86	109.12	58.34	55.73	79.20	65.67	97.46	98.53
formamide	61.16	85.11	57.26	55.08	74.80	64.48	82.03	82.78
formic acid	56.63	76.11	52.88	50.94	70.74	59.51	80.30	80.83
indole	75.68	102.60	72.67	71.83	83.45	75.10	87.24	87.83
methanal	53.50	82.21	49.92	46.43	69.44	60.48	79.57	80.75
methane	59.29	115.66	51.67	45.48	76.70	66.27	94.97	96.48
methanol	58.40	99.43	53.70	50.29	77.11	63.43	95.91	97.12
methyl ether	62.88	106.10	58.67	55.46	78.78	65.41	96.99	98.06
mNA	74.62	94.78	72.54	71.69	82.54	74.29	91.85	92.53
neopentane	67.84	121.09	64.04	61.52	81.84	66.77	97.69	98.82
pNA	76.80	95.08	74.75	73.86	84.24	76.77	91.98	92.61
thymine	71.93	95.14	69.64	68.26	80.34	71.28	93.51	94.27
uracil	71.02	89.43	68.76	67.35	79.11	71.05	88.44	90.68
valine	70.77	109.47	68.32	67.03	81.92	68.18	98.78	99.32
water	38.52	60.61	37.03	33.52	71.45	47.32	78.74	79.14
average	65.43	96.25	62.18	59.94	78.98	67.40	91.15	92.01

Atomic Polarizability

When a molecule is subjected to an external electrostatic potential, the induced dipole moment on each atom can be calculated with the Mulliken, Hirshfeld, Hirshfeld-I, and Becke partition schemes (i.e., the second term in Eq. 15), and the corresponding atomic polarizability $\left({\widehat{\alpha }}^{\mathit{IAD}}\right)$ can be calculated with Eq. 18. In general, $\left({\widehat{\alpha }}^{\mathit{IAD}}\right)$ is a nonsymmetric 3 × 3 matrix, and its diagonalization leads to three principal polarizability components, which are not necessarily perpendicular to each other.

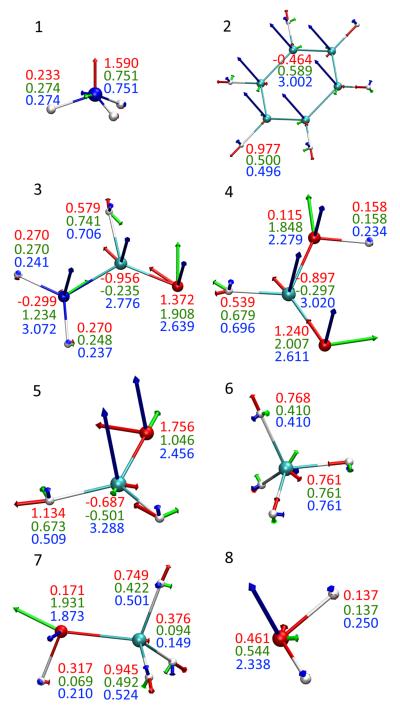
The three principal polarizability components were obtained under the Hirshfeld-I partitioning scheme for eight molecules, and the results are shown in Fig. 6. Overall, both the magnitudes and directions of the atomic polarizability components appear to be sensitive to the local connectivity. Here are some observations for different atom types:

• Nonpolar hydrogen atoms (those connected to carbon atoms). The three principal polarizabilies of the hydrogen atoms are (0.410, 0.410, 0.768) for methane and (0.496, 0.500, 0.977) for benzene, with the largest components (0.768 or 0.977) pointing along the C-H bond in both molecules. For methanol, the three components are (0.422, 0.501, 0.749) or (0.492, 0.524, 0.945), again with the largest component along the C-H bond. It is somewhat disturbing that the two methyl hydrogen atoms closer to the hydroxyl group appear to be significantly more polarizable, because all charge models in this work predict small variations in the charges on the three hydrogen atoms (0.0477, 0.0477, and 0.0807 e under the Hirshfeld-I scheme and 0.0160, 0.0160, and 0.0805 e under the MK-ESP scheme). The atomic polarizabilities of the hydrogen atoms connected to carbonyl carbon atoms also vary significantly: the three components are (0.509, 0.673, 1.134) for methanal, with a rather large component (1.134) along the C-H bond; while the atomic polarizabilities are more isotropic for nonpolar hydrogens in formamide and formic acid: (0.579, 0.706, 0.741) for formamide, and (0.539, 0.679, 0.696) for formic acid, where the smallest components (0.579 or 0.539) point nearly along the C-H bond.

• Polar hydrogen atoms (those connected to oxygen or nitrogen atoms). Compared to nonpolar hydrogen atoms, whose atomic polarizabilities range from 0.410 to 1.134, the polar hydrogen atoms have smaller atomic polarizabilities, mostly likely because these hydrogen atoms lose a significant fraction of their electrons to their neighboring atoms and thus become less polarizable. The three components are (0.137, 0.137, 0.250) for water, with the largest component (0.250) along the direction perpendicular to the molecular plane. The hydroxyl hydrogen in formic acid has a more isotropic atomic polarizability of (0.158, 0.158, 0.234), with the largest component also perpendicular to the molecular plane; in contrast, methanol has a less isotropic atomic polarizability of (0.069, 0.210, 0.317), with the largest component (0.317) within the C-O-H plane and nearly perpendicular to the O-H bond. Compared to hydroxyl hydrogens, atomic polarizabilities of amine hydrogen atoms are similar in magnitude but are more isotropic: (0.233, 0.274, 0.274) for ammonia, and (0.241, 0.270, 0.270) or (0.237, 0.248, 0.270) for the two amine hydrogens in formamide.

• Carbon atoms. As expected, the atomic polarizability of the carbon atom in methane is perfectly isotropic with a value of 0.761 along all directions. Carbon atoms in benzene, on other hand, are extremely anisotropic: they are most polarizable perpendicular to the molecular plane with a component of 3.002 (suggesting that the π-electrons are most polarizable); and the value is 0.589 along the six-membered ring, and most interestingly, the polarizability is −0.464 along C-H bonds. In other words, an electric field along the C-H bond will generate an opposing response. The atomic polarizabilities of carbonyl carbon atoms are even more anisotropic with two negative components: (−0.956, −0.235, 2.776) for formamide, (−0.897, −0.297, 3.020) for formic acid, and (−0.687, −0.501, 3.288) for methanal, with the largest component (2.776 or 3.020 or 3.288) perpendicular to the molecular plane (again suggesting that the π-electrons are most polarizable), and the negative components lie in the molecular plane.

• Oxygen atoms. Carbonyl oxygens have very large atomic polarizabilities: (1.372, 1.908, 2.639) for formamide; (1.240, 2.007, 2.611) for formic acid; (1.046, 1.756, 2.456) for methanal, with the largest components (2.639 or 2.611 or 2.456) all perpendicular to the molecular plane (i.e., π-electrons are most polarizable). But even the smallest component, which lies along the C=O bond, is quite significant (1.372 or 1.240 or 1.046). Hydroxyl oxygen atoms also have large atomic polarizabilities: (0.115, 1.848, 2.279) for formic acid, (0.171, 1.873, 1.931) for methanol, and (0.461, 0.544, 2.338) for water, all with a large component of polarizability (2.279 or 1.873 or 2.338) lying perpendicular to the plane formed by the oxygen atom and its two neighbors. The component that bifurcates its neighboring atoms has a large fluctuation (1.848 or 1.931 or 0.544) among the three molecules. Meanwhile, the third component is much smaller in magnitude.

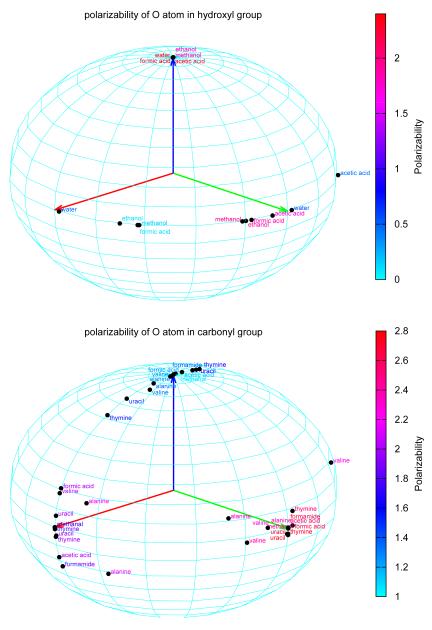
  To further investigate the transferability of atomic polarizabilities, the principal polarizability components of hydroxyl oxygen atoms and carbonyl oxygen atoms appearing in all of the 21 molecules are projected into the atomic local frame¹²⁰ and are plotted in Fig. 7. For hydroxyl oxygen atoms, the z component of the polarizability, i.e., the component perpendicular to the plane formed by the oxygen atom and its neighbors, is very consistent in all the molecules. But the other two components are scattered and have large fluctuations in magnitude. For the carbonyl oxygen atom, all of the three components vary significantly from molecule to molecule. As such, this figure demonstrates some degree of transferability for the computed atomic polarizabilities.

• Nitrogen atoms. The dominant component of the atomic polarizability (1.590) of the nitrogen atom in ammonia lies along the axis of C₃ symmetry. The other two components are degenerate and the magnitude (0.751) is about one half of the first component. On other hand, the nitrogen atom in formamide has much larger component (3.072) of polarizability perpendicular to the H-N-C plane. The second component (1.234) points along the N-C bond. And the third one has a small negative value (−0.299).

Fig. 6.

Atomic polarizability $\left({\widehat{\alpha }}^{\mathit{IAD}}\right)$ under Hirshfeld-I scheme for 1. Ammonia. 2. Benzene. 3. Formamide. 4. Formic acid. 5. Methanal. 6. Methane. 7. Methanol. 8. Water.

Fig. 7.

Atomic polarizabilities from various functional groups.

Overall, with the exceptions of the carbon atom in methane (which is in a high symmetry local environment) and the hydrogen atoms in hydroxyl groups, the atomic polarizabilities as computed in this work are rather anisotropic. As an extreme case, the three components of the atomic polarizability of the hydroxyl oxygen atom in formic acid can differ in magnitude by a factor of 20 (i.e., 0.115 versus 2.279). Some components can even be negative, such as for benzene carbon, carbonyl carbon, and amide nitrogen atom. The importance of anisotropy in the polarizability has also been investigated several times before^121–123 and a computationally feasible solution has also been presented.¹²⁴

As a further investigation of the transferability of computed atomic polarizabilities (and thus their applicability in extended systems), a calculation on the water pentamer¹²⁵ (shown in Fig. 3) was performed. The central water molecule is embedded in an inhomogeneous electrostatic environment generated by the four other water molecules. Marenich et al. noticed that the total polarizability (including both the charge transfer term and local deformation of electron density) of buried atoms can be reduced or quenched by its surrounding atoms.¹²⁶ We observe the same for this water pentamer under the Hirshfeld partition scheme. Table 9 shows that the polarizability of the oxygen atom in the central water molecule is more isotropic and is around 1.61 a.u., while the atomic polarizability components of the oxygen atoms in the other water molecules are less isotropic and are in the range from 1.86 to 2.23 a.u.. However, Hirshfeld-I analysis indicates that the average atomic polarizabilities of the oxygen atom in the central water molecule (1.68) are larger than those of the surrounding oxygen atoms: 1.19 for the two hydrogen bond acceptor water molecules; and 1.36 for the two hydrogen bond donor water molecules. Besides, these water molecules differ from the gas-phase water molecule (see Fig. 6) in terms of their atomic polarizability with a varying degree: gas (1.11) < acceptor (1.19) < donor (1.36) < central (1.68).

Table 9.

The principal polarizability components (a.u.) of the oxygen atoms in the water pentamer and the net charge of each water molecule under Hirshfeld and Hirshfeld-I schemes. x: the direction perpendicular to the water plane. y: the direction bifurcating the hydrogen atoms. z: the direction perpendicular to the x-y plane.

	Hirshfeld					Hirshfeld-I
	polarizability				net charge	polarizability				net charge
	x	y	z	average		x	y	z	average
central	1.63	1.61	1.61	1.61	0.004	2.46	1.50	1.08	1.68	0.005
acceptor	1.90	1.94	1.86	1.90	0.139	2.50	0.76	0.30	1.19	0.076
donor	1.96	2.23	2.04	2.08	−0.141	2.27	1.39	0.42	1.36	−0.078

Conclusions

The static molecular polarizability, which is the response of a molecule to an external electric field, was computed in this work for 21 small molecules using density functional theory and a finite-difference scheme. Altogether, nine charge population schemes (Löwdin, Mulliken, Becke, Hirshfeld, Hirshfeld-I, NPA, CM5, CHELPG, MK-ESP) were employed to compute the charge fluctuation contribution to the molecular polarizability. Four schemes (Mulliken, Becke, Hirshfeld, Hirshfeld-I), for which atomic electronic densities are well-defined, can also yield the induced dipole contributions from each atom to the molecular polarizability. Our results show that:

• The fluctuating charge contribution to the molecular polarizability is found to be rather significant with all nine charge schemes, with its ratio ranging from 59.9% with the Hirshfeld or CM5 scheme to 96.2% with the Mulliken scheme for the 21 small molecules included in this study.

• The atomic polarizabilities, as computed from the induced atomic dipoles for 8 small molecules using the Hirshfeld-I scheme, are clearly anisotropic for the vast majority of atoms. For example, the out-of-plane polarizability of benzene carbon atoms or carbonyl carbon atoms can be significantly larger than the other components, meaning that π electrons are more polarizable than other electrons. Some components of the computed atomic polarizabilities are even negative.

This suggests to us that (a) more emphasis probably should be placed on the charge fluctuating terms in future polarizable force field development; (b) an anisotropic polarizability might be more suitable than an isotropic one in polarizable force fields based entirely or partially on the induced atomic dipoles.

On the other hand, this work has several limitations:

• This work does not address the Pauli repulsion or dispersion effects, which are strongly coupled to the polarization effect (the main focus of this work) in condensed-phase simulations. We note that Pauli repulsion has been included in a quantum mechanical manner in ab initio-derived force fields such as the effective fragment potential.¹²⁷

• While the significance of charge fluctuations within the molecules is clearly demonstrated, this work does not provide any new route forward to account for the charge fluctuation effect via a force field.

• Arguably in the computation of atomic polarizabilities using Eq. 18, one can use the effective electric field on individual atoms instead of the applied external field.

• The atomic polarizabilities as computed using Eq. 18 showed some, albeit limited, transferability across molecules. Therefore, more work is needed to turn such observations into practical force fields.

For the last point, one potential approach to move forward is to extend this study to many more compounds and gain a more complete understanding of atomic polarizabilities (as computed from the induced atomic dipoles), especially their anisotropy. Then one could use that understanding to develop a proper parameterization scheme and, since the polarizability in condensed phase (even in water pentamer) can significantly differ from that in the gas phase, ^128–131 use QM/MM calculations to fit anisotropic atomic polarizabilities in a self-consistent fashion.^132,133

During the course of decomposing the molecular polarizabilities, we have also reconfirmed several known facts about atomic charges:

• Mulliken and Löwdin charges have a stronger basis set dependence than other charges. Hirshfeld-I, NPA, CHELPG, and MK-ESP charges show moderate basis-set dependence. Becke, Hirshfeld and CM5 are the least basis-set dependent charge schemes.

• Compared to basis-set dependence, the dependence on the density functional approximation is weaker but still not negligible.

• Two ESP-based schemes, CHELPG and MK-ESP, best reproduce the dipole moments as computed from the quantum mechanical electron density. Hirshfeld charges, which are systematically smaller than other charges, lead to underestimated molecular dipole moments. As a significant improvement, the Hirshfeld-I scheme well reproduces both the magnitudes and the directions of the molecular dipole moments. NPA, on other hand, yields significantly overestimated molecular dipole moments. Löwdin and Becke charge schemes perform better than Mulliken charge scheme, but less well than Hirshfeld-I, CHELPG, and MK-ESP schemes.

• For a subset of 12 molecular complexes from the S22 database, the amount of charge transfer between the two monomers generally falls between 0.01 and 0.1 e, but these amounts are noticeably dependent on the charge scheme. Surprisingly, Hirshfeld charges, which are relatively small compared to other charges, predict the largest amount of charge transfer for 4 out of 12 complexes and also the largest mean unsigned average for the 12 complexes. On the other hand, NPA charges, which tend to be larger than other charges, predict the smallest amount of charge transfer for 9 out of 12 complexes and also the smallest average across the 12 complexes.

We note that the energy stabilization associated with charge transfer has been investigated for the water dimer,^134,135 but its effect in other complexes has yet to be investigated systematically. If the charge transfer interaction energies are shown to be substantial, it will be even more desirable to include explicit charge fluctuation terms in future polarizable force fields.