Synonymous and Nonsynonymous Distances Help Untangle Convergent Evolution and Recombination

Abstract

When estimating a phylogeny from a multiple sequence alignment, researchers often assume the absence of recombination. However, if recombination is present, then tree estimation and all downstream analyses will be impacted, because different segments of the sequence alignment support different phylogenies. Similarly, convergent selective pressures at the molecular level can also lead to phylogenetic tree incongruence across the sequence alignment. Current methods for detection of phylogenetic incongruence are not equipped to distinguish between these two different mechanisms and assume that the incongruence is a result of recombination or other horizontal transfer of genetic information. We propose a new recombination detection method that can make this distinction, based on synonymous codon substitution distances. Although some power is lost by discarding the information contained in the nonsynonymous substitutions, our new method has lower false positive probabilities than the comparable recombination detection method when the phylogenetic incongruence signal is due to convergent evolution. We apply our method to three empirical examples, where we analyze: 1) sequences from a transmission network of the human immunodeficiency virus, 2) tlpB gene sequences from a geographically diverse set of 38 Helicobacter pylori strains, and 3) Hepatitis C virus sequences sampled longitudinally from one patient.

1 Introduction

The field of phylogenetics aims to describe evolutionary relationships among homologous sequences, by inferring a phylogeny, or evolutionary tree (Felsenstein, 2004). In the estimation of a phylogenetic tree from a molecular sequence alignment, the absence of recombination is frequently assumed, meaning that every site along the sequence alignment has the same evolutionary history/phylogeny. Implications of recombination on tree estimation (Posada and Crandall, 2002; Schierup and Hein, 2000) and downstream analyses (Anisimova et al., 2003; Arenas and Posada, 2010a,b) have motivated the development of a plethora of tests for the presence of recombination (Awadalla, 2003; Martin et al., 2011). Most of these methods try to test whether there are segments of the sequence alignment that support different phylogenies; if so, such phylogenetic incongruence is used as evidence of recombination (Grassly and Holmes, 1997; McGuire et al., 1997; Posada and Crandall, 2001). However, another evolutionary force can produce an observed data pattern similar to the one produced by recombination. Suppose that the same selective pressure acts upon two sequences to make them appear more closely related to each other than they are under the true evolutionary history. Now, if this phenomenon, known as convergent evolution (Wake et al., 2011), occurs between these two sequences only at a localized region of the alignment, then it will appear as if this region has a different evolutionary history than the remainder of the alignment, leading to an observed phylogenetic incongruency. To our knowledge, no existing method for detecting phylogenetic incongruence can distinguish between recombination and convergent evolution. In this paper, we develop a method that can accomplish this task.

As a starting point, we consider the Dss method proposed by McGuire et al. (1997) and implemented in the TOPALi software (Milne et al., 2004). Dss, an abbreviation for \difference in the sum of squares,” is a sliding window approach that scans across the sequence alignment in question, with the following assumption: if a recombination breakpoint is present within any given window, then the portions of the window on opposite sides of the breakpoint would have distinct evolutionary trees. Our proposed modification is to base the method on a measure of evolutionary distance that considers only synonymous substitutions: the codon changes that do not result in amino acid changes. Since synonymous substitutions provide ‘neutral' information about evolutionary relationships of sequences under study (Lemey et al., 2005; Yang, 2006; O'Brien et al., 2009), we postulate that using a distance metric which considers only synonymous substitutions within the Dss framework would still allow for recombination detection, but will avoid the false positives resulting from convergent evolution. Thus, we develop a new test statistic, and a novel parametric bootstrap method to access the distribution of this statistic under the null hypothesis of no recombination in order to assess statistical significance.

To test our new recombination detection method, we first proceed via simulations to compare its performance to the original Dss statistic, both in terms of their ability to identify true recombination events, and to avoid false positives due to convergent evolution. We also examine three real data examples. The first is a human immunodeficiency virus (HIV) dataset, which comes from nine Belgian patients that belong to a known HIV transmission chain (Lemey et al., 2005). This dataset has been of particular interest because phylogenetic reconstructions can be compared to the known transmission chain, providing a real data example in which estimation procedures can be validated. In their work, Lemey et al. (2005) studied two distinct HIV genes: pol and env, and concluded that the pol gene was under convergent selective pressures, whereas the env gene was not. Here, we revisit this question with our method, by examining a concatenated alignment of the pol and env genes. Our second real data example is a sequence alignment of the tlpB gene encoding the methyl-accepting chemotaxis protein in Helicobacter pylori. The importance of the TlpB protein lies in its role as a chemoreceptor and also in colonizing the bug to the gastric mucosa of its host (Croxen et al., 2006). Interestingly, using multiple recombination detection statistics, we found evidence of recombination in tlpB. Therefore, we choose this important gene to analyze the distribution of recombination signals across synonymous and nonsynonymous substitutions via our Dss statistics, and to determine where there is evidence of actual recombination events. Finally, we investigate a Hepatitis C virus (HCV) sequence alignment from serum samples collected over roughly 10 years from one chronically infected individual (Palmer et al., 2012). In their work, Palmer et al. (2012) examined sequences of the hypervariable region 1 (HVR1) of the HCV genome and found evidence of recombination between two distinct viral populations residing in the individual. However, HVR1 is subject to selective pressure, as antibody responses to HCV infection target this region (Zibert et al., 1995). Thus, we analyze this dataset with our Dss statistics to again test whether the recombination signal is due to a true recombination, or due to convergent evolution.

2 Methods

2.1 Evolutionary Distances

Let Y be a matrix that represents a DNA sequence alignment, composed of row vectors y₁, …, y_n, where n is the number of taxa/species/sequences. Then, y_k = (y_k1, …, y_kL), where L is the length, or number of sites in the sequence alignment. For a given DNA sequence alignment, one common summary of the data is the distance matrix d = {d_kl}, where each element d_kl is the distance between sequences k and l, for k; l ∈ (1, …, n). Intuitively, each pairwise distance simply indicates how different two sequences are from each other. For example, two sequences that are identical at every site along the alignment would have a distance of 0, under most sensible measures of distance.

Typically, one assumes a substitution model that is defined by the rates of change between the possible states. For a pair of taxa, the evolution of each site (y_ks; y_ls) for s ∈ (1, …, L) can thus be described by a continuous-time Markov chain (CTMC) with infinitesimal generator Λ = {λ_ij} for i, j, ∈ (1, …, M), where M is the number of states (e.g. for DNA nucleotide data, M = 4 as the state space is {A; C; G; T}; for DNA codons, M = 64 as the state space is {A; C; G; T}³), and the rate of leaving state i is ${\lambda }_i\equiv {\sum }_{j\ne i}^M{\lambda }_{ij}$ With stationary distribution π ≡ (π₁, …, π_M), we then can calculate distances for each pair (k; l) as

$${\widehat{d}}_{kl}=\sum _{i=1}^M{\widehat{\pi }}_i{\widehat{\lambda }}_i,$$ (1)

with the necessary parameter estimates being calculated from the data. As this quantity is equal to the average number of jumps in a stationary continuous-time Markov chain, evolutionary distances are thus defined as the expected number of substitutions per site, according to the given continuous-time Markov chain model.

The notion of an evolutionary distance can be generalized to consider certain subsets of substitutions. For example, it is sometimes of biological interest to count only transitions (A ⇌ G and C ⇌ T), or transversions (A ⇌ T, A ⇌ C, G ⇌ T, and G ⇌ C). A variety of ad-hoc strategies could be used to account for this (Felsenstein, 2004), but it can also be formally incorporated into the framework of CTMC models of DNA evolution as was demonstrated by O'Brien et al. (2009). First, we define the set L to be the subset of the lattice {1, …, M}² that indicates the substitutions which we wish to count; that is, (i; j) ∈ 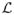if i → j is a substitution of interest. Then, we can express distances for any labeled subset of substitutions as

$${\widehat{d}}_{\mathcal{L}}=\sum _{i=1}^M{\widehat{\pi }}_i\sum _{j\ne i}^M{\widehat{\lambda }}_{ij}{1}_{\{(i,j)\in \mathcal{L}\}},$$ (2)

for each pair of sequences (k; l). The indicator function 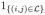in (2) is equal to 1 if i → j is a substitution of interest, and 0 if it is not. In this manner, the labeled distance metric does not count the substitutions that are not of interest. In this work, we specifically appeal to the labeled subset known as synonymous substitutions: the changes in codon state which do not result in a change in amino acid.

2.2 Distance-Based Recombination Detection: Dss Statistic

The Dss method for the detection of recombination is based upon evolutionary distances. First, with an estimated distance matrix, one can infer a phylogeny, which consists formally of a topology τ and branch lengths b. The tree distance t_kl(τ; b) between taxa k and l is then the sum of the branch lengths between them on any particular topology. With d̂_kl estimated from DNA sequence data as above, least squares phylogenetic inference then proceeds by finding

$$\underset{\mathit{\tau },\mathbf{b}}{\text{argmin}}\sum _{k,l}{\left[{\widehat{d}}_{kl}-t_{kl}(\mathit{\tau },\mathbf{b})\right]}^2,$$ (3)

which is the usual least squares criterion. The solution (τ̂, b̂) to (3) then gives the least squares phylogeny.

Now, we define recombination as an exchange of genetic material between two taxa that results in different evolutionary histories for the different respective parts of the sequence alignment. The Dss method then uses a sliding window approach (McGuire et al., 1997; McGuire and Wright, 2000; Milne et al., 2004), as illustrated in Figure 1, where the two panels show a window (in red) moving across a sequence alignment.

Figure 1.

Illustration of two overlapping sliding windows, shown as red boxes, across a sequence alignment of four taxa. The vertical grey lines divide each window in half.

First, the average of all estimated pairwise distances from the entire sequence alignment is recorded as d̄. Next, the distance matrix is estimated with a DNA substitution model for the first half of a given window, along with its mean, w̄^{1}. This distance matrix is then standardized by multiplying each entry by d̄/w̄^{1}, and the resulting standardized distance matrix for the first half of the window is recorded as ${\widehat{\mathbf{d}}}^{\{1\}}=\{{\widehat{d}}_{kl}^{\{1\}}\}$. Using phylogenetic least squares as described above, we then calculate

$$\underset{\mathit{\tau },\mathbf{b}}{\text{argmin}}\sum _{k,l}{\left[{\widehat{d}}_{kl}^{\{1\}}-t_{kl}(\mathit{\tau },\mathbf{b})\right]}^2.$$ (4)

The estimated topology is recorded as τ̂^{1}, and the minimized value of the sum of squares in (4) is recorded as ${\mathit{SSa}}_w^F$.

For the second half of the window, again the distance matrix is estimated, with its mean stored as w̄^{2} and again the standardized distance matrix is calculated by multiplying each entry byn d̄/w̄^{2} to obtain ${\widehat{\mathbf{d}}}^{\{2\}}=\{{\widehat{d}}_{kl}^{\{2\}}\}$. Now, we calculate

$${\mathit{SSb}}_w^F=\underset{\mathbf{b}}{min}\sum _{k,l}{\left[{\widehat{d}}_{kl}^{\{2\}}-t_{kl}({\widehat{\mathit{\tau }}}^{\{1\}},\mathbf{b})\right]}^2.$$ (5)

That is, the topology from the first half is imposed as fixed in (5), and only the branch lengths are optimized according to the sequence alignment of the second half of the window.

For each window, we then have ${\mathit{Dss}}_w^F=({\mathit{SSa}}_w^F-{\mathit{SSb}}_w^F)$. The entire procedure is repeated in the reverse direction, by starting with a window at the end of the alignment, swapping the roles of each half of the window, and then sliding it backwards across the sequence alignment; this gives ${\mathit{Dss}}_w^B$ for each window. Then, $Ds{s}_w=max({\mathit{Dss}}_w^F,{\mathit{Dss}}_w^B)$. Finally, here we consider only the maximum Dss statistic from all windows, giving us $Ds{s}_{\mathit{max}}=\underset{w}{max}(Ds{s}_w)$.

Our modification of the Dss statistic uses estimates of labeled distances for synonymous substitutions, estimated by the method developed by O'Brien et al. (2009), replacing d̄ and ${\widehat{d}}_{kl}^{\{·\}}$ in the calculation of Dss_max above. The original Dss method tests for discrepant _kl phylogenies throughout windows across the sequence alignment. However, it cannot distinguish between the case where the discrepancies are actually due to an exchange of genetic material, as opposed to convergent selective pressure. In other words, with the Dss method, the null hypothesis is that the sequence alignment has one true evolutionary history that has been affected neither by recombination nor convergent evolution, and evidence against the null hypothesis may be due to either recombination or convergent evolution, or due to the presence of both of these events.

With our new synonymous Dss statistic, our null hypothesis remains the same, but our new test will detect only departures from the null that are due to an exchange of genetic material. Under the assumption that selective pressure acts on the amino acid level, synonymous substitutions are presumed to be neutral, and therefore distances based upon them would ignore selective pressures. In this manner, potential false positive signals for recombination due to selection can be avoided.

2.3 Modified Parametric Bootstrap

To assess statistical significance, McGuire and Wright (2000) propose a parametric boot-strap to generate the null distribution of the test statistic. Under this parametric bootstrap, the distribution of Dss_max is simulated under the null hypothesis as follows: first, the Ordinary Least Squares tree for the entire sequence alignment is obtained, under the chosen model of substitution. In this manner, the data are treated as if the sequences were inherited through one true tree and substitution model, in accordance with the null hypothesis. Next, sequence data are simulated under this tree, B times. Finally, the Dss values are calculated under the same procedure as outlined above for each simulated sequence alignment, and saving only the maximum from each simulated realization. Thus, one obtains the distribution of the maximum Dss statistic under the null hypothesis. This gives the basis for determining how extreme an observed Dss statistic is, and we calculate the Monte Carlo estimate of the p-value as the proportion of simulated null Dss values that are more extreme than our observed value in question.

However, we must make important modifications to the parametric bootstrap for assessing statistical significance of the Dss statistic as first proposed by McGuire and Wright (2000). First, we estimate the distances between sequences on the codon scale (e.g. the expected number of substitutions per codon site). Using this distance matrix, we then estimate the least squares tree, which represents the null hypothesis of the evolutionary history of the sequences: with no recombination or convergent evolution. Next, we estimate codon substitution parameters from the codon model proposed by Nielsen and Yang (1998): κ (the transition/transversion ratio) and Ω = (Ω₁; Ω₂; Ω₃) where each Ω_i is a nonsynony-mous/synonymous rate ratio, with corresponding proportions p = (p₁; p₂; p₃) where each p_i represents the probability that Ω_i will be selected as the nonsynonymous/synonymous rate ratio for any given site. This mixture of three codon models allows for estimation of variable nonsynonymous/synonymous rate ratios at each site, to simulate the bootstrap data as similarly as possible to the evolutionary process that created the original data. With the null evolutionary history, κ, Ω and p estimated from the sequence data, we then simulate our parametric bootstrap sequence alignment datasets. Using these, we calculate the original Dss statistic and the synonymous Dss statistic in the manner described above, to then obtain the distribution of the maximum, for each.

2.4 Implementation

All analyses have been performed using the R package synDss, in which we implemented the proposed methodology. The package contains our implementation of the original Dss method, our synonymous Dss method, and modified parametric bootstrap. The source code and binaries are available at http://evolmod.r-forge.r-project.org/#synDss.

3 Results

3.1 Simulations: Power and Type I Error

To assess performance of each statistic, we simulate sequences under a codon model using the software package PAML (Yang, 2007). Three basic scenarios are considered: 1) null; 2) true recombination event; 3) localized convergent evolution. For each scenario, we consider a sequence alignment with five taxa, and we set κ = 2 (transition/transversion ratio), and sample (nonsynonymous/synonymous rate ratio) from a discrete mixture model with values Ω = (0:1; 0:8; 3:2). We used three sets of sampling probabilities: p₁ = (0:74; 0:24; 0:02), p₂ = (0:85; 0:14; 0:01) and p₃ = (0:99; 0:009; 0:001) to produce average synonymous substiution proportions of 50%, 60% and 75% respectively.

Under the null scenario, we assume that every site along the sequence alignment is inherited according to one true evolutionary history. To simulate this, we provide PAML with one true phylogeny with five tips (shown in panel A of Figure 2), and simulate codon sequences along this phylogeny. Each codon sequence consists of 1032 codon sites (or 3096 nucleotides).

Figure 2.

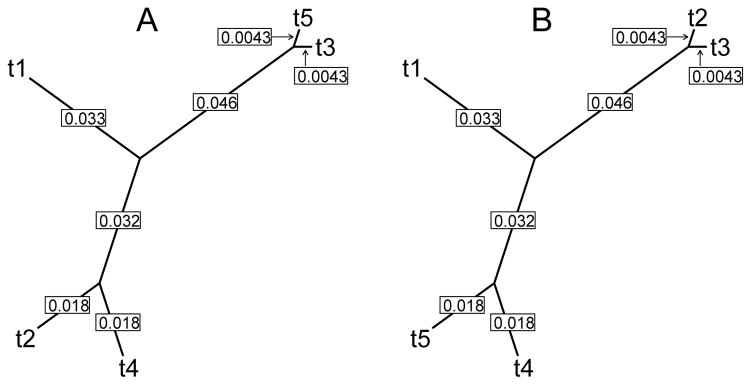
Phylogenies used for simulations. Numbers indicate branch lengths, in expected number of substitutions per site between two nodes.

For the scenario with a true recombination event, we use two phylogenies corresponding to each side of the recombination breakpoint (shown in panels A and B of Figure 2, which are identical except that taxa 2 and taxa 5 are swapped). Partial sequence alignments of length 400 and 632 codons are simulated according to each phylogeny respectively, and then concatenated to form one mosaic sequence alignment that is 1032 codons in length.

For the scenario of localized convergent evolution, we simulate codon sequences along one true phylogeny, and then choose a region upon which to have selection act. Specifically, we use the latter 632 codons as this region (as in the recombination scenario). In this region, we again target taxa 2 and taxa 5, but here we make substitutions to change differing amino acids each into another (concordant) amino acid. We choose only codon sites in which this convergent evolution could occur with one nucleotide change in each of the sequences, and select a proportion of these sites, uniformly at random, in which to make this change. To make scenarios comparable, we convert the same proportion, on average, of all sites that have codon variations initially: we set this proportion to 25% in all cases. Noting that our convergent evolution scheme can only act on sites which had nonsynonymous substitutions initially (since some sequences at these sites must be in different amino acid states), the proportion of eligible sites which get converted at random must be adjusted according to the percentage of nonsynonymous substitutions in each scenario (described above), in order to maintain the overall proportion of 25% of all variable sites that will be converted.

Finally, for every scenario, we also vary the branch lengths, to effectively vary the number of substitutions, or diversity, in each simulation. The branch lengths shown in Figure 2 are the original set of branch lengths. We consider the original branch lengths, and also branch lengths that are scaled by 0:80 and 0:67 relative to the original branch lengths, to result in scenarios of \high diversity,” \medium diversity,” and \low diversity,” respectively.

With α = 0:05, Type I error probabilities under 1000 replicates of a simulated null scenario appear to be well-behaved, with estimated Type I error probabilities of 6:6% and 6:3% for the original Dss and synonymous Dss tests, respectively. Distributions of the p-values resemble a uniform distribution, as shown in Supplementary Figure S1.

Next, we examine power to detect recombination, under the scenario with a true recombination event. We vary the expected number of substitutions (diversity) and proportion of synonymous substitutions, and examine the corresponding effect on the power of each version of the test statistic. Histograms of p-values from the original Dss statistic and synonymous Dss statistic from one scenario are shown in Supplementary Figure S2, where we observe 90% power with the original Dss test statistic, and 76% power with our synonymous Dss test statistic. The results from all scenarios are shown in Table 1. Our synonymous Dss statistic has reduced power in every case, which is to be expected since we have reduced the amount of information used. The reduction in power is less dramatic in the scenarios where a greater proportion of the substitutions are synonymous (bottom row of Table 1), since less information is being discarded in these cases.

Table 1.

Power of each test under the recombination scenario. Each column represents one set of branch lengths (equivalently, the diversity), which correspond to each average power of the original Dss test. Each cell represents the power of the synonymous Dss statistic, with 95% confidence intervals in parentheses. In each scenario, 100 simulated replications were analyzed.

	Power of original Dss
	99%	90%	85%
50% syn	66 (56.6, 75.4)	38 (28.4, 47.6)	20 (12.1, 27.9)
60% syn	79 (70.9, 87.1)	48 (38.1, 57.9)	34 (24.6, 43.4)
75% syn	87 (80.3, 93.7)	76 (67.5, 84.5)	62 (52.4, 71.6)

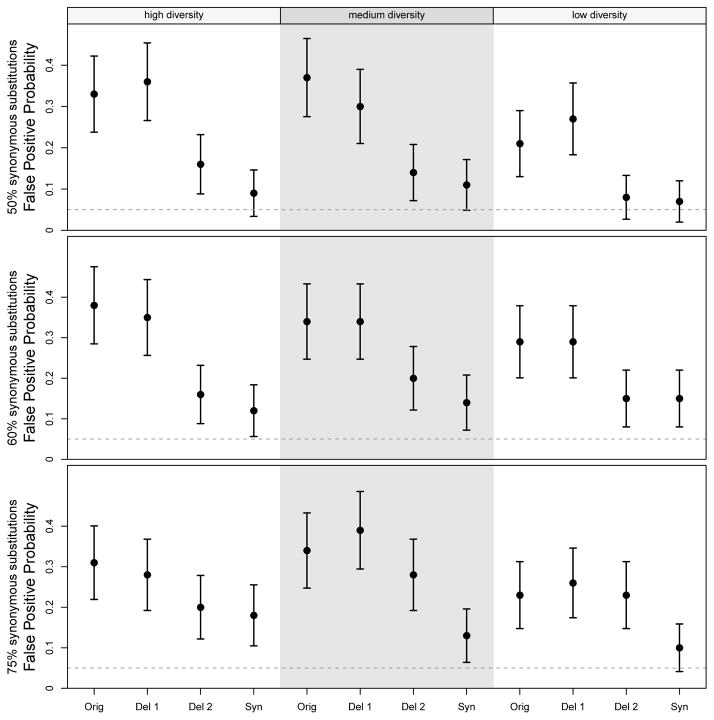
Under the scenario of convergent evolution, we compare the false positive probabilities under the original Dss statistic and the synonymous Dss statistic. That is, while the Dss statistic detects phylogenetic incongruence from any cause, we want to determine if the synonymous Dss statistic can avoid giving a significant p-value when the phylogenetic incongruence is due to convergent evolution. Under every scenario, we observe that the false positive probability of the synonymous Dss method is substantially lower than that of the original Dss statistic, as shown in Figure 3. For example, under high diversity and 50% synonymous substitutions, the estimated false positive probability for the original Dss statistic is 33%, vs. 9% for the synonymous Dss statistic. Results from all scenarios are shown in Figure 3, labeled as \Orig” and \Syn” respectively.

Figure 3.

False positive probability of each test under the convergent evolution scenario. Using the same branch length sets (diversity) and synonymous substitution proportions as in the recombination scenarios, we induce convergent evolution on the alignment instead of a true recombination. “Orig” refers to the original Dss statistic; “Del 1” refers to the case in which we remove a proportion of substitutions corresponding to the non-synonymous substitution proportion (and thus keeping a proportion corresponding to the synonymous substitution proportion); “Del 2” is similar to “Del 1” except that we also shrink the window size by the corresponding proportion; “Syn” refers to the synonymous Dss statistic. Error bars represent 95% confidence intervals based on the asymptotic binomial variance, using the observed false positive probability as p̂ to obtain standard errors. In each scenario, 100 simulated replications were analyzed.

We next examine whether this reduction in false positive probability might simply be due to the fact that the synonymous Dss statistic uses less information; that is, it considers only synonymous substitutions. To answer this question, we first examine the effect of removing a proportion of sites, corresponding to the proportion of synonymous substitutions. For example, under the scenario with 75% synonymous substitutions, we retain 75% of the alignment sites at random, and then obtain the original Dss statistic. We observe that the false positive rate under these simulations are similar to that of the original Dss statistic, as shown in Figure 3, labeled as \Del 1.”

However, this effort suffers from the fact that, while the sequence alignments are shorter, our window size has remained the same, thus resulting in fewer windows across the alignments. In our exploration of the Dss statistic behavior, we have noticed trends between window count and Power / Type I error (not shown) indicating that the \Del 1” regime is probably anti-conservative. Thus, we perform another validation experiment in which we also shrink the window size by the corresponding proportion; that is, if we removed 50% of the sites, we also shrink the window size by 50%. This is shown in Figure 3 as \Del 2.” Based on our experimentation with the relationship between window size and power (not shown), we believe this to be a conservative effort, and yet in all nine scenarios, we still obtain higher Type I error probabilities under this regime than that of the synonymous Dss statistic.

Finally, for the scenarios with 50% synonymous substitutions, we perform one additional set of experiments. Noting that in these scenarios, a nonsynonymous Dss statistic would have, on average, the same loss of information as our synonymous Dss statistic, we thus create a nonsynonymous Dss statistic in an analogous manner to which we created our synonymous Dss statistic, using labeled distances for nonsynonymous substitutions. We then run this nonsynonymous Dss statistic on the same set of data for each of the 50% synonymous substitution scenarios. In the high diversity case, we obtain a false positive probability of 19%, which is substantially higher than the synonymous Dss statistic's false positive probability of 7%. For medium and low diversity, we obtain false positive probabilities of 13% and 7% respectively, which are identical to their respective estimated false positive probabilities from the synonymous Dss statistic.

For our simulation studies, we set the number of bootstrap replicates to B = 100. We are able to use B = 500 for the real data analyses, but it would have been prohibitively time consuming to do this for the simulations. Although the resulting accuracy of significance level thresholds may thus be of some concern, we found through a brief examination that the value of the 95% significance level threshold does not move substantially with B = 100 on different parametric bootstrap runs with the same original datasets.

3.2 Data Analysis I: Belgian HIV Transmission Chain

Phylogenetic analyses of HIV sequences are useful in characterizing its transmission and spread, and these analyses are particularly relevant to elucidating the development of HIV drug resistance (Lemey et al., 2005). However, while the typically high mutation rates and short generation times for HIV are conducive towards a phylogenetic reconstruction, phylogenetic inference can be confounded by the high recombination rates, and selective pressures imposed by antiretroviral therapy and the host immune system (Rambaut et al., 2004). Our method is the first to address the important issue of distinguishing between recombination and convergent evolution, and thus we apply it here.

Of particular interest are the pol and env genes of HIV-1, which are responsible for replication (Hill et al., 2005) and cell entry (Coffin et al., 1997), respectively. These two genes were studied through a transmission chain of nine Belgian HIV-positive patients (Lemey et al., 2005), in which it was found that a phylogenetic reconstruction using the sequenced env gene was compatible with the known transmission history among these nine patients; on the other hand, the phylogenetic reconstruction using the pol gene sequences was not compatible with the transmission history. This raised the question of whether selective pressures might be the cause of this incongruity.

Specifically, Lemey et al. (2005) explored whether the selective pressure may have been due to antiretroviral drug therapies applied to HIV-positive patients in the transmission chain. They hypothesized that patients on similar antiretroviral drug treatments may invoke convergent evolution on their HIV strains, due to the fact that their respective HIV viruses may develop the same drug resistance-associated mutations. By examinating known drug resistance-associated mutations within the pol gene, they found this was in fact the case with two of their individuals: \Patient A” and \Patient I.” That is, these two individuals shared specific amino acid substitutions that have been identified by the International AIDS Society as being associated with clinical resistance to HIV antiretroviral drugs (Johnson et al., 2003).

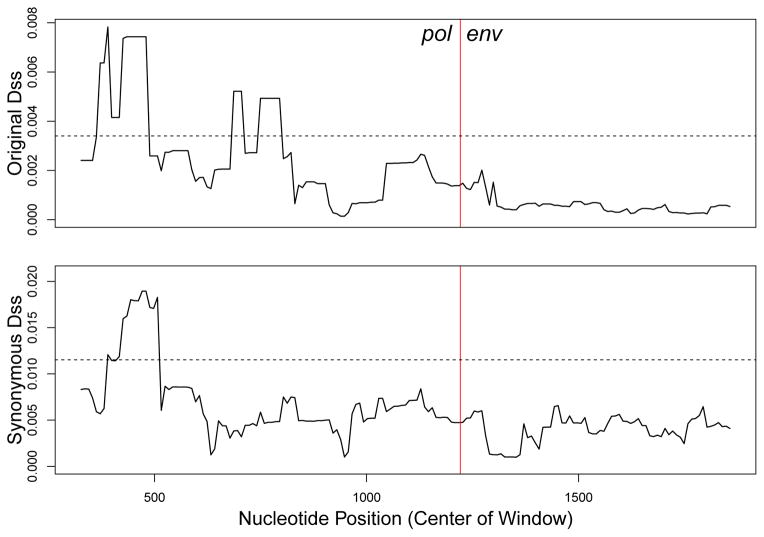
Following this observation, Lemey et al. (2005) then constructed phylogenetic trees for the pol gene based on synonymous distances and nonsynonymous distances separately, using the Syn-SCAN software (Gonzales et al., 2002). The synonymous tree was compatible with the transmission history, while the nonsynonymous tree was not, and showed Patient A's strains clustering with those of Patient I. For an illustration, see Figure 4 from the work by Lemey et al. (2005). Thus, they concluded that the pol gene was under convergent selective pressure. Here, we revisit this question by examining the behavior of each Dss statistic on a concatenated pol-env sequence alignment. That is, if we join the two sequence alignments together as one, will either recombination detection method indicate the presence of intergenic or intragenic recombination?

Figure 4. Dss statistic landscapes for pol-env concatenation.

Dotted horizonal lines represent the 95% significance level for each test, from a parametric bootstrap with B = 500. The red vertical lines represent the boundary between the two genes, with pol on the left, and env on the right.

The dataset consists of nine individuals, with multiple samples taken longitudinally from some of them, for a total of 13 sequences. Results from our analyses are shown in Figure 4. Our analysis used a window size of 636 nucleotides (or 212 codons) and a step size of 9 nucleotides (or 3 codons). To assess statistical significance, we used a parametric bootstrap with the number of replications set to B = 500. We observe that both the original Dss statistic and the synonymous Dss statistic cross their 95% bootstrap significance thresholds, suggesting the presence of a recombination event, as opposed to convergent evolution.

3.3 Data Analysis II: H. pylori tlpB gene

One of the most common diseases in the world is chronic gastritis. The human-adapted motile Gram-negative bacteria Helicobacter pylori is the major causative agent of chronic gastritis, in addition to causing stomach and duodenal ulcers and gastric cancer (Feldman et al., 1998). Infection by H. pylori is typically acquired by ingestion, with person-to-person transmission occurring most commonly through vomit, saliva or feces (Feldman, 2001; Parsonnet et al., 1999). Due to the emergence of antibiotic-resistant strains, treatment of H. pylori has begun to fail in roughly 20–30% of cases (Graham, 2009), which points to the need for a better understanding of the evolutionary processes that drive H. pylori diversity and survival.

Here, we focus on tlpB, the gene that encodes the TlpB methyl-accepting chemotaxis protein. This protein is crucial to H. pylori’s ability to colonize the stomach of its host, as it is responsible for its pH taxis, or movement in response to high acidity (Croxen et al., 2006). TlpB allows the bacterium to sense the pH of its surroundings, and move toward an optimal pH zone. Due to these functional roles, TlpB is a potential target of the immune response by the infected host. Thus, recombination is a potential diversification mechanism that could be used by TlpB to avoid elimination by the host's immune response. To investigate this, we selected tlpB gene sequences from 38 completely sequenced H. pylori genomes of globally representative isolates. Recombination detection analyses by PhiPack (Bruen et al., 2006) involving three different statistics { Pairwise Homoplasy Index (p<0.0001), Maximum χ² (p=0.005) and Neighbor Similarity Score (p<0.0001) { detected evidence of recombination in this gene. Additionally, we ran a multiple change-point recombination detection method DualBrothers (Minin et al., 2005) implemented in the R package rbrothers (Irvahn et al., 2013). This recombination detection tool found that the posterior probability of at least one break-point remains at 1.0 even when the prior probability of this event is lowered from 0.5 to 0.001, providing strong evidence in favor of presence of recombination (Supplementary Figures S3–S5).

However, there remained a possibility that this recombination signal was actually a result of convergent evolution. Especially for H. pylori that shows extensive genomic diversity, it could be a common scenario that an excess of convergent mutations created an illusion of recombination, thereby confusing traditional recombination detection algorithms. With the same tlpB sequence alignment dataset from 38 isolates, our aim is to determine whether our Dss analysis concludes that there is truly a recombination signal, or whether it was actually due to convergent evolution.

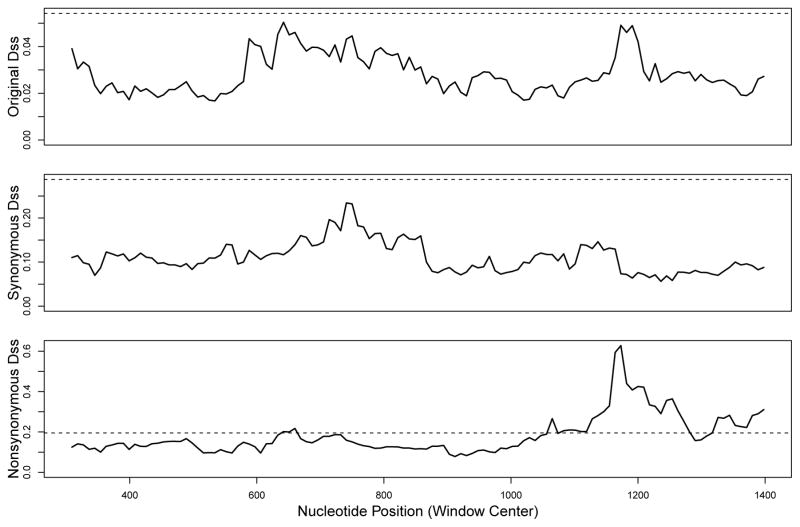
Here, we perform analyses with a window size of 600 nucleotides (200 codons), and step size of 9 nucleotides (3 codons). The sequence alignment was 1695 nucleotides (565 codons), yielding approximately 122 windows across the alignment. To obtain significance threshold levels, we use the parametric bootstrap with the number of replications set at B = 500. Results from our analyses are shown in Figure 5. We observe that neither the original Dss statistic nor the synonymous Dss statistic crosses its respective 95% bootstrap significance threshold. However, the original Dss statistic was very close, and in fact gave a bootstrap p-value of 0.058. In contrast, the synonymous Dss statistic did not come quite as close to its 95% bootstrap significance threshold, and gave a bootstrap p-value of 0.14.

Figure 5.

Dss statistic landscape for H. pylori tlpB gene. Dotted horizonal line represents the 95% significance level for each test, from a parametric bootstrap with B = 500.

It might be a possibility that the lack of signal with the synonymous Dss statistic was due to a loss of power. However, we found that the nonsynonymous Dss statistic did cross its 95% bootstrap significance threshold (shown in the bottom panel of Figure 5), with a bootstrap p-value of 0. Also, an examination of the sequence alignment revealed that there was approximately a 1.5:1 ratio of synonymous substitutions to nonsynonymous substitutions. Therefore, any loss of power observed with the synonymous Dss statistic should also be observed with the nonsynonymous Dss statistic. These results demonstrate that the signal observed in the original Dss statistic was driven primarily by nonsynonymous substitutions. Absence of any such signal with the synonymous Dss statistic strongly suggests that the recombination signal in the nonsynonymous changes was actually due to convergent evolution, most likely in response to adaptive selection pressures.

3.4 Data Analysis III: HCV

HCV is an RNA virus that is estimated to infect roughly 3% of the human population worldwide, and is a leading cause of liver disease and liver cancer (WHO, 2003). Overall, treatment success has been limited, and thus it has been recognized that a greater understanding of the virus' evolutionary behavior is crucial to effective prevention and treatment of HCV infection (Gray et al., 2012). Indeed, specifically the matter of whether genetic recombination occurs in HCV has important implications regarding resistance development against antiretroviral treatments used against the diseases that are caused by HCV infection (Morel et al., 2011).

Similar to HIV, HCV mutates very rapidly within an infected host, which makes treatment difficult, but also should reveal patterns that will lead to a greater understanding of the link between the evolution of the virus and progression of disease (Okamoto et al., 1992; Smith et al., 1997). Curiously, however, there have been few reports of recombination occuring in HCV, despite the fact that recombination can be an important diversification mechanism in positive sense RNA viruses (González-Candelas et al., 2011). One potential reason is that simultaneous infection by two or more HCV types might be rare (Viazov et al., 2000; Tscherne et al., 2007). Additionally, it has been postulated that the viability of recombinant strains is poor in vivo (Prescott et al., 1997).

Here, we investigate a sequence alignment of the hypervariable region 1 (HVR1) of HCV, from serial samples taken over 9.6 years from a single infected patient (Palmer et al., 2012). In the initial study, Palmer et al. (2012) found evidence of recombination between two HVR1 subpopulations within the patient. However, this genetic region is subject to strong selective pressures as the envelope glycoprotein is targeted by the host antibody responses (von Hahn et al., 2007). Thus, we analyze this sequence alignment with our Dss statistics, to determine whether our analysis corroborates the original findings of Palmer et al. (2012), or whether this recombination signal is confounded by convergent evolution.

We perform analyses with a window size of 144 nucleotides (48 codons) with a step size of 6 nucleotides (2 codons). The sequence alignment was 324 nucleotides long (108 codons), which gives 31 windows across the alignment. As noted in Section 3.1, one issue is the choice of window size and step size, as we noticed a relationship between window count and power/type I error. Based on our simulations, we thus aimed for a window count of approximately 100 whenever possible. However, this became infeasible with this dataset, because the sequence alignment has a length of only 324 codons. Thus, for this dataset, we were only able to construct window sizes and step sizes that resulted in 31 windows total, without making the window size too small to recover phylogenies in each window size with any accuracy.

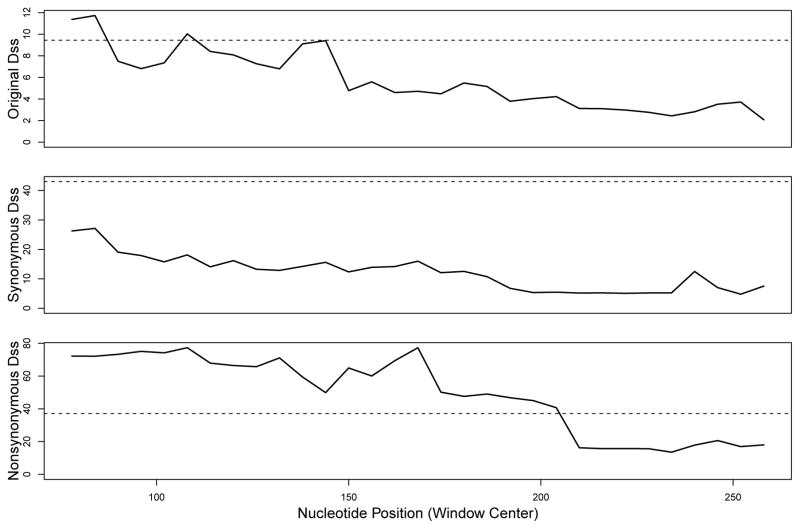
Results from our analyses are shown in Figure 6, with significance threshold levels obtained from the parametric bootstrap with B = 500. We observe that the original Dss statistic crosses its 95% bootstrap significance threshold, whereas the synonymous Dss statistic does not. Additionally, the nonsynonymous Dss statistic crosses its 95% bootstrap significance threshold, suggesting that the lack of signal with the synonymous Dss statistic was not simply due to a loss of power. This is further supported by an examina tion of the raw counts of synonymous vs. nonsynonymous substitutions in this sequence alignment, as there are in fact slightly more synonymous substitutions than nonsynonymous substitutions. Thus, we find statistically significant evidence that the recombination signal in HVR1 sequences is actually due to convergent evolution, and not recombination, since a true recombination event should have manifested itself in the synonymous Dss analysis.

Figure 6.

Dss statistic landscapes for HVR1 of HCV alignment. Dotted horizonal lines represent the 95% significance level for each test, from a parametric bootstrap with B = 500.

4 Discussion

In this work, we have introduced the synonymous Dss statistic, developed to give a statistical method which allows us to distinguish between recombination and convergent evolution. Since convergent evolution acting at a single site will not confuse recombination detection methods, we are concerned only with convergent evolution that acts at multiple sites located in close proximity to each other. Our simulations show that while our synonymous Dss statistic loses some power compared to the original Dss statistic, it does have a lower false positive probability when the signal is due to convergent evolution. Furthermore, we provide some verification that this lower false positive probability is not simply due to the loss of power, as suggested by the false positive probabilities of the various scenarios in which we remove a comparable portion of the information in the sequences, shown in Figure 3.

Our real data analyses highlight the usefulness of our methodology when dealing with situations where both recombination and convergent evolutionary may be participating in the evolution of molecular sequences. We find evidence contrary to the conclusion by Lemey et al. (2005) that convergent evolution has occurred in the pol gene lineage of HIV; instead, we find evidence for the occurrence of a recombination event. The benefit of using our method is that we have created a statistical testing framework for addressing precisely this question. In contrast, Lemey et al. (2005) examined phylogenies constructed with synonymous and nonsynonymous substitutions separately, basing their conclusion on whether each phylogeny matched the known transmission chain. However, Lemey et al. (2005) had difficulty providing a measure of statistical significance for their findings; in contrast, our method naturally assigns statistical significance to our individual findings. Furthermore, Lemey et al. (2005) implicitly assumed that the entire pol gene had one evolutionary history, and likewise for the env gene. If recombination had occurred within either gene, then this assumption would be violated. Similarly, Lemey et al. (2005) compared the synonymous and nonsynonymous trees of the entire pol gene, while convergent evolution is most likely to be localized to a subset of sites, making it difficult to detect using distances based on the whole alignment. In contrast, our sliding window method is able to separate the contributions of synonymous and nonsynonymous substitutions to the local phylogenetic incongruence signal, which we believe to be an important advantage.

Croxen et al. (2006) found that tlpB mutant strains were deficient in colonization due to their inability to respond to the pH gradient. More recently, engineered mutational analysis showed the disruption in urea-binding and thermal stabilization of the mutational variants (Sweeney et al., 2012). Also, the work demonstrated reduced chemotactic responses of urea-binding variants to acid. These experimental results suggested the possibility that the natural mutational variations in the TlpB protein could arise from adaptive selection pressures. While the gene showed recombination signals via traditional statistics, our novel approach detected the signal to be due to the presence of convergent nonsynonymous (i.e. amino acid replacement) mutations. Such events of repeated, independent (i.e. phylogenetically unlinked) accumulation of mutations at specific amino acid positions of encoded proteins represents powerful evidence of adaptive events (Christin et al., 2012; Tenaillon et al., 2012). Taken together, our results, on one hand, indicated the presence of adaptive evolution of the H. pylori tlpB gene via convergent nonsynonymous mutations. On the other hand, this study depicted the promise of our approach to differentiate convergent mutational events from recombination.

As noted by González-Candelas et al. (2011), there has been some debate regarding the occurrence of recombination as a diversification mechanism in HCV. The reports of in vivo recombination have been questioned as being due to either PCR artifacts or misidentification due to convergent evolution. Here, we find evidence that the recombination signal found by Palmer et al. (2012) in their HVR1 sequence alignment is due to convergent evolution. As the occurrence of recombination in HCV continues to be called into question, our results side with the notion that empirical evidence of recombination of HCV sequences should be interpreted with caution, because of a possibility of false positives due to convergent evolution.

A fundamental question that one might ask is how our method is advantageous over simply removing sites that contain nonsynonymous substitutions during a recombination detection analysis. An illustration of the answer can be observed by considering an alignment containing a large number of sequences, in which multiple substitutions per site would not be uncommon. Thus, if two substitutions had occurred at a particular site, then one substitutions could be synonymous and the other could be nonsynonymous. To use the brute-force approach of removing sites that contain nonsynonymous substitutions would necessarily remove the information contained in the synonymous substitution that had occurred at that site; that is, to remove the site means to remove the entire column from the sequence alignment, so all of the information contained in that site is lost. In contrast, our approach of counting synonymous substitutions under the framework laid out by O'Brien et al. (2009) removes the nonsynonymous mutation information in a more elegant manner, avoiding the total loss of information that would result from removing entire sites.

A potential future development would be to create a coherent method to disintangle recombination and convergent evolution without a convoluted three-way comparison, between the original Dss statistic, the synonymous Dss statistic, and the nonsynoymous Dss statistic. That is, in this study, we would conclude that there is evidence for recombination if both the original Dss statistic and the synonymous Dss statistic show a positive signal. If the original Dss statistic shows a positive signal but the synonymous Dss statistic does not, then we would conclude that this is evidence of convergent evolution, further validated if the nonsynonymous Dss statistic also showed a positive signal. It would be preferable if a methodology could produce one coherent statistic to evaluate in order to answer this question, instead of two or three.

Finally, there is the potential that our concept could be implemented in other recombination detection regimes, specifically those that are likelihood-based. It is well documented that sliding window recombination detection methodology, such as that of the Dss statistic, has drawbacks. For example, the behavior of the test statistic is somewhat influenced by the window size chosen, and there are few guidelines on how to select this tuning parameter (McGuire and Wright, 2000). Also, a multiple comparisons issue exists, since each window produces a value of the test statistic. Although this issue is handled by considering only the maximum statistic value from the alignment and performing an appropriate parametric bootstrap test for statistical significance, this strategy prevents estimating locations of recombination break-points with confidence. Thus, it may be advantageous to import our concept of synonymous recombination detection into a likelihood-based framework, such as those proposed in (Husmeier and Wright, 2003), or in (Minin et al., 2005; Suchard et al., 2003).