Abstract
In this paper, 3D particle focusing in a straight channel with asymmetrical expansion–contraction cavity arrays (ECCA channel) is achieved by exploiting the dean-flow-coupled elasto-inertial effects. First, the mechanism of particle focusing in both Newtonian and non-Newtonian fluids was introduced. Then particle focusing was demonstrated experimentally in this channel with Newtonian and non-Newtonian fluids using three different sized particles (3.2 μm, 4.8 μm, and 13 μm), respectively. Also, the effects of dean flow (or secondary flow) induced by expansion–contraction cavity arrays were highlighted by comparing the particle distributions in a single straight rectangular channel with that in the ECCA channel. Finally, the influences of flow rates and distances from the inlet on focusing performance in the ECCA channel were studied. The results show that in the ECCA channel particles are focused on the cavity side in Newtonian fluid due to the synthesis effects of inertial and dean-drag force, whereas the particles are focused on the opposite cavity side in non-Newtonian fluid due to the addition of viscoelastic force. Compared with the focusing performance in Newtonian fluid, the particles are more easily and better focused in non-Newtonian fluid. Besides, the Dean flow in visco-elastic fluid in the ECCA channel improves the particle focusing performance compared with that in a straight channel. A further advantage is three-dimensional (3D) particle focusing that in non-Newtonian fluid is realized according to the lateral side view of the channel while only two-dimensional (2D) particle focusing can be achieved in Newtonian fluid. Conclusively, this novel Dean-flow-coupled elasto-inertial microfluidic device could offer a continuous, sheathless, and high throughput (>10 000 s−1) 3D focusing performance, which may be valuable in various applications from high speed flow cytometry to cell counting, sorting, and analysis.
I. INTRODUCTION
Particle focusing is very important and essential for separating,1 sorting, counting,2 detecting, and analysis in numerous biological and chemical applications. Three-dimensional (3D) particle focusing, where particles can eventually form one single equilibrium position in flow field, is the most desirable focusing condition in various microfluidic applications such as the flow cytometers used for the detection and enumeration of bio-particles. Various microfluidic devices were designed to realize the particle migration and focusing to one or several equilibrium positions in a Newtonian fluid. The migration of particles is based on their intrinsic physical characteristics such as particle size, shape, density, polarizability, and magnetic susceptibility. Focusing techniques can be classified to two categories: active methods and passive methods. Active methods are based on the application of external force fields. Various active methods have been proposed, such as dielectrophoresis (DEP),3–6 magnetophoresis,7,8 acoustophoresis,9 and optical tweezers.10 These active methods can provide precise control of target bio-particles. However, they have a low throughput and require extra, expensive device components for the external forces. Passive methods are based on the microchannel geometrical effects and hydrodynamic forces,11 such as pinched flow fractionation (PFF),12 hydrodynamic filtration,13 Dean-flow coupled inertial effects,14,15 deterministic lateral displacement (DLD),16 and surface acoustic wave (SAW)-induced streaming.17 These passive methods are simple, effective, and have a high throughput.
Recently, particle manipulation including focusing and separation in non-Newtonian fluids has gained significant attention because the positive first normal stress difference (N1) arising in pressure driven flows of dilute polymer solutions can lead suspended particles or cells to migrate to the mid–plane of the channel.18–21 Leshansky et al.20 observed that the particles migrate toward the centreline due to the imbalance in the first normal stress difference between the centreline and the walls in a slit channel. These particles are two-dimensionally focused under the conditions of negligible inertia and dominant elasticity. However, in planar rectangular channels, the elasticity results in particle migration towards the centreline and the corners of the channel which corresponds to the low first normal stress regions, so this approach cannot be directly applied to 3D focusing. Yang et al.22 reported that the number of multiple equilibrium positions can be reduced to one equilibrium at the centreline by properly adjusting the flow rate due to the synergetic effect of inertia and viscoelasticity. By balancing the elastic and inertial forces, he demonstrated particle focusing on a flow centreline of a square microchannel by using a synergetic combination of elasticity and inertia of viscoelastic fluid flow. D'Avino et al.23 performed 3D numerical simulations and experiments to demonstrate particle focusing through viscoelasticity-induced migration in pressure-driven flows in simple cylindrical micropipes. Seo et al.24 investigated the elasto-migration of microparticles in a microscale pipe flow of viscoelastic fluids using a holographic technique, and evaluated the effects of blockage ratio, flow rate, and entry length on particle migration. Lu and Xuan25 presented an experimental study of continuous particle separation in viscoelastic solutions via a combined action of elastic and inertial lift forces, which is termed as elasto-inertial pinched flow fractionation (eiPFF).
3D particle focusing and separation are achieved in Newtonian fluid in channels with expansion–contraction cavity arrays by Je-Kyun Park's group.26 He exploits the dean flow effects and inertial effects and also uses the aid of sheath flow to realize 3D focusing. In this paper, 3D sheathless particle focusing in the ECCA channel which also used the geometry of expansion-contraction cavity arrays was demonstrated by exploiting the Dean-flow-coupled elasto-inertial effects. The differences are that in the ECCA channel, the viscoelastic fluid is used instead of the Newtonian fluid, and thus 3D particle focusing can be sheathless and easily realized. In this paper, we demonstrated particle focusing experimentally in this channel under Newtonian and non-Newtonian fluids using three different sized particles (3.2 μm, 4.8 μm, and 13 μm), respectively. The influences of flow rate and distance from the inlet on focusing performance were also studied. The particles are focused on the cavity side in a Newtonian fluid by the synthesis of inertial and Dean-drag force, whereas on the opposite cavity side in a non-Newtonian fluid due to the addition of viscoelastic force. Besides, the Dean effects in the ECCA channel improve the particle focusing performance compared with that of in straight channel. To the authors' best knowledge, the Dean-flow-coupled elasto-inertial focusing in such a device has not been explored yet. This Dean-flow-coupled elasto-inertial microfluidic device reported here could offer a continuous, sheathless, and high throughput (>10 000 s−1) 3D focusing performance, which may be valuable in various applications from high speed flow cytometry to cell counting, sorting, and analysis.
II. THEORETICAL BACKGROUND
A. Particle focusing in Newtonian fluids
Recently, inertial effect was used for various microfluidic applications such as focusing,27,28 separation,29,30 and filtration.31,32 Di Carlo's group14,33 and Toner's group34 comprehensively reviewed and summarized the phenomenon of inertial migration. Focusing in straight channels has been discussed in detail by Zhou and Papautsky.35 In a straight channel, the inertial migration of particles is driven by two different types of forces: the shear gradient lift force FLS and wall lift force FLW. The sum of the two inertial lift forces, which is called the net inertial lift force, was first derived by Asmolov,36 and later simplified by Di Carlo14 as follows:
| (1) |
| (2) |
where , , and are the fluid density, mean velocity, and dynamic viscosity, respectively; a is the spherical diameter of the particles; = 2wh/(w + h) is the hydraulic diameter for a rectangular channel with w and h as the width and height of the channel cross section. The lift coefficient of net inertial lift force is a function of the position of the particles within the cross section of channel and the channel Reynolds number .14
The Dean flow, or the secondary rotational flow, can also contribute to the particle migration. Focusing using Dean force coupled-migration has been discussed by Nivedita and Papautsky37 and Je-Kyun Park.26 A pressure gradient in a radial direction is induced when fluid flows within the curved or an ECCA channel to satisfy the mass balance between inner-wall (or cavity side) and outer-wall (the opposite cavity side) regions. Thereby, two counter rotating vortices at the channel are generated. The secondary flow is characterised by two dimensionless numbers: the Dean number De = Re(H/2R)1/2 and the curvature ratio δ = H/2R, where H is the width of the channel and R is the radius of the channel curvature. The straight channel with ECCA channel arrays can also induce rotational flow due to the abrupt change of cross sectional area and produces a Dean-like counter-rotating flow when the fluid in the contraction area accelerates. Because of the difference between particle velocity and fluid velocity in a cross sectional plane, a secondary flow drag is induced,
| (3) |
where and are the lateral velocities of fluid elements and particles in a cross sectional plane, respectively.
The equilibrium positions are determined by the ratio of FL/FD. When the inertial lift force is dominant (FL≫FD), the focusing is achieved mainly with the inertial force only. When dean flow is dominant (FD≫FL), no focusing is achieved. When FL is comparable to FD, new focusing positions can be adjusted.
According to the ratio of FL/FD, the ratio of particle size and channel dimension a/Dh play an important role in determining the focusing behaviour. Focusing can only be achieved when a/Dh is larger than 0.07,2,38 so if the particle is too small or the channel is too large, particle focusing cannot be achieved.
B. Particle focusing in non-Newtonian fluids
Particle migration and focusing in a non-Newtonian viscoelastic fluid is different than that in Newtonian fluids. In non-Newtonian viscoelastic fluid, the elastic force is determined by the intrinsic properties of the medium. The elastic effects of a non-Newtonian fluid in the channel flow can be characterized by Wi, which is defined as the ratio between two time constants,
| (4) |
where is the relaxation time of the fluid and is the characteristic time of the channel flow. The characteristic time is approximately equal to the inverse of the average (characteristic) shear rate, , which is 2Vm/w or 2Q/hw2 in a rectangular channel. is the average velocity and w and are the channel width and height, respectively.
For pressure-driven flows in rectangular channels, the elasticity results in particle migration towards the centreline and the corners of the channel which corresponds to the low first normal stress N1 regions, where N1 is defined as . Actually, both the 1st and 2nd normal stress N1 and N2 can contribute to the particle migration, where N2 = . Because N1 is much larger than N2,39,40 thus the effects of N2 can be neglected in diluted PEO solutions. The elastic force can be assumed to stem from the imbalance in the distribution of N1 over the size of the particle20,41
| (5) |
where a is the particle radius, is the ratio of the solvent to solution viscosity, and is the non-dimensional local shear rate.
The number of multiple equilibrium positions can be reduced to one at the centreline by properly adjusting the flow rate due to the synergetic effect of inertia and viscoelasticity. The competition between the elasticity and the inertia determines the particle migration. Since the elasticity and inertia is represented by Wi and Rc, respectively, the elasticity number (the ratio between these two numbers (Wi/Rc)) can be used to measure the relative importance of elastic forces to inertial effects, which is defined as
| (6) |
If the medium does not yield apparent shear-thinning viscosity, El is independent of the flow rate and only dependent on fluid viscosity and relaxation time in a specific channel.
C. Principle of Dean-flow-coupled elasto-inertial particle focusing
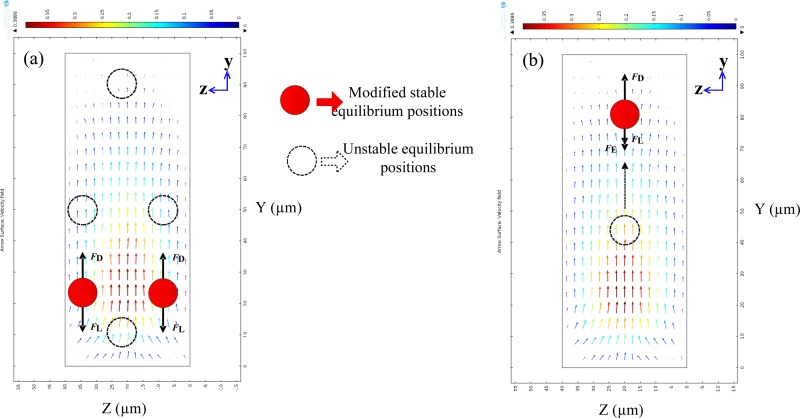
The Dean-flow-coupled elasto-inertial particle focusing is to harmonize three kinds of forces: Lift force FL, including the shear-gradient lift force (FLS), wall-repulsion force (FLW); the Dean drag force FD resulting from the curved channel geometry; and elastic force FE induced by the nature of the viscoelastic medium. Fig. 1 shows the simulation results of the flow field in the cross section 10 μm away from the cavity along the x direction and the schematic illustration of the focusing mechanism in Newtonian (a) and non-Newtonian (b) fluid at the outlet in the ECCA channel. The magnitude of the secondary flow field in this simulation is represented by . When particles flowing in straight channels in Newtonian fluid, the shear gradient lift force pushes particles away from the centreline of the channel where corresponds to the low shear rate region, while the wall lift force drives particles away from the channel wall. The four equilibrium positions are formed as shown in Fig. 1(a) (the four black dashed circles). When the particles are not in straight channels but in ECCA channels with a Newtonian fluid, the effects of inertial migration and secondary flow act in superposition on the particles, thus the four equilibrium positions induced by Lift force FL in rectangular channels are destroyed by the dean drag force FD and particles become stable in two modified equilibrium positions, Fig. 1(a) (the red circles). The arrows in Fig. 1 represent the magnitude and direction of the secondary flow field induced by the abrupt contraction of the channel. When particles flowing in ECCA channels with a viscoelastic non-Newtonian fluid, the elastic force FE should be considered, which is directed away from the wall and decays with increasing distance from the wall. In a straight rectangular channel with non-Newtonian fluids, the particles tend to migrate to the centreline of the channel by the synergetic effect of inertia and viscoelasticity. In ECCA channels, the particles become unstable when an additional secondary flow drag is exerted on the particles. Subsequently, a new equilibrium position can be achieved near the channel wall by the combined effects of lift force FL, elastic force FE, and the Dean drag force FD, as shown in Fig. 1(b). Finally, 3D particle focusing is realized in an ECCA channel with the combined effect of Dean-flow-coupled elasto-inertial forces.
FIG. 1.
Simulation results of the flow field in the cross section 10 μm away from the cavity along the x direction and the schematic illustration of the focusing mechanism in Newtonian (a) and non-Newtonian (b) fluid. (a) The red circles represent two equilibrium positions that resulted from a balance between the inertial lift force FL and secondary flow drag FD. (b) The red circle represents the single equilibrium position by the synergetic effect of inertia, secondary flow, and viscoelasticity. The dashed circles are the unstable equilibrium positions. The arrows represent the magnitude and direction of the secondary flow field induced by the abrupt contraction of the channel.
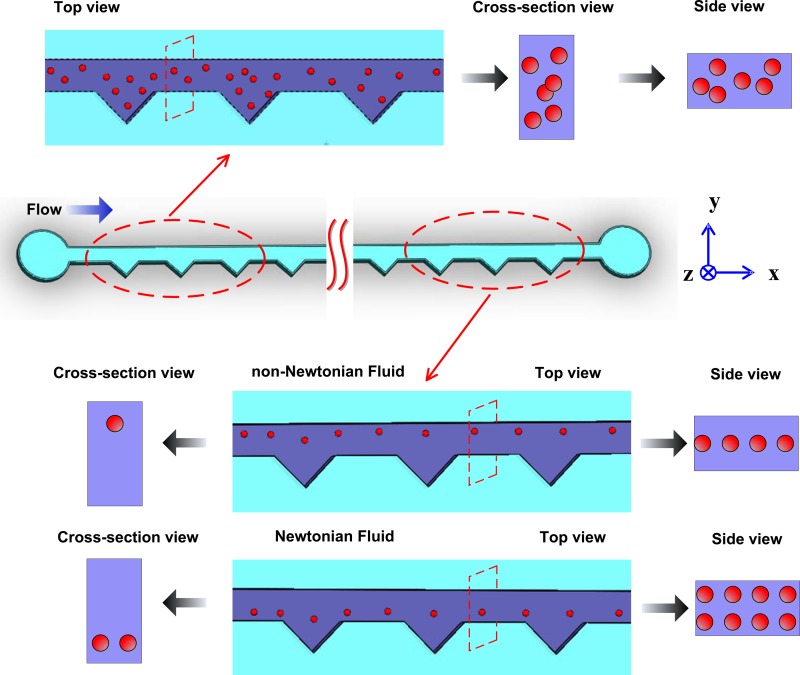
After a comprehensive review of the working principle of particle focusing in Newtonian and non-Newtonian fluid, particle focusing experiments were performed using both Newtonian and non-Newtonian fluids in the ECCA channel. Fig. 2 shows the schematic diagram of particle focusing in Newtonian and non-Newtonian fluids in the ECCA channel. There are 26 repeated expansion–contraction triangular cavities in this channel, while only the inlet and outlet sections of the channel are illustrated here. Particles are randomly injected to the inlet, so from the top view, cross section view, and side view in the amplified inlet section the particles are dispersed. As the particle suspension flows, particles are driven into a single line along the channel wall on the opposite cavity side in non-Newtonian fluid with the Dean-flow-coupled elasto-inertial effects described above. However, in a Newtonian fluid, because there is no elastic effect induced by the polymers, particles are focused to two equilibrium positions on the cavity side at the outlet in a Newtonian fluid as result of Dean and inertial effects.
FIG. 2.
Schematic diagrams of particle focusing in Newtonian and non-Newtonian fluids in the ECCA channel. Particles are randomly injected to the inlet, and finally focused in a single line on the opposite cavity side at the outlet in non-Newtonian fluid in Dean-coupled elasto-inertial effects, while focused to two equilibrium positions on the cavity side at the outlet in Newtonian fluid in the combination of Dean and inertial effects.
III. EXPERIMENTS
A. Design and fabrication of the microfluidic device
The right angled isosceles triangular cavities are patterned on one side of a straight channel. The channel has a cross section of 100 μm × 40 μm (width × height). The longest edge of the triangle is L1 = 900 μm, and the space between two adjacent cavities is uniform at L2 = 900 μm. The total length of the straight channel is L0 = 48 mm, including 26 repeated expansion–contraction triangular cavities. Its schematic geometry is shown in Figure 3.
FIG. 3.

The schematic geometry of the microfluidic channel with triangular expansion–contraction cavity arrays, L0 = 48 mm, L1 = 900 μm, L2 = 900 μm.
The device was fabricated by standard photolithography and soft lithography techniques. The fabrication included rapid prototyping on a silicon master, polydimethylsiloxane (PDMS) replica moulding, and sealing through plasma oxidation. Briefly, photoresist (SU-8 2025, MicroChem Co., Newton, MA) was spun on a silicon wafer at 2000 rpm to a thickness of 40 μm, and then exposed to UV light through a designed mask using a mask aligner system (ABM, San Jose, CA). After that the photoresist on the silicon wafer was developed in an SU-8 developer solution and rinsed by isopropylalcohol (IPA) to create a positive replica of channel geometry. A PDMS mixture with a 10:1 ratio of base to agent (Dow Corning, Midland, MI) was poured over the silicon master, degassed to remove bubbles in a vacuum oven, and cured at 100 °C for 45 min. After the PDMS was cured and taken out of silicon master, the inlet and outlet holes were punched with a custom needle tip. Finally, the PDMS slide was bonded with another PDMS slide after exposure to oxygen plasma (PDC-002, Harrick Plasma, Ossining, NY) for 3 min.
B. Suspending fluid and particles
In this work, two kinds of fluids were prepared: Newtonian fluid (deionized water) and Non-Newtonian fluid (moderate elasticity fluid). For the moderate elasticity fluid, PEO (poly(ethylene oxide), Mw = 2 000 000, Sigma-Aldrich) was added to deionized water in 500 ppm. The density of the fluid matches with the polystyrene (PS) particles (1.05 g cm3). The PEO solution is considered to have a constant shear viscosity of 3.12 × 10−3 Pa s under the present experimental conditions and its relaxation time is 9.1 × 10−3 s. The viscosity for deionized water is 1.0 × 10−3 Pa s. Tween 20 (0.01 wt. %, Sigma-Aldrich) was added to all the solutions to prevent particle-particle adhesion.
Internally dyed fluorescent polystyrene microspheres were purchased from Thermo Fisher Scientific., USA. A particle suspension was prepared by diluting 3.2 μm (Product No. G0300, CV < 5%), 4.8 μm (Product No. G0500, CV < 5%), and 13 μm (Product No. G1000, CV < 5%) particles to the concentration of ∼107 particles ml−1 by deionized water and PEO solution, respectively. This concentration was considered to be low enough to neglect any interaction between particles in the micro-channel. Before the experiment, the particles are shaken by a vortex device to guarantee a good suspension.
C. Experimental setup
The particle suspensions were transferred to a 1 ml syringe, and then introduced into the microfluidic chip through a silicon tube by a syringe pump (Legato 100, Kd Scientific). The outflow of the particle suspension was collected in a glass bottle. The microfluidic chip was placed on an inverted microscope (CKX41, Olympus, Japan), and illuminated by a mercury arc lamp. The images of the fluorescent particles were observed and captured by a CCD camera (Rolera Bolt, Q-imaging, Australia) which had a maximum capturing speed of 50 frames/s. The fluorescent images were then post-processed and analysed with the software Q-Capture Pro 7 (Q-imaging, Australia). The flow rate in the experiment was increased from 10 μl min−1 to 300 μl min−1, which corresponds to an average fluid velocity from 0.04 m s−1 to 1.2 m s−1. A profile of the fluorescent intensity was taken from the outlet of the last cavity to examine the focusing performance of this microfluidic device in both Newtonian and non-Newtonian fluid.
IV. RESULTS AND DISCUSSION
A. Effects of elasticity on particle migration
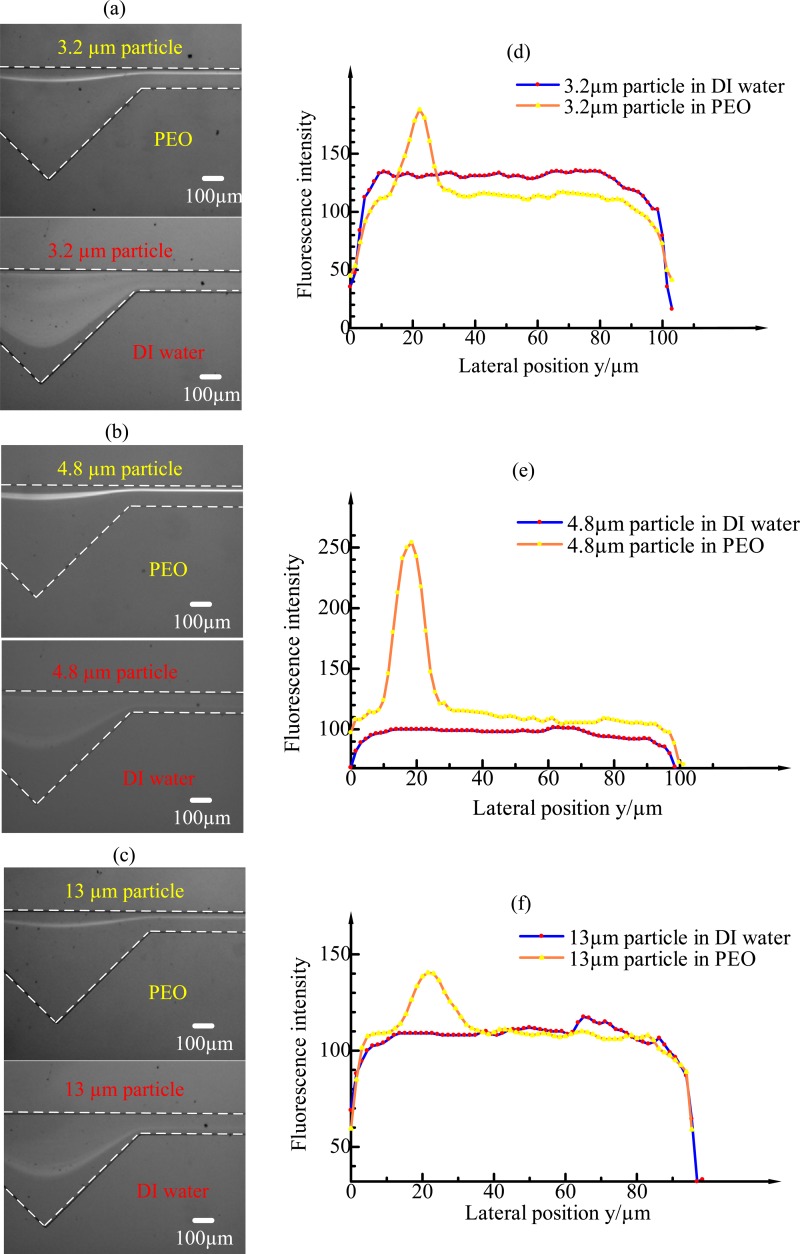
To investigate the effects of elasticity on particle migration, experiments were carried out in both Newtonian and non-Newtonian fluids in ECCA channels using three different particle sizes (3.2 μm, 4.8 μm, and 13 μm) with the flow rate increasing from 10 μl min−1 to 300 μl min−1. The results show that particles are more easily and better focused in non-Newtonian fluid. Fig. 4 shows the fluorescent images of 3.2-μm, 4.8-μm, and 13-μm particles at the outlet under the flow rate of 60 μl min−1 in Newtonian and non-Newtonian fluids, respectively, and corresponding intensity profiles for each particle type along the width of the channel. In the 500-ppm PEO solution, the three particle types were focused very well at the flow rate of 60 μl min−1 (Rc = 4.62, Wi = 45.48, El = 9.84) and in a specific range of flow rate around 60 μl min−1 as well. The particles experience the lift force FL, the Dean drag force FD and the elastic force FE at the same time, and an equilibrium position was observed on the opposite of cavity side due to the combined effects of the three forces. In a Newtonian fluid, however, no obvious particle focusing is observed at the outlet under 60 μl min−1 flow rate with the 3.2-μm and 4.8-μm particle size. The 13-μm particles begin to focus from 60-μl min−1 flow rate under the effects of the lift force FL, the Dean drag force FD. In this experiment, the hydrodynamic diameter Dh = 2wh/(w + h) ≈ 60, and a/Dh is approximately 0.05, 0.08, and 0.22 for 3.2-μm, 4.8-μm, and 13-μm particles, respectively. This phenomenon is consistent with the theory that particle focusing can only be achieved when a/Dh is larger than 0.07.2,28,33 It can also be seen from the fluorescent intensity profile (Figs. 4(d)–4(f)) that the particles in DI water are mostly dispersed, while in PEO solution the particles are tightly focused. The width of the focusing line (derived from the difference of lateral position in the fluorescence intensity profile at 70% intensity peak) in PEO solution is similar to the diameter of the particles. We can conclude that single-particle focusing is achieved in the x-y plane. Compared with particle focusing in a Newtonian fluid, the elasticity in a non-Newtonian fluid accelerates the particle focusing, improves the focusing performance, and finally focuses particles on the opposite side of cavity. Besides, particle focusing in non-Newtonian fluid requires less external energy and less pressure is exerted on the microfluidic device.
FIG. 4.
The fluorescent images of 3.2-μm, 4.8-μm, and 13-μm particles at the outlet under the flow rate of 60 μl min−1 in Newtonian and non-Newtonian fluids, respectively, and corresponding fluorescent intensity profiles for each particle type along the width of the channel.
B. Effects of dean flow induced by expansion–contraction cavity arrays in ECCA channels
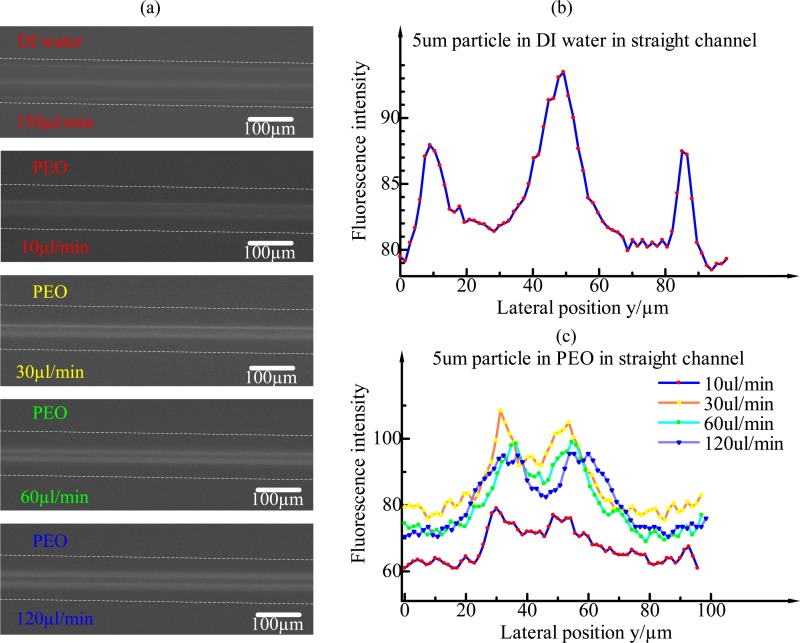
In order to investigate the effects of Dean flow induced by expansion–contraction cavity arrays in ECCA channels, the particle distribution in a straight rectangular channel with cross section 100 μm × 50 μm (width × height) (Fig. 5) was compared with that in the ECCA channel (Fig. 4). As is known that particles focus in rectangular channels to four or two equilibrium positions centred at the faces of the channels at moderate flow rates of a Newtonian fluid as shown in Fig. 5(a). In a non-Newtonian fluid, Yang et al. demonstrated that multiple particle equilibrium positions can be reduced to a single particle stream along the channel centreline when elastic and inertial forces are synergistically balanced,22 which was termed as elasto-inertial particle focusing. The dimension of the microchannel cross section used in Yang's experiments was 50 μm × 50 μm, and particle size was 5.9 μm. Finally, particles formed a single line at the centre of the channel at only several microlitres per minute. Whereas in the 100 μm × 50 μm rectangular channel, single-particle focusing was not achieved due to a wider width, Fig. 5(a). This can be explained by the shape of velocity profile along the channel width. Velocity distribution along the width becomes increasingly flat as the channel width becomes wider. The fluid shear rate is very small along a large central area. As the particles tend to migrate towards the low shear rate region in a viscoelastic fluid, the particles in 100 μm × 50 μm rectangular channel can only distribute in a wide central area along the width of the channel, Fig. 5.
FIG. 5.
(a) The fluorescent images of 4.8-μm particles at the outlet in a straight rectangular channel under the flow rate of 150 μl min−1 in DI water and in PEO under different flow rates, respectively. (b) The fluorescent intensity profile in DI water. Particles focus to four equilibrium positions centred at the faces of the channels. The middle fluorescent intensity peak, which is higher than the other two peaks, represents two overlap equilibrium positions. (c) The fluorescent intensity profiles in PEO under different flow rates. Particles in 100 μm × 50 μm channel can only distribute in a wide central area along the width of the channel without the aid of secondary flow.
With the aid of the Dean flow induced by expansion–contraction cavity arrays, the particles can be tightly focused to a single line on the opposite cavity side in moderate flow rates although the channel dimension is still 100 μm × 50 μm in rectangular section as shown in Fig. 4. A further advantage is that in the ECCA channel the flow rate that allows particle focusing can be dozens of or even hundreds of microlitres per minute, which is much higher than that in a straight channel, resulting in a higher throughput (>10 000 s−1). So this Dean-flow-coupled elasto-inertial microfluidic device could offer a continuous, sheathless, and high-throughput focusing performance.
C. Effects of different flowing conditions
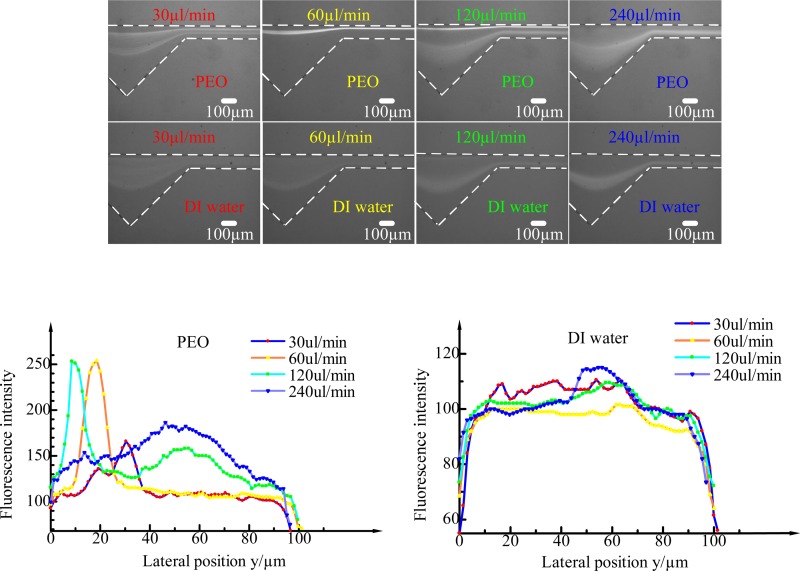
As the inertial lift force, secondary force and elastic force are all related to the flow rate. Under different flowing conditions, the particles will experience different dominant forces, which will lead to different particle distributions. Take 4.8-μm particle as an example, the 4.8-μm particles distribution was observed under different flowing conditions in 500 ppm PEO fluid and DI water, as is shown in Fig. 6. The flow rate Q varies from 10 μl min−1 to 300 μl min−1, which corresponds to the levels of Rc ranging from 0.77 to 23.10, Wi ranging from 7.58 to 227.4, and El of 9.84 which is independent of the flow rate. In DI water, Wi and El are both zero since Newtonian fluid does not exhibit elastic properties. When the flow rates are relatively low (<30 μl min−1, Rc = 2.31, Wi = 22.74, El = 9.84) with 500 ppm PEO solution, the inertial effect and the Dean effect are negligible, while elastic force is dominant, and the particles are randomly distributed. As the flow rate increases, the inertial and Dean drag forces being exerted on a particle competes with elastic force, and the particles gradually migrate to the opposite side of the cavity in the channel and focused tightly (as shown in Fig. 6 at 60–μl min−1 flow rate in PEO (Rc = 4.62, Wi = 45.48, El = 9.84)) due to the balance of the lift force FL, Dean drag force FD and elastic force FE. The focusing range is approximately from 30 μl min−1 to 120 μl min−1. When the flow rate reaches 120 μl min−1 (Rc = 9.24, Wi = 90.96, El = 9.84), another focusing line occurs on the cavity side. This is partly because inertia and secondary flow effects begin to dominant the particle migration. Consequently, the elastic force was eventually overwhelmed by the inertial force all the particles migrate and focus on the cavity side when the flow rate reaches 240 μl min−1 (Rc = 18.48, Wi = 181.92, El = 9.84). In DI water, the particles are dispersed until the flow rate reaches 120 μl min−1, then the particles are focused on the cavity side of the channel under the combined effect of the lift force FL and the Dean drag force FD. The minimum focusing flow rate in a Newtonian fluid is higher than that in a non-Newtonian fluid and the focusing performance in a Newtonian fluid is not as good as in a PEO solution. That is to say, the elastic effect accelerates and improves the particle focusing performance. It can also be seen from the fluorescent intensity profiles of particles flowing with different flow rates in 500 ppm PEO and DI water.
FIG. 6.
The fluorescent images of 4.8 μm particle at the outlet at the flow rate of 30 μl min−1, 60 μl min−1, 120 μl min−1, 240 μl min−1 in 500 ppm PEO and DI water fluids, respectively, and corresponding fluorescent intensity profiles for different flow rates along the width of the channel.
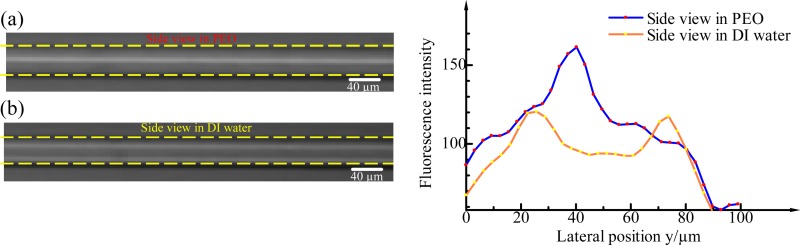
D. Side view of the channel
We checked if the focusing is three-dimensional focusing in Newtonian and non-Newtonian fluids in this ECCA channel by imaging the side view of the channel, Fig. 7. Fig. 7(a) is the side view of the channel when particles flowing in 500 ppm PEO solution at a flow rate of 60 μl min−1. It is verified that the particles flowing in non-Newtonian fluid is not only focused in the x-y plane but also forms a single line in the centreline of the channel in the x-z plane. That means, the 3D particle focusing in non-Newtonian fluid in this ECCA channel is realized by properly balancing the effects of inertia, secondary flow, and elasticity. This phenomenon was not observed for the case of a Newtonian fluid when particles focused in DI water in x-y plane as shown in Fig. 7(b) in 240 μl min−1. Instead, the particles in DI water are focused in two lines along the two channel walls in the x-z plane due to the synergetic effect of inertia and secondary flow, which is not suitable for practical applications such as one-by-one particle counting or sorting. It is confirmed that the equilibrium positions are reduced to a single one by the additional elasticity effect in PEO solution in the ECCA channel. It is also obvious from the corresponding fluorescent intensity profiles in PEO and DI water, respectively. In a PEO solution, only one fluorescence intensity peak exists in the middle of the lateral side view, while there are two peaks in DI water.
FIG. 7.
Fluorescent images of the side view of the channel when particle focusing in 500 ppm PEO solution and DI water, respectively, and corresponding fluorescent intensity profiles.
E. Effects of different distances from the inlet
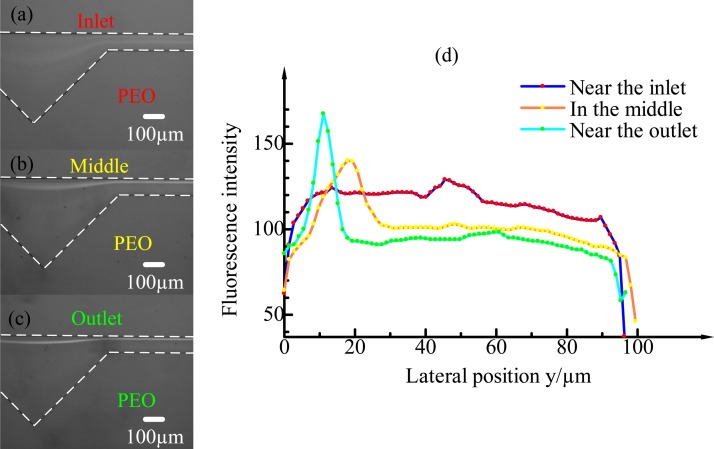
The particle distribution also strongly depends on the distance from the inlet. Fig. 8 shows the fluorescent images of 4.8-μm particle distributions at three different distances from the inlet in the 500-ppm PEO solution. Fig. 8(a) shows that particles at the inlet are randomly distributed along the radial direction. However, at the middle of the channel, approximately 2.5 mm from the inlet that almost all the particles have already migrated and been confined within a narrow band along the channel wall on the opposite side of cavity. Finally, at the outlet of the channel, strict particle focusing is observed. It can also be seen from the fluorescent intensity profiles at three different distances from the inlet that particle focusing strongly depends on the distance from the inlet. The focusing width at the outlet of the channel is approximately 5 μm, which is the same size of particles, indicating single-line particle focusing.
FIG. 8.
4.8 μm particle distributions in the ECCA channel at different distances from the inlet in 500 ppm PEO. (a) At the inlet, no focusing is observed and the particles are still randomly distributed. (b) At the middle of the channel (approximately 2.5 cm from the inlet), the particles are confined within a narrow band along the channel wall on the opposite side of the cavity. (c) At the outlet of the channel (approximately 4.5 cm from the inlet), 3D focusing on a line is achieved. (d) The fluorescence intensity profiles at the inlet, middle, and outlet.
V. CONCLUSION
To summarize, 3D particle focusing was demonstrated in a straight channel with asymmetrical expansion–contraction cavity arrays (ECCA channel) by exploiting the Dean-flow-coupled elasto-inertial effects. By properly controlling the flow rates to harmonize the inertial force, viscoelastic force, and Dean-drag force, 3D particle focusing in non-Newtonian fluid along the opposite side of cavities was achieved. Particle focusing under Newtonian and non-Newtonian fluids using three different sized particles (3.2 μm, 4.8 μm, and 13 μm) were demonstrated. The particles were focused on the cavity side in a Newtonian fluid by the synthesis of inertial and Dean-drag force, whereas on the opposite cavity side in a non-Newtonian fluid due to the addition of the viscoelastic force. Compared with particle focusing in Newtonian fluid in an ECCA channel and in non-Newtonian fluid in a straight channel, it can be concluded that particles in non-Newtonian fluid in the ECCA channel are more easily and better focused. Moreover, the effect of Dean-flow-coupled elasto-inertial focusing can be fully developed as the flowing distances from the inlet becomes longer. This Dean-flow-coupled elasto-inertial microfluidic device could offer a continuous, sheathless, and high-throughput (>10 000 s−1) 3D focusing performance, which may be valuable in various applications from high speed flow cytometry to cell counting, sorting, and analysis.
ACKNOWLEDGMENTS
This work was supported by the University of Wollongong—China Scholarship Council joint scholarships (CSC No. 201406690028).
References
- 1. Whitesides G. M., “ The origins and the future of microfluidics,” Nature 442(7101), 368–373 (2006). 10.1038/nature05058 [DOI] [PubMed] [Google Scholar]
- 2. Bhagat A. A. S., Kuntaegowdanahalli S. S., Kaval N., Seliskar C. J., and Papautsky I., “ Inertial microfluidics for sheath-less high-throughput flow cytometry,” Biomed. Microdevices 12(2), 187–195 (2010). 10.1007/s10544-009-9374-9 [DOI] [PubMed] [Google Scholar]
- 3. Kang Y., Li D., Kalams S. A., and Eid J. E., “ DC-Dielectrophoretic separation of biological cells by size,” Biomed. Microdevices 10(2), 243–249 (2008). 10.1007/s10544-007-9130-y [DOI] [PubMed] [Google Scholar]
- 4. Li M., Li S., Cao W., Li W., Wen W., and Alici G., “ Continuous particle focusing in a waved microchannel using negative dc dielectrophoresis,” J. Micromech. Microeng. 22(9), 095001 (2012). 10.1088/0960-1317/22/9/095001 [DOI] [Google Scholar]
- 5. Yan S., Zhang J., Alici G., Du H., Zhu Y., and Li W., “ Isolating plasma from blood using a dielectrophoresis-active hydrophoretic device,” Lab Chip 14(16), 2993–3003 (2014). 10.1039/C4LC00343H [DOI] [PubMed] [Google Scholar]
- 6. Kang K. H., Kang Y., Xuan X., and Li D., “ Continuous separation of microparticles by size with Direct current-dielectrophoresis,” Electrophoresis 27(3), 694–702 (2006). 10.1002/elps.200500558 [DOI] [PubMed] [Google Scholar]
- 7. Hejazian M., Li W. H., and Nguyen N.-T., “ Lab on a chip for continuous-flow magnetic cell separation,” Lab Chip 15(4), 959–970 (2015). 10.1039/C4LC01422G [DOI] [PubMed] [Google Scholar]
- 8. Zeng J., Chen C., Vedantam P., Brown V., Tzeng T. R. J., and Xuan X., “ Three-dimensional magnetic focusing of particles and cells in ferrofluid flow through a straight microchannel,” J. Micromech. Microeng. 22(10), 105018 (2012). 10.1088/0960-1317/22/10/105018 [DOI] [Google Scholar]
- 9. Heyman J. S., “ Acoustophoresis separation method,” U.S. patent 5,192,450 (9 March 1993).
- 10. MacDonald M. P., Spalding G. C., and Dholakia K., “ Microfluidic sorting in an optical lattice,” Nature 426(6965), 421–424 (2003). 10.1038/nature02144 [DOI] [PubMed] [Google Scholar]
- 11. Karimi A., Yazdi S., and Ardekani A. M., “ Hydrodynamic mechanisms of cell and particle trapping in microfluidics,” Biomicrofluidics 7(2), 021501 (2013). 10.1063/1.4799787 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Yamada M., Nakashima M., and Seki M., “ Pinched flow fractionation: continuous size separation of particles utilizing a laminar flow profile in a pinched microchannel,” Anal. Chem. 76(18), 5465–5471 (2004). 10.1021/ac049863r [DOI] [PubMed] [Google Scholar]
- 13. Crowley T. A. and Pizziconi V., “ Isolation of plasma from whole blood using planar microfilters for lab-on-a-chip applications,” Lab Chip 5, 922–929 (2005). 10.1039/b502930a [DOI] [PubMed] [Google Scholar]
- 14. Di Carlo D., “ Inertial microfluidics,” Lab Chip 9(21), 3038–3046 (2009). 10.1039/b912547g [DOI] [PubMed] [Google Scholar]
- 15. Zhang J., Li M., Li W. H., and Alici G., “ Inertial focusing in a straight channel with asymmetrical expansion–contraction cavity arrays using two secondary flows,” J. Micromech. Microeng. 23(8), 085023 (2013). 10.1088/0960-1317/23/8/085023 [DOI] [Google Scholar]
- 16. Davis J. A., Inglis D. W., Morton K. J., Lawrence D. A., Huang L. R., Chou S. Y., Sturm J. C., and Austin R. H., “ Deterministic hydrodynamics: taking blood apart,” Proc. Natl. Acad. Sci. 103(40), 14779–14784 (2006). 10.1073/pnas.0605967103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Friend J. and Yeo L., “ Microscale acoustofluidics: Microfluidics driven via acoustics and ultrasonics,” Rev. Mod. Phys. 83(2), 647 (2011). 10.1103/RevModPhys.83.647 [DOI] [Google Scholar]
- 18. D'Avino G., Maffettone P. L., Greco F., and Hulsen M. A., “ Viscoelasticity-induced migration of a rigid sphere in confined shear flow,” J. Non-Newtonian Fluid Mech. 165(9), 466–474 (2010). 10.1016/j.jnnfm.2010.01.024 [DOI] [Google Scholar]
- 19. Huang P. Y., Feng J., Hu H. H., and Joseph D. D., “ Direct simulation of the motion of solid particles in Couette and Poiseuille flows of viscoelastic fluids,” J. Fluid Mech. 343, 73–94 (1997). 10.1017/S0022112097005764 [DOI] [Google Scholar]
- 20. Leshansky A. M., Bransky A., Korin N., and Dinnar U., “ Tunable nonlinear viscoelastic ‘focusing’ in a microfluidic device,” Phys. Rev. Lett. 98(23), 234501 (2007). 10.1103/PhysRevLett.98.234501 [DOI] [PubMed] [Google Scholar]
- 21. Ho B. P. and Leal L. G., “ Migration of rigid spheres in a two-dimensional unidirectional shear flow of a second-order fluid,” J. Fluid Mech. 76(04), 783–799 (1976). 10.1017/S002211207600089X [DOI] [Google Scholar]
- 22. Yang S., Kim J. Y., Lee S. J., Lee S. S., and Kim J. M., “ Sheathless elasto-inertial particle focusing and continuous separation in a straight rectangular microchannel,” Lab Chip 11(2), 266–273 (2011). 10.1039/C0LC00102C [DOI] [PubMed] [Google Scholar]
- 23. D'Avino G., Romeo G., Villone M. M., Greco F., Netti P. A., and Maffettone P. L., “ Single line particle focusing induced by viscoelasticity of the suspending liquid: Theory, experiments and simulations to design a micropipe flow-focuser,” Lab Chip 12(9), 1638–1645 (2012). 10.1039/c2lc21154h [DOI] [PubMed] [Google Scholar]
- 24. Seo K. W., Byeon H. J., Huh H. K., and Lee S. J., “ Particle migration and single-line particle focusing in microscale pipe flow of viscoelastic fluids,” RSC Adv. 4(7), 3512–3520 (2014). 10.1039/C3RA43522A [DOI] [Google Scholar]
- 25. Lu X. and Xuan X., “ Continuous microfluidic particle separation via elasto-inertial pinched flow fractionation (eiPFF),” Anal. Chem. 87(12), 6389–6396 (2015). 10.1021/acs.analchem.5b01432 [DOI] [PubMed] [Google Scholar]
- 26. Lee M. G., Choi S., and Park J. K., “ Inertial separation in a contraction–expansion array microchannel,” J. Chromatogr. A 1218(27), 4138–4143 (2011). 10.1016/j.chroma.2010.11.081 [DOI] [PubMed] [Google Scholar]
- 27. Di Carlo D., Irimia D., Tompkins R. G., and Toner M., “ Continuous inertial focusing, ordering, and separation of particles in microchannels,” Proc. Natl. Acad. Sci. 104(48), 18892–18897 (2007). 10.1073/pnas.0704958104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Oakey J., R. W. Applegate, Jr. , Arellano E., Carlo D. D., Graves S. W., and Toner M., “ Particle focusing in staged inertial microfluidic devices for flow cytometry,” Anal. Chem. 82(9), 3862–3867 (2010). 10.1021/ac100387b [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Di Carlo D., Edd J. F., Humphry K. J., Stone H. A., and Toner M., “ Particle segregation and dynamics in confined flows,” Phys. Rev. Lett. 102(9), 094503 (2009). 10.1103/PhysRevLett.102.094503 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Di Carlo D., Jon F., Irimia D., Tompkins R. G., and Toner M., “ Equilibrium separation and filtration of particles using differential inertial focusing,” Anal. Chem. 80(6), 2204–2211 (2008). 10.1021/ac702283m [DOI] [PubMed] [Google Scholar]
- 31. Mach A. J. and Di Carlo D., “ Continuous scalable blood filtration device using inertial microfluidics,” Biotechnol. Bioeng. 107(2), 302–311 (2010). 10.1002/bit.22833 [DOI] [PubMed] [Google Scholar]
- 32. Bhagat A. A. S., Kuntaegowdanahalli S. S., and Papautsky I., “ Enhanced particle filtration in straight microchannels using shear-modulated inertial migration,” Phys. Fluids 20(10), 101702 (2008). 10.1063/1.2998844 [DOI] [Google Scholar]
- 33. Amini H., Lee W., and Di Carlo D., “ Inertial microfluidic physics,” Lab Chip 14(15), 2739–2761 (2014). 10.1039/c4lc00128a [DOI] [PubMed] [Google Scholar]
- 34. Martel J. M. and Toner M., “ Inertial focusing in microfluidics,” Annu. Rev. Biomed. Eng. 16, 371–396 (2014). 10.1146/annurev-bioeng-121813-120704 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Zhou J. and Papautsky I., “ Fundamentals of inertial focusing in microchannels,” Lab Chip 13(6), 1121–1132 (2013). 10.1039/c2lc41248a [DOI] [PubMed] [Google Scholar]
- 36. Asmolov E. S., “ The inertial lift on a spherical particle in a plane Poiseuille flow at large channel Reynolds number,” J. Fluid Mech. 381, 63–87 (1999). 10.1017/S0022112098003474 [DOI] [Google Scholar]
- 37. Nivedita N. and Papautsky I., “ Continuous separation of blood cells in spiral microfluidic devices,” Biomicrofluidics 7(5), 054101 (2013). 10.1063/1.4819275 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Bhagat A. A. S., Kuntaegowdanahalli S. S., and Papautsky I., “ Continuous particle separation in spiral microchannels using dean flows and differential migration,” Lab Chip 8(11), 1906–1914 (2008). 10.1039/b807107a [DOI] [PubMed] [Google Scholar]
- 39. Magda J. J., Lou J., Baek S. G., and Devries K. L., “ Second normal stress difference of a Boger fluid,” Polymer 32(11), 2000–2009 (1991). 10.1016/0032-3861(91)90165-F [DOI] [Google Scholar]
- 40. Pathak J. A., Ross D., and Migler K. B., “ Elastic flow instability, curved streamlines, and mixing in microfluidic flows,” Phys. Fluids 16(11), 4028–4034 (2004). 10.1063/1.1792011 [DOI] [Google Scholar]
- 41. Tehrani M. A., “ An experimental study of particle migration in pipe flow of viscoelastic fluids,” J. Rheol. 40(6), 1057–1077 (1996). 10.1122/1.550773 [DOI] [Google Scholar]