The Role of Aromaticity, Hybridization, Electrostatics, and Covalency in Resonance-Assisted Hydrogen Bonds of Adenine–Thymine (AT) Base Pairs and Their Mimics

Abstract

Hydrogen bonds play a crucial role in many biochemical processes and in supramolecular chemistry. In this study, we show quantum chemically that neither aromaticity nor other forms of π assistance are responsible for the enhanced stability of the hydrogen bonds in adenine–thymine (AT) DNA base pairs. This follows from extensive bonding analyses of AT and smaller analogs thereof, based on dispersion-corrected density functional theory (DFT). Removing the aromatic rings of either A or T has no effect on the Watson–Crick bond strength. Only when the smaller mimics become saturated, that is, when the hydrogen-bond acceptor and donor groups go from sp² to sp³, does the stability of the resulting model complexes suddenly drop. Bonding analyses based on quantitative Kohn–Sham molecular orbital theory and corresponding energy decomposition analyses (EDA) show that the stronger hydrogen bonds in the unsaturated model complexes and in AT stem from stronger electrostatic interactions as well as enhanced donor–acceptor interactions in the σ-electron system, with the covalency being responsible for shortening the hydrogen bonds in these dimers.

1 Introduction

Hydrogen bonds play a crucial role in many biochemical processes and supramolecular chemistry.¹ After observing the X-ray diffraction images of DNA obtained by Rosalind Franklin, Watson and Crick proposed in 1953 that hydrogen bonds are essential for the working of the genetic code.² In DNA, the two helical strands of nucleotides are held together by the hydrogen bonds that arise between a purine- and a pyrimidine-derived nucleic base, that is, adenine–thymine (AT) or guanine–cytosine (GC).

Gilli et al.³ proposed that the hydrogen bonds in DNA base pairs are reinforced by π assistance, the so-called resonance-assisted hydrogen bonding (RAHB). The resonance of the conjugated double bonds assists the hydrogen bonds by charge delocalization, which results in a shortening of the distance between proton donor and proton acceptor. They proposed that the RAHB interaction occurs for inter- and intramolecular systems. Numerous theoretical studies have been devoted to study these inter- and intramolecular RAHBs.⁴,5a For the DNA base pair, the resonance assistance, as proposed by Gilli et al., is presented in Scheme 1 with the upper Lewis structure.

Scheme 1.

Resonance-assisted hydrogen bonding in adenine–thymine (AT)

In previous work,⁵ we established theoretically that, for the hydrogen bonds in DNA base pairs, the electrostatic interactions and orbital interactions are of equal importance, and that, indeed, the π electrons provide an additional stabilizing component. This finding was reconfirmed by others.4g,4j However, our work⁵ also showed computationally that the synergetic interplay between the delocalization in the π-electron system and the donor–acceptor interactions in the σ-electron system was small, that is, the simultaneous occurrence of the π and σ interactions is only slightly stronger than the sum of each of these interactions occurring individually. Recently, we showed that the intriguing cooperativity in guanine quartets, which can occur in the telomeric part of the chromosome, originates from the charge separation that goes with donor–acceptor orbital interactions in the σ-electron system, and not from the strengthening caused by resonance in the π-electron system.4i Also in this case the π delocalization provides only an extra stabilization to the hydrogen bonds.

In the present paper, we study the resonance assistance to the hydrogen bonds of AT and its smaller analogs (see Scheme 2), because the Lewis structure of AT in Scheme 1 as proposed by Gilli et al.³ suggests that the smaller mimic can also give the same resonance assistance. Also, our previous work on the Watson–Crick base pairs based on high-level density functional theory (DFT) computations,5a showed that the hydrogen bonds affected mainly the atomic charges of the blue part in Scheme 1. However, the resonance of the π electrons encompasses a larger part of the adenine nucleobase as can be seen in the lower (green) part of Scheme 1, suggesting that we can remove the 5-membered ring of the purine base, but we cannot remove the 6-membered ring. For the pyrimidine base, the resonance structures suggest that we need to incorporate all frontier atoms.

Scheme 2.

Adenine (A) and its smaller analogs (A′ and A“) and Thymine (T) and its smaller analogs (T′ and T”).

To validate the charge rearrangements suggested by resonance structures, the number of π electrons will be made smaller in the monomers by going from A, to A′ and A“ and from T to T′ and T”. All the possible pairing combinations will be taken into account (AT, AT′, AT“, A′T, A′T′, A′T”, A“T, A”T′ and A“T”, see Scheme 2). This computational investigation determines if the π assistance is exclusively due to aromaticity,⁶,4f or if the sp²-hybridization of the proton donor and acceptor atoms already accounts for the π charge delocalization. The logical follow-up question is to address the importance of hybridization by comparison of sp² and sp³ hybridized dimers. The latter hydrogen bonds are known to be longer when the difference is only the saturation of the molecules, but the complex has the same front atoms participating in the hydrogen bonds.

The computational analyses of the DNA base pair AT and its smaller mimics are based on dispersion-corrected density functional theory (DFT-D3).⁷ The small geometrical and bonding differences computed for the hydrogen bonds of AT and its mimics are explained with our quantitative Kohn–Sham molecular orbital (MO) and corresponding energy decomposition analyses (EDA).⁸ They reveal that the π assistance is independent of the number of π electrons of the monomers, but it is essential that the proton donor and acceptor atoms have π electrons.

2 Computational Methods

2.1 General procedure

All calculations were performed using the Amsterdam Density Functional (ADF) program (2013) developed by Baerends, Ziegler, and others.^9,10 The MOs were expanded in a large uncontracted set of Slater-type orbitals (STOs) containing diffuse functions: TZ2P (no Gaussian functions are involved).10i The basis set is of triple-ζ quality for all atoms and has been augmented with two sets of polarization functions, that is, 2p and 3d on H and 3d and 4f on C, N, and O. The 1s core shells of carbon, nitrogen, and oxygen were treated by the frozen-core approximation.10c An auxiliary set of s, p, d, f, and g STOs was used to fit the molecular density and to represent the Coulomb and exchange potentials accurately in each self-consistent field cycle.10a,10b

The calculations were done with DFT using the BLYP functional^11,12 with dispersion corrections as developed by Grimme,7e BLYP-D3(BJ). Dispersion corrections are applied using the DFT-D3(BJ) method, developed by Grimme,7f which contains the damping function proposed by Becke and Johnson.¹³ In this approach, the density functional is augmented with an empirical term correcting for long-range dispersion effects, described by a sum of damped interatomic potentials of the form C₆/(R⁶+c) added to the usual DFT energy.⁷ Equilibrium structures were optimized using analytical gradient techniques.¹⁰

Geometries were optimized in the gas phase with C_S symmetry. All stationary points were verified to be minima through vibrational analysis. For the dispersion-corrected functional, the basis set superposition error (BSSE) on the bond energy was not calculated because the dispersion correction7e has been developed such that the small BSSE effects5c are absorbed into the empirical potential. The BLYP-D₃(BJ)/TZ2P geometries and bond energies for the AT and GC base pairs are in line with benchmarks and other work.⁷

2.2 Bonding Energy Analysis

The hydrogen-bond energy ΔE of the dimer is defined as:

1

where E_dimer is the energy of the dimer, optimized in C_s symmetry, and E_monomer1 or E_monomer2 are the energies of the monomers adenine, thymine, or one of their smaller analogs, optimized in C₁ symmetry, that is, without any geometrical constraint. The overall bond energy ΔE is made up of two major components:

2

In this formula, the preparation energy (ΔE_prep) is the amount of energy required to deform the monomers from their equilibrium structure to the geometry that they acquire in the dimer. The interaction energy (ΔE_int) corresponds to the actual energy change when the prepared monomers are combined to form the pair.

The interaction energy is examined in the hydrogen-bonded model systems in the framework of the Kohn–Sham MO model using a quantitative energy decomposition analysis (EDA) into electrostatic interaction, Pauli repulsive orbital interactions, and attractive orbital interactions:^8,14,15,19

3

The term ΔV_elstat corresponds to the classical electrostatic interaction between the unperturbed charge distributions of the prepared (i.e. deformed) bases and is usually attractive. The Pauli-repulsion (ΔE_Pauli) comprises the destabilizing interactions between occupied orbitals and is responsible for any steric repulsion. The orbital interaction (ΔE_oi) in any MO model, and therefore also in Kohn–Sham theory, accounts for charge transfer (i.e. donor–acceptor interactions between occupied orbitals on one moiety with unoccupied orbitals of the other, including the HOMO–LUMO interactions) and polarization (empty/occupied orbital mixing on one fragment due to the presence of another fragment). The term ΔE_disp accounts for the dispersion corrections as introduced by Grimme and co-workers.7e,7f

The orbital interaction energy can be further decomposed into the contributions from each irreducible representation (Γ) of the interacting system [Eq. (4)] using the extended transition state (ETS) scheme developed by Ziegler and Rauk.¹⁴ Our approach differs in this respect from the Morokuma scheme¹⁵ which instead attempts a decomposition of the orbital interactions into polarization and charge transfer. In systems with a clear σ/π separation (such as our planar DNA base pair AT and its equivalents), the symmetry partitioning in our approach proves to be most informative.

4

2.3 Analysis of the Charge Distribution

The electron density distribution is analyzed using the Voronoi deformation density (VDD) method introduced in ref. ¹⁶. The VDD charge (Q_A) is computed as the (numerical) integral of the deformation density Δρ(r)=ρ(r)−Σ_Bρ_B(r) associated with the formation of the molecule from its atoms in the volume of the Voronoi cell of atom A [Eq. (5)]. The Voronoi cell of an atom A is defined as the compartment of space bounded by the bond midplanes on and perpendicular to all bond axes between nucleus A and its neighboring nuclei (cf. the Wigner–Seitz cells in crystals).10h,¹⁷

5

Here, ρ(r) is the electron density of the molecule, and Σ_Bρ_B(r) the superposition of atomic densities ρ_B of a fictitious promolecule without chemical interactions that is associated with the situation in which all atoms are neutral. The interpretation of the VDD charge (Q_A) is rather straightforward and transparent. Instead of measuring the amount of charge associated with a particular atom A, Q_A directly monitors how much charge flows, due to chemical interactions, out of (Q_A>0) or into (Q_A<0) the Voronoi cell of atom A, that is, the region of space that is closer to nucleus A than to any other nucleus.

The chemical bond between two molecular fragments can be analyzed by examining how the VDD atomic charges of the fragments change due to the chemical interactions. In ref. 5a, however, we have shown that [Eq. (5)] leads to small artifacts that prohibit an accurate description of the subtle changes in atomic charges that occur in the case of weak chemical interactions, such as hydrogen bonds. This is due to the so-called front-atom problem that, in fact, all atomic-charge methods suffer from. To resolve this problem and, thus, enable a correct treatment of even subtle changes in the electron density, the change in VDD atomic charges (ΔQ_A) is defined by [Eq. (6)], which relates this quantity directly to the deformation density, ρ_dimer(r)−ρ₁(r)−ρ₂(r), associated with forming the overall molecule (i.e. the base pair) from the joining of monomer 1 and 2.5a

6

Again, ΔQ_A has a simple and transparent interpretation: it directly monitors how much charge flows out of (ΔQ_A>0) or into (ΔQ_A<0) the Voronoi cell of atom A as a result of the chemical interactions between monomer 1 and 2 in the dimer.

This functionality is extended to also enable a decomposition of the charge redistribution per atom ΔQ_A into a component associated with the Pauli repulsion (ΔE_Pauli) and a component associated with the bonding orbital interactions (ΔE_oi):

7

This charge decomposition constitutes a complete bond analysis tool that mirrors the ΔE_Pauli and ΔE_oi terms occurring in the bond energy decomposition of [Eq. (3)] described in Section 2.2 (note that ΔV_elstat is not associated with any charge redistribution nor the empirical ΔE_disp).

The Pauli repulsion (ΔE_Pauli) is the energy change associated with going from the superposition of unperturbed monomer densities ρ₁+ρ₂ to the wave function Ψ⁰_dimer=N Â [Ψ₁ Ψ₂] that properly obeys the Pauli principle through explicit antisymmetrization (Â operator) and renormalization (N constant) of the product of monomer wave functions.¹⁸ The deformation density, Δρ(r)=ρ_dimer−ρ₁−ρ₂, associated with the formation of the dimer from the monomers is now divided into two components [Eq. 8]:

8

Here, Δρ_Pauli=ρ⁰_dimer−ρ₁−ρ₂ is associated with the Pauli repulsive orbital interactions, and Δρ_oi=ρ_dimer-ρ⁰_dimer is associated with the bonding orbital interactions; ρ⁰_dimer is the density belonging to Ψ⁰_dimer.

Thus, the change in atomic charge caused by Pauli repulsion between the monomers in the complex is defined by [Eq. (9)], and the corresponding change caused by charge transfer and polarization is given by [Eq. (10)].

9

10

With [Eq. (9) and (10)], we are able to measure quantitatively and separately the charge redistributions associated with the energy component (ΔE_Pauli) and with the orbital interaction component (ΔE_oi).

The ΔQ_A,Pauli and ΔQ_A,oi can be further decomposed into contributions from the various irreducible representations (Γ) of the dimer, for example, the σ and the π component (for the planar, C_s symmetric dimers):

11

12

Here, the density (ρ^Γ) is obtained as the sum of orbital densities of the occupied molecular orbitals belonging to the irreducible representation (Γ) [Eq. 13]:

13

It appears that, in particular, the decomposition of ΔQ_A^σ into a Pauli repulsion and a bonding orbital interaction component makes it possible to reveal small charge-transfer effects that are otherwise masked by the charge redistribution caused by Pauli repulsion (see Section 3.3).

3 Results and Discussion

3.1 Structure and stability of AT and its analogs

To study the importance of the π electrons and aromaticity on the hydrogen bonds of the DNA base pair AT, we have investigated computationally all the possible dimers of A and its smaller mimics A′ and A“ with T and its smaller mimics T′ and T”. The hydrogen-bond distances and energies calculated at the BLYP-D3(BJ)/TZ2P level of theory for the possible dimers (AT, AT′, AT“, A′T, A′T′, A′T”, A“T, A”T′, and A“T”) are shown in Figure 1. The optimal structures of these dimers have been obtained in C_S symmetry, and C₁ symmetry for monomers.

Figure 1.

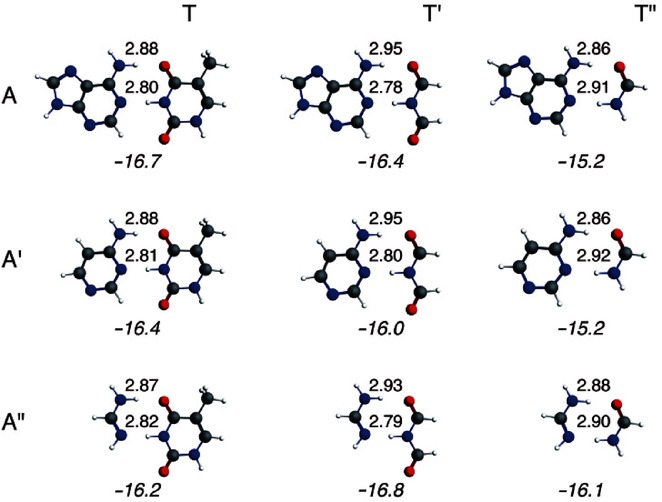
Hydrogen-bond distances (in Å) and energies (in kcal mol⁻¹) for adenine–thymine (AT) and its smaller analogs at the BLYP-D3(BJ)/TZ2P level of theory.

From this computational investigation, it can be deduced that the hydrogen-bond energy changes slightly from −16.8 kcal mol⁻¹ to −15.2 kcal mol⁻¹, when the size of the aromatic system or the number of π electrons is varied. However, the difference in energy between the largest system, AT, and the smallest dimer, A“T”, is only 0.6 kcal mol⁻¹. The geometrical changes in the hydrogen-bond distances are more pronounced (>0.1 Å) when the number of π electrons is modified. From A to A′ and A“, the N6(H)⋅⋅⋅O4 and N1⋅⋅⋅(H)N3 distances are approximately similar when pairing with T, T′, or T”. However, when we keep A (or A′, A“) the same and pair it with T, T′, and T”, the pattern in the hydrogen-bond distances changes: for T and T′, the N6–O4 distance is larger (by 0.05–0.08 Å) than the N1–N3 distance, whereas for T“ the N6–O4 distance is shorter (by 0.2–0.6 Å) than the N1–N3 distance.

3.2 Nature of the hydrogen-bond interaction

In the next part, we will discuss the nature of the hydrogen bonds in AT and its smaller mimics. Previous work,5a on the nature of the Watson–Crick base pairs AT and GC revealed the importance of electrostatic and covalent interactions in the bonding mechanism.

Electronic structure of A versus A′ and A“ and of T versus T′ and T”

Previously, we shown that A and T are electronically complementary, that is, the proton- acceptor atoms have a negative charge whereas the corresponding protons they face are all positively charged. This is also the case for the smaller mimics of A and T (as can be seen in Figure 2). The differences in charge of the atoms N1 and H6 for A, A′, and A“, and of H3 and O4 for T, T′, and T” are small, as expected from the small differences in hydrogen-bond energies and lengths.

Figure 2.

VDD atomic charges (in me⁻) of the prepared monomers (see [Eq. (5)]).

Next, we consider the possibility of charge-transfer interactions in the σ-electron system. Figure 3 displays the basic features in the electronic structures of the DNA bases A and T that lead to the donor–acceptor orbital interactions: a lone pair on a proton-acceptor nitrogen or oxygen atom pointing toward and donating charge into the unoccupied σ* orbital of an N−H group of the other base. This leads to the formation of a weak covalent bond which is σ_LP+σ*_N−H bond. For a complete description of the covalent component in the hydrogen bonds of AT, see ref. 5a.

Figure 3.

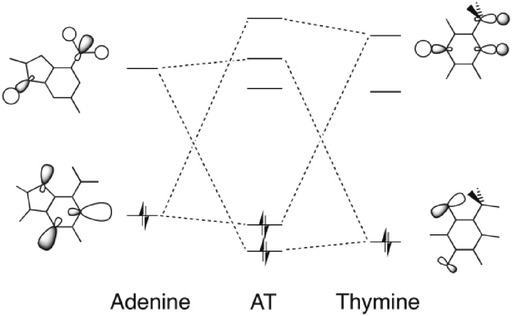
Molecular orbital diagram with the most pronounced donor–acceptor interactions in the N6(H)⋅⋅⋅O4 and N1⋅⋅⋅(H)N3 hydrogen bonds between adenine and thymine.

For the same donor–acceptor interactions to occur in the different dimers, the smaller mimics of A and T need to possess similar frontier orbitals in the σ electronic system. In Figure 4, the frontier orbitals of A, A′, A“, T, T′, and T” are depicted. The orbitals are very similar except for the σ_HOMO−1 of A“ and T”, which have only one proton-acceptor nitrogen or oxygen atom, respectively, and therefore, also have only one lone-pair character orbital. The donor–acceptor interactions occur between the σ_HOMO−1 and σ_HOMO of A (or A′, A“) and the σ_LUMO or σ_LUMO+1 of T (or T′, T”) for the N⋅⋅⋅(H)N hydrogen bond. For the other hydrogen bond, N(H)⋅⋅⋅O, the interaction occurs between the σ_HOMO-1 and σ_HOMO of T (or T′, T“) and the σ_LUMO or σ_LUMO+1 of A (or A′, A”). Note that for A“, the donor–acceptor interactions occur only between the σ_HOMO of A” and the σ_LUMO or σ_LUMO+1 of T, T′, or T“ for the N⋅⋅⋅(H)N hydrogen bond, and for T”, the donor–acceptor interactions occur between the σ_HOMO of T“ and the σ_LUMO or σ_LUMO+1 of A, A′, or A” for the N(H)⋅⋅⋅O hydrogen bond.

Figure 4.

Frontier orbitals of the monomers (HOMO−1, HOMO, LUMO, and LUMO+1) in the σ electronic system, with their corresponding energies (eV).

The donor–acceptor interactions in the σ electronic system lead to small depopulations of the occupied σ-orbitals and small populations of the unoccupied σ-orbitals of the monomers when they form the complex. In Table 1, the values of Gross populations for the σ_HOMO-1, σ_HOMO, σ_LUMO, and σ_LUMO+1 of the different monomers are given. The Gross populations are obtained from the calculation where the prepared monomers (that is in the geometry that they acquire in the dimer) are combined together to form the dimer. The values of the Gross populations are small (mostly less than 0.10 electrons), which are in line with previous work on hydrogen bonds.5a Other orbitals can also be slightly depopulated such as the σ_HOMO−3 or σ_HOMO−2, or slightly populated such as the σ_LUMO+2 or σ_LUMO+3, but as these are not the main interactions, we have left them out of Table 1.

Table 1.

Bonding analyses and populations for adenine—thymine (AT) and its smaller analogs.^[a]

	AT	AT′	AT′′	A′T	A′T′	A′T“	A”T	A“T′	A”T“
Bond energy [kcal mol−1]
ΔE	−16.7	−16.4	−15.2	−16.4	−16.0	−15.2	−16.2	−16.8	−16.1
ΔEprep	1.8	2.0	1.4	1.8	1.9	1.5	2.3	2.5	1.8
ΔEint	−18.5	−18.4	−16.7	−18.3	−17.9	−16.7	−18.5	−19.4	−17.9
Bond energy decomposition [kcal mol−1]
ΔEPauli	39.9	39.4	32.0	38.6	37.9	31.3	38.2	38.2	32.3
ΔVelstat	−31.9	−31.2	−27.3	−31.0	−30.0	−26.8	−31.2	−31.5	−28.4
ΔEdisp	−5.4	−5.0	−3.9	−5.3	−4.9	−3.9	−4.1	−3.8	−3.4
ΔEoi	−21.1	−21.6	−17.5	−20.5	−20.8	−17.2	−21.5	−22.2	−18.5
ΔEσ	−19.5	−20.0	−15.9	−19.0	−19.3	−15.6	−19.7	−20.4	−16.6
ΔEπ	−1.6	−1.6	−1.6	−1.5	−1.6	−1.6	−1.8	−1.9	−1.9
Gross populations of A [e−]
σLUMO+1	0.01	0.01	0.01	0.01	0.01	0.02	0.02	0.02	0.02
σLUMO	0.01	0.01	0.02	0.02	0.01	0.02	0.01	0.01	0.01
σHOMO	1.95	1.95	1.97	1.96	1.95	1.97	1.88	1.87	1.91
σHOMO−1	1.97	1.97	1.98	1.96	1.96	1.98	2.00	2.00	2.00
Gross populations of T [e−]
σLUMO+1	0.04	0.00	0.03	0.03	0.01	0.03	0.06	0.01	0.04
σLUMO	0.01	0.08	0.02	0.01	0.08	0.02	0.01	0.10	0.03
σHOMO	1.97	1.98	1.95	1.97	1.98	1.95	1.97	1.98	1.95
σHOMO−1	1.99	1.97	2.00	1.99	1.97	2.00	1.99	1.98	2.00

[a] Energies and geometries computed at BLYP-D3(BJ)/TZ2P in C_s symmetry for the pair and C₁ for monomer.

Quantitative decomposition of the hydrogen-bond energy

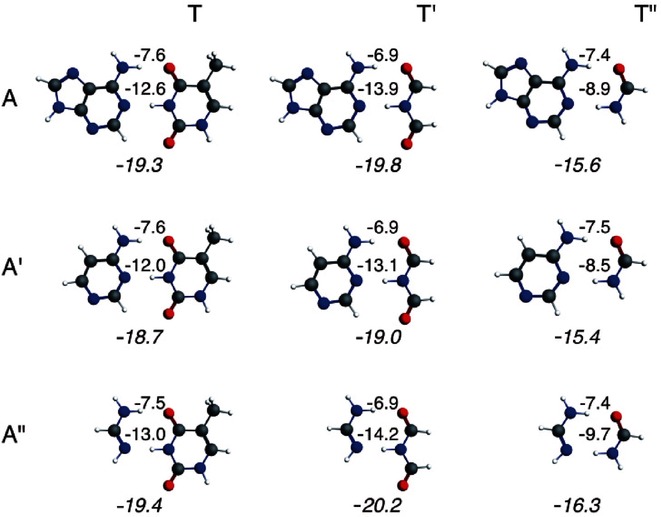
In the previous part, we established that the mimics of A and T have suitable charge distributions for electrostatically attracting each other. After having established the occurrence of σ charge transfer and π polarization (see also previous work), ^[5a] we want to quantitatively assess the importance of the various components of the dimerization energy as we did for the Watson–Crick base pair AT. Thus, we have carried out the bond energy decomposition for the different dimers (see Table 1).

The bond energy is first decomposed into a preparation energy (ΔE_prep) for the deformation of the monomers and the interaction energy between the monomers (ΔE_int). The former is small (1.4 to 2.5 kcal mol⁻¹) as the monomers are only slightly deformed due to the hydrogen bonds. The trend of the bond energy is followed by the interaction energy. The values of the interaction energy deviate somewhat more and are between −16.7 kcal mol⁻¹ and −19.4 kcal mol⁻¹.

Further decomposition of the interaction energy shows that, in all cases, the electrostatic interaction (ΔV_elstat) is not capable of providing a net bonding interaction as it only compensates partly the Pauli-repulsive orbital interactions (ΔE_Pauli). Without the bonding orbital interactions, (ΔE_oi), the monomers would repel each other. The orbital interaction is divided into a σ component and a π component. ΔE_σ consists mainly of the electron donor–acceptor interactions mentioned above. The π component (ΔE_π) accounts basically for the polarization in the π system, which turns out to partly compensate the local buildup of charge caused by the charge-transfer interactions in the σ system (see Section 3.3 on charge redistribution). The dispersion term comprises the correction for dispersion interactions and lies between −3.8 kcal mol⁻¹ and −5.4 kcal mol⁻¹.

The σ-orbital interaction term (ΔE_σ) is the sum of the donor–acceptor interactions in both hydrogen bonds. To get a quantitative estimate of how large each donor–acceptor interaction is in the individual N(H)⋅⋅⋅O and N⋅⋅⋅(H)N bond, we used the same technique as in ref. 5a, where we removed σ and π virtuals for the AT base pairs. In this previous work,5a we removed the π virtuals of both bases to switch off the polarization in the π electronic system. Furthermore, we removed the σ virtuals from one base to switch off the donor–acceptor interactions of one of the hydrogen bonds. The same procedure was followed for the A, T, and their analogs. The σ interactions of the hydrogen bonds, ΔE_σ (σ,–;σ,–), were analyzed without occurrence of the π polarization (that is, the π virtuals were removed in the calculation from both monomers). Comparison of ΔE_σ from Table 1 and ΔE_σ(σ,–;σ,–) from Figure 5 shows that when the π polarization is allowed, the donor–acceptor interactions are only 0.3 kcal mol⁻¹ lower. Therefore, we can conclude that also for the smaller mimics of A and T, the synergy between σ and π is small. Figure 5 also displays the donor–acceptor interactions in the individual hydrogen bonds’ ΔE_σ(σ,–;–,–) for N(H)⋅⋅⋅O with the σ virtuals removed from T, T′, or T“ and ΔE_σ(–,–;σ,–) for N⋅⋅⋅(H)N with the σ virtuals removed from A, A′, or A”.

Figure 5.

ΔE_σ(σ,–;σ,–) of both hydrogen bonds, ΔE_σ(σ,–;–,–) for the N(H)⋅⋅⋅O hydrogen bond, and ΔE_σ(–,–;σ,–) for the N⋅⋅⋅(H)N hydrogen bond (see main text).

The synergism within the σ system between charge transfer from one base to the other through one hydrogen bond, and back through the other hydrogen bond can be investigated by comparison of ΔE_σ(σ,–;σ,–) with the sum of ΔE_σ(σ,–;–,–) and ΔE_σ(–,–;σ,–). In accordance with our previous work, the values show that the hydrogen bonds donating charge in opposite directions operate independently. Furthermore, the N⋅⋅⋅(H)N hydrogen bond is twice as strong as the N(H)⋅⋅⋅O hydrogen bond for the dimers with T and T′, but for the dimers with T“, the hydrogen bonds are of equal strength.

3.3 Charge redistribution due to hydrogen bonding

Up until now, our investigation has shown that the smaller mimics of A and T have the same bonding characteristics as the dimer AT, which implies that for these hydrogen bonds, the atoms participating in the hydrogen bonds do not need to be connected to an aromatic ring to achieve this strength of hydrogen bonding. In this part, we want to investigate the electronic rearrangements in the σ and π electronic system due to the formation of the hydrogen bonds. For this purpose, we use the partitioning of the VDD atomic charges into σ and π components, see Section 2.3, [Eq. (11)–(12)]. (For the charge rearrangements due to the Pauli repulsive interaction see Figures S1 and S2 in the Supporting Information).

The σ and π charge rearrangements for the nine dimers are depicted in Figure 6 and 7 respectively. The ΔQ^σ_A,oi values reveal a clear charge-transfer picture for AT and its equivalents: negative charge is lost on the electron-donor atoms, whereas there is a significant accumulation of negative charge on the nitrogen atoms of the electron-accepting N−H bonds (see Figure 6). The π-electron density of the bases is polarized in such a way that the build-up of charge arising from charge-transfer interactions in the σ system is counteracted and compensated: the electron-donor atoms gain π density and the nitrogen atoms of the electron-accepting N−H bonds lose π density (compare ΔQ^σ_A,oi and ΔQ^π_A,oi in Figure 6 and 7). This π charge rearrangement is in agreement with the Lewis structure proposed by Gilli et al.³ (see Scheme 1). The charge rearrangements for T“ are somewhat smaller than for T and T′, which is in line with the weaker orbital interactions for T”. Furthermore, we see that the charge rearrangements in σ and π electronic systems do not depend on the aromatic ring.

Figure 6.

Voronoi deformation density (VDD) atomic charges (ΔQ^σ_A,oi, in me⁻) associated with the formation of the different dimers. The contributions stemming from the σ electrons are given.

Figure 7.

Voronoi deformation density (VDD) atomic charges (ΔQ^π_A,oi, in me⁻) associated with the formation of the different dimers. The contributions stemming from the π electrons are given.

3.4 sp² versus sp³ hybridization

In the previous section, we established that the number of π electrons does not influence the hydrogen-bond energy; that is, the strength of the hydrogen bonds of AT and its smaller analogs deviate less than 1.6 kcal mol⁻¹ from each other. This leads us to conclude that the hydrogen donor and acceptor atoms do not need to be part of an aromatic ring to establish this strong hydrogen bonding—but do they need to be sp² hybridized? If so, how does the sp² hybridization assist the hydrogen bonds, which result in a shortening of the distance between proton donor and proton acceptor?³

This part will address this question if the hydrogen donor and acceptor atoms need to be sp²-hybridzed atoms by comparing A“T” (sp²) to a“t” (sp³), see Figure 8. The latter exists in the chair and boat conformation and, in analogy to cyclohexane, the chair conformation is 4.8 kcal mol⁻¹ lower in energy (see Supporting Information). The hydrogen-bond energy of the sp²-hybridized A“T” is 7.9 kcal mol⁻¹ stronger bound than its saturated equivalent (see Table 2). This cannot be attributed to the π electrons as the π polarization in the sp²-hybridized A“T” amounts only to −1.9 kcal mol⁻¹ (see Table 1). At the equilibrium structures, all the bonding components of the interaction energy, ΔE_oi and ΔV_elstat, are smaller for a“t”, than for A“T”, but the Pauli repulsion is also smaller in the case of a“t”.

Figure 8.

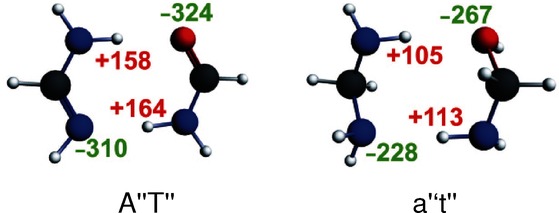
Atomic Voronoi deformation density (VDD) charges (in me⁻) for front atoms in A“T” and a“t”.

Table 2.

Bonding analyses for adenine—thymine small analogs A“T” and a“t”.^[a]

	A“T”	A“T” at R[sp3][b]			a“t′′	a”t′ at R[sp2][b]
Distances [Å]
N(H)⋅⋅⋅O	2.88	3.09			3.09	2.88
N⋅⋅⋅(H)N	2.90	3.14			3.14	2.90
Bond energy [kcal mol−1]
ΔE	−16.1	−14.4			−8.2	−6.7
ΔEprep	1.8	1.8			0.7	0.7
ΔEint	−17.9	−16.2			−8.9	−7.4
ΔEPauli	32.3	15.0			16.4	34.3
ΔVelstat	−28.4	−18.5			−14.4	−23.8
ΔEdisp	−3.4	−2.7			−3.4	−4.2
ΔEoi	−18.5	−10.0			−7.5	−13.7
ΔEσ	−16.6	−8.9
ΔEπ	−1.9	−1.1
Gross populations: N(H)⋅⋅⋅O [e−]
σLUMO+1 of A“	0.02	0.02		LUMO+1 of a”	0.01	0.01
σLUMO of A“	0.01	0.01		LUMO of a”	0.01	0.02
σHOMO of T“	1.95	1.97		HOMO of t”	2.00	2.00
σHOMO−1 of T“	2.00	2.00		HOMO−1 of t”	1.98	1.96
Gross populations: N⋅⋅⋅(H)N [e−]
σLUMO+1 of T“	0.04	0.03		LUMO+1 of t”	0.02	0.02
σLUMO of T“	0.03	0.02		LUMO of t”	0.01	0.01
σHOMO of A“	1.91	1.94		HOMO of a”	1.95	1.93
σHOMO−1 of A“	2.00	2.00		HOMO−1 of a”	1.99	1.99
Orbital energies of A“ [eV]				Orbital energies of a” [eV]
σLUMO+1	0.29			LUMO+1	0.30
σLUMO	−0.39			LUMO	−0.24
σHOMO	−5.80			HOMO	−5.31
σHOMO−1	−10.86			HOMO−1	−5.60
Orbital energies of T“ [eV]				Orbital energies of t” [eV]
σLUMO+1	0.18			LUMO+1	0.41
σLUMO	−0.64			LUMO	−0.49
σHOMO	−5.85			HOMO	−5.77
σHOMO−1	−9.80			HOMO−1	−6.54
Overlap < Α“|Τ” > for N(H)⋅⋅⋅O				Overlap < a“|t” > for N(H)⋅⋅⋅O
<σLUMO+1|σHOMO>	0.11	−0.10		<LUMO+1|HOMO−1>	−0.08	−0.08
<σLUMO|σHOMO>	0.09	−0.08		<LUMO|HOMO−1>	−0.12	−0.11
Overlap < Α“|Τ” > for N⋅⋅⋅(H)N				Overlap < a“|t” > for N⋅⋅⋅(H)N
<σHOMO|σLUMO+1>	0.27	0.26		<HOMO|LUMO+1>	−0.15	0.14
<σHOMO|σLUMO>	0.23	0.21		<HOMO|LUMO>	0.10	−0.10

[a] Energies and geometries computed at BLYP-D3(BJ)/TZ2P level of theory: A“T” in C_s symmetry, and a“t” in C₁ symmetry (chair conformation). [b] A“T” has been elongated to the distance of a“t”, R(sp³), and a“t” compressed to the distance of A“T”, R(sp²).

To analyze where the difference due to hybridization comes from, we compressed a“t” to the distance R(sp²), that is, the hydrogen-bond distances of A“T”. We also expanded A“T” to the distances of R(sp³), that is, the hydrogen-bond distances of a“t”. At R(sp²), the interaction energy of A“T” amounts to −17.9 kcal mol⁻¹, and −7.4 kcal mol⁻¹ for a“t”. Comparison of the components of the interaction energy at the R(sp²) distance for both dimers reveals that the stronger interaction energy of A“T” can be ascribed to the stronger electrostatic interaction as well as the larger orbital interaction. We see that both dimers have almost the same Pauli interaction (32.3 for A“T” and 34.3 for a“t”). The electrostatic interaction and the orbital interaction are both stronger (by 4.6 kcal mol⁻¹ and 4.8 kcal mol⁻¹, respectively) for A“T” than for a“t” at the distance R(sp²). The π resonance only amounts to −1.9 kcal mol⁻¹ (see Table 2). The smaller ΔV_elstat for a“t” compared with A“T”, at the same R(sp²) distance, can be understood with the atomic Voronoi deformation density charges depicted in Figure 8. The absolute values of the VDD charges of the front atoms in a“t” are smaller than in the A“T”.

The decomposition of the interaction energy is presented in graphical form in Figure 9 at the R(sp²) and R(sp³) distances. The augmentation of Pauli repulsion by compressing the dimers A“T” and a“t” from R(sp³) to the R(sp²) distance has to be overcome by the attractive contributions to the bonding energy. The electrostatic interaction gains for both dimers equally, and the dispersion correction does not change much by the compression. The largest difference due to the shortening is seen in the orbital interaction: A“T” gains more rapidly (blue line in ΔE_oi) than a“t” (red line in ΔE_oi). Decomposition of ΔE_oi of A“T” into ΔE_σ and ΔE_π of A“T” shows that it is the σ component in the orbital interaction (green line) that is responsible for strengthening the hydrogen bonds for the sp²-hybridized dimers, as it increases more rapidly. This results in an equilibrium structure of A“T” with shorter hydrogen bonds than for a“t”.

Figure 9.

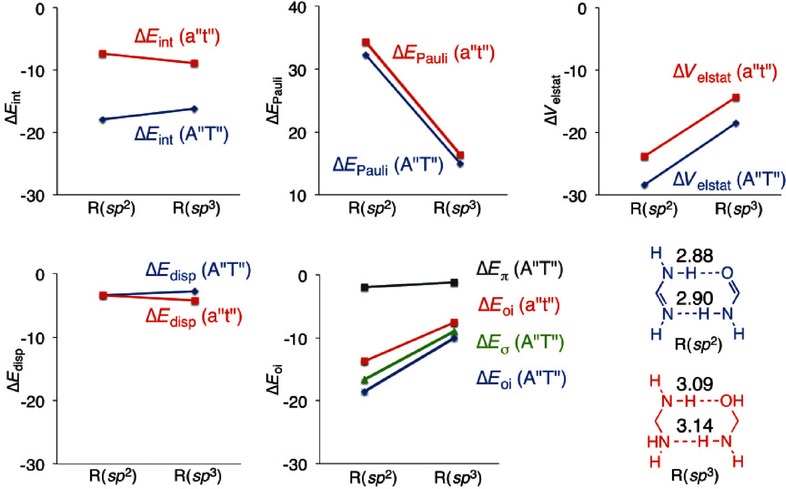
Energy decomposition analysis for A“T” and a“t” at the equilibrium distance R(sp²) of A“T” and at the equilibrium distance R(sp³) of a“t”.

We are left with the question why the σ component of the orbital interaction is much more favorable for sp² than sp³. To understand this, we performed Kohn–Sham MO analysis on the hydrogen bonds in A“T” and a“t” at the R(sp²) and R(sp³) distances (see Table 2). The Gross populations and the energies of the frontier orbitals are given, together with the overlap between the frontier orbitals in Table 2. The N(H)⋅⋅⋅O hydrogen bond in A“T” is explained by a charge-transfer interaction of 0.05 electrons from the σ_HOMO of T“ to the σ_LUMO and σ_LUMO+1 of A” (0.02 and 0.01 electrons, respectively). For a“t” this charge transfer is smaller: 0.02 electrons from the HOMO−1 of t“ to the LUMO and LUMO+1 of a” (both 0.01 electrons). The electron donation and acceptance within one hydrogen bond of the dimers are not exactly of the same magnitude because there is also polarization (mixing between occupied and unoccupied) on the same monomer due to the presence of the other monomer. The smaller charge-transfer interaction in a“t” has its origin in the lower lying electron donor orbital (HOMO−1 at −6.54 eV for t“ and σ_HOMO at −5.85 eV for T”). The accepting orbitals of A“ and a” do not differ so much in energy, and the overlap between the frontier orbitals is of the same size in the N(H)⋅⋅⋅O hydrogen bond of A“T” and a“t”.

The charge transfer in the N⋅⋅⋅(H)N hydrogen bond is also larger in A“T” than in a“t”. The σ_HOMO of A“ donates 0.09 electrons into the accepting orbitals of T”, whereas the HOMO of a“ donates only 0.05 electrons in the accepting orbitals of t”. In this case, the HOMO–LUMO gap between frontier orbitals cannot be held responsible for this difference as it amounts to 5.2 eV for A“T” and 4.8 eV for a“t” (nor the HOMO–LUMO+1 gap which amounts to respectively 6.0 eV and 5.7 eV). However, the overlap between the frontier orbitals in A“T” is twice as large than for a“t”: <σ_HOMO|σ_LUMO> amounts to 0.23 and <HOMO|LUMO> to 0.10, respectively (see Table 2). This is merely the consequence of the σ_HOMO of A“ and σ_LUMO of T” being somewhat better directed towards each other due to the sp²-hybridization (see Figure S3 in the Supporting Information).

Thus, the sp²-hybridized dimer has shorter hydrogen bonds for two different reasons: 1) because of the smaller HOMO–LUMO gap in the σ electronic system for one hydrogen bond and 2) because the overlap between the frontier orbitals in the σ system is better than in the sp³ system for the other hydrogen bond.

4 Conclusions

In the present paper, we studied the π assistance to the hydrogen bonds of AT and its analogs. This investigation determined that the π assistance is not exclusively due to aromaticity, but that the sp²-hybridization of the proton donor and acceptor atoms already accounts for the π charge delocalization. This follows from extensive computational analyses of the DNA base pair AT and its smaller mimics (AT′, AT“, A′T, A′T′, A′T”, A“T, A”T′, and A“T”, see Scheme 1) based on dispersion-corrected density functional theory (DFT-D3). The pair A“T”, which is the smallest equivalent, lacks the aromatic rings of AT, but the hydrogen-bond energy is very similar to the bonding energy of AT. The small geometrical and bonding differences computed for the hydrogen bonds of A“T” and the other equivalents of AT are explained with our quantitative Kohn–Sham molecular orbital (MO) and corresponding energy decomposition analyses (EDA). They reveal that the π assistance is independent of the number of π electrons of the monomers, but it is essential that the proton donor and acceptor atoms have π electrons to arrive at similar hydrogen-bond energies for all the mimics of AT.

Thus, the small sp²-hybridized dimer was compared with its sp³ equivalent and subjected to a Kohn–Sham MO analysis to understand where the strengthening and shortening of the hydrogen bonds comes from. The hydrogen-bond energy of the sp² system (A“T”) amounts to −16.1 kcal mol⁻¹, and of the equivalent sp³ dimer (a“t”) to −8.2 kcal mol⁻¹. This could not be explained with the assistance by the π electronic system, because the polarization in the π electronic system is only 2 kcal mol⁻¹. The MO analysis revealed that the stronger hydrogen bonds in the sp² systems can be ascribed to enhanced electrostatic interactions and also better covalent interactions. The shorter hydrogen bonds in the sp²-hybridized dimer are ascribed to two different reasons: 1) for the N(H)⋅⋅⋅O hydrogen bond it can be explained with the smaller HOMO–LUMO gap in the σ electronic system of A“T”, and 2) for the N⋅⋅⋅(H)N hydrogen bond, the reason can be found in the larger overlap between the frontier orbitals in the σ system of the sp² system than in the sp³ system. Thus, it is not the assistance by the π electrons; rather, the stronger covalent interaction in the hydrogen bonds of unsaturated dimers compared with the covalency in saturated dimers that is the reason for the experimental finding of smaller hydrogen-bond distances for resonance-assisted AT and its smaller analogs.

Supporting Information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re-organized for online delivery, but are not copy-edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.