Design and in vivo evaluation of more efficient and selective deep brain stimulation electrodes

Abstract

Objective

Deep brain stimulation (DBS) is an effective treatment for movement disorders and a promising therapy for treating epilepsy and psychiatric disorders. Despite its clinical success, the efficiency and selectivity of DBS can be improved. Our objective was to design electrode geometries that increased the efficiency and selectivity of DBS.

Approach

We coupled computational models of electrodes in brain tissue with cable models of axons of passage (AOPs), terminating axons (TAs), and local neurons (LNs); we used engineering optimization to design electrodes for stimulating these neural elements; and the model predictions were tested in vivo.

Main results

Compared with the standard electrode used in the Medtronic Model 3387 and 3389 arrays, model-optimized electrodes consumed 45–84 % less power. Similar gains in selectivity were evident with the optimized electrodes: 50 % of parallel AOPs could be activated while reducing activation of perpendicular AOPs from 44–48 % with the standard electrode to 0–14 % with bipolar designs; 50 % of perpendicular AOPs could be activated while reducing activation of parallel AOPs from 53–55 % with the standard electrode to 1–5 % with an array of cathodes; and, 50 % of TAs could be activated while reducing activation of AOPs from 43–100 % with the standard electrode to 2–15 % with a distal anode. In vivo, both the geometry and polarity of the electrode had a profound impact on the efficiency and selectivity of stimulation.

Significance

Model-based design is a powerful tool that can be used to improve the efficiency and selectivity of DBS electrodes.

1. Introduction

Deep brain stimulation (DBS) is an established therapy for neurological disorders, wherein 100–200 Hz electrical pulses are delivered to specific regions of the brain. DBS is effective in treating movement disorders, including Parkinson’s disease and essential tremor (Limousin et al., 1999, Montgomery, 1999) and shows promise for treating epilepsy and psychiatric disorders (Kuhn et al., 2010, Mayberg et al., 2005). Despite the clinical success of DBS, some aspects of the therapy require further development.

The energy efficiency of stimulation is one aspect of DBS that can be improved. Implantable pulse generators (IPGs) powered by non-rechargeable primary batteries last 3–5 years (Ondo et al., 2007), which is much shorter than the required duration of treatment. Consequently, patients must undergo repeated IPG replacement surgeries, obligating them to incur repeatedly the risks associated with surgery, which include infection (Boviatsis et al., 2010, Bronstein et al., 2011) and misprogramming (Okun et al., 2005). Rechargeable IPGs, which have longer predicted battery lives, are an alternative to primary-cell devices. In some cohorts, a majority of the patients were highly satisfied with the rechargeable stimulators (McAuley et al., 2013, Timmermann et al., 2013, Waln and Jimenez-Shahed, 2014); whereas in other cohorts, some patients felt that the burden of recharging was not worth the extra battery life (Harries et al., 2012, Lam and Rosenow, 2010). Whether a patient prefers a primary-cell or rechargeable IPG, improved efficiency can impact the cost and acceptability of DBS.

There are a number of approaches for improving stimulation efficiency including modifying the stimulation waveform (Foutz and McIntyre, 2010, Sahin and Tie, 2007, Wongsarnpigoon and Grill, 2010) or altering the material properties of the electrode (Cogan, 2008, Merrill et al., 2005). Examples of latter include surface roughening (Norlin et al., 2002) and electrode coatings (Cogan, 2008). Additionally, efficiency may be improved by increasing the area and/or perimeter of the electrode (Golestanirad et al., 2013, Howell and Grill, 2014, Wei and Grill, 2005).

Another aspect of DBS that requires development is stimulation selectivity, or the ability to activate target neural elements over non-target elements, as suboptimal lead placement is a common failure mode of DBS (Ellis et al., 2008, Okun et al., 2008, Okun et al., 2005). Lead deviations of 2–3 mm can preclude some or all potential clinical benefits (Bronstein et al., 2011, Ellis et al., 2008, Okun et al., 2008, Okun et al., 2005), and in some cases, generate side-effects by stimulation of non-target neural elements (Okun et al., 2008). For example, DBS of cerebellar afferents in the ventral intermediate nucleus of thalamus masks tremor-associated burst activity in essential tremor (Birdno et al., 2012). Activation of cerebellar afferents, however, may be limited by activation of non-target projection neurons in the ventral caudal nucleus of thalamus, which can cause uncomfortable paresthesias (Keane et al., 2012). Small lead misplacements can sometimes be overcome by reprogramming (Kuncel and Grill, 2004), but larger misplacements may require an additional surgery to reposition the lead (Ellis et al., 2008).

Improvements in selectivity may be possible by altering the configuration (i.e., the geometry and polarity) of the stimulation electrodes. For example, with a standard clinical lead, such as the Medtronic Model 3387 or Model 3389, selectivity may be improved by altering the geometry of the individual electrodes (Butson and McIntyre, 2006), segmenting the electrodes into many smaller electrodes (Buhlmann et al., 2011, Martens et al., 2011), or by combining the electrodes in multipolar configurations to shape the volume of tissue activated (Keane et al., 2012).

The goal of the current study was to design electrodes that improved the efficiency and selectivity of DBS. We coupled a computational model of a cylindrical electrode array in brain tissue with cable models of neural elements and used engineering optimization to design electrode configurations that increased the efficiency and selectivity of DBS. Subsequently, prototype electrodes were tested in vivo. Electrodes with greater stimulation efficiency will increase the lifetime of primary-cell IPGs and increase the recharge intervals of rechargeable IPGs, and electrodes with greater stimulation selectivity may reduce the sensitivity of clinical outcomes to malpositioning of the electrode, thereby reducing side effects. Preliminary results of this study were presented in a conference paper (Howell and Grill, 2013).

2. Methods

2.1. Computational model of DBS

We constructed a finite element method model in COMSOL Multiphysics v3.4 (COMSOL Inc., Burlington, MA) consisting of a three-contact cylindrical electrode array surrounded by a cubic (60 mm × 60 mm × 60 mm) volume of brain tissue (0.2 S/m (Gabriel et al., 2009)) (figure 1a). A 0.5 mm thick layer of tissue immediately surrounding the electrode represented the glial scar (0.1 S/m (Grill and Mortimer, 1994)), and the electrical conductivities of the encapsulation and brain tissue were homogeneous, isotropic and purely resistive (Bossetti et al., 2008). The origin in the model was located at the geometric center of electrode 2.

Figure 1.

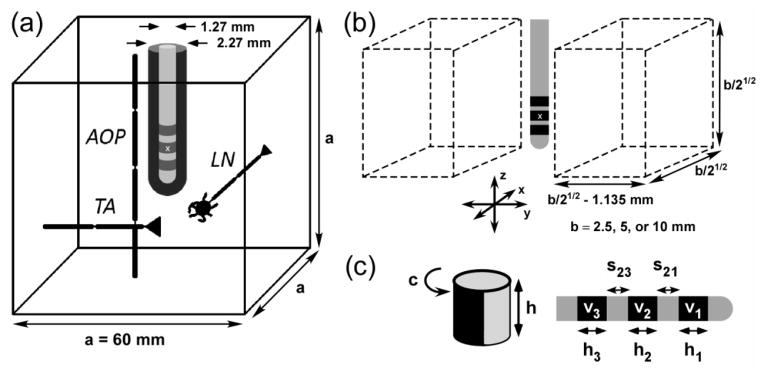
A computational model for design and analysis of deep brain stimulation (DBS) electrodes. (a) A finite element method model of an electrode array surrounded by encapsulation tissue (0.1 S/m) and brain tissue (0.2 S/m) was coupled to cable models of neural elements: AOPs = axons of passage, TAs = terminating axons, and LNs = local neurons. (b) Neural elements were distributed in two rectangular prisms that were displaced on either side of the x-z plane. (c) The three-electrode array (right) was parameterized using eight variables: 3 electrode heights (h₁, h₂, and h₃), 2 interelectrode spacings (s₂₁ and s₂₃), and 3 applied potentials (v₁, v₂, and v₃). In monopolar stimulation (left), electrodes 1 and 3 were modeled as insulating boundaries, and electrode 2 was parameterized by its height, h, and normalized circumference, c. The origin (x) is located at the geometric center of electrode 2.

A normal current density of 0 A/mm² (i.e., a Neumann boundary condition) was imposed on the electrode shaft to model a perfect insulator. Fixed potentials of X V (i.e., Dirichlet boundary conditions), where − 10 < X < 10, were imposed individually on the three contacts, and 0 V was imposed on the outer tissue boundary. The electric potentials were calculated by solving Laplace’s equation,

$$\nabla ·(\sigma ·\nabla \mathrm{\Phi })=\nabla ·\stackrel{\rightharpoonup }{J}=0,$$ (1)

where ∇ is the divergence operator, σ is the conductivity and J⃑ is the current density. The injected current was calculated by integrating the current density over the surface of the electrode,

$$\stackrel{\rightharpoonup }{J}=\sigma ·\stackrel{\rightharpoonup }{E},$$ (2)

where E⃑ is the electric field.

The NEURON simulation environment (v7.1) (Carnevale and Hines, 1997) was used to implement cable models of neural elements, including myelinated axons of passage (AOPs) (McIntyre et al., 2002), terminating axons (TAs), and local neurons (LNs) (McIntyre et al., 2004). The axons of all neural elements were 2.5 μm in diameter (Assaf et al., 2008, Barazany et al., 2009) and 40 mm in length. AOPs, TAs, and LNs were placed in the tissue according to defined reference points, which were the middle node of Ranvier, the axon terminal, and the center of the soma, respectively. Populations consisted of 100 elements with axons oriented parallel (z direction) and perpendicular (x direction) to the electrode shaft (figure 1b). The two halves of the population were uniformly distributed in two rectangular prisms displaced by ± 1.135 mm on either side of the z = 0 plane (figure 1b). This displacement included the radius of the lead (0.635 mm) plus a 0.5 mm thick region representing the glial scar that forms after chronic implantation (Haberler et al., 2000). The region of glial scar contained no neural elements because chronic inflammation within and around this region can lead to neurodegeneration and/or cell death (McConnell et al., 2009).

Modeling studies (Butson et al., 2007, Keane et al., 2012, Kuncel et al., 2008) predict that neural elements up to 3 mm from the electrode surface are activated at typical DBS parameter settings (e.g., 3 V, 90 μs, and 130–185 Hz) (Kuncel and Grill, 2004). In DBS for the treatment of psychiatric disorders, stimulation amplitudes up to 10 V are required to achieve a therapeutic effect (Holtzheimer and Mayberg, 2011), and at these higher stimulation amplitudes, elements > 3 mm from the electrode surface may be activated (Butson et al., 2007). To encompass this range of distances, the dimensions of the rectangular prisms were chosen so that the furthest neural element in the population had a least one point on its axon or soma that was < 2.5 mm, 5 mm, or 10 mm from the origin.

The source driving polarization of the neural membrane is proportional to the spatial centered second difference of the potentials, δ²Φ (Rattay, 1986), so the potentials were calculated using ~ 1 million 3^rd order Lagrangian elements, as 3^rd order elements prevented large discontinuities when calculating δ²Φ (Howell et al., 2014). Refinement of the mesh (i.e., splitting elements into smaller elements) from ~320,000 to 1 million cubic elements resulted in changes of < 1 % in the mean absolute relative difference of both the interpolated potentials and corresponding stimulation thresholds of model neurons.

The interpolated potentials were used in NEURON to stimulate the neural elements. To isolate the effect of electrode geometry during model optimization, neural elements were stimulated with a 100 μs monophasic rectangular pulse. However, biphasic stimulation was used in our experiments, and for that reason, the performance of all optimal designs was quantified post hoc during stimulation with a short 100 μs cathodic phase followed by a long 900 μs anodic phase. Since the conductivities were linear, the potentials at a specific stimulation voltage were calculated by multiplying the 1 V solutions by a scalar, and the threshold stimulation voltage to activate each model axon was calculated using a bisection algorithm (relative error < 1 %).

2.2. Design of electrodes with increased stimulation efficiency and selectivity

The computational model of DBS was used with engineering optimization to design electrode geometries that could efficiently activate AOPs, TAs, and LNs; selectively activate parallel AOPs over perpendicular AOPs; or selectively activate parallel TAs over AOPs. The three-electrode array was parameterized using eight parameters (figure 1c): three electrode heights (h₁, h₂, and h₃ ≥ 0.1 mm), two inter-electrode spacings (s₂₁ and s₂₃ ≥ 0.1 mm), and three applied potentials (v₁, v₂, and v₃). In preliminary work (Howell and Grill, 2013), we allowed the radius of the electrode to vary between 0.1 and 1 mm. The optimal radius for efficient activation of AOPs was > 0.635 mm. However, a larger diameter electrode, although potentially more efficient, would damage more tissue upon implantation, so r was held constant at 0.635 mm. If the optimal solution identified by the genetic algorithm (GA, see below) resembled a single contact (i.e., s₂₁ and s₂₃ were equal to 0.1 mm), then contacts 1 and 3 were treated as insulation, contact 2 was parameterized by its height (h) and normalized circumference (c), and a post hoc brute force search was conducted on the reduced parameter space: 1 mm ≤ h ≤ 15 mm in increments of 0.5 mm and 0.1 ≤ c ≤ 1 in increments of 0.1.

For each electrode configuration (i.e., geometry and polarity), we calculated the electric potentials, stimulation thresholds for activation of each neural element, and subsequently, the cost functions quantifying efficiency or selectivity. The cost function for stimulation efficiency was the average power required to activate 50 % of the population of neural elements (P₅₀):

$$P_{50}={PW}^{-1}\underset{0}{\overset{PW}{\int }}\frac{V^2(t)}{R_a}dt,$$ (3)

where V(t) is the applied voltage and PW is the duration of the rectangular pulse. The efficiency of the optimal electrode design was quantified by calculating a relative power usage (RPU), which is 100 times the ratio of P₅₀ with the optimal design to P₅₀ with the standard electrode (height = 1.5 mm and radius = 0.635 mm) that is used in the Medtronic Model 3387, the Medtronic Model 3389, and the Boston Scientific Vercise arrays. Selectivity was quantified by constructing a curve, p(x), of the proportion of a population of neural elements activated versus selected proportions of a population of other neural elements and minimizing or maximizing the (normalized) area under the curve:

$$\mathit{AUC}={100}^{-1}\underset{0}{\overset{100}{\int }}p(x)dx.$$ (4)

We used a genetic algorithm (GA) to search the parameter space and optimize the cost function (MATLAB v2008b, Global Optimization Toolbox). The initial geometry was selected randomly within the bounds of the parameter space. Each generation consisted of 20 solutions: the 2 fittest solutions and 18 progeny, which were generated by mating (i.e., randomly swapping parameters between) nine random pairs of parent vectors. Mating was conducted by creating a random binary vector (of 0s and 1s) for each vector pair and exchanging the elements of the parent vectors where the elements of the corresponding binary vectors were equal to 1. Mutations were introduced by adding random numbers to each element of the progeny vector. The random numbers for each element were generated from a Gaussian distribution with a mean of zero and a standard deviation equal to the difference in the parameter between the first two generations. The standard deviation of the Gaussian distribution for each parameter decreased linearly so that it reached zero at the maximum number of generations. The GA terminated when the average change in the cost function was < 0.1 % over 100 iterations, or after 150 iterations.

Optimizations were repeated ten times on three independent populations of 100 neural elements to ensure that the results were not the result of a specific population, and a post hoc brute force search was conducted on a subset of the parameter space surrounding the best GA solution to determine whether a better solution existed.

The sensitivity of the efficient electrode designs to changes in model parameters was assessed by quantifying how RPU changed when the 900 μs charge-balancing phase was removed from the stimulus pulse (i.e., monophasic stimulation), when the encapsulation tissue was replaced with brain tissue, when the diameter of target axons was increased from 2.5 μm to 15 μm in increments of 2.5 μm, and when the load of the electrode tissue interface (ETI) impedance was included. For the ETI analysis, the double-layer capacitance (C_dl) and Faradaic resistance (R_f) were set to the minimum or maximum values measured in vivo (see Sections 2.3 and 3.4.1). The sensitivity of the selective electrode designs to changes in model parameters was assessed when the 900 μs charge-balancing phase was removed from the stimulus pulse (i.e., monophasic stimulation) and when the axons were rotated about the y axis in the xz plane. The angle of rotation for each fiber was randomly sampled from a normal distribution with mean = 0 ° and standard deviation = 7.5 °.

Simulations were also conducted to determine whether the electrodes of the 3387, the 3389, and the Vercise arrays could be configured to approximate the potentials of the novel electrode configurations that resulted from the optimization. The 3387 and 3389 have four electrodes, 1.5 mm in height and 0.635 mm in radius, with (edge-to-edge) inter-electrode spacings of 1.5 mm and 0.5 mm, respectively. The Vercise array has eight electrodes with the same height, radius, and inter-electrode spacing of the 3389 array. If the standard clinical array did not achieve an RPU or AUC that was within 5 % of the corresponding optimal configuration, further simulations were conducted to assess whether an array with more electrodes and a smaller inter-electrode spacing could achieve RPU and AUC to within 5 % of the optimal configurations.

2.3. Measurements of stimulation efficiency and selectivity in vivo

Two sets of prototype electrodes were fabricated to test the model-based designs in cats (figure 2). Prototypes were fabricated by sputter depositing a chrome adhesion layer followed by a gold metal layer onto a planar polyimide substrate, and planar substrates were wrapped around and bound to a rigid steel shaft to form cylindrical electrode arrays. The set of electrode designs for measuring efficiency in vivo consisted of a long cylinder (LC) with a height of 6 mm, a long hemi-cylinder (LHC) electrode with a height of 6 mm, and the standard electrode with a height of 1.5 mm. The LC, LHC, and standard electrode all had radii of 0.635 mm. Selectivity was measured in vivo using a five-electrode array that could be configured to approximate the potentials produced by the optimal electrode configurations. Each electrode had a height of 1 mm and a radius of 0.635 mm, and the inter-electrode spacing was 0.2 mm. Since the size of the neural tissue targeted in the cat was small compared to that of humans, we focused on the optimal configurations for stimulating neural elements ≤ 2.5 mm from the origin.

Figure 2.

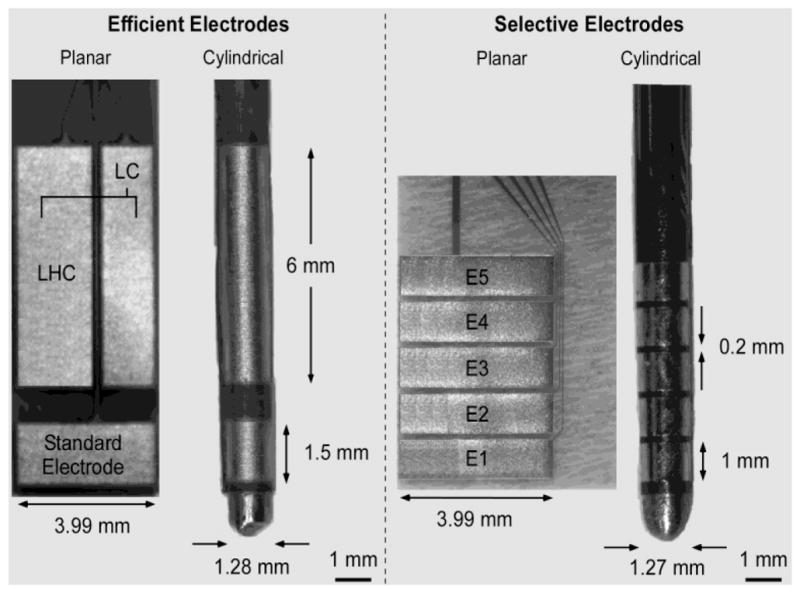
Prototype electrodes for experimental measurement of stimulation efficiency and selectivity. Photomicrographs of two sets of planar and cylindrical electrode designs for measuring the efficiency (left) and selectivity (right) of electrical stimulation in vivo. LHC = long hemicylinder, LC = long cylinder, and E = electrode. The standard electrode has the geometry of the contacts used in the Medtronic Model 3387 and 3389 arrays, and the Boston Scientific Vercise system array.

Acute in vivo experiments were conducted in anesthetized cats using a protocol approved by the Institutional Animal Care and Use Committee at Duke University. Anesthesia was induced with ketamine HCL (Ketaset 35 mg/kg IM, supplemented as required at 15 mg/kg during surgical preparation) and maintained with alpha chloralose (65 mg/kg IV, supplemented at 15 mg/kg). In one set of experiments, the planar electrode designs were oriented parallel or perpendicular to the cat sciatic nerve (figure 3a), and an isolated stimulator was used to deliver a 0.5 Hz train of voltage-regulated, asymmetric pulses with a short 100 μs cathodic phase followed by a long 900 μs anodic phase. Performance was assessed using a repeated measures design: in each animal, we tested all the efficient or selective planar electrode designs, and we repeated the experiments for measuring efficiency and selectivity in a total of seven and five cats, respectively.

Figure 3.

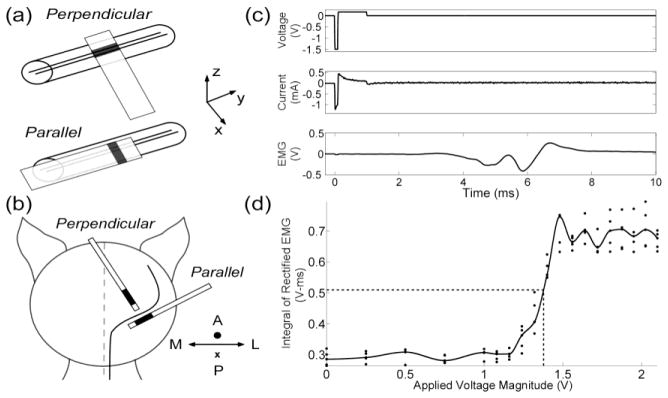
Measuring the efficiency and selectivity of prototype electrodes in vivo. (a) Planar electrode designs (see figure 2) were oriented parallel or perpendicular to the sciatic nerve. (b) Cylindrical electrode designs were implanted parallel or perpendicular to corticospinal axons in the posterior limb of the internal capsule. A = anterior, P = posterior, M = medial, and L = lateral. (c) The applied voltage, applied current, and evoked electromyographic responses (EMGs) were recorded during stimulation. (d) The EMG was rectified and integrated, and a fitted spline was used to calculate the voltage (and average power) required to evoke a half maximal response.

In a second set of experiments, brain surgery was performed under 1 % isoflurane anesthesia, and the electrode was implanted parallel or perpendicular to axons in the posterior limb of the internal capsule (Duerden et al., 2011) (figure 3b) – located 7 mm anterior, 10.5 mm lateral, and 10 mm above the interaural line (Nicholson, 1965, Snider and Niemer, 1961). Stimulus trains consisted of 30 voltage-regulated rectangular pulses with a short 300 μs cathodic phase followed by a long 700 μs anodic phase delivered at 350 Hz. Voltage amplitudes were varied between 0 V and 5 V, focusing the majority of values between the stimulation threshold for evoking an electromyographic response (EMG) and the amplitude at which the EMG was maximal. Voltage amplitudes were repeated five times. C_dl, R_f, and the access resistance (R_a) of each electrode were determined by using nonlinear regression to fit a three-element Randles equivalent circuit to the average current transient (Equation 5) recorded at each voltage amplitude (figure 3c).

$$I(t)=\frac{V_o}{R_a+R_f}\left(\frac{R_f}{R_a}exp(\frac{-t}{\tau })+1\right)$$ (5)

$$\tau =\frac{C_{dl}{R}_f{R}_a}{R_a+R_f}$$ (6)

V_o is the amplitude of the applied voltage. The efficiency and selectivity of the cylindrical electrode designs were measured in ten and five cats, respectively.

Measurements were taken using an isolated, low noise amplifier (SR560, Stanford Research, Sunnyvale, CA): the applied voltage was measured from the output of the isolated stimulator, and the current was measured from the voltage drop across a 25 Ω resistor in series with the implanted electrode and tissue load. The measured current waveforms were averaged across five repetitions, and the product of the voltage and current waveforms was used to calculate the average electrical power transferred over time (figure 3c). EMGs were measured differentially between two 29-gauge multi-stranded stainless steel wires (Cooner Wire, Chatsworth, CA). In the sciatic nerve experiments, the EMG electrodes were implanted in the ipsilateral peroneus muscles, and in the brain experiments, the EMG electrodes were implanted in the contralateral extensor digitorum muscles. EMGs were AC coupled, amplified by a gain of between 100 and 500, and bandpass filtered with lower and upper cutoff frequencies of 3 Hz and 3 kHz, respectively (SR560). The EMG was rectified and integrated to quantify the average magnitude of the signal over time. Data were sampled and stored using the MATLAB Data Acquisition toolbox (Mathworks, Natick, MA).

Stimulation efficiency was quantified by calculating the average power required to evoke a half maximal EMG (P₅₀) and comparing it to P₅₀ of the standard clinical electrode used in the 3387, 3389, and Vercise arrays (figure 2a). Stimulation selectivity was measured by calculating the ratio of the voltage required to evoke a half maximal EMG (V₅₀) when oriented parallel to the target fibers to V₅₀ when oriented perpendicular to the target fibers.

The location of implanted electrodes was determined from post mortem histology. Animals were perfused with 10 % formalin (~ 4 % formaldehyde). The brain was removed and immersed in a 10 % formalin (~ 4 % formaldehyde) solution for two days, immersed in a 30 % sucrose solution for one week, and frozen in optimal cutting temperature (OCT) medium at −80 °C. 30 μm thick brain slices were stained using 0.1 % cresyl violet, and electrode placement was determined by overlaying images of the stained tissue with a brain slice of the target region from a cat brain atlas (www.brainmuseum.org).

2.4. Statistical analysis

We fitted a spline to the EMG data to calculate V₅₀ or P₅₀ (figure 3d). The dependent variable in our statistical analysis was the natural logarithm of the ratio of V₅₀ or P₅₀ of one electrode in one orientation to the V₅₀ or P₅₀ of a second (same) electrode in the same (second) orientation. Three statistical tests were conducted. First, for a given orientation and electrode design, a Lilliefors test was conducted on the distributions of ln(V₅₀) or ln(P₅₀) across experiments to test the null hypothesis that ln(V₅₀) or ln(P₅₀) was normally distributed. Second, if there was not enough evidence to reject the null hypothesis of the Lilliefors test across all designs and orientations, a repeated measures analysis of variance (ANOVA) was conducted to test the hypothesis that ln(V₅₀) or ln(P₅₀) across all electrodes in both orientations came from the same normal distribution. Finally, if the null hypothesis of the ANOVA was rejected, post hoc paired comparisons were made using Fisher’s least significant difference test. Data are presented as the mean ± standard error, and all statistical tests were conducted at a 95 % confidence level (α < 0.05).

3. Results

We used a computational model of DBS and engineering optimization to design electrodes intended to increase the efficiency and selectivity of DBS. The efficiency and selectivity of the prototype electrodes were subsequently measured in vivo. Biphasic stimulation was used in the experiments; therefore, unless stated otherwise, the performance of the optimal designs reflects stimulation with a short 100 μs cathodic phase followed by a long 900 μs anodic phase.

3.1. Computational analysis of efficient electrode designs

Optimizations of the eight design parameters were conducted to determine what three-electrode configurations (figure 1) minimized the power required to stimulate parallel or perpendicular neural elements (AOPs, TAs, and LNs). Optimal solutions yielded parameters sets where s₂₁ and s₂₃ were much smaller than h₁, h₂, and h₃; and s₂₁ and s₂₃ were > h₁ and h₃, and v₁ and v₃ were close to 0 V. Since these solutions resembled monopolar stimulation with a single electrode, electrodes 1 and 3 were replaced with insulation, and electrode 2 was optimized with parameters c and h.

Electrodes with relatively large (height to diameter) aspect ratios were more efficient at stimulating neural elements oriented perpendicular to the electrode shaft (figure 4a). For example, long electrodes with h between 3.5 and 10 mm and c between 0.5 and 0.8 consumed 45–84 % less power than the standard clinical electrode when activating populations of perpendicular AOPs, TAs, and LNs. In contrast, electrodes with relatively small aspect ratios were more efficient for stimulating parallel neural elements. The geometry of the standard electrode was close to optimal for stimulating parallel AOPs and TAs, and altering h and c decreased power consumption by only 14 % when stimulating parallel LNs (figure 4a).

Figure 4.

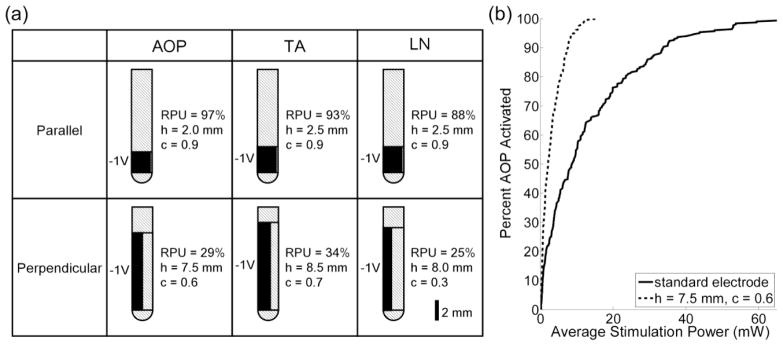
Optimal monopolar electrode geometries for efficiently activating neural elements ≤ 5 mm from the origin. (a) Optimal geometries and corresponding relative power usage (RPU) when stimulating a population of AOPs (column 1), TAs (column 2), and LNs (column 3) oriented either parallel (row 1) or perpendicular (row 2) to the electrode shaft. AOP = axon of passage, TA = terminating axon, LN = local neuron, h = height, c = normalized circumference, and RPU is 100 times the ratio of the average stimulation power required to activate 50 % of the neural elements (P₅₀) with the optimal design to P₅₀ with the standard clinical electrode (see section 2.2) in a cathodic configuration. (b) Input-output curves of average stimulation power versus percentage of perpendicular AOPs activated for electrodes: the electrode in row 2, column 1 of part a and the standard electrode in a cathodic configuration.

Four additional analyses were conducted to assess how sensitive the efficiency of the optimal electrode geometries were to changes in the model parameters. Since the solutions were qualitatively similar across the different neural elements, analyses were conducted only for stimulation of AOPs. The efficiency of the optimal designs was sensitive to an increase in fiber diameter above 5 μm and the presence of the ETI, but insensitive to the presence of encapsulation tissue and changing the waveform from biphasic to monophasic (Table 1).

Table 1.

Sensitivity of stimulation efficiency to changes in model parameters^a

Case		Baselineb (RPU)	Monophasic Stimulation	RPU					ETIc		No ET
				Fiber diameter (μm)
Distance (mm)	Orientation			5	7.5	10	12.5	15	Min.	Max.
2.5	parallel	96	94	98	106	111	106	108	101	107	90
5	parallel	97	96	94	93	93	94	92	97	93	98
10	parallel	74	72	70	68	66	65	64	78	67	80
2.5	perpendicular	55	56	69	75	77	74	73	70	70	61
5	perpendicular	29	29	36	39	42	41	43	46	37	35
10	perpendicular	20	20	23	25	26	27	27	39	28	23

^aStimulation of axons of passage. See Section 2.2 for a summary of the sensitivity analyses.

^bBiphasic stimulation of axons with diameters of 2.5 μm and ET present. RPU = relative power usage (see Section 2.2).

^cThe effect of the ETI was assessed at the minimum C_dl and R_f, or maximum C_dl and R_f values.

Abbreviations: ETI = electrode-tissue interface, ET = encapsulation tissue.

3.2. Computational analysis of selective electrode designs

3.2.1. Selectivity based on orientation

Optimizations of the eight design parameters were conducted to determine electrode configurations that maximized selectivity of parallel AOPs over perpendicular AOPs and vice versa. An asymmetric bipolar configuration was the optimal solution for selectively activating parallel AOPs over perpendicular AOPs (figure 5a). When neural elements were placed up to 2.5 mm, 5 mm, and 10 mm from the origin, asymmetric bipolar configurations activated 50 % of target parallel AOPs while limiting activation of non-target perpendicular AOPs to 0 %, 14 %, and 8 %, respectively, whereas the standard electrode activated almost 50 % of the non-target elements (figure 5).

Figure 5.

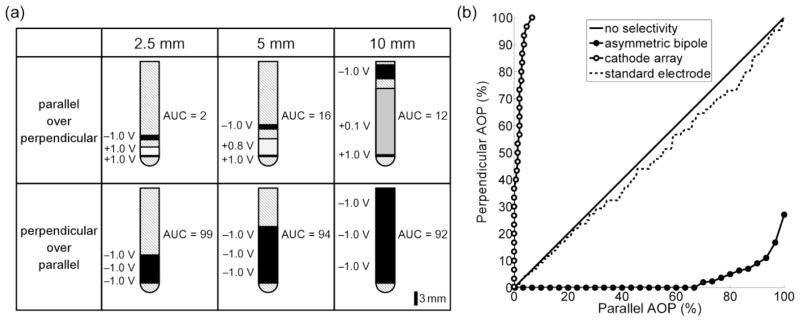
Optimal three-electrode configurations for selectively activating axons of passage (AOPs) based on their orientation. (a) Optimal electrode configurations and corresponding normalized area under curve (AUC, see Equation 4) when stimulating parallel AOPs over perpendicular AOPs (row 1) and perpendicular AOPs over parallel AOPs (row 2). Elements were placed ≤ 2.5 mm (column 1), 5 mm (column 2), and 10 mm (column 3) from the origin. The configurations shown in rows 1 and 2 are referred to as asymmetric bipoles and cathodes arrays, respectively. Note, in row 2, the edge-to-edge spacings between electrodes are all 0.1 mm, which could not be resolved in the image. (b) Curves of the percent of perpendicular AOPs activated versus select percentages of parallel AOPs when elements were placed ≤ 2.5 mm from the origin. For comparison, the standard clinical electrode (see section 2.2) was used to stimulate AOPs in a cathodic configuration.

The optimal configuration for selectively activating perpendicular AOPs over parallel AOPs was an array of cathodes. When neural elements were placed up to 2.5 mm, 5 mm, and 10 mm from the origin, an array of cathodes activated 50 % of target perpendicular AOPs while limiting activation of non-target parallel AOPs to 1 %, 3 %, and 5 %, respectively, whereas cathodic monopolar stimulation with the standard electrode activated more than 50 % of the non-target elements (figure 5).

Additional analyses were conducted to assess how sensitive the performance of the optimal tripolar electrode geometries was to changes in the waveform shape and axon orientation. Aside from selective stimulation of parallel AOP over perpendicular AOP that were placed ≤ 10 mm from the origin, the selectivity of the optimal electrode designs was insensitive to shifts in the axon orientation and changing the waveform from biphasic to monophasic (Table 2).

Table 2.

Sensitivity of stimulation selectivity to changes in model parameters^a

Distance (mm)	Orientations	Baselinea (AUC)	AUC
			Monophasic Stimulation	Angular Shiftsb
2.5	parallel over perpendicular	2	0	6
5	parallel over perpendicular	16	17	19
10	parallel over perpendicular	12	22	23
2.5	perpendicular over parallel	99	99	100
5	perpendicular over parallel	94	93	93
10	perpendicular over parallel	92	91	89

^aBiphasic stimulation of axons with diameters of 2.5 μm. AUC = area under curve (see Section 2.2)

^bShifts in axon orientations sampled from a normal distribution (mean = 0°, standard deviation = 7.5°).

3.2.2. Selectivity based on type of neural element

Optimization of the eight design parameters was conducted to identify electrode configurations that maximized selectivity of parallel TAs over parallel and perpendicular AOPs. An anode distal to the target population was the optimal solution for selectively activating TAs over AOPs. When neural elements were placed up to 2.5 mm, 5 mm, and 10 mm from the origin, distal anodes activated 50 % of target parallel TAs while limiting activation of non-target parallel AOPs to 2 %, 15 %, and 2 %, respectively; whereas monopolar anodic stimulation with the standard electrode activated 64 %, 43 %, and 100 % of non-target elements, respectively (figure 6). Selectivity was greatest when distal anodes were used to activate parallel TAs over perpendicular AOPs (figure 6a).

Figure 6.

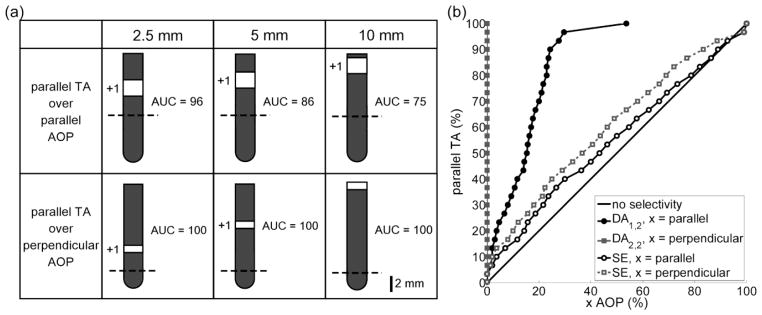
Optimal electrode configurations for selectively activating terminating axons (TAs) over axons of passage (AOPs). (a) Optimal electrode configurations and corresponding normalized area under the curve (AUC, see Equation 4) when stimulating parallel TAs over parallel AOPs (row 1) and parallel TAs over perpendicular AOPs (row 2) when neural elements were placed ≤ 2.5 mm (column 1), 5 mm (column 2), and 10 mm (column 3) from the origin. The dashed line denotes z = 0. (b) The percentage of parallel TAs versus selected percentages of parallel or perpendicular AOPs for the distal anodes in row 1, column 2 (DA_1,2) and row 2, column 2 (DA_2,2) in part a. For comparison, the standard electrode (SE) in an anodic configuration was used to stimulate parallel TAs over AOPs.

3.3. Efficiency and selectivity of clinical arrays

We conducted additional simulations to determine whether the 3387, 3389, and Vercise arrays could be configured to approximate the performance of the optimal electrode configurations (figures 4a, 5a, and 6a). The clinical arrays performed on par with the asymmetric bipole configurations and distal anode configurations but worse than the efficient monopolar configurations and selective cathode array configurations (Table 3).

Table 3.

Using electrode arrays to approximate the optimal model electrode configurations^a

Description			Performance (RPU or AUC)b of Arrays
Case	Orientation	Element	Optimalc	3387	3389	Vercise	12-electrode
Efficiency	parallel	AOP	97	100	100	100	95
Efficiency	parallel	TA	93	100	100	100	87
Efficiency	parallel	LN	88	100	100	100	77
Efficiency	perp.	AOP	29	161	284	283	32
Efficiency	perp.	TA	34	161	282	282	39
Efficiency	perp.	LN	25	161	284	283	36
Selectivity	parallel over perp.	AOP over AOP	16	28	11	11	13
Selectivity	perp. over parallel	AOP over AOP	94	84	84	86	96
Selectivity	parallel over parallel	TA over AOP	86	86	86	86	86
Selectivity	parallel over perp.	TA over AOP	100	99	99	99	100

^aBiphasic stimulation of neural elements ≤ 5 mm from origin.

^bRelative power usage (RPU) for efficiency and area under curve (AUC) for selectivity (see Section 2.2).

^cSee figures 4a, 5a, and 6a for optimal 3-electrode configurations.

Abbreviations: AOP = axon of passage, TA = terminating axon, LN = local neuron, perp. = perpendicular.

We also tested a 12-electrode array whose contacts were approximately 0.9 mm in height and spaced by 0.1 mm. The 12-electrode array was able to achieve a performance that was relatively close to the performance of all ten optimal electrode configurations (Table 3). It should be noted that in a few cases the clinical and 12-electrode arrays performed marginally better than the optimal designs. Using more than three contacts increased the total perimeter of the configurations, which decreased the electrode impedance (Howell and Grill, 2014, Wei and Grill, 2005), leading to slight improvements in performance.

3.4. Measuring stimulation efficiency and selectivity in vivo

3.4.1. Efficient prototype electrodes

The electrical properties (i.e., R_a, R_f, and C_dl) of LHC, LC, and the standard electrode were determined by fitting Equation 5 to the current transient recorded during voltage-regulated stimulation (figure 3c). The relationship between R_a and the electrode geometry observed in vivo was predicted by the computational model (figure 7a). R_f values were between 21 kΩ and 3.9 × 10³ kΩ, corresponding to a range of specific Faradaic resistances (i.e., r_f) between 1.3 kΩ-cm² and 490 kΩ-cm²; and the range of C_dl values was between 0.64 and 6.9 μF, corresponding to specific double-layer capacitances (i.e., c_dl) between 6.8 and 41 μF/cm².

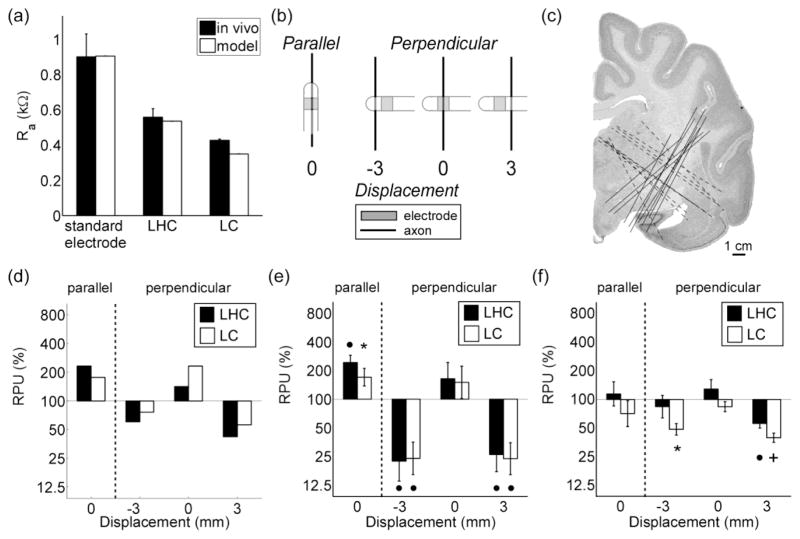
Figure 7.

Measuring the stimulation efficiency of optimized electrode designs in vivo. (a) The access resistance (R_a) of the prototype electrodes measured in vivo compared to R_a of the electrodes calculated from the computational model. LC = long cylinder and LHC = long hemicylinder. (b) Electrodes were oriented either parallel or perpendicular to target axons. In the perpendicular orientation, electrodes were displaced ± 3 mm from the long axis of the axon bundle. (c) Locations of electrode tracks in the brain stimulation experiments. (d) Computational results. Relative power usage (RPU) is 100 times the ratio of the average power required to activate 50 % of the AOPs (P₅₀) with the optimal design to P₅₀ with the standard electrode in a cathodic configuration. RPU in the (e) sciatic nerve (n = 7) and (f) brain (n = 10) stimulation experiments is the same as part c, except P₅₀ is the average power required to evoke a half maximal EMG. A repeated-measures ANOVA revealed a significant effect of electrode geometry on the relative P₅₀ that depended on the orientation and distance of the electrode in parts d (p = 0.0105) and e (p = 0.0242), and post hoc comparisons were made using a Fisher’s least significant difference (FLSD) test. An asterisk, bullet, and plus sign denote a p value of < 0.05, < 0.01, and < 0.001, respectively, in the FLSD test.

We quantified the stimulation efficiency of each prototype electrode with respect to the standard electrode by calculating its RPU. Parallel to the sciatic nerve (n = 7), LHC and LC were less efficient than the standard electrode, as their RPU was significantly greater than 100 %, which agreed with the results from the computational model (figure 7c). However, when oriented perpendicular to the sciatic nerve, LHC and LC performed on par with the standard electrode (figure 7d). This unexpected result was attributed to differences in the distributions of neural elements between the model and cat sciatic nerve. Perpendicular axons in the model were located near the electrode, along the shaft, and below the tip of the electrode (Figure 1b), whereas target fascicles in the experiments only lay adjacent to the electrode (Figure 7b). To emulate better the distributions of perpendicular axons in the computational model, we displaced the stimulating electrode ± 3 mm mediolaterally from the long axis of the sciatic nerve (figure 7b). When oriented perpendicular to the nerve and displaced by ± 3 mm, the RPU of LHC and LC were significantly < 100 %, indicating that they were more efficient than the standard electrode (figure 7d). This dependence of stimulation efficiency on displacement was also observed in the model (figure 7c).

In brain stimulation experiments (n = 10), LHC performed on par with the standard electrode when oriented both parallel and perpendicular to axons in the posterior IC, whereas LC was more efficient than the standard electrode when oriented perpendicular to the target axons and displaced ± 3 mm from their long axis (figure 7e). Post-mortem histology confirmed that the electrode tracts passed through the posterior IC in all experiments (figure 7f).

3.4.2. Selective prototype electrodes

We used a five-electrode array (figure 2) to measure the selectivity of an asymmetric bipole and cathode array, which were the two optimal electrode configurations for activating AOPs based on their orientation (figure 5a). We also used the five-electrode array to measure the selectivity of a guarded cathode, which is a cathode surrounded by two anodes, and a single electrode or monopole (figure 8a). The guarded cathode was tested because its selectivity was similar to that of the asymmetric bipole when neural elements were placed ≤ 2.5 mm from the origin (results not shown), and the monopolar configuration was tested because it was expected to have no orientation-dependent selectivity (figure 5b). We confirmed that the relationship between R_a and the electrode configuration predicted by the computational model was observed in vivo (figure 8c).

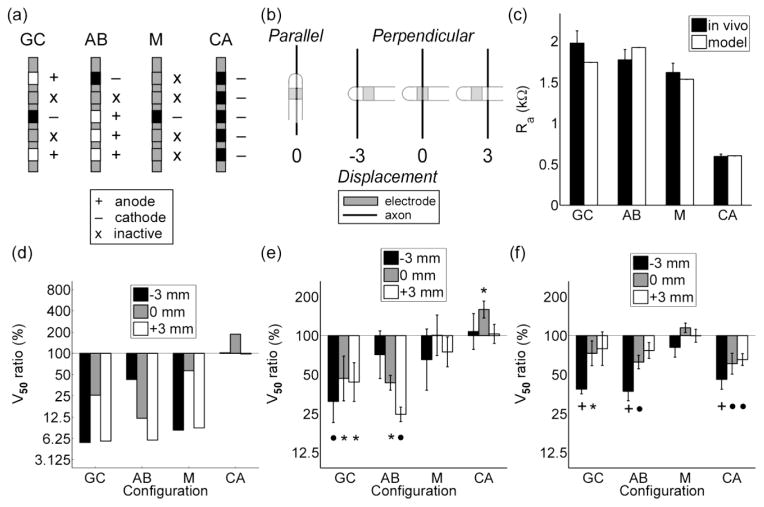
Figure 8.

Measuring the stimulation selectivity of optimal electrode designs in vivo. (a) Four electrode configurations were tested: GC = guarded cathode, AB = asymmetric bipole, M = monopole, and CA = an array of cathodes. (b) Electrode configurations were oriented parallel or perpendicular to target axons. Electrodes in the perpendicular orientation were displaced ± 3 mm from the long axis of the axons. (c) The access resistance (R_a) of the electrode configurations measured in vivo compared to R_a calculated from the model. (d) The voltage required to activate 50 % of modeled AOPs (V₅₀) in the parallel orientation to V₅₀ in the perpendicular orientation. V₅₀ is the same in (e) the sciatic nerve (n = 5) and (f) brain (n = 5) stimulation experiments, except V₅₀ denotes the voltage required to evoke a half maximal EMG. A repeated-measures ANOVA revealed a significant effect of electrode configuration on the V₅₀ ratio that depended on the orientation and distance of the electrode in parts e (p = 0.0280) and f (p = 0.0288). Post hoc comparisons were made using a Fisher’s least significant difference (FLSD) test. An asterisk, bullet, and plus sign denote a p value of < 0.05, < 0.01, and < 0.001, respectively, in the FLSD test.

The selectivity of the four configurations was quantified using the ratio of V₅₀ in the parallel orientation to V₅₀ in the perpendicular orientation. In the sciatic nerve experiments (n = 5), the V₅₀ ratio of the guarded cathode and the asymmetric bipole were significantly less than 100 when oriented parallel to the axon, the V₅₀ ratio of the monopolar configuration did not differ significantly between the two orientations, and the V₅₀ ratio of an array of cathodes was greater than 100 when oriented parallel to the axons (figure 8e). The selectivity of all four configurations depended on their displacement from the long axis of the nerve. Similar results were observed in brain experiments (n = 5), with the exception of the array of cathodes, which had significantly smaller V₅₀ ratio when oriented parallel to the axon (figure 8f). The selectivity for each configuration measured in vivo compared well with the predictions from the model-based analysis (figure 8d).

In the brain experiments, the array of cathodes activated parallel AOPs selectively over perpendicular AOPs (figure 8f). We predicted that this unexpected result might be explained by the geometry of the targeted corticospinal axons, which are not straight, like the axons in the sciatic nerve. We used anatomical images from a cat atlas (Snider and Niemer, 1961) and spline fits to approximate the trajectory of CS axons, and additional simulation and experiments were conducted to test our prediction (figure 9). With straight axons, cathode array configurations consisting of 4 or 5 electrodes had larger stimulation thresholds than a monopolar configuration when oriented parallel to the modeled AOPs, whereas with curved CS axons, all thresholds with cathode arrays were less than the monopolar threshold (figure 9c). Similar results were observed in two additional experiments (figure 9d).

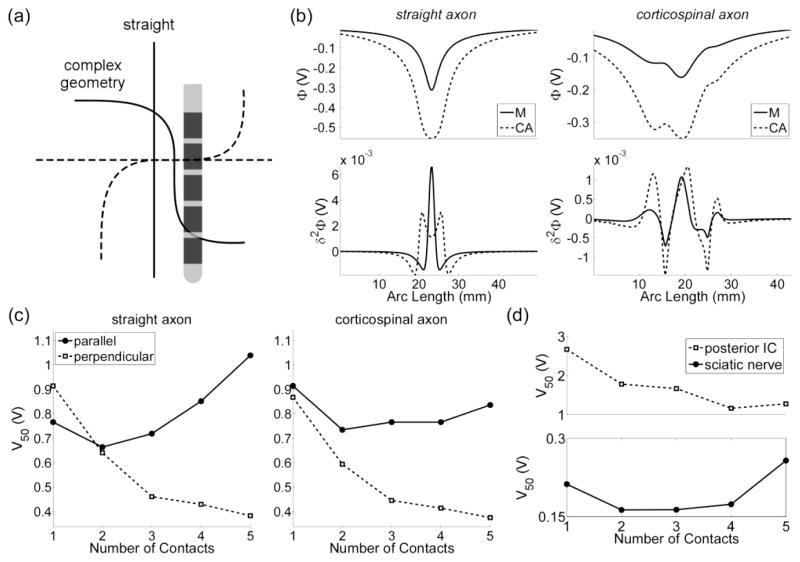
Figure 9.

The effect of axon geometry on stimulation thresholds. (a) A straight axon and corticospinal axon with bends oriented parallel (solid line) and perpendicular (dashed line) to a five-electrode array. (b) The potentials (top) and the second difference of the potentials (δ²Φ, bottom) when either one (M) or five contacts (CA) in a cathodic configuration was used to stimulate the target axons. (c) The voltage required to activate 50 % of a population of modeled axons (V₅₀) when the array was oriented either parallel or perpendicular to the axons. (d) The voltage required to evoke a half maximal EMG (V₅₀) when the array was oriented parallel to the posterior internal capsule (IC, top) and sciatic nerve (bottom).

4. Discussion

We combined computational models of electric potentials and neurons and used engineering optimization to design novel electrode configurations for efficient and selective DBS. In vivo measurements of EMGs evoked by either peripheral nerve or brain stimulation were used to quantify the performance of prototype electrodes. Electrode geometry and polarity had profound effects on the efficiency and selectivity of stimulation, which depended on the orientation and type of the neural elements, and the optimal electrode designs exhibited significant improvements in efficiency and selectivity compared to the standard clinical electrode. Further, the results suggest that there is no universal electrode geometry or configuration that is optimal for all DBS targets, but demonstrate the potential performance improvements that can accrue from target-specific electrode designs.

4.1. Principles for electrode design

The increases in efficiency of some, but not all, of the efficient designs could be explained by decreases in the electrode impedance, and the increases in efficiency and selectivity were better explained by examining the second difference of the potentials (δ²Φ). Therefore, we analyzed δ²Φ of the optimal electrode designs to understand the origin of the results and how they might translate into principles for electrode design.

The results reveal that efficiency can be improved by using long cylindrical electrodes with relatively large (height to diameter) aspect ratios to stimulate perpendicular neural elements (figure 4a). Increasing h increases electrode area, which reduces R_a, reduces R_f, and increases C_dl. Therefore, the efficiency of longer electrodes could be explained, in part, by a decrease in the electrode impedance. The other factor that explained the efficiency of the long cylindrical electrodes was their proximity to the neural elements. Increasing h brought the electrode surface closer to excitable regions (e.g., nodes of Ranvier or the axon hillock) of perpendicular neural elements distributed along the insulated region of the shaft. Since the magnitude of the potentials is greatest near the electrode surface, the stimulation thresholds of these distal elements were decreased.

Increasing h also decreased the gradient of the potentials along the electrode shaft, which translated to a reduction in δ²Φ (figure 10a). This explains why LC and LHC, despite having a smaller R_a, were less efficient than the standard electrode in activating parallel AOPs, and it also explains why longer electrodes, or, similarly, an array of closely spaced cathodes, were selective in activating perpendicular AOPs over parallel AOPs (figure 5a). The selectivity of long cylindrical electrodes has been studied in a computational model of electrical stimulation of the retina (Rattay and Resatz, 2004), and a longer electrode, the Model 3391, is currently used to stimulate the anterior internal capsule in DBS for the treatment of obsessive compulsive disorder.

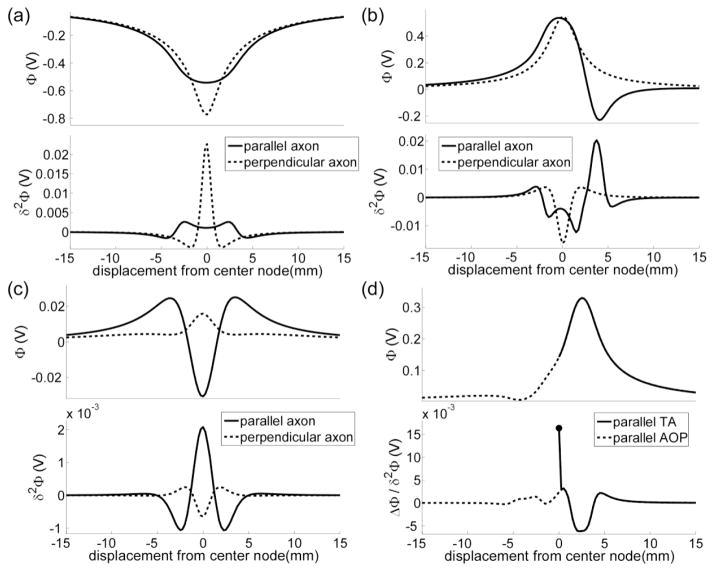
Figure 10.

The effect of electrode geometry and polarity on the force driving polarization of the neural membrane. Shown are the potentials and second difference of the potentials (δ²Φ) generated by (a) a long cylindrical electrode (figure 4a), (b) an asymmetric bipole (figure 5a), (c) a guarded cathode (figure 8a), and (d) a distal anode (figure 6a) across the nodes of Ranvier of an axon of passage (AOP). The filled circle in d denotes the first difference of the potentials (ΔΦ) at the terminal of a terminating axon (TA).

The results also revealed that multipolar configurations, such as an asymmetric bipole and a guarded cathode, can improve selectivity when activating neural elements based on their orientation. This can be explained by considering how δ²Φ = (Φ_n+1−2Φ_n + Φ_n−1) depends on orientation, where n denotes the n^th node of Ranvier. Parallel to the electrode shaft, the potentials change sign (figures 10b and 10c), and δ²Φ can be as large as |Φ_n+1+2Φ_n+Φ_n−1|, where | | denotes the absolute value. However, perpendicular to the electrode shaft, the potentials are either positive, negative, or zero. Since the potentials perpendicular to the electrode do not change sign (figures 10b and 10c), δ²Φ is only as large as 2|Φ_n|. Bipolar and tripolar electrode configurations are currently used in spinal cord stimulation for the treatment of chronic pain (Holsheimer et al., 1998, Holsheimer and Wesselink, 1997, North et al., 2002, Sankarasubramanian et al., 2011) and may hold promise for increasing spatial targeting of the therapeutic elements in DBS for essential tremor (Keane et al., 2012).

A single electrode in an anode configuration distal to the target population can improve selective activation of TAs over AOPs (figure 6a). The selectivity of the distal anode can be explained in two parts. First, the excitability of a TA is different from an AOP (Rubinstein, 1993) because the force driving polarization at the axon terminal is proportional to the first difference of the potentials (ΔΦ) (Rattay, 1999). For example, when an anode is centered at the origin, ΔΦ in the z direction is positive when z > 0, zero when z = 0, and negative when z < 0. Therefore, half the terminals of a population of parallel TAs (in the z direction) are depolarized, while the other half are hyperpolarized. As the anode is displaced progressively in the positive z direction, terminals that were previously hyperpolarized are now depolarized. Because |ΔΦ|, in general, is greater than |δ²Φ|, TAs are activated at lower stimulation thresholds.

ΔΦ is symmetric, and displacing a cathode in the negative z direction can also reduce the stimulation thresholds of TAs. Therefore, the second reason the distal anode configuration is selective for activating TAs over AOPs is that an anode depolarizes AOPs less than a cathode, as the maximum δ²Φ of the former is markedly less than that of the latter. In other words, a distal anode strongly depolarizes the terminals of TAs, reducing their stimulation thresholds, while also minimizing depolarization of AOPs (figure 10d). Although the performance of the distal anode for selective stimulation of TAs over AOPs has not been measured in vivo, anodes, in general, have been studied for selective microstimulation of LNs over AOPs (Lu et al., 2008, McIntyre and Grill, 2000, Wang et al., 2012) and selective stimulation of local retinal ganglion cells over passing axons of distal retinal ganglion cells (Schiefer and Grill, 2006).

4.2. Differences between computational and in vivo results

The goal of this study was to design electrodes that improved the efficiency and selectivity of DBS, which employs chronically implanted electrodes. However, we tested the predictions of our model in acute experiments, where the glial scar had not yet formed. Removing the model glial scar did not have a marked impact on the model predictions (Table 1); therefore, the presence or absence of the glial scar did not explain differences between the predicted and observed results.

The majority of alpha motor axons in cat peripheral nerves have diameters < 10 μm (Fabricius et al., 1994). Although our model predicted that the RPU of longer electrodes increased with increasing fiber diameter (Table 1), LC and LHC were still more efficient for stimulation of perpendicular neural elements. In fact, the measured RPUs were markedly smaller than what was predicted for stimulation of perpendicular axons < 2.5 mm from the electrode (Table 1), and we believe this underestimation of efficiency may be due to differences in the electrical properties between nerve and brain.

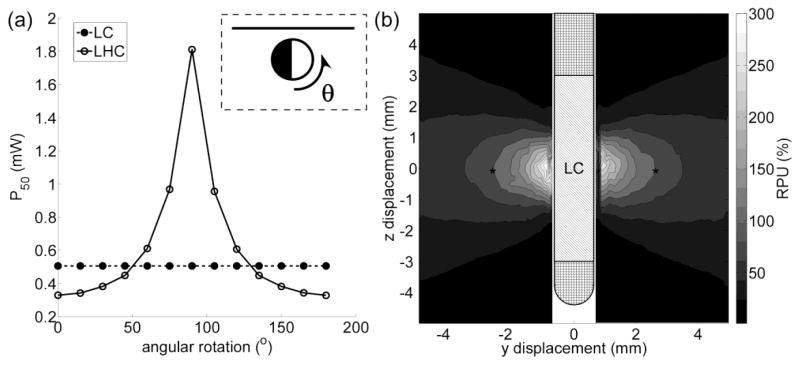
In the brain experiments, the LHC, rather than being more efficient, was less efficient than the LC (figure 7f). Since most axons in the brain have diameters < 4 μm (Assaf et al., 2008, Barazany et al., 2009, Yagishita et al., 1994), this discrepancy could not be explained by changes in fiber diameter. We predicted that LHC was less efficient than LC because of its axial asymmetry; therefore, additional simulations were conducted to assess how the performance of LHC varied with axial rotations (figure 11a). Rotating LHC about its axis markedly reduced its efficiency; thereby the difference between model and experiment could be explained by suboptimal alignment of LHC with the target axons.

Figure 11.

Evaluating the stimulation efficiency of the long cylinder (LC) and long hemicylinder (LHC) in cathodic configurations. (a) P₅₀ of LC and LHC at different rotations about their axes. P₅₀ is the average power required to activate 50 % of axons of passage (AOPs) oriented perpendicular to the electrode shaft. Inset: cross-section of LHC at an angular rotation (θ) of 0° with respect to a target AOP (solid line) and the direction of rotation. (b) The efficiency of LC in activating individual perpendicular AOPs. The relative power usage (RPU) is 100 times the ratio of the average power required to activate an individual AOP with the LC to the average power required to activate an individual AOP with the standard electrode (see section 2.2) in a cathodic configuration. The asterisks denote the equi-value contour of RPU = 100.

Another difference between the predicted and observed results was that the efficiency of the LC and the standard electrode were not significantly different when oriented parallel to the target brain axons (figure 7e). Recall, long electrodes, despite having a smaller impedance than the standard electrode, were expected to be less efficient because increasing h decreased δ²Φ parallel to the electrode axis (figure 10a), resulting in increased stimulation thresholds. Indeed, the computational model was able to reproduce the relationship between R_a and electrode geometry (figure 7a), as well as the impact of the ETI impedance on the predicted efficiency. However, the model did not account for the heterogeneous and anisotropic electrical properties of the tissue, which can alter the shape of the potential distribution and resulting excitation thresholds (Chaturvedi et al., 2010).

The results of the experiments to measure selectivity were consistent with many of the model predictions (figures 5 and 8e). In the sciatic nerve experiments, the asymmetric bipolar and guarded cathode configurations were selective in activating parallel AOPs over perpendicular AOPs. Moreover, the monopolar configuration showed no selectivity based on orientation, and the array of cathodes was selective in activating perpendicular AOPs over parallel AOPs. Similar results were observed in brain experiments, except for the array of cathodes, which was selective in activating parallel AOPs over perpendicular AOPs (figure 8f). We predicted that this unexpected result might be explained by the geometry of the targeted corticospinal axons.

Many corticospinal (CS) axons in the IC originate from the motor cortex (Lemon, 2008). In cats, CS axons travel from rostral to caudal, and as they pass through the IC, they course medially to form the cerebral peduncle (Snider and Niemer, 1961). Our electrode designs were implanted in the posterior IC, caudal to the optic chiasm and rostral to the cerebral peduncle, so we predicted that there would be bends in CS axons rostral and caudal to the target region.

The bends in the CS axons had an impact on the model predictions. When axons were straight and oriented parallel to an array of cathodes, decreases in electrode impedance that resulted from increasing the number of stimulation electrodes did not progressively decrease V₅₀ (figure 9c) because decreases in δ²Φ parallel to the cathode array (figure 10a) were eventually large enough to counteract the effect of decreasing impedance. This effect was observed when stimulating the sciatic nerve, where axons are straight, but not when stimulating axons with bends in the posterior IC (figure 9d), which the model predicted (figures 9c). Therefore, the geometry of the axon is a crucial parameter to consider in future studies.

4.3. Considerations for a versatile electrode array

No single configuration of electrodes was both optimally efficient and selective at stimulating neural elements across the cases tested, suggesting there is no universal electrode geometry or configuration that is optimal for all DBS targets. Fabrication of a multitude of different electrode designs for different DBS applications is not practical. Instead, an array with many electrodes (Keane et al., 2012) can be used to approximate closely the potential distributions of optimal configurations.

A 12-electrode array could be configured so that it, in most cases, performed on par with the optimal configurations (Table 3). Indeed, by increasing the number of contacts, the versatility of an array in approximating many optimal configurations can be improved, but most clinical arrays are limited to < 10 electrodes due to physical limitations (e.g., the number of wires that can fit inside the shaft). As new technologies emerge, it will be possible to construct arrays with tens to hundreds of electrodes on a flexible substrate (Viventi et al., 2011), where thin film metal traces, rather than wires, are used to connect the electrodes to the stimulator.

4.4. Limitations

One limitation of this study was the choice of animal model for testing the electrode designs. Targets in DBS for movement disorders, including the subthalamic nucleus and the ventral intermediate nucleus of thalamus, span a length scale of 1–10 mm in humans (Keane et al., 2012, Slavin et al., 2006), and the neural volumes activated at therapeutic stimulation levels are predicted to span similar length scales (Butson et al., 2007). In contrast, the cat sciatic nerve (Grill and Mortimer, 1996) and the posterior IC (Nicholson, 1965) span a length scale of 1–3 mm, and in these tissues, EMG activity in a single muscle group can be evoked by activating a small population of axons that occupy a length scale of < 1 mm.

The smaller volumes of tissue in the cat were a challenge for assessing the efficiency of electrodes that were intended for use in humans. For example, compared to the standard electrode, LC was more efficient at activating > 90 % of perpendicular AOPs but less efficient at activating a small subset of the AOPs located near the center of the electrode (figure 11b). To emulate the presence of perpendicular axons distal to the electrode (i.e., along the shaft insulation and below the shaft tip), we displaced the electrodes ± 3 mm when oriented perpendicular to the target axons. While many of the qualitative trends observed experimentally could be reproduced with the model (figures 7d and 8d), experiments in larger animals may provide more accurate evaluation of improved electrode designs.

Another limitation was the choice of straight axon trajectories in the model analysis. Although the trajectory of an axon is never perfectly straight, it was a reasonable approximation. In DBS of the internal globus pallidus, activation of AOPs that course approximately perpendicular to the electrode array has been observed at therapeutic stimulation settings (Johnson and McIntyre, 2008). In subthalamic nucleus DBS, activation of AOPs in the anterior internal capsule, which course approximately parallel to the electrode array in humans (Miocinovic et al., 2006), improved PD symptoms in rats (Gradinaru et al., 2009). And, evidence from non-human primates suggest that axons from the lenticular fasciculus, which course approximately perpendicular to the electrode array, may also be therapeutic targets (Miocinovic et al., 2006). As a further example, in DBS of the ventral intermediate nucleus of the thalamus, TAs from the cerebellothalamic tract that course approximately parallel to the implanted array are predicted to be the therapeutic targets (Birdno et al., 2012). Therefore, while the results do not reveal an optimal configuration for any particular region, they do identify what types of configurations may improve efficiency and/or selectivity for different possible orientations of neural elements that might be encountered across anatomical targets.

Although the simplified FEM model did not account for heterogeneity or anisotropy of brain tissues, it reproduced the dependence of R_a on the electrode configuration (figures 7a and 8c) and had two advantages: model solution times were less than thirty minutes, allowing us to study a very large parameter space of possible electrode designs; and the effects of electrode geometry and polarity on the potentials could be studied in isolation from other variables, such as heterogeneities in the conducting volume, that may also affect the potential distribution (Astrom et al., 2006). The simplified model, however, did not reproduce all of the experimental findings. It is possible that discrepancies between the model and experiments may be due to anisotropy and heterogeneity in the conductivity of brain tissue and/or the geometry of the target neural elements (figure 9), and future computational models should account for these features when designing electrodes for specific DBS applications (Butson et al., 2007, Chaturvedi et al., 2010, Frankemolle et al., 2010).

5. Conclusion

Model-based engineering optimization was used to design electrodes that improved the efficiency and selectivity of DBS. Electrodes with heights greater than the standard clinical electrode contact were the most efficient for stimulating neural elements oriented perpendicular to the long axis of the electrode, and electrodes with geometries similar to the standard clinical electrode were the most efficient for stimulating parallel neural elements. Bipolar and tripolar electrode configurations were the most selective for activating parallel axons over perpendicular axons. An array of cathodes with short interelectrode spacing, or equivalently, an elongated cylindrical electrode, was the most selective for activating perpendicular axons over parallel axons; and an anode displaced from the center of the target region was the most selective for selectively activating terminating axons over passing axons. The performance of these designs could not be explained solely by differences in their electrical properties, suggesting that field-shaping effects from changing electrode geometry and polarity can be on par with or greater than the effects of decreasing electrode impedance.