Mass weighted urn design - a new randomization algorithm for unequal allocations

Abstract

Unequal allocations have been used in clinical trials motivated by ethical, efficiency, or feasibility concerns. Commonly used permuted block randomization faces a tradeoff between effective imbalance control with a small block size and accurate allocation target with a large block size. Few other unequal allocation randomization designs have been proposed in literature with applications in real trials hardly ever been reported, partly due to their complexity in implementation compared to the permuted block randomization. Proposed in this paper is the mass weighted urn design, in which the number of balls in the urn equals to the number of treatments, and remains unchanged during the study. The chance a ball being randomly selected is proportional to the mass of the ball. After each treatment assignment, a part of the mass of the selected ball is re-distributed to all balls based on the target allocation ratio. This design allows any desired optimal unequal allocations be accurately targeted without approximation, and provides a consistent imbalance control throughout the allocation sequence. The statistical properties of this new design is evaluated with the Euclidean distance between the observed treatment distribution and the desired treatment distribution as the treatment imbalance measure; and the Euclidean distance between the conditional allocation probability and the target allocation probability as the allocation predictability measure. Computer simulation results are presented comparing the mass weighted urn design with other randomization designs currently available for unequal allocations.

1. Introduction

Unequal treatment allocations have been frequently employed in clinical trials motivated by ethical, economical, trial efficiency, or trial feasibility considerations [1,2]. They are more commonly used in Bayesian adaptive trials [3], early phase trials, and trials using response adaptive randomization [4]. Researches on unequal allocation randomization designs involve new concepts and challenges which are not relevant to equal allocation randomization designs. To facilitate the further discussion, the following concepts are defined:

1.1. Conventional unequal allocations versus optimal unequal allocations

Unequal allocations can be classified into two categories: optimal allocations and conventional allocations. Optimal allocations are derived from pre-defined optimization algorithms [1], and may include rational or irrational numbers. For example, in a two-arm trial with a binary outcome testing the simple difference between the response rates p_A and p_B, the optimal allocation which minimizes the total number of failures is $1:\sqrt{p_A∕p_B}$. If the goal is to maximize the power of the trial under a fixed sample size, the optimal allocation is $1:\sqrt{p_A(1-p_A)∕\left[p_B(1-p_B)\right]}$, known as Neyman allocation [1,2]. Assume p_A = 0.35 and p_B = 0.20, these two allocations are 1:1.3229, and 1:1.1924 respectively. Another instance where an unequal allocation is statistically desirable is when (m – 1) treatments are compared to a single control using the Dunnett procedure, in which, the optimal allocation is 1 for each of the treatment arms and $\sqrt{m-1}$ for the control arm [1,5]. When m = 3, the optimal allocation is $1:1:\sqrt{2}$. Optimal unequal allocations are frequently used in Bayesian adaptive trials [3]. Connor et al. recently reported a design for a three-arm trial with a binary outcome aiming to identify the best treatment [6]. If the success rates obtained from the initial balanced phase of 300 subjects are 51%, 55%, and 64% respectively for the three arms, an unequal allocation of 6:11:33 is desired for the next 100 subjects in order to maximize the likelihood of identifying the best or the worst one among the three arms. Conventional allocations, sometimes called convenient allocations, are usually composed by small integers. Dumville et al. searched the Cochrane Library, Medline, PubMed and the Science Citation Index, and identified 65 trials with unequal allocations [7]. Among them, 64 (98%) trials used allocations with integers no greater than 4. Of the 56 two-arm trials, 53 (95%) used allocations 1: 2, 1:3, or 2:3. None of the trials Dumville searched used optimal unequal allocations. In fact, there is no randomization design currently available that is able to directly target optimal allocations, except the complete randomization, which is vulnerable to unwanted treatment imbalances.

1.2. The desired allocation, the target allocation, and the achieved allocation

The desired allocation is defined based on the study design or derived from accumulated study data. The target allocation is used by the randomization algorithm. The achieved allocation is the treatment distribution obtained in a randomization procedure. The distinction between the desired allocation and the target allocation occurs when the randomization design cannot target the desired allocation. For example, if the desired optimal allocation is 1:1.3229, one may choose a randomization design to target the allocation 2:3 or 3: 4. The difference between the desired allocation and the target allocation is defined as the allocation accuracy. The difference between the target allocation and the achieved allocation is defined as the allocation precision. The expected value of the difference between the treatment distribution under the desired allocation and the distribution under the target allocation is proportional to the sample size. As the sample size increase, so does the impact of the allocation accuracy.

1.3. Pre-generated randomization sequence and conditional allocation probability

Historically, a randomization sequence was generated before the trial started, and was kept in a secure place, such as sequentially numbered sealed envelopes locked in a file cabinet. When a subject was ready for randomization, the envelope with the smallest sequence number is opened for treatment assignment. Cases of suspicious selection biases and frauds associated with this old practice have been reported [8]. As computers have become widely available, a pre-generated randomization sequence can be stored in a computerized randomization system. Randomization codes are then used sequentially for treatment assignments. This method cannot handle unexpected, yet unavoidable, situations associated with study drug supply problems and clinical site trial operation misconducts [9]. As a better alternative to the pre-generated randomization sequence, an explicit conditional allocation probability formula allows randomization assignments being generated in real-time by a central computerized randomization system, adapting the entire randomization history. This approach not only eliminates prior randomization treatment assignment concealment failures, but also allows covariate adaptive randomization for treatment imbalance controls beyond stratification and response adaptive randomization [10].

In summary, desired features for a good unequal allocation randomization design include:

• High allocation accuracy to ensure that the target allocation of the randomization algorithm is close enough to the desired allocation.

• A consistent allocation precision to ensure that at any time point in the study the treatment imbalance between the achieved allocation and the target allocation is controlled within a pre-specified tolerated limit.

• A simple method for the calculation of the conditional allocation probability to ensure an easy implementation of the randomization algorithm.

In Section 2, currently available unequal allocation randomization designs are reviewed, and the need for a better design is presented. In section 3, the mass weighted urn design is proposed, followed by the evaluation of its statistical properties and performance comparison with other randomization designs in Section 4. Section 5 presents more discussions on the desired features for unequal allocation randomization designs and limitation of the proposed mass weighted urn design.

2. Background

Currently available unequal allocation randomization designs include the complete randomization (CP), the permuted block randomization (PBR), the modified Wei's urn design (mUD) described by Rosenberger and Lachin [1], the maximal procedure (MP) proposed by Berger et al. [11,12], the brick tunnel randomization (BTR) and its modified version, the wide brick tunnel randomization (WBT) propose by Kuznetsova and Tymofyeyev [13,14], and the block urn design (BUD) proposed by Zhao and Weng [15]. Consider a target allocation r₁:r₂:···:r_m, where r_j (j =1,2,···,m) are integers without common divisor greater than 1. Let $R={\sum }_{j=1}^m{r}_j$ be the sum of allocation elements, and w_j = r_j / R so that ${\sum }_{j=1}^m{w}_j=1$. Let n_ij be the number of subjects assigned to treatment j in the first i subjects, and p_ij be the probability of assigning subject i to treatment j. CR directly applies the target allocation probability to each treatment assignment, i.e:

$$p_{ij}\left(CP\right)=w_j(i=1,2,\dots ;j=1,2,\cdots ,m)$$ (1)

It offers the lowest allocation predictability at the cost of a weak treatment imbalance control. Although it is extremely easy to implement, CR has rarely been used in practice. PBR sequences can be obtained based on an urn model [1,16]. Letb = αR be the block size with α being a positive integer. The conditional allocation probability for PBR is:

$$p_{ij}\left(PBR\right)=\frac{b{w}_j+b{w}_{j}k-n_{i-1,j}}{b+bk+i+1},(i=1,2,\cdots ;j=1,2,\cdots ,m)$$ (2)

Here k = int[(i –1) / b] is the number of completed blocks among the first (i –1) assignments. Pre-generated PBR sequences are frequently used in practice. With formula (2), a PBR assignment can be generated in real-time when needed. The conditional allocation probability for BUD is:

$$p_{ij}\left(BUD\right)=\frac{b{w}_j+R{w}_j{k}^{\ast }-n_{i-1,j}}{b+R{k}^{\ast }-i+1},(i=1,2,\cdots ;j=1,2,\cdots ,m)$$ (3)

Here k* is the number of complete balanced sets of R assignments among the first (i –1) subjects [15]. For both PBR and BUD, treatment imbalance is controlled by the block size. A small block size offers a tighten imbalance control. Meanwhile, it may reduce the accuracy of the target allocation. For example, for a desired allocation $1:\sqrt{2}:\sqrt{3}$, choosing 10:14:17 as the target allocation results a good allocation accuracy with a weak imbalance control because the minimal block size is 41. Choosing target allocation 2:3: 4 allows a block size as small as 9 at the cost of a noticeable allocation accuracy loss.

Rosenberger and Lachin described the mUD for two-arm trials with unequal allocation w₁ : w₂, where w₁ + w₂ =1. Starting from αw₁ and αw₂ balls in the urn for the two arms respectively, if a ball for arm 1 is drawn, βw₂ balls are added to the urn for arm 2; and if a ball for arm 2 is drawn, βw₁ balls are added to the urn for arm 1 [1]. Although it was not explicitly mentioned, it is assumed that the selected ball is returned to the urn after the treatment assignment, same as the original Wei's urn design [18]. By extending this model to m ≥ 2 scenarios, the conditional allocation probability for mUD is:

$$p_{ij}\left(mUD\right)=\frac{\alpha w_j+\beta (i-1-n_{i-1,j})w_j}{\alpha +\beta {\sum }_{h=1}^m(i-1-n_{i-1,h})w_h},(i=1,2,\cdots ;j=1,2,\cdots ,m)$$ (4)

As i increases, the number of balls in the urn increases, and the treatment imbalance control decreases. For large trials, mUD has a weak treatment imbalance control similar to the complete randomization [16], a limitation associated with the original urn design proposed by Wei for equal allocations [18].

Proposed by Berger, MP ensures that all permissible randomization sequences, under the condition of a given sequence length and the maximal tolerated imbalance (MTI), have the same chance being selected [12]. Equal probability sequence is important for designed-based randomization tests in which the type I error is assessed based on the permutation of all permissible sequences under the randomization design. Proposed by Kuznetsova and Tymofyeyev, BTR ensures that the unconditional allocation probability for each treatment assignment in the randomization sequence equals to the target allocation ratio [13,19]. Preserving the unconditional allocation ratio helps selection bias prevention. However, few randomization designs offer both the equal probability sequence and the preserved unconditional allocation ratio. Consider a trial with a target allocation 2:3 between arms A and B, using MP with MTI = 2, there are 8 possible sequences for the first 5 assignments: ABABB, ABBAB, ABBBA, BAABB, BABAB, BABBA, BBAAB, and BBABA. Giving each sequence the same probability of 1/8, the unconditional allocation ratio is 1:1 for the third subject and 3:5 for the other 4 subjects; none of them equals to the target allocation ratio 2:3 [13]. On the other hand, if BTR is applied to preserve the unconditional allocation ratio, sequences 1, 4, 7 and 8 have 1/10 chance being used, and the other 4 sequences have 3/ 20 chance being used [13], none of them equals to 1/ 8. What is common to MP and BTR is that both do not offer an explicit formula for the calculation of conditional allocation probabilities. Salama et al. provided an algorithm for the generation of MP randomization sequence [12]. It helps for short sequences and conventional allocations with small integers. The extensive amount of calculation and complex logic rules discouraged the MP being applied to more general unequal allocation trial scenarios. The creation of a BTR sequence involves a complex iterative procedure for the calculation of transition probabilities from each permissible allocation node to each permissible next node under the unconditional allocation ratio preserving condition. This procedure becomes more complex when the trial involves m < 2 arms and target allocations with large integers. BTR does not have a parameter to adjust the tradeoff between the allocation predictability and treatment imbalance. In the 5-assignment sequence discussed above, 36% assignments are deterministic, making BTR vulnerable to selection bias. For this reason, Kuznetsova and Tymofyeyev proposed the WBT by expending the BTR allocation space [14]. While the allocation predictability is improved in WBT, the implementation complexity is also increased, making it even harder being used in practice.

While each of these currently available unequal allocation randomization designs has some advantages and disadvantages, a better design is needed to simultaneously provide high allocation accuracy, a consistent imbalance control, and an explicit formula for conditional allocation probability, while maintain a low level of allocation predictability.

3. Method

3.1. The conceptual model for the mass weighted urn design

Unlike in traditional urn designs where each ball in the urn always has the same chance to be selected, in the mass weighted urn design (MWUD) the probability a ball being selected is proportional to its mass. Each ball can have its mass as a real number, such as an integer, a rational number, or an irrational number. Consider a study comparing m treatments with a target allocation W = (w₁,w₂,···,w_m), where w_j > 0 (j =1,2,···,m) and ${\sum }_{j=1}^m{w}_j=1$. There are m balls in the urn, each represents one treatment. Let T_i be the treatment allocation for the i^th subject, and x_ij be the mass of the ball for treatment j after treatment assignment T_i. Initially each ball has its mass proportional to the target allocation, i.e. x_0,j = αw_j (j =1,2,···,m). Here α is a parameter controlling the maximal tolerated treatment imbalance. The MWUD procedure follows the steps below:

• Step 1: When eligible subject i is ready for randomization, among all balls with a positive mass, a ball is randomly drawn from the urn with the probability proportional to its mass. The subject is assigned to the treatment associated with the selected ball, denoted as T_i.

• Step 2: One unit mass is taken from the selected ball, and redistributed among the m balls, including the selected ball, based on the target allocation ratio. Then, the selected ball is returned to the urn.

• Step 3: Repeat the steps 1 to 2 until the end of the study.

After treatment assignment T_i, the contents of the urn are changed as follows:

$$x_{ij}=\{\begin{array}{cc}{x}_{i-1,j}-1+w_j\hfill & j=T_i\hfill \\ x_{i-1,j}+w_j\hfill & j\ne T_i\hfill \end{array}\phantom{\}}(i=1,2,\cdots )$$ (5)

The total mass of the m balls in the urn ${\sum }_{j=1}^m{x}_{ij}\equiv \alpha$, (i = 0,1,2,···) is a constant. In certain circumstances, a ball could have a negative mass. When this situation occurs, that ball is not available for the next random draw, and the associated treatment is excluded from the randomization for the next subject. After the randomization for the next subject to one of the other treatments, that ball will receive its share of the redistributed mass. It will become available for randomization as soon as its mass turns to positive.

3.2. The conditional allocation probability

With the mass weighted urn model, the conditional allocation probability p_ij is fully determined by the current contents of the urn, i.e. X_i–1 = (x_i–1,1, x_i–1,2,···, x_i–1,m). Let N_i = (n_i,1,n_i,2,···,n_i,m) be the treatment distribution among the previous i subjects. Before T_i, there is:

$$x_{i-1,j}=\alpha w_j+(i-1-n_{i-1,j})w_j-(1-w_j)n_{i-1,j}=\alpha w_j-n_{i-1,j}+(i-1)w_j$$ (6)

The conditional allocation probability for MWUD is:

$$p_{ij}\left(MWUD\right)=\frac{x_{i-1,j}}{\alpha }=w_j-\frac{n_{i-1,j}-(i-1)w_j}{\alpha }=w_j-\frac{1}{\alpha }{\delta }_{i-1,j}(j=1,2,\cdots ,m)$$ (7)

Here δ_i–1,j = n_i–1,j –(i –1)w_j represents the difference between the observed number of assignments to treatment j and the desired number of assignments to treatment j among the (i – 1) subjects under the target allocation. It is noticed that formula (7) may have negative values when α is small. To solve this problem, negative values of x_i–1,j is replaced by zero, and the remaining conditional allocation probability items are rescaled so that their sum equals to 1. With this scenario taken into account, the following formula is used for implementation of MWUD:

$$p_{ij}\left(MWUD\right)=\frac{\max [\alpha w_j-n_{i-1,j}+(i-1)w_j,0]}{{\sum }_{h=1}^m\max [\alpha w_h-n_{i-1,h}+(i-1)w_h,0]}(j=1,2,\cdots ,m)$$ (7a)

For example, in a three-arm trial with the targeting allocation of 1:2:3 = 1/6:1/3:1/2 and α = 3, if the first subject is assigned to arm 1, the conditional allocation probabilities obtained from (7) are −1/9, 4/9, 6/9 respectively for the three arms. By replace −1/9 with 0 and rescale 4/9 and 6/9 based (7a) we have 0, 2/5, 3/5 as the conditional allocation probabilities for assigning the second subject to the three arms respectively.

With the conditional allocation probability P_i = (p_i1, p_i2,···, p_im), a random variable Y ~ Uniform(0,1) is employed to facilitate the subject randomization procedure. Subject i is assigned to treatment j if:

$${\sum }_{k=0}^{j-1}{p}_{ij}<y_i\le {\sum }_{k=0}^j{p}_{ik}(\text{where}{p}_{i0}\equiv 0;i=1,2,\cdots ;j=1,2,\cdots m)$$ (8)

3.3. The maximal treatment imbalance

The primary goal of using a restricted randomization design is to control treatment imbalance so that the difference between the achieved treatment distribution and the desired allocation is within a tolerated range. Let H_i = (iw₁,iw₂,···,iw_m) be the treatment distribution under the target allocation. The treatment imbalance d_i is defined as the Euclidian distance between N_i and H_i:

$$d_i=\Vert {\mathbf{N}}_i-{\mathbf{H}}_i\Vert =\sqrt{{\sum }_{j=1}^m{(n_{ij}-i{w}_j)}^2}=\sqrt{{\sum }_{j=1}^m{\delta }_{ij}^2}(i=1,2,\cdots )$$ (9)

Here δ_ij = n_ij –iw_j (i =1,2,···; j =1,2,···,m) represents the imbalance component in treatment j after assignment T_i. For two-arm equal allocation trials, formula (9) is reduced to $d_i=\mid n_{i1}-n_{i2}\mid ∕\sqrt{2}$, proportional to the absolute difference of the two treatment group sizes. Based on the definition of δ_ij, at any given time point i, there is:

$${\sum }_{j=1}^m{\delta }_{ij}={\sum }_{j=1}^m{n}_{ij}-1{\sum }_{j=1}^m{w}_j=0(i=1,2,\cdots )$$ (10)

According to (7) and (8), if δ_ij > αw_j, there are p_i+1,j < 0, T_i+1 ≠ j, n_i+1,j = n_ij, and δ_i+1,j =δ_ij – w_j. The maximum of δ_ij occurs when δ_i+1,j is in its minimal positive value and the ball j is selected:

$$\max ({\delta }_{ij}\mid i=1,2,\cdots )\le \alpha w_j+(1-w_j)=(\alpha -1)w_j+1(j=1,2,\cdots ,m)$$ (11)

Based on (10), there is:

$$\min ({\delta }_{ij}\mid i=1,2,\cdots )>0-{\sum }_{h=1,h\ne j}^m\max \left({\delta }_{ih}\right)\ge -(\alpha -1)(1-w_j)-(m-1)$$ (12)

Comparing (11) and (12), there is max(δ_ij)<|min(δ_ij)|. Therefore, the treatment imbalance d_i defined by (9) will not exceed the limit below:

$$\max (d_i\mid i=1,2,\cdots )<\sqrt{{\sum }_{j=1}^m{((\alpha -1)(1-w_j)+(m-1))}^2}<(\alpha +m-2)\sqrt{m}$$ (13)

For example, for target allocation $1:\sqrt{2}:\sqrt{3}=0.2412:0.3411:0.4177$ with α = 4, there is:

$$\max (d_i\mid i=1,2,\cdots )<\sqrt{{4.2764}^2+{3.9767}^2+{3.7469}^2}=6.9384$$

In reality, at any given time point in a sequential allocation procedure, there could be no more than one imbalance component δ_ij reaches its maximum or its minimum. The actual maximal treatment imbalance will be smaller than the one given in (13). Formula (13) indicated that the proposed MWUD provides a consistent treatment imbalance control throughout the study. The maximal imbalance, measured by the Euclidian distance between the observed treatment distribution and the targeted treatment distribution, is capped through parameter α.

3.4. The allocation predictability

Allocation predictability is an important property for randomization designs. For two-arm equal allocation trials, the correct guess probability defined based on the Blackwell and Hodges’ convergence strategy [20] and the proportion of deterministic assignments are widely employed as the measures for allocation predictability [16,10]. For trials with m ≥ 2 and unequal allocations, a generally applicable assessment for allocation predictability is needed. CP uses the target allocation probability for each treatment assignment, and has the lowest allocation predictability. Therefore, the difference between the conditional allocation probability P_i = (p_i1, p_i2,···, p_im) and the target allocation probability W = (w₁,w₂,···,w_m) can be a generalizable measure for the allocation predictability:

$$g_i=\Vert {\mathbf{P}}_i-{\mathbf{W}}_i\Vert =\sqrt{{\sum }_{j=1}^m{(p_{ij}-w_{ij})}^2}(i=1,2,\cdots )$$ (14)

Insert (7) and (9) into (14), there is:

$$g_i=\Vert {\mathbf{P}}_i-{\mathbf{W}}_i\Vert =\sqrt{{\sum }_{j=1}^m{\left[\frac{{\delta }_{i-1,j}}{\alpha }\right]}^2}=\frac{d_{i-1}}{\alpha }(i=1,2,\cdots )$$ (15)

Formula (15) indicated that for MWUD, when both are measured by the Euclidian distance, the allocation predictability of a treatment assignment is proportional to the treatment imbalance prior to that treatment assignment.

4. Results

The MWUD described in Section 3 applies to all target allocations, equal or unequal, two arms or more than two arms, and is easy for implementation due to the simple formula for conditional allocation probability (7a). In this section, the statistical and operation properties of this new randomization design are assessed with computer simulations and are compared to those of PBR, mUD, and CR.

4.1. A sample MWUD randomization sequence

Consider a trial with a target allocation $1:1:\sqrt{2}$ and a sample size of 300. Table 1 shows the details of MWUD process with α = 4, including information before, during, and after the first 10 and last 10treatment assignments. Using formulas (7a), conditional allocation probability can be easily calculated based on the target allocation, the current treatment distribution and the parameter α. Treatment assignment T_i is made based on (8). The treatment imbalance and the allocation predictability are measured by (9) and (14) respectively. Under the target allocation $1:1:\sqrt{2}=0.2929:0.2929:0.4142$, a deterministic assignment to treatment 1, 2, or 3 has the predictability of 0.8703, 0.8703, and 0.7174 respectively. The observed allocation predictability is much lower than those of deterministic assignments, indicating a high level of allocation randomness. Based on formula (13), the treatment imbalance cap for this trial setting is 6.9346. Observed treatment imbalances are much smaller than this cap. This sample randomization sequence demonstrates that the proposed MWUD is able to achieve the optimal target allocation accurately and precisely while maintaining a low allocation predictability.

Table 1. A Sample Randomization Procedure with Mass Weighted Urn Design.

Number of treatment arms = 3; Target Allocation = 1: 1: √2; Sample size n = 300; α = 4.

i	Before Assignment			During Assignment						After Assignment
	n i-1,1	n i-1,2	n i-1,3	p i,1	p i,2	p i,3	g i	x i	T i	d i	ni,2/ni,1	ni,3/ni,1
1	0	0	0	0.293	0.293	0.414	0	0.664	3	0.717
2	0	0	1	0.366	0.366	0.268	0.179	0.718	2	0.738
3	0	1	1	0.439	0.189	0.371	0.184	0.098	1	0.297	1	1
4	1	1	1	0.263	0.263	0.475	0.074	0.763	3	0.420	1	2
5	1	1	2	0.336	0.336	0.328	0.105	0.044	1	0.712	0.5	1
6	2	1	2	0.159	0.409	0.432	0.178	0.314	2	0.594	1	1
7	2	2	2	0.232	0.232	0.536	0.149	0.350	2	1.309	1.5	1
8	2	3	2	0.305	0.055	0.639	0.327	0.147	1	1.609	1	0.667
9	3	3	2	0.129	0.129	0.743	0.402	0.727	3	0.891	1	1
10	3	3	3	0.202	0.202	0.596	0.223	0.006	1	1.567	0.75	0.75
......
291	85	85	120	0.278	0.278	0.445	0.037	0.033	1	0.964	0.988	1.395
292	86	85	120	0.101	0.351	0.548	0.241	0.250	2	1.163	1	1.395
293	86	86	120	0.174	0.174	0.652	0.291	0.709	3	0.446	1	1.407
294	86	86	121	0.247	0.247	0.505	0.111	0.937	3	0.272	1	1.419
295	86	86	122	0.321	0.321	0.359	0.068	0.621	2	0.745	1.012	1.419
296	86	87	122	0.394	0.144	0.462	0.186	0.905	3	0.856	1.012	1.430
297	86	87	123	0.467	0.217	0.316	0.214	0.735	3	1.392	1.012	1.442
298	86	87	124	0.540	0.290	0.169	0.348	0.132	1	0.692	1	1.425
299	87	87	124	0.364	0.364	0.273	0.173	0.468	2	0.731	1.011	1.425
300	87	88	124	0.437	0.187	0.377	0.183	0.318	1	0.323	1	1.409

α: Parameter used by the mass weighted urn design.

i: Randomization sequence order.

n_i-1,j: Treatment distribution before subject i. (j=1,2,3).

p_i,j: Conditional allocation probability for subject i. (j=1,2,3)

g_i: Allocation predictability for subject i.

x_i: Random number

T_i: Treatment assignment for subject i.

d_i: Treatment imbalance for subject i.

d_i: Treatment imbalance after subject i.

n_i,j/n_i,1: Allocation ratio between arm j and 1, (j=2,3)

4.2. Performance comparison with alternative designs for optimal unequal allocation

Computer simulations are conducted for a trial with a desired optimal allocation $1:\sqrt{2}:\sqrt{3}$ and a sample size of 100, comparing MWUD with CR, PBR, and mUD. The CR, mUD, and MWUD directly target the optimal allocation. Three conventional allocations are used as the target allocation for PBR. They are 2:3:4,5:7:8, and 10:14:17. The minimal block size b = 9, 20, or 41, is used for each scenario respectively. Four levels of parameter α, 2, 4, 6, and 8, are used for MWUD. Fifty thousand replications are run for each simulation scenario.

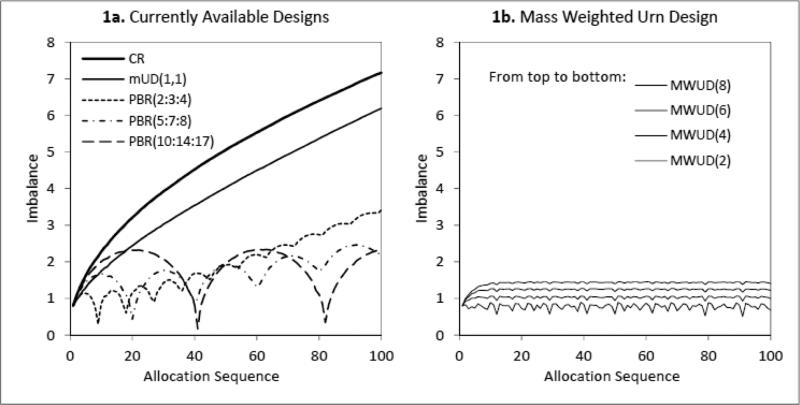
Figure 1a and 1b show the treatment imbalance for each assignment in the randomization sequence averaged across simulation runs. Figure 1a indicates that mUD has a treatment imbalance increasing as the sequence increases, similar to CR. PBR with a small block size has a low allocation accuracy, due to the difference between the desired allocation and the target allocation. The treatment imbalance grows along with the allocation sequence. With a large block size, the target allocation is closer to the desired allocation. However, this occurs only at the end of each block. The treatment imbalance in the middle of each block increases as the block size increases. In Figure 1b, the proposed MWUD demonstrates its capacity of accurately targeting the optimal allocation with a consistent imbalance control throughout the randomization sequence. Table 2 lists the average treatment imbalance and the average allocation predictability for the 9 simulation scenarios. Results show that the MWUD with parameter α equals to 4 or 6 offers better overall performance when compared to CR, mUD, and PBR for optimal unequal allocation $1:\sqrt{2}:\sqrt{3}$. It can be expected that as the sample size increases, the advantageous of the MWUD over other designs will become even more significant.

Figure 1.

Treatment Imbalances for Optimal Unequal Allocation

Desired allocation = $1:\sqrt{2}:\sqrt{3}$, Sample size = 100, Simulation = 50,000/scenario

Table 2. Performance comparison between MWUD and alternative designs.

Optimal allocation = 1: √2: √3, sample size = 100, simulation = 50,000 per scenario

Randomization design	Target allocation	Parameter	Average Allocation Predictability*	Average Treatment Imbalance†
Complete randomization	1: √2: √3		0	4.8072
Modified Urn Design	1: √2: √3	α = 1, β = 1	0.0586	3.9141
Permuted Block Randomization (block size = b)	2 : 3 : 4	b = 9	0.2841	1.9584
	5 : 7 : 8	b = 20	0.2121	1.7374
	10 : 14 : 17	b = 41	0.1378	1.8466
Mass Weighted Urn Design	1: √2: √3	α = 2	0.3480	0.7747
		α = 4	0.2501	1.0268
		α = 6	0.2032	1.2359
		α = 8	0.1747	1.4134

^†Calculated based on the Euclidean distance between the desired treatment distribution and the achieved treatment distribution, averaged across the randomization sequence and the simulation runs.

^*Calculated based on the Euclidean distance between the desired allocation probability and the conditional allocation probability, averaged across the randomization sequence and the simulation runs.

4.3. Tradeoff between treatment imbalance and allocation predictability

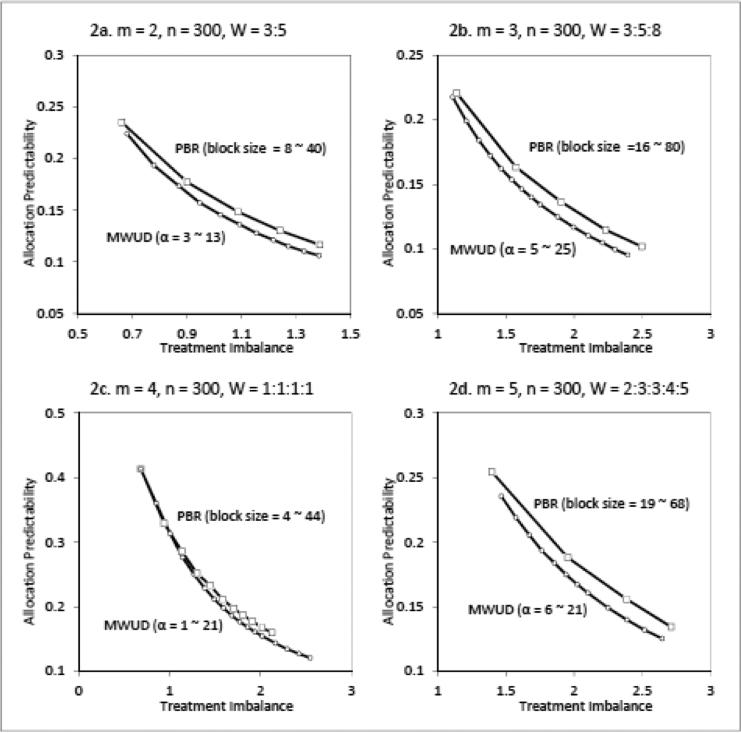
A tradeoff between treatment imbalance and allocation predictability is commonly exist in all restricted randomization designs. For a specific randomization design, a reduction in imbalance tolerance is often associated with an increase in allocation predictability, and vice versa. However, for different randomization designs, with the same cost in allocation predictability, the gain in treatment balancing are not always the same [16]. To compare the proposed MWUD to the most commonly used PBR with the focus on the tradeoff performance between treatment imbalance and allocation predictability, four trial scenarios are simulated: (1) a two-arm trial with desired allocation 3:5; (2) a three-arm trial with desired allocation 3:5:8; (3) a four-arm trial with equal allocation 1:1:1:1; and (4) a five-arm trial with desired allocation 2:3:3:4:5. In all these cases, the desired allocation can be directly targeted by both PBR and MWUR, so the simulation results solely represent the tradeoff mechanism of each design. For this purpose, wide ranges of block size b for PBR and parameter α for MWUD are simulated. The sample size for all simulation scenarios is set to 300 so that the periodical variation of treatment imbalance and allocation predictability can be reduced by taking the average across the sample size. To gain stable estimates, each simulation scenario is repeated 5000 times. Figure 2 shows that in the three unequal allocation scenarios, MWUD demonstrates better performances than PBR. With the same level of treatment imbalance control, MWUD provides lower allocation predictability than PBR. Contrasted with the discrete block sizes available in PBR, a continuous space for parameter α is offered in MWUD. In addition, the high proportion of deterministic assignments associated with PBR has been considered as one of the major risk factor for selection bias [10,16,17, 21]. When α ≥ 3, deterministic assignments are almost eliminated from MWUD sequence. For equal allocations, there is no big difference between MWUD and PBR with regards to the tradeoff performance. In fact, it is not hard to prove that MWUD with α =1 is identical to PBR with block size b = m.

Figure 2.

Performance Comparison between MWUD and PBR for Conventional Allocation Sample size = 300, Simulation = 5,000/scenario

4. Discussion

Originally created by Friedman [22], the urn model with integer components had been used to illustrate various randomization designs for sequential clinical trials, including Wei's urn design [18], Chen's Ehrenfest urn design [23], and Zhao and Weng's BUD [15], the commonly used PBR [1, 16], and the mUD [1]. The use of continuous contents, such as the mass weighted rule, in an urn model is not new [24]. It allows the MWUD to target any desired unequal allocation in the real number domain without approximation. After using conventional allocations with small integers for decades, people may challenge the relevance of having allocations with real numbers. The growing use of Bayesian adaptive design and response adaptive designs call for unequal allocation designs better than the commonly used PBR. It is important to realize that, compared to PBR, the proposed MWUD offers better tradeoff performance between treatment imbalance control and allocation predictability, equally easy implementation with a simple formula for the calculation of conditional allocation probability. The accurate allocation targeting of MWUD is an additional advantageous feature for an unequal allocation randomization design.

A consistent unconditional allocation probability for each treatment assignment in a randomization sequence is a good feature for a randomization design [13,14,19]. To exam this feature for MWUD, consider a two-arm trial with target allocation w₁ : w₂. Without the loss of generality, assume w₁ ≤ w₂ and w₁ + w₂ =1. Let p_i1 and p_i2 =1– p_i1 be the conditional allocation probability, u_i1 and u_i2 = 1 –u_i1 be the unconditional allocation probability for treatment assignment T_i. Let n_i1 and n_i2 =i–n_i1 be the observed treatment distribution after T_i. The unconditional allocation probability for T₁ is u_1,1 = p_0,1 = w₁. The unconditional allocation probability for T₂ is:

$$u_{2,1}\left(MWUD\right)=\{\begin{array}{cc}{w}_1\frac{(\alpha +1)w_1-1}{\alpha }+w_2\frac{(\alpha +1)w_1}{\alpha }=w_1\hfill & \text{if}\alpha \ge \frac{w_1}{w_2}\hfill \\ w_2\frac{(\alpha +1)w_1}{\alpha }=w_1+\frac{(w_2-\alpha w_1)w_1}{\alpha }\hfill & \text{if}\alpha <\frac{w_1}{w_2}\hfill \end{array}\phantom{\}}$$ (16)

This result indicates that when α < w₂ / w₁, the unconditional allocation probability u_2,1 will be greater than the target allocation w₁. For example, when w₁ =1/ 4, w₂ = 3/4, and α = 2 < w₂/ w₁ = 3, the unconditional allocation probability u_2,1 =1/ 4+1/ 32. This fact shows that MWUD does not hold the allocation ratio preservation feature. Similar issue occurs to the mUD. Under the same trial setting, consider mUD with parameters α = 4, and β = 8, so that the urn starts with 1 ball for arm 1 and 3 balls for arm 2. If a ball is drawn for arm 1, 6 balls are added to the urn for arm 2. If a ball is drawn for arm 2, 2 balls are added to the urn for arm 1.

$$u_{2,1}\left(mUD\right)=\frac{1}{4}\times \frac{1}{4+3\times 2}+\frac{3}{4}\times \frac{1+1\times 2}{4+1\times 2}=\frac{1}{4}+\frac{3}{20}$$ (17)

Computer simulations are conducted to exam the magnitude of the shift in the unconditional allocation probability of MWUD for a two-arm trial with allocation 2:3. Results are shown in Table 3. . . In this specific case, when α ≥ 2 the unconditional allocation probability shift is trivial. In general, α ≥ 4 is recommended for MWUD, so that the concerns for the unconditional allocation probability shift can be eased. It is worth to point out that, compared to the unconditional allocation probability shift, the high proportion of deterministic assignments with conditional allocation probability equals to 1.0 is a more harmful factor inviting selection bias, especially when perfect blinding is not available.

Table 3. Estimation of unconditional allocation probability for MWUD.

Allocation = 2:3. Simulation replicate = 10,000 per scenario

Sequence	α = 1	α = 2	α = 3	α = 4	α = 5	α = 6
1	0.4	0.4	0.4	0.4	0.4	0.4
2	0.3967	0.4001	0.3983	0.3998	0.4010	0.4002
3	0.3226	0.3974	0.4000	0.4012	0.4012	0.4007
4	0.4288	0.3951	0.4006	0.4013	0.4009	0.4002
5	0.3396	0.3977	0.3984	0.4021	0.4003	0.4020
6	0.4000	0.4014	0.3959	0.4015	0.4028	0.4032
7	0.3978	0.3965	0.3972	0.4010	0.3998	0.4030
8	0.3177	0.3974	0.3985	0.4000	0.3996	0.4022
9	0.4219	0.3963	0.3995	0.4006	0.4005	0.4024
10	0.3205	0.3930	0.4016	0.3999	0.3997	0.4007

Unconditional probability is estimated based on the average conditional allocation probability for each assignment in the sequence across simulation runs.

In addition to computer simulation studies under limited trial setting scenarios, further works are needed to explore the statistical properties of MWUD with different approaches. It is also worth to extend the implementation of this unequal allocation randomization design in trials where baseline covariate balancing is desired.