Self-removal of condensed water on the legs of water striders

Significance

Condensing water droplets can be self-removed from the legs of water striders in a three-step mechanism. First, droplets migrate inside the texture and grow. Then, drops are suddenly expelled out of the hairs, owing to the elastic deformation of the network of setae by growing drops. Ultimately, condensed drops are expelled from the leg. Self-removal of condensing water prevents a major source of risk for the creature, whose hydrophobicity would reverse if setae were impregnated by water. The design of the legs therefore provides a remarkable example where the conjunction of hydrophobicity, geometry, and flexibility yields water repellency both at large and very small scales.

Abstract

The ability to control drops and their movements on phobic surfaces is important in printing or patterning, microfluidic devices, and water-repellent materials. These materials are always micro-/nanotextured, and a natural limitation of repellency occurs when drops are small enough (as in a dew) to get trapped in the texture. This leads to sticky Wenzel states and destroys the superhydrophobicity of the material. Here, we show that droplets of volume ranging from femtoliter (fL) to microliter (μL) can be self-removed from the legs of water striders. These legs consist of arrays of inclined tapered setae decorated by quasi-helical nanogrooves. The different characteristics of this unique texture are successively exploited as water condenses, starting from self-penetration and sweeping effect along individual cones, to elastic expulsion between flexible setae, followed by removal at the anisotropic leg surface. We envision that this antifogging effect at a very small scale could inspire the design of novel applicable robust water-repellent materials for many practical applications.

When a vapor condenses on a rough hydrophobic surface, liquid nuclei naturally appear within the roughness, forming tiny droplets stuck in the texture (1–3). Without the assistance of external forces, dew tightly adheres to the surface in the so-called Wenzel state, which most often destroys the superhydrophobicity of the material (4, 5). An applicable robust water-repellent surface thus requires an additional mechanism to expel these condensates from the texture (6). It has been reported in the literature that nanotextures (such as found on the surface of lotus leaves or cicada wings) might generate adhesion forces small enough to permit an efficient conversion of surface energy (coming from droplet coalescence) into kinetic energy, so that droplets can be mobilized (7–9). However, contact angle hysteresis effects are generally dominant at a small scale, so that a key challenge for antifogging materials lies in the generation of a force able to expel droplets from microtextures.

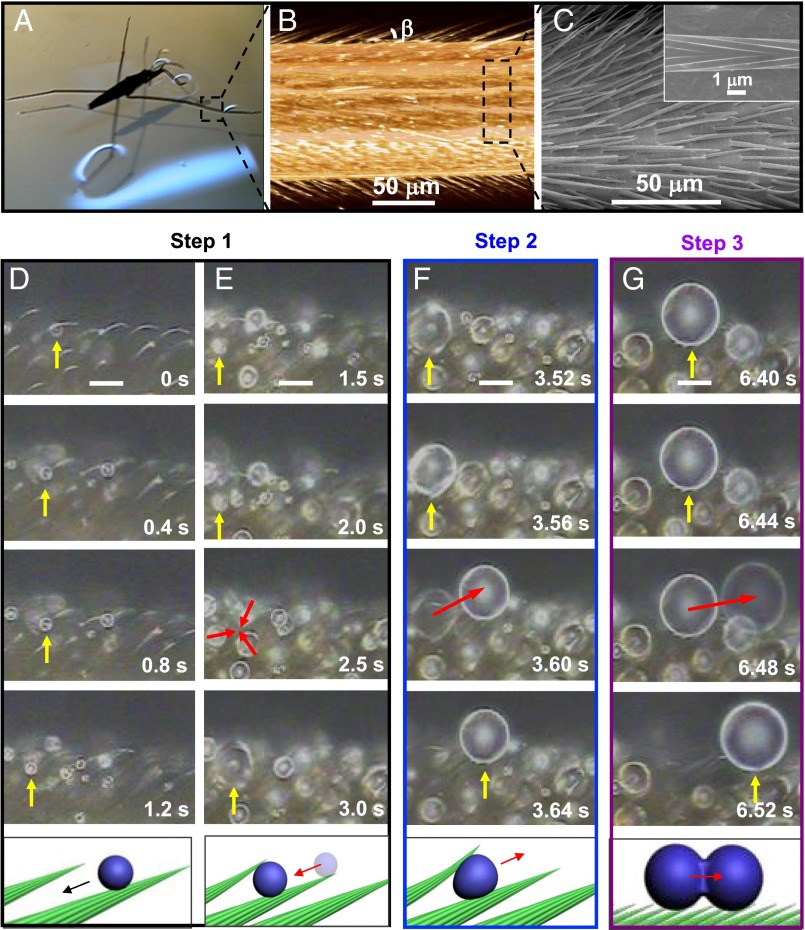
Water striders (Gerris remigis, Fig. 1A) living at the water surface in a highly humid environment offer a remarkably simple solution to this problem. Without any external force, tiny condensed droplets in the range of femtoliters (fL) to microliters (μL) get removed from striders’ legs, owing to the presence of oriented conical setae. A Gerris leg is a centimeter-size cylinder (of typical diameter 150 μm) decorated by an array of inclined tapered hairs characterized in Fig. 1 B and C by micro X-ray computed tomography (XCT) and scanning electron microscopy (SEM). Individual setae have a length L = 40–50 μm, a maximum diameter of ∼3 μm, and an apex angle of ∼5°. They make regular arrays with a mutual distance of 5–10 μm, and are tilted by an angle β = 25–35° to the base of the leg (Fig. 1 B and C and Fig. S1). In addition, longitudinal or quasi-helicoidal nanogrooves are found on the seta surface (10), as shown in Fig. 1C, Inset.

Fig. 1.

Cascade of self-motions for water droplets condensing on a leg of water strider. (A) G. remigis, an insect commonly called water strider, lives at the surface of water in a highly humid environment. (B) Micro-XCT and (C) SEM images of a strider’s leg. It is composed of tilted conical setae, and nanogrooves decorate each seta (Inset). (D–G) Water condensation in a leg placed in a fog: as we follow the drop pointed out by a yellow arrow, three successive dynamical steps are observed, eventually leading to the expulsion of water. Magnification is kept constant (scale bar, 15 μm), and time is indicated in each picture. Corresponding movie is Movie S1. (D and E, step 1) Tiny droplets self-propel on single setae, before stopping when contacting another seta. Then, droplets grow by merging with neighbors (red arrows) (F, step 2) As condensation proceeds, a growing drop deforms the surrounding setae enough to generate an elastic force able to expel it at t = 3.6 s out of the structures (red arrow). Image persistence is used to give the feeling of this quick motion. (G, step 3) At the leg surface, coalescence between neighboring drops produces directional motion at t = 6.48 s (red arrow). Again, image persistence is used to suggest fast motion. Hence droplets at a micrometric scale can be self-removed, a key fact for keeping legs dry in a humid atmosphere.

Fig. S1.

Microstructure of water strider leg. (A and B) Micro-XCT images indicate that the surface of water strider leg is composed of setae array, which is oriented toward the tip of the leg with ∼27° tilt angle. (C and D) SEM images of water strider leg reveal that the setae are all conical with an apex angle of ∼5°, in a periodicity of 5–10 μm between the neighboring setae. (E and F) Magnified SEM images show that the setae are composite of nanogrooves in longitudinal or quasi-helix orientation.

Fig. 1 D–G and Movie S1 show what happens when a Gerris leg is placed in a mist. Micrometric drops condense at the setae surface, and it is first observed that these droplets slowly move away from the seta tip and sink inside the texture (Fig. 1D). This motion stops when the liquid reaches proximal setae, and drops keep on growing owing to condensation and coalescence (Fig. 1E)––the usual growth events in a breath (Fig. 1). Drops above a critical size push away the setae they contact, as revealed by their shape: they slightly elongate in the direction parallel to the setae, until they get suddenly expelled out of the hairs (Fig. 1F). Once at the top of the setae, drops still grow but coalescence is biased, and water moves along a preferred direction, which also contributes to remove it from the leg surface (Fig. 1G).

This sophisticated mechanism of drop expulsion can be divided into three steps, as proposed in Fig. 1. In step 1, droplets self-propel along the surface of single conical hairs (Movie S2) and then grow. In step 2, the growth deforms the setae array, which leads to expulsion (Movie S3). In step 3, coalescence at the leg surface results in a rapid anisotropic motion of the merged drops along the surface or away from it (Movies S4 and S5). Gerris live at the water surface in a highly humid environment, and they must repel water not only at a large scale to keep floating, but also at the scale of microdrops forming from the surrounding atmosphere, in particular on the side of the leg directly facing water. By exploiting the unique design of their legs, water striders seem to be able to remove dew at a femtoliter scale, a key condition for avoiding a gradual penetration of water in the leg textures, which would lead to failure of the superhydrophobicity needed by insects to stay at the water surface.

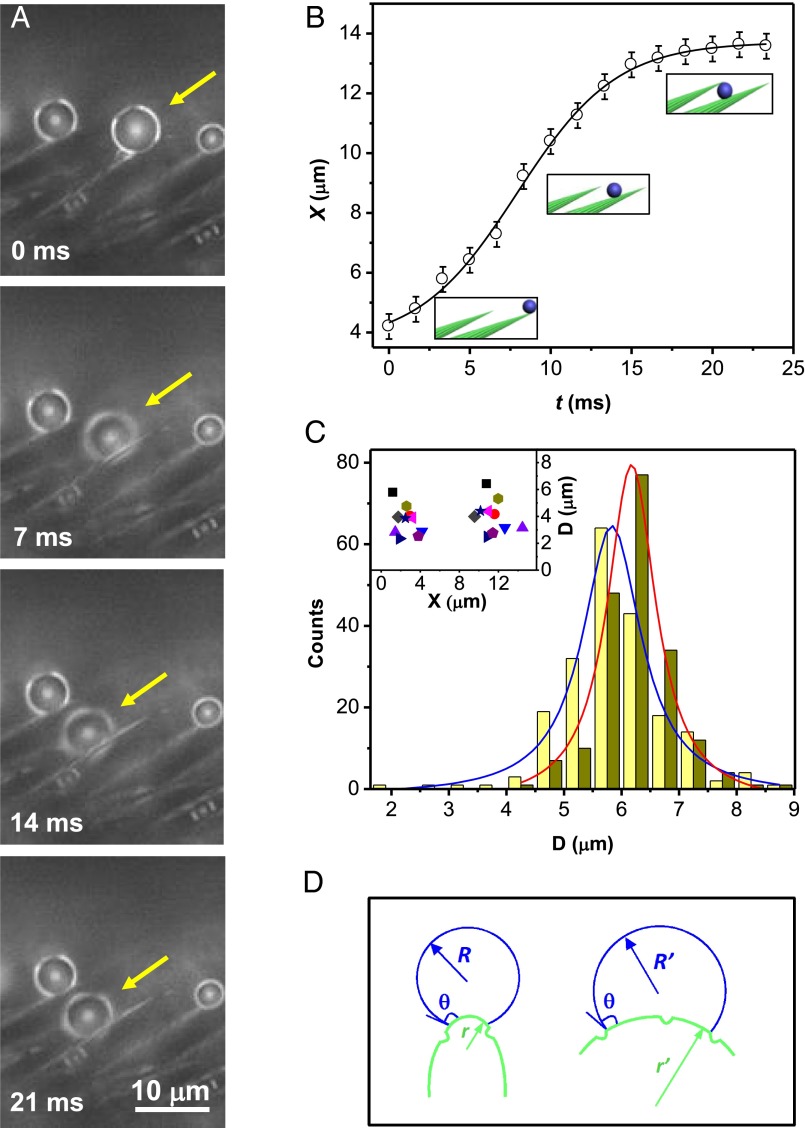
To follow the trajectory X(t) of drops and the associated dynamical phenomena during condensation, we used high-speed imaging (films shot at 1,000 frames per second) mounted on a microscope. Small water droplets (below 3 fL) from the mist randomly condense on the setae and start moving along them, from tip to base (step 1, Fig. 2A). The velocity in this phase can reach about 1 mm/s before decreasing: The drop stopped after it traveled by typically 10 μm, a distance comparable yet smaller than the setae length (Fig. 2B). We statistically analyzed the size distribution of 200 such mobile droplets (Fig. 2C), and found diameters ranging from 2 to 9 μm, with an average size of 5.7 ± 0.9 μm at the beginning of motion, and 6.2 ± 0.9 μm at the end (blue and red distributions in Fig. 2C, respectively). These drops generally do not coalesce with each other, but just move individually along the seta, which explains why both distributions nearly overlap. Fig. 2C also shows that droplets need to be large enough (around 3–4 μm) to move––at smaller scales, pinning forces can overcome the force driving the motion; hence continuous condensation triggers movement. Another way of capturing these different facts consists of comparing the position X and diameter D of 10 droplets between beginning and end of motion (Fig. 2C, Inset, where each symbol corresponds to a drop). This plot confirms that the volume does not change significantly during motion and that droplets stop at a well-defined position, typically 10–15 μm away from the seta tip. This first dynamical step seems to contradict dew expulsion, and it may be exploited by creatures to sweep tiny drops or contaminants along the setae.

Fig. 2.

Droplets self-propelling along single conical setae (step 1). (A) As a strider leg is exposed to a fog, tiny droplets first condense at the tip of setae, before spontaneously moving toward their base. We follow the drop pointed out by a yellow arrow, and observe that it self-propels and sinks within the texture by 10 μm in less than 20 ms. Corresponding movie is Movie S2. (B) Typical plot of droplet position X as a function of time t: Water travels by a distance comparable to the seta length at a roughly constant velocity (around 0.5 mm/s) before stopping. Origin of X is chosen at the seta tip. (C) Statistics of 200 self-propelling droplets, of diameter ranging from 2 to 9 μm. Their average sizes at beginning and end of motion are 5.7 ± 0.9 μm (in blue) and 6.2 ± 0.9 μm (in red), respectively. (Inset) The diameter and position of 10 droplets (each one designated by a symbol) before and after moving confirm that drops generally do not coalesce with others, but just move individually along setae and stop at a well-defined position, typically 10–15 μm away from the seta tip. (D) For a droplet at the surface of a single seta, the conical geometry provides an asymmetric surface energy landscape, which generates a motion (see text).

Self-propulsion is remarkable at this scale, where surface effects and specifically contact angle hysteresis could impede motion. Three facts facilitate mobility. (i) Setae are hydrophobic, so that drops are naturally ejected on one side of the cone (as seen in Fig. 2A), instead of being axisymmetric (11), which minimizes the solid–liquid contact and the associated pinning. (ii) Substructures (nanogrooves; Fig. 1C, Inset) should amplify the hydrophobicity of setae, and contribute to drop mobility. (iii) The cone geometry provides curvature gradients (Fig. 2D and Fig. S2), and thus an asymmetric surface energy landscape, which permits a motion (12–15). A simple argument allows us to understand the origin of the driving force. Let us consider a conical substrate with a Young contact angle close to 90° (a typical hydrophobicity). In such a case, a comparison between surface energies as drops move along the cone reduces to liquid–vapor energies, because solid–liquid and solid–vapor interfaces have common surface tensions. A drop on a seta tip, that is, on a substrate of radius r much smaller than its own radius R, has a surface energy E ∼ 4πR²γ, denoting γ as the surface tension of water. When water moves to regions of larger and larger r (Fig. 2D), its shape becomes closer and closer to a hemisphere of radius R′ = 2^1/3R, which it becomes on a substrate of infinite radius. Then its surface energy simply writes E′ ∼ 2πR′²γ ∼ 2^5/3πR²γ, that is, an energy smaller than E by 2^−1/3, i.e., about 25%: Drops in this case are drawn by surface tension. The driving force should be smaller if the apparent angle θ is larger than 90°, owing to the presence of nanogrooves: then, the liquid far from the tip forms a spherical cap of radius $R^{\prime }=R{\left(1/2-\left(3\cos \mathit{\theta }/4\right)+\left({\cos }^3\mathit{\theta }/4\right)\right)}^{-\left(1/3\right)}$ sitting on a cylinder (12, 16–18), of corresponding surface energy E′:

$$E^{\prime }=E\left[1-\frac{{\left(1+\text{cos}\mathit{\theta }\right)}^2}{4R^{\prime 2}}\frac{1}{H^2}\right],$$ [1]

denoting H as the mean curvature of the solid. Curvature decreases as water goes from the tip to the seta base, and so does the energy E′ (Figs. S3–S5).

Fig. S2.

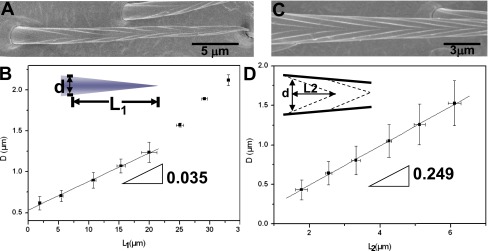
Conical structure of setae and their nanogrooves. (A and B) The diameters of setae (D) in different positions away from the tip (L₁) present conical structures with conicity ($D/2L$) of 0.035. (C and D) The diameters of V-shaped nanogrooves (D) in different positions away from the tip of V-shape (L₂) present similar conical structures with conicity ($D/2L$) of 0.249.

Fig. S3.

Drop motion on a single conical seta. When placed in fog, very tiny droplets (identified by numbers 1 and 2) could be condensed on the tip of seta (0 s). As water condensation continues, droplet 1 spontaneously rolled on a single conical seta from the tip to the base (0.163 s), and coalesced with droplet 2 to form larger water drops (droplet 1 + 2, 0.199 s). Similarly, this new larger drop could also move directionally to the base of setae (from 0.316 to 0.444 s), showing a self-propelled motion behavior.

Fig. S5.

Drop motion on a superhydrophobic conical copper wire. For a superhydrophobic conical copper wire, drops could move toward the base of the wire when placed in mist.

Fig. S4.

Drop motion on a hydrophobic conical copper wire. For a hydrophobic conical copper wire, condensed drops could coalesce anisotropically toward the base of the wire when placed in mist.

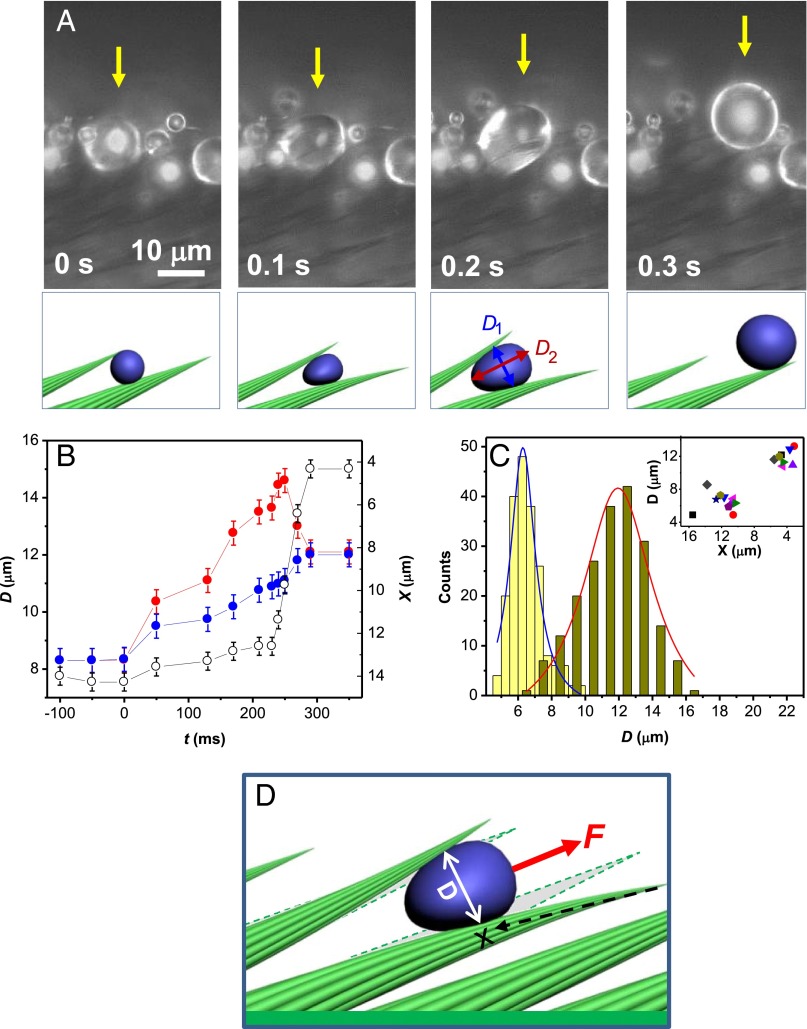
Once drops stop within the setae, they grow owing to further condensation and coalescence with neighbors (Fig. 1E). We show in Fig. 3A the sudden dynamical event following this stage, corresponding to step 2 in Fig. 1F. Water moves (or jumps) in the direction opposite to the one in step 1, until its complete expulsion from the array of setae. Big droplets (about 1 pL) eventually sit at the tips of setae, from which they can be easily removed. Drop anisotropy in step 2 first increases, as guessed in Fig. 3A and observed in Fig. 3B, where we plot transverse and longitudinal diameters D₁ and D₂ as a function of time (blue and red data). The anisotropy factor D₂/D₁ increases from 1 to about 1.3, while drop position X remains fixed, until the anisotropy factor relaxes to 1, which corresponds to the jump (fast increase of X). The isotropic drop observed after expulsion always has a diameter larger than its transverse diameter before expulsion, because averaging on 200 drops shows an increase from ∼6.5 μm to ∼12.5 μm, as reported in Fig. 3C with blue and red distributions, respectively. This can also be seen in Fig. 3C, Inset, where 10 individual drop sizes are followed as they are expelled out of the array of setae. All these features can be understood by the ability of hairs to deform as a trapped drop grows. Drop elongation is a signature of this process, and we indeed observe that the typical diameter of expelled drops compares with the average distance between setae: Elastic deformation provides the energy necessary to expel the liquid out of the texture (Fig. 3D).

Fig. 3.

Expulsion of water out of the setae (step 2). (A) As condensation proceeds, drops inside the texture grow and deform the array of setae, so that the arising elastic force can expel them out of the hairs. Here, we follow the drop pointed out by a yellow arrow, and note that it is deformed when it jumps. Corresponding movie is Movie S3. (B) Position X (empty symbols) and principal diameters D₁ (in blue) and D₂ (in red, D₁ < D₂) of the drop, as a function of time t. Just before its expulsion, the drop becomes strongly anisotropic. Origin of time is defined at the onset of anisotropy. (C) Diameter distribution of 200 drops: The drop after expulsion (in red) is always larger than before expulsion (in blue). Diameter and position changes of 10 droplets (each one designated by a symbol) confirm the drop deformation and its expulsion in step 2 (C, Inset). (D) As a growing drop gets larger than the distance between hairs, elastic energy arising from the setae deformation can generate a force F able to expel the drop out of the texture.

As a condensing drop gets larger than the distance between setae (Fig. 3D), setae get distorted. The bending energy E of a single seta scales as KC², denoting K and C as the bending constant and the seta curvature, respectively (19). For a hair of Young's modulus Y and typical radius r, K scales as Yr⁴L. Because of the high stiffness of setae, we expect the deformation to be small (ε << L) and the curvature to vary as ε/X², where X is now the distance between the bottom of the cone and the drop. Hence we get E ∼ Yr⁴Lε²/X⁴. Simply assuming that drops are larger than the space between setae, we can write ε ∼ D and deduce that the force F expelling the drop out of the grass scales as Yr⁴LD²/X ⁵. The main force opposing drop ejection is the sticking force due to contact angle hysteresis Δθ, because the weight is negligible at such scale. The corresponding resisting force is F_r ∼ γD(cosθ_r – cosθ_a), where advancing and receding angles are written θ_a = θ + Δθ/2 and θ_r = θ − Δθ/2, respectively (20). For Δθ << θ, we get F_r ∼ γDsinθΔθ. Water can be expelled from the setae provided that F(X = L) is larger than F_r, which yields an ejection criterion based on drop diameter:

$$D\mathrm{>}{D}_c=\frac{\mathit{\gamma }{L}^4}{Y{r}^4}\sin \mathit{\theta }\hspace{0.17em}\mathrm{\Delta }\mathit{\theta }\mathit{.}$$ [2]

This criterion is highly sensitive to the geometry of setae: it varies as the fourth power of their aspect ratio L/r, which shows that flexible hairs can accurately “select” drops of a given size. This is especially true in more general cases where L and r are tuned independently, allowing in principle the selection of droplet size in a wide range. Here (with γ ∼ 72 mN/m, L ∼ 40 μm, r ∼ 1 μm, and Y ∼ 10⁸ J/m³), we expect from Eq. 2 a critical diameter D_c on the order of 10 μm, comparable to our observations.

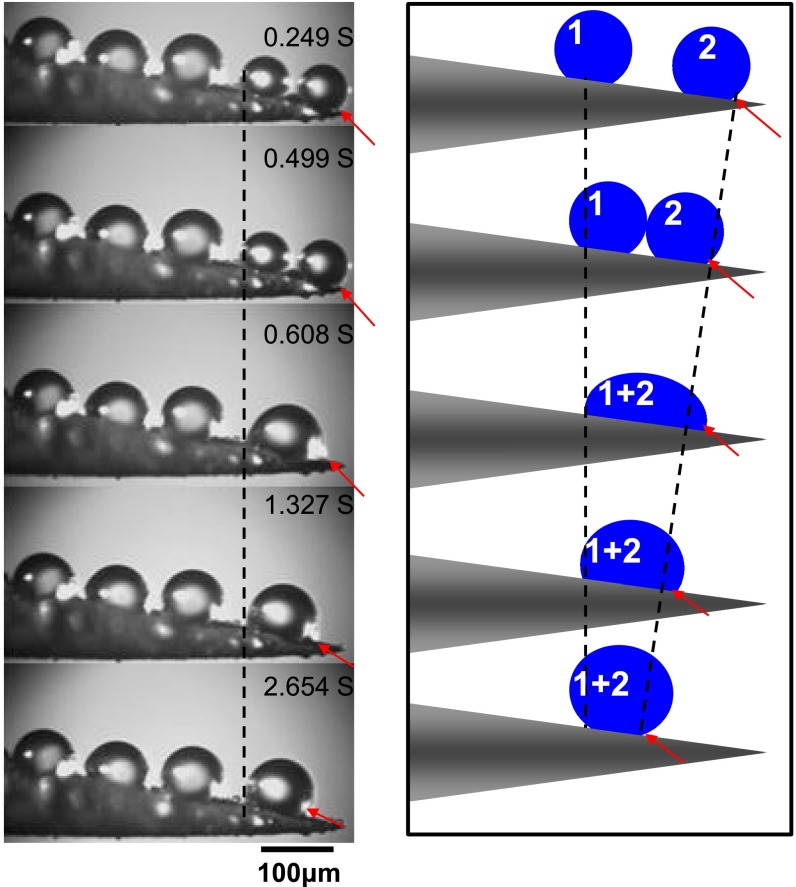
Once expelled, drops can be evacuated by leg vibrations, or by directly contacting the water surface. However, note that a third regime of propulsion along the texture is observed during condensation, which also participates in the evacuation of dew (step 3 in Fig. 1). When droplets (at a picoliter or nanoliter scale) merge at the leg surface, the center of gravity of the resulting drop is found in Fig. 4A to be shifted, in the direction of “easy” motion––that is, in the direction favored by the anisotropic contact angle hysteresis at the setae surface. Tilted setae form a kind of ratchet that promotes directional movement in the direction of smaller adhesion (21–24) (Fig. S6), when activated by vibrations or coalescence. The amplitude of the jump is one drop size, as expected for an anisotropic coalescence. Drops sometimes can even take off and jump out of the leg (Fig. 4B), a direct expulsion event such as encountered on cicada wings or lotus leaves (8, 25). Contrasting with the latter examples, water here takes off with an oblique angle, a consequence of anisotropic adhesion: One droplet remains pinned while the other one moves to it, which yields horizontal momentum as drops merge and thus explains the oblique trajectory at takeoff.

Fig. 4.

Directional removal of drop on the anistropic setae array (step 3). (A and B) Coalescence at the leg surface results in a rapid directional motion of merged drops along the surface (A) or away from it (B). On the ratchet made by tilted setae, liquid–solid adhesion is anisotropic, which drives the liquid along the inclined cones. Droplets involved in coalescence are pointed out by yellow arrows. Corresponding movies are Movies S4 and S5.

Fig. S6.

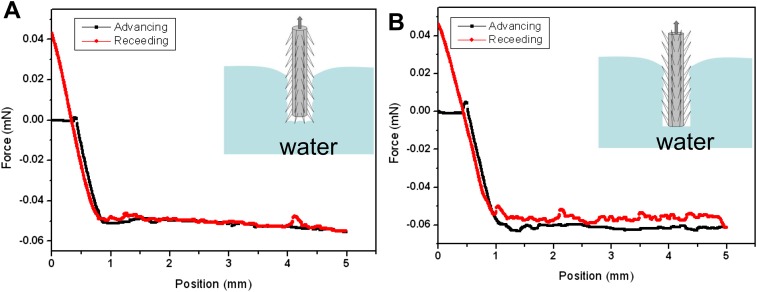
Anisotropic wetting behavior of water strider leg: force curves for water strider's leg in both (A) against-scale (AS) and (B) with-scale (WS) orientations show different wetting behavior influenced by the oriented setae contributions.

The sophisticated textures of the legs of G. remigis provide a unique ensemble of functions. Robust superhydrophobicity is first necessary to deform the water surface in such a way that creatures’ weight can be opposed by Laplace pressure. The anisotropy of textures is also exploited to have gliding and resisting directions, allowing the strider to control its movements (23, 26). Here we showed that the texture also provides expulsion of condensed droplets, which prevents a major source of risk for the creature, whose hydrophobicity would reverse (in a fatal way) if setae were impregnated by water as humid air condenses. Compared with the few cases of natural antifogging materials reported in the literature, the observed behavior is original: Paradoxically, the droplets first migrate inside the texture, which might help to capture microdroplets condensed there, and possibly contaminants; this sweeping step is followed by a sudden expulsion of the liquid out of the hairs, found to be caused by elastic deformations in the network of setae around the growing water drop. Adding textures to a solid surface can provide multifunctions, such as for cicada wings, where both antireflective and water-repellent properties are generated at once (8). We have here a remarkable example where the conjunction of hydrophobicity, geometry, and flexibility provides both water repellency at a large scale (the pond) and at a very small scale (the dew). We anticipate that the self-removal behavior of droplets on Gerris legs will inspire the design of novel robust superhydrophobic materials for many practical applications, such as self-cleaning surfaces, antidew materials, dropwise condensers, and microfluidic devices.

Methods

Water striders (G. remigis) were captured in Beijing, China. The optical images of a water strider leg were recorded by a digital video camera (WV-CP280/CH, Panasonic). Microstructures were observed by a field-emission scanning electron microscope (JEOL, JSM-6700F) at an accelerating voltage of 3.0 KV. Micro-XCT measurements were conducted in air, using a 3D MicroXCT-200 (Xradia Inc.). The source setting of the voltage and current was 90 kV and 88 μA, respectively.

In the observation of self-removal of condensed water, one leg of water strider was fixed in a chamber with a humidity ranging between 90% and 99%, as provided by an ultrasonic humidifier using Milli-Q water at room temperature. The behavior of condensed water drops was recorded by high-speed imaging (video camera Phantom V9.1, films shot at 1,000 frames per second) mounted on a microscope (BX51, Olympus Co., Ltd.).