What the fly’s nose tells the fly’s brain

Significance

This work is significant for three reasons. First, a new way the brain represents information is identified, one in which the information present in a large population of neurons can be gotten from a small subset of any neurons rather that from a subset of certain specific neurons. Second, the nature of the combinatorial code used to specify odor identity is identified, and this same type of code may be used in other contexts. Third, the way fly olfaction works can potentially provide a model for understanding the function of important vertebrate brain regions that appear to share the same neural circuit architecture.

Abstract

The fly olfactory system has a three-layer architecture: The fly’s olfactory receptor neurons send odor information to the first layer (the encoder) where this information is formatted as combinatorial odor code, one which is maximally informative, with the most informative neurons firing fastest. This first layer then sends the encoded odor information to the second layer (decoder), which consists of about 2,000 neurons that receive the odor information and “break” the code. For each odor, the amplitude of the synaptic odor input to the 2,000 second-layer neurons is approximately normally distributed across the population, which means that only a very small fraction of neurons receive a large input. Each odor, however, activates its own population of large-input neurons and so a small subset of the 2,000 neurons serves as a unique tag for the odor. Strong inhibition prevents most of the second-stage neurons from firing spikes, and therefore spikes from only the small population of large-input neurons is relayed to the third stage. This selected population provides the third stage (the user) with an odor label that can be used to direct behavior based on what odor is present.

A hallmark of at least three major brain structures found in essentially all vertebrates—cerebellum, hippocampus, and olfactory system—is an architecture with three stages of information processing (Fig. 1). In the first stage (the encoder), information arriving from other brain areas is assembled into a combinatorial code and relayed, with a massive expansion of neuron number, to the second stage. This code is “broken” by the second stage (the decoder), and passed to the third stage, where the desired pieces of decoded information are selected for use in other brain regions.

Fig. 1.

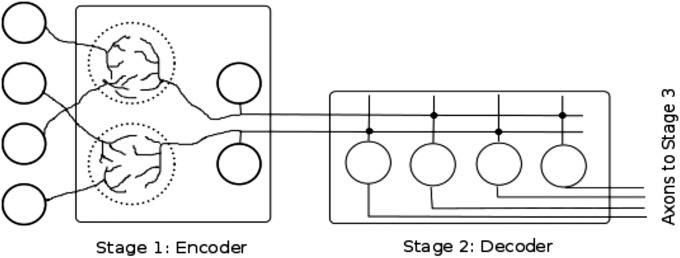
Schematic representation of the Marr motif. Four sensory neurons at the left (circles represent their cell bodies) send their axons to two regions of neuropil (dotted circles) in the first (encoder) stage of the three-stage circuit. Additional circuitry (not illustrated) produces interactions between the two neuropil regions. Dendrites of the two stage 1 projection neurons (cell bodies of precerebellar neurons are the circles) collect and format the sensory information as a combinatorial code. This coded information is then sent over the precerebellar neuron axons to stage 2 (decoder). Synaptic connections (dark dots) are made on the dendrites of four stage 2 neurons (granule cell bodies represented by four circles), and the output, the broken code, is sent at the right of the diagram to stage 3 (not represented). Additional circuitry responsible for breaking the combinatorial code in the second stage is not shown.

The first proposal for the operation of this three-stage processing architecture was made by Marr (1), over four decades ago, to explain the function of the cerebellum, and I shall refer to the first two (encoder/decoder) stages of the architecture as the Marr motif. According to Marr, the encoder stage provides the pattern (neuronal activity compiled in precerebellar nuclei) that is relayed to cerebellar granule cells (the decoder stage). In granule cells, the pattern provided by the precerebellar neurons is separated by spreading the information over many more neurons (there are many more granule cells than precerebellar neurons), and by quieting most of the granule cells with strong inhibition from Golgi inhibitory neurons. These inhibitory neurons collect the output of many granule cells and feed it back to them. Finally, in the third stage (Purkinje cells), some parts of the separated pattern relayed by the granule cells are selected for labeling by concurrent climbing fiber activity that adjusts the strength of synapses conveying the chosen signals to Purkinje cells. Whenever labeled signals happened to recur, the modified synapses cause selected Purkinje cells change their firing rates and provide an output based on the tagged signals.

Although Marr’s proposal has been enormously influential, we still do not understand the combinatorial code (Marr’s pattern) generated by the precerebellar neurons, nor do we know how it is decoded by the granule cells (Marr’s pattern separation). What appears to be this same three-stage architecture is used by Drosophila for the first three levels of its olfactory system (2), but the fly system is much smaller, simpler, and more completely understood than any vertebrate version. Here I exploit the simplicity and extensive knowledge about the fly olfactory system to learn the properties of the combinatorial odor code, and how it is decoded. My hope is that what is learned from the fly will help us understand the similar three-level architecture in vertebrates.

Results

I will consider (see Fig. 1) only the first two stages (the Marr motif) of the fly’s three-stage architecture. The first stage is the antennal lobe (corresponding to the encoder stage precerebellar nuclei) and the second stage consists of Kenyon cells of the mushroom body (corresponding to the decoder stage cerebellar granule cells). The basic outline of the process is quite simple: the antennal lobe collects information from olfactory receptor neurons and reformats this information into a combinatorial code, which is sent to the mushroom body. The mushroom body then converts the combinatorially coded odor into a unique output that can be used by the fly to identify the odor.

My discussion is divided into five sections. In the first section, I present information about the fly’s olfactory system that is needed in the later sections, and in the second section I describe how olfactory information is represented in the main cell type of the mushroom body, the Kenyon cells. The third section identifies properties of the combinatorial code constructed in the antennal lobe, and these properties are used in the fourth section to explain how a unique Kenyon cell output is generated for each odor. In the last section I identify some idealizations made in the earlier sections and explain the consequences of departures from these idealizations.

Structure and Function of the Fly Olfactory System.

Information about the fly’s odor environment is delivered to the first stage of the three-stage olfactory system architecture, the antennal lobe, by axons of olfactory receptor neurons (ORNs) (3). Each of these ORNs expresses just one of the adult fly’s ∼50 odorant receptors (the actual best current estimate is 54; ref. 4), and all ORNs expressing that receptor converge on a structure in the antennal lobe called a glomerulus. Each of the about 50 glomeruli is a spherical neuropil structure with three main components: (i) ORN axon terminals, (ii) dendrites of several projection neurons that send modified odor information from ORN terminals to Kenyon cells in the mushroom body, and (iii) circuitry for modifying the ORN input to give the odor code the right properties. These modifications include lateral inhibition from other glomeruli onto ORN axon terminals to adjust the firing rate of projection neurons so they are mostly independent of odor concentration (a gain control mechanism; refs. 5–7, 9, 10), and other mechanisms to spread information about the odor environment more evenly over all of the glomeruli (3, 6, 7, 9, 10). Projection neurons have a background firing rate of about 5 Hz. The projection neurons from a glomerulus do not increase their rate much for most odors, but a lot (>300 Hz) for some odors (8). Generally, different odors produce the highest projection neuron firing rates for different glomeruli but, of course, the same odor always produces the same average response in the same glomeruli. Projection neurons in the antennal lobe send their output to two major brain regions, the lateral horn (11, 12) (where evolution has designed circuits to deal with specific odors) and the mushroom body (where the fly can learn to recognize arbitrary odors). In the following, I will not consider the lateral horn, but will focus on the mushroom body, which contains the second stage of the Marr motif.

The mushroom body (13, 14) is a large (for the fly brain) structure with a neuropil calyx that contains the dendrites of many intrinsic neurons, the Kenyon cells (the Kenyon cell bodies are grouped just next to the calyx), and with two elongated lobes, one vertical and one horizontal, to which Kenyon cell axons project. The Kenyon cells and their associated circuitry constitute the second stage of the Marr motif (corresponding to the cerebellar granule cells), and the lobes contain the third stage (corresponding to the cerebellar Purkinje cells) of the three-stage architecture. This third stage will not be considered in most of the following discussion.

All axon terminals of antennal lobe projection neurons are found in special structures, called microglomeruli (15), in the mushroom body calyx. Each microglomerulus contains three main components: (i) a single large axon terminal from an antennal lobe projection neuron, (ii) dendritic structures, called claws, from about 10 Kenyon cells, each of which is postsynaptic to the single projection neuron terminal, and (iii) GABAergic terminals from a single anterior paired lateral (APL) neuron that also form synapses on Kenyon cell claws. Each Kenyon cell has about six claws (16), so one Kenyon cell collects information from only about 6 of the 50 glomeruli. The single APL neuron (only one on each side of the brain) sends its dendrites into the mushroom body lobes to collect the output from all of the Kenyon cell axons, and this APL neuron inhibits all Kenyon cells by sending its axons to the calycal microglomeruli to terminate on Kenyon cell dendrites (18–20).

Three experimental observations will be important in the following discussion. First, the 50 glomeruli send odor information to about 2,000 Kenyon cells, so there is a 40-fold expansion from antennal lobe to mushroom body. Second, each Kenyon cell collects odor information from only about 10% of the glomeruli, and it takes this sample randomly (16, 17). Third, most odors do not produce synaptic currents in most Kenyon cells, but even when Kenyon cells do receive synaptic input on presentation of an odor, only about 5% of those Kenyon cells fire spikes reliably (21); this sparsity of firing is the result of the winner-take-all circuit formed by the inhibitory APL neuron (18).

A Distributed Representation of Olfactory Information in the Mushroom Body.

In this section I will argue that the mushroom body uses a distributed representation of odor information rather than the more familiar localized representation. I make the distinction between these two ways information is represented by comparing the mammalian visual cortex (V1) with the mushroom body. V1 has a retinotopic map of the visual world but, on a finer scale, this visual area has a pinwheel organization where neurons with the same orientation preference are found along the spokes of the pinwheel, and neurons with the same receptive field size (spatial frequency) are arranged in concentric rings around the pinwheel center (note that V1 neurons are jointly selective for orientation and spatial frequency) (22). This means that all of the information about one tiny patch of the visual world can be found in the neurons making up one pinwheel. I have just described a localized representation: a specific group of cells can give you a specific part of all information available.

In contrast, I will argue that, for the mushroom body, one can get all of the information available about the fly’s odor environment from a specific number of any Kenyon cells, no matter which ones are chosen. In this sense, the information is distributed because the number of neurons, not their identity, is what matters.

I pointed out above that each Kenyon cell receives input from six glomeruli selected at random (16). To see why this gives a distributed representation of the odor information provided by the 50 glomeruli, I need to formalize this statement to make a connection with a new field of mathematics and computer science called compressed sensing (23).

We start with an empty list s with places for 50 numbers. Call this list s the signal, and fill it with the 50 projection neuron firing rates generated, at some particular time, by all of the glomeruli. Now create an empty table $\left(\text{call}\hspace{0.17em}\text{it}\hspace{0.17em}\mathbf{R}\right)$ that has 2,000 rows (one for each Kenyon cell) and 50 columns (one for each glomerulus). For the first Kenyon cell, fill the first row of the table with 1s and 0s, and place a 1 wherever the first Kenyon cell receives synaptic input from the corresponding glomerulus and the number 0 if it does not. The first row will, then, contain all zeros except at six random locations where 1s are present (because the Kenyon cells receive olfactory information collected randomly by six claws). Repeat the same procedure for all 2,000 Kenyon cells so that the table $\mathbf{R}$ has six randomly placed ones on each row (a row for each Kenyon cell) with the rest of the entries = 0. This table $\mathbf{R}$ is a random matrix (its entries are selected at random) and $\mathbf{R}$ is called the sensing matrix or connection matrix.

Now multiply the signal s by the sensing matrix $\mathbf{R}$, and call the result r. This r is a 2,000-long list of olfactory inputs (measured as spikes per second) received by each Kenyon cell:

$$\mathbf{r}=\mathbf{R}\mathbf{s}.$$

The matrix multiplication is carried out by multiplying each entry in the first row by the corresponding entry in the signal s (first by first, second by second, etc.) and then adding up all of the products and putting the sum in the first entry of $\mathbf{r}$. Repeat for all rows (all Kenyon cells), and the list r will contain the total number of spikes per second that each Kenyon cells is receiving from the antennal lobe glomeruli.

What I just described is called a random projection, and if one looks at any 50 of the 2,000 entries in the Kenyon cell synaptic input list r, one can always get back the original signal s. That is, all of the information the fly has about its odor environment is available to any 50/2,000 Kenyon cells.

To actually get back olfactory information in s (the projection neuron firing rate produced in each glomerulus) from r (the total olfactory input into each Kenyon cell), pick any 50 Kenyon cells (50 rows of R) and extract their inputs from the list r and their corresponding 50 rows from the large matrix R. This procedure gives a new shorter 50-long list $\tilde{\mathbf{r}}$ and a new 50 × 50 square matrix $\tilde{\mathbf{R}}$. This matrix $\tilde{\mathbf{R}}$ has an inverse ${\tilde{\mathbf{R}}}^{-1}$ because $\tilde{\mathbf{R}}$ is a random matrix, and such matrices are known to (almost) always have an inverse. All of the olfactory information in any 50/2,000 entries in $\tilde{\mathbf{r}}$, then, can be recovered with

$$\mathbf{s}={\tilde{\mathbf{R}}}^{\mathbf{-1}}\tilde{\mathbf{r}},$$

because there are 50 simultaneous linear equations (from $\tilde{\mathbf{R}}$ and $\tilde{\mathbf{r}}$) and 50 unknowns (in the list $\mathbf{s}$). This means that the synaptic input to of any 50 Kenyon cells always contains all of the available odor information in the antennal lobe.

Actually, things are somewhat better than I just described. The main result from the new field of compressed sensing is that, depending on how much redundancy there is in the signal s, all of the information about the odor represented by r is, in fact, present in fewer, generally many fewer, than 50 entries in r (24). Based on experience from many types of signals, one would expect that any one or two dozen entries of the 2,000-long list r of Kenyon cell inputs would show everything the fly can know about the odor present.

The reason for using the random projection to give a 40-fold expansion (from 50 glomeruli to 2,000 Kenyon cells) is to provide many different representations of the odor for the Kenyon cells to pick between to find an output that best characterizes the odor and is very likely to be different from the Kenyon cell output for almost any other odor. If only 20 of the 2,000 numbers in r are needed to define the odor, the expansion is 100-fold rather than 40-fold, and the Kenyon cells are given more representations, and thus more chances to find the representation that best characterizes the odor. The collection of Kenyon cells that reliably fire in response to a particular odor constitutes the neural ‘tag’ associated with that odor. How the Kenyon cells choose an odor’s tag is the subject of the following two sections.

We know that the odor information in the antennal lobe is indeed mapped to the Kenyon cells by a random projection (16), but is it true, as just predicted, that the antennal lobe response to an odor can be recovered from any small sample of Kenyon cell activity? Campbell et al. (25) showed that behavioral performance to odor presentations could be predicted from 25 randomly selected Kenyon cells out of a larger population of neurons whose activity in response to odors had been measured using calcium imaging. Thus, as predicted, the odor information is distributed over a large number of neurons, and this information can be recovered from a randomly selected small subset of the entire population.

Properties of the Combinatorial Odor Code.

We know that the Kenyon cells decode the combinatorial odor code—that is, they provide the tag associated with any odor—because flies have been shown to use the output of Kenyon cells to learn odors that have been paired with reward or punishment (26). The previous section demonstrated that odors are represented in a distributed way over the population of Kenyon cells, but to see how these cells provide a (close to) unique output for each odor, we need to know properties of the combinatorial code produced by the antennal lobe. That is the task undertaken in this section.

The purpose of the odor code generated by the antennal lobe is to let the fly identify as many odors as possible. The combinatorial odor code, then, that best accomplishes this should provide the greatest survival value for the fly. In other words, the code should be the most informative one. According to information theory (27), the best combinatorial odor code should be the one with maximum entropy. Entropy is precisely defined and roughly has to do with how many distinct odors can be coded for by the antennal lobe. Maximum entropy codes are known to have two properties used in the following paragraphs.

A single glomerulus and its projection neurons constitute an information channel, and I now focus on such a channel. We know that, if an odor is selected at random, our glomerulus usually will not respond much, but for some odors it will respond well, and sometimes, for odors that bind best to its odorant receptor protein, the odor response for that glomerulus will be maximal. For the kth glomerulus, then, the probability density $p_k\left(r\right)$ that specifies the firing rate r should be in a class of well-known functions that are maximum entropy (first property of a maximum entropy code; ref. 27). We know that the gain control mechanism in the antennal lobe sets the average firing rate across all glomeruli (6, 7, 9). A likely probability density function, then, would be an exponential $p_k\left(r\right)=\alpha e^{-\alpha r}$ because this function, according to information theory, maximizes the entropy if the mean firing rate averaged over many different odors (here $1/\alpha$) is constrained to have some particular value (27). We do not know in advance, however, if there are other constraints on $p_k\left(r\right)$. For example, if the variance as well as the mean were constrained, the probability density function with maximum entropy would be Gaussian.

The total entropy of the combinatorial code is the sum of the contributions from each of the 50 glomeruli (entropy is additive) and, according to information theory, this total entropy is maximized if all of the channels have the same probability density function (second property of a maximum entropy code; ref. 27). I therefore drop the subscript k that identifies the glomerulus, and call the common maximum entropy density function $p\left(r\right)$.

Notice that the fact that all glomeruli have odor responses that obey the same probability density function does not mean that all glomeruli have the same rate r for a randomly selected odor. On the contrary, each glomerulus usually responds differently for every odor and always the same way for the same odor. The function $p\left(r\right)$ just says what fraction of the odors cause what rate, and nothing about what that rate is for any given glomerulus and odor.

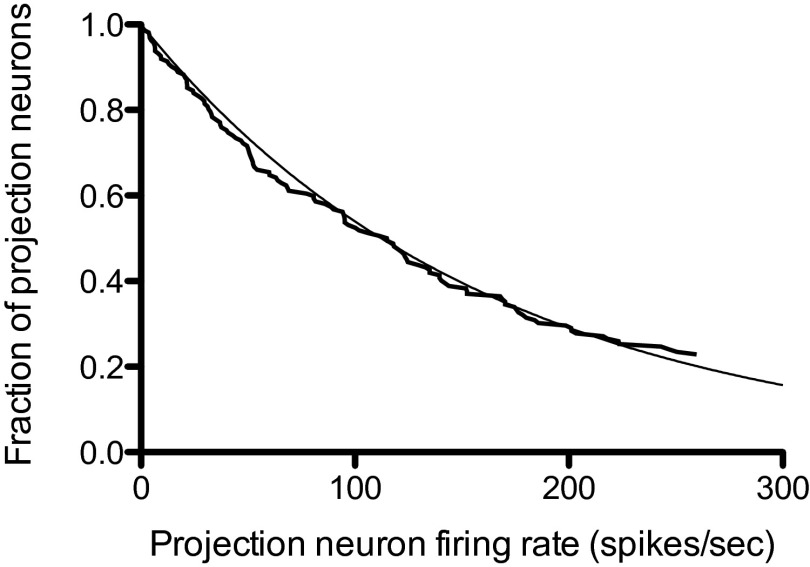
The density function $p\left(r\right)$ does not depend explicitly on either the odor or the glomerulus identity, so a histogram of firing rates across all glomeruli and for a large number of odors should be an exponential (or some other maximum entropy function, depending on what is constrained). Measuring the firing rates associated with all glomeruli for a large number of odors would be prohibitively difficult, but Bhandawat et al. (8) have approximated this ideal experiment by recording the projection neuron firing rates in response to 18 odors for seven glomeruli. The histogram of the peak firing rates for this dataset [from figure S2 of Bhandawat et al. (8)] is presented here in Fig. 2 where the observed fraction of neurons with a firing rate greater than or equal to the rate on the abscissa is displayed, and an exponential distribution function is superimposed. Because the sample size of projection neurons is small (only 126), the sample does not include any of the fastest firing (and therefore lowest probability) neurons. This means that a single free parameter (the average firing rate across the entire projection neuron population) must be estimated; the value found was $1/\alpha =162$ spikes per second. I conclude that the combinatorial odor code is well approximated by a maximum entropy code with an exponential distribution function for the firing rates.

Fig. 2.

Observed probability distribution for fraction of neurons (ordinate) with projection neuron firing rates greater than or equal to the value given on the abscissa (spikes per second). Data from ref. 8. An exponential probability distribution with an average rate of 162 spikes per second is superimposed on the observed distribution.

Decoding the Maximum Entropy Code by Kenyon Cells.

With the properties of the combinatorial odor code just described, I can calculate what fraction of the Kenyon cell population is depolarized by how much in response to an odor chosen at random. My description is, however, only a probabilistic one, so I have no idea which glomeruli are responding to the odor and which Kenyon cells are depolarized by what amount. This calculation will be the first step in understanding how a (close to) unique response to an odor is generated.

My final result of this calculation is summarized here: The probability that a Kenyon cell has a particular depolarization v is approximately Gaussian, and this means that Kenyon cells with the largest depolarizations are rare. The second step in understanding the “trick” Kenyon cells use to tag odors is to recognize that an inhibitory feedback from the Kenyon cells onto themselves permits only the rare, most depolarized Kenyon cells to fire spikes in response to an odor. Two different, randomly selected odors, then, are unlikely to cause the same Kenyon cells to fire spikes, so the tags for two different odors rarely overlap.

Experiments have shown that the average Kenyon cell depolarization, produced by activation at a single claw, is $v=ar$, where v is the Kenyon cell depolarization (mV), r is the projection neuron firing rate (hertz) and $a=5.4\times {10}^{-3}$ mV/Hz [figure S6 in Gruntman and Turner (28)]. This relation between v and r can be used to eliminate r in favor of v in the probability density $p\left(r\right)$ to show that, for a single claw, a random odor will produce a Kenyon cell depolarization v with a probability

$$w_1\left(v\right)=\lambda e^{-\lambda v}.$$

Here, $w_1\left(v\right)$ is the probability density function for depolarization by synaptic activity at a single claw, and $\lambda =1/162a=0.87$ mV⁻¹ (remember that the mean firing rate of olfactory projection neurons is $\alpha =162$ Hz). For two claws, because the claws sample glomeruli at random, the probability density $w_2\left(v\right)$ is the convolution $w_1\left(v\right)\mathrm{\ast }{w}_1\left(v\right)$, which is

$$w_2\left(v\right)={\lambda }^2{\displaystyle \underset{0}{\overset{v}{\int }}du{e}^{-\lambda u}{e}^{-\lambda \left(v-u\right)}}$$

$$={\lambda }^{2}v{e}^{-\lambda v}.$$

This equation says that if a single claw gives a depolarization u, and the second claw gives a depolarization $\left(v-u\right)$ the probability density that a pair of claws gives a depolarization v is $e^{-\lambda u}{e}^{-\lambda \left(v-u\right)}$; to find the total probability, add this joint probability density up over all possible values of u. The function $w_2\left(v\right)$ is known as a γ density function with shape parameter 2. Because Kenyon cells have six claws, a random odor will depolarize a Kenyon cell by v mV with a probability density $w_6\left(v\right)$ that is a sixfold convolution of $w_1\left(v\right).$ The result of this convolution is a γ density function with shape parameter 6:

$$w_6\left(v\right)=\frac{{\lambda }^6}{5!}{v}^5{e}^{-\lambda v}.$$

For a γ density with a shape parameter j, the mean of v is $j/\lambda$ and the variance if $j/{\lambda }^2$. As the shape parameter j increases, the γ density approaches a Gaussian, and $w_6\left(v\right)$ is not too far off from a Gaussian. Thus, we can say that the probability density of a Kenyon cell depolarization caused by a randomly selected odor would be approximately normally distributed, a very simple result.

The expected fraction of the Kenyon cells with each possible depolarization v for a random odor is described by $w_6\left(v\right),$ and the winner-take-all circuit provided by the APL neuron (18) permits only a small fraction—about 5%—of the Kenyon cells (those most depolarized) to fire spikes (21, 29). Thus, the most depolarized Kenyon cells provide the spiking output, and constitute the odor’s tag. Because the antennal lobe projection neurons with the highest firing rates are rare, it is very unlikely that two randomly chosen odors will cause the same Kenyon cells to fire (the probability that a pair of odors happen to strongly depolarize the same Kenyon cell is the square of two small numbers, which is very small indeed). Statistically, then, a pair of odors will probably have nonoverlapping tags.

Often, one will be able to find a pair of odors that bind to odorant receptor proteins in very similar ways. This particular odor pair would activate very similar patterns of Kenyon cell firing and it would be difficult, or perhaps impossible, for the fly to discriminate between the two odors. If that particular odor pair needed to be discriminated, presumably evolution would have selected odorant receptors that would cause activation of different Kenyon cell pairs. Because the theory presented here is a statistical one, this sort of question cannot be addressed.

Consequences of Variability in Kenyon Cell Properties.

In the earlier sections, I assumed three things: (i) all Kenyon cells have six claws, (ii) all Kenyon cells are interchangeable and sample all glomeruli with the same probability, and (iii) all synapses made by projection neurons onto Kenyon cells have the same strength. In fact, the number of Kenyon cell claws ranges from around 1 to 11 (16), three classes of Kenyon cells with different properties and different targets for their axons are known (14, 30), and the synaptic strength varies considerably from one synapse to the next (28), whereas I used the mean value. Relaxing these simplifying assumptions changes my results quantitatively, but does not alter the main conclusions. Some consequences of the first two of these simplifications are described here and, in the Supporting Information, I discuss nonuniform sampling of glomeruli by different Kenyon cells classes, and address the assumption that all projection neurons make synapses with the same strength on Kenyon cells.

I noted earlier that streams of parallel Kenyon cell axons run vertically and horizontally to define the two lobes of the mushroom body. The vertical lobe is divided into two sublobes called α and ${\alpha }^{\prime }$, and the horizontal lobe is divided into three sublobes termed β, ${\beta }^{\prime }$, and γ. Furthermore, three distinct classes of Kenyon cells are recognized (13) based on the destination of their axons. These three classes are called $\alpha /\beta$, ${\alpha }^{\prime }/{\beta }^{\prime }$, and γ because those sublobes are their targets.

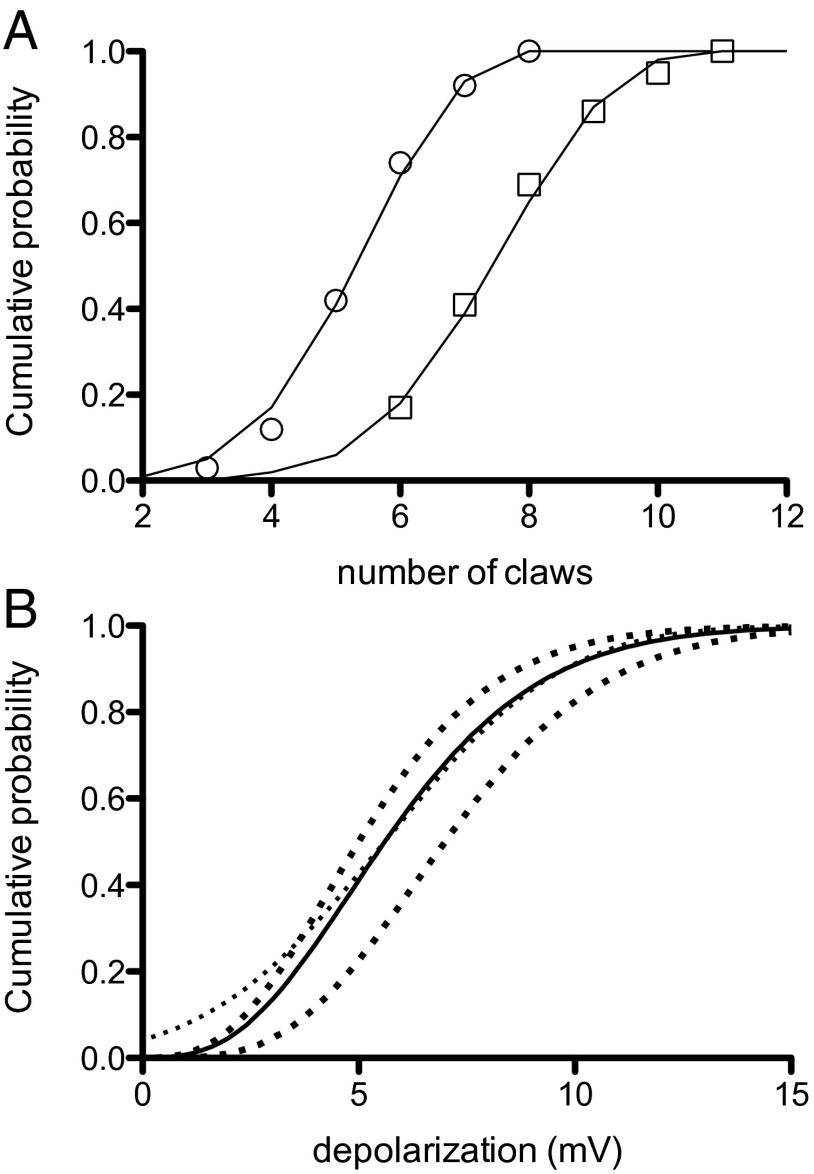
Caron et al. (16) published counts of the number of claws for all three Kenyon cell types. The average number of claws, 5.75 (range = 2–8), was not different between the $\alpha /\beta$ and ${\alpha }^{\prime }/{\beta }^{\prime }$ types (hereafter called the non-γ Kenyon cells), whereas the γ Kenyon cell type has an average of 7.8 claws (range = 5–11). The cumulative probability distributions for the Caron et al. (16) claw data (from their supplementary table 1) are plotted here in Fig. 3A where they are fitted to binomial distributions. Both distributions have a probability of 0.715 for adding a claw, and the non-γ Kenyon cells have at most 8 claws, whereas the γ Kenyon cells have a maximum of 11.

Fig. 3.

Probability distributions for Kenyon cell claw number and its effect on the depolarization of Kenyon cells by projection neurons. (A) Graphs for cumulative probability of claw number (non-γ Kenyon cell Left, γ type Right). The smooth curves are binomial distributions. (B) Calculated probability distribution for depolarization of Kenyon cells by antennal lobe input (solid curve), a normal probability distribution (light dotted). The heavy dotted curves to the left of the solid curve is the distribution for non-γ Kenyon cells (Left), and for γ Kenyon cells (Right).

In the preceding section, I used the observed exponential distribution of antennal lobe projection neuron firing rates to calculate the probability density function for the depolarization of Kenyon cells. In this earlier calculation, however, I assumed that all Kenyon cells have six claws, a value close to the one observed for the non-γ class. In that section, I found that, for a Kenyon cell with c claws, the density function is

$$w_c\left(v\right)=\frac{{\lambda }^c}{\left(c-1\right)!}{v}^{\left(c-1\right)}{e}^{-\lambda v},$$

where $w_c\left(v\right)$ is the probability density for depolarization v of a Kenyon cell with c claws, and λ = 0.87 mV⁻¹. When the number of claws c follows a binomial distribution $B\left(p,N\right)$ $(p=.715$ is the probability of a claw and maximum claw number is N = 8 for non-γ Kenyon cells and $N=11$ for γ Kenyon cells) the probability density $w\left(N,v\right)$ is

$$w\left(N,v\right)={\displaystyle \sum _{c=1}^{N}B\left(p,N\right)w_c\left(v\right)}$$

for a depolarization v. The corresponding cumulative probability distribution is $W\left(N,v\right)={\displaystyle {\int }_0^{v}duw\left(N,u\right)}$.

Of the ∼2,000 Kenyon cells, 1/3 are of the γ type and 2/3 are of the non-γ $\left(\alpha /\beta \mathrm{+}{\alpha }^{\prime }/{\beta }^{\prime }\right)$ type. If I assume that synaptic strength of projection neurons onto Kenyon cells is the same for all types, the cumulative probability distribution $P\left(v\right)$ for the depolarization v caused by any odor is $P\left(v\right)=\frac{2}{3}W\left(8,v\right)+\frac{1}{3}W\left(11,v\right)$. $P\left(v\right)$ is plotted in Fig. 3B (solid line), where it can be seen to be close to a normal distribution (the light dotted curve superimposed) for depolarizations greater than about 5 mV. This distribution describes the depolarization of all Kenyon cells for any odor, and the winner-take-all circuit restricts the actual firing to those Kenyon cells that happen to have depolarizations greater than about 10 mV. These particular Kenyon cells would then provide the neural tag for the odor.

Because the non-γ and γ types of Kenyon cells have different numbers of claws, I have also included the probability distributions for the depolarization for both types separately in Fig. 3B. The dark dotted curve on the left of Fig. 3B is the distribution for the non-γ class $\left[W\left(8,v\right)\right]$ and the dark dotted curve on the right for the γ class $\left[W\left(11,v\right)\right]$.

Discussion

The final picture of the fly olfactory system is quite simple. The antennal lobe formulates the most informative odor code possible (technically a maximum entropy code), based on information from ORNs and from constraints (like gain control) provided by the antennal lobe circuitry. Because of the structure of this code, most projection neurons fire slowly, but a very few projection neurons respond with high firing rates in a small fraction of the glomeruli. Each Kenyon cell in the mushroom body combines information from about six glomeruli, selected at random, and those cells that best (in a statistical sense) characterize the odor are ones with largest depolarizations. The output of the mushroom body, then, is based on a winner-take-all circuit that permits firing only of the most depolarized Kenyon cells. Thus, the Kenyon cells that are permitted to fire spikes provide tags for a pair of randomly selected odors that are unlikely to overlap.

My motivation for this work was to learn how one example of the Marr motif works and, to identify the Marr motif in the fly, I relied on what appeared to be analogous architectures across vertebrate and insect brain regions. I am not, however, the first to notice these same parallels between insect and vertebrate brains; indeed, similarities between the mushroom bodies and vertebrate olfactory system, hippocampus, and cerebellum have long been discussed (31–33). To be explicit about the parallels I identify, I include Table 1.

Table 1.

Marr motif correspondences for fly and vertebrates

Brain region	Stage 1: encoder	Stage 2: decoder
Fly olfactory system	antennal lobe	mushroom body (Kenyon cells)
Vertebrate olfactory system	olfactory bulb	piriform cortex (layer ii)
Cerebellum	precerebellar nuclei	cerebellar granule cells
Hippocampus	entorhinal cortex	dentate granule cells

To apply the conclusions I have reached to other systems (cerebellum, vertebrate olfaction, and the hippocampus), two steps are required. First, it must be verified that the combinatorial code generated by the various brain regions is maximum entropy, and that the decoding step uses distributed information and a winner-take-all circuit to establish statistically nonoverlapping tags for distinct inputs. This task will likely be difficult, and will presumably require many small steps. Second, even if it turned out that the identified Marr motif structures generally work the same way, the actual brain structures that appear to use this motif all have quite different functions, and we must discover what specializations and embellishments are used on top of a generic architecture to account for what makes, for example, the cerebellum different from the hippocampus, or the olfactory bulb different from the antennal lobe. Whatever is finally established about structures that seem to use the Marr motif, I hope that the framework I presented here will be useful for studying them.

In the main text, I initially treated all Kenyon cells (KCs) as if they were interchangeable, but then relaxed this requirement to take account of the fact that the mushroom body has three classes of KCs defined according to which lobe they send their axons. The vertical lobe is divided into two sublobes called α and ${\alpha }^{\prime }$ and the horizontal lobe is divided into $\beta ,$ ${\beta }^{\prime }$, and γ sublobes. Because the KCs that project to the α lobe also project to $\beta ,$ and the ones projecting to ${\alpha }^{\prime }$ also send their axons to ${\beta }^{\prime },$ the first two classes of KCs are known as $\alpha /\beta$ and ${\alpha }^{\prime }/{\beta }^{\prime }$. The third KC class, the γ KCs, projects only to the γ lobe. For convenience, when I consider the combined KCs of the $\alpha /\beta$ and ${\alpha }^{\prime }/{\beta }^{\prime }$ types, I will identify them at non-γ KCs. There are 1,370 non-γ KCs $\left(1\text{,}000\alpha /\beta \mathrm{+}370{\alpha }^{\prime }/{\beta }^{\prime }\right)$ and 670 γ KCs, which together make just over 2,000 total KCs (15). Here I consider differences in the sensing matrix (connection matrix) $\mathbf{R}$ (see main text) between the non-γ and γ KCs, and variability in strength of projection neuron (PN) synapses onto KCs.

Nonuniform Sampling of Glomeruli by KCs

I initially assumed that all KCs sampled six glomeruli randomly with equal probabilities so that every row of $\mathbf{R}$ had six entries equal to 1 (the other entries = 0) distributed randomly along the row according to a uniform distribution. The text later showed that the number of entries per row varied according to a binomial distribution with a mean that differs between non-γ and γ KCs; I still assumed, however, that all glomeruli are sampled with equal probability. Now I relax that assumption by taking into account the data from Carron et al. (16), which shows that different glomeruli are sampled randomly, but with different probabilities.

The relative frequency for sampling a glomerulus is replotted [from Carron et al. figure S2 (16)] in my Fig. S1 for the non-γ and γ KC types. My Fig. S1 is based on histograms in the Carron et al. figure S2 with data from their figure reordered to run from largest to smallest relative frequencies. Data in my Fig. S1A is based on 278 PN synapses onto 84 $\alpha /\beta$ KCs + 35 PN synapses onto ${\alpha }^{\prime }/{\beta }^{\prime }$ 14 KCs and in Fig. S1A on 354 PN synapses onto 102 γ KCs. Note that the numbers n assigned to glomeruli are different between my Fig. S1 A and B (each is arranged from largest to smallest relative frequency) and both are different from the standard order in Carron et al. figure S2.

Fig. S1.

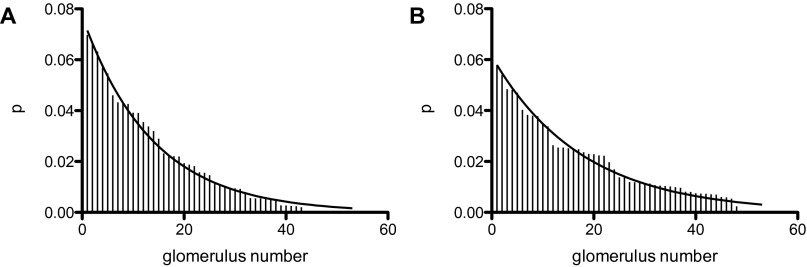
Relative frequency of a KC sampling a glomerulus vs. glomerulus number. Non-γ KCs in A and γ KCs in B. Data from Carron et al. (16), Fig. S2. Smooth lines according to a distribution (see Nonuniform Sampling of Glomeruli by KCs).

The descriptive theory (smooth lines in Fig. S1) is a geometric distribution normalized to range from glomerulus number $n=\mathrm{1,2}\hspace{0.17em}.\hspace{0.17em}.\hspace{0.17em}.\hspace{0.17em}54$. The equation used for $p\left(n,a\right),$ the probability that glomerulus n will be sampled by a KC, is

$$p\left(n,a\right)=\frac{a{\left(1-a\right)}^n}{{\displaystyle {\sum }_{k=1}^{54}a{\left(1-a\right)}^k}},$$

where n is the glomerulus index (the glomeruli are numbered from 1 to 54 in order of decreasing probabilities) and a is a parameter that determines the probability $p\left(n,a\right);$ the value of $a=0.07$ for non-γ KCs and $a=0.055$ for γ KCs. Thus, two different sensing matrices, ${\mathbf{R}}_{\overline{\mathbf{\gamma }}}$($1\text{,}370\hspace{0.17em}\times \hspace{0.17em}54$ with ${\mathbf{r}}_{\overline{\mathbf{\gamma }}}$ 1,370 long) for non-γ KCs and ${\mathbf{R}}_{\gamma }$($670\hspace{0.17em}\times \hspace{0.17em}54$ with ${\mathbf{r}}_{\gamma }$ long) for γ KCs, are required. To construct these matrices, generate—for each KC—the number of nonzero entries for that row of the sensing matrix with the appropriate binomial distribution for the KC type, and then distribute these entries over that KC row in the sensing matrix according to $p\left(n,a\right)$ using the appropriate value for a for the KC type. Note that rarely the same glomerulus may be sampled twice (or, very rarely, more than twice) by the same KC.

Strength of PN Synapses onto Kenyon Cells

In the main text, I assumed that the sensing matrix (also called connection matrix) $\mathbf{R}$ (the 2,000 × 50 matrix that specified the relation between the firing rate of projections neurons and the total spike rate input into the KCs) had 44 zeros and 6 ones distributed at random across each row. I have discussed the fact that the number of ones per row is not six but rather follows a binomial distribution, and that different glomeruli are sampled with different probabilities. Here I show that the sensing matrix is more complicated with uniformly distributed random numbers replacing the ones as entries because of random variability in synaptic strength. Note that the sensing matrix $\mathbf{R}$ as described above only specified the total number of presynaptic spikes arriving at the synapses of a KC, but not the postsynaptic effect of these arrivals. In the main text, I replaced the entries of the sensing matrix—all of which had a value of 0 or 1—with the average postsynaptic depolarization produced by the a given rate of presynaptic impulse arrivals. However, the postsynaptic depolarization for a given arrival rate is actually stochastic. Therefore, the entries equal to 1 must be replaced by random variables. Here I identify the probability distribution of these random variables.

The data described here appeared in figure 6S of Gruntman and Turner (28). They optically stimulated a small set of antennal lobe projection neurons and then recorded the membrane potential from KCs that received synaptic input from only a single claw. For 16 such neurons, they measured the amplitude of the first excitatory synaptic potential (EPSP) elicited by the stimulus. Gruntman and Turner provided me with their original list of EPSP amplitudes for each of the 16 KCs that is used in the following analysis.

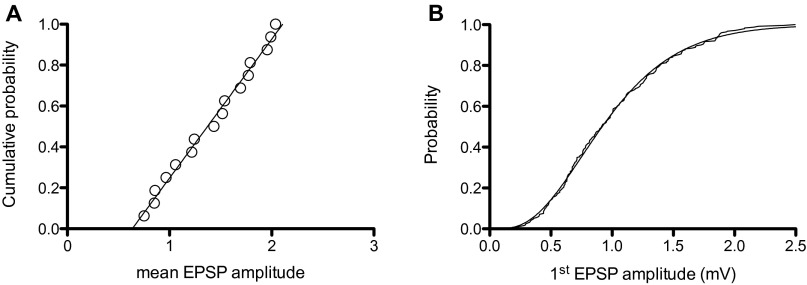
In Fig. S2A I have plotted a cumulative histogram of the mean EPSP amplitudes, and fitted it with a straight line with an ordinate value that ranges from 0 to 1 and EPSP amplitudes that range from 0.588 to 1.76 mV. Thus, the synaptic strength of these synapses is uniformly distributed over a threefold range [0.59,1.8] with a probability density of 0.85. The coefficient of variation for these 16 claw synapses is constant, so a possible source for the variability is the number of acetylcholine receptors per synapse.

Fig. S2.

Properties of the antennal lobe projection neuron synapses onto KCs. (A) The cumulative distribution function for synaptic strength at 16 single claw synapses [the mean amplitude (mV) for the first EPSP]. The fitted straight line has a slope of 0.85 (B). Cumulative histogram for all EPSP amplitudes (235 observations) scaled for each claw to have a mean = 1. This histogram has been fitted to a Γ distribution function with scale factor = 4 and shape factor = 4.

Because one would expect the EPSP amplitude distribution for all claw synapses to be described by the same function, I have divided the observed EPSP amplitudes by the mean for that claw, plotted the cumulative histogram for all 253 EPSPs from the 16 KCs in Fig. S2B, and I also carried out a sanity check by showing that the observed mean of 253 scaled EPSP amplitudes = 1. The claw synapses are constructed with separated fingers of the claw having a single active zone (15) and the average number of such separated active zones is 4. The simplest consistent basis for the observed variability would be for each active zone to produce an exponentially distributed contribution to the total EPSP amplitude. Because there are four active zones per KC synapse on a single claw, the EPSP amplitude should have a $\mathrm{\Gamma }$ distribution with a shape factor of 4. And because the individual KC EPSP amplitudes have been scaled to have a mean of 1, the scale factor should also be 4. The $\mathrm{\Gamma }$ distribution superimposed on the cumulative histogram in Fig. S2B is this function.

Thus, the sensing matrix should not have zeros and six randomly placed (according to the distributions in Fig. S1) ones per row, but rather zeros and nonzero entries at locations chosen at random from a binomial distribution with a probability of adding a claw of 0.715 and the appropriate mean number of claws for the KC type for that row. The nonzero entries in each row are drawn from a uniform probability density over the range [0.69,2.1] with a probability density of 0.71 that replaces the ones of the earlier sensing matrix. Note that the range of uniformly distributed EPSP amplitudes is a different from the observed range because the grand mean of all EPSP amplitudes was used when converting the total input spike rate into depolarization with the linear relation between total rate and mean depolarization.

As a biophysical theory for the distribution of synaptic strengths and the corresponding EPSP amplitudes, what I have just laid out is unsatisfactory because identification for sources in the variation of EPSP amplitudes from claw to claw is too unconstrained. As a description of the data, however, it is very accurate as far as it goes. The problem is that the types of KCs that provided the sample upon which Fig. S2 is based are unknown, too few KCs with a single claw activation are available, and those that are available represent activation by only a few types of glomeruli. The value of the description is that it shows what the actual sensing matrix should look like, and indicates what types of experiments would ideally be needed to find the actual sensing matrix. It also identifies one source in the variability of olfactory system functioning that is the basis for the observed variability in fly behavior in response to odors.