Three-dimensional model of surfactant replacement therapy

Significance

To our knowledge, this paper presents the first structural model of surfactant replacement therapy (SRT), the delivery of liquid bolus surfactant mixtures into the lung airways. SRT has succeeded in premature neonates with surfactant deficiency but mostly failed in adults with acute respiratory distress syndrome, which claims ∼74,500 lives annually in the United States at a 39% mortality rate. Our model incorporates the fluid mechanics of the liquid bolus propagating through a branching airway tree with gravity effects. It reveals well-mixed distributions in the neonatal lung, but poorly mixed, highly nonlinear distribution features in adult lungs. The model suggests adult SRT failures are likely due to inadequate delivery, while providing a rational basis for successful protocols.

Abstract

Surfactant replacement therapy (SRT) involves instillation of a liquid-surfactant mixture directly into the lung airway tree. It is widely successful for treating surfactant deficiency in premature neonates who develop neonatal respiratory distress syndrome (NRDS). However, when applied to adults with acute respiratory distress syndrome (ARDS), early successes were followed by failures. This unexpected and puzzling situation is a vexing issue in the pulmonary community. A pressing question is whether the instilled surfactant mixture actually reaches the adult alveoli/acinus in therapeutic amounts. In this study, to our knowledge, we present the first mathematical model of SRT in a 3D lung structure to provide insight into answering this and other questions. The delivery is computed from fluid mechanical principals for 3D models of the lung airway tree for neonates and adults. A liquid plug propagates through the tree from forced inspiration. In two separate modeling steps, the plug deposits a coating film on the airway wall and then splits unevenly at the bifurcation due to gravity. The model generates 3D images of the resulting acinar distribution and calculates two global indexes, efficiency and homogeneity. Simulating published procedural methods, we show the neonatal lung is a well-mixed compartment, whereas the adult lung is not. The earlier, successful adult SRT studies show comparatively good index values implying adequate delivery. The later, failed studies used different protocols resulting in very low values of both indexes, consistent with inadequate acinar delivery. Reasons for these differences and the evolution of failure from success are outlined and potential remedies discussed.

Since the early 1980s, surfactant replacement therapy (SRT) has been successful in applications to prematurely born neonates to treat their lack of surfactant production, which normally initiates late in gestation (1). Because surfactant reduces the surface tension between the air and the lung’s liquid lining, its deficiency creates high surface tensions and collapsed, stiff lungs making them difficult to inflate. The resulting clinical entity of labored breathing and poor oxygenation is called neonatal respiratory distress syndrome (NRDS), or hyaline membrane disease, and is a risk of premature birth increasing with decreasing gestational age. The incidence is ∼1% of all births, equating to 40,000 cases annually in the United States (2). The mortality associated with NRDS dropped from 4,997 deaths in 1980 to 861 in 2005, and SRT played an important role in this success (3).

SRT has also been tried in adults whose surfactant systems are compromised by acute respiratory distress syndrome (ARDS). ARDS results from overwhelming infections, mechanical injuries, and other insults either directly or indirectly to the lung. ARDS cases in the United States total 190,600 annually with a 39% mortality rate yielding 74,500 deaths (4). Although some early SRT large-animal and adult clinical trials were successful (5–8), subsequent studies were failures (9–11). The field is looking for direction, with concerns ranging from the delivered surfactant biochemistry to the persistence of the underlying ARDS disease to the adequacy of delivery (12). The model presented here addresses the delivery issue and shows that simulations of these adult SRT studies produce significantly different delivery distributions that can explain success vs. failure.

Effective drug delivery is a major medical challenge. First mathematical models for i.v. (13), oral (14), and aerosol (15) modalities contributed to the development of those fields simulating drug uptake, distribution, metabolism, and elimination. The role of models is to interpret data mechanistically, predict outcomes, follow treatment courses, relate dose to response, establish safety criteria, design new drugs and delivery strategies, compare animal experiments to human applications, and tailor protocols to patient specific circumstances. To our knowledge, the work presented here is the first structural model of SRT with the same goals. It quantifies the physics of two-phase fluid flow, air and liquid, into a branching network of airways representing the lung (16–18). Our model provides a mechanistic foundation for SRT delivery, which turns out to be a highly nonlinear process. A working SRT model can have a significant impact on this field, moving it from a process of informed trial and error to one that harnesses the underlying fundamental mechanisms.

In SRT, the instilled mixture can form a liquid plug in the trachea (19), which then propagates through the tracheobronchial tree by forced inspiratory airflow. As the liquid plug propagates distally, it coats the airway walls, losing some of its mass, and also splits at bifurcations. Our mathematical model considers these two important steps in sequence. For step A (airway), the propagating plug deposits some content onto the airway walls into a trailing film. This deposition, or coating, reduces efficiency because less surfactant mixture reaches the acinus. Our experimentally validated theory predicts the trailing film thickness as a function of plug viscosity, speed, surface tension, and tube radius from computational fluid dynamics results (17). Then, in step B (bifurcation), the plug splits at an airway bifurcation in an uneven manner due to gravity, favoring the steepest downhill daughter tube, so reduces distribution homogeneity. The larger the structure (adult lungs), the greater is this reduction. For this step, we compute the ratio of the split volumes from conservation of momentum and mass. This split ratio depends on the plug speed, viscosity, surface tension, bifurcation geometry, and orientation with gravity (20, 21). Each step is performed sequentially through a 3D tree construct with the geometrical features of the conducting airways (22, 23) (Materials and Methods). The time period for the flow is a single forced inspiration. A larger fluid velocity yields more even splitting, improving homogeneity, but leaves a thicker wall deposition layer, reducing efficiency. The resulting distribution of SRT depends on the competition between these two fluid mechanical phenomena.

Results

Two sizes of lung are simulated (Materials and Methods): a 1-kg premature neonate and a 70-kg adult. The surfactant bolus starts as a plug in the distal trachea for both, because that would normally be the outlet of an endotracheal tube. However, for adults, we also simulate a bronchoscopic instillation at generation 3 or 4 of the airway tree. The lungs are in left lateral decubitus (LLD) or right lateral decubitus (RLD) positions. Two (RLD, LLD) positions are used for an entire treatment protocol. Only the supine position is used for bronchoscopic delivery. Assuming a symmetric airway tree, we use the published properties of surfactant mixtures (viscosity, density, surface tension) and the instilled volume taken from clinical studies. Then the airflow rate, which drives the plug flow during a forced inspiration, is varied to cover a wide range of possibilities.

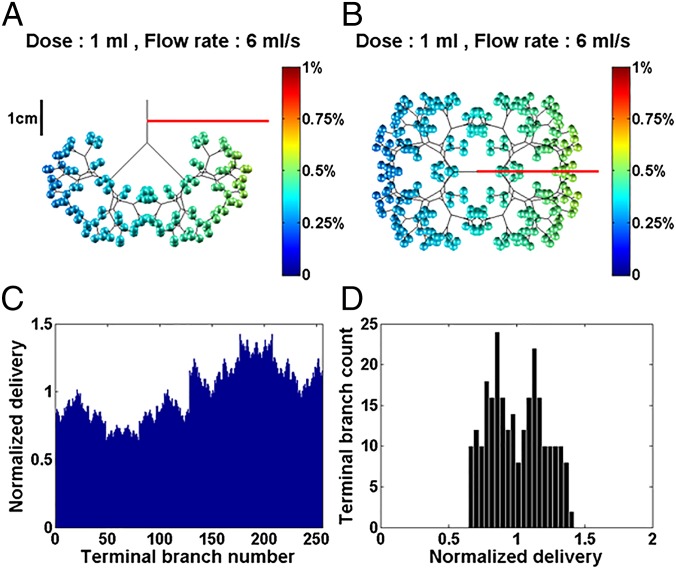
To appreciate the delivery in just one of the positions, Fig. 1 represents a single instillation into a 1-kg LLD neonate. The instilled dose volume, V₀, is 1 mL, the mixture viscosity is μ = 30 cP, typical of Survanta (Ross Products Division, Abbott Laboratories), Infasurf (ONY, Inc.), and Curosurf (Chiesi Farmaceutici) (24, 25), and the imposed flow rate is 6 mL/s. We choose a symmetric airway tree with eight generations plus a trachea. Fig. 1A shows a front view and Fig. 1B shows a top view of this 3D tree and its 256 terminations. These terminations are assumed to be the entrance into the acinar region that contains the alveoli. A 1-cm ruler scale is shown. The acini are color coded for their received amount, V_i (i = 1–256), calculated as a percentage of the dose delivered to the acinar region. Note that, even though the neonate is in the LLD position, the instilled volume is delivered to acini in both lungs, with a preference for the left lung that is lower in the gravity field.

Fig. 1.

The 1-kg neonate in the LLD position with viscosity µ = 30 cP, dose volume of 1 mL, and flow rate of 6 mL/s. The airway tree is symmetric with eight generations plus trachea, 256 acini. The efficiency index is η = 52.8%. (A) Front view. (B) Top view of the 3D model with color-coded amounts percentages in the acini. (C) Normalized delivery V_N(i) plotted vs. i = 1–256 acini. (D) Histogram showing homogeneity index is 1/SD = 4.9. See text for definitions.

One of the challenges for modeling is how best to compare results from different protocol simulations. Generating 3D images, like Fig. 1 A and B, which can be rotated with differing viewpoints, is an important first step. However, it becomes difficult simply to compare images and extract quantitative information for determining the preferred protocol. To address this issue, we define and generate two global measures of the distribution, the “efficiency index” and the “homogeneity index,” both defined as follows. The efficiency index, η, is the percentage of the instilled dose volume, V₀, reaching the acini, $\mathit{\eta }\mathrm{=100}\times {\displaystyle {\sum }_{\mathit{i}\mathrm{=1}}^{\mathit{M}}{\mathit{V}}_{\mathit{i}}/{\mathit{V}}_{\mathrm{0}}}$ (M = 256). Here η = 52.8%, so approximately one-half of V₀ deposits on the airway walls and one-half is delivered to the acini.

Fig. 1C plots each acinar amount normalized by the total acinar delivered amount. We define the normalized delivery as ${\mathit{V}}_{\mathit{N}\hspace{0.17em}}\left(\mathit{i}\right)\mathit{=}{\mathit{V}}_{\mathit{i}}\mathit{/}(\mathit{\eta }{\mathit{V}}_{\mathrm{0}}/\mathrm{100})$. In this example, every acinus receives surfactant, but the left lung ($\mathrm{129}\le \mathit{i}\le \mathrm{256}$) is favored over the right ($\mathrm{1}\le \mathit{i}\le \mathrm{128}$) due to the LLD position. Fig. 1D is a histogram of Fig. 1C arranged in amount groups. The average value of the histogram is 1, but its SD is an inverse measure of homogeneity. We therefore define a homogeneity index as 1/SD. Here, the calculated value is SD = 0.20; hence the homogeneity index is about 4.9.

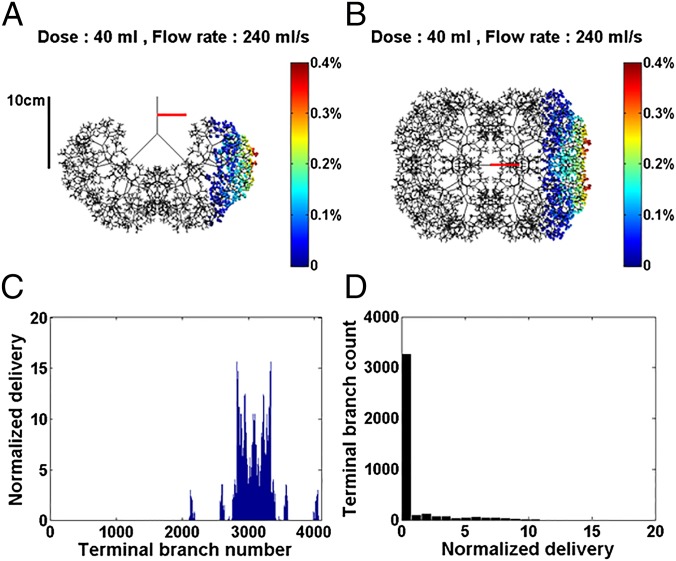
Next, we model SRT for a 70-kg adult using a symmetric airway tree having 12 generations plus a trachea. Fig. 2 shows an adult single instillation with dose volume of 40 mL and flow rate of 240 mL/s. A 10-cm ruler gives the scale. Note the very different resulting distribution shown in Fig. 2 A and B, compared with the neonate, simply based on size. No surfactant mixture reaches the acini of the right lung, and that delivered to the left lung is very inhomogeneous. For this case, the efficiency index is η = 13.0%, about one-fourth of the neonate value. Fig. 2C shows the normalized delivery in all M = 4,096 acini. More than 3,000, i.e., about 75% of the acini, do not receive any surfactant at all. The histogram in Fig. 2D shows the homogeneity index to be 1/SD = 0.41, less than 1/10th the neonatal value.

Fig. 2.

The 70-kg adult in the LLD position with viscosity µ = 30 cP, dose volume of 40 mL, and flow rate of 240 mL/s. The airway tree is symmetric with 12 generations plus trachea, 4,096 acini. The efficiency index is η = 13.0%. (A) Front view. (B) Top view of the 3D model with color-coded amounts percentages in the acini. (C) Normalized delivery V_N(i) plotted vs. i = 1–4,096 acini. (D) Histogram showing homogeneity index is 1/SD = 0.41. See text for definitions.

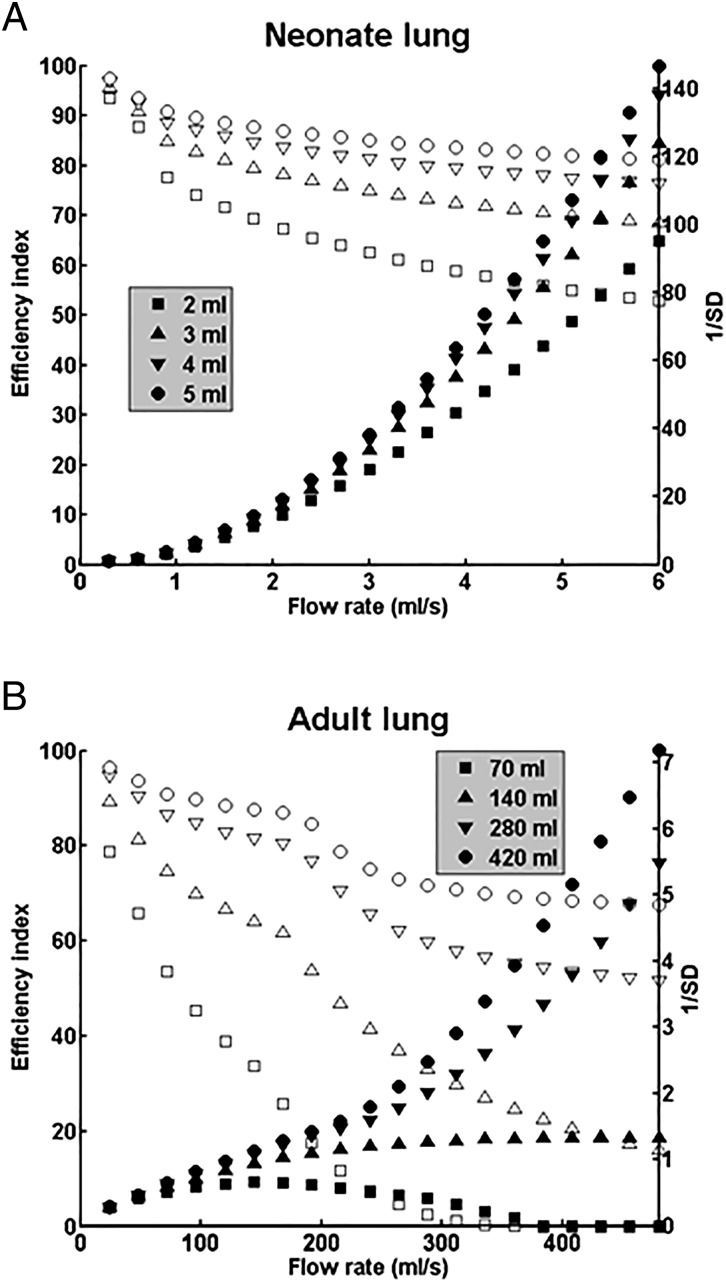
Having calculated delivery into a neonate and adult at one flow rate, one dose volume, and one position, we now use the model to simulate a broader range of treatment protocols in Fig. 3. The efficiency index (open symbols) and the homogeneity index (filled symbols) are plotted vs. the flow rate, for four different total doses in the neonate (Fig. 3A) and four in the adult (Fig. 3B). Each total dose is divided into equal portions for delivery, one-half per position for two positions, LLD and RLD, a delivery mode relevant to the clinical studies we discuss and model (6, 9–11). For the neonate, Fig. 3A shows that increasing flow rate has opposite effects on efficiency and homogeneity. Efficiency decreases with increasing flow rate due to thicker trailing films coating the airway walls, whereas homogeneity increases because the split ratio at each bifurcation is shifted more toward unity, i.e., more equal plug splitting as the fluid velocity increases.

Fig. 3.

(A) Efficiency index η (open symbols) and homogeneity index 1/SD (filled symbols) as functions of the tracheal flow rate for total dose volumes of 2, 3, 4, and 5 mL in the 1-kg neonate lung, which are from reported neonatal SRT protocols (26). For each total dose value, one-half is delivered in each of two positions, RLD and LLD. (B) Same positions and plot as in A, but in the 70-kg adult lung for total dose volumes of 70, 140, 280, and 420 mL The first three dose volumes are from reported adult SRT protocols, 70 mL (9, 10) and 140 and 280 mL (6).

The effect of dose volume is also significant. The recommended dose volume per kg for neonates depends on the surfactant and its concentration, Survanta (25 mg/mL × 4 mL/kg = 100 mg/kg), Infasurf (35 mg/mL × 3 mL/kg = 105 mg/kg), and Curosurf (80 mg/mL × 1.25 mL/kg = 100 mg/kg or × 2.5 mL/kg = 200 mg/kg) (26). We have chosen the dose volumes to be 2, 3, 4, or 5 mL to reflect this range. Increasing the dose volume increases both efficiency and homogeneity at any given flow rate, because more available volume reduces plug ruptures. Increases in homogeneity with dose volume are consistent with rabbit experiments (27). Over a wide range of flow rates, the neonatal treatment simulation yields very high homogeneity and efficiency indexes. For example, at 6 mL/s, η is in the range of 60–85% depending on the dose volume, whereas 1/SD is in the range of 100–140.

By contrast, Fig. 3B shows the 70-kg adult case where the efficiencies are somewhat lower than those of the neonate, whereas the homogeneity index is an order of magnitude smaller than the neonate, up to 1/SD = 7. For the adult, the influence of dose volume can be critical. Three of the four dose volumes are chosen from published protocols: 70 mL (1 mL/kg) (9, 10); 140 mL (2 mL/kg) and 280 mL (4 mL/kg) (6); and 420 mL (6 mL/kg) appears as an upper limit. Increasing flow rate again reduces efficiency and increases homogeneity, except for the 70-mL example. For that dose volume, there is a very low local maximum of 1/SD ∼ 0.6 at a flow rate of 150 mL/s. For flow rates of 350 mL/s or higher, both η and 1/SD are essentially zero. Again, increasing the dose volume increases the homogeneity index for any given flow rate.

Clinicians have used bronchoscopic instillation to improve SRT results in adults (7, 8). Fig. 4A presents homogeneity and efficiency plots for two types of supine bronchoscopic instillation for a total dose of 320 mL: either 8 instillations of 40 mL injected at generation 3 of the tracheobronchial tree (corresponding to lobar bronchi), or 16 instillations of 20 mL injected at generation 4 (corresponding to segmental bronchi). Fig. 4 B and C displays two examples of distributions of surfactant corresponding to one instillation of either case. Note that the n = 3 instillation subtends a larger portion (1/8th) of the distal lung than the n = 4 case (1/16th). In both cases, efficiency is generally high, η > 80%, because coating the larger airways is avoided, and homogeneity has maximal values 1/SD ∼ 10.

Fig. 4.

(A) Homogeneity, 1/SD, and efficiency, η, for simulating two types of multiple bronchoscopic instillations, either 8 × 40-mL instillations at the end of generation n = 3 (triangles) or 16 × 20-mL instillations at the end of generation n = 4 (inverted triangles). In both cases, the patient is in the supine position. (B) Top view of the distribution of delivered surfactant at generation n = 3. The gravity vector is displayed in red. (C) Top view of the distribution of delivered surfactant at generation n = 4.

Discussion

The model assumption of the instilled surfactant bolus starting as a plug in the distal trachea is likely met by the neonatal applications. However, for the adult studies, the plug probably starts more distally in some gravity-dependent pooling location, looking more like Fig. 4 B and C. Under those circumstances, the model would overpredict the homogeneity and underpredict the efficiency. Nevertheless, there are important and striking differences for adult simulations regarding dose volume. In ref. 6, Survanta (25 mg/mL phospholipid) was used, so the 140 mL (2 mL/kg) and 280 mL (4 mL/kg) dose volumes shown in Fig. 3B correspond to 50 and 100 mg/kg molecular doses, respectively. The model shows comparatively good efficiency and homogeneity for an adult lung, and the clinical study found a significant improvement in mortality with SRT, 18.8% SRT (n = 43) vs. 43.8% control (n = 16). Mortality was reduced by one-half, led by the 280-mL group. Transition to a higher concentration surfactant was then tested in 40-kg sheep with saline-lavage induced ARDS (5). They used Venticute (Nycomed) (1 mg/mL recombinant surfactant protein C, 50 mg/mL phospholipid), which is twice the phospholipid concentration of Survanta. Three concentration mixtures were used at only one dose volume, 4 mL/kg. The resulting molecular doses were 25 mg/kg using 6.25 mg/mL, 100 mg/kg using 25 mg/mL, and 200 mg/kg using 50 mg/mL. All three molecular doses led to improved gas exchange with the two higher doses performing the best.

The large multinational studies of adult SRT for ARDS involved hundreds of patients (n = 224 SRT, n = 224 control) (9) and (n = 419 SRT, n = 424 control) (10). Using Venticute at 50 mg/mL concentration, the dose volume was 1 mL/kg, keeping the molecular dose at 50 mg/kg as in ref. 6, but at 70 mL instead of 140 mL There was no improvement in mortality for these studies (9, 10). Our simulation is the 70-mL curve of Fig. 3B showing significantly lower values of efficiency and homogeneity compared with the 140- or 280-mL curves. The surfactant mixtures coat the airways in all scenarios, a requisite “coating cost.” However, a 70-mL dose volume does not have much remaining mixture, if any, to enter the acinus as in Fig. 2. The 140- or 280-mL dose volumes have sufficient material to pay the coating cost and still deliver surfactant to the acinus, particularly ample for 280 mL. The 4 mL/kg dose volume for the sheep (5) is also in this surplus dose volume range. Our model strongly suggests that inadequate delivery may be a major cause for the failure of these later studies (9, 10). The simulations for all of the above are for one treatment sequence. However, in practice, the clinical treatments are often repeated, likely improving the cumulative acinar delivery but probably not the cumulative homogeneity. Improving homogeneity could result from additional position choices, for example. Also, some of the surfactant mixture lost to airway coating may eventually reach the acinar region due to gravity. That would improve efficiency but probably not homogeneity. However, the arrival rate may be too slow to keep up with its possible neutralization in the ARDS alveoli.

A common assumption in drug delivery is that the medication distributes uniformly in a well-mixed compartment. Examples are the blood or extracellular fluid. In those cases, doubling the concentration and halving the delivered volume yields the same molecular dose and, presumably, the same clinical outcome. For SRT, the neonatal lung is well mixed in these simulations as judged by its high values of 1/SD. Lower/higher surfactant concentrations (Survanta, 25 mg/mL, vs. Curosurf, 80 mg/mL) given at higher/lower dose volumes (Survanta, 4 mL/kg, vs. Curosurf, 1.25 mL/kg) yield equivalent molecular doses of 100 mg/kg and similar successful results. This notion holds for neonates but is a misleading concept for an adult lung. The adult lung is a poorly mixed compartment, as indicated by its lower 1/SD values. In the adult clinical studies, the shift from higher (140 and 280 mL) to lower (70 mL) dose volumes, while doubling the surfactant concentration, appears to rely on the well-mixed compartment assumption. However, the values of η and 1/SD drop to near zero when 70 mL is simulated due to the coating cost. So for adult SRT, the liquid dose volume is critical and has a significant impact on the flow physics. It is the physics, as modeled by Eqs. 1 and 2, which determines the distribution quality reflected by η and 1/SD. Clearly, the protocol in ref. 6 can be revisited by clinicians with some confidence that it was very effective as prescribed. All subsequent studies deviated from that prescription and failed.

Bronchoscopic delivery to segmental bronchi in adult SRT has been successful in improving oxygenation and lung compliance in ref. 8 (n = 8 SRT, n = 8 control) and ref. 7 (n = 27 SRT). The latter also found an improved mortality rate compared with the expected rate. In these studies, ∼400 mL of Alveofact (Boehringer Ingelheim Pharma) (50 mg/1.2 mL phospholipid bovine derived) was delivered equally divided into 19 segmental bronchi. These studies fall into the n = 4 curve of Fig. 4A showing high efficiency and homogeneity, i.e., η = 85%, 1/SD = 7 at 250 mL/s flow rate.

The transition from well-mixed (neonates) to poorly mixed (adults) lung compartments is an issue of size. Increasing size increases gravity effects, through the Bond number, and available surface area for airway coating. Both are proportional to the square of the characteristic length. So SRT is a particularly nonlinear, complex process. The nonlinearity of SRT reflects the essential difference that airways are designed for optimal gas exchange (28), not optimal surfactant mixture delivery. Of course, there is a maximum volume one can deliver safely to an ARDS lung. In ref. 11, a total dose of 600 mL of HL 10 (LEO Pharmaceutical Products) (50 mg/mL porcine-derived surfactant) was divided into two positions at ∼8.5 mL/kg. That high-dose volume appears to have been too much, because the study was terminated prematurely due to worsening results for the SRT (n = 208) vs. non-SRT (n = 210) patients. Their protocol, however, was designed to create the liquid plug in the distal trachea. Adult SRT dose volumes of 70 mL (9, 10) and 600 mL (11) differ by an order of magnitude, a clinical situation clearly reflecting the need for a model. The 2–4 mL/kg surfactant instillations in ref. 6 and the 4 mL/kg in ref. 5 appear to be in a “sweet spot” in the dose volume parameter range where 1 mL/kg is too little and 8.5 mL/kg is too much.

The extensions of this SRT model are numerous. Using the more general form of Eq. 2, any airway tree geometry can be modeled: adult, neonate, and all age groups in between. It can also include important variations due to airway disease as well as patient-specific geometries from imaging. Experimental animal lungs can also be modeled, allowing quantitative predictions to the human application. Positioning, dose volumes, flow rates, surfactant properties, and point of instillation can be explored for any and all combinations.

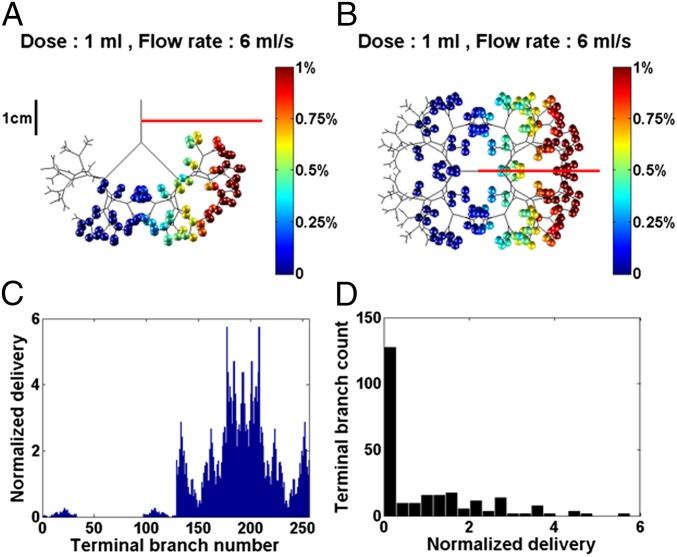
Because fluid viscosity, density, and surface tension are in the model, drug manufacturers can learn how the physical properties of their mixtures influence delivery and tailor them accordingly. For example, the synthetic surfactant mixture Exosurf (Glaxo-Wellcome) has a viscosity of ∼3 cP, which is 1/10th that of Survanta, Curosurf, and Infasurf. That difference has a profound effect on the computed distribution, as shown in Fig. 5, where the same neonatal protocol used for Fig. 1 is repeated, but with the much lower viscosity of Exosurf. Notice that the front and top distribution views are quite heterogeneous, unlike those of Fig. 1. Although there is an improvement of efficiency using Exosurf, increasing η from 52.8 to 82%, the homogeneity is significantly reduced, decreasing 1/SD from 4.9 to 0.79. For 2 mL split equally into two doses, LLD and RLD, delivered at 6 mL/s, the cumulative homogeneity index is 1/SD = 1.77, compared with ∼95 using a 30-cP viscosity shown in Fig. 3A. The treatment efficiency is η = 82%. Consequently, even the neonatal lung can be a poorly mixed compartment if the viscosity is too small.

Fig. 5.

The 1-kg neonate in the LLD position with viscosity µ = 3 cP, dose volume of 1 mL, flow rate of 6 mL/s. The efficiency index is η = 82%. (A) Front view. (B) Top view. (C) Normalized delivery V_N(i) vs. i = 1–256. (D) Histogram showing 1/SD = 0.79.

Exosurf is no longer on the market, having been outperformed in clinical comparative studies. A major reason given is its lack of important surfactant associated proteins which are included in the animal-derived surfactants of Survanta (bovine), Infasurf (calf), and Curosurf (porcine) (26). However, our model raises a different issue, that of the mixture viscosity, rather than its biochemistry. Increasing the viscosity of a mixture with inert additives can be far less costly for an industry than adding specific proteins. Extending beyond SRT, instilled surfactant mixtures have many other uses as a safe vehicle to deliver additional constituents into the lung such as gene therapy to airway epithelium, antibiotics, glucocorticoids, immunosuppressive agents, insulin, stem cells, and nanoparticles (29).

In summary, we have presented a first structural model of SRT. From the two-step process, applied stepwise through 3D airway tree structure, the model predicts a 3D delivery distribution to the acini. Two global parameters are derived from this distribution: the efficiency index, η, and the homogeneity index, 1/SD. Examples are shown for neonatal and adult applications, although any size or species of lung can be used. The neonatal airway tree is found to be a well-mixed compartment for high enough surfactant viscosity, whereas the adult airway tree is not. The influence of gravity on plug splitting at bifurcations is far greater in the adult due to the size and causes reductions in the homogeneity of delivery. The values of η and 1/SD strongly depend on the adult dose volume, better for higher volumes. This observation likely explains the success of higher volume–lower concentration adult SRT compared with lower volume–higher concentration failed adult SRT. Successful adult bronchoscopic delivery protocols also carry higher values of η and 1/SD in our model.

Materials and Methods

When liquid is instilled into the airway tree via an endotracheal tube, it will form a liquid plug either immediately or within a few generations. The following forced inspirations blow the liquid plug into the branching network of airways. We simplify this complex flow into two separate steps as the plug propagates from the airflow: step A (airway), deposition of liquid from the plug onto the airway walls into a trailing film; and step B (bifurcation), liquid plug splitting at an airway bifurcation.

For step A, the airway deposition or coating, Fig. 6A shows the rear meniscus of a long plug propagating along a tube of radius a, at speed U_p. The fluid viscosity, µ, and surface tension, σ, combine with U_p and a to create the trailing film of thickness h. This deposited film reduces the plug volume, so less is delivered distally. If the remaining local plug volume in any airway is fully deposited into the trailing film, the plug ruptures, reinstating continuous gas flow, but halting further delivery downstream from that point (30–32). That reduces overall efficiency as well as homogeneity. We have developed a computational solution for the dependence of h on the parameters (17), which was our previous theory lacking 3D structure and gravity effects. It is shown in Eq. 1, where H = h/a as a function of the plug capillary number, $\mathit{C}{\mathit{a}}_{\mathit{P}}\mathit{=}\mathit{\mu }{\mathit{U}}_{\mathit{P}}/\mathit{\sigma }$:

$$\mathit{H}\left(\mathit{C}{\mathit{a}}_{\mathit{P}}\right)\mathit{=}\frac{\mathit{h}}{\mathit{a}}\mathit{=}\mathrm{0}\mathrm{.36}\left(\mathrm{1-}{\mathit{e}}^{\mathrm{-2}\mathit{C}{\mathit{a}}_{\mathit{P}}^{\mathrm{0}\mathrm{.523}}}\right)\mathrm{.}$$ [1]

Fig. 6.

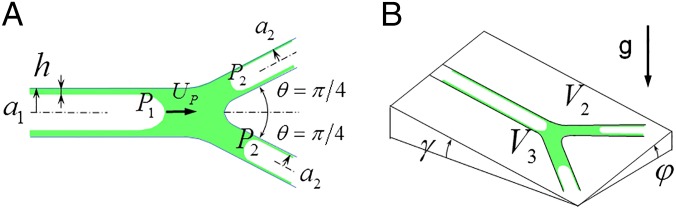
(A) Plug splitting at a symmetric bifurcation showing the deposited trailing film thickness h, plug speed U_p, equal branch angles θ = π/4, parent radius a₁, daughter radii a₂, upstream pressure P₁ and downstream pressures P₂. (B) Split volumes V₂ and V₃, roll angle φ, and pitch angle γ are shown for the bifurcation plane with respect to a plane perpendicular to gravity.

H increases rapidly with $\mathit{C}{\mathit{a}}_{\mathit{P}}$ from H = 0 to an asymptotic value of H = 0.36, covering 85% of that within the range $\mathrm{0}\le \mathit{C}{\mathit{a}}_{\mathit{P}}\le \mathrm{1}$. As H increases, more of the plug’s volume coats the wall. Consequently, less surfactant mixture flows downstream, reducing the delivery efficiency. The amount deposited onto an airway, V_D, divided by the airway volume, V_A, is the deposition ratio, ${\mathit{R}}_{\mathit{D}}\mathit{=}{{\mathit{V}}_{\mathit{D}}/{\mathit{V}}_{\mathit{A}}\mathit{=}\mathrm{1-}\left(\mathrm{1-}\mathit{h}/\mathit{a}\right)}^{\mathrm{2}}$, which has the range 0 ≤ R_D ≤ 0.59 given the maximum H = 0.36.

For step B, plug splitting at the bifurcation, we have analyzed this phenomenon previously (20, 21), establishing agreement between theory and benchtop experiments. In Fig. 6A, the liquid plug starts in the 1-parent tube with radius a₁, gas pressure P₁, and initial volume V₀. The bifurcation is chosen to be symmetric with total branch angle 2θ = π/2, equal daughter radii a₂, and equal end gas pressures P₂. Asymmetric bifurcations may also be chosen. Fig. 6B shows that the 2-daughter receives volume V₂ and the 3-daughter receives V₃. The sum ${\mathit{V}}_{\mathrm{2}}\mathrm{+}{\mathit{V}}_{\mathrm{3}}$ equals V₀ minus the deposited volume into the trailing film, h, according to Eq. 1. In this example, V₂ < V₃, indicating the 3-daughter is downhill with respect to gravity from the indicated roll, φ, and pitch, γ, angles. Balancing the forces includes pressure jumps across the three menisci using the Law of Laplace, viscous pressure drops according to Poiseuille flow with gravity terms, and an inertial term for the velocity change at the junction. From the balance, we can derive an equation for the split ratio, R_s = V₂/V₃:

$${\mathit{R}}_{\mathit{s}}\mathit{=}\frac{\mathit{ReCa+}\mathrm{16}\mathit{Ca}{\tilde{\mathit{V}}}_{\mathrm{0}}\left(\mathrm{1-}{\mathit{R}}_{\mathit{D}}\left(\mathit{C}{\mathit{a}}_{\mathit{P}}\right)\right)\frac{\mathit{1}}{{\mathit{\lambda }}^{\mathrm{4}}}\mathrm{-2}\mathit{Bo}{\tilde{\mathit{V}}}_{\mathit{0}}\left(\mathrm{1-}{\mathit{R}}_{\mathit{D}}\left(\mathit{C}{\mathit{a}}_{\mathit{P}}\right)\right)\left(\sin \mathit{\theta }\sin \mathit{\phi +}\cos \mathit{\theta }\sin \mathit{\gamma }\right)}{\mathit{ReCa+}\mathrm{16}\mathit{Ca}{\tilde{\mathit{V}}}_{\mathit{0}}\left(\mathrm{1-}{\mathit{R}}_{\mathit{D}}\left(\mathit{C}{\mathit{a}}_{\mathit{P}}\right)\right)\frac{\mathit{1}}{{\mathit{\lambda }}^{\mathrm{4}}}\mathit{+}\mathrm{2}\mathit{Bo}{\tilde{\mathit{V}}}_{\mathit{0}}\left(\mathrm{1-}{\mathit{R}}_{\mathit{D}}\left(\mathit{C}{\mathit{a}}_{\mathit{P}}\right)\right)\left(\sin \mathit{\theta }\sin \mathit{\phi }\mathrm{-cos}\mathit{\theta }\sin \mathit{\gamma }\right)},$$ [2]

where additional dimensionless parameters are as follows: the Reynolds number Re = ρU₁a₁/µ; the radius ratio λ = a₂/a₁; the Bond number Bo = ρga₁²/σ, which contains the gravity effect; and the dimensionless dose volume Ṽ = V₀/πa₁³, where V₀ is the dimensional dose volume instilled into the tube. The tube capillary number is related to the plug capillary number by Ca = µU₁/σ = (1 − H(Ca_P))²Ca_P. U₁ is the average airflow rate into the tube divided by the tube cross-sectional area. R_S = 1 means the plug splits evenly which is the most homogenous split. R_S = 0 means all of the parent plug flows into the downhill daughter tube and none into the uphill daughter tube, the most inhomogeneous result. So the range of R_S is 0 ≤ R_S ≤ 1.

Ca and Re depend on the airway flow speed, which decreases rapidly as one progresses into the airway tree with its increasing total cross-sectional area. Typical tracheal values are Ca ∼ 1.5 adult and ∼ 0.5 neonatal. Likewise, typical tracheal values are Re ∼ 500 adult and ∼ 300 neonatal. Unlike Ca and Re, however, Bond numbers are vastly different between adult and neonate due to the dependence on a₁². Tracheal Bo ∼ 25 adult and ∼ 1 neonate, a ratio that is maintained for the remaining generations as airway diameters become smaller. So gravity effects, which promote inhomogeneity, are much stronger in an adult lung. Additional parameter values include viscosity, which we choose to be 30 cP, for Survanta, Curosurf, and Infasurf, and 3 cP, for Exosurf, and the static surface tension, which we chose to be σ = 30 dyn/cm (33).

Any airway tree can be inputted. For simplicity, we assume a symmetric airway structure. The purpose of this simple tree geometry is to allow us to focus on the fluid mechanical phenomena that govern the eventual distribution and are fundamental to the process. Similar symmetric tree assumptions are common for complicated flows in airways (34, 35). Introducing patient-specific lung geometries and generally asymmetric trees are planned for future work, but at this stage would mask asymmetries inherent to the basic fluid mechanics with gravity effects.

The airway diameters, D_n, at generation n obey the relationship D_n = D₀2^−n/3 (22) where D₀ (n = 0) is the tracheal airway diameter. Hence the diameter ratio is D_n+1/D_n = 2^−1/3 = 0.79. The branch angle 2θ between daughter tubes will be 90° (θ = π/4) and airway lengths, L_n = 3D_n. The 1-kg neonate has D₀ = 0.4 cm, and terminal bronchiole diameter, 0.05 cm. There are 256 acinar terminations (acini) fed by eight generations plus the trachea. The 70-kg adult tracheal diameter is taken to be D₀ = 1.72 cm. The terminal bronchiole diameter is 0.1 cm, and there are 4,096 acinar terminations, fed by 12 generations plus the trachea. To model an airway network in three dimensions requires us to relate successive bifurcation planes when passing from one generation to the next. Parent tube, A, and daughter tubes, B and C, form the ABC plane for the first bifurcation. Then parent tube C and daughter tubes, D and E, form a new plane, CDE, which we take to be perpendicular to plane ABC.

The two-step process starts with step A. The plug propagates down the length of an airway losing volume to the tube wall by H in Eq. 1. Step A governs efficiency for an individual airway. Reaching the bifurcation the plug splits, step B, over zero distance at the junction. Gravity makes the split unequal, so step B governs homogeneity for that bifurcation. The assumption is that the gravity effects of splitting are governed by the difference in elevations of the two daughter plugs. Plugs that may extend over more than one generation would have upstream influence on the fluid pressure at the end of the forward parent tube, which is equal to the entrance pressure into the forward daughters, i.e., the split point pressure. However, the split ratio comes from the relative pressures between the daughters, which cancel the split point pressure. The model assumes no other influence. More detailed, 3D computational fluid mechanics would be needed to address this potential issue. Each daughter receives its portion based on R_S in Eq. 2, and then the steps are repeated in each daughter to the next bifurcations, etc. This process continues until the plug in an airway either ruptures from losing all of its volume to deposition, or is delivered to tree termination or acinus.