Segmentation of the Aortic Valve Apparatus in 3D Echocardiographic Images: Deformable Modeling of a Branching Medial Structure

Abstract

3D echocardiographic (3DE) imaging is a useful tool for assessing the complex geometry of the aortic valve apparatus. Segmentation of this structure in 3DE images is a challenging task that benefits from shape-guided deformable modeling methods, which enable inter-subject statistical shape comparison. Prior work demonstrates the efficacy of using continuous medial representation (cm-rep) as a shape descriptor for valve leaflets. However, its application to the entire aortic valve apparatus is limited since the structure has a branching medial geometry that cannot be explicitly parameterized in the original cm-rep framework. In this work, we show that the aortic valve apparatus can be accurately segmented using a new branching medial modeling paradigm. The segmentation method achieves a mean boundary displacement of 0.6 ± 0.1 mm (approximately one voxel) relative to manual segmentation on 11 3DE images of normal open aortic valves. This study demonstrates a promising approach for quantitative 3DE analysis of aortic valve morphology.

1 Introduction

Echocardiography is the most commonly used imaging modality for heart valve assessment and has a prominent role in valve diagnostics and surgical planning. Heart valve segmentation in echocardiographic data, particularly 3D echocardiographic (3DE) images, is a means of extracting visual and quantitative information about valve morphology. However, image segmentation in this context is particularly challenging due to the signal dropouts and noise that are characteristic of this imaging modality, as well as the fact that many clinically relevant valve landmarks are defined geometrically rather than by distinctive image intensity characteristics. For example, several components of the aortic valve complex, such as the sinotubular junction (STJ), the commissures, and the basal attachments of the aortic cusps, are identified anatomically rather than by characteristic image intensity patterns.

Deformable modeling methods are well suited for tasks like shape-guided heart valve segmentation in 3DE images. These methods capture the geometry of an image region by deforming parametric surfaces under the influence of external data-driven forces and internal regularization forces. Shape constraints imposed on the deformable model can fill in areas of intensity inhomogeneity or establish boundaries between anatomical components that are not demarcated by image gradients. Once a parametric model of the valve is obtained, it can be interactively visualized, quantitatively analyzed, and statistically compared to other valve geometries.

Several deformable modeling methods for heart valve segmentation in 3DE images have been proposed. Ionasec et al developed a fully automatic technique for segmenting the aortic and mitral valves in 3DE images [1]. Given a database of manually landmarked images, machine learning algorithms globally locate and track several valve landmarks throughout the cardiac cycle. A spline model fitted through these points with the aid of learned boundary detectors represents valve geometry. In other work [2,3], the mitral and aortic leaflets are represented with a deformable model known as a continuous medial representation (cm-rep), which explicitly parameterizes the leaflets' medial axis (or morphological skeleton) [4]. The latter representation is volumetric; it defines the structure as one with locally varying thickness. One advantage of employing a geometrical model that explicitly defines thickness is that leaflet thickness is an important tissue parameter in biomechanical valve simulation [5].

While cm-rep has been effectively used to describe mitral and aortic leaflet morphology in 3DE images, applying it to the entire aortic valve complex (including the sinuses of Valsava) is challenging. The heart valve leaflets themselves can be described in terms of a single non-branching medial manifold. However, the entire aortic valve complex has a branching medial representation, in which the basal attachments of the aortic cusps are seams that join the medial manifolds of the cusps and sinuses. The cm-rep methodology described in [4] has the limitation that medial axes are difficult to explicitly parameterize along curves at which medial surfaces meet. Attempts to do so have been relatively ad hoc [6,7] and do not strictly adhere to the medial axis definition originally proposed in [8].

To overcome the challenge of modeling structures with branching medial topologies, a new boundary-centric deformable medial modeling paradigm has been proposed [9]. Rather than explicitly parameterizing a structure's medial axis and determining its boundary algorithmically as in [4], the new paradigm explicitly describes the model's boundary and implicitly maintains medial axis topology by imposing geometric constraints on the boundary of the model as it deforms. Since these constraints are nearly identical at the interior of the medial axis and along branch curves, the framework supports medial modeling of structures with branching medial axes while adhering to the medial axis definition in [8]. To date, the feasibility of modeling branching structures with this boundary-centric paradigm has only been demonstrated with a toy example and has not yet been translated to any real-world applications. The contribution of the present work is to leverage this paradigm for visual, quantitative, and statistical shape analysis of the aortic valve in 3DE images. This work conceptually demonstrates that deformable medial modeling is not limited to anatomical structures with simple shape; it is potentially applicable to a wider range of clinical problems that involve anatomical structures with complex geometries.

2 Materials and Methods

2.1 Background on Medial Axis Representation

Medial axis representation, which describes an object's geometry in terms of its morphological skeleton [8], combines the attractive features of boundary and region-based shape representations by defining a continuous relationship between the structure's boundary and interior. Suppose an object represented by the set $S\subset {\mathbb{R}}^N$ has a smooth boundary ∂S. The medial axis transform (MAT) of S is a mapping between points on ∂S and points on the object's interior that are centers of the maximally inscribed balls (MIBs) of S. An MIB is defined as a ball B inscribed in S that satisfies the condition that there exists no other ball B′ ⊂ S such that B ⊂ B′ Note that in 3D the centers of the MIBs define a continuous surface, i.e. a medial manifold. Multiple medial manifolds join at seams, which are curves in 3D.

In the deformable medial modeling framework originally proposed in [4], a 3D cm-rep is a discretized model of an object's continuous medial axis comprising one or more medial manifolds. Object thickness is parametrically represented as a scalar field defined over the medial manifold(s). The deformable medial model is defined by tuples of values {m, R}, where m refers to the 3D coordinates of points on the medial manifold(s) and R is the radial thickness associated with m, or equivalently the distance between m and the closest point on ∂S. During model deformation, the values {m, R} are updated to capture the medial geometry of the target object, and the model's boundary is derived analytically by inverting the MAT. Model deformation is an optimization problem that maximizes the overlap of the cm-rep with an image region. Constraints that ensure valid medial geometry are enforced as soft penalties in the objective function.

Alternatively, in the constrained boundary-centric deformable medial modeling framework proposed in [9], ∂S is explicitly parameterized and the MAT of S is encoded by grouping tuples of points on ∂S using “medial links”. For example, two boundary points x₁, x₂ ∈ ∂S are defined as being medially linked if they are both members of the same MIB in S. Note that MIBs may be associated with one, two, or three medially linked boundary points depending on their position along the medial axis (Fig. 1a). This boundary-centric approach to medial representation leverages the fact that transformations of S that preserve medial links also preserve the branching structure of the medial axis. The following are the sufficient conditions for a transformation to preserve medial links. A ball with center m ∈ S and radius R is tangent to ∂S at a point x if and only if m = x − RN where N is the outward unit normal to ∂S at X. Such a ball is an MIB in S if ∀y ∈ ∂S, ‖y − m‖ ≥ R. This observation leads to the condition that two points x₁, x₂ ∈ ∂S are medially linked if and only if there exists R < 0 such that x₁ − RN₁ = x₂ − RN₂ and ‖y − (x₁ − RN₁)‖ < R for all y ∈ ∂S. In [9], constrained optimization is used to ensure that these conditions are satisfied during model deformation. Additional hard constraints are used to enforce geometric quality on the discretization of ∂S during deformation. Since the constraints are nearly the same on the interior of the medial axis as they are along branch curves, this latter approach to deformable medial modeling circumvents the challenge of explicitly parameterizing the medial axis at branch curves.

Fig. 1.

(a) Diagram of 2D medial geometry showing an object's boundary (gray), medial axis (dashed green curves), and several MIBs (black circles). Centers of MIBs (red, pink, blue) are associated with one, two, or three linked boundary points (marked by colored lines) depending on their location along the medial axis. The blue point is a branch point in the medial axis. Note that this diagram is 2D for illustrative purposes only; model fitting is performed entirely in 3D. (b) Model of the aortic root and cusps viewed from the ascending aorta. (c) Deformable model of the aortic valve apparatus, clipped with respect to the red reference rectangle in (b). The model's medial manifolds are green and boundary is gray. Blue arrows point to branch points where the medial manifolds of the cusps and sinuses meet. (d) Slice of the original 3D image oriented with respect to the red reference rectangle in (b). (RC = right coronary cusp, LC = left coronary cusp, NC = non-coronary cusp).

2.2 Medial Modeling of the Aortic Valve Complex

The aortic valve apparatus is an anatomic structure with a branching medial axis, meaning that the medial axis consists of several surfaces that meet at curves, referred to as seams. Our delineation of the aortic valve extends from the outflow of the left ventricle to the STJ and includes the bulbous aortic sinuses and three cusps (Fig. 1b–c). The aortic root is modeled as a tubular shape to which three fin-like structures (the aortic cusps) are attached. The semilunar attachments of the cusps are seams in the medial axis. Free edges occur at the level of the left ventricular outflow and STJ, as well as the cusps' free margins.

Deformable modeling requires a pre-defined model, or template, of the anatomic structure of interest. Template generation involves manual interaction, but the deformable model is generated only once and thereafter is used to segment new instances of the target structure. To obtain a medial model of the aortic valve complex, the 3D Voronoi skeleton of a manually segmented valve is first generated (Fig. 2a–b). Then a triangulated mesh is created with an interactive tool that allows the user to select and triangulate points on the object's skeleton. The result is a coarse representation of the aortic valve's medial axis, shown in Fig. 2c. To obtain a boundary mesh from the skeleton, a duplicate of the medial mesh is created and the two copies of the mesh are “inflated” to give the aortic root walls and cusps finite thickness (Fig. 2d). Connectivity and vertex modifications are made to ensure proper medial linkage. Medial links are encoded on the boundary mesh by assigning each vertex i a medial link index. $M_i\in \mathbb{N}$. Any two mesh vertices i,j that satisfy M_i = M_j are considered medially linked, meaning that they are members of the same MIB. Boundary vertices may be medially linked to two, three, or no other boundary vertices depending on where the MIB is located on the medial axis (on the interior, along a seam, or on an edge).

Fig. 2.

The boundary template generation process. (a) Manual segmentation of the aortic valve complex viewed from the side. (b) Voronoi skeleton of the manual segmentation. (c) Triangulated mesh of the medial axis. (d) Boundary mesh (translucent) generated from the medial mesh (red). (e) Three views of the final template from a side (left), ventricular (center), and aortic (right) perspective. (LVO = left ventricular outflow).

Multi-atlas Segmentation

To guide model fitting to a target 3DE image, a preliminary segmentation of the aortic valve apparatus is obtained by multi-atlas label fusion. Briefly, a collection of atlases (3DE images and labels for the aortic valve components) is registered to a target image, first with a landmark-guided affine transformation and then diffeomorphic deformable registration. The candidate segmentations generated by each atlas are fused to create a consensus segmentation using the weighted voting method detailed in [10]. Five manually identified landmarks are used for registration initialization: three aortic commissures and two points marking the centers of the outflow tract at the level of left ventricle and the STJ. The reference atlas set is described in Section 2.3.

Model Fitting

In [9], the fitting of a medially constrained parametric boundary model to a target image is implemented as an iterative closest point (ICP) surface-matching problem. Since ICP is sensitive to initialization, deformable registration between the template in Fig. 2 and the multi-atlas segmentation of the target image is first performed to initialize the template prior to ICP surface matching. Then during ICP surface matching, the objective function of the constrained optimization function incorporates both the dissimilarity between the deforming model and target multi-atlas segmentation, as well as irregularity of the deforming mesh. The constraints include the inequalities described in Section 2.1 that preserve medial linkages, as well as mesh quality constraints. The variables in the optimization problem are the boundary vertex coordinates, as well as additional “helper” variables (such as the unit normal vector to each boundary vertex) introduced in order to make the constraints quadratic. Optimization is performed using the Ipopt method [11].

2.3 Dataset and Segmentation Evaluation

Automated segmentation of the aortic valve apparatus was evaluated in a leave-one-out cross-validation on a set of transesophageal 3DE images obtained from 11 human subjects with normal aortic valve morphology. These subjects underwent cardiac surgery for reasons unrelated to the aortic valve. The images were acquired pre-operatively with the iE33 platform (Philips Medical Systems, Andover, MA) using a 2 to 7 MHz matrix-array transducer. For each subject, a 3DE image of the aortic valve at mid systole was selected for analysis. The images were exported with an approximate size of 224 × 208 × 208 voxels with nearly isotropic resolution of 0.4 to 0.8 mm. To evaluate segmentation accuracy, each 3DE dataset was segmented using the other 10 datasets as reference atlases for multi-atlas segmentation. The automated and manual segmentations were compared based on symmetric mean boundary displacement.

3 Results

The original boundary mesh of the aortic valve complex had 433 vertices and 866 triangles. Fig. 3 illustrates a representative deformable model of the aortic valve (fitted to the results of multi-atlas segmentation) overlaid on the corresponding manual segmentation.

Fig. 3.

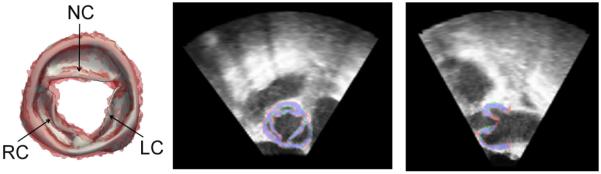
(Left) Fitted model of the aortic valve complex (gray) overlaid on the manual segmentation (red) as viewed from the ascending aorta. (Right) Cross-sections of the 3DE image of the aortic valve with the manual segmentation in red and the model fitting in green. Overlap of the manual and automated segmentations is shown in blue. (RC = right coronary cusp, NC = non-coronary cusp, LC = left coronary cusp).

The mean boundary displacement (MBD) between the manual segmentations and the deformable model fitted to the results of multi-atlas segmentation was 0.6 ± 0.1 mm. The MBD and the mean difference in the radial thickness are shown in color on a mean model of the aortic valve in Fig. 4. For reference, the MBD between the manual segmentations and the deformable models fitted directly to the manual segmentations was 0.4 ± 0.03 mm, and the MBD between the manual and multi-atlas segmentations without any model fitting was 0.6 ± 0.1 mm.

Fig. 4.

Mean boundary displacement (top row) and mean difference in radial thickness (R_diff, bottom row) are displayed in color on a mean model of the aortic valve complex. The valve is shown from three viewpoints: aortic (left), side (center), and ventricular (right) perspectives. (LC = left coronary, NC = non-coronary, RC = right coronary, STJ = sinotubular junction, LVO = left ventricular outflow).

4 Discussion

This study is the first to demonstrate that deformable medial modeling can effectively represent an anatomical structure with a branching medial topology in a way that adheres to Blum's original definition of the medial axis. By preserving the branching configuration of the medial axis during model deformation, the method produces patient-specific anatomical shape representations that have inter-subject point correspondences and can be statistically compared in a straightforward manner. The method extends the utility of medial modeling for medical image and statistical shape analysis since many structures in the human body have complex geometries that cannot be represented in terms of a non-branching morphological skeleton.

The aortic valve has a branching medial geometry that is well suited for the deformable modeling paradigm proposed in [9]. To assess the ability of the deformable medial model to capture this complex geometry, the model was fitted directly to the 11 manual segmentations and the MBD was computed. The resulting MBD of 0.4 ± 0.03 mm demonstrates that the medial model can indeed capture the shape of the aortic valve apparatus. The MBD between the manual segmentation and the medial models fitted to the results of multi-atlas segmentation (0.6 ± 0.1 mm) was on the order of one voxel. The similarity of the multi-atlas and manual segmentations (without model fitting) was nearly identical, suggesting that improvements in multi-atlas segmentation could enhance the accuracy of deformable medial modeling. The advantage of a medial representation over the multi-atlas segmentation alone is that the model identifies landmarks and facilitates statistical comparison of shape features such as thickness.

The manual versus automatic segmentation comparison in this study is on par with one of few studies on automatic aortic valve segmentation in 3DE images, wherein the authors report an MBD of 1.54 ± 1.17 mm [1]. As shown in Fig. 4, the localized MBD is uniformly low across most of the sinus segments and cusps, with the largest error occurring at the STJ. This localized error is not surprising, since the STJ is an anatomical boundary rather than an intensity-based boundary in the 3DE image. While this study is a proof of concept of the branching medial modeling framework proposed in [9], future work will focus on the clinical application of medial modeling of the aortic valve apparatus, including image segmentation of pathological cases and of the valve at multiple time points in the cardiac cycle.