Nonparametric Bayesian Bi-Clustering for Next Generation Sequencing Count Data

Abstract

Histone modifications (HMs) play important roles in transcription through post-translational modifications. Combinations of HMs, known as chromatin signatures, encode specific messages for gene regulation. We therefore expect that inference on possible clustering of HMs and an annotation of genomic locations on the basis of such clustering can contribute new insights about the functions of regulatory elements and their relationships to combinations of HMs. We propose a nonparametric Bayesian local clustering Poisson model (NoB-LCP) to facilitate posterior inference on two-dimensional clustering of HMs and genomic locations. The NoB-LCP clusters HMs into HM sets and lets each HM set define its own clustering of genomic locations. Furthermore, it probabilistically excludes HMs and genomic locations that are irrelevant to clustering. By doing so, the proposed model effectively identifies important sets of HMs and groups regulatory elements with similar functionality based on HM patterns.

1 Introduction

Histones are proteins that package DNA into structural units called nucleosomes. Through post-translational modifications, histones play key roles in transcription (Bernstein et al. (2002); Roh et al. (2005)), chromosomal segregation (Andersson et al. (2009)), and DNA repair. Combinations of such histone modifications (HMs) are known as the “histone code”, which modulates chromatin structure to regulate gene expression. For example, combinations of HMs have been linked to cancer prognosis (Kurdistani (2007)) and clinical decisions (Kurdistani (2011)).

Recently, several HM patterns have been shown to be associated with various classes of regulatory elements, known as chromatin signatures (Bernstein et al. (2006)). For example, distinct and predictive chromatin signatures are used to characterize active promoters and enhancers (Heintzman et al. (2007); Heintzman et al. (2009)). These results lead us to look for more such patterns. We expect that regulatory elements with similar functionality are likely to share similar patterns of some subset of HMs. We conjecture that annotating genomic location on the basis of such patterns could be a promising step towards deciphering the histone code.

We consider data from ChIP-Seq experiments, which are applications of next generation sequencing (NGS) technology and will be introduced in the next Section. The sequencing data is a matrix of HM counts, with rows representing genomic locations and columns representing HMs. Traditional one-dimensional clustering techniques aim to partition either the HMs or genomic locations. While useful, such clustering methods are often inadequate to identify co-localized HMs that are important factors in deciding functions of genomic regions. In addition, how genomic regions cluster should depend on which subset of HMs we focus on. Difierent HM sets might partition genomic locations in difierent ways, which might indicate difierent cellular or chromatin states.

These considerations lead us to consider two-dimensional clustering. Getz et al. (2000) presented a coupled two-way clustering approach that employs hierarchical clustering to each separate dimension, combining the clustering results along each dimension in a problem-specific manner. Later, Cheng and Church (2000) introduced the concept of biclustering to find biclusters within a data matrix. They proposed a quantitative measure as a guide to search for biclusters in gene expression data. Lazzeroni and Owen (2002) developed the plaid model that describes gene expression data as a sum of biclusters. In their model, each bicluster contains a group of genes expressed similarly within a given set of samples, indicating the presence of a particular biological process. Turner et al. (2005) proposed an improved algorithm for fitting the plaid model. Li et al. (2009) reported an effective and computationally efficient biclustering algorithm, QUBIC, to identify overlapping biclusters by employing a combination of qualitative measures of gene expression data and a combinatorial optimization technique.

We extend these approaches to incorporate two important new features: first, we develop models for discrete count data as opposed to continuous measurements. Second, we introduce full model-based inference that defines a posterior probability model for the random partitions, including a full probabilistic description of the associated uncertainties. Specifically, we propose a nonparametric Bayesian local clustering Poisson model (NoB-LCP) to close this gap in the existing literature. The proposed method builds on Lee et al. (2013a) who developed bi-directional clustering for continuous protein activation data. The proposed NoB-LCP model clusters any two HMs (columns) together if they give rise to the same partition of genomic locations. That is, the partitions of genomic locations (rows) are nested within clusters of HMs, with a separate partition of locations for each HM cluster. This definition of HM clusters based on inducing the same (nested) clustering of genomic locations distinguishes the proposed model from most currently used models, including Bayesian nonparametric approaches, that define clusters based on common parameters in the sampling model. We will refer to the column clusters as “HM clusters” and to the row clusters as “location clusters”. Location clusters can be used to define difierent functional signatures that are characterized by subsets of HMs, while HM clusters suggest unique combinatory patterns that annotate chromatin states. One advantage of nonparametric Bayesian clustering is that it provides model-based posterior probability models for the random partitions. It entirely avoids the problem of specifying the number of clusters in advance. Another key difierence between NoB-LCP and other biclustering methods is that we allow that some HMs and some genomic locations might not meaningfully cluster with the other HMs or locations. In practice, experimental data usually include noisy rows and/or columns that are irrelevant to the scientific problem being addressed. Excluding them significantly increases the power of detecting meaningful signals in the remaining rows and columns.

The paper proceeds as follows. We introduce the motivating application and the data set in Section 2. In Section 3, we present probability models and computational methods for posterior inference. We present a simulation study in Section 4, and in Section 5, we report inference results on the ChIP-Seq data. We conclude with a discussion in Section 6.

2 ChIP-Seq Data

ChIP-Seq integrates chromatin immunoprecipitation (ChIP) with massively parallel DNA sequencing (Seq) to identify genome-wide expression patterns of DNA-binding proteins. ChIP-Seq data record the counts of sequence tags mapped onto non-overlapping positions that cover the genome. By applying HM-specific antibodies, ChIP-Seq experiments can record the counts of DNA fragments that include a certain HM. And the fragments are mapped to specific locations across the whole genome. A large count of DNA fragments indicates high occurrence of the targeted HM.

We consider a ChIP-Seq experiment for CD4+ T lymphocytes (Barski et al. (2007); Wang et al. (2008)), in which 39 types of HMs, including 18 acetylations, 20 methylations, and a special histone modification H2A.Z, are reported. We focus on genomic locations with at least one enriched HM for meaningful inference and use the peak- calling program SICER (Zang et al. (2009)) to decide enrichment. SICER parameters were set to W SIZE=200, GAP SIZE=600, EVALUE=1000, FRAG SIZE=150. Also any adjacent windows with unchanged SICER calls for the 39 HM counts are merged to create larger regions.

3 Methodology

3.1 Probability Model

The ChIP-Seq data is arranged in an N × G matrix Y = [y_ig ] with each element y_ig representing the read count for HM g in genomic location i, i = 1, 2, …, N and g = 1, 2, …, G. Here, genomic locations are defined as windows of 200 base pairs. We start the model construction with a random partition of HMs {1, …, G} into non-overlapping subsets C_q as {1, …, G} = ${\bigcup }_{q=0}^Q{C}_q$. The unusual indexing starting with q = 0 is in anticipation of the upcoming discussion. The number Q + 1 of subsets is random itself. It is part of the random partition {C₀, …, C_Q}. In the following discussion we find it convenient to index the partition equivalently by cluster membership indicators c_g, g = 1, …, G with c_g = q if g ∈ C_q. Under the proposed model some HMs are singled out as not giving rise to a nested partition of genomic locations. We refer to these HMs as the “idle HMs”, and to the remaining ones as “active HMs”. We use the special cluster C₀ to combine the idle HMs, i.e., c_g = 0 for all idle HMs. Assume that there are G^′ < G active HMs and (G − G^′) idle HMs. We propose a zero-enriched Pólya urn (Sivaganesan et al. (2011)) prior for c = (c₁, c₂, …, c_G)^T:

$$P\left(c\right)={\pi }_0^{G^{\prime }}{(1-{\pi }_0)}^{G-G^{\prime }}\frac{{\alpha }^Q{\Pi }_{q=1}^Q\Gamma \left(p_q\right)}{{\Pi }_{q=1}^{G^{\prime }}(\alpha +g-1)}$$ (1)

where p_q is the number of HMs in HM set q and α is the total mass parameter of the Pólya urn scheme. Under this model, c_g = 0 with probability (1 − π₀), i.e., HM g falls into the idle HM set with probability (1 − π₀). When c_g is non-zero, HM g is either assigned to an existing active HM set q with probability proportional to p_q, or assigned to a new singleton active HM set with probability proportional to α. We refer to (1) as a nonparametric Bayesian prior model. The Pólya urn is traditionally considered a nonparametric Bayesian model since it can be constructed as the partition that is implied by the ties under i.i.d. sampling from a probability measure with a Dirichlet process prior. See, for example, a recent review by Lee et al. (2013b).

Next, we consider clustering of genomic locations for each of the Q active HM sets. Recall that the partition of locations is nested within HM sets, i.e., we want to allow for a difierent set of location clusters with respect to each HM cluster. We define r_q = (r_q1, r_q2, …, r_qN)^T to be the N cluster labels r_qi ∈ {0, …, D_q } that describe the partition of genomic locations corresponding to the q-th HM set. Again we allow for a special cluster r_qi = 0 of inactive genomic locations that do not meaningfully co-cluster with other loci with respect to the q-th HM set. We assume that r_q includes D_q active location clusters with r_qi = d indicating that locus i is assigned to active location cluster d, and r_qi = 0 indicating that genomic location i is assigned to the idle location cluster. Let $\mathbf{r}={({\mathbf{r}}_1^T,\dots ,{\mathbf{r}}_Q^T)}^T$. We assume independent zero-enriched Pólya urn priors for each r_q given by

$$P(r\mid c)=\prod _{q=1}^{Q}P\left(r_q\right)\text{and}P\left(r_q\right)={\pi }_1^{m_q}{(1-{\pi }_1)}^{N-m_q}\frac{{\beta }^{D_q}{\Pi }_{d=1}^{D_q}\Gamma \left(n_{qd}\right)}{{\Pi }_{i=1}^{m_q}(\beta +i-1)}.$$ (2)

Note that Q is random and depends on c. In (2), for a given active HM set q, n_qd is the number of genomic locations in the active location cluster d(> 0) and $m_q={\Sigma }_{d=1}^D{n}_{qd}$. In addition, β is the total mass parameter of the Pólya urn. The cluster label r_qi is allowed to be 0 with probability (1 − π₁), characterizing the idle location cluster.

The described prior probability model can be characterized as a partition of HMs and a nested partition of locations, nested within each (active) cluster of HMs. In words, we identify subsets of HMs that are characterized by the fact that genomic locations cluster into the same subsets with respect to all HMs in a HM cluster. These subsets will provide important information on the co-location patterns of HMs and actionable target HMs for diagnosis and prognosis. In addition, the resulting clusterings of genomic regions can be examined and integrated with other information (e.g., transcription binding sites) to potentially achieve better understanding of gene regulation.

Given c and r, we now define a sampling model for the observed counts y_ig. Let Poi(θ) denote a Poisson distribution with mean θ. We start with a Poisson sampling model for the count data, i.e.,

$$y_{ig}~\text{Poi}\left({\theta }_{ig}\right).$$

The prior probability model for θ_ig makes use of the clustering. Let Ga(a, b) denote a gamma distribution with mean a/b. We define P (θ_ig | c, r) as follows. Assume c_g = q and r_qi = d. The model gives meaning to the partition of locations by assuming a shared rate ${\tilde{\theta }}_{dg}$ for all locations in the same location cluster, i.e., θ_ig = ${\tilde{\theta }}_{dg}$ for all i with r_qi = d. But HMs in the same HM cluster share the same partition of locations only, not the same rate, i.e., ${\theta }_{jh}={\tilde{\theta }}_{dh}\ne {\tilde{\theta }}_{dg}$ for all (h, j) with c_h = q and r_qj = d and h ≠ g. We assume

$${\tilde{\theta }}_{dq}\stackrel{iid}{~}\text{Ga}(k_{0g},{\lambda }_{0g}),$$

For the idle genomic locations in the active HM sets, i.e., r_qi = 0 with q > 0, we assume a priori ${\theta }_{ig}\stackrel{iid}{~}\text{Ga}(k_{1g},{\lambda }_{1g})$. For idle HMs, i.e., c_g = 0, we assume ${\theta }_{ig}\stackrel{iid}{~}\text{Ga}(k_{2g},{\lambda }_{2g})$ for all locations i. Note that taking a Poisson sampling model with parameter θ_ig and a gamma prior for θ_ig, we equivalently constructed a negative binomial sampling model for the count data, which provides additional variabilities to account for potential over dispersion.

Finally, denoting with Beta(a, b) a beta distribution with parameters (a, b), we assume conditionally conjugate priors

$${\pi }_0~\text{Beta}(a_0,b_0),{\pi }_1~\text{Beta}(a_1,b_1).$$

The beta hyperprior on π₀ and π₁ is important to allow for inference about the number of active HMs and locations, as it allows adjustment of the priors p(c | π₀) and p(r_q | c, π₁) to adapt to the level of noise in the data. See, for example Scott and Berger (2010) for a discussion of this multiplicity correction feature.

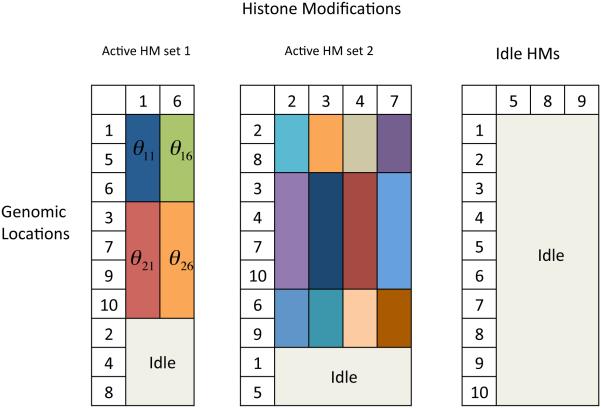
Figure 1 is a graphical illustration of the proposed NoB-LCP model. It demonstrates the core idea of how we define local clusters. In Figure 1, we assume that 9 HMs belong to two active HM sets and and an idle HM set, including HMs 5, 8 and 9. In the two active HM sets, cells in off-white are idle genomic locations. The rest of cells marked with the same color in the same column form local clusters of genomic locations (rows). Difierent colors indicate difierent values of parameters ${\tilde{\theta }}_{dg}$. Within each local cluster, the colors are the same across the genomic locations but difierent across difierent HMs. We define an active HM set as the set of HMs that partition the genomic locations in the same way, regardless of the actual values of ${\tilde{\theta }}_{dg}$. This highlights the important difierence between NoB-LCP and other clustering methods that often assume common values of ${\tilde{\theta }}_{dg}$ for items in the same cluster. In other words, in Figure 1, the cells in each local cluster would be marked in the same color across both genomic locations and HMs.

Figure 1.

An illustration of the proposed NoB-LCP model with 9 HMs and 10 genomic locations. There are two active HM sets and an idle HM set, including HMs 5, 8, 9. In the two active HM sets, cells in off-white are idle genomic locations. The rest of the cells marked with the same color in the same column form local clusters of genomic locations (rows). Difierent colors indicate difierent values of parameters ${\tilde{\theta }}_{dg}$.

In summary, the joint model is:

$$P(\mathbf{Y},\mathbf{c},\mathbf{r},\theta ,\mathbf{k},\lambda ,{\pi }_0,{\pi }_1)=P(\mathbf{Y}\mid \theta )P(\theta \mid \mathbf{c},\mathbf{r},\mathbf{k},\lambda )P(\mathbf{r}\mid \mathbf{c})P\left(\mathbf{c}\right)P\left({\pi }_0\right)P\left({\pi }_1\right).$$ (3)

3.2 Markov Chain Monte Carlo Simulations

We carry out posterior inference using MCMC simulation. Letting [x | y, z] generically denote a transition density that updates an unknown parameter x conditional on currently imputed values for y and z, we propose a Gibbs sampler that iterates over the following sampling steps that draw random values from the transition densities:

$$[\mathbf{r}\mid \mathbf{Y},\mathbf{c},{\pi }_1],[\mathbf{c}\mid \mathbf{Y},\mathbf{r},{\pi }_0],[\theta \mid \mathbf{Y},\mathbf{c},\mathbf{r}],[{\pi }_0\mid \mathbf{c}],[{\pi }_1\mid \mathbf{c},\mathbf{r}]$$

We start by generating r_qi, q = 1, …, G^′, i = 1, …, N, from its full conditional posterior distribution. When resampling r_qi and c_g, we marginalize over θ.

Let Q denote the currently imputed number of active HM clusters. A challenge in constructing a valid transition probability arises when c_g = Q + 1 is considered, i.e., when we consider placing g into a new, (Q + 1)-th, singleton HM cluster. The problem is that a proposal c_g = Q + 1 gives rise to a new partition r_Q+1 of locations. We use the pseudo prior mechanism of Carlin and Chib (1995) to construct an MCMC scheme. We introduce a set of auxiliary variables ${\tilde{\mathbf{r}}}_g=({\tilde{r}}_{ig},i=1,2,\dots ,N)$, g = 1, 2, …, G, and augment the probability model with a pseudo prior $P({\tilde{\mathbf{r}}}_g\mid {\pi }_1)$. Let $p_{1g}({\tilde{\mathbf{r}}}_g\mid {\pi }_1)$ denote the conditional posterior of the location partition with respect to a singleton HM cluster {g}. We define $P({\tilde{\mathbf{r}}}_g\mid {\pi }_1)=p_{1g}({\tilde{\mathbf{r}}}_g\mid {\pi }_1)$. Think of ${\tilde{r}}_g$ as a potential genomic location partition with respect to a singleton HM set {g}. In other words, when a new singleton HM set is proposed for c_g, the proposal distribution for the genomic location clusters under this new HM set is determined by imputed value ${\tilde{r}}_g$. Lastly we draw θ, π₀ and π₁ whose full conditional posterior distributions are in closed forms. More MCMC technical details are included in the Appendix.

3.3 Posterior Inference

A practical challenge related to posterior inference is the need to summarize a distribution over random partitions. Medvedovic et al. (2004) initially addressed this problem by estimating posterior probabilities that any two HMs are clustered together. They evaluated probabilities H_gh = P (c_g = c_h | data) of pair-wise co-clustering, and used H as a distance matrix for a (deterministic) hierarchical clustering algorithm. Alternatively, Dahl (2006) proposed a point estimate of a random partition under a Dirichlet process mixture model by reporting a least-squares partition. Specifically, the least-squares clustering c^LS is the observed clustering c which minimizes the Frobenius distance (L₂ norm for matrices) between S^c and H, where S^c is an association G × G matrix whose (g, g^′) element is an indicator that HM g is clustered with HM g^′. We include HMs in the idle HM set by letting $s_{g,g^{\prime }}^c$ = 0 for all g^′ if c_g = 0. Following Dahl (2006), we propose a least-square summary

$${\mathbf{c}}^{LS}=\text{arg}{\text{min}}_c\parallel S^c-H{\parallel }^2,$$

as a point estimate of the clustering of HMs, which minimizes the sum of the squared deviation of association matrix S from the matrix H of the posterior pairwise co-clustering probabilities. Given c^LS, we compute ${\mathbf{r}}_q^{LS}$, the least square estimate of the clustering for genomic locations, based on the same formulation.

4 Simulation Studies

4.1 Simulation setup

We conducted simulation studies to evaluate the performance of the proposed NoB-LCP model. We compared posterior inference with the simulation truth and with inference under two alternative clustering methods, the plaid model and the QUBIC. Furthermore, to show the importance of zero-enriched Pólya urn priors which allow some HMs or genomic locations to be idle, we performed a sensitivity analysis by using regular Pólya urn priors without zero-enrichment as the prior for the random partitions of HMs and genomic locations. It means that we let π₀ = 1 and π₁ = 1 in (1) and (2) respectively.

We simulated a data matrix Y with N = 300 genomic locations and G = 18 HMs. We let 13 out of 18 HMs belong to two active HM sets, in which HMs 1-7 belonged to set 1 and HMs 8-13 to set 2. The remaining 5 HMs, HMs 14–18, belonged to the idle HM set. We assumed that the active HM set 1 partitioned the genomic locations into four location clusters including one idle location cluster, i.e., D₁ = 3, and that the active HM set 2 partitioned the genomic locations into three location clusters including one idle location cluster, i.e., D₂ = 2. We generated location cluster labels, r_qi, for each active HM set assuming that a genomic location belonged to one of the location clusters with equal probability. In keeping with the definition of the idle HM set (q = 0), we did not generate location clusters with respect to the idle HMs with c_g = 0. We fixed ${\tilde{\theta }}_{dg}$ for all the active location clusters for each of the 13 HMs residing in the active HM set as listed in Table 1. Finally, denoting with NB(mean = a, size = b) a negative binomial distribution with mean=a, variance=a+a²/b and with Unif(0, 1) a Uniform distribution on (0, 1), the remaining θ_ig were independently generated from NB(mean = µ, size = 1), where µ ~ Unif(0, 10), including the idle genomic locations in the active HM sets and all the genomic locations in the idle HM set. The NB distribution was chosen to examine the sensitivity of posterior inference with respect to deviations from the assumed Poisson sampling model.

Table 1.

The true mean counts for active genomic location clusters, ${\tilde{\theta }}_{dg}$, in the simulated data.

		HM 1	HM 2	HM 3	HM 4	HM 5	HM 6	HM 7
HM set 1	cluster 1	11	9	7	13	13	9	13
	cluster 2	15	7	15	7	9	7	7
	cluster 3	13	11	9	9	7	11	15

		HM 8	HM 9	HM 10	HM 11	HM 12	HM 13
HM set 2	cluster 1	9	15	9	11	7	9
	cluster 2	11	11	15	9	13	7

4.2 Simulation Results

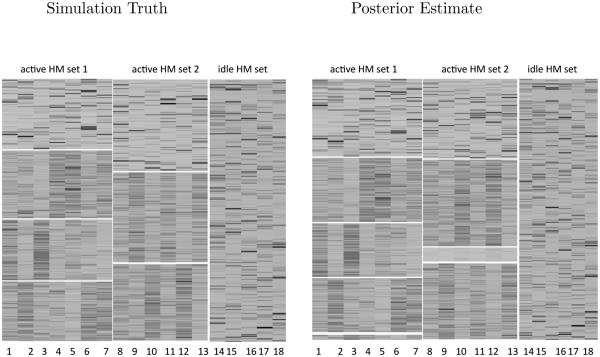
The left panel of Figure 2 shows the heatmaps of y_ig under the simulation truth. After rearranging the HMs and the genomic locations within each active HM set according to the simulation truth, we can clearly observe the local clustering patterns in the data. In the active HM sets, the idle genomic locations, which are located in the first row block, do not show a noticeable pattern: the colors are more or less randomly scattered. In contrast, the active genomic locations in the columns corresponding to active HM sets show clear patterns and the colors are more homogeneous within each location cluster. In the idle HM set, since the genomic locations do not cluster, the corresponding color mapping exhibits large variability.

Figure 2.

Heatmaps of the HM sets in the simulation truth versus the identified HM sets under the NoB-LCP model. The first row block of each active HM set is the idle genomic location cluster for that HM set. The remaining blocks are active genomic location clusters. The division of genomic location clusters is indicated by white horizontal lines

We applied the proposed NoB-LCP model to the simulated data. In the MCMC posterior simulation, we initialized the HMs allocation variable c using the clustering result from hierarchical clustering by cutting the dendrogram to achieve two active HM sets and one idle HM set. HMs 2, 4, 5 and 6 belonged to active HM set 1, HMs 8, 11 and 13 belonged to active HM set 2 and the remaining belonged to the idle HM set. The initial values and priors of π₀ and π₁ were set to 0.5 and Beta(1, 1), respectively. We fixed parameters k_0g and λ_0g by setting the mean of ${\tilde{\theta }}_{dg}$ equal to g-th column mean of Y and setting the variance of ${\tilde{\theta }}_{dg}$ equal to 10. Finally, k_1g, λ_1g, k_2g and λ_2g were computed by setting the mean of θ_ig equal to g-th column mean of Y and variance equal to 50. After 10,000 MCMC iterations with 5,000 burn-in, the Markov chains converged and mixed well. We conducted convergence diagnostics using the R package coda and found no evidence for convergence problems. Traceplots and empirical autocorrelation plots (not shown) for the imputed parameters indicate a well mixing Markov chain. For example, the empirical autocorrelation of π₀ and π₁ is practically zero beyond lag 2. The simulation was carried out on a MacBook Pro laptop with 2.53 GHz Intel Core and 8GB memory. Computation was completed in 2.5 hours.

The least-squares summary of the posterior on c was c^LS = (1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 0, 0, 0, 0, 0). Conditional on c^LS, we further calculated the least-squares estimates of genomic location clusters for active HM sets, r^LS, q = 1, 2. Figure 2 right panel shows that the NoB-LCP model correctly detected the two active HM sets in the simulation data: HMs 1-7 belonged to the active HM set 1 and HMs 8-13 belonged to the active HM set 2, the remaining HMs belonged to the idle HM set, consistent with the simulation truth. Tables 2 and 3 show that there are five estimated active genomic location clusters and one idle genomic location cluster for HM set 1, where clusters {0, 1, 2, 3} dominate and largely overlap with the four true genomic location clusters. And the model identified four active genomic location clusters and one idle genomic location cluster with respect to HM cluster 2, where clusters {0, 1, 2} dominated and largely overlapped with the three true genomic location clusters of true HM set 2.

Table 2.

The number of genomic locations in each genomic location cluster for active HM sets.

	0	1	2	3	4	5
active HM set 1	89	75	63	64	1	8
active HM set 2	91	101	18	89	1	-

Table 3.

Comparisons of the location cluster membership estimated by the NoB-LCP model with the true location cluster membership.

HM set 1
${\mathbf{c}}_1^{LS}$
cTRUE	0	1	2	3	4	5
d=0	80	0	0	0	0	0
d=1	3	68	1	1	1	3
d=2	5	0	61	1	0	4
d=3	0	7	1	60	0	1

HM set 2
${\mathbf{c}}_2^{LS}$
cTRUE	0	1	2	3	4
d=0	87	0	0	18	0
d=1	3	85	17	0	0
d=2	1	4	84	0	1

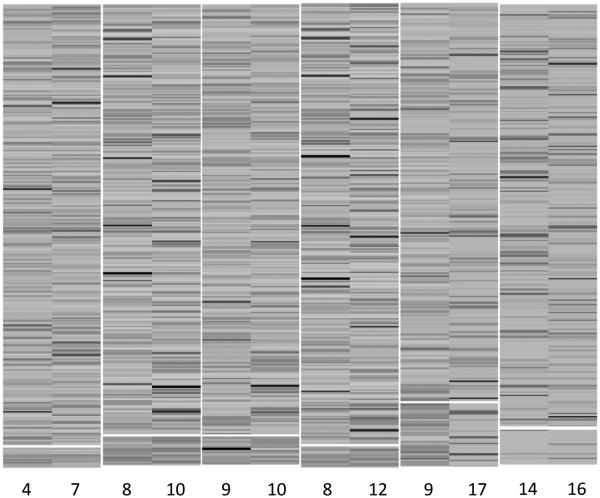
For comparison, the two alternative methods, the plaid model and QUBIC, were applied to the same simulated data. Figure 3 shows the heatmaps of HMs in two biclusters identified by the plaid model. The first bicluster included 18 genomic locations of HMs 8, 9, 10, 11 and 12, all of which belonged to true genomic location cluster d = 0 of true HM set 2. The second bicluster included 37 genomic locations of HMs 14 and 15, which belonged to the idle HM set under the simulation truth. The QUBIC method detected 23 biclusters, 17 of which only included one single HM and the other six included two HMs. Figure 4 shows the heatmaps of HMs in the six biclusters with two HMs. Some of those six biclusters included idle HMs such as HMs 14, 16 and 17, and others included either idle genomic locations, active genomic locations, or multiple active location sets. For example, bicluster 1 included 15 genomic locations of HMs 4 and 7, among which 7 belonged to the true genomic location cluster d = 1 of true HM set 1, and 5 belonged to the true genomic location cluster d = 2 of true HM set 1; bicluster 2 included 21 genomic locations of HMs 8 and 10, among which 17 belonged to the true genomic location cluster d = 2 of true HM set 2.

Figure 3.

Heatmaps of HMs in two biclusters of the simulated data identified by the plaid model. The division of genomic locations is indicated by white horizontal lines. Below the white line is the detected bi-cluster.

Figure 4.

Heatmaps of HMs in six biclusters for the simulated data identified by QUBIC. The division of genomic locations is indicated by white horizontal lines. Below the white line is the detected bi-cluster.

Next we replaced the zero-enriched Pólya urn priors in (1) and (2) with regular Pólya urn priors. And we used the same hyperparameters and initialized the parameters as before, except for c. We initialized c by letting HMs 1-13 belong to active HM set 1 and HMs 14-18 belong to active set 2. After 10,000 iterations of MCMC simulation with 5,000 burn-in, the Markov chains converged and mixed well.

The least-squares summary of the posterior on c was c^LS = (1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2). Conditional on c^LS, we further calculated the least-squares estimates of genomic location clusters for active HM sets, ${\mathbf{r}}_q^{LS}$, q = 1, 2. Figure 5 shows the heatmaps of two detected active HM sets. Compared to the simulation truth, the model with regular Pólya urn priors failed to difierentiate the two active HM sets. In addition, many small and meaningless genomic location clusters nested within two active HM sets can be observed.

Figure 5.

Heatmaps of HMs in two active HM sets for the simulated data identified by the model with regular Pólya urn priors without zero-enrichment. The division of genomic locations is indicated by white horizontal lines.

5 ChIP-Seq Data Analysis

We present local clustering results for the ChIP-Seq data described in Section 2. For demonstration purpose, we apply our NoB-LCP model to clustering of promoters and insulators, both of which are important regulatory elements. Information on the genomic location for promoters was obtained from the UCSC Genome Browser (Fujita et al. (2011)). Read counts were recorded for all genomic locations and all HMs. The insulator information was obtained from the CTCFBSDB (Bao et al. (2008)), a CTCF binding site database to identify insulators.

We consider a small subset of the ChIP-Seq data covering randomly selected 50 genomic locations in promoter regions and 50 genomic locations in insulator regions. The data is a 100 × 39 matrix with genomic locations as rows and HMs as columns. To fit the NoB-LCP model, c is initialized by the clustering determined by a (deterministic) hierarchical clustering algorithm. We chose parameters k_0g and λ_0g by fixing the prior variance of ${\tilde{\theta }}_{dg}$ at Var(${\tilde{\theta }}_{dg}$) = 10, and matching the mean of ${\tilde{\theta }}_{dg}$ with the column means of the data matrix. Similarly, k_1g, λ_1g, k_2g and λ_2g are chosen by fixing the prior variance at 50, and matching the prior mean of θ_ig with the column means. Finally, π₀ and π₁ are initially set to 0.5 and we used a₀ = b₀ = a₁ = b₁ = 1, i.e., uniform hyperpriors. After 10,000 iterations with a 5,000 burn-in for MCMC posterior simulation, we evaluated convergence diagnostics (R package coda) and found no evidence for practical convergence problems. The chain mixed well.

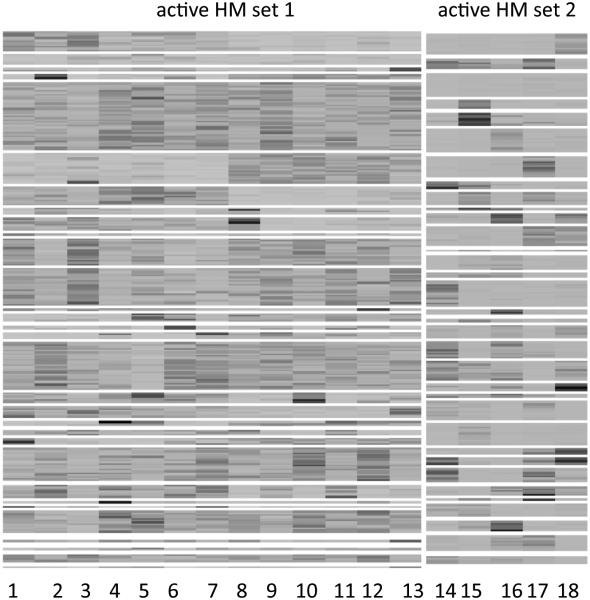
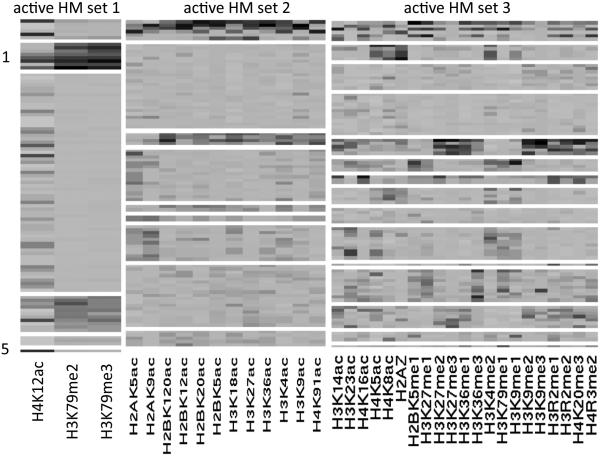
We compute the least-squares estimates c^LS and r^LS to summarize posterior inference. The NoB-LCP model identifies 3 active HM sets, each of which partitions genomic locations difierently. Figure 6 shows the heatmaps of all active HM sets. These three sets are candidates of co-localized HMs that relate to gene transcription. In addition, the heatmap shows genomic location clusters nested in each active HM set.

Figure 6.

Heatmaps of three active HM sets for ChIP-Seq data. White horizontal lines indicate division of location clusters.

Posterior inference distinguishes difierent types of regulatory elements and clusters similar types together reasonably well. For example, active HM set 1 includes the following HMs: H4K12ac, H3K79me2, H3K79me3. Genomic location clusters 1 and 5 in active HM set 1 include only promoter regions, in which H4K12ac, H3K79me2 and H3K79me3 clearly show relatively high expression in Figure 6. Our results are consistent with previous findings that H4K12ac counts are elevated in the promoter and transcribed regions of active genes (Wang et al. (2008)), H3K79me2 and H3K79me3 are important histone markers for the prediction of promoter regions (Wang et al. (2009); Weishaupt et al. (2010)). Out of the 12 HMs in active HM set 2, all of them are acetylations; out of the 21 HMs in active HM set 3, 15 of them are methylations. From this fact, we can conjecture that the same types of histone modifications (methylations, acetylations, etc.) are more likely to be clustered together.

In addition, highly correlated HM patterns can be identified by our model. For example, active HM set 2 includes the following HMs: H2BK120ac, H2BK12ac, H2BK20ac, H2BK5ac, H3K18ac, H3K27ac, H3K36ac, H3K4ac, H3K9ac, and H4K91ac, which were reported to have relatively high correlation according to Wang et al. (2008).

For comparison, we applied the plaid model and QUBIC to the same ChIP-Seq data.

The plaid model did not report any biclusters. QUBIC found 57 biclusters, but none of them provide us clear divisions of regulatory elements. In addition, it is not easy to extract useful information from so many biclusters.

Finally, we used a qq-plot to validate the assumed sampling model. Assuming a Poisson/gamma hierarchical sampling model, we have implicitly defined a negative binomial marginal sampling model. The negative binomial model allows larger variabilities in modeling the counts. We made a qq-plot of the empirical c.d.f. of the observed ChIP-Seq data versus simulated data sampled from the imputed negative binomial distribution. We can see a linear relationship between two quantiles, suggesting that the hierarchical sampling model is well calibrated (Figure not shown).

6 Discussion

We propose a nonparametric Bayesian local clustering Poisson model for a count data matrix. The NoB-LCP model detects local clustering patterns by performing simultaneous clustering on columns and rows of a data matrix. Idle local clusters are introduced to better separate noisy HMs and location from the actual signals in the genomics data. Through simulation studies and the analysis of ChIP-Seq data we demonstrate the effectiveness of our model in grouping regulatory elements with similar functionality based on HMs patterns.

In this paper, we used zero-enriched Pólya urn priors to model random partitions of HMs and genomic locations. Although partitions do not allow overlap between the partitioning subsets in one imputation of the parameters, posterior inference could still report positive (marginal) posterior probability for membership in multiple clusters for the same HM (reporting such probabilities also requires a resolution of the label switching problem). Alternatively, one could use feature allocation models, such as the Indian buffet processes (Griffiths and Ghahramani (2005)) as priors for a random allocation of HMs to subsets, including membership in multiple subsets.

Appendix: MCMC details

Joint pdf

$$\begin{array}{cc}\hfill p(\mathbf{Y},\mathbf{c},\mathbf{r},\theta ,{\pi }_0,{\pi }_1)& =p\left({\pi }_0\right)p\left({\pi }_1\right)p\left(\mathbf{c}\right),p(\mathbf{r}\mid \mathbf{c})p(\theta \mid \mathbf{c},\mathbf{r},\mathbf{k},\lambda )p(\mathbf{Y}\mid \theta )\hfill \\ \hfill & =p\left({\pi }_0\right)p\left({\pi }_1\right)p\left(\mathbf{c}\right)\prod _{q=1}^Q[p\left({\mathbf{r}}_q\right)\hfill \\ \hfill & \times \prod _{d=1}^{D_q}\left\{\prod _{g\in V_q}(p({\tilde{\theta }}_{dg}\mid k_{0g},{\lambda }_{0g})\prod _{i\in R_{qd}}p(y_{ig}\mid {\tilde{\theta }}_{dg})\right\}\hfill \\ \hfill & \times \prod _{g\in V_q}\prod _{i\in R_{s0}}\left(p({\theta }_{ig}\mid k_{1g},{\lambda }_{1g})p(y_{ig}\mid {\theta }_{ig})\right)]\hfill \\ \hfill & \times \prod _{g\in V_0}\prod _{i=1}^N\left(p({\theta }_{ig}\mid k_{2g},{\lambda }_{2g})p(y_{ig}\mid {\theta }_{ig})\right)\hfill \end{array}$$

where V_q = {g | c_g = q, g = 1, …, G} is the set of HMs in an HM set q, q = 0, …, Q, and R_qd = {i | r_qi = d, i = 1, …, N } is the set of genomic locations in genomic location cluster d corresponding to HM set q for q = 1, …, Q and d = 1, …, D_q. We include λ and k in the conditioning sets to indicate the relevant (fixed) hyperparameters.

The prior probability distributions of c and r_q are a zero-enriched Pólya urn scheme given in Equations (1) and (2) of the main paper.

Full conditional

• (i) Update θ

  • (a) For active HMs (c_g > 0) and active genomic locations (r_qi > 0), q = 1, …, Q and d = 1, …, D_q,

    $${\tilde{\theta }}_{dg}\mid k_{0g},{\lambda }_{0g},\mathbf{c},{\mathbf{r}}_q,{\mathbf{y}}_q~\text{Gamma}(k_{0g}+\sum _{i\in R_{qd}}^N{y}_{ig},{\lambda }_{0g}+n_{qd}).$$
  • (b) For active HMs (c_g > 0) and idle genomic locations (r_qi = 0), i = 1, …, N,

    $${\theta }_{ig}\mid k_{1g},{\lambda }_{1g},\mathbf{c},{\mathbf{r}}_q,{\mathbf{y}}_g~\text{Gamma}(k_{1g}+y_{ig},{\lambda }_{1g}+1).$$
  • (c) For idle HM set (c_g = 0), i = 1, …, N,

    $${\theta }_{ig}\mid k_{2g},{\lambda }_{2g},\mathbf{c},{\mathbf{y}}_g~\text{Gamma}(k_{2g}+y_{2g},{\lambda }_{2g}+1).$$
• (ii) Update π₀

  $${\pi }_0\mid \mathbf{c}~\text{Beta}(a_0+G^{\prime },b_0+G-G^{\prime })$$
• (iii) Update π₁

  $${\pi }_1\mid \mathbf{r}~\text{Beta}(a_1+\sum _q\sum _{i}I(r_{qi}>0),b_1+NQ-\sum _q\sum _{i}I(r_{qi}>0)),$$

  where I is an indicator function: I(r_qi > 0) = 1 if r_qi > 0; I(r_qi > 0) = 0 if r_qi = 0.

• (iv) Update r_q

  Update r_q for active HM sets, q = 1, …, Q and i = 1, …, N.

  Remove ${\theta }_i^q$, define $m_q^{-},{\theta }^{q-},D_q^{-},{\mathbf{r}}_q^{-},n_q^{-}\text{and},R_{qd}^{-}$, and integrate with respect to θ. We find

  $$\begin{array}{cc}\hfill p& (r_{qi}=d\mid \mathbf{c},{\mathbf{r}}_q^{-},{\mathbf{k}}_0,{\lambda }_0,\mathbf{y})\hfill \\ \hfill & \{\begin{array}{cc}\hfill & \propto ({\pi }_1\frac{n_{qd}^{-}}{\beta +m_q^{-}}{\prod }_{g\in V_q}\frac{1}{y_{iq}!}{\Pi }_{g\in V_q}\frac{\Gamma (k_{0g}+{\Sigma }_{i\in R_{qd}^{-}\bigcup \left\{i\right\}}y{l}_q)}{\Gamma (k_{0g}+{\Sigma }_{i\in R_{qd}^{-}}y{l}_q)}\hfill \\ \hfill & \times \frac{{({\lambda }_{0g}+n_{qd}^{-})}^{k_{0g}+{\Sigma }_{i\in R_{qd}^{-}}y{l}_q}}{{({\lambda }_{0g}+n_{qd}^{-}+1)}^{k_{0g}+{\Sigma }_{i\in R_{qd}^{-}\bigcup \left\{i\right\}}y{l}_q}}ifd=1,\dots ,D_q^{-},\hfill \\ \hfill & \propto {\pi }_1\frac{\beta }{\beta +m_q^{-}}{\Pi }_{g\in V_q}\frac{\Gamma (k_{0g}+y_{ig})}{\Gamma \left(k_{0g}\right)}\frac{{\left({\lambda }_{0g}\right)}^{k_{0g}}}{{({\lambda }_{0g}+1)}^{k_{0g}+y_{ig}}{y}_{ig}!}ifd=D^{-}+1,\hfill \\ \hfill & \propto (1-{\pi }_1){\Pi }_{g\in V_q}\frac{\Gamma (k_{1g}+y_{ig})}{\Gamma \left(k_{1g}\right)}\frac{{\left({\lambda }_{1g}\right)}^{k_{1g}}}{{({\lambda }_{1g}+1)}^{k_{1g}+y_{ig}}{y}_{ig}!}ifd=0.\hfill \end{array}\phantom{\}}\hfill \end{array}$$

• (v) Update c

  Remove c, and define G^{′ −}, Q⁻, p⁻, c⁻ and n⁻. Sample c_g as follows: c_g ∈ {0, 1,, …, Q⁻, (Q⁻ + 1)}. Note that c_g = 0 implies becoming idle, 1 ≤ c_g ≤ Q⁻ joining one of the existing HM sets, and c_g = Q⁻ + 1 starting a new singleton HM set.

  $$p(c_g=q\mid {\mathbf{y}}_g)\propto \{\begin{array}{cc}p(c_g=0)p({\mathbf{y}}_g\mid c_g=0)\hfill & q=0\hfill \\ p(c_g=0)p({\mathbf{y}}_g\mid c_g)\hfill & q=1,\dots ,Q^{-}\hfill \\ p(c_g=Q^{-}+1){\Sigma }_{r}p(\mathbf{r}\mid c_g=Q^{-}+1)p({\mathbf{y}}_g\mid \mathbf{r})\hfill & q=Q^{-}+1.\hfill \end{array}\phantom{\}}$$
  The marginalization of r is dificult and computationally intensive. To avoid this problem, we consider a pseudo prior $p({\tilde{\mathbf{r}}}_g\mid {\mathbf{y}}_g)$ and let $r_{Q^{-}+1}={\tilde{\mathbf{r}}}_g$. Finally, after canceling ${\Pi }_{g^{\prime }=1}^{G}p({\tilde{\mathbf{r}}}_g\mid {\mathbf{y}}_g)$, we have the following:

  $$p(c_g=q\mid {\mathbf{y}}_g)\propto \{\begin{array}{cc}p(c_g=0)p({\mathbf{y}}_g\mid c_g=0)\hfill & q=0\hfill \\ p(c_g=0)p({\mathbf{y}}_g\mid c_g)\hfill & q=1,\dots ,Q^{-}\hfill \\ p(c_g=Q^{-}+1)p\left({\mathbf{r}}_{Q^{-}+1}\right)p({\mathbf{y}}_g\mid {\mathbf{r}}_{Q^{-}+1})\hfill & q=Q^{-}+1.\hfill \end{array}\phantom{\}}$$
  For joining an existing cluster, q = 1, …, Q⁻,

  $$\begin{array}{cc}\hfill p(c_g=q\mid {\mathbf{c}}^{-},\text{rest})& \propto {\pi }_0\frac{p_q^{-}}{\alpha +G^{\prime -}}\hfill \\ \hfill & \times \prod _{d=1}^{D_q}\left[\frac{{\lambda }_{0g}^{K_{0g}}}{\Gamma \left(k_{0g}\right)}\frac{\Gamma (k_{0g}+{\Sigma }_{i\in R_{qd}}{y}_{ig})}{{(n_{qd}+{\lambda }_{0g})}^{(k_{0g}+{\Sigma }_{i\in R_{qd}}{y}_{ig})}}\prod _{i\in R_{qd}}\frac{1}{y_{iq}}\right]\hfill \\ \hfill & \times \prod _{i\in R_{qd}}\frac{\Gamma (k_{1g}+y_{ig})}{\Gamma \left(k_{1g}\right)}\frac{{\left({\lambda }_{1g}\right)}^{k_{1g}}}{{({\lambda }_{1g}+1)}^{k_{1g}+y_{ig}}{y}_{ig}{!}^{’}}\hfill \end{array}$$

  for starting a new (singleton) cluster

  $$\begin{array}{cc}\hfill p(c_g=Q^{-}+1\mid {\mathbf{c}}^{-},\text{rest})& \propto {\pi }_0\frac{\alpha }{\alpha +G^{\prime -}}{\pi }_1^{m_q}{(1-{\pi }_1)}^{(N-m_q)}\frac{{\beta }^{D_q}{\Pi }_{d=1}^{D_q}\Gamma \left(n_{qd}\right)}{{\Pi }_{i=1}^{m_q}(\beta +i-1)}\hfill \\ \hfill & \times \prod _{d=1}^{D_q}\left[\frac{{\lambda }_{0g}^{K_{0g}}}{\Gamma \left(k_{0g}\right)}\frac{\Gamma (k_{0g}+{\Sigma }_{i\in R_{qd}}{y}_{ig})}{{(n_{qd}+{\lambda }_{0g})}^{(k_{0g}+{\Sigma }_{i\in R_{qd}}{y}_{ig})}}\prod _{i\in R_{qd}}\frac{1}{y_{iq}}\right]\hfill \\ \hfill & \times \prod _{i\in R_{qd}}\frac{\Gamma (k_{1g}+y_{ig})}{\Gamma \left(k_{1g}\right)}\frac{{\left({\lambda }_{1g}\right)}^{k_{1g}}}{{({\lambda }_{1g}+1)}^{k_{1g}+y_{ig}}{y}_{ig}{!}^{’}}\hfill \end{array}$$

  and for joining the inactive cluster

  $$p(c_g=0\mid {\mathbf{c}}^{-},\text{rest})\propto (1-{\pi }_0)\prod _{i=1}^N\frac{\Gamma (k_{2g}+y_{ig})}{\Gamma \left(k_{2g}\right)}\frac{{\left({\lambda }_{2g}\right)}^{k_{2g}}}{{({\lambda }_{2g}+1)}^{k_{2g}+y_{ig}}{y}_{ig}!}.$$