Modeling Protein Expression and Protein Signaling Pathways

Abstract

High-throughput functional proteomic technologies provide a way to quantify the expression of proteins of interest. Statistical inference centers on identifying the activation state of proteins and their patterns of molecular interaction formalized as dependence structure. Inference on dependence structure is particularly important when proteins are selected because they are part of a common molecular pathway. In that case, inference on dependence structure reveals properties of the underlying pathway. We propose a probability model that represents molecular interactions at the level of hidden binary latent variables that can be interpreted as indicators for active versus inactive states of the proteins. The proposed approach exploits available expert knowledge about the target pathway to define an informative prior on the hidden conditional dependence structure. An important feature of this prior is that it provides an instrument to explicitly anchor the model space to a set of interactions of interest, favoring a local search approach to model determination. We apply our model to reverse-phase protein array data from a study on acute myeloid leukemia. Our inference identifies relevant subpathways in relation to the unfolding of the biological process under study.

1. INTRODUCTION

In this article, we consider the statistical analysis of high-throughput protein expression data. We focus on the identification of patterns of protein interactions, capitalizing on both a molecular interrogation protocol called reverse-phase protein array (RPPA) technology and prior biological pathway knowledge.

RPPAs (Tibes et al. 2006) represent a high-throughput proteomic technology that provides a quantification of the expression for specifically targeted proteins selected from molecular pathways. Unlike traditional microarrays in which thousands of gene probes are immobilized on glass or fabric slides and are hybridized against samples from individuals, in RPPA, one immobilizes individual samples on the slides and hybridizes them against a single antibody that recognizes only one protein. This is why the technology is named reverse phase. Figure 1 presents an image of RPPA, in which 40 individual patient samples containing whole cellular protein repertoires are printed in 40 batches. Each batch can be recognized as a square of four-by-four dots. For quantification purposes, each sample is diluted serially in eight steps so that the resulting strength of the dilutions are full strength, 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, and 1/128 of the full strength. Duplicates are produced for each dilution, resulting in a total of 16 spots for each sample, shown as the four-by-four square on the slide. Each slide is probed with an antibody that represents one specific protein. The antibody can be detected by amplified fluorescent, colorimetric, or chemiluminescent assays. After each slide is hybridized against the antibody, signal intensities for all the samples on the slide are measured by scanning the slide using a specially designed scanner. Quantification of each sample is based on the intensities of the 16 spots. In our application, we base our analysis on results obtained from the SuperCurve software (http://bioinformatics.mdanderson.org/Software/OOMPA). Currently, researchers are able to deposit over a thousand patient samples on one RPPA, making the technology particularly attractive for pathway analysis. In general, the availability of protein-specific antibodies remains a limitation of RPPA, but this issue lies outside the scope of this article.

Figure 1.

(a) A typical reverse-phase protein array with 40 samples shown as the 40 batches on the slide. Each batch represents one individual sample with 16 spots, which are the results of duplicates of eight-step dilutions. (b) Normalized RPPA intensities for 51 proteins and 531 AML patients.

Statistical research in the estimation of dependence patterns has mainly centered on Bayesian networks (Jansen et al. 2003; Friedman 2004; Pittman et al. 2004; Sebastiani and Ramoni 2005). Other recent attempts on network models include the work on finding differentially expressed gene sets (often belonging to a genetic pathway) by Efron and Tibshirani (2006) and Newton et al. (2007). Recent extensions to this framework (Shojaie and Michailidis 2009, 2010) show how the introduction of explicit prior information about gene–gene interactions improves power in the differential analysis of gene sets. The innovative work by these authors still stops short of modeling specific interaction among the genes. In fact, in the setting of estimating gene–gene interactions, recent contributions have highlighted how well-established computational techniques often perform poorly in very-high-dimensional settings (Dobra et al. 2004; Scott and Carvalho 2008). In this regard, some progress has been reported when the analysis is carried out using convenient probabilistic schemes, such as Gaussian Markov random fields (MRFs) (Wong, Carter, and Khon 2003; Jones et al. 2005; Scott and Carvalho 2008), or functional transformation schemes (Telesca et al. 2009).

In the case of RPPA data, the curse of dimensionality is somewhat mitigated by the fact that the technology looks at a limited set (typically < 200) of proteins for expression and activation states, which represents a fraction of the estimated 4 million proteins and activation states thought to occur in the human proteome. Furthermore, in typical protocols, one is not dealing with the n ≪ p paradigm, as large sample sizes can easily be analyzed. On the other hand, when investigating dependence, some issues that are inherently associated with high-throughput molecular interrogation persist: (1) the sampling distribution of proteomic abundance is usually non-Gaussian, rendering the convenient Gaussian graphical models framework inadequate as a model for protein interactions; and (2) RPPA experiments often target specific biological pathways. It is therefore important that the prior specification exploit available prior information on such targeted pathways.

We address issue (1) following the formalism introduced by Telesca et al. (2010), modeling the sampling distribution of protein abundance as a heavy-tailed mixture distribution and defining dependence at a hidden level, between binary indicators of inactive and active states. Addressing issue (2) defines a key feature of the proposed model, as our formulation introduces an informative prior that assigns high prior probability mass to the model space surrounding the target pathway. Mukherjee and Speed (2008), for example, suggested a similar approach in the context of Gaussian directed acyclic graphical (DAG) models. Our approach is also comparable to that described by Airoldi et al. (2007) in a data integration context. From a methodological perspective, we extend the work of Telesca et al. (2010) in two fundamental directions. First, we introduce a fully general dependence prior between hidden multivariate binary random quantities, and second, we propose a framework for Bayesian model determination that allows a local search for interactions, penalizing the model space as a function of a discrepancy measure between the target pathway and random departures from its graphical topology.

The rest of this article is structured as follows. We introduce the proposed analysis framework and probability model in Section 2. Statistical inference based on Markov chain Monte Carlo (MCMC) sampling from the posterior distribution of interest is discussed in Section 3. In Section 4, we illustrate our approach through the analysis of an RPPA dataset from a set of patients diagnosed with acute myeloid leukemia (AML). We conclude with a critical discussion of our contribution in Section 5.

2. DEPENDENT MIXTURE MODEL

We consider protein expression data in the form of a G × T matrix Y = [y_gt], with the generic element y_gt denoting the observed molecular expression for protein g in sample t, where g = 1, …, G and t = 1, … T. The sampling model for Y is defined conditionally on a latent variable e_gt, representing an indicator of class membership in a mixture density and is described in Section 2.1. We argue that e_gt is likely to represent the biologically meaningful signal of protein activation better than the noisy row intensities y_gt. A key feature of the model is a graphical model to parameterize a dependent prior on e = [e_gt]. The graph reflects the dependence structure between proteins. The strength of this dependence is indexed by an additional set of parameters β. In summary, the probability model is defined as

$$p(\mathbf{Y},\mathit{e},\mathit{\beta },\mathcal{G})=\underset{2.1}{\underbrace{p(\mathbf{Y}\mid \mathit{e})}}\underset{2.2}{\underbrace{p(\mathit{e}\mid \mathit{\beta },\mathcal{G})}}\underset{2.3}{\underbrace{p(\mathit{\beta }\mid \mathcal{G})p(\mathcal{G})}}.$$ (1)

Underbraced numbers indicate the subsections where each sub-model is discussed.

2.1 Sampling Model: p(Y |e)

We assume that the sampling distribution of y_gt has heavy tails and follows a mixture of a normal distribution and two scale mixtures of uniform distributions. Let e_gt denote a latent trinary indicator, e_gt ∈ {−1, 0, 1}, indexing three possible distribution functions. Also, let ỹ_gt = y_gt − (α_t + μ_g) denote a normalized measure of relative abundance, corrected for a protein-specific effect μ_g and a sample-specific effect α_t. Using f (·) to generically denote a probability density function, we write the sampling distribution of ỹ_gt as

$$f({\stackrel{\sim }{y}}_{gt}\mid e_{gt})=f_{-1}({\stackrel{\sim }{y}}_{gt})I(e_{gt}=-1)+f_0({\stackrel{\sim }{y}}_{gt})I(e_{gt}=0)+f_1({\stackrel{\sim }{y}}_{gt})I(e_{gt}=1),$$ (2)

where $f_{-1}(·)=U(-k_g^{-},0),f_0(·)=N(0,{\sigma }_g^2),f_1(·)=U(0,k_g^{+}),k_g^{\pm }>0$, and I(A) denotes an indicator of the event A. Such normal–uniform mixtures have been previously introduced by Parmigiani et al. (2002) and Dean and Raftery (2005) for the robust analysis of high-throughput cDNA microarrays. Recently, Telesca et al. (2010) have extended the original formulation of Parmigiani et al. (2002), defining mixing proportions via a multivariate probit link.

Conditional on e_t = (e_gt, g = 1, …, G), the observed abundance measurements y_gt are exchangeable in (2). Later, in Section 2.2, we will exploit the trinary indicators e_gt to model conditional dependence between protein abundance measurements. For each protein g, the marginal distribution of e_g = (e_g1, …, e_gT)′ is trinomial, with T possible trials, support {−1, 0, 1}, and probabilities ${\pi }_g^{-}=p(e_{gt}=-1),{\pi }_g^{+}=p(e_{gt}=1)$, and ${\pi }_g^0=1-({\pi }_g^{+}+{\pi }_g^{-})$.

In the foregoing formulation, ${\sigma }_g^2$ denotes the variance of the baseline distribution for protein g. The mixture distribution models overdispersion relative to f₀(·) through the tail parameters $k_g^{-}$ and $k_g^{+}$. We will require that $min(k_g^{-},k_g^{+})>5{\sigma }_g$ to account for heavy tails in the proteomic distribution of abundance. More precisely, marginalizing over ${\kappa }_g^{\pm }$, the sampling model (2) is heavy tailed compared with the central normal distribution.

We propose the following conditionally conjugate hierarchical normal prior for the remaining parameters in (2): ${\mu }_g~N(m_{\mu },{\tau }_{\mu }^2),1/{\sigma }_g^2~\text{Ga}({\gamma }_{\sigma },{\lambda }_{\sigma }),{\alpha }_t~N(0,{\tau }_{\alpha }^2),1/k_g^{-}~\text{Ga}({\gamma }_k,{\lambda }_k)$, and finally, $1/k_g^{+}~\text{Ga}({\gamma }_k,{\lambda }_k)$. Additionally, we will require ${\sum }_{t=1}^T{\alpha }_t=0$, for likelihood identifiability.

2.2 Modeling Dependence: p(e | β, )

We model dependence between proteins using the formalism of graphical models (Lauritzen 1996). A graph = {V, E} is an algebraic structure composed of a set of vertices V and a set of edges E ⊆ V × V. When the set of vertices V represents a collection of random quantities, the edge structure E is often used to identify the full set of conditional independence relations between the components of V via the global Markov property associated with (Besag 1974). Details, including whether edge set E is allowed to include directed edges, that is, ordered pairs of nodes, or only undirected edges, that is, unordered pairs, depend on the specific graphical model and are discussed below.

Regulatory relationships between proteins may include causal loops and dynamic reciprocal regulation (see Figure 2). This motivates the assumption that the set of conditional dependence relationships characterizing protein interactions is well represented by a class of graphical models known as reciprocal graphs (Koster 1996). These graphs allow for directed (e.g., a → b) and undirected edges (e.g., a − b), loops (e.g., a → b, b → c, c → a), and reciprocal relationships (e.g., a → b, b → a), where a, b, c ∈ V. Provided there are no directed edges between vertices of the same undirected path (e.g., a − b, b − c, c → a), this class of models has a clear causal interpretation and equivalent Markov classes may be defined via graphical moralization (Koster 1996; Lauritzen 1996).

Figure 2.

A protein interaction pathway produced by combining known protein–protein interactions from the literature. This network wiring diagram shows the connectivity of the receptor tyrosine kinase to the MAPK (mitogen-activated protein kinase), Akt, STAT, Bcl-2 (B-cell lymphoma 2), and p53 signaling proteins. (We are able to measure a large percentage of the molecules using the RPPA for AML patients. The relationships between proteins suggested in this diagram will be considered as prior information for the proposed probability model.) The online version of this figure is in color.

Our notation = {V, E} defines a reciprocal graph. Each corresponds to one and only one moral (undirected) graph 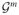= {V, E^m}, where E^m represents the set of undirected edges moralized from E. While we use a directed graph to interpret the pathway diagram, in the absence of a time-course experiment, the data can only inform about an equilibrium distribution. For the development of the sampling model, it therefore suffices to consider the implied conditional independence structure of the equilibrium distribution. We will represent this by G^m. We proceed in the following way. We start with a prior on G; this induces a prior on G^m. Conditional on G^m, we define a sampling model for the observed data. Finally, posterior updating provides the desired posterior inference on G. In this process, it is important to note that we only learn about the features of G that would change G^m. This process parallels inference in an analysis of variance (ANOVA) model that can only inform about identifiable contrasts. The prior on the directed graph can be thought of as prior regularization.

The mapping → 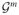is via the moralization procedure. Henceforth, notation with superscript m will always refer to the moralized graph. The mapping is not one to one, as the same undirected graph may correspond to different directed structures, (Markov equivalence, Lauritzen 1996). In , standard MRF properties apply (Besag 1974). In particular, if we denote ne(g) as the set of neighbors of protein g (a ∈ ne(b) if and only if {a, b} ∈ E^m), then it is assumed that the abundance of protein g is conditionally independent of any other protein, given its neighbors ne(g).

We specify a joint distribution over the latent indicators e_t = (e_1t, …, e_Gt)′, (t = 1, …, T), which is consistent with the Markov structure spanned by a given reciprocal graph , through its moral representation 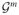. We first reduce the trinary e_gt to a binary indicator z_gt. We do so because in RPPA studies, researchers usually focus on protein activations. We thus define an auxiliary indicator z_gt = 2I {e_gt = 1} − 1 ∈ {−1, 1}, which we will use to describe dependence across proteins.

Next, we construct a joint probability model for z_t = (z_gt, g = 1, …, G). The reduction to the multivariate binary vector z_t greatly simplifies this modeling step. Following the arguments by Hammersley and Clifford (1971) and Besag (1974), given G and the neighborhood structure encoded in a moral graph 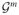, the joint distribution p(z_t) can be defined in its full generality through the complete conditional probabilities p(z_gt | z_(\g,t)). More precisely, let exp[Q(z_t)] ∝ p(z_t), then there exists an expansion of Q(z_t), unique on Ω = {−1, 1}^G and of the form:

$$Q({\mathit{z}}_t)=\sum _{1\le g\le G}{z}_{gt}{H}_g(z_{gt})+\sum _{1\le g\le h\le G}{z}_{gt}{z}_{ht}{H}_{gh}(z_{gt},z_{ht})+\cdots +z_{1t}{z}_{2t}\dots z_{Gt}{H}_{1,2,\dots ,G}(z_{1t},z_{2t},\dots ,z_{Gt}).$$ (3)

The Hammersley–Clifford theorem (Besag 1974) postulates that while the H-functions may be chosen arbitrarily, for any set of labels (1 ≤ g, h, …, s ≤ G), H_g,h,…,s may be nonnull if and only if the set of proteins labeled (g, h, …, s) forms a clique in the moral graph 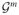. A clique is a subset of proteins in which each pair of proteins is connected by an edge.

The binary nature of z_gt allows us to, without loss of generality, replace any nonnull H-function with a single arbitrary parameter (Cox 1972; Besag 1974) and we can therefore write

$$Q(z_t)=\sum {\alpha }_g{z}_{gt}+\sum {\beta }_{gh}{z}_{gt}{z}_{ht}+\cdots +{\beta }_{1,2,\dots ,G}{z}_{1t}{z}_{2t}\dots z_{Gt}.$$ (4)

The foregoing formulation is a representation result for any multivariate distribution p(z). Later, conditioning on a particular graphical model will substantially reduce the number of terms appearing in (4). In fact, when considering p(z_t | ), the function Q(z_t | ) will only include sets of vertices forming cliques in the moralized graph 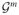. Finally, the definition of a joint distribution over the original trinary indicators e_t is completed with the conditional probability p(e_gt = −1 | z_gt = −1) = exp(γ_g)/{1 + exp(γ_g)}, (g = 1, …, G).

In summary, we have mapped to 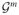and then indexed all possible joint probability models on e_t that respect the conditional independence structure represented in 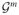by (4).

2.3 Priors Over Interaction Parameters and Graphical Structures: p(β | ) p( )

We introduce an informative class of priors for the unknown graph . In words, our prior model is based on a pathway diagram that summarizes substantive prior information about the biochemical pathway of interest. First, we interpret the pathway diagram as a known and fixed reciprocal graph = {V, E₀}. Here, we assume that the biochemical pathway is displayed as a set of nodes corresponding to proteins and edges between nodes. We assume that all edges are directed. In general, a reciprocal graph could also include undirected edges, subject only to the constraint that there be no directed edges between nodes of the same (undirected) pathway component (Koster 1996). We do not make use of this feature in our implementation, as all edges in the original pathway are indeed directed.

Conceptually, we write p( ) ∝ f {d( , )}, where d(·, ·) is a discrepancy measure and f′ ≤ 0, so that graphs that deviate from are assigned a lower prior probability. A similar approach was introduced by Mukherjee and Speed (2008) for Gaussian DAGs.

Let A^c denote the complement of set A and define $d({\mathcal{G}}_0,\mathcal{G})=\mid E^c\cap E_0\mid +\delta \mid E\cap E_0^c\mid$, δ > 1. Here, |E| identifies the number of edges in a graph = {V, E}. This defines a discrepancy measure d( , ) as the weighted sum of edges dropped from and edges added to . If we assume for a moment δ = 1, then d( , ) reduces to the number of changed edges relative to . A weight δ > 1 allows us to include a notion of parsimony by using an increased penalty for adding edges compared with dropping edges. For a given d(·, ·), we assume that

$$p(\mathcal{G}\mid \phi )\propto f\{d({\mathcal{G}}_0,\mathcal{G})\}={\phi }^{d({\mathcal{G}}_0,\mathcal{G})},$$ (5)

where we assume φ~ (a_φ, b_φ). The prior (5), with δ = 1, is equivalent to assuming exchangeable coin flips to determine each edge, with odds of matching edges in equal to φ. Similar probability models have been shown to provide in several contexts automatic multiplicity correction in the posterior (Scott and Berger 2008). For any given φ, the expected density of a graph¹ is computed as $\overline{d}(\mathcal{G}\mid \phi )=(\mid E_0^c\mid \frac{{\phi }^{\delta }}{1+{\phi }^{\delta }}+\frac{\mid E_0\mid }{1+\phi })\frac{1}{G(G-1)}$, which is a decreasing function of δ. Furthermore, the distribution of the graph density d( | φ) has mode at $\frac{\mid E_0\mid }{G(G-1)}$ and variance decreasing with δ. A key property of (5) is therefore the informative nature of the prior, maximized at the prior guess , leading to posterior simulation being a local exploration of the model space. This is in sharp contrast to alternate approaches that allow for global model exploration by using prior probability models that are far more diffuse over the model space. If desired, further structural restrictions are easily incorporated in this framework by introducing changes in d( , ). For example, this function could be defined in ways that force the inclusion of a subset of edges, say $E_0^{\ast }$, or in ways that introduce discrete cutoffs to the overall model size.

Our model is completed by defining normal priors over the interaction parameters (β_gh, β_ghk, …), (∀ g < h < k …) so that ${\beta }_u\mid \mathcal{G}~N({\eta }_u,{\sigma }_{\beta }^2)$, for any generic index of the parameter vector β. The mean value η_u is used to represent an important feature of typical molecular pathway representations. Pathway diagrams usually include a distinction between stimulatory and inhibitory interactions. In Figure 2, for example, edges between proteins are labeled with an arrowed-tip (i → j) if interactions observed a priori are of a stimulatory nature, and with a bullet-tip (—•) if prior interactions are inhibitory.

We formalize the definition of stimulatory and inhibitory relationships, following the framework introduced in Section 2.2 and focusing on second-order interactions parameters β_gh, (g < h). More precisely, indexing protein activation with binary indicators z_gt ∈ {−1, 1}, we assume that protein g stimulates the activation of protein h if p(z_gt = 1 | z_ht = 1) > p(z_gt = 1 | z_ht = −1). Similarly, for inhibitory relationships, we assume p(z_gt = −1 | z_ht = 1) > p(z_gt = −1 | z_ht = −1). It is easy to verify that these definitions motivate the choice of η_u > 0 for stimulatory and η_u < 0 for prior inhibitory interactions. In the absence of prior information, η_u is simply set to 0.

For reference, we summarize the complete model. Let ${\mathbf{\lambda }}_g={({\kappa }_g^{-},{\kappa }_g^{+},s_g)}^{\prime }$; we have

$$\begin{array}{ll}\text{Sampling}\text{model}:\hfill & {\stackrel{\sim }{y}}_{gt}\mid e_{gt}=e,{\mathbf{\lambda }}_g~f_e({\stackrel{\sim }{y}}_{gt}),\hfill \\ \hfill & {\stackrel{\sim }{y}}_{gt}=y_{gt}-({\alpha }_t+{\mu }_g)\hfill \\ \text{Autologistic}:\hfill & p({\mathit{z}}_t\mid \mathcal{G},\mathit{\beta })\propto exp\{{\sum }_g{\alpha }_g{z}_{gt}+{\sum }_{(g,h)\in E^m}{\beta }_{gh}{z}_{gt}{z}_{ht}\}\hfill \\ \text{Graphical}\text{model}\text{prior}:\hfill & p(\mathcal{G}\mid \phi )\propto {\phi }^{d({\mathcal{G}}_0,\mathcal{G})}\hfill \\ \text{Hyperpriors}:\hfill & {\beta }_{ij}\mid \mathcal{G}~N({\eta }_{ij},{\sigma }_{\beta }^2),(i,j)\in E^m\text{and}\phi ~\text{Beta}(a,b),\hfill \end{array}$$

where the trinary indicator e_gt is an elaboration of the binary indicator z_gt for activation, with $log\frac{p(e_{gt}=-1\mid z_{gt}=-1)}{p(e_{gt}=0\mid z_{gt}=-1)}={\gamma }_g$ and e_gt = 1 when z_gt = 1.

In our analysis, we consider a default prior setting inspired by the considerations in Jiang (2007). Specifically, we choose ${\sigma }_{\beta }^2=\frac{1}{2\pi }{e}^{\frac{1}{\sqrt{\mid E\mid }}},\phi ~\text{Beta}(T,m_G^{\varsigma })$, and $\delta =\nu \sqrt{m_G}$, where m_G = G(G − 1), and ζ and ν are positive constants. This simplifies tuning and sensitivity analyses to the choice of two parameters: ζ > 0, regulating overall sparsity, and ν > 0, defining prior deviation penalties from .

3. POSTERIOR COMPUTATION AND INFERENCE

3.1 Stochastic Search and MCMC Computation

We are interested in identifying patterns of molecular interactions, as informed by experimental data and guided by a prior pathway. The full model is determined by mixture membership indicators e, a conditional dependence configuration summarized in a graph , MRF parameters β, and a collection of parameters θ, which we assume contains all remaining random quantities with the exception of Y. Our inference centers on the posterior distribution p(e, , β, θ |Y), which fully summarizes the available evidence on protein abundance and protein expression profiles similarities.

The posterior probability model is not available in closed form. However, it is conceptually straightforward to define MCMC simulation from this target distribution. In particular, we could proceed as usual and draw the parameters of interest sequentially or in random order from the full conditional posterior distributions of θ, e, β, and . Updating of e and θ can be implemented via standard Gibbs sampling.

Unfortunately, updating β and remains problematic (Green and Richardson 2002). The complete conditional posterior for β and depends on e only indirectly through z. Recall that we further summarized the trinary indicators e into binary indicators z ∈ {−1, 1}^G of protein activation. The conditional posterior of β is given by

$$p(\mathit{\beta }\mid Y,\mathit{z},\mathcal{G},\mathit{\theta })=p(\mathit{\beta }\mid \mathit{z},\mathcal{G},\mathit{\theta })\propto p(\mathit{z}\mid \mathit{\beta },\mathcal{G},\mathit{\theta })\pi (\mathit{\beta }\mid \mathcal{G},\mathit{\theta }),$$ (6)

where

$$p(\mathit{z}\mid \mathit{\beta },\mathcal{G},\mathit{\theta })=\prod _{t=1}^T\frac{exp\{Q({\mathit{z}}_t)\}}{g(\mathit{\beta })},g(\mathit{\beta })=\sum _{\mathit{z}}exp\{Q({\mathit{z}}_t)\},$$

and the sum Σ_z is over all 2^G possible realizations of z.

The full conditional distribution of β is therefore defined in terms of a partition function g(β), which requires summation over all possible 2^G realizations of z_t, for any t = 1, …, T. This quantity can be evaluated efficiently only for a very small G. This is often not the case in RPPA studies, which leaves us with the problem of devising a feasible strategy to update β. Similar considerations apply for updates involving , with the further complication that changes in define changes in the dimensionality of the parameter vector β.

This problem is well known in the literature on MRFs and several solutions have been proposed, based on ad-hoc approximation to the partition function of interest (Green and Richardson 2002; Friel et al. 2009). In the following, we propose a solution based on MCMC ingenuity and show that exploiting a transition kernel that updates mixture indicators e and dependence parameters β in a joint fashion is possible without calculation of g(β).

3.2 Updating β

To update β, we consider a Metropolis–Hastings (MH) transition kernel that involves also changes in z and consequently in e. For any generic element of β, say β_u (u ⊂ {1, …, M}), we consider a proposal distribution $({\beta }_u^{\prime },{\mathit{e}}^{\prime })~q({\beta }_u^{\prime })p({\mathit{e}}^{\prime }\mid {\beta }_u^{\prime },{\mathit{\beta }}_{(\backslash u)},\mathcal{G},\mathit{\theta })$, where q(·) is an arbitrary proposal density and possibly dependent on the previous values β_u, whereas p(e | β, , θ) is the conditional prior defined in Section 2.2. In our implementation, for all i > j = 1, …, G, we consider a random-walk proposal $q({\beta }_{ij}^{\prime }){=}_{d}N({\beta }_{ij},s_{\beta })$, where s_β is calibrated at burn-in to achieve acceptance rates between 30% and 70%.

Draws from e′| β′, , θ may then be obtained easily via a short Gibbs run, based on full conditionals p(e_gt | e_\g, β′, , θ). It is easy to verify that for the construction of a standard MH transition kernel the newly proposed values (e′, ${\beta }_{ij}^{\prime }$) must be accepted with probability

$$\rho ({\beta }_u,\mathit{e},{\beta }_u^{\prime },{\mathit{e}}^{\prime })=min\left\{\frac{p(Y\mid {\mathit{e}}^{\prime },\mathit{\theta })}{p(Y\mid \mathit{e},\mathit{\theta })}\frac{\pi ({\beta }_{ij}^{\prime }\mid \mathcal{G},\mathit{\theta })}{\pi ({\beta }_{ij}\mid \mathcal{G},\mathit{\theta })}\frac{q({\beta }_{ij})}{q({\beta }_{ij}^{\prime })};1\right\}.$$ (7)

The structure of the proposal distribution allows for the elimination of the partition function g(β), at the cost of having to simulate G × T mixture indicators for each β_ij. Gains in efficiency could be further achieved by considering block updates for the elements of β. Our approach is similar to that of Møller et al. (2006).

In short, we replace the problem of evaluating the partition function with a problem of approximate prior simulation. The resulting MCMC provides an approximation to the desired posterior only to the extent to which the prior Gibbs simulation can be considered a draw from the prior. A systematic discussion of related MCMC schemes appears in the work of Andriew and Roberts (2009), who also discussed several more elaborate variations of this strategy. Further precision may be achieved by considering exact simulation from e | β, , θ (Propp and Wilson 1996), but this would come at a higher computational cost. In fact, the asymptotic validity of the proposed computation and a favorable comparison with exact sampling methods have recently been discussed by Liang (2010). A comparative review of alternate computational strategies associated with similar probability models (Ising and Potts models) has been compiled by Zhou and Schmidler (2009).

3.3 Updating via Reversible-Jump MCMC (RJ-MCMC)

Updating involves changes in β and its dimensionality. We are therefore faced with two complications, one associated with the evaluation of the partition function g(β), as explained above, and the other associated with the need to maintain detailed balance across dimensions. To solve this problem, we combine the reversible-jump algorithm of Green (1995) with the approach described in Section 3.2. More precisely, we follow Giudici and Green (1999) and propose the following transitions:

1. Select an edge (i, j) at random. If (i, j) ∈ E, propose its elimination; otherwise, if (i, j) ∉ E, propose its birth. This corresponds to moving from the current graph to a new graph , with moral representation .

2. Assume the move in Step 1 involves a birth. Propose a set of, say k, new interaction parameters ${\mathit{\beta }}_k^{\prime }~q({\mathit{\beta }}_k^{\prime })$ in correspondence to new undirected edges in the moral graph . In our implementation, we consider a proposal density based on local logistic regressions. More precisely, if we propose the birth of an interaction parameter β_ij involving z_i and z_j, we define: a = Σ_t I{z_it = −1, z_jt = −1}, b = Σ_t I{z_it = −1, z_jt = 1}, c = Σ_t{z_it = 1, z_jt = −1}, and d = Σ_t I{z_it = 1, z_jt = 1}. We calculate ${\widehat{\beta }}_{ij}=log(\frac{ad}{bc})/2$ and ${\delta }_{\beta }=\sqrt{(1/a+1/b+1/c+1/d)}$. Here, β̂_ij estimates the log odds ratio for a logistic regression involving z_i and z_j The parameter δ_β is a standard large-sample approximation to SE(β̂_ij). The proposal density is then constructed as a normal approximation to the conditional likelihood surface so that $q({\beta }_{ij}^{\prime }){=}_{d}N({\widehat{\beta }}_{ij},{\delta }_{\beta }^2)$.

3. Propose new values for the mixture indicators e′ ~ p(e′| β′, , θ). Draws are made from the conditional prior defined in Section 2.2.

4. Accept Steps 1–3 with probability ρ_b( , ):

   $${\rho }_b(\mathcal{G},{\mathcal{G}}^{\prime })=min\left\{\frac{p(Y\mid {\mathit{e}}^{\prime },\mathit{\theta })}{p(Y\mid \mathit{e},\mathit{\theta })}\frac{\pi ({\mathcal{G}}^{\prime })}{\pi (\mathcal{G})}\frac{p({\beta }_k^{\prime })}{q({\mathit{\beta }}_k^{\prime })};1\right\}.$$

The reverse move, involving the death of a random edge (i, j), is implemented by setting to 0 the elements of β disappearing from and it is accepted with probability ρ_d ( , ) = 1/ρ_b( , ).

The transition probability for includes a proposal for elements of β. One could therefore drop the transition probability described in Section 3.1.1, and still maintain irreducibility. However, without Section 3.1.1, the resulting MCMC demonstrates far slower mixing.

We conclude by summarizing the overall MCMC. We use notation x_−i to indicate the vector x without the element x_i, and [x | y, z] to generically indicate a transition probability that changes x and depends on the currently imputed values of y, z. Each iteration in the proposed posterior simulation algorithm involves the following transition sequence:

$$[\mathit{\theta }\mid \mathit{e},\beta ,{\mathcal{G}}^m,\mathbf{Y}],[e_{gt}\mid {\mathit{e}}_{-gt},\mathit{\beta },{\mathcal{G}}^m,\mathit{\theta },\mathbf{Y}],[{\beta }_{ij}\mid {\mathit{\beta }}_{-ij},\mathit{e},\mathit{\theta },{\mathcal{G}}^m],[\mathcal{G}\mid \mathit{e},\mathit{\beta },\mathit{\theta }].$$

4. SIMULATED DATA

We carried out a small simulation experiment to validate inference under the proposed model, to investigate the impact of prior choices and to compare with alternate approaches. In brief, we simulated data under a model that differs from the proposed sampling model. Hypothetical data were sampled as: $Y_{ij}~{\pi }_{ij}^{-}N(-c,v^2)+(1-{\pi }_{ij}^{-}-{\pi }_{ij}^{+})N(0,1)+{\pi }_{ij}^{+}N(c,v^2)$, where the mixing proportions depend on the realizations of a matrix normal random quantity W ~ (M, Σ, I_T) through a multivariate probit link (Chib and Greenberg 1998) so that ${\pi }_{ij}^{-}=p(w_{ij}<-1)$ and ${\pi }_{ij}^{+}=p(w_{ij}>1)$. The concentration matrix Σ⁻¹ was structured via structural equations to encode a notion of true dependence in a reciprocal graph. We fitted our model using a misspecified network prior. Given the true set of edges E^* (in our example, | E^* |= 50), we consider $E_0=\{E^{\ast }\backslash E_1^{\ast }\}\cup \stackrel{\sim }{E}$, with $E_1^{\ast }\subset E^{\ast }$ omitted from the prior edge set (in our example, $\mid E_1^{\ast }\mid =20$) and Ẽ serving as a random misspecification set including false edges (in our example, |Ẽ| = 30). Ideally, this prior would mimic what is often the case in practice, where a prior pathway may include edges that do not play a relevant role in the biological process under investigation (Ẽ) as well as previously unidentified but relevant interactions ( $E_1^{\ast }$).

Figure 3(a) explores robustness of protein activation inference to data arising from misspecified sampling models, by comparing inference on protein activation with the simulation truth. Figure 3(b) shows receiver operating characteristic (ROC) curves for selecting edges in the graph and compares inference under the proposed model, under GeneNet (Schäfer and Strimmer 2005) and under a model with exchangeable Bernoulli priors on all edges. Figure 3(c) shows similar ROC curves under alternate priors with the proposed model, comparing the proposed informative prior (5) and two relatively noninformative priors. Details and sensitivity analyses are reported in the supplementary materials to this article, available online. Overall, we found that a sampling model mimicking a potential data generative process is likely to provide some advantages over standard multivariate Gaussian calculations. Furthermore, we remark how using prior information as a source of structural constraints on the model space can provide a substantial advantage in the identification of meaningful interactions.

Figure 3.

Simulated data. Panel (a) shows ROC curves for the correct classification of into activated versus nonactivated proteins. Panels (b) and (c) show ROC curves for reporting edges as present or not. In panel (b), we compare different models. In panel (c), we compare alternate priors under the proposed model (δ = 50 and 100, corresponding to ζ = 1 and 2, respectively). The online version of this figure is in color.

5. EXAMPLE: ANALYSIS OF RPPA DATA

5.1 A Study in Acute Myeloid Leukemia

The current classification of AML uses the French–American–British system based on morphological features, along with flow cytometric analysis of surface marker expression, cytogenetics, and assessment of recurrent molecular abnormalities. These classification schemes have prognostic relevance, but with the exception of acute promyelocytic leukemia, they generally do not alter therapeutic recommendations (Mrozek et al. 2007). Furthermore, the predictive abilities of prognostic models based on current clinical and laboratory features are generally low, with less than half of the outcomes explained by these features. Researchers have recently started to investigate genomic and proteomic features for prognosticating AML. Proteins within signaling pathways that exhibit heterogeneous expression in AML are often prognostic, a characteristic that has been studied by researchers such as Kornblau et al. (2006) and Tanner et al. (2001). These authors find that distinct molecular abnormalities and patterns of pathway activation in leukemic cells collectively suggest potential targets for therapeutic intervention. Consequently, knowledge allowing rational evaluation of targeted therapies on an individualized basis in AML is sorely needed. As part of a knowledge-learning process, expression levels and activation process of a single protein or a limited number of proteins have been studied by Kornblau et al. (1994), Kornblau et al. (2000), and Kreuter et al. (2006).

The natural next step is formal inference on different patterns of pathway activation and modification. This requires inference on the joint probability distribution for multiple proteins in a pathway. The proposed model and the inference approach are built to facilitate such inference.

We use data from a large AML study based on RPPA. Specifically, we have probed protein samples from 531 newly diagnosed, primary, refractory, and relapsed AML patients. The objective of this experiment was to investigate interactions of important protein markers related to AML. We selected 51 proteins involved in signal transduction, apoptosis, and cell cycle regulatory pathways (Figure 2) and studied their expression pro-files in all 531 samples. An important feature of the AML data under study is that the number of samples (n = 531) is much greater than the number of proteins (p = 51). This feature facilitates principled model-based inference and model assessment and contrasts inference for RPPA data with inference for many other high-throughput genomic platforms.

The targeted interactions are illustrated in Figure 2, where we present a comprehensive signaling network map for the selected proteins based on the three pathways. The signaling network map was developed to show signaling interactions based on published articles from PubMed searches as well as from the connections map in Signal Transduction Knowledge Environment (http://www.stke.org).

5.2 Data Analysis

Using a desktop scanner at an optical resolution of 1200 dpi, we scanned the hybridized RPPA slides and saved them as TIFF files. The protein expression intensity of each spot was measured with an automated software program, MicroVigene^™ (VigeneTech, Inc., North Billerica, MA). The dilution series of the samples provided a dilution–concentration–expression curve, providing relative expression intensities that were read off in the linear part of the curve. We used these numbers for data preprocessing and calculation after standardization and topographical normalization (for details, refer to the SuperCurve software at http://bioinformatics.mdanderson.org/Software/OOMPA). Good preprocessing of data from any high-throughput experiments in general, and RPPA data in particular, is critically important. We used SuperCurve as it is the best currently available model-based and principled implementation of inference to quantify RPPA data.

We estimate protein pathway structure by combining prior knowledge of protein interaction and RPPA measurements. Specifically, given the prior consensus pathway in Figure 2, we use the proposed probability model to update our prior knowledge, combining the qualitative information about the consensus pathway with quantitative information from RPPA data (Figure 1). We fit the model presented in Section 2 to this set of 51 proteins. Reported inference is based on 500,000 MCMC samples (thinned by 10) after discarding 100,000 samples for burn-in.

In Figure 4 (left panel), we illustrate the fit of the proposed model to the AML protein expression data reported in Figure 1. Defining ${\pi }_{gt}^{+}=p(e_{gt}=1\mid Y)$ and ${\pi }_{gt}^{-}=p(e_{gt}=-1\mid Y)$, we follow Parmigiani et al. (2002) and define a probability of expression (POE) scale $p_{gt}^{\ast }\in [-1,1]$. This quantity represents a univariate posterior summary, designed to relate directly to the mixture indicator labels e_gt ∈ {−1, 0, 1} and may be considered as the normalized scale for raw intensities y_gt. Here, we show how the original abundance measurement is translated into a POE on the new scale (p^*). Plotting the raw correlation coefficients versus the the simple correlation estimated in the p^* scale (Figure 4, right panel), we note that the two measures of association are clearly correlated, with a tendency of stronger agreement toward large absolute values of the correlation coefficients.

Figure 4.

RPPA study: (Left panel) Centered protein abundance y_gt versus POE scale intensities ( $p_{gt}^{\ast }=E(p_{gt}^{+}-p_{gt}^{-})$). (Right panel) Raw simple correlation estimates versus simple correlations in the POE scale.

Our inference on molecular interaction is based on posterior edge inclusion probabilities, P{(i, j) ∈ E or (j, i) ∈ E | Y)}. These quantities are estimated directly from the RJ-MCMC output as the percentage of iterations where the edge is included in the current graphical structure . In Figure 5, we represent the posterior edge inclusion probabilities for all possible protein interactions, against expected posterior interactions E(β_ij | Y). Solid diamonds denote edges originally included in the prior pathway . Our differential penalization scheme favors edges in the target pathway, but still allows for the model to explore interactions that are not included in the prior. Reporting a final pathway may be based on several criteria (Telesca et al. 2009). Here, we consider the median model (Barbieri and Berger 2004; Scott and Berger 2008). That is, we select edges with posterior inclusion probability greater than 0.5.

Figure 5.

Panel (a): Posterior expected interactions E(β_u | Y) versus posterior edge inclusion probabilities p((i, j ) or (j, i) ∈ E | Y). Solid diamonds correspond to edges originally included in the prior pathway. Panel (b): Median model identified selecting edges with posterior inclusion probability greater than 0.5. Arrows define stimulatory relationships, whereas dotted arrowheads define inhibitory relationships. Edge thickness is proportional to the absolute size of the posterior expected interaction parameters.

The selected posterior network is reported in Figure 5. The edge thickness is proportional to the absolute value of the associated expected posterior interaction parameter E(β_ij | Y). We distinguish between stimulatory and inhibitory relationships. Following the argument introduced in Section 2.3, we base our inference on the sign of the posterior mean E(β_ij | Y ). For a generic edge index u, a positive posterior mean is interpreted as stimulation, whereas a negative sign is interpreted as inhibition. In the figure, we represent stimulation with arrows and inhibition with dotted arrowheads.

Our analysis identifies two main subpathways [Akt/mTOR (protein kinase B/mammalian target of rapamycin) and STATs (signal transducers and activators of transcription)] as groups of proteins exhibiting significant similarities in their overabundance patterns across samples. The Akt/mTOR pathway is known to be a key player in cell growth, proliferation, and survival. Recent literature identifies this pathway as a strong contributor to proliferation and drug resistance in AML [a comprehensive review is provided by Martelli et al. (2009)]. The second active pathway involves the family of STAT proteins (STAT3/STAT5). These molecules are known to act as important regulators in hematopoiesis (blood cell formation), and their upregulation via β-catenin (BCAT) has been documented by several authors (Boeuf et al. 2001; Hao et al. 2006). In the same pathway, we also recover key interactions between the STAT proteins and extracellular signal-regulated kinase (ERK) (Jain et al. 1998). The important role of STAT5 in AML was also recently noted by Kornblau et al. (2010).

Some of our results are surprising. For example, pPTEN (phosphatase and tensin homolog) is inactivated when phosphorylated and therefore cannot inhibit Akt phosphorylation. The negative relationship between pPTEN and pAkt-308 seems, therefore, contrary to canonical expectations (Wan and Helman 2003). The PTEN–Akt pathway is however of great interest in oncology, and this finding may prove useful in the search for possible feedback regulatory interactions or latent oncogenes [see, e.g., the discussion in Palomero, Dominguez, and Ferrando (2008)]. Likewise, one would expect the pAkts to have an edge with pGSK-3 (glycogen synthase kinase 3) instead of total Akt. On the other hand, the inferred diagram confirms evidence that, in active form, Akt phosphorylates a wide variety of downstream substrates. Also, the diagram highlights MTOR as a main activator of the serine p70S6K (p70S6 kinase), possibly contributing to tumor cell survival. Furthermore, the fact that MTOR signaling is confirmed to operate downstream makes it a promising therapeutic target for AML patients (Chen et al. 2010).

These unexpected findings may simply represent misidentified relationships or may reflect regulatory feedback within the system. At the same time, however, they may define the basis for genuinely novel discoveries. While this analysis is exploratory in nature, we believe it provides a principled hypothesis generation instrument for further experimental investigation. This instrument may prove particularly significant in a disease like AML, where standard chemotherapy is too often not fully effective and where there is a great need for new therapeutic strategies.

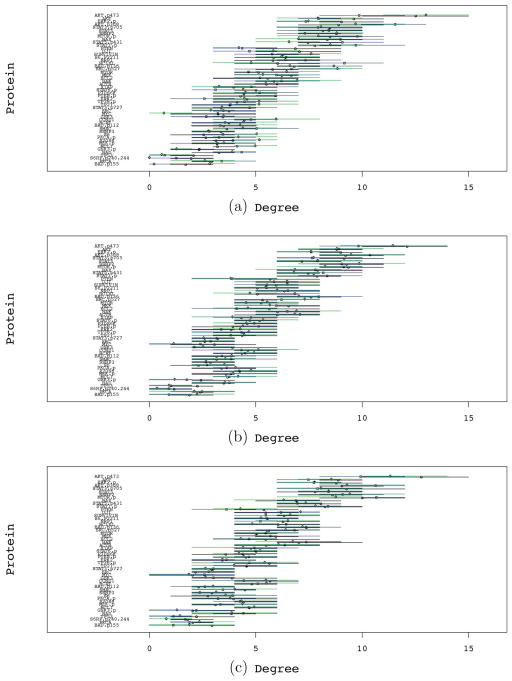
We assess the sensitivity of our inference with respect to prior settings by repeating our analysis for a range of values associated with prior hyperparameters. We summarize the posterior distribution of the proteomic pathway by analyzing the degree of each protein. As we consider reciprocal graphs, the degree of a vertex (protein) is defined as the number of edges incident to the vertex, with reciprocal relationships counted twice. A summary of our results is reported in Figure 6, where we represent the posterior mean degree associated with each protein and 95% credible intervals. Our analysis considered varying levels of prior sparsity (ζ = 0.5, 1.0, and 2.0), as well as varying degrees of prior pathway faithfulness, by considering pathway departure penalties, ν = 0.5, 1.0, and 2.0. We found that our results are robust to varying degrees of prior pathway faithfulness and overall sparsity. The proteomic degree distribution is maintained in agreement with respect to the order and magnitude of the expected number of neighbors. We observed some added instability associated with increasing levels of the sparsity parameter ζ > 2. However, posterior degree distributions are, for the large majority, significantly overlapping for most proteins over wide ranges of prior hyperparameters.

Figure 6.

Posterior mean degree and associated 95% CI by protein. Panels (a), (b), and (c) correspond to increasing sparsity penalties = 0.5, 1.0, and 2.0, respectively. For each protein, we report the posterior mean vertex degree evaluated in relation to three settings of the pathway deviation penalty parameter ν [ν = 0.5 (black), ν = 1.0 (blue), ν = 2.0 (green)]. The online version of this figure is in color.

6. DISCUSSION

We have proposed a probabilistic framework for the analysis of RPPA data. We focus on assessing the probability of protein–protein interactions by considering patterns of similarity characterized by hidden states of activation (as compared with inactive states).

Our probability model makes explicit use of prior information regarding evidence of protein interactions reported in the literature. This allows for the definition of a prior over graphical structures that explicitly anchors the model to known patterns of interaction, still allowing for a local search of new interaction patterns. Among the appealing features of the prior defined in this article is the explicit consideration of edge direction and the possibility of feedback loops between proteins.

We observed strong robustness of posterior inference about the pathway, to the setting of prior hyperparameters. This is expected as RPPA data are often characterized by large sample sizes. We however maintain that careful tuning and diagnostic checks are often required and are useful tools to assess sensitivity to the prior.

The large sample sizes characterizing RPPA data provide a unique opportunity for principled probabilistic modeling. At the same time, we are fully aware that departure from the multivariate Gaussian framework comes at a technical and computational cost. Particularly, computations involving partition functions, like the one reported in Section 3.1, characterize an entire area of research (Møller et al. 2006, Friel et al. 2009) and are known to be potentially problematic in high-dimensional settings. The strategy suggested in our article relies on the ability to simulate from a multivariate binary distribution in a fast and reliable fashion. Therefore, if the number of proteins or samples is very large, one may consider alleviating the computation burden via parallelization across samples and/or relying on alternate approximation strategies (Besag 1974; Green and Richardson 2002; Friel et al. 2009). While a full review of this problem would be perhaps too ambitious for this application, we defer the reader to Zhou and Schmidler (2009) for a comparative discussion of alternate computational strategies.

On a related subject, it is worth noting that even standard Gaussian MRF representations are not fully immune from computational difficulties, as closed-form expressions are usually only available upon assuming very stringent restrictions (decomposability) on the graph topologies admitted for inference (Giudici and Green 1999; Roverato 2002; Wong, Carter, and Khon 2003; Atay-Kays and Massam 2005, among others). In contrast, the general Hammersley–Clifford representation (Hammersley and Clifford 1971; Besag 1974) does not prescribe unrealistic restrictions on the graph of interest and provides a very flexible recipe for the definition of conditional dependence relationships.

Finally, in this article, we model dependence between protein by assuming that there are no significant alterations in patterns of covariation between different subsets of patients. While this is beyond the scope of this work, our formulation provides a straightforward basis for methodological extensions aimed at allowing for formal tests of differential pathway activation, both in a supervised and in an unsupervised fashion. These possible developments will be particularly useful in the analysis of proteomic studies of AML, since the disease is markedly heterogeneous, with numerous underlying genetic aberrations, and we still lack a strategy for the treatment of different subtypes of AML based on the current knowledge about genetic markers.