The innervation of the muscle spindle: a personal history

Abstract

I present a brief review of current understanding of the innervation of the mammalian muscle spindle, from a personal historical perspective. The review begins with comparative studies on the numbers of spindle afferents and considers how their relative abundance may best be assessed. This is followed by an examination of the distribution and some functional properties of the motor innervation. The primary ending is the subject of the final section, in particular, I look at what can be learned from serial sectioning and volumetric reconstruction, and present new results on a model and simulations concerning sensory terminal deformation during stretch.

Inside every old person is a young person wondering ‘What happened?’ (attributed to Terry Pratchett)

Introduction

I was introduced to the muscle spindle 45 years ago (1969) when I joined the department of Human Biology and Anatomy in Sheffield as a postgraduate student under the supervision of Nigel James. The neural component of the muscle spindle had first been described just over a century before (Kuhne, 1863) and the intervening years had seen the establishment of the key structural and functional elements both of the bundle of intrafusal muscle fibres and of their innervation (see Matthews, 1964, for review). In addition to two kinds of sensory ending – known as primary and secondary since Ruffini (1898) – the muscle spindle has its own efferent, or fusimotor, innervation (Leksell, 1945; Kuffler et al. 1951). In the view prevailing at the time I began my studentship, mammalian muscle spindles were seen as two essentially separate systems of intrafusal muscle fibres whose only common innervation was the single primary ending. Ian Boyd, in his monumental paper of 1962, was unequivocal in his conclusion: ‘From this work it is quite certain that mammalian muscle spindles contain two distinct types of intrafusal muscle fibre’. And Matthews’ (1962) demonstration of the two functional categories of dynamic and static fusimotor fibre in the same year could readily be accounted for on the basis of Boyd’s ‘nuclear bag muscle fibre system’ and ‘nuclear chain muscle fibre system’. But the 1960s saw the rapid introduction of new and improved microtechniques, including enzyme histochemistry and electron microscopy, to studies of muscle spindles; dissenting voices quoted histochemical evidence in particular suggesting that there might be more than two kinds of intrafusal fibre. Part of Boyd’s (1962) evidence for his two systems of intrafusal muscle fibres had been his conviction that the nuclear bag and nuclear chain fibres were always separately innervated by fusimotor axons; chief among the dissenters was David Barker, recently arrived from Hong Kong as professor of Zoology in Durham, whose main focus of criticism was that this was untrue. Together with Ip (Barker & Ip, 1963) he had developed a modified de Castro technique that allowed whole spindles to be teased from entire muscles impregnated en bloc with silver nitrate. Despite a reputation for capriciousness, favourable silver-impregnated preparations presented a stunningly clear picture of the complete innervation of the spindle, and the teased, silver-impregnated preparations frequently showed instances of common innervation by single fusimotor axons of the two morphological types of muscle fibre. So when I began my work on the spindle in 1969 I was fortunate to be able to make use of a battery of microtechniques – enzyme histochemistry, silver impregnation, electron microscopy and ultramicrotomy – that were relatively new to such studies. Among the conclusions from my postgraduate work (Banks, 1973) was that there were not two but three distinct kinds of intrafusal fibre, at least in rabbit and guinea pig, which were the species I had studied. When I joined David Barker’s group soon after receiving my PhD, Mike Stacey, Dave Harker and I extended this conclusion to cat and rat spindles as well as carrying out a direct correlation of histochemical and ultrastructural properties of their intrafusal fibres (Banks et al. 1977b). This was to provide the catalyst for a rapid expansion in our understanding of the innervation of the spindle, especially of the pattern of motor innervation whose resolution had been so intimately involved with the number of intrafusal fibre types.

In this paper I have been given the opportunity to review those features of the sensory and motor innervation of muscle spindles and their intrafusal fibres that seem to me likely to be most important in any full understanding of the functional role of the spindle in motor control, and that I have had the good fortune to have worked on. The sheer richness of their innervation provides the clearest demonstration, if one were needed, that spindles are a crucially important component of the system of motor control, as its provision requires the expenditure of considerable metabolic and spatial resources. For example, the nerve to the cat soleus muscle contains some 450 myelinated axons, but only about a third (155) of them are the α motoneurons carrying motor commands to around 25 000 extrafusal muscle fibres (for the sources of data quoted here, see Banks, 2005). From a total of 180 afferent axons, the 56 spindles and 45 tendon organs present in the muscle between them account for the same numbers of group I axons as well as 70 of group II, with the balance made up of a few group II or III afferents most likely supplying free endings and paciniform corpuscles. The remaining 115 myelinated axons are γ efferents providing an exclusive motor supply to around just 360 intrafusal muscle fibres.

I shall begin my review with comparative studies on the numbers of spindle afferents and consider how their relative abundance may best be assessed. Next I shall examine the distribution and some functional properties of the motor innervation; and I shall end with a closer look at the primary ending, in particular what can be learned from serial sectioning and volumetric reconstruction.

On the abundance of spindle afferents

I begin not by examining the numbers of afferents directly, which I shall consider later, but with a look at the numbers of spindles in different muscles, for which much more data are available. As each spindle of necessity receives at least one afferent, this will give us an idea of the minimum number of afferents. The fullest set of data for any one species is that accumulated by Voss and his group for the human, and summarised by him just as I was beginning my own studies on the spindle (Voss, 1971). It comprises almost 22 000 spindles in total, distributed among 139 named muscles only two of which, mylohyoideus and pterygoideus lateralis, lacked spindles. Some paraspinal muscles are missing from the data set, so the system of human skeletal muscles must contain in excess of 44 000 spindles and at least the same number of group Ia afferents supplying their primary sensory endings. To take two particular examples: the counts for lumbricalis manus IV and gluteus maximus are respectively 28 and 629 spindles, but the lumbrical is almost 600 times smaller (1.3 g) than the gluteal muscle (748 g). Is it possible to compare these values meaningfully, for such a wide range of muscles? And if it is possible, how may it be done?

Voss himself seems to have thought that some sort of integrated volume of all the spindles in a given muscle, when expressed as a proportion of the muscle’s volume, would make a suitable basis for comparisons (Voss, 1937), but this appears to have been founded purely on a priori conviction rather than empirical or theoretical evidence. He also considered an integrated length of the spindles, but recognising the impracticality of both methods, he settled instead on the number of spindles per gram of adult muscle mass, usually known as spindle density (Voss, 1937). Although some authors used other measures from time to time, most, including myself initially, accepted spindle density uncritically; even now new reports and textbook accounts appear, giving values of spindle density as a supposed reliably simple, direct measure of comparative spindle abundance.

I began to have doubts about the usefulness of spindle density when, in the early 1980s David Barker proposed that we should write a monograph on the spindle. One of the chapters assigned to me was on the number and distribution of spindles, and although neither the chapter nor the monograph was completed, I hope that my work on them was not wasted; with Mike Stacey I published a short paper (Banks & Stacey, 1988) where we demonstrated that spindle density is itself non-linearly related to muscle mass, thus making direct linear comparisons of spindle densities derived from muscles of different size seriously misleading. Instead, having adopted an allometric approach and finding a clear linear regression between log-transformations of spindle-count and muscle-mass data sampled across three species (rat, cat, human), we suggested that the residuals of the regression relationship could provide an unbiased measure of spindle abundance, applicable to muscles of different size (Banks & Stacey, 1988). Eventually, nearly two decades later, and after accumulating as much relevant data as I could find in the literature or obtain experimentally in a series of undergraduate final-year projects, I published a much more complete and rigorous analysis of this problem (Banks, 2006).

The non-linearity of spindle density in relation to muscle mass was, of course, present in Voss’s (1971) data but was overlooked for many years, certainly by me. I offer this as a salutary lesson to young scientists. My graphical analysis (Banks, 2006) of the complete set of data from Voss (1971) is reproduced in Fig.1. The slope of the overall regression relationship shows that spindle number tends to increase as a fractional power function of muscle mass. I will return to the value of the slope shortly, but for now I wish to emphasise that the residual values are homogeneously distributed and, suitably corrected when back-transformed (see Banks, 2006), do indeed provide an unbiased comparative measure of relative spindle abundance. Lumbricalis manus IV and gluteus maximus, with which I introduced this section, are indicated in Fig.1. Though occurring at almost the extreme ends of the range of muscle mass, after back-transformation and correction each is found to have almost exactly the number of spindles expected for muscles of their size, based on the regression, so each has a relative abundance of 1.0 (Banks, 2006). The data in Fig.1 are coded according to regional location. Regression relationships for two of the groups, shoulder and head position/neck, are also included. The mean residual values for the two groups, −0.57 and 1.09 ln units, respectively, differ very highly significantly (t > 6.78, P < 0.001), and represent a range of relative abundance of a little over fivefold. Vestibulo-collic reflexes play a central role in maintenance of a stable head position during changes of body position in locomotion and postural adjustments (Wilson, 1992); the wealth of proprioceptive information derived from the muscles involved is presumably a necessary component of the head-positioning system, although monosynaptic reflexes, perhaps not surprisingly, are weak. By contrast, the relative paucity of spindles in shoulder muscles may be related to the great freedom of movement of the upper limb at the shoulder and probably a much greater requirement for descending cortical control. Finally, I will mention one other comparison of physiological interest – between a group of 24 muscles that I identified as physiological flexors and 31 I identified as physiological extensors, all from the upper and lower limbs. Although the groups overlapped considerably, the mean residual value for the flexors (0.18 ln unit) was significantly greater (anova, F₁ > 5.25, P < 0.05) than that for the extensors (−0.05 ln unit).

Fig 1.

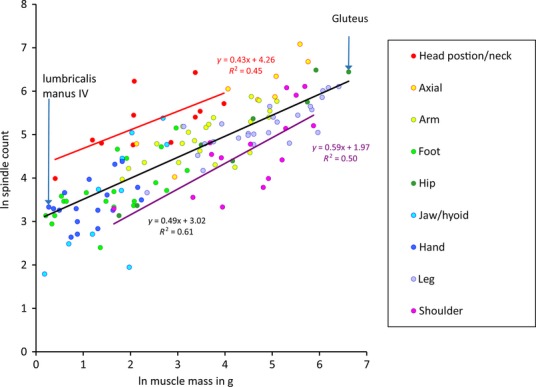
The relationship of number of spindles and muscle size for human muscles. Scatter plot of logarithmically transformed spindle counts against muscle mass using data from Voss (1971). The least-squares regressions of ln (spindle number) vs. ln (muscle mass) are shown together with their respective equations, as follows: total sample in black; head position and neck muscles in red; shoulder muscles in purple. Lumbricalis manus IV and gluteus maximus are indicated as specific examples. Modified from Banks (2006).

The tendency of spindle number to increase as a fractional power function of muscle mass is also seen across species that differ progressively in body size by about an order of magnitude (Banks & Stacey, 1988; Banks, 2006). No other species has been sampled as extensively as the human, however, and mostly only sporadic data have been published. But for the cat, rat and guinea pig, samples of at least 32, 26 and 76 muscles, respectively, are available (see Banks, 2006, for references to original sources). The rat and guinea pig have similar body sizes, so to minimise bias while retaining as much information as possible, I constructed two sets of data – (i) rat, cat and human; (ii) guinea pig (Cavia), cat and human – such that data were included only if they were available for muscles homologous in at least two of the three species in each set (identified by anatomical homonymy). Both sets showed similar distributions; the data for guinea pig, cat and human are plotted in Fig.2. The continuous line is the regression of ln spindle number on ln muscle mass, treating all the muscles of the three species as a single group. Its slope (0.36) and that for the rat, cat and human set (0.35) are virtually identical, and contain within their 95% confidence limits the isometric condition (0.33) (Banks, 2006). The rightmost dashed line is the regression relationship for the complete human sample replotted from Fig.1. Its slope (0.49) differs significantly from the isometric condition, but is of course very close to that of a square root function (0.5).

Fig 2.

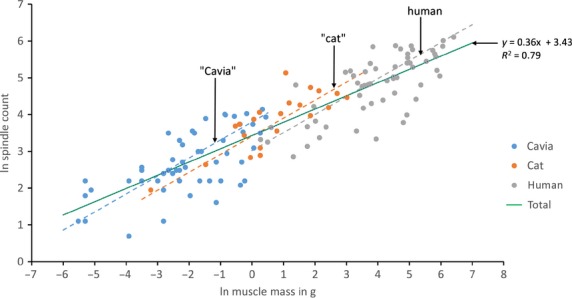
The relationship of number of spindles and muscle size for muscles from three species of mammal, differing in body size by about an order of magnitude. Scatter plot of logarithmically transformed spindle counts against muscle mass for samples of muscles from guinea pig (Cavia), cat and human. Muscles are only included if they are homologous in at least two species. The least-squares regression of ln (spindle number) vs. ln (muscle mass) for the total sample is shown together with its equation by the continuous line. Dashed lines show the regression relationship for the complete human sample of Fig.1 in its original location (human) and displaced by 3 ln units twice successively along the total regression line (‘cat’ and ‘Cavia’).

Initially it had seemed as though the relationship between spindle number and muscle mass would be the same both across and within species (Banks & Stacey, 1988), but this is clearly not so. Nevertheless, I thought that underlying the different regression relationships there ought to be a more fundamental level where they could be unified. I was able to do this by introducing a variable W, which I called the characteristic width (Banks, 2006), such that spindle number (N_s, let us say) is some function of W:

Now suppose that muscle volume is proportional to W²L_f, where L_f is the mean extrafusal fibre length. In the isometric condition all lengths scale proportionately, thus the mass of homologous muscles scaling isometrically will do so in proportion to the cube of some arbitrary length L, assuming constant physical density (ρ), and N_s will scale as the cube root of muscle mass. For heteronymous muscles within a single species, however, L_f is constant, so muscle mass will vary as a function of W² and N_s will scale as the square root of muscle mass. W² is clearly related, but not identical, to the physiological cross-sectional area. If this model is accurate it ought to apply to other species apart from the human, but the limited sample sizes available for non-human species prevented a direct test. Instead I have included in Fig.2 the outcome of an approximately isometric scaling model of the human data, in which the (human) regression line is shifted along the interspecific regression line by 3 ln mass units (ca. 20-fold) twice in succession. This is equivalent to, say, a species of 80 kg body mass scaling isometrically to one of 4 kg, then to one of 200 g. The shifted lines are labelled as ‘cat’ and ‘Cavia’ to indicate that whereas they are located within the individual data for the cat and the guinea pig, they are, of course, not derived from those data. Indeed, homologous muscles do not occupy exactly comparable locations with respect to the regression lines, which is to be expected as the guinea pig and cat are only approximately miniature versions of the human. This all indicates the importance of regulating spindle number in relation to muscle mass and function in a controlled way through selection pressure, but of course says nothing of the mechanism by which it is achieved. Whereas the genetic programs controlling spindle number and muscle mass are unlikely to be entirely independent, it would seem they are separable under selective breeding to some extent (Lionikas et al. 2013).

The above analysis would serve to define the relative abundance of all spindle afferents if there was a known relationship between the number of spindles and the number of afferents. When I began my doctoral studies, this was still a possibility; it was known that spindles varied in the number of sensory endings they possessed, but not whether this was deterministic, and it was unclear whether the population of afferents varied characteristically from muscle to muscle (Ruffini, 1898; Barker, 1962; Boyd, 1962). Moreover, almost everything that was then known about the sensory innervation was derived from a few hindlimb muscles of the cat, as reviewed by Matthews (1972) and Barker (1974). By the early 1980s, however, we had gathered enough evidence, still mainly from the cat hindlimb, to be fairly sure that once the number of spindles in a muscle had been set by the instructional role of the first afferents to arrive in development, the number of additional afferents received by any particular spindle was determined at random, but that the mean number of these additional afferents per spindle was probably deterministic and might vary characteristically from muscle to muscle (Banks et al. 1982). Further progress was slow, as it usually depended on the accumulation of material from control experiments carried out in connexion with work in Durham on reinnervation (for example, Banks & Barker, 1989) or in Calgary with Manuel Hulliger on the neuropathic effects of pyridoxine megavitaminosis (Hulliger, M. and Banks, R. W., unpublished in full). The method used for the studies was the Barker & Ip (1963) teased, silver-impregnation technique. After a run of failures to obtain useable results with the technique, I set out systematically to investigate the steps involved and found that the total exposure to silver ion during incubation in AgNO₃ solution was critical, and that prior to its reduction to metallic silver the distribution of silver ion did not reach a stable end-point. This enforced methodological detour remains unpublished (although the outcome was reported in Banks, 1999b), but it did at least generate some comparative data for the rat.

Finally, together with Manuel Hulliger, Hassan Saed and Mike Stacey, I felt that we had enough information to answer some important questions concerning the pattern of innervation of muscle spindles and other encapsulated mechanoreceptors in muscle (Banks et al. 2009): did the number and distribution of spindle afferents, particularly those ending as secondaries, vary independently of spindle number; if they did, were they characteristic for different muscles; did the number of other encapsulated mechanoreceptors, in particular the tendon organ, vary in similar ways; are there interspecific differences? Previous studies, including our own (Banks et al. 1982), had been based on incompletely sampled muscles, but we had found that the full analysis required a large sample of muscles whose complete afferent supply to their spindle populations was known, because spindles close to the main intramuscular nerve trunks tended to show a more complex sensory innervation than more distant spindles. The statistical demonstration of this result was based on the peculiar structure of the cat tenuissimus, but a clear example from flexor digitorum longus, also from the cat hindlimb, is illustrated in Fig.3.

Fig 3.

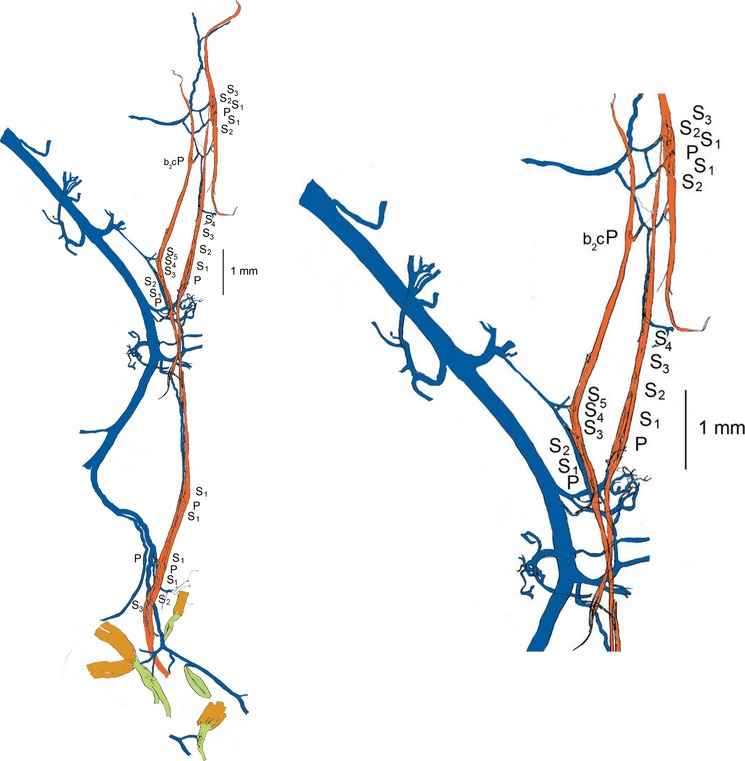
Tracing of a portion of the intramuscular nerve (blue), silver-impregnated and teased, from a flexor digitorum longus muscle of the cat, together with seven spindles (red) that were located close to the nerve. The sensory complement of each spindle is given alongside its equatorial region; all had a single primary ending (P) together with a variable number (0–5) of secondary endings (S). Each sensory ending is supplied by a separate afferent axon; the mean number of afferents per spindle additional to that a single primary, N_A, for this group is 2.86, whereas for the remainder of the muscle (more distant from the main intramuscular nerve) N_A > 1.7. The intramuscular nerve shown here also supplies three tendon organs and a Pacinian corpuscle (green). Part of the tracing is enlarged on the right, to show detail more clearly; b₂c signifies a spindle that lacked a bag₁ fibre.

Despite the positional bias within a muscle, this time (Banks et al. 2009) we confirmed the random nature of the overall frequency distribution of the sensory complements of the spindles for several particular muscles, rather than a single mixed sample. For most muscles even a simple Poisson distribution did not differ significantly from the observed data, as judged by the chi-square goodness-of-fit test, though binomial distributions gave better fits. The observed distribution for the tenuissimus muscle is compared with the best-fitting binomial in Fig.4.

Fig 4.

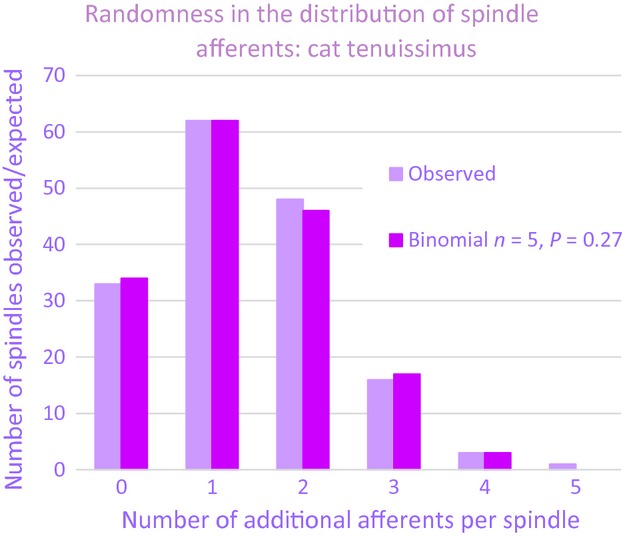
Histograms showing the observed and best-fitting binomial frequency distributions of cat tenuissimus spindles with different numbers of afferent axons additional to that supplying a single primary ending and for which the observed mean number of such afferents, N_A > 1.37.

The hypothesis behind this analysis is that the first afferents to arrive in the muscle primordium do not have to locate a myotube that is predetermined to develop as part of a spindle, but instead cause primary myotubes that they happen to encounter to switch their genetic program from one causing the expression of the default extrafusal phenotype to one generating the first of the spindle’s set of intrafusal muscle fibres. They will become the group Ia afferents as they mature (Kucera et al. 1988). Later-arriving afferents, mostly corresponding to group II afferents (Kucera et al. 1988), must then locate the incipient spindles. One obvious way they might do this is to recognise the earlier instructional afferents somewhere in the nerve and simply follow them to their spindles. If the association of a later-arriving afferent with one of the instructional afferents is a stochastic process, the observed distributions are to be expected.

We constructed the theoretical distributions for each muscle using the mean number of afferent fibres in each spindle additional to the one presumed to have initiated the development of the spindle. For convenience, I shall refer to this value here as N_A. Analysis of five muscles from the cat hindlimb that were multiply sampled showed significant differences between at least some of them, so demonstrating that N_A is characteristic for a particular muscle. The muscles formed part of our largest sample from a single species (the cat), where N_A ranged from 0.42 (calcaneometatarsalis) to 3.49 (rectus capitis posterior). As with the relative abundance of spindles, there was some evidence for regional differences: values of N_A for the three axial muscles in the sample were higher than those for all but two (popliteus and abductor digiti quinti medius) of the 19 appendicular muscles; and the intrinsic muscles of the hind foot had a significantly lower average N_A (1.12, n > 10) than the remainder of the hind limb (1.79, n > 8; for details of the statistical analysis see Banks et al. 2009). Nevertheless, even within the group of intrinsic foot muscles there was at least one clear specialisation that could plausibly be linked to function, in that the three muscles controlling the position of the 5th digit, and thus presumably the stability of the foot, had values of N_A as high or higher than any other muscle of the group (Fig.5).

Fig 5.

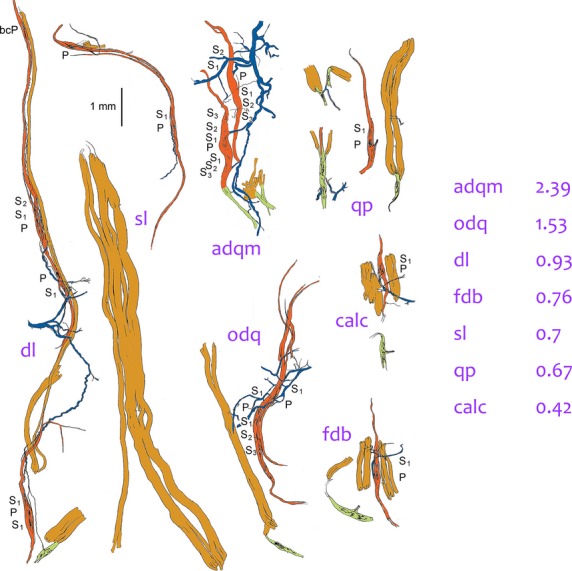
Tracings of groups of muscle spindles, tendon organs and extrafusal muscle fibres teased from intrinsic hind-foot muscles of the cat, all drawn to the same scale. Colour code as in Fig.3. dl, deep lumbrical (flexor profundus); the tendon organ is a rare occurrence in this muscle; extrafusal muscle fibres (light brown) extend the full length of the fascicle alongside the group of spindles. sl, superficial lumbrical (flexor superficialis; two spindles partially in parallel shown above an extrafusal fascicle. adqm, abductor digiti quinti medius: one of the spindles is in series with a tendon organ. odq, opponens digiti quinti. qp, quadratus plantae; the short pole of the spindle is complete. calc, calcaneometatarsalis. fdb, flexor digitorum brevis. Note that the spindles are longer than the extrafusal muscle fibres in calc and fdb. Values of N_A for each of these muscles are given on the right.

In the cat most spindles possess a single ending at the equator, supplied by one large afferent, and known since Ruffini (1898) as the primary ending, but in a small number of spindles in our sample (22/1363, including nine from extensor digitorum longus alone) a second, equally large, afferent contributed another primary ending to the equatorial region. The great majority of additional afferents, however, end on either side of the primary as Ruffini’s secondary endings (1800/1822 in our sample). In any particular spindle, when secondary endings are present, the afferents are always smaller than that supplying the primary ending and they become progressively smaller as their endings are located further from the primary ending (S₁, S₂ and so on; Banks et al. 1982).

We obtained the remainder of our data (Banks et al. 2009) from samples of rat (four muscles), rabbit (five muscles) and guinea pig (one muscle). Apart from the rat masseter, all were from the hind limb. Their values of N_A fell within the range seen in the cat. Primary and secondary endings were supplied by separate afferents in all 214 rabbit and 15 guinea pig spindles, whereas some afferents in the rat (34/528 to the 197 spindles) ended in mixtures of primary-like and secondary-like terminals. All but one of these were additional to at least one afferent supplying primary-ending terminals; moreover, the incidence of multiple primary-ending afferents was very high in all muscles of the rat (151/331 additional afferents), especially the masseter, where up to five afferents might contribute primary terminals to a single spindle and four was quite common (8/77 spindles).

At the present time, when entire genomes are readily available, it may seem strange that we know so little about the way a sensory system of such importance in motor control is organised. But we cannot read this information from the genome; it can only be obtained by patient collection of structural and functional data that may lead us towards a more complete understanding. So, for example, we can see from the interspecific regression relationship (Fig.2) that doubling the size of homologous skeletal muscles is associated on average with a 1.28-fold increase in spindle number. Why should this be? When, presumably, so many other features of the organisation of the muscles are changing, is it merely coincidence that the slope is so close to the isometric condition of 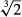The number of spindles and the total number of spindle afferents are characteristic properties of a particular muscle, but neither spindles nor afferents are evenly distributed throughout the muscle, instead being subject to random variation. Does this randomness matter functionally? Probably not (Eldred et al. 1998). As we shall see in the following section, some aspects of the organisation of the intrafusal motor supply are also subject to random variation. In this case, however, we know even less about any possible functional significance.

The motor innervation

The publication of our paper (Banks et al. 1977b) in which we clearly established that mammalian muscle spindles regularly contained three types of intrafusal muscle fibre might be taken as a turning point in studies on the intrafusal motor innervation. The argument about whether or not nuclear-bag and nuclear-chain fibres were separately innervated had already been resolved by David Barker, Yves Laporte and their colleagues; to put it in their own words (Barker et al. 1973):

Our results show that the [dual] model has outlived its use, since we have found that among the spindles innervated by a static γ axon the terminals may be distributed either to bag fibres or to chain fibres, and are most frequently distributed to both.

But until it was recognised that the morphological category of ‘nuclear-bag fibre’ actually consisted of two, biochemically and functionally, very different kinds of fibre, now known as bag₁ and bag₂, interpretation of these results in terms of the known functional categories of dynamic and static axons remained challenging. Brown & Butler (1973), for example, having introduced the technique of glycogen depletion to muscle-spindle studies, recognised that static axons could activate nuclear-bag and nuclear-chain fibres together, but argued that in such circumstances the bag-fibre contribution did not affect the output of the primary ending. The best clue at that time as to what was actually happening is to be found in the study by Bessou & Pagès (1973), using their technique of direct observation of spindles with intact nerve and blood supply. To quote the authors again:

All dynamic γ axons innervated bag fibres but in many spindles the stimulation of several static γ axons elicited contractions in bag fibres which were never found to contract when dynamic γ axons were stimulated.

In passing, I will also note a very prescient observation by Bessou & Pagès (1973) concerning what would later come to be called the bag₁ fibre: ‘These contractile characteristics of bag fibres innervated by dynamic γ axons look like those of tonic muscle fibres of the frog…’ Although enzyme histochemistry and electron microscopy were showing that the bag₁ fibre had characteristics of a slow fibre, its tonic nature was not generally recognised until 1980 and the introduction of immunohistochemical studies on myosin by Pierobon-Bormioli et al. (1980).

In principle, the techniques of direct observation and glycogen depletion were to an extent complementary in that a direct observation experiment permitted the actions of all motor axons innervating a single spindle to be determined, whereas a glycogen-depletion experiment could demonstrate the complete distribution of a single motor axon among all the spindles innervated by it. After the separate identities of bag₁ and bag₂ fibres were recognised, a very satisfying level of agreement concerning the distribution of static and dynamic axons was rapidly achieved (my review in Progress in Neurobiology sets out the details: Banks, 1994a). It was clear that dynamic actions always involved the bag₁ fibre (but only rarely also involved bag₂ or chain fibres), whereas static actions always involved the bag₂ fibre, the chain fibres, or both bag₂ and chain fibres together. But some conflicting results remained concerning the static fusimotor innervation. David Barker had a foot in both camps. He continued to collaborate with Yves Laporte following Yves’ move to the Collège de France in Paris, and they began to use the glycogen-depletion technique which indicated that static fusimotor axons seemed capable of activating all three kinds of intrafusal fibre with bag₁ being depleted about as often as bag₂ (Barker et al. 1976). If the bag₁ fibre was innervated by both dynamic and static axons, as the results indicated, did the nature of its action on the response of the primary-ending to stretch depend on the type of fusimotor axon activating it? Some time earlier, David had begun another collaborative experiment with Paul Bessou’s group in Toulouse, including Elżbieta Jankowska. The experiment involved the iontophoretic injection of a fluorescent dye, Procyon Yellow, through micropipette electrodes used to record from intrafusal fibres in the region of convergence movements directly observed in intrafusal muscle fibres when activated by fusimotor axons. Although the experiment had been conceived before bag₁ and bag₂ fibres had been differentiated, their separate identification became possible during analysis of the results, mainly thanks to electron microscopical observations by Mike Stacey. The inferred intrafusal distributions of dynamic and static axons were generally similar to those derived from glycogen depletion, with the exception that static axons were never seen to activate bag₁ fibres (Barker et al. 1978). Nevertheless, the authors stated that: ‘Whereas it is generally agreed that static γ axons activate bag₂ and chain fibres, opinions differ as to whether they also ever activate bag₁ fibres’; and having asked ‘Is it significant that our static sample does not include a bag₁ fibre?’, gave several rather indirect reasons why it was not. Just a few years later I was able to present a clear reason why it was, based on reconstructions of the entire innervation of spindles from another Durham-Toulouse collaboration (Banks, 1981).

Scientists looking back over their careers will often acknowledge the importance that chance or serendipity has played. In my case what subsequently turned out to be one of my most important decisions can be traced back to the happenstance that I had initially learned my microtechnique in the electron microscopy laboratory run by Geoffrey Meek in Sheffield, where one of the techniques I acquired was a simple method for cutting resin-embedded tissue blocks into so-called semi-thin serial sections (typically 1 μm thick) using an ultramicrotome equipped with glass knives (Banks, 1999a). When we had completed the work on intrafusal fibre types (Banks et al. 1977b), I was casting around for my next project and David Barker told me of a series of tenuissimus muscles that had been fixed for electron microscopy by Paul Bessou and Bernard Pagès in Toulouse following their observation and location of foci of convergence movements in intrafusal muscle fibres activated by either dynamic or static axons. The idea had been to investigate the structure of the neuromuscular junctions that were confidently expected to occur at these foci, in particular those of the dynamic axons, as Paul and Bernard had shown that only junctional potentials could be obtained from intrafusal fibres on dynamic stimulation (Bessou & Pagès, 1972). The histological analysis was to be carried out in Durham, but David had put the material aside for the time being, after most of the foci initially investigated had been found to lack any motor ending. It was clear, however, that there had to be motor endings somewhere on the fibres whose movements had been observed and my fateful decision was to ask if I could use serial sectioning to find them. David agreed: a couple of years and about 30 000 sections later we had found that (Banks et al. 1978):

Contrary to expectation, motor endings on the bag₁ fibres seldom occurred at the sites of convergent movement. Only two cases of coincidence occurred among sixteen foci and 21 motor endings; otherwise focus and nearest ending were separated by distances of 0.85–2.5 mm.

A consideration of why the foci of sarcomere shortening did not coincide with the locations of motor endings would take me too far from the subject of this review, and we did not have a clear idea at the time, but it now seems likely to be due in the main to the tonic nature of the bag₁ fibre; thus, when it is activated by dynamic fusimotor input there is a rapid increase in relatively stable cross-bridge formation causing the polar region centred on the motor ending to become much stiffer, but without overt shortening in much of the region.

The quality of the sections and their effective close spacing (1 μm) when reduced to two-dimensional photomicrographs (Fig.6) meant that I now had a resource capable of defining the motor innervation in unprecedented clarity by the straightforward, if time-consuming, process of reconstruction. Simple schematic reconstructions, to scale only on the long axis of the spindle, revealed the distributions of all afferent and efferent axons from the intramuscular nerve to their endings on individual intrafusal muscle fibres (Fig.7). Only three complete spindles and an incomplete one, in which just the equatorial and one polar region were sectioned, were reconstructed in this way. But they were enough to decide between the apparently conflicting evidence from glycogen-depletion and direct observational studies as to whether static axons innervated bag₁ and bag₂ fibres more or less equally often. Of the 26 motor axons innervating the reconstructed spindles, 22 were identified as purely fusimotor γ fibres; of these, 18 supplied bag₂ (5), chain (5) fibres or both together (8), and none of the 18 made any form of contact with the bag₁ fibres. I could conclude that (Banks, 1981):

Fig 6.

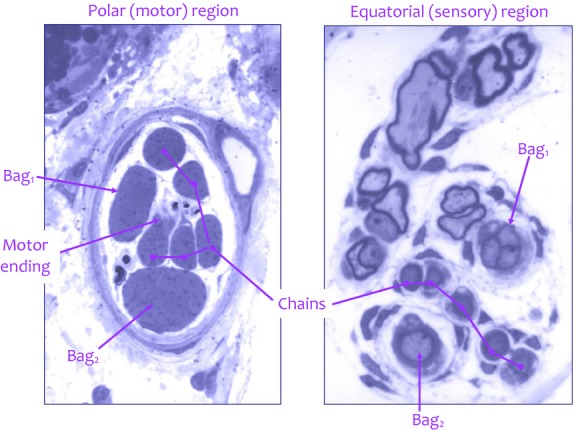
Examples of semi-thin (1-μm-thick) transverse sections through the polar (left) and equatorial (right) regions of a cat tenuissimus spindle, serially sectioned throughout its length. The polar-region section passes through a motor ending on a chain fibre, and the equatorial-region section passes through the primary ending, which is reconstructed in Figs1 and 2. Toluidine blue; width of each image is 85 μm.

Fig 7.

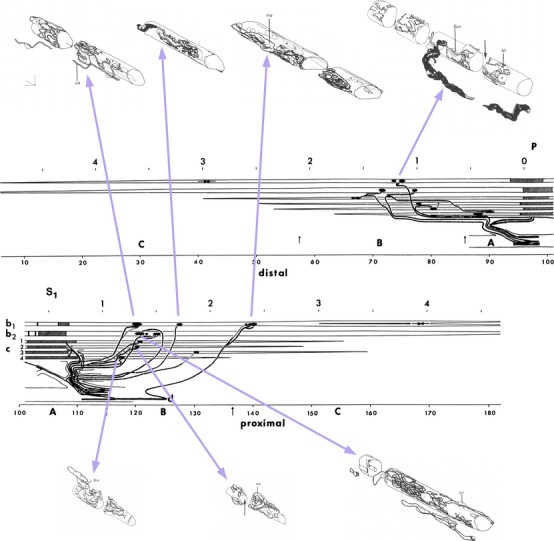
Semi-schematic and axonometric reconstructions of a cat tenuissimus spindle from serial, semi-thin sections. The semi-schematic reconstruction is divided into distal and proximal halves, and shows the lengths of the intrafusal muscle fibres, the positions of their motor (black oval shapes) and sensory (hatched rectangular shapes) nerve endings, and the distribution of the afferent and efferent axons. The scale above each half is in mm; below each half is the number of microscope slides in the series, with 50 sections per slide. A, B, C separated by vertical arrows indicate the expanded periaxial space (A), the polar region enclosed by capsule (B), and the extracapsular polar region (C). Horizontally opposed arrows in the bag₁ fibre (b₁) indicate the locations of foci of sarcomere convergence seen on stimulation of a dynamic β axon that was subsequently found by this reconstruction to supply all motor endings on the bag₁ fibre. All the bag₁ motor endings, and a selection of motor endings on the bag₂ (b₂) and chain (c) fibres, are shown in axonometric reconstructions above and below the semi-schematic. Axonometric scales are 10 μm. For full details and electron micrographs taken in the gaps marked by vertical arrows see Banks (1994b).

Analysis of the results clearly indicates that the bag₁ intrafusal muscle fibre usually does not receive a static fusimotor input via trail innervation. In contrast to the highly selective innervation of bag₁ fibres, almost half the axons supplying bag₂ or chain fibres branched to terminate on both types of fibre.

My results were later borne out by the Glasgow group (Arbuthnott et al. 1982; Sutherland et al. 1985) and by Kucera in Boston (1985), but it was already evident that the depletion of bag₁ fibres during prolonged static γ activation was artefactual, and Yves Laporte’s group soon showed that it was associated with fatigue of the bag₂ or chain fibres (Decorte et al. 1984).

There are two aspects of intrafusal motor innervation that I have glossed over in the preceding account, and that I now need to introduce briefly: the so-called β axons that have a skeletofusimotor distribution; and the use of the terms trail, p₁ plate and p₂ plate to categorise intrafusal motor endings. Motor innervation of intrafusal muscle fibres by branches of skeletomotor axons was already well known from non-mammalian tetrapods when it was also found to occur in mammals by Bessou et al. in Toulouse (1965). In non-mammals it may provide the only intrafusal motor supply, so to some it undoubtedly then represented little more than an evolutionary oddity when it was discovered in mammals, with their highly developed, purely fusimotor, γ system. But over the next 25 or 30 years Yves, Françoise, Léna Jami, Julien Petit, and others, working in Paris and making extensive use of the glycogen-depletion technique, characterised the mammalian skeletofusimotor system thoroughly, and demonstrated that it was an important component of mammalian intrafusal motor innervation. A detailed account is given in my earlier review (Banks, 1994a); here I must content myself with a list of the following salient features:

1. Both dynamic and static fusimotor types occur;

2. Intrafusal glycogen depletion produced by stimulation of dynamic β axons was essentially identical to that produced by dynamic γ axons;

3. Static β axons almost always produced glycogen depletion in chain fibres, but typically only the longest one or two fibres in one pole;

4. The extrafusal distributions of dynamic and static β axons respectively consisted of slow (type I) and fast (type IIA or IIB) fibres;

5. There was no difference between the extrafusal components of the motor units and their purely skeletomotor counterparts.

The final item on the list raises, in my opinion, an important point about scientific nomenclature. The term ‘β axon’ is, in effect, a name and as such has the unfortunate property of suggesting the existence of a distinct category of objects. It appears that in this context β was first used for no better reason than that it comes between α and γ in the Greek alphabet. It could be treated as an hypothesis (β axons are different from both α and γ axons) in which case it has not been substantiated and is probably wrong: β axons appear to be α axons that just happen to innervate both intrafusal and extrafusal fibres. Mammalian skeletofusimotor fibres (an accurate descriptive phrase rather than a name) is admittedly a bit cumbersome, so we seem to be stuck with β axon, at least for the time being.

The use of the terms ‘trail, p₁ plate and p₂ plate’ also originally represented an implicit categorical hypothesis, but in addition it illustrates a subtle change of use of the kind that occurs frequently in science due to advances in knowledge. The terms were introduced by David Barker to designate what he argued were three different types of intrafusal motor ending, and for some years formed part of the evidence he presented in his intellectual skirmishes with Ian Boyd concerning the structure and innervation of the spindle that so often enlivened meetings of the Physiological Society in the 1970s. This phase in the life of the terminology culminated in a major paper in the Philosophical Transactions of the Royal Society (Barker et al. 1970). The three hypothetical categories were used to inform the debate on the number of types of intrafusal muscle fibre, and were incorporated into the linked hypotheses that static γ axons ended as trail endings, dynamic γ axons ended as p₂ plates, and skeletofusimotor axons ended intrafusally as p₁ plates. These three hypotheses were to be tested in experiments designed to establish directly the histological properties of functionally identified fusimotor axons. Characterisation of the endings confidently expected to be found at the sites of sarcomere convergence was to have been one of these experiments. When I eventually found the endings responsible for eliciting the observed contractions, as described above, we already knew from the independent evidence of histochemistry and electron microscopy that there were three kinds of intrafusal fibre, so now, rather than identifying an ending and asking on what kind of fibre was it located, we could identify the different types of fibre and ask what all of their motor endings were like. And so I made a series of axonometric reconstructions of all the motor endings in the serially sectioned spindles (Fig.7) (Banks, 1981). There were too few endings (27) to use in a quantitative assessment of the trail, p₁ plate and p₂ plate categories, but the reconstructions seemed to work quite well, so I thought it might be fun to do the same with the primary sensory endings. I will return to the primary endings at the end of this review; I mention their reconstructions here because they indicated that there were consistent features of those parts of primary endings associated with each type of intrafusal muscle fibre, which ought to be clearly visible in teased, silver-impregnated spindles. We soon found that that was indeed the case (Banks et al. 1982), so we could now identify bag₁ and bag₂ fibres in our teased material and could gather a sample of silver-impregnated intrafusal motor endings large enough for quantitative analysis. The complete sample included the endings of known skeletofusimotor axons, known static γ axons, and presumed dynamic γ axons remaining on bag₁ fibres after removal of skeletofusimotor axons by differential degeneration after denervation. There were significant differences between the population statistics of these three groups, to which we could now justifiably give the names p₁ plate, trail and p₂ plate by definition rather than hypothesis (Banks et al. 1985).

Just as the number of sensory endings varies from spindle to spindle, even within a single muscle, so also does the number of motor axons supplying those spindles. For example, in one tenuissimus muscle (C883 in Banks, 1994b) the number of motor axons received by each of 17 spindles ranged from 2 to 10, despite all of the spindles possessing a similar complement of intrafusal fibres: one bag₁, one bag₂ and a variable number of chain fibres, probably between 2 and 5, most commonly 4. Why is this, and how does it come about? The first question is, I think, the more difficult and I will return to it when I have looked at some aspects of the physiological effects of the motor innervation. How the observed patterns of motor axonal distribution come about is, of course, a developmental question. The answer, by random association of a particular axon with a particular spindle, is the same whether the total efferent population is examined, or some part of it such as γ axons supplying bag₂ and chain fibres. The evidence for this conclusion is that each of the observed distributions may be accurately modelled with binomial statistics (Banks, 1994b). There is a little more to the story, however, involving a difference in behaviour between the purely fusimotor γ axons and the mixed, skeletofusimotor (β) axons. When the efferents were segregated into probable or possible γ axons and probable or possible β axons, a clear correlation emerged between the number of γ axons and the number of afferent axons entering a spindle, but there was no correlation whatsoever between the numbers of β axons and afferent axons. The most obvious explanation for this difference is that γ axons, being purely fusimotor, must find their way to the already developing spindles and they may do so by accompanying afferent axons or following pathways laid down by them, whereas skeletofusimotor (β) axons only become so by virtue of the accidental encounter of branches of α axons with developing spindles, any α axon apparently being capable of forming intrafusal connexions. This randomness should not be seen as detracting from the functional importance of the skeletofusimotor innervation, only that it does not matter which particular α motoneuron establishes contact with any particular spindle.

In their 1976 paper on glycogen depletion, while considering the limitations of the technique for demonstrating the complete motor innervation of the spindle, David Barker and his colleagues Françoise Emonet-Dénand, Dave Harker, Léna Jami and Yves Laporte (Barker et al. 1976) wrote that:

Theoretically it should be possible to correlate patterns of motor control of primary-ending discharge with patterns of fusimotor innervation, but such a correlation would require not only very precise location of several spindles supplied by the same axon (not so easily achieved), but also a more detailed analysis of the alterations of sensory discharge resulting from fusimotor activation.

There was one preparation where the first of these conditions could be met due to the narrowness of the muscle and the orderly arrangement of its spindles (see Fig.9); that was the cat tenuissimus, which I was taught by Paul Bessou and Bernard Pagès when I went to Toulouse in 1978 on an MRC/INSERM exchange fellowship. The second condition was addressed most comprehensively perhaps by Ian Boyd who used direct observation of tenuissimus spindles with intact nerve and blood supply to characterise the effects of contraction in each type of intrafusal fibre on primary- and secondary-ending responses (Boyd, 1981). Ian then went on to argue that there were two kinds of static γ axon, each one always supplying either the bag₂ or chain fibres, though not exclusively so (Boyd, 1986). If true, this might confer a degree of independent control of the bag₂ and chain fibres (as indicated by some central stimulation experiments from Glasgow; Gladden & McWilliam, 1977a,b), but the known histology ruled out anything approaching the homogeneity shown by extrafusal motor units or the distribution of dynamic γ axons.

Fig 9.

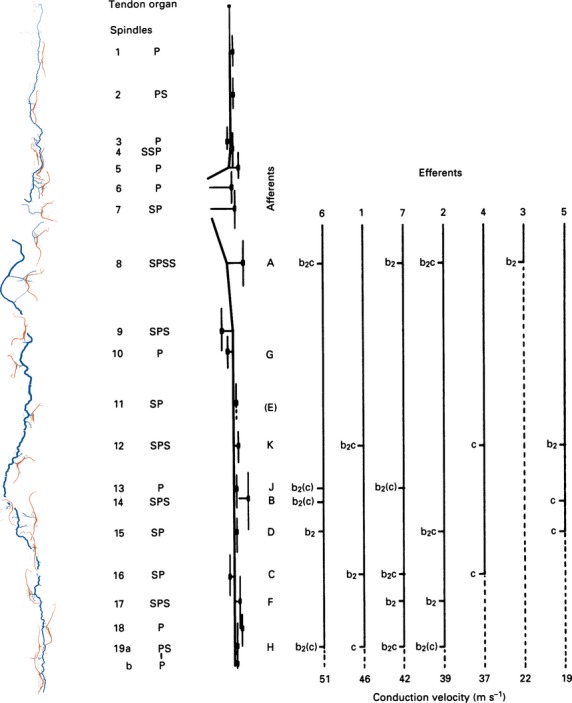
Graphic representation of the distribution of γ-efferents among the spindles supplied by the distal nerve branch in a cat tenuissimus muscle, together with a tracing and a schematic diagram of the arrangement of the spindles and their nerve supply in the whole muscle. At the left, the spindles and nerve supply are shown as tracings of the silver-impregnated, teased preparations made following the physiological experiment. Spindle sensory regions were located in the intact muscle and marked with epimysial stitches. Next right is a schematic diagram of the nerve supply, with spindles represented by short vertical lines. Recorded afferents were all from primary endings; they are identified alphabetically according to the order in which they were isolated in dorsal-root filaments, and are positioned opposite their corresponding spindle. Efferents are identified according to their order of isolation in ventral-root filaments, and are positioned according to their conduction velocities. Afferent E was initially isolated but was lost before any motor actions could be tested. Otherwise all combinations were tested, and the probable intrafusal distribution of the motor axons, based on the afferent responses, are given. P, primary ending; S, secondary ending; b₂(c) signifies that the axon supplied either bag₂ alone or bag₂ and chain fibres together. Modified from Banks (1991).

The idea that there are two kinds of static γ axon could not be tested on the evidence then available, so a more direct test was needed, one that could substantially meet the theoretical ideal of Barker et al. (1976). Once we had the capability to identify all three types of intrafusal muscle fibre in teased, silver-impregnated preparations (Banks et al. 1985) it was evident that in principle the distribution of fusimotor axons within and between spindles could be mapped in the physiologically accessible part of the cat tenuissimus. The practical feasibility of the experiment was shown by some key histophysiological correlations, such as the driving action of chain fibres and the biasing action of bag₂ (Fig.8). These correlations were independent of Ian Boyd’s (1981) catalogue of actions, and generally in agreement with it, but on their own could not test Ian’s hypothesis of two types of static γ axon. What was required were matrices of large numbers of interactions; in the most complete matrices I was able to test the actions of eight or nine static γ axons on seven primary endings, yielding 26 actual from 56 potential and 23 actual from 63 potential interactions, all potential interactions having been tested (Fig.9) (Banks, 1991). I had expected to find that nearly all the static γ axons would supply both bag₂ and chain fibres somewhere in their complete distribution, though by chance some might supply either bag₂ or chain fibres more often than others, as this had been shown many years before by Barker et al. (1973). I had also expected not to find any support for the separate existence of two kinds of static γ axon. Both these expectations were borne out; but the most important result was unexpected – there was a clear relationship between the distribution of the static γ axons and their conduction velocity (Fig.9) (Banks, 1991). As far as I am aware, no one had predicted this; I reported it with scientific sang-froid that belied my excitement at the discovery (Banks, 1991):

Fig 8.

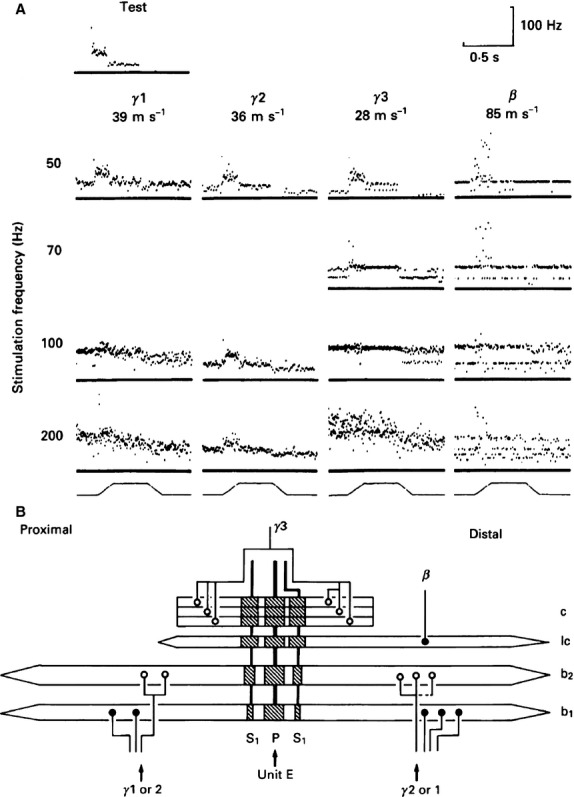
(A) Instantaneous frequency displays showing the responses to ramp-and-hold stretch, indicated at the bottom of each column, of a primary ending (conduction velocity 92 ms⁻¹) in the absence (test) and the presence of fusimotor stimulation at different frequencies. Zero frequency is marked by a continuous baseline in each response plot. All the motor axons were static in action but only two drove the primary ending at the stimulus frequency, including the β. Conduction velocities of the motor axons are given below each one’s identifier. (B) Schematic diagram of the innervation of the spindle that contained the primary ending whose responses are shown in (A). There were probably four static motor axons (the connexion shown by the dashed line is uncertain), all of which were isolated in L7 ventral root. Note that the bag₁ fibre received only β innervation, as judged by the nature of its end plates. ○, trail plate; ●, p₁ plate (as defined by Banks et al. 1985). In this and following figures, abbreviations are: P, primary ending; S, secondary ending; b₁, bag₁ fibre; b₂, bag₂ fibre; c, chain fibre; lc, long chain fibre (a and b from Banks, 1991).

The static γ axons showed some differential distribution according to their conduction velocities: faster-conducting axons were likely to be more widely distributed among spindles but less likely to innervate chain fibres alone than were more slowly conducting axons.

To return now to the question I posed earlier: why should there be a wide variation in the number of motor axons supplying spindles with similar numbers and types of intrafusal fibre? My sample of cat tenuissimus spindles with a full complement of intrafusal fibres (bag₁, bag₂ and chain) each received from 2 to 13 motor axons, with an average of 7.36 per spindle (Banks, 1994b). In virtually every case, therefore, this would be sufficient in principle to supply all three fibre types separately, and in more than half of all spindles to supply even the individually contractile poles of the different fibre types separately, if either of these conditions were beneficial. Actually both histology and physiology agree on the high degree of segregation between the dynamic (bag₁) and static (bag₂/chain) systems, consistent with separate dynamic and static modulation being of prime functional importance in motor control, at least in the cat. Thus the developmental program is capable of delivering an essentially segregated motor innervation when needed. What, then, about the bag₂/chain system? Here the number of γ axons entering the tenuissimus sample ranged from 1 to 7 with a mean of 3.74, still sufficient to innervate the bag₂ and chain fibres completely separately in almost every case, yet this occurred in only one of 12 spindles that each received at least two presumed static γ axons (see fig. 5 of Banks, 1994b). Conversely, the poles of the bag₂ and chain fibres were supplied completely separately by those axons in 10 of the 12 spindles. It would seem clear, then, that the wide variation in the number of motor axons is not so as to ensure segregation of the bag₂ and chain fibres comparable to that between these two and the bag₁ fibre; perhaps it serves rather to provide individual primary endings with a level of integration of fusimotor command signals above that which needed simply to activate the intrafusal fibres.

If there is only one kind of static γ axon why should the axons innervate bag₂ and chain fibres together? Emonet-Dénand et al. (1997) showed that:

The coactivation of bag₂ and chain fibers, at presumed physiological frequencies, enables primary endings to continuously signal changes of length over a large range of stretch velocities independently of the average muscle length.

Moreover, by stimulating groups of static γ axons with different conduction velocity ranges, Emonet-Dénand et al. (2001) went on to show that:

Stimulation of each group prevented ensemble discharges [of several afferents] from falling to very low levels during shortening phases. However, this effect was clearly larger when the group of fast-conducting axons was stimulated. [T]his stronger effect supports the view that static γ axons with faster conduction velocities are more likely to supply more bag₂ fibers than slower ones.

I shall end this section with a brief account of an unfinished experiment carried out with, and utterly dependent on, my dear friend Manuel Hulliger. I hope I am correct in recalling that we discussed the germ of the idea when Manuel and I met at a symposium organised by Tony Taylor and Arthur Prochazka at the Sherrington School of Physiology in 1980. The idea was, in view of the integration of intrafusal actions and length changes at the primary ending, to create a kind of look-up table of primary responses to a wide range of stretch and fusimotor stimulation in combinat-ion. Diagnosing fusimotor actions typically involved stimul-ation of axons at constant high rates, most often 100 impulses s⁻¹. Such rates are, of course, quite artificial; natural rates, for example during locomotion, where they are modulated with the step cycle up to around 50 impulses s⁻¹, are also subject to apparently random inter-impulse variability (Taylor et al. 2006). In creating our look-up table we would aim to use (pseudo-) randomly varying patterns of fusimotor stimulation with low mean rates of perhaps 30 impulses s⁻¹. Circumstances meant that the germ lay dormant for more than a decade; then, in 1992, I was granted a term’s research leave which Manuel generously hosted in his laboratory in Calgary. We first carried out a series of experiments on the existence and interaction of separate pacemaker or encoding sites (that is to say, sites of action-potential generation) in the primary ending (Banks et al. 1997); then, when I returned to Calgary for another extended stay in 1995, we began the experiment that we were calling ‘multiple low-rate gammas’. The protocol was to isolate as many primary-ending afferents and fusimotor efferents (preferably γ, but β if necessary) as possible and to group them into unique combinations of one afferent with a pair of dynamic and a pair of static axons that activated it, then to catalogue the fusimotor actions singly and in combination, with each axon stimulated by an individual and exactly reproducible pseudorandom pattern of impulses. The technical challenge of such a regime of stimulation was considerable; I am certain that Manuel was one of the few who could have met it. The key element was a real-time, heuristic, stimulus artefact cancellation device (SACAD) developed by Manuel and his small team of electronic and software engineers (Boris Kacmar and William Morrow). I returned to Calgary on research leave again in 1998; we began the final practical experiment on 18 December and finished it the following day, my 51st birthday, just a few hours before I boarded my flight back to Britain. Its success was a memorable present. So far we have published the method in some detail (Hulliger & Banks, 2009), but the mass of data awaits full analysis. As an illustration I give just one example of a primary ending responding to stimulation of a pair of dynamic γ axons and a pair of static γ axons during a series of trapezoidal stretches of the parent muscle, peroneus tertius (Fig.10). Note, in particular, the highly reproducible passive responses, as well as, during combined fusimotor stimulation, the almost complete occlusion of the static by the dynamic effects while the muscle is being stretched, conversely the occlusion of the dynamic by the static effects while the muscle is being released, and varying amounts of summation of the separate effects while the muscle is a constant length.

Fig 10.

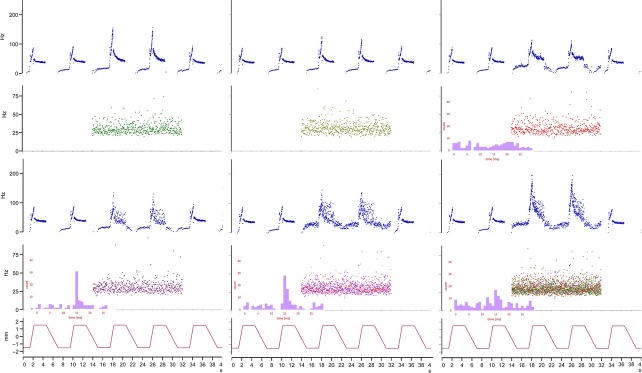
The effects of stimulation of up to four fusimotor axons with individually repeatable, pseudo-randomly varying patterns at low mean rates (30 impulses s⁻¹ with normally distributed inter-stimulus intervals of 20% coefficient of variation) on the response of a primary ending in cat peroneus tertius to a series of trapezoidal muscle-stretches. Instantaneous frequency plots with cross-correlograms shown as insets when the static axons are active; upper right, between the primary output and γ 3; all three in lower row, between the primary output and γ 4. Muscle length in mm is given at the bottom of each column. Unpublished results obtained with Manuel Hulliger.

Reconstructing the primary ending

The primary sensory ending, truly the sine qua non of the muscle spindle thanks to its instructional role in development, has been studied for well over a century. Ruffini (1898) gave it its name and provided one of the fullest early descriptions (though by no means the only one; see, for example, Huber & DeWitt, 1897). The description ‘annulo-spiral’ also dates from those early accounts, which were based on whole-mount methylene blue or gold chloride preparations. But our familiarity with the ending may lead us to overlook important questions by taking too much for granted; questions such as: why is the ending so large; why does it have an annulo-spiral form; why are all the equatorial nuclei of the intrafusal muscle fibres required? I don’t think there are any clear answers to any of these, but if we could answer them they may well have important consequences beyond their immediate significance to spindle physiology. So if any additional justification were needed to take a closer look at the primary ending, it would probably be to undermine any sense of complacency we might have that we already know all of the most significant aspects of its function.

I had toyed with a very simple reconstruction of the equatorial region of the guinea pig spindle in my PhD thesis (published in Banks & James, 1973), but this was as much concerned with recognition of the three types of intrafusal muscle fibre as with the sensory innervation. Once we could identify the different kinds of fibre, and when I was in possession of high quality semi-thin serial sections, the opportunity to make axonometric reconstructions of sensory endings was too great to ignore, even though there was no particular reason to expect any major new insights; after all, we had already shown using schematic reconstructions that the (usually) two first-order branches of the Ia afferent axon of cat spindles supplied the bag₁ fibre separately from the bag₂ and chain fibres (Banks et al. 1977a). The axonometric reconstructions (Fig.11), however, revealed consistent details of the sensory terminals associated with each type of intrafusal fibre that, together with the preterminal branching structure, we could recognise in teased, silver-impregnated spindles (Banks et al. 1982). I have already mentioned the importance this finding had for much of our subsequent work. But the reconstructions had a major drawback, which was that they could only represent one viewpoint without doing the whole exercise again. To overcome it, I made a solid three-dimensional reconstruction from serial longitudinal sections (Banks, 1986), but what was undoubtedly more important in that study were the quantitative measurements made in relation to sensory-terminal shape and deformation under maintained stretch. Within the last few years another opportunity, this time to make virtual, interactive reconstructions by computer, with all the added bonus of ease of quantitation, again became too great to ignore. Using scanned images of the original photomicrographs of the primary ending shown in Fig.11, manual tracing of the key elements, and the reconstruct program (Fiala, 2005) the reconstruction now provides a resource as a database of primary-ending geometry (Fig.12).

Fig 11.

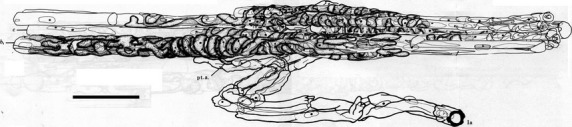
Axonometric reconstruction of the primary sensory ending of a cat tenuissimus spindle made from serial, semi-thin sections. One of the sections from the series is shown in Fig.6 (right). In this ending, the bag₁ and bag₂ fibres were separated by the (5) intervening chain fibres; in this view the bag₁ is at the front; bag₂ at the rear is obscured by the chain fibres. Scale bar: 50 μm (modified from Banks et al. 1982).

Fig 12.

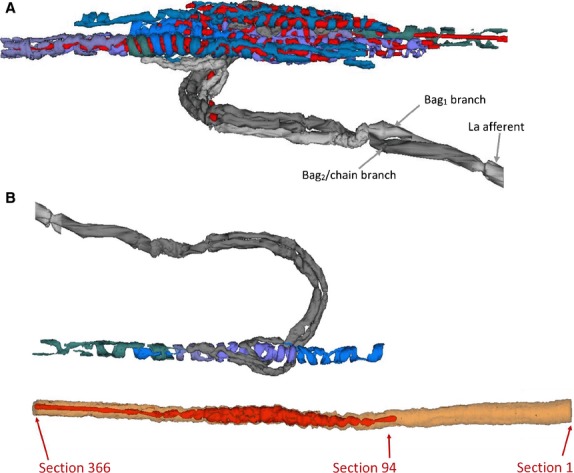
(A) The primary ending of Fig.1 generated using the reconstruct program of Fiala (2005). The output of the program is interactive; the view chosen here corresponds with that of Fig.1 but the outlines of the intrafusal fibres are omitted; sensory terminals, shades of blue/purple; nuclei, red; myelinated axon and branches, shades of grey. (B) Sensory terminals of the bag₂ fibre from the spindle of Figs6, 1 and 2A, with the equatorial region of the fibre shown separately below. The sensory terminals occupied the region between sections 94 and 366, a distance of 273 μm.

I will end with an example of its use in simulations based on a model of sensory-terminal deformation in which the terminals are supposed to be squeezed between the basal lamina and the intrafusal muscle fibre (Banks, 1986). In particular, I will examine the consequent changes in shape of the annulo-spiral terminals using a two-component model and simulations based on data derived from bag₂ fibres of cat tenuissimus spindles. Direct observation of isolated muscle spindles has shown that the equatorial region, where the primary ending is located, behaves like a pure spring (Poppele et al. 1979), so extension (strain) of the equatorial region is directly proportional to tension (stress). The reconstructed bag₂ fibre and its primary sensory terminals are shown separately in Fig.12. Areal and volumetric data derived from it (Table1) were obtained respectively by integration of the relevant profile perimeters and areas given by reconstruct, and nominal section thickness of 1 μm. Geometrical properties of profiles of the sensory terminals of three bag₂ fibres cut in longitudinal section are shown in Fig.13 and Table2, which include both measured data and data derived by trigonometry assuming the terminal profiles to be lenticular (biconvex circular). In the first component of the model a constant volume segment of the bag₂ fibre including one complete helical turn of an annulo-spiral terminal is extended by a longitudinal force (Fig.14A). The simulation (Fig.14B) shows the changes in terminal length (T), lead angle (θ) and segment diameter (D) with respect to segment length (L) of a 10-μm-long segment with volume of 950 μm³, based on the mean volume for 1-μm segments in the bag₂ fibre of the spindle in Fig.12. (The observed pitch of the annulo-spiral terminal varies between about 10 and 20 μm in bag₂, based on spindles 4, 5 and 10 of Banks, 1986). In the second component of the model, for simplicity, the terminal profile seen in longitudinal section through the muscle fibre is assumed to deform symmetrically under tension transmitted equally by the basal lamina and the muscle fibre (Fig.15A,B). The volume of the helical turn is about 450 μm³ and is assumed to be constant. For a 1% increase in segment length from 10 to 10.1 μm, the helical length of the terminal is approximately constant (it actually decreases by 0.39%; see Fig.14B), therefore the profile area is also constant. In the simulation (Fig.15C) the length of the membrane (or profile circumference) and its incremental and total strains are plotted with respect to the longitudinal strain in the muscle fibre-terminal system for a profile of area 12 μm², based on spindles 4, 5 and 10. And so, using realistic values obtained from experimental data, I conclude that stretching the equatorial region of the bag₂ fibre does not result in lengthening of the annulo-spiral sensory terminal, which instead undergoes membrane strain due to deformation in the longitudinal plane of the intrafusal fibre. The amount of stress that results in these strains is unknown, but a reasonable estimate is that it is about 1 kPa (see fig. 5 in Odegard et al. 2008). Assuming a maximum cross-sectional area for the intrafusal muscle fibre of 100 μm², the force producing that stress would be 100 pN.

Table 1.

Terminal, fibre and nuclear areas and volumes relating to the bag₂ fibre of Fig.2

	Surface area (μm2)	Volume (μm3)
Terminal 1	2904	2233
Terminal 2a	3441	2669
Terminal 2b	1522	1161
Terminal 3a	3323	2237
Terminal 3b	721	547
Totals	11 912	8846
Fibre	10 240	25 863
Nuclei	6185	6951

Fig 13.

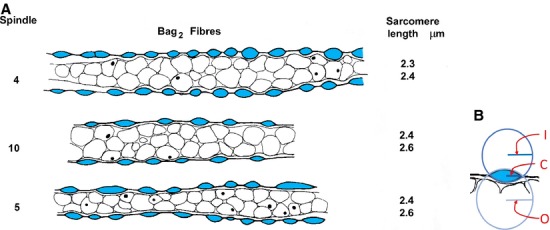
(A) Tracings of longitudinal sections through the equatorial regions of bag₂ fibre from spindles 4, 5 and 10 (from Banks, 1986). Profiles of primary-ending terminals are shown in blue; equatorial nuclei are shown in outline, some with nucleoli visible as black dots. Sarcomere lengths are the means of 50 sarcomeres proximal and distal to the sensory endings for each bag₂ fibre. (B) Method of obtaining the data in Table2 from the tracings in (A). I, radius of circle fitting the curvature of the inner membrane of a sensory-terminal profile; O, radius of circle fitting the curvature of the outer membrane of a sensory-terminal profile; C, half the length of the common chord of I and O.

Table 2.

Measured and derived terminal dimensions, and sarcomere lengths, of bag₂ fibres from three spindles (4, 5 and 10 of Banks, 1986)

Measured terminal dimensions (means)				Derived terminal dimensions						Measured
Spindle	Radius of outer curvature (O), μm	Radius of inner curvature (I), μm	Half length of chord (C), μm	Outer segment area, μm2	Inner segment area, μm2	Total area, μm2	Outer membrane length, μm	Inner membrane length, μm	Total membrane length, μm	Mean sarcomere length, μm
4	3.8	3.5	2.9	5.4	6.3	11.7	6.6	6.8	13.4	2.35
10	4.9	5.1	3.4	6.4	6.1	12.5	7.5	7.4	15.0	2.5
5	3.8	7.7	3.2	7.9	3.0	10.9	7.6	6.6	14.2	2.5
	Measured data from Banks (1986)

Fig 14.

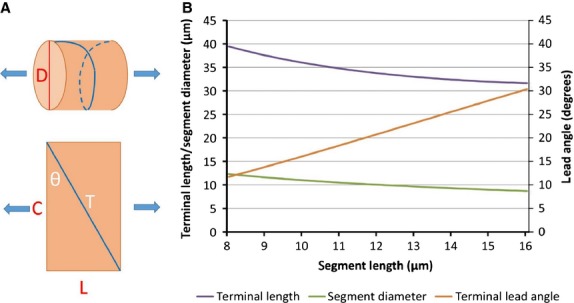
(A) Model of annulo-spiral sensory terminal deformation under longitudinal stress, component 1. Geometrical model of a bag₂ fibre segment containing one turn of an annulo-spiral terminal, represented by a helix wound on a cylinder. (B) Model of annulo-spiral sensory terminal deformation under longitudinal stress, simulation 1. Variation of terminal length (T), segment diameter (D), and lead angle (θ) with segment length (L) for a segment of volume 950 μm³ in model component 1.

Fig 15.

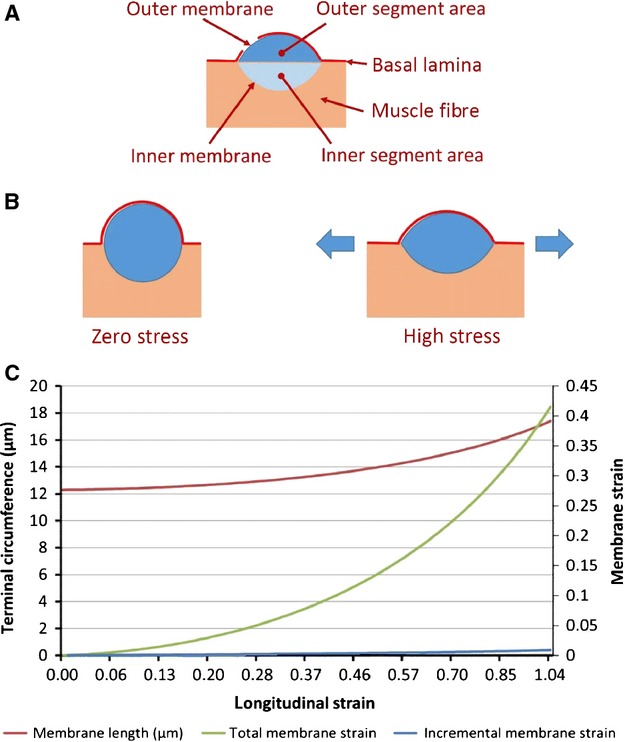
(A) Derived terminal dimensions given in Table2 and used in the model of annulo-spiral sensory terminal deformation under longitudinal stress, component 2 and simulation 2. (B) Model of annulo-spiral sensory terminal deformation under longitudinal stress, component 2. Geometrical model of a bag₂ fibre sensory terminal undergoing symmetrical deformation in response to longitudinal stretch of the fibre. The terminal profile is assumed to adopt a minimum energy (circular) section at zero stress, and to deform to a biconvex lens shape of progressively greater radii with increasing stress. (C) Model of annulo-spiral sensory terminal deformation under longitudinal stress, simulation 2. Variation of terminal circumference, and absolute and incremental membrane strain with longitudinal strain for a helical turn of volume 450 μm³ in model component 2.

Closing remarks

These observations bring me near to the topic of mechanotransduction in the peripheral terminals of low-threshold mechanoreceptors, including the sensory endings of the spindle, and mark an appropriate end to my present subject. For the last 15 years I have been extremely fortunate to have been able to work on aspects of mechanotransduction with another very dear friend, Guy Bewick, and Guy will take up that subject elsewhere in these proceedings.

The present review has given me the opportunity to reflect on our present understanding of the ways in which the sensory and motor innervation of mammalian muscle spindles are organised, and to try to draw out at least some of the principles involved, using examples from my own work. The subdivision of intrafusal muscle fibres into three types emerged as one such common principle of the organisation of mammalian muscle spindles, another is the importance of random events in ontogeny while still ensuring the delivery of functionally important aspects of spindle innervation. It is perhaps worth underlining the primacy of experimental observation here. Undoubtedly our understanding of the internal working of the muscle spindle and of its role in motor control is largely dependent on the identification of such organisational principles, but in most cases they would have been unlikely, if not impossible, to be predicted in advance of their discovery. Similar considerations must surely apply in many areas of bioscience, even in these post-genomic times. It must often happen that we obtain data whose significance only emerges later, sometimes much later, so we should not eschew these data simply because we do not immediately understand their importance. And finally, to any young scientists who may read this, I would say: do not seek for certainty; be ready always to doubt and not to take anything for granted; and do not be afraid to question even widely held opinion.

Conflict of interest

The author confirms that he has no conflict of interest to declare.