Abstract
A main goal of population geneticists is to study patterns of gene flow to gain a better understanding of the population structure in a given organism. To date most efforts have been focused on studying gene flow at either broad scales to identify barriers to gene flow and isolation by distance or at fine spatial scales in order to gain inferences regarding reproduction and local dispersal. Few studies have measured connectivity at multiple spatial scales and have utilized novel tools to test the influence of both environment and geography on shaping gene flow in an organism. Here a seascape genetics approach was used to gain insight regarding geographic and ecological barriers to gene flow of a common reef sponge, Stylissa carteri in the Red Sea. Furthermore, a small-scale (<1 km) analysis was also conducted to infer reproductive potential in this organism. At the broad scale, we found that sponge connectivity is not structured by geography alone, but rather, genetic isolation in the southern Red Sea correlates strongly with environmental heterogeneity. At the scale of a 50-m transect, spatial autocorrelation analyses and estimates of full-siblings revealed that there is no deviation from random mating. However, at slightly larger scales (100–200 m) encompassing multiple transects at a given site, a greater proportion of full-siblings was found within sites versus among sites in a given location suggesting that mating and/or dispersal are constrained to some extent at this spatial scale. This study adds to the growing body of literature suggesting that environmental and ecological variables play a major role in the genetic structure of marine invertebrate populations.
Keywords: Environmental gradient, isolation by distance, isolation by environment, porifera, relatedness, seascape genetics
Introduction
Historically, gene flow in the marine realm was thought to generate panmictic populations semiconnected ones following a stepping stone trajectory, or completely isolated groups. However, it is now widely accepted that genetic connectivity can take any combination of the above-mentioned trajectories and can differ given the temporal and spatial scale at which it is investigated (Selkoe et al. 2008). It is thus noted that conducting population genetics studies at various temporal and spatial scales can yield a more accurate picture of the genetic distribution of a species (Wiens 1989; Levin 1992).
Studies conducted at various geographic scales are useful to determine the importance of spatial heterogeneity on shaping genetic connectivity. For example, many marine studies have explored the effect of increasing spatial distance on gene flow (Isolation by Distance, IBD) (reviewed in Hellberg 2007; Jones et al. 2009; Selkoe and Toonen 2011), but the direct relationship between geographic distance and genetic distance is not always linear. Often, correlations are weak and significant only due to large sample sizes (as explained by Jenkins et al. 2010), and IBD relationships do not always hold at multiple spatial scales. Processes operating at one spatial scale can influence recruitment, survival, and admixture in ways that go undetected if a study is conducted at a larger spatial scale (Manel and Holderegger 2013). More recently, this has been shown to occur frequently with invertebrate populations (Gorospe and Karl 2013; Ordóñez et al. 2013). Many abiotic and biotic factors are known to influence marine invertebrate population dynamics and these factors operate at diverse spatial scales (see review by Sanford and Kelly 2011). Temperature, light, and salinity gradients exist at fine vertical scales to large latitudinal scales. Gradients in primary productivity, nutrient availability, and predator abundance can exist at yet other scales (see review by Sanford and Kelly 2011). Thus, the combination of the various scales of factors that influence marine invertebrates yields population contingencies that are much more complex than those resulting from genetic drift alone.
Recently, a metric known as Isolation by Environment (IBE) has been utilized to analyze the effect of increasing environmental heterogeneity on genetic structure (e.g., Selkoe et al. 2008; Nanninga et al. 2014; Wang and Bradburd 2014). While analyzing the influence of environmental factors driving genetic variation among populations is not as common as simply testing for IBD, the few studies that have tested for IBE show the importance of considering both geography and environment before drawing conclusions regarding barriers to population connectivity (e.g., Crispo et al. 2006; Cushman et al. 2006; Wang and Summers 2010; Lee and Mitchell-Olds 2011; Wang 2013; Nanninga et al. 2014). Most notably at large scales, environmental heterogeneity can promote genetic divergence, which could impact juvenile settlement, larval survival, and mortality, as well as promote potential differences in reproductive success (Selkoe et al. 2006, 2008; Schmidt et al. 2008). Environment has been shown to be particularly important in segregating long-lived sessile organisms that have wide-range dispersal (Goreau 1959; Kinzie 1973; Paine et al. 2009; Baldeck et al. 2013). Further to this, transplant experiments have shown that mature organisms experience higher mortality in non-native habitats (Marshall et al. 2010; Prada and Hellberg 2013) and local adaptation has been shown to reach 71% in some plants (Leimu and Fischer 2008). Yet, despite the fact that sponges are both long living and sessile, the extent to which environmental condition promotes local adaptation in phylum Porifera is yet untested.
Sponges are among the most ancient metazoans making them target organisms for many evolutionary studies (e.g., Li 1998; Srivastava et al. 2010), yet to date, only approximately ten population genetics studies conducted at ecologically relevant time scales (e.g., using highly variable microsatellite markers) have been published (reviewed in Uriz and Turon 2012). Several of these studies confirm the inherent complexity of sponge population biology as four of these studies have reported strong genetic structure at small spatial scales (<1 km) (Duran et al. 2004; Blanquer et al. 2009; Blanquer and Uriz 2010; Guardiola et al. 2011), one study found genetic differentiation even at the scale of tens of centimeters (Calderón et al. 2007), and yet other studies found genetic structure at large spatial scales (>100 km) (Dailianis et al. 2011; Chaves-Fonnegra et al. 2015). These studies and others conducted using mitochondrial and nuclear markers (e.g., DeBiasse et al. 2009; López-Legentil and Pawlik 2009) suggest that while dispersal is limited in some species, there is no general pattern of strict isolation, isolation by distance, or panmixia in phylum Porifera.
The aim of this study was to assess the broad and fine-scale population genetic structure of a common Indo-Pacific reef sponge, Stylissa carteri, and determine factors that influence population differentiation. As a member of the order Halichondrida, Stylissa carteri is thought to have indirect and internal reproduction with a parenchymella type I larvae, although gametogenesis is yet unstudied in the genus Stylissa (Maldonado 2006). Members of phylum Porifera are thought to disperse through an often-short pelagic larval phase (Uriz et al. 1998), and once settled, the sessile adult sponge is dependent on the constraints of its surrounding environment in terms of food availability (Lesser 2006), reproductive potential (Maldonado and Young 1996), and predation (Pawlik et al. 2013). At the broad scale, genetic connectivity was explored using Bayesian clustering, IBD, and IBE analyses to determine whether barriers to gene flow are due in part to geographic and/or environmental factors. At finer scales, we investigated the presence of limited larval dispersal and/or nonrandom mating by evaluating spatial autocorrelation analysis within 50-m transects and comparing the proportion of full-siblings among individuals in a hierarchical design (transect/site/location). Taken together, the results gathered yield valuable information regarding the importance of environmental heterogeneity in the Red Sea and how this heterogeneity predicts gene flow and potentially local adaptation in a sessile marine organism.
Materials and Methods
Study system
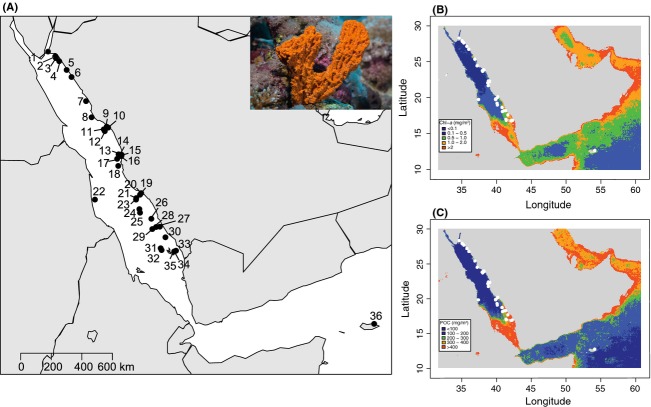
The Red Sea is an understudied system (Berumen et al. 2013) known for its high endemism (14–50% depending on the taxa see Roberts et al. 1992; Randall 1994; Cox and Moore 2000; DiBattista et al. 2013), its extreme salinity (37–42‰), and temperature ranges (20–32°C) (Raitsos et al. 2011). Extending from 30°N to 12.5°N, the Red Sea is marked by a latitudinal environmental gradient in primary productivity and turbidity, both increasing in southern waters (Raitsos et al. 2013; Fig.1). The study subject, Stylissa carteri, has a widespread Indo-Pacific distribution (Hooper and Van Soest 2004) and is abundant in coastal Red Sea waters (with the exception of the Gulf of Aqaba) typically between 5 and 15 m in depth (E. C. Giles, unpubl. data).
Figure 1.
(A) Sampling sites in the Red Sea and northwest Indian Ocean. Photograph of Stylissa carteri from the Red Sea (Photograph credit: Tane Sinclair-Taylor). Contour maps of 9-year averaged Red Sea chlorophyll (B) and particulate organic carbon (C). More information can be found in Tables S1 and S2.
Sample collection
Sponge tissue samples (n = 966) were collected by SCUBA between October 2012 and February 2014 from a total of 36 reef sites. A total of 34 of those sites span 1500 km of Saudi Arabian coastline, one is off the coast of Sudan, and one is off the coast of Socotra in the Indian Ocean (Fig.1, Table1). Approximately 1 g of tissue was cut from each sponge and stored in 96% ethanol until further analysis was undertaken. Select samples were analyzed by traditional taxonomy and verified as Stylissa carteri by two sponge taxonomic experts (Lisa Goudie and Nicole de Voogd).
Table 1.
Summary statistics for Stylissa carteri listed from northernmost to southernmost sampled sites (Site Number, Location, Site Name, 1fine-scale sampling was conducted, GPS). The number of samples amplified (N), allelic diversity (NA), observed heterozygosity (HO), unbiased expected heterozygosity (uHE), and fixation index (FIS) are given for each population. Values are averaged over 9 loci
| Site number | Location | Site name | GPS coordinates | N | NA | HO | HE | FIS |
|---|---|---|---|---|---|---|---|---|
| 1 | North | Gulf of Aqaba | 28.185, 34.638 | 7 | 3.111 | 0.313 | 0.485 | 0.3743* |
| 2 | North | Jazirat Burcan | 27.910, 35.065 | 14 | 4.556 | 0.452 | 0.533 | 0.1565 |
| 3 | North | Shi’b Pelam | 27.817, 35.107 | 11 | 3.889 | 0.364 | 0.499 | 0.2807 |
| 4 | North | Jaz’air Sila | 27.638, 35.306 | 7 | 4 | 0.5 | 0.59 | 0.1663** |
| 5 | North | An Numan | 27.139, 35.751 | 20 | 4.556 | 0.389 | 0.528 | 0.2703** |
| 6 | North | Ras Al-Ubayd | 26.736, 36.044 | 12 | 4.333 | 0.426 | 0.544 | 0.2251** |
| 7 | North | Shaybarah | 25.362, 36.913 | 8 | 3.222 | 0.361 | 0.46 | 0.2272 |
| 8 | Yanbu | Marker9 | 24.443, 37.248 | 11 | 4.556 | 0.444 | 0.625 | 0.2988** |
| 9 | Yanbu | Reef21 | 23.907, 38.153 | 44 | 5.889 | 0.42 | 0.59 | 0.2902** |
| 10 | Yanbu | Refinery1 | 23.853, 38.240 | 54 | 6.333 | 0.39 | 0.538 | 0.2765** |
| 11 | Yanbu | 7Sisters | 23.753, 37.974 | 24 | 5.889 | 0.349 | 0.595 | 0.4194** |
| 12 | Yanbu | Tistis | 23.651, 38.035 | 22 | 4.889 | 0.313 | 0.546 | 0.4322** |
| 13 | Thuwal | Shib Nazar1 | 22.331, 38.863 | 72 | 6.889 | 0.38 | 0.564 | 0.3245** |
| 14 | Thuwal | Al Fahal | 22.312, 38.978 | 22 | 5.444 | 0.399 | 0.549 | 0.2769** |
| 15 | Thuwal | Abu Shoosha | 22.305, 39.049 | 24 | 6.444 | 0.416 | 0.597 | 0.3065** |
| 16 | Thuwal | Fsar | 22.227, 39.030 | 24 | 5.667 | 0.446 | 0.533 | 0.1636** |
| 17 | Thuwal | Abu Madafi1 | 22.074, 38.778 | 24 | 5 | 0.42 | 0.522 | 0.2014** |
| 18 | Jeddah | Obhur | 21.671, 38.844 | 20 | 5.111 | 0.38 | 0.597 | 0.3665** |
| 19 | Al-Lith | Whale Shark Reef1 | 20.119, 40.220 | 71 | 6.111 | 0.375 | 0.553 | 0.3207** |
| 20 | Al-Lith | Reef31 | 20.031, 40.147 | 46 | 6.222 | 0.385 | 0.549 | 0.2977** |
| 21 | Al-Lith | MarMar1 | 19.838, 39.921 | 27 | 5.667 | 0.354 | 0.548 | 0.3495** |
| 22 | Sudan | Sanganeb | 19.753, 37.448 | 11 | 4.111 | 0.392 | 0.525 | 0.2671** |
| 23 | Al-Lith | Malatu1 | 19.752, 39.910 | 57 | 6.556 | 0.365 | 0.522 | 0.3013** |
| 24 | Farasan Banks | Abu Dauqa | 19.209, 40.109 | 15 | 4.667 | 0.413 | 0.525 | 0.2182* |
| 25 | Farasan Banks | Dolphen Lagoon | 19.005, 40.148 | 12 | 4.333 | 0.354 | 0.465 | 0.2488** |
| 26 | Farasan Banks | Ablo Island | 18.660, 40.827 | 19 | 4.667 | 0.365 | 0.516 | 0.2976** |
| 27 | Farasan Banks | Marka Island | 18.209, 41.335 | 27 | 4.778 | 0.436 | 0.575 | 0.2465** |
| 28 | Farasan Banks | Atlantis Shoal | 18.189, 41.111 | 16 | 5.556 | 0.502 | 0.621 | 0.1943* |
| 29 | Farasan Banks | Shib Radib | 18.073, 40.886 | 44 | 6.667 | 0.393 | 0.538 | 0.2729** |
| 30 | Wassalyat Shoals | Mamali Kabir | 17.605, 41.671 | 37 | 5.556 | 0.405 | 0.577 | 0.3005** |
| 31 | Farasan Islands | Baghlah | 16.980, 41.385 | 9 | 3.778 | 0.444 | 0.519 | 0.1504 |
| 32 | Farasan Islands | Dhi Dahaya | 16.875, 41.440 | 28 | 5.667 | 0.376 | 0.551 | 0.3178** |
| 33 | Farasan Islands | Zahrat Durakah | 16.840, 42.305 | 24 | 4.889 | 0.416 | 0.522 | 0.2031** |
| 34 | Farasan Islands | Abulad Island | 16.798, 42.199 | 46 | 5.778 | 0.43 | 0.572 | 0.25** |
| 35 | Farasan Islands | Tiger Head | 16.791, 42.199 | 29 | 4.889 | 0.441 | 0.55 | 0.2013** |
| 36 | Soccotra | Soccotra | 12.670, 54.178 | 12 | 3.222 | 0.367 | 0.426 | 0.1442 |
Significant (FIS) values are indicated
P < 0.05
P < 0.01 (FDR correction).
At eight of the 36 reef sites, sampling was conducted to determine fine-scale structure patterns both within and among sites. At each of three locations (Yanbu, Thuwal, and Al-Lith), transects were sampled in different sites (at Yanbu and Thuwal, two sites yielding four transects were sampled, and at Al-Lith, four sites yielding eight transects were sampled). Sites were separated by no more than 30 km, 38 km, and 52 km at Yanbu, Thuwal, and Al-Lith, respectively. At each of the eight sites (Site 9, Site 10, Site 13, Site 17, Site 19, Site 20, Site 21, Site 23, indicated in Table1), two belt transects 50 m x 4 m were laid on the leeward side of the reef and an effort was made to sample all Stylissa carteri individuals within each transect. As individuals were sampled, their depth and location within the transect were recorded.
Genetic analysis
The DNA was extracted from 200 to 250 mg of sponge tissue with cell lysis immersion in 600 μL of 1% 2-mercaptoethanol RLT buffer (Qiagen, Germany) and shaking incubation or overnight proteinase K incubation at 56°C (Qiagen). Following cell lysis, the DNA extraction method proceeded via the Allprep DNA/RNA mini Kit (Qiagen).
Nine microsatellite markers were used. Marker details and PCR parameters are specified in Giles et al. (2013) and summarized in Table S1. The microsatellite markers were combined into five multiplex mixes based on fragment sizes and fluorescent dye tags. For loci that did not amplify at first, PCRs were redone without multiplexing. Positive PCR products were diluted with Hi-Di formamide (Applied Biosystems) and GeneScan 500-LIZ size standard (Applied Biosystems, CA, USA) and run on an ABI 3730xl genetic analyzer (Applied Biosystems) for fragment size identification. All samples with more than one missing loci were removed from the dataset.
Samples were genotyped using the software GENEMAPPER 4.0 (Applied Biosystems). Allelic frequencies, number of alleles (NA), observed (HO), and unbiased expected heterozygosities (uHE) were estimated for each site using the software Genalex (v6.5; Peakall and Smouse 2012). Calculations were made for the inbreeding coefficient (FIS), and tests for linkage disequilibrium (LD) and deviations from Hardy–Weinberg proportions (HWE) were determined using Genepop (Raymond and Rousset 1995; Rousset 2008). Tests for significant deviations from LD and HWE were made using permutations via Markov chain reshuffling (10,000 dememorizations, 1000 batches, and 10,000 iterations per batch). Corrections for multiple testing were made using false discovery rate (FDR, Benjamini and Hochberg 1995). Furthermore, the data were tested for the presence of null alleles using MICROCHECKER (v2.2.3; Van Oosterhout et al. 2004).
Clonality within the entire dataset was determined by measuring the number of 100% multilocus matches (Genalex v6.5). To avoid over-representation of individual genotypes, one of each of the members of a clonal pair was removed from the dataset for subsequent genetic analyses.
Broad-scale structure
Bayesian clustering via the program STRUCTURE (v2.3.4 Pritchard et al. 2000) was employed to ascertain the most likely number of populations (K-clusters). An admixture model was used with sampling location as a prior. Allele frequencies were assumed to be correlated among populations. The model was run for values of K from 1 to 20. For each K, the model was run 10 times with a burn-in step of 300,000 iterations and 500,000 subsequent iterations. STRUCTURE Harvester (Earl and vonHoldt 2012) was used to determine which K best describes the data according to the highest averaged maximum-likelihood score and Evanno’s delta K.
We also examined population genetic differentiation via the analysis of molecular variance (AMOVA) using the program Genalex. The AMOVA was run four times, once without regional classification of the samples, once with a two-region classification, once with a three-region classification, and once with a four-region classification. The regional classifications were made based on results from the STRUCTURE (v2.3.4 Pritchard et al. 2000) analysis and based on the knowledge that Socotra represents a distant and potentially unique population as samples from this site are the only ones which were taken outside of the Red Sea. Thus, the two-region classification scheme included sites 1–32 and 36 in one region and sites 33–35 in the second region. The three-region classification scheme included sites 1–32 in the first region, sites 33–35 in the second region, and Site 36 as the third region. The four-region classification scheme included sites 1–29 and 31–32 in one region, Site 30 as a region, sites 33–35 as a region, and Site 36 as a region (see Table1 for site information). Significant pairwise FST comparisons were determined based on FDR. Finally, pairwise population FST and GST estimates were calculated in Genalex using the same AMOVA framework with 9999 permutations to test for significance. Pairwise FST and GST values were calculated for the 36 pairwise comparisons; pairwise values for Site 36 were calculated using only eight loci as one loci would not amplify for the Socotra samples.
Geographic analysis
Pairwise geographic distance (Euclidean distance in km) was calculated between each of the 35 sample sites following Nanninga et al. 2014. To investigate the determinants of genetic distance in the Red Sea, the Socotra data was withheld from all subsequent analysis as (1) this site is outside the area of primary interest; (2) it is geographically isolated from all the other sites; and (3) it appears to be very distinct (highest pairwise FST are with this site) from the rest of the dataset, probably due to its geographic isolation. Thus, the inclusion of this disparate site could confound meaningful results about processes within the Red Sea.
Using a Mantel test with 9999 permutations, pairwise matrices of linearized FST (FST / (1 − FST)) and geographic distance were compared to determine the degree of isolation by distance (IBD) of S. carteri populations. Pearson correlation coefficients were calculated for the linear relationship between geographic distance and genetic distance. Regressions were made twice, once using raw matrices and secondly on matrices standardized by subtracting the mean and dividing by the standard deviation of the dataset.
Environmental analysis
Environmental data were gathered from the NASA Giovanni website using the MODIS-Aqua 4 km database (http://oceancolor.gsfc.nasa.gov) with standard NASA estimate algorithms. Color radiometry measurements of sea surface temperature (day DSST °C and night NSST °C), colored dissolved organic matter (CDOM), chlorophyll a (CHLA mg/m3), and particulate organic carbon (POC mg/m3) were used as the environmental criteria in this study. All criteria for the 9-year winter season (October 2003 to May 2012) and annual (January 2003 to December 2012) time frame were averaged and downloaded yielding a value of SST, CDOM, CHLA, and POC for the entire Red Sea and northwest Indian Ocean for winter and annual means. Due to seasonal cloud cover/shallow sea level, there was a lack of satellite data for summer months; thus, this time frame was excluded from the study. The data used for the environmental analysis were selected because they are the most robust available measurements of large-scale environmental criteria for the Red Sea. The raw data for the five environmental criteria assessed were averaged because it is thought that processes such as reproduction, dispersal, and ultimately gene flow happen over demographic to evolutionary time scales. Contour maps of the 9-year annual averages of CHLA and POC for the entire Red Sea and northwest Indiana Ocean were made in R using the raw data downloaded from MODIS-Aqua (Fig.1).
These datasets were then mined for the values that corresponded to the point (4 km2 resolution) nearest to the 36 sample site locations in this study (Table S2). Pairwise environmental distance (Euclidean distance in km) was calculated between each of the 35 sample sites located within the Red Sea following Nanninga et al. 2014 for all environmental criteria and the two time periods in question. Using Mantel tests with 9999 permutations, pairwise matrices of linearized FST (FST / (1 − FST)) and environmental distance were compared to determine the degree of isolation by environment (IBE) of S. carteri populations. Pearson correlation coefficients were calculated for the linear relationship between environmental distance and genetic distance and significance tests were made (α = 0.05).
Multiple matrix regression
Multiple matrix regression with randomization (MMRR) was used to determine which model best explained the observed trend in genetic distance (Wang 2013). The MMRR analysis was performed in R with 9999 permutations. The matrices used for this analysis were standardized by subtracting the mean and dividing by the standard deviation.
Fine-scale structure
Genetic structure at the scale of 50 m was analyzed using the belt transect samples for eight of the 36 sample sites. Spatial autocorrelations generated in Genalex were used to test whether S. carteri multilocus genotypes were randomly distributed in space (within each transect) or not (following Smouse and Peakall 1999). Samples were binned into 5 m distance class sizes, and 999 permutations were used to determine the 95% confidence intervals around the null hypothesis of no spatial autocorrelation. All statistics were generated for each 50-m transect individually yielding two replicates for each of the eight reef sites.
Genetic structure at the scale of 50 m and at slightly larger scales (100–200 m depending on distance between 50-m transects) was also explored using the same belt transect samples in a hierarchical design. We used a likelihood-based approach implemented in KINGROUP v2 (Konovalov et al. 2004) to identify likely full-sibling pairs among all samples of each site. Two individuals were accepted as full-sibs if the LOD-score associated P value was ≤ 0.01. Significance testing was built based on the distribution of LOD scores from simulated 10,000 full-sibling pairs and unrelated pairs of individuals. The type II error associated with estimating the full-sibling pairs was estimated to be 34–35%. As a conservative measure, we chose to minimize type I error: that is, accept truly unrelated individual pairs as being full-sibs, at the expenses of type II error: rejecting pairs of individuals as being full-siblings when they truly are full-siblings. We estimated the proportion of full-siblings within transects, among transects within sites, and among sites within each location. We then compared the proportions of full-siblings: (1) within transects vs. among transects (within each site) and (2) within sites vs among sites (within each location) using a χ2 test of proportions conducted in R. We expected that if nonrandom mating or limited dispersal is occurring in a given location, the proportion of full-siblings within transects or within sites would be higher than the proportion of full-siblings among transects or among sites.
Results
Summary statistics
A total of 966 samples were genotyped at the nine microsatellite loci with the exception of the Socotra samples (n = 12) for which loci sc90 would not amplify. As the S. carteri microsatellite markers were developed on Red Sea samples, it is possible that a mutation in the primer-binding region of the more divergent Socotra samples is causing faulty amplification at this locus. The missing data of the Socotra samples did not affect the summary statistic analysis, as results were identical when analysis was made with and without loci sc90 and with and without the Socotra samples. In addition, of the 966 samples, 16 clonal pairs with identical multilocus genotypes were recovered (Table S3). Clones were more commonly found within sites (14 of the 16 pairwise comparisons) than among sites (2 of the 16 comparisons). One individual from each of the clonal pairs was removed from the dataset yielding a working dataset of 950 individuals with unique multilocus genotypes. All analysis was completed on the dataset with 950 individuals.
Overall, the data show a clear pattern of low heterozygosity (mean Ho = 0.399, mean He = 0.528), which was consistent at all sample site locations (Table1). This was met with a consistent and high inbreeding coefficient (FIS ranged from 0.1442 to 0.4322) that was significant in 31 of the 36 sites. The allelic diversity ranged from 1 to 10 alleles per locus for any given site. While some deviations from HWE were found, no loci showed significant deviations (using FDR correction) from HWE at all sites tested (Table S4). Loci sc65 and sc88 showed no deviation from HWE, loci sc83 showed deviation from HWE in just two sites, and the remaining six loci showed deviations from HWE in approximately half of the sites tested. MICROCHECKER indicated the possible presence of null alleles in all loci as was to be expected with the observed heterozygote deficiencies. However, no loci showed the presence of null alleles at all sites. Null alleles were detected on average in 11 of 36 (99% CI) sites for a given locus. The lack of a clear pattern in deviations from HWE along with the findings of other studies that have shown reduced heterozygosities in sponge populations (Duran et al. 2004; Whalan et al. 2005; Duran and Rützler 2006; Guardiola et al. 2011; Chaves-Fonnegra et al. 2015) suggests that this is not a primer-binding artifact but rather a biological phenomenon that exists in sponge populations. Hence, these markers were considered suitable for the study at hand. Lastly, the tests for LD yielded zero significant values for linkage disequilibrium using FDR correction (1199 multiple comparisons).
Broad-scale structure
The STRUCTURE analysis indicated that K = 2 and K = 4 are the most probable number of population clusters (Fig.2 and Fig. S1). The STRUCTURE plot based on K = 2 (Fig.2A) shows that all individuals are experiencing admixture but sites 33–35 (Zahrat Durakah, Abulad Island, Tiger Head, all from the Farasan Islands) are different from the rest of the dataset. The K = 4 plot (Fig.2B) again supports the uniqueness of sites 33–35, but it also supports separation of sites 30 and 36. To clarify, Site 30 (Wassalyat Shoals) forms one cluster, sites 33–35 (Zahrat Durakah, Abulad Island, Tiger Head, all from the Farasan Islands) form a second cluster, Site 36 (Socotra) forms a third cluster, and the rest of the dataset forms the fourth cluster.
Figure 2.
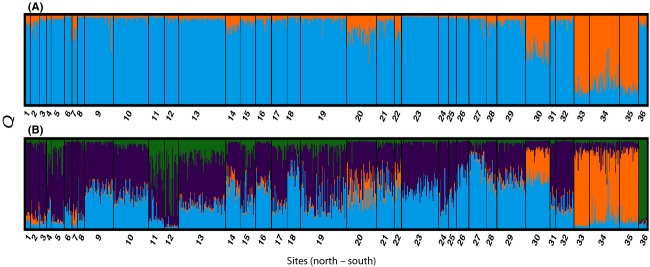
Large-scale population genetic differentiation inferred via Bayesian clustering. Prior information about the geographic origin of the samples was given. Best inferred clustering scheme was K = 2 (A) measured using Evanno’s delta K and K = 4 (B) determined from the mean estimated Ln(K). More information found in Fig. S1.
The AMOVA indicates that the overall molecular variance among populations (36 sites) is low. When no regional classification of sites was used, the variation among populations was 4% (P = 0.001). When two regions were indicated (Region 1: sites 1–32 and Site 36 Socotra; Region 2: sites 33–35), the variation among populations was 3% (P = 0.001), while the variation among regions was 6% (P = 0.001). When a three-region classification was used (Region 1: sites 1–32; Region 2: sites 33–35; Region 3: Site 36 Socotra), the variation among populations was 2% (P = 0.001), while the variation among regions was 7% (P = 0.001). Likewise, when a four-region classification was used (Region 1: sites 1–29, 31–32; Region 2: Site 30; Region 3: sites 33–35; Region 4: Site 36), the variation among populations was 2% (P = 0.001), while the variation among regions was 7% (P = 0.001). In addition, there were many significant pairwise population comparisons with FST values ranging from 0 to 0.284 and GST values ranging from −0.011 to 0.077 (Table2). All pairwise comparisons with sites 30 (Mamali Kabir: Wassalyat Shoals), 33 (Farasan Islands: Zahrat Durakah), and 36 (Socotra: Socotra) were significant. Overall, the southern sites from the Farasan Banks, Farasan Islands, and Socotra were often significantly different from the rest of the dataset.
Table 2.
Pairwise population structure based on nine1 microsatellite loci. Sites are indicated north to south (1–36). FST values are below the diagonal and GST values are above the diagonal. Values in bold show significant values based on FDR (alpha = 0.05)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | −0.006 | 0.005 | −0.008 | 0.015 | 0.006 | 0.019 | −0.004 | 0.014 | 0.019 | 0.003 | 0.005 | 0.006 | 0.002 | 0.008 | 0.012 | 0.015 | 0.023 | 0.012 | 0.006 | 0.018 | 0.050 | 0.011 | 0.008 | 0.009 | 0.044 | 0.031 | 0.031 | 0.029 | 0.040 | 0.014 | 0.016 | 0.044 | 0.030 | 0.052 | 0.082 | |
| 2 | 0.000 | −0.004 | 0.004 | 0.001 | 0.003 | 0.009 | 0.001 | 0.006 | 0.007 | −0.001 | 0.015 | 0.002 | 0.001 | 0.003 | 0.003 | −0.002 | 0.015 | 0.014 | 0.004 | 0.005 | 0.027 | 0.010 | 0.000 | 0.008 | 0.021 | 0.025 | 0.020 | 0.011 | 0.027 | −0.005 | −0.002 | 0.042 | 0.023 | 0.045 | 0.074 | |
| 3 | 0.011 | 0.000 | 0.012 | −0.004 | 0.001 | 0.015 | 0.004 | 0.003 | −0.001 | 0.006 | 0.026 | 0.001 | −0.002 | 0.004 | 0.001 | −0.001 | 0.008 | 0.010 | 0.012 | 0.004 | 0.020 | 0.001 | 0.007 | −0.011 | 0.021 | 0.023 | 0.025 | 0.006 | 0.033 | −0.003 | −0.003 | 0.057 | 0.034 | 0.053 | 0.055 | |
| 4 | 0.000 | 0.009 | 0.023 | 0.010 | 0.010 | 0.032 | 0.002 | 0.008 | 0.017 | −0.004 | 0.006 | 0.001 | 0.000 | 0.002 | 0.008 | 0.007 | 0.007 | 0.009 | 0.008 | 0.000 | 0.035 | 0.014 | 0.021 | 0.018 | 0.027 | 0.009 | 0.025 | 0.015 | 0.021 | 0.013 | 0.015 | 0.032 | 0.018 | 0.040 | 0.044 | |
| 5 | 0.020 | 0.003 | 0.000 | 0.015 | −0.004 | 0.013 | 0.007 | 0.008 | 0.006 | 0.004 | 0.023 | 0.002 | 0.008 | 0.013 | 0.006 | 0.003 | 0.017 | 0.014 | 0.023 | 0.016 | 0.037 | 0.011 | 0.007 | 0.008 | 0.028 | 0.023 | 0.018 | 0.017 | 0.030 | 0.006 | 0.002 | 0.056 | 0.033 | 0.053 | 0.087 | |
| 6 | 0.015 | 0.007 | 0.001 | 0.021 | 0.000 | 0.006 | 0.001 | 0.006 | 0.005 | 0.004 | 0.021 | 0.005 | 0.006 | 0.012 | 0.008 | 0.012 | 0.013 | 0.014 | 0.022 | 0.013 | 0.041 | 0.014 | 0.004 | 0.008 | 0.033 | 0.029 | 0.024 | 0.022 | 0.029 | 0.008 | 0.001 | 0.061 | 0.043 | 0.061 | 0.100 | |
| 7 | 0.025 | 0.006 | 0.022 | 0.036 | 0.026 | 0.013 | 0.011 | 0.020 | 0.025 | 0.025 | 0.033 | 0.024 | 0.029 | 0.021 | 0.019 | 0.023 | 0.033 | 0.023 | 0.034 | 0.041 | 0.073 | 0.030 | 0.007 | 0.027 | 0.055 | 0.054 | 0.039 | 0.037 | 0.047 | 0.007 | 0.011 | 0.053 | 0.035 | 0.057 | 0.134 | |
| 8 | 0.000 | 0.003 | 0.008 | 0.002 | 0.015 | 0.002 | 0.012 | 0.007 | 0.013 | 0.001 | 0.011 | 0.002 | 0.008 | 0.002 | 0.008 | 0.008 | 0.014 | 0.006 | 0.006 | 0.013 | 0.046 | 0.012 | −0.001 | 0.018 | 0.031 | 0.017 | 0.011 | 0.017 | 0.032 | 0.004 | 0.004 | 0.044 | 0.027 | 0.042 | 0.080 | |
| 9 | 0.025 | 0.010 | 0.004 | 0.014 | 0.015 | 0.011 | 0.026 | 0.016 | 0.009 | 0.007 | 0.023 | 0.005 | 0.005 | 0.004 | 0.001 | 0.004 | 0.003 | 0.007 | 0.013 | 0.006 | 0.031 | 0.009 | 0.008 | 0.012 | 0.017 | 0.016 | 0.010 | 0.014 | 0.022 | 0.000 | 0.002 | 0.047 | 0.027 | 0.047 | 0.062 | |
| 10 | 0.033 | 0.013 | 0.000 | 0.032 | 0.012 | 0.009 | 0.040 | 0.029 | 0.018 | 0.011 | 0.025 | 0.007 | 0.005 | 0.012 | 0.004 | 0.008 | 0.006 | 0.017 | 0.019 | 0.008 | 0.025 | 0.008 | 0.015 | −0.003 | 0.015 | 0.021 | 0.024 | 0.019 | 0.029 | 0.007 | 0.002 | 0.060 | 0.039 | 0.058 | 0.071 | |
| 11 | 0.000 | 0.000 | 0.008 | 0.000 | 0.007 | 0.006 | 0.025 | 0.001 | 0.014 | 0.022 | 0.003 | 0.002 | 0.005 | 0.004 | 0.008 | 0.006 | 0.014 | 0.010 | 0.013 | 0.007 | 0.037 | 0.013 | 0.014 | 0.016 | 0.020 | 0.017 | 0.018 | 0.019 | 0.027 | 0.004 | 0.008 | 0.051 | 0.034 | 0.050 | 0.061 | |
| 12 | 0.012 | 0.028 | 0.049 | 0.014 | 0.046 | 0.040 | 0.040 | 0.022 | 0.045 | 0.049 | 0.007 | 0.014 | 0.025 | 0.017 | 0.025 | 0.021 | 0.028 | 0.013 | 0.020 | 0.027 | 0.070 | 0.028 | 0.029 | 0.033 | 0.049 | 0.043 | 0.032 | 0.050 | 0.050 | 0.025 | 0.026 | 0.048 | 0.039 | 0.051 | 0.089 | |
| 13 | 0.005 | 0.003 | 0.002 | 0.000 | 0.006 | 0.010 | 0.032 | 0.005 | 0.011 | 0.015 | 0.004 | 0.028 | 0.002 | 0.010 | 0.004 | 0.001 | 0.009 | 0.008 | 0.009 | 0.006 | 0.035 | 0.006 | 0.007 | 0.007 | 0.023 | 0.012 | 0.013 | 0.015 | 0.027 | 0.002 | 0.003 | 0.049 | 0.027 | 0.049 | 0.069 | |
| 14 | 0.004 | 0.002 | 0.000 | 0.000 | 0.015 | 0.012 | 0.035 | 0.015 | 0.009 | 0.012 | 0.009 | 0.047 | 0.004 | 0.000 | −0.003 | 0.002 | 0.003 | 0.008 | 0.003 | −0.002 | 0.014 | 0.002 | 0.010 | −0.001 | 0.015 | 0.011 | 0.016 | 0.002 | 0.016 | 0.000 | 0.002 | 0.040 | 0.022 | 0.038 | 0.045 | |
| 15 | 0.016 | 0.004 | 0.008 | 0.001 | 0.026 | 0.025 | 0.017 | 0.006 | 0.009 | 0.026 | 0.007 | 0.033 | 0.021 | 0.000 | −0.003 | 0.005 | 0.004 | 0.006 | 0.004 | 0.003 | 0.024 | 0.009 | 0.006 | 0.014 | 0.012 | 0.013 | 0.010 | 0.004 | 0.018 | −0.009 | 0.007 | 0.037 | 0.022 | 0.032 | 0.039 | |
| 16 | 0.025 | 0.004 | 0.002 | 0.013 | 0.014 | 0.017 | 0.025 | 0.018 | 0.002 | 0.008 | 0.013 | 0.048 | 0.008 | 0.000 | 0.000 | 0.002 | 0.003 | 0.005 | 0.006 | 0.001 | 0.023 | 0.003 | 0.001 | 0.004 | 0.005 | 0.011 | 0.007 | 0.002 | 0.016 | −0.009 | −0.002 | 0.047 | 0.026 | 0.044 | 0.062 | |
| 17 | 0.023 | 0.000 | 0.000 | 0.009 | 0.009 | 0.021 | 0.023 | 0.010 | 0.007 | 0.015 | 0.008 | 0.035 | 0.003 | 0.005 | 0.005 | 0.003 | 0.011 | 0.004 | 0.006 | 0.000 | 0.034 | 0.002 | 0.012 | 0.002 | 0.019 | 0.019 | 0.019 | 0.010 | 0.028 | −0.003 | −0.001 | 0.050 | 0.026 | 0.050 | 0.059 | |
| 18 | 0.031 | 0.028 | 0.015 | 0.006 | 0.029 | 0.022 | 0.045 | 0.025 | 0.007 | 0.014 | 0.025 | 0.052 | 0.016 | 0.006 | 0.010 | 0.007 | 0.019 | 0.013 | 0.012 | 0.007 | 0.018 | 0.008 | 0.015 | 0.012 | 0.016 | 0.011 | 0.009 | 0.012 | 0.019 | 0.004 | 0.006 | 0.053 | 0.031 | 0.047 | 0.053 | |
| 19 | 0.027 | 0.024 | 0.018 | 0.015 | 0.030 | 0.028 | 0.027 | 0.013 | 0.014 | 0.034 | 0.019 | 0.025 | 0.017 | 0.014 | 0.012 | 0.010 | 0.005 | 0.026 | 0.011 | 0.010 | 0.054 | 0.007 | 0.015 | 0.017 | 0.033 | 0.023 | 0.012 | 0.021 | 0.029 | 0.004 | 0.010 | 0.048 | 0.030 | 0.049 | 0.066 | |
| 20 | 0.017 | 0.009 | 0.024 | 0.015 | 0.045 | 0.043 | 0.040 | 0.014 | 0.027 | 0.039 | 0.026 | 0.040 | 0.021 | 0.007 | 0.007 | 0.011 | 0.010 | 0.025 | 0.020 | 0.006 | 0.034 | 0.010 | 0.009 | 0.015 | 0.024 | 0.021 | 0.017 | 0.013 | 0.031 | 0.000 | 0.010 | 0.032 | 0.018 | 0.029 | 0.054 | |
| 21 | 0.034 | 0.016 | 0.015 | 0.002 | 0.033 | 0.029 | 0.059 | 0.027 | 0.016 | 0.025 | 0.019 | 0.060 | 0.019 | 0.000 | 0.012 | 0.009 | 0.005 | 0.018 | 0.023 | 0.014 | 0.021 | 0.006 | 0.015 | 0.005 | 0.007 | 0.012 | 0.021 | 0.006 | 0.021 | −0.001 | 0.005 | 0.050 | 0.032 | 0.051 | 0.043 | |
| 22 | 0.072 | 0.054 | 0.041 | 0.058 | 0.068 | 0.082 | 0.110 | 0.089 | 0.058 | 0.049 | 0.065 | 0.129 | 0.062 | 0.027 | 0.043 | 0.042 | 0.059 | 0.037 | 0.097 | 0.064 | 0.047 | 0.038 | 0.046 | 0.021 | 0.025 | 0.035 | 0.047 | 0.018 | 0.035 | 0.015 | 0.022 | 0.064 | 0.044 | 0.058 | 0.055 | |
| 23 | 0.029 | 0.020 | 0.004 | 0.030 | 0.022 | 0.028 | 0.047 | 0.026 | 0.018 | 0.018 | 0.029 | 0.058 | 0.015 | 0.005 | 0.022 | 0.008 | 0.007 | 0.020 | 0.016 | 0.021 | 0.013 | 0.076 | 0.010 | −0.002 | 0.017 | 0.020 | 0.016 | 0.013 | 0.033 | 0.003 | 0.004 | 0.064 | 0.039 | 0.063 | 0.062 | |
| 24 | 0.006 | 0.000 | 0.011 | 0.026 | 0.013 | 0.008 | 0.010 | 0.000 | 0.011 | 0.025 | 0.017 | 0.048 | 0.010 | 0.013 | 0.004 | 0.000 | 0.013 | 0.021 | 0.024 | 0.010 | 0.026 | 0.073 | 0.018 | 0.016 | 0.023 | 0.024 | 0.009 | 0.014 | 0.030 | −0.006 | 0.003 | 0.059 | 0.033 | 0.057 | 0.100 | |
| 25 | 0.022 | 0.018 | 0.000 | 0.038 | 0.017 | 0.015 | 0.044 | 0.035 | 0.021 | 0.000 | 0.028 | 0.062 | 0.012 | 0.000 | 0.026 | 0.009 | 0.004 | 0.023 | 0.031 | 0.030 | 0.021 | 0.041 | 0.000 | 0.027 | 0.016 | 0.029 | 0.036 | 0.015 | 0.038 | 0.006 | 0.000 | 0.068 | 0.043 | 0.065 | 0.061 | |
| 26 | 0.075 | 0.041 | 0.040 | 0.049 | 0.053 | 0.065 | 0.085 | 0.063 | 0.033 | 0.030 | 0.037 | 0.093 | 0.042 | 0.030 | 0.024 | 0.009 | 0.035 | 0.034 | 0.061 | 0.046 | 0.022 | 0.047 | 0.036 | 0.036 | 0.031 | 0.017 | 0.020 | 0.015 | 0.025 | 0.006 | 0.010 | 0.077 | 0.052 | 0.070 | 0.065 | |
| 27 | 0.054 | 0.046 | 0.043 | 0.015 | 0.043 | 0.054 | 0.079 | 0.033 | 0.030 | 0.042 | 0.032 | 0.080 | 0.022 | 0.021 | 0.024 | 0.019 | 0.030 | 0.022 | 0.043 | 0.040 | 0.030 | 0.066 | 0.042 | 0.039 | 0.050 | 0.032 | 0.015 | 0.008 | 0.022 | 0.009 | 0.017 | 0.059 | 0.038 | 0.057 | 0.060 | |
| 28 | 0.043 | 0.040 | 0.049 | 0.038 | 0.033 | 0.048 | 0.063 | 0.021 | 0.021 | 0.050 | 0.034 | 0.063 | 0.027 | 0.031 | 0.020 | 0.016 | 0.032 | 0.017 | 0.025 | 0.032 | 0.035 | 0.087 | 0.033 | 0.014 | 0.069 | 0.040 | 0.030 | 0.020 | 0.022 | 0.009 | 0.013 | 0.055 | 0.031 | 0.044 | 0.088 | |
| 29 | 0.053 | 0.020 | 0.010 | 0.028 | 0.030 | 0.040 | 0.056 | 0.033 | 0.026 | 0.036 | 0.037 | 0.094 | 0.029 | 0.005 | 0.009 | 0.003 | 0.017 | 0.026 | 0.039 | 0.026 | 0.017 | 0.035 | 0.025 | 0.021 | 0.026 | 0.029 | 0.016 | 0.038 | 0.022 | −0.004 | 0.009 | 0.056 | 0.033 | 0.052 | 0.047 | |
| 30 | 0.069 | 0.051 | 0.060 | 0.037 | 0.054 | 0.055 | 0.071 | 0.064 | 0.043 | 0.056 | 0.051 | 0.095 | 0.052 | 0.032 | 0.036 | 0.030 | 0.049 | 0.038 | 0.056 | 0.061 | 0.048 | 0.067 | 0.065 | 0.051 | 0.069 | 0.048 | 0.043 | 0.044 | 0.042 | 0.014 | 0.024 | 0.058 | 0.031 | 0.056 | 0.078 | |
| 31 | 0.025 | 0.000 | 0.000 | 0.023 | 0.010 | 0.015 | 0.005 | 0.006 | 0.000 | 0.013 | 0.003 | 0.046 | 0.003 | 0.000 | 0.000 | 0.000 | 0.000 | 0.005 | 0.006 | 0.001 | 0.007 | 0.031 | 0.006 | 0.000 | 0.011 | 0.012 | 0.014 | 0.018 | 0.000 | 0.024 | −0.010 | 0.043 | 0.021 | 0.043 | 0.055 | |
| 32 | 0.025 | 0.000 | 0.000 | 0.023 | 0.005 | 0.002 | 0.011 | 0.006 | 0.005 | 0.005 | 0.014 | 0.050 | 0.008 | 0.003 | 0.011 | 0.000 | 0.000 | 0.012 | 0.019 | 0.018 | 0.009 | 0.038 | 0.008 | 0.003 | 0.001 | 0.018 | 0.031 | 0.022 | 0.016 | 0.046 | 0.000 | 0.048 | 0.028 | 0.050 | 0.074 | |
| 33 | 0.092 | 0.081 | 0.105 | 0.066 | 0.107 | 0.114 | 0.069 | 0.087 | 0.087 | 0.112 | 0.095 | 0.091 | 0.087 | 0.074 | 0.067 | 0.084 | 0.084 | 0.099 | 0.086 | 0.058 | 0.097 | 0.117 | 0.119 | 0.099 | 0.122 | 0.140 | 0.105 | 0.105 | 0.102 | 0.107 | 0.079 | 0.086 | 0.001 | 0.002 | 0.093 | |
| 34 | 0.058 | 0.044 | 0.062 | 0.036 | 0.063 | 0.081 | 0.046 | 0.056 | 0.053 | 0.074 | 0.066 | 0.076 | 0.050 | 0.042 | 0.045 | 0.048 | 0.047 | 0.061 | 0.057 | 0.036 | 0.065 | 0.083 | 0.076 | 0.056 | 0.077 | 0.096 | 0.071 | 0.063 | 0.062 | 0.059 | 0.038 | 0.054 | 0.004 | 0.008 | 0.078 | |
| 35 | 0.098 | 0.086 | 0.099 | 0.079 | 0.100 | 0.115 | 0.082 | 0.085 | 0.089 | 0.109 | 0.096 | 0.097 | 0.089 | 0.072 | 0.063 | 0.082 | 0.088 | 0.089 | 0.090 | 0.057 | 0.100 | 0.110 | 0.119 | 0.096 | 0.119 | 0.130 | 0.106 | 0.085 | 0.096 | 0.105 | 0.081 | 0.091 | 0.006 | 0.017 | 0.085 | |
| 36 | 0.205 | 0.234 | 0.213 | 0.177 | 0.235 | 0.262 | 0.284 | 0.228 | 0.195 | 0.218 | 0.191 | 0.235 | 0.171 | 0.172 | 0.182 | 0.214 | 0.199 | 0.180 | 0.201 | 0.196 | 0.178 | 0.210 | 0.209 | 0.249 | 0.220 | 0.230 | 0.192 | 0.224 | 0.195 | 0.225 | 0.232 | 0.215 | 0.243 | 0.208 | 0.228 |
Values are calculated with 9999 permutations of the full dataset.
Only eight loci were used for calculating FST and GST for Site 36 as loci sc90 would not amplify for these samples.
Geographic analysis
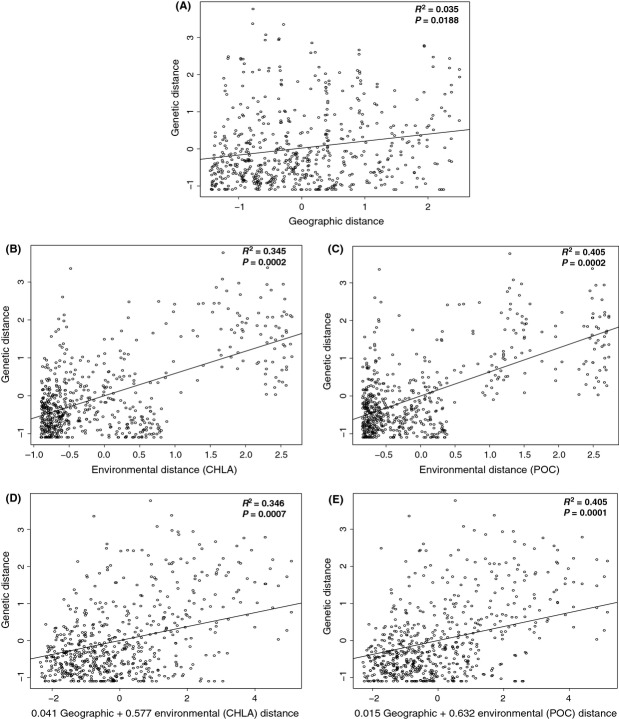
Overall, the IBD Mantel tests show a weak positive (unstandardized matrices R2 = 0.0354, standardized matrices R2 = 0.035) but significant (unstandardized matrices P = 0.001, standardized matrices P = 0.0188) relationship between geographic distance and genetic distance (Fig.3A and Fig. S3), suggesting that geographic distance does not strongly influence genetic structure.
Figure 3.
IBD and IBE analyses. The Mantel test scatterplot of IBD shows genetic distance (FST / (1 − FST)) as a function of geographic distance (A) (Soccotra samples were withheld from all IBD and IBE analysis). The multiple matrix regression with randomization (MMRR) analyses shows IBE relationships between chlorophyll and genetic distance (B) and particulate organic matter and genetic distance (C) and for the combined effects of geographic and chlorophyll distances on genetic distance (D) as well as geographic and particulate organic matter distance on genetic distance (E). All data were standardized to a mean of zero and a standard deviation of one (unstandardized IBD plot can be seen in Figure S3).
Environmental analysis
The IBE Mantel tests comparing environmental distance (NSST, DSST, CHLA, POC, CDOM) with genetic distance (FST / (1 − FST)) and geographic distance (GGD) yielded several significant correlations (α = 0.05). Geographic distance was significantly correlated with all environmental criteria, yet correlations with CHLA, POC, and CDOM were weak, R2 = 0.065, 0.075, and 0.031, respectively. Genetic distance was also strongly correlated with several of the environmental measurements, and these correlations were consistent for the two time frames (annual and winter) studied (Table3). The consistency in results suggests that there is no seasonal effect of environment on genetic structure, or at least that it is not detectable in this study. Genetic distance was significantly correlated with annual CHLA (P = 0.0000, R2 = 0.3446, m = 13.052), annual POC (P = 0.0000, R2 = 0.4045, m = 4839.3), winter CHLA (P = 0.0010, R2 = 0.3399, m = 12.784), and winter POC (P = 0.0000, R2 = 0.4070, m = 4927.5) (Table3).
Table 3.
IBE Mantel test results of full dataset comparing genetic distance (LinFST) and geographic distance (GGD) with five environmental criteria gathered from 9-year averages of night sea surface temperature (NSST), day sea surface temperature (DSST), chlorophyll a (CHLA), particulate organic carbon (POC), and colored dissolved organic matter (CDOM) for the entire year (Annual) and October to May (Winter). R2 is indicated below the diagonal; P values are indicated above the diagonal. Calculations are based on 9999 permutations
| LinFST | GGD | NSST | DSST | CHLA | POC | CDOM | |
|---|---|---|---|---|---|---|---|
| Annual | |||||||
| LinFST | 0.0190 | 0.1480 | 0.1200 | 0.0000 | 0.0000 | 0.2990 | |
| GGD | 0.0353 | 0.0000 | 0.0000 | 0.0050 | 0.0040 | 0.0020 | |
| NSST | 0.0110 | 0.8391 | 0.0000 | 0.1750 | 0.1320 | 0.0250 | |
| DSST | 0.0149 | 0.8630 | 0.9821 | 0.1150 | 0.0990 | 0.0100 | |
| CHLA | 0.3446 | 0.0650 | 0.0066 | 0.0161 | 0.0000 | 0.4230 | |
| POC | 0.4045 | 0.0751 | 0.0112 | 0.0225 | 0.8630 | 0.3960 | |
| CDOM | 0.0020 | 0.0306 | 0.0156 | 0.0222 | 0.0005 | 0.0008 | |
| Winter | |||||||
| LinFST | 0.0190 | 0.1140 | 0.1680 | 0.0010 | 0.0000 | 0.2777 | |
| GGD | 0.0353 | 0.0000 | 0.0000 | 0.0080 | 0.0040 | 0.3650 | |
| NSST | 0.0121 | 0.8668 | 0.0000 | 0.1630 | 0.1110 | 0.4300 | |
| DSST | 0.0069 | 0.8630 | 0.9860 | 0.2350 | 0.1690 | 0.4100 | |
| CHLA | 0.3399 | 0.0615 | 0.0069 | 0.0028 | 0.0000 | 0.3260 | |
| POC | 0.4070 | 0.0713 | 0.0137 | 0.0067 | 0.8556 | 0.2460 | |
| CDOM | 0.0027 | 0.0002 | 0.0000 | 0.0000 | 0.0008 | 0.0026 | |
Multiple matrix regression
Multiple matrix regression with randomization (MMRR) was used to determine whether ecological isolation (CHLA and POC) or geographic isolation is more likely contributing to the observed genetic structure in this study. The MMRR analysis showed that environmental distance (both CHLA and POC) is a stronger predictor of genetic distance than geographic distance (Fig.3) and in the combined models of geographic distance and environmental distance, geography contributes minimally to the strength of the model (Fig.3D–E). Overall, the best models for predicting genetic distance were the model employing only particulate organic carbon distance and the combined model of particulate organic carbon and geography (Fig.3C and E). These models accounted for 40% of the variation in genetic distance.
Fine-scale structure
The spatial autocorrelation analysis of the 16 belt transects taken at 8 sites revealed no significant genetic autocorrelation at the scale of 50 m (Fig.4); that is, at this scale, the genotypes distribution seems to be random in all sites. In all analyses, the autocorrelation coefficient, r, was not significantly different from random expectations.
Figure 4.
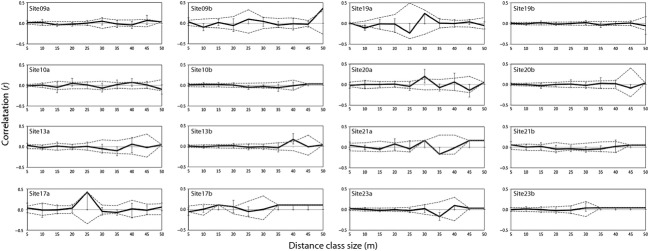
Small-scale spatial autocorrelation analysis for eight reef sites (9, 10, 13, 17, 19, 20, 21, 23) with two transects taken at each site. The relationship between geographic distance and genetic distance at the scale of 50 m is shown with correlograms. Distance class sizes of 5 m were chosen to highlight small spatial scales. The dashed gray lines represent 95% confidence intervals based on 999 permutations of individual locations among all individuals.
Overall, full-sibling pairs within transects, within sites, and among sites represented a small proportion of all pairwise comparisons. The proportion of full-sibling pairs ranged from 5.19% to 7.22% within transects, 4.72% to 6.24% among transects, 4.96% to 6.74% within sites, and 3.92% to 4.84% among sites (Fig.5). There was no significant difference (P > 0.05) between the proportion of full-siblings within transects vs. among transects at any of the three sampling locations (Yanbu χ2 = 0.68, df = 1, P = 0.20; Thuwal χ2 = 0.08, df = 1, P = 0.39; Al-Lith χ2 = 2.01, df = 1, P = 0.08; Fig.5A). There was, however, a significantly higher proportion of full-siblings within sites vs. among sites at Yanbu (χ2 = 10.29, df = 1, P = 0.00) and Al-Lith (χ2 = 29.32, df = 1, P = 0.00) (Fig.5B). This pattern was not seen at Thuwal; there was no significant difference between the proportion of full-siblings within and among sites (χ2 = 0.0593, df = 1, P = 0.4038). Overall, these results indicate that while at Thuwal individuals seem to be distributed randomly regardless of the scale, at Yanbu and Al-Lith, more related individuals are found at slightly larger than 50 m scales (100–200 m within sites) than is to be expected by chance (10–45 km among sites).
Figure 5.
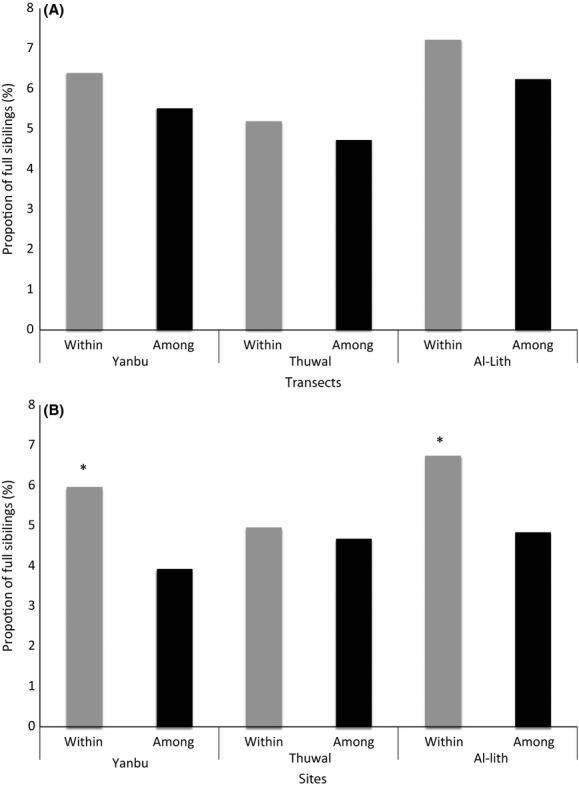
The proportion of significant full-sibling pairs within vs. among transects (A) and within vs. among sites (B). Significantly different proportions (P value < 0.05) of full-siblings are shown (*).
Discussion
Overall, our broad-scale results suggest that environment is a better predictor of genetic structure of S. carteri than is geographic distance. Our fine-scale results indicate that at the scale of 50 m, genetic correlations are no different from random expectations, but at the scale of hundreds of meters, the results suggest that local dynamics might be important. Here we discuss the implications of our findings and propose hypotheses that could link these findings with biological processes that could be tested in future studies.
In terms of the broad-scale patterns that are seen in the data herein gathered, it seems that gene flow can be achieved throughout great distances in this species, at least in the north and central Red Sea. However, the southern region of the Red Sea, namely the Farasan Islands, seems genetically distinct from the rest of the Red Sea. Additionally in the Red Sea, there is evidence for restricted gene flow at Wassalyat Shoals, which lies in the transition zone between the Farasan Islands and the complex Farasan Banks (the southernmost area of the relatively genetically homogenous remainder of the Red Sea). Furthermore, in the northwest Indian Ocean, Socotra could represent another genetic cluster. The finding of strong genetic structure in the Farasan Islands is interesting in that it is similar to the results recently published in another study (Nanninga et al. 2014), yet Nanninga and colleagues found a genetic break in populations of an anemonefish, Amphiprion bicinctus, in the southern Red Sea at 19°N which is considerably further north than the genetic break found in this study (around 16°N). The reason for the difference in this exact location of this genetic break may be due to a difference in the biology of the two species (e.g., the active swimming and sensory capabilities of fish larvae or a wider environmental tolerance for one of the species), a question warranting further investigation. Regardless of the exact location of the boundary, it is notable that the southern Farasan Islands and potentially the Wassalyat Shoals of the Red Sea appear to host populations exhibiting this type of genetic break compared to the rest of the Red Sea. From this, we gather that there could be differential larval survival of S. carteri from the southern Red Sea. It is possible the nutrient poor waters found in the north and central Red Sea could present a boundary to larval survival for those individuals originating from the southern Red Sea (implying some level of local adaptation). And while in the past local adaptation was thought to be limited in marine invertebrates and restricted to only those species with very short dispersal distances, it has now been found that local adaptation occurs in many marine invertebrates, including those with planktonic dispersal (see review by Sanford and Kelly 2011). Further to this, a recent study of a sessile reef dweller has shown that strong selection on larvae produces locally adapted adults with narrow hybrid zones (Prada and Hellberg 2014).
The lack of a strong relationship between geographic distance and genetic distance in the IBD analysis indicates that long-range dispersal or stochastic colonization over many generations is allowing for a high degree of admixture within the Red Sea. It is possible that the inherent biological dispersal capability of S. carteri is most likely not a driving factor contributing to the genetic separation of the Farasan Islands from the rest of the Red Sea. But rather, it is hypothesized that gene flow is limited by other factors such as environmental heterogeneity or circulation boundaries. The IBE results indicate that environmental heterogeneity could be influencing gene flow. Most notably, the strong correlation between chlorophyll distance and genetic distance, and between particulate organic carbon distance and genetic distance indicate that differential primary productively might be associated with population divergence. However, further tests including transplant experiments are needed to fully determine whether or not the well-documented environmental gradient of highly oligotrophic waters in the north to central Red Sea and the more nutrient rich southern Red Sea (Raitsos et al. 2011, 2013, Table S2) are promoting local adaptation through either pre- or postrecruitment barriers to gene flow.
It is noted that the physical circulation of the Red Sea must be considered when determining barriers to gene flow in this region. The 9-year annual mean surface circulation model produced by Sofianos and Johns (2003) presents two notable circulation features in the southern Red Sea; these include the boundary current switch in the southern end of the Red Sea around 14.5°N and an anticyclonic gyre centered around 15–16°N. These physical features could create a pocket of isolation on the eastern side of the Red Sea, south of the boundary switch (14.5°N) that would be maintained by the turbulence effect of the eddy. However, the proposed pocket of isolation lies south of the southern Farasan Islands including sites 33–35. Because the sites in which we have detected barriers to gene flow lie north of this pocket where the model predicts a dominant northward flow north of 16°N, there is no large observable circulation feature that would promote isolation of sites 33–35. This suggests that circulation processes are not the only determining factor in this system. Overall, these observations are purely qualitative; thus, until the effect isolation by circulation is explicitly tested, and more sites in the southern and western Red Sea are studied, circulation cannot be ruled out as a predictor of genetic structure. But, the lack of a well-resolved Red Sea-wide circulation model and the difficulty of sampling reefs off the coast of Sudan, Yemen, and Somalia currently limit the ability to adequately address the influence of circulation in this system.
While we found no evidence for deviations from random mating at the scale of 50 m, the evidence for a greater proportion of full-siblings at scales of 100–200 m in Stylissa carteri assemblages suggests that dispersal might be limited to hundreds of meters or, alternatively, reproductive strategies in this organism might be complex. Besides potential dispersal limitation at scales slightly larger than 50 m, it is possible that low observed heterozygosity and high inbreeding coefficient (FIS) are the consequence, to some extent, of sporadic self-fertilization events. While the presence of null alleles cannot be completely ruled out, self-fertilization or asexual reproduction is relatively common in sponge populations and occurs in all classes within phylum Porifera (see review by Uriz and Turon 2012). It is possible that the reproductive mode of this sponge could be triggered by environmental fluctuations, or after environmental events that drastically diminish population densities. It is well documented that asexual reproduction can be favorable following habitat perturbation thereby allowing for rapid recolonization (Bell 1982; Trivers 1985). Though the extent to which this holds true for sponges is not well understood, it has, however, been shown in Antarctic sponges that asexual reproduction can allow for an increase in sponges with favorable genotypes in a relatively unchanging habitat (Carvalho 1994). Regardless of the known mechanism that might be promoting nonrandom mating, the lack of significant differences in the proportion of full-siblings within vs. among transects paired with the significantly greater proportion of full-siblings within sites vs. among sites indicates that there could be some site-specific structure at scales slightly larger than 50 m but less than the thousands of meters assessed with the among-site comparisons.
This study supports the growing body of literature supporting the importance of the environmental landscape in shaping the genetic structure of marine invertebrate populations (see review by Sanford and Kelly 2011); this study also represents the first evidence for a potential latitudinal environmental gradient influence on sponge population genetic structure. Besides providing important theoretical insights into sponge population dynamics, this study presents important information concerning the Red Sea ecosystem. This information is useful for the planning of marine protected areas by highlighting regions that appear to have frequent genetic exchange. In a broader biogeographic context, these results may help to clarify some of the underlying mechanisms that created or that maintain high endemism levels within the Red Sea.
Acknowledgments
We would like to thank the KAUST Bioscience Core Lab for providing assistance with laboratory procedures, Fieldwork and logistic support was provided by the KAUST Coastal and Marine Resources Core Lab and Amr Gusti, and Dream Divers. This project would not be possible if not for sample collections made possible by Joseph D. DiBattista, Tane H. Sinclair-Taylor, James D. Reimer, the KAUST Reef Ecology Lab, and many others who helped in the field. We thank Equipe Cousteau and Sudanese partners; the Wildlife Conservation General Administration, The Red Sea Government and The Red Sea University. We thank Nicole de Voogd and Lisa Goudie for taxonomic confirmation of some samples. Financial support came from KAUST baseline research funds (to TRR and MLB), a KAUST award CRG-1-BER-002 (to MLB), and National Geographic Society Grant 9024-11 (to J.D. DiBattista). For support in Socotra, we kindly thank the Ministry of Water and Environment of Yemen, staff at the Environment Protection Authority (EPA) Socotra, and especially Salah Saeed Ahmed, Fouad Naseeb, and Thabet Abdullah Khamis, as well as Ahmed Issa Ali Affrar from Socotra Specialist Tour for handling general logistics.
Conflict of Interest
None declared.
Data Accessibility
Genotypes: Dryad Data Repository doi: 10.5061/dryad.h2 h08. MMRR code: Dryad Data Repository doi: 10.5061/dryad.kt71r (Wang 2013).
Supporting Information
Additional Supporting Information may be found in the online version of this article:
Table S1. Primer multiplex mixes for nine microsatellite loci for Stylissa carteri.
Table S2. Environmental data gathered for each of the 36 sample sites.
Table S3. Summary of Multilocus Genotype matches for detection of clonal pairs in the dataset.
Table S4. Tests for HWE for nine microsatellite loci (sc58, sc65, sc72, sc88, sc90, sc56, sc83, sc82, sc96) at 36 populations.
Figure S1. STRUCTURE Harvester results indicate that K = 4 using the natural log of the maximum likelihood as score (A) and K = 2 using the using Evanno’s delta K (B) are the most probable number of theoretical data clusters.
Figure S2. Large-scale population genetic differentiation as measured with Bayesian clustering via STRUCTURE (v2.3.4 Pritchard et al. 2000). Population prior was given; the number of clusters plotted is three (K = 3).
Figure S3. Mantel test scatterplot of IBD shows genetic distance (FST / (1 − FST)) as a function of geographic distance.
Figure S4. Photograph of Stylissa carteri in the Red Sea (photograph credit: Tane Sinclair-Taylor).
References
- Baldeck CA, Harms KE, Yavitt JB, John R, Turner BL, Valencia R, et al. Habitat filtering across tree life stages in tropical forest communities. Proc. Biol. Sci. 2013;280:20130548. doi: 10.1098/rspb.2013.0548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bell G. The masterpiece of nature: the evolution and genetics of sexuality. Berkeley: University of California Press; 1982. [Google Scholar]
- Benjamini Y. Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. Series B (Methodol.) 1995;57:289–300. [Google Scholar]
- Berumen ML, Hoey AS, Bass WH, Bouwmeester J, Catania D, Cochran JEM, et al. The status of coral reef ecology research in the Red Sea. Coral Reefs. 2013;32:737–748. [Google Scholar]
- Blanquer A. Uriz MJ. Population genetics at three spatial scales of a rare sponge living in fragmented habitats. BMC Evol. Biol. 2010;10:13. doi: 10.1186/1471-2148-10-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blanquer A, Uriz M. Caujapé-Castells J. Small-scale spatial genetic structure in Scopalina lophyropoda, an encrusting sponge with philopatric larval dispersal and frequent fission and fusion events. Mar. Ecol. Prog. Ser. 2009;380:95–102. [Google Scholar]
- Calderón I, Ortega N, Duran S, Becerro M, Pascual M. Turon X. Finding the relevant scale: clonality and genetic structure in a marine invertebrate (Crambe crambe, Porifera) Mol. Ecol. 2007;16:1799–1810. doi: 10.1111/j.1365-294X.2007.03276.x. [DOI] [PubMed] [Google Scholar]
- Carvalho GR. Evolutionary genetics of aquatic clonal invertebrates: concepts, problems and prospects. In: Beaumont AR, editor. Genetics and evolution of aquatic organisms. London: Chapman & Hall; 1994. pp. 291–323. [Google Scholar]
- Chaves-Fonnegra A, Feldheim K, Secord J. Lopez JV. Population structure and dispersal of the coral excavating sponge Cliona delitrix. Mol. Ecol. 2015;24:1447–1484. doi: 10.1111/mec.13134. [DOI] [PubMed] [Google Scholar]
- Cox C. Moore PD. Biogeography: an ecological and evolutionary approach, 6th edn. Oxford: Blackwell; 2000. [Google Scholar]
- Crispo E, Bentzen P, Reznick DN, Kinnison MT. Hendry AP. The relative influence of natural selection and geography on gene flow in guppies. Mol. Ecol. 2006;15:49–62. doi: 10.1111/j.1365-294X.2005.02764.x. [DOI] [PubMed] [Google Scholar]
- Cushman SA, McKelvey KS, Hayden J. Schwartz MK. Gene flow in complex landscapes: testing multiple hypotheses with causal modeling. Am. Nat. 2006;168:486–499. doi: 10.1086/506976. [DOI] [PubMed] [Google Scholar]
- Dailianis T, Tsigenopoulos CS, Dounas C. Voultsiadou E. Genetic diversity of the imperilled bath sponge Spongia officinalis Linnaeus, 1759 across the Mediterranean Sea: patterns of population differentiation and implications for taxonomy and conservation. Mol. Ecol. 2011;20:3757–3772. doi: 10.1111/j.1365-294X.2011.05222.x. [DOI] [PubMed] [Google Scholar]
- DeBiasse MB, Richards VP. Shivji MS. Genetic assessment of connectivity in the common reef sponge, Callyspongia vaginalis (Demospongiae: Haplosclerida) reveals high population structure along the Florida reef tract. Coral Reefs. 2009;29:47–55. [Google Scholar]
- DiBattista JD, Berumen ML, Gaither MR, Rocha LA, Eble JA, Choat JH, et al. After continents divide: comparative phylogeography of reef fishes from the Red Sea and Indian Ocean. J. Biogeogr. 2013;40:1170–1181. [Google Scholar]
- Duran S. Rützler K. Ecological speciation in a Caribbean marine sponge. Mol. Phylogenet. Evol. 2006;40:292–297. doi: 10.1016/j.ympev.2006.02.018. [DOI] [PubMed] [Google Scholar]
- Duran S, Pascual M, Estoup A. Turon X. Strong population structure in the marine sponge Crambe crambe (Poecilosclerida) as revealed by microsatellite markers. Mol. Ecol. 2004;13:511–522. doi: 10.1046/j.1365-294x.2004.2080.x. [DOI] [PubMed] [Google Scholar]
- Earl DA. vonHoldt BM. STRUCTURE HARVESTER: A website and program for visualizing STRUCTURE output and implementing the Evanno method. Conserv. Genet. Resour. 2012;4:359–361. [Google Scholar]
- Giles EC, Saenz-Agudelo P, Berumen ML. Ravasi T. Novel polymorphic microsatellite markers developed for a common reef sponge, Stylissa carteri. Mar. Biodivers. 2013;43:237–241. [Google Scholar]
- Goreau TF. The ecology of Jamaican coral reefs I. Species composition and zonation. Ecology. 1959;40:67–90. [Google Scholar]
- Gorospe KD. Karl SA. Genetic relatedness does not retain spatial pattern across multiple spatial scales: dispersal and colonization in the coral, Pocillopora damicornis. Mol. Ecol. 2013;22:3721–3736. doi: 10.1111/mec.12335. [DOI] [PubMed] [Google Scholar]
- Guardiola M, Frotscher J. Uriz MJ. Genetic structure and differentiation at a short-time scale of the introduced calcarean sponge Paraleucilla magna to the western Mediterranean. Hydrobiologia. 2011;687:71–84. [Google Scholar]
- Hellberg ME. Footprints on water: the genetic wake of dispersal among reefs. Coral Reefs. 2007;26:463–473. [Google Scholar]
- Hooper JNA. Van Soest RWM. Book Review: Systema Porifera. Guide to the classification of sponges. Invertebr. Syst. 2004;18:233–234. [Google Scholar]
- Jenkins DG, Carey M, Czerniewska J, et al. A meta-analysis of isolation by distance: relic or reference standard for landscape genetics? Ecography. 2010;33:315–320. [Google Scholar]
- Jones GP, Almany GR, Russ GR, et al. Larval retention and connectivity among populations of corals and reef fishes: history, advances and challenges. Coral Reefs. 2009;28:307–325. [Google Scholar]
- Kinzie RA. The zonation of West Indian gorgonians. Bull. Mar. Sci. 1973;23:93–155. [Google Scholar]
- Konovalov DA, Manning C. Henshaw MT. KINGROUP: a program for pedigree relationship reconstruction and kin group assignments using genetic markers. Mol. Ecol. Notes. 2004;4:779–782. [Google Scholar]
- Lee C-R. Mitchell-Olds T. Quantifying effects of environmental and geographical factors on patterns of genetic differentiation. Mol. Ecol. 2011;20:4631–4642. doi: 10.1111/j.1365-294X.2011.05310.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leimu R. Fischer M. A meta-analysis of local adaptation in plants. PLoS ONE. 2008;3:e4010. doi: 10.1371/journal.pone.0004010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lesser MP. Benthic-pelagic coupling on coral reefs: feeding and growth of Caribbean sponges. J. Exp. Mar. Biol. Ecol. 2006;328:277–288. [Google Scholar]
- Levin S. The problem of pattern and scale in ecology: the Robert H. MacArthur award lecture. Ecology. 1992;73:1943–1967. [Google Scholar]
- Li C. Precambrian sponges with cellular structures. Science. 1998;279:879–882. doi: 10.1126/science.279.5352.879. [DOI] [PubMed] [Google Scholar]
- López-Legentil S. Pawlik JR. Genetic structure of the Caribbean giant barrel sponge Xestospongia muta using the I3-M11 partition of COI. Coral Reefs. 2009;28:157–165. [Google Scholar]
- Maldonado M. The ecology of the sponge larva. Can. J. Zool. 2006;84:175–194. [Google Scholar]
- Maldonado M. Young C. Effects of physical factors on larval behavior, settlement and recruitment of four tropical demosponges. Mar. Ecol. Prog. Ser. 1996;138:169–180. [Google Scholar]
- Manel S. Holderegger R. Ten years of landscape genetics. Trends Ecol. Evol. 2013;28:614–621. doi: 10.1016/j.tree.2013.05.012. [DOI] [PubMed] [Google Scholar]
- Marshall D, Monro K, Bode M, Keough M. Swearer S. Phenotype-environment mismatches reduce connectivity in the sea. Ecol. Lett. 2010;13:128–140. doi: 10.1111/j.1461-0248.2009.01408.x. [DOI] [PubMed] [Google Scholar]
- Nanninga GB, Saenz-Agudelo P, Manica A. Berumen ML. Environmental gradients predict the genetic population structure of a coral reef fish in the Red Sea. Mol. Ecol. 2014;23:591–602. doi: 10.1111/mec.12623. [DOI] [PubMed] [Google Scholar]
- Ordóñez V, Pascual M, Rius M. Turon X. Mixed but not admixed: a spatial analysis of genetic variation of an invasive ascidian on natural and artificial substrates. Mar. Biol. 2013;160:1645–1660. [Google Scholar]
- Paine CET, Harms KE. Ramos J. Supplemental irrigation increases seedling performance and diversity in a tropical forest. J. Trop. Ecol. 2009;25:171–180. [Google Scholar]
- Pawlik JR, Loh TL, McMurray SE. Finelli CM. Sponge communities on Caribbean coral reefs are structured by factors that are top-down, not bottom-up. PLoS ONE. 2013;8:5. doi: 10.1371/journal.pone.0062573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peakall R. Smouse PE. GenAlEx 6.5: genetic analysis in Excel. Population genetic software for teaching and research – an update. Bioinformatics. 2012;28:2537–2539. doi: 10.1093/bioinformatics/bts460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prada C. Hellberg ME. Long pre-reproductive selection and divergence by depth in a Caribbean candelabrum coral. Proc. Natl Acad. Sci. USA. 2013;119:53–60. doi: 10.1073/pnas.1208931110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prada C. Hellberg ME. Strong natural selection on juveniles maintains a narrow adult hybrid zone in a broadcast spawner. Am. Nat. 2014;184:702–713. doi: 10.1086/678403. [DOI] [PubMed] [Google Scholar]
- Pritchard JK, Stephens M. Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155:945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raitsos DE, Hoteit I, Prihartato PK, et al. Abrupt warming of the Red Sea. Geophys. Res. Lett. 2011;38:L14601. [Google Scholar]
- Raitsos DE, Pradhan Y, Brewin RJW, Stenchikov G. Hoteit I. Remote sensing the phytoplankton seasonal succession of the Red Sea. PLoS ONE. 2013;8:6. doi: 10.1371/journal.pone.0064909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Randall JE. Twenty-two new records of fishes from the Red Sea. Fauna of Saudi Arabia. 1994;14:259–275. [Google Scholar]
- Raymond M. Rousset F. An exact test for population differentiation. Evolution. 1995;49:1280–1283. doi: 10.1111/j.1558-5646.1995.tb04456.x. [DOI] [PubMed] [Google Scholar]
- Roberts CM, Shepherd ARD. Ormond RFG. Large-scale variation in assemblage structure of Red Sea butterflyfishes and angelfishes. J. Biogeogr. 1992;19:239–250. [Google Scholar]
- Rousset F. GENEPOP’007: A complete re-implementation of the GENEPOP software for Windows and Linux. Mol. Ecol. Resour. 2008;8:103–106. doi: 10.1111/j.1471-8286.2007.01931.x. [DOI] [PubMed] [Google Scholar]
- Sanford E. Kelly MW. Local adaptation in marine invertebrates. Annu. Rev. Mar. Sci. 2011;3:509–535. doi: 10.1146/annurev-marine-120709-142756. [DOI] [PubMed] [Google Scholar]
- Schmidt PS, Serrão EA, Pearson GA, et al. Ecological genetics in the North Atlantic: environmental gradients and adaptation at specific loci. Ecology. 2008;89:S91–S107. doi: 10.1890/07-1162.1. [DOI] [PubMed] [Google Scholar]
- Selkoe K. Toonen R. Marine connectivity: a new look at pelagic larval duration and genetic metrics of dispersal. Mar. Ecol. Prog. Ser. 2011;436:291–305. [Google Scholar]
- Selkoe KA, Gaines SD, Caselle JE. Warner RR. Current shifts and kin aggregation explain genetic patchiness in fish recruits. Ecology. 2006;87:3082–3094. doi: 10.1890/0012-9658(2006)87[3082:csakae]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- Selkoe KA, Henzler CM. Gaines SD. Seascape genetics and the spatial ecology of marine populations. Fish Fish. 2008;9:363–377. [Google Scholar]
- Smouse PE. Peakall R. Spatial autocorrelation analysis of individual multiallele and multilocus genetic structure. Heredity. 1999;82(Pt 5):561–573. doi: 10.1038/sj.hdy.6885180. [DOI] [PubMed] [Google Scholar]
- Sofianos SS. Johns WE. An Oceanic General Circulation Model (OGCM) investigation of the Red Sea circulation: 2. Three-dimensional circulation in the Red Sea. J. Geophys. Res. 2003;108:3066. [Google Scholar]
- Srivastava M, Simakov O, Chapman J, et al. The Amphimedon queenslandica genome and the evolution of animal complexity. Nature. 2010;466:720–726. doi: 10.1038/nature09201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trivers RL. Social evolution. Menlo Park: Benjamin/Cummings Publishing; 1985. [Google Scholar]
- Uriz MJ. Turon X. Sponge ecology in the molecular era. Adv. Mar. Biol. 2012;61:345–410. doi: 10.1016/B978-0-12-387787-1.00006-4. [DOI] [PubMed] [Google Scholar]
- Uriz M, Maldonado M, Turon X. Martí R. How do reproductive output, larval behaviour, and recruitment contribute to adult spatial patterns in Mediterranean encrusting sponges? Mar. Ecol. Prog. Ser. 1998;167:137–148. [Google Scholar]
- Van Oosterhout C, Hutchinson WF, Wills DPM. Shipley P. MICRO-CHECKER: Software for identifying and correcting genotyping errors in microsatellite data. Mol. Ecol. Notes. 2004;4:535–538. [Google Scholar]
- Wang IJ. Examining the full effects of landscape heterogeneity on spatial genetic variation: a multiple matrix regression approach for quantifying geographic and ecological isolation. Evolution. 2013;67:3403–3411. doi: 10.1111/evo.12134. [DOI] [PubMed] [Google Scholar]
- Wang IJ. Bradburd GS. Isolation by environment. Mol. Ecol. 2014;23:5649–5662. doi: 10.1111/mec.12938. [DOI] [PubMed] [Google Scholar]
- Wang IJ. Summers K. Genetic structure is correlated with phenotypic divergence rather than geographic isolation in the highly polymorphic strawberry poison-dart frog. Mol. Ecol. 2010;19:447–458. doi: 10.1111/j.1365-294X.2009.04465.x. [DOI] [PubMed] [Google Scholar]
- Whalan S, Johnson MS, Harvey E. Battershill C. Mode of reproduction, recruitment, and genetic subdivision in the brooding sponge Haliclona sp. Mar. Biol. 2005;146:425–433. [Google Scholar]
- Wiens J. Spatial scaling in ecology. Funct. Ecol. 1989;3:385–397. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table S1. Primer multiplex mixes for nine microsatellite loci for Stylissa carteri.
Table S2. Environmental data gathered for each of the 36 sample sites.
Table S3. Summary of Multilocus Genotype matches for detection of clonal pairs in the dataset.
Table S4. Tests for HWE for nine microsatellite loci (sc58, sc65, sc72, sc88, sc90, sc56, sc83, sc82, sc96) at 36 populations.
Figure S1. STRUCTURE Harvester results indicate that K = 4 using the natural log of the maximum likelihood as score (A) and K = 2 using the using Evanno’s delta K (B) are the most probable number of theoretical data clusters.
Figure S2. Large-scale population genetic differentiation as measured with Bayesian clustering via STRUCTURE (v2.3.4 Pritchard et al. 2000). Population prior was given; the number of clusters plotted is three (K = 3).
Figure S3. Mantel test scatterplot of IBD shows genetic distance (FST / (1 − FST)) as a function of geographic distance.
Figure S4. Photograph of Stylissa carteri in the Red Sea (photograph credit: Tane Sinclair-Taylor).
Data Availability Statement
Genotypes: Dryad Data Repository doi: 10.5061/dryad.h2 h08. MMRR code: Dryad Data Repository doi: 10.5061/dryad.kt71r (Wang 2013).