Homogeneous Coordinates in Motion Correction

Abstract

Purpose

Prospective motion correction for MRI and other imaging modalities are commonly based on the assumption of affine motion, i.e. rotations, shearing, scaling and translations. In addition it often involves transformations between different reference frames, especially for applications with an external tracking device. The goal of this work is to develop a computational framework for motion correction based on homogeneous transforms.

Theory and Methods

The homogeneous representation of affine transformations uses 4×4 transformation matrices applied to 4-dimensional augmented vectors. It is demonstrated how homogenous transforms can be used to describe the motion of slice objects during an MRI scan. Furthermore, we extend the concept of homogeneous transforms to gradient and k-space vectors, and show that the 4^th dimension of an augmented k-space vector encodes the complex phase of the corresponding signal sample due to translations.

Results

The validity of describing motion tracking in real space and k-space using homogeneous transformations only is demonstrated on phantom experiments.

Conclusion

Homogeneous transformations allows for a conceptually simple, consistent and computationally efficient theoretical framework for motion correction applications.

Introduction

Motion correction in MRI is becoming increasingly important due to its ability to maximize effective spatial resolution and image quality by virtually freezing patient motion. This is achieved by locking the scan geometry to the mobile object reference frame, based on feedback from a system that tracks object motion. Object motion can be either derived from MR navigators (1-3), MR-visible markers (4,5), or using external tracking devices (e.g. optical camera systems (6-9)). Once information about object motion is available, motion correction can be performed prospectively by updating the imaging gradients and slice objects (6,7,9), retrospectively by implicitly or explicitly updating the k-space trajectory used during image reconstruction (10), or by a combination of both approaches (11,12). Many motion correction techniques are based on the assumption of rigid body object motion, and calculations commonly involve several coordinate systems (i.e. reference frames). This is particularly true for external tracking devices, whose internal coordinate system is different from that frame of the scanner (7-9,13).

Rigid body motion involves rotations and translations. Homogeneous coordinates and transformations (represented by augmented 4-dimensional, or 4D, vectors and 4x4 matrices) allow for a matrix formulation for both translations and rotations. Homogeneous transforms have been previously used in motion corrected MRI. For example, Aksoy et al. (6,11) used homogeneous matrices to model the calibration process and calculate gradient updates. The effect of affine transformations on the k-space signal is described in (14) and (15). However, most current commercial implementations still describe position in terms of slice offsets (i.e. translations), and the orientation of slices and the field-of-view in terms of gradient rotations (8,9). Additionally, gradient orientation and slice offsets are usually treated as completely separate entities. These approaches may lead to lengthy and complicated calculations when transformations between multiple reference frames are involved.

In this work, we demonstrate how the complete chain of transformations including the camera reference frame, the initial slice orientation and position and resulting updates can be described using homogeneous transformations only. We further introduce augmented 4D gradient and k-space vectors that allow for a direct application of homogeneous transformations to k-space coordinates and gradient orientations.

Theory

Reference frames

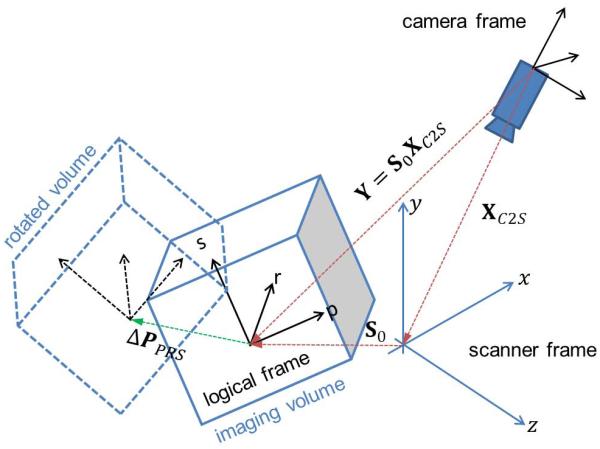
A motion correction system with an external tracking device typically involves three stationary reference frames: camera, scanner and the logical frame at the start of the scan (Figure 1). The camera frame is the internal reference frame of the tracking device. The stationary scanner frame is the reference frame of the MRI machine as defined by the orientation and direction of the physical gradient fields (XYZ-frame) used for spatial encoding. The logical frame depends on the initial orientation of the imaging volume or slice, and describes the spatial encoding process in terms of logical gradients (e.g. phase, read, slice direction or PRS-frame).

Figure 1.

Reference frames and transformations for a typical system using an external motion tracking device (here: camera) that does not directly track in the in the scanner frame.

Motion correction is commonly conceptualized and implemented as a two step process. First, the primary tracking data (in the internal reference frame of the tracking system) are transformed into scanner coordinates (XYZ), and object motion is calculated in scanner coordinates. This is achieved using an experimentally determined “cross-calibration” transformation, which describes the camera pose in the XYZ-frame (9,11,16). In step 2, motion in scanner coordinates is used to adjust the gradient orientation matrix and slice positions and FOV, i.e. to update the logical reference frame.

One major reason for using a two-step approach is that external motion tracking systems are not fully integrated into commercial scanners. Consequently, the external tracking system typically acts as an independent front-end that provides tracking data to the scanner. Updates to the logical reference frame are subsequently performed on the scanner using internal software algorithms available. Furthermore, since current scanner environments typically treat the gradient matrix, slice objects, and FOV properties as separate entities, calculations for rotations and translations are usually performed separately as well, which can result in rather complex algorithms. In the following sections, we describe how the consistent use of homogeneous transformations can dramatically simplify calculations required for motion correction, and lead to more efficient implementations.

Rigid body motion and homogeneous transformations

Rigid body motion involves a combination of rotations (3×3 matrix R̂) and translations (3×1 column vector d̂ = (d_x, d_y, d_z)^T). However, rotations and translations of a 3-dimensional vector r̂ can be expressed as a single matrix multiplication if the position vector r̂ is augmented by a 4^th dimension. The augmented 4×1 vector r is of the form r = (r̂, 1)^T = (r_x, r_y, r_z, 1)^T with the 4^th coefficient set to a constant value of 1. Here, the hat is used to indicate regular 3D vectors and matrices, and omitted when using augmented 4D coordinates (homogeneous transforms). Transformation of an augmented vector r is then written as

$${\mathbf{r}}^{\prime }=\mathbf{Ar}$$ [1]

where A is a 4×4 homogeneous transform matrix of the form $\mathbf{A}=\left(\begin{array}{cc}\hfill \widehat{\mathbf{R}}\hfill & \hfill \widehat{\mathbf{d}}\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right)$ It can be easily verified that Eq.[1] is equivalent to a vector rotation and subsequent translation. Furthermore, it is easy to proof that the transpose of A is ${\mathbf{A}}^T=\left(\begin{array}{cc}\hfill {\widehat{\mathbf{R}}}^T\hfill & \hfill 0\hfill \\ \hfill {\widehat{\mathbf{d}}}^T\hfill & \hfill 1\hfill \end{array}\right)$ and the inverse is ${\mathbf{A}}^{-1}=\left(\begin{array}{cc}\hfill {\widehat{\mathbf{R}}}^{-1}\hfill & \hfill -{\widehat{\mathbf{R}}}^{-1}\widehat{\mathbf{d}}\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right)$.

Representing slices and imaging volume as homogeneous matrices

First, rather than treating slice (or imaging volume) offsets and the rotation matrix as two separate objects, we represent a slice object as a single homogeneous matrix that combines translations and rotations. Specifically, a given slice is characterized by the offset of its center relative to (physical) isocenter, as well as its rotation relative to the scanner reference frame (Figure 1). Thus, the initial slice object is represented by its homogeneous matrix S₀ relative to the XYZ-frame. S₀ maps the augmented gradient (see below) vector g_PRS (phase, read, slice, 0) in the logical frame to the physical frame by

$${\mathbf{g}}_{XYZ}=\left({\mathbf{S}}_0^{-1}\right){\mathbf{g}}_{PRS}$$ [2]

“Logical cross calibration” and transforming motion from the camera to logical frame

Once slice objects are represented as homogeneous matrices, it is possible to describe the process of motion correction in a simplified framework. First, we define the “logical cross calibration” Y as the pose of the camera relative to the logical frame. Specifically, for any slice i with initial orientation S_0i, the associated logical cross calibration Y_i is defined as:

$${\mathbf{Y}}_{\mathbf{i}}={\mathbf{S}}_{0i}\mathbf{X}$$ [3]

where X is the “conventional” cross-calibration (from camera to physical coordinate frame).

The primary measurement of object motion occurs in the reference frame of the tracking device, and is calculated relative to the initial pose of the tracking marker P_cam(t = t₀) at time point t = t₀, typically at the start of the imaging sequence. P_cam(t) represents a subsequent pose of the maker at time t in the camera frame. Object motion A(t) as seen by the camera is then given by

$$\mathbf{A}\left(\mathrm{t}\right)={\mathbf{P}}_{cam}\left(t\right){\mathbf{P}}_{cam}^{-1}\left(t_0\right)$$ [4]

The logical cross calibration Y_i from Eq. [3] allows the direct transformation of poses in the camera frame into poses in the logical frame, resulting in P_prs(t₀) = Y_iP_cam(t₀) and P_prs(t) = Y_iP_cam(t). Therefore, motion B(t) in the logical PRS-frame is given by

$$\mathbf{B}\left(\mathrm{t}\right)={\mathbf{P}}_{prs}\left(t\right){\mathbf{P}}_{prs}^{-1}\left(t_0\right)={\mathbf{Y}}_i\mathbf{A}\left(t\right){\mathbf{Y}}_{\mathbf{i}}^{-1}$$ [5]

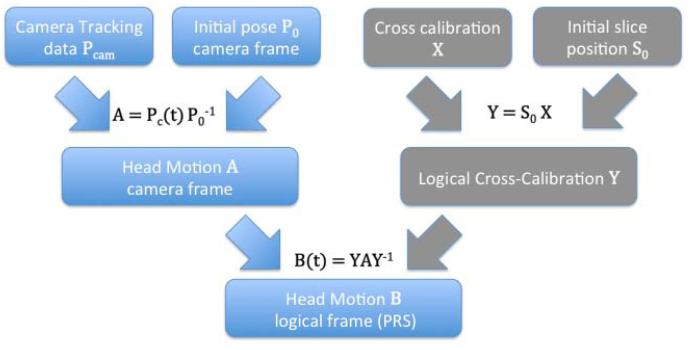
As shown in Figure 2, the proposed algorithm starts by initializing the logical cross calibration (for each slice) at the start of a given scan. Subsequent motion correction updates in logical coordinates can then be calculated as per Eq. [5], and require a single matrix operation. It is then trivial to extract the necessary rotational and translational changes from the homogeneous matrix B(t), and update the rotation matrix and slice position accordingly.

Figure 2.

One step transformation from motion in camera frame directly to motion in logical frame. For each slice, a “logical cross calibration” Y is calculated and stored at the start of the scan, and then used repeatedly in calculating motion updates in logical coordinates.

Augmented K-space

In this section, we extend the use of homogenous coordinates to k-space and the MR signal equation, and introduce augmented 4D gradient and k-space vectors.

The received signal s(t) in MRI is commonly written as

$$s\left(t\right)=\int \rho \left(\widehat{\mathbf{r}}\right)e^{i\Phi (\widehat{\mathbf{r}},t)dV}$$ [6]

with ρ(r̂) being the complex valued spin density at spatial location r̂ = (r_x, r_y, r_z)^T·Φ(r̂, t) is the accumulated phase of a single spin at position r̂ due to the influence of temporally and spatially varying gradient field ĝ = (g_x, g_y, g_z)^T. The phase variation Φ at position r̂ is given by integrating the effects of the magnetic field gradient over time:

$$\Phi (\widehat{\mathbf{r}},t)=\gamma {\int }_0^t{\widehat{\mathbf{r}}}^T\widehat{\mathbf{g}}d{t}^{\prime }$$ [7]

By defining the k-space variable as $\widehat{\mathbf{k}}\left(t\right)=\gamma {\int }_0^t\widehat{\mathbf{g}}d{t}^{\prime }$ and under the assumption of a stationary object, Eq.[7] can be rewritten as the scalar product of the spatial position with the k-space vector.

$$\Phi (\widehat{\mathbf{r}},t)={\widehat{\mathbf{r}}}^T\widehat{\mathbf{k}}\left(t\right)$$ [8]

Phase evolution in case of rigid body motion and homogeneous representation

Equations [6] to [8] demonstrate that spatial encoding in MRI is ultimately based on a periodic phase pattern imposed on the object’s magnetization, as determined by the scalar product of r̂ and k̂. In analogy to the augmented 4×1 spatial vector r = (r̂, 1)^T = (r_x, r_y, r_z, 1)^T, we now define an augmented gradient vector as g = (g_x, g_y, g_z, c₀)^T, with the 4^th component c₀ yet to be determined. We also define an augmented k-space vector as

$$\mathbf{k}\left(t\right)=\gamma {\int }_0^t\mathbf{g}\left(t^{\prime }\right)d{t}^{\prime }=\left(\begin{array}{c}\hfill \gamma {\int }_0^t{g}_{x}d{t}^{\prime }\hfill \\ \hfill \gamma {\int }_0^t{g}_{y}d{t}^{\prime }\hfill \\ \hfill \gamma {\int }_0^t{g}_{z}d{t}^{\prime }\hfill \\ \hfill \gamma {\int }_0^t{c}_{0}d{t}^{\prime }\hfill \end{array}\right)=\left(\begin{array}{c}\hfill k_x\hfill \\ \hfill k_y\hfill \\ \hfill k_z\hfill \\ \hfill {\phi }_0\hfill \end{array}\right)$$ [9]

The 4^th component φ₀ is still undetermined (c₀), but it will become clear below that φ₀ represents an initial phase. Rewriting the phase evolution of Eq. [7] during rigid body motion for an initial position r₀ in terms of homogeneous coordinates yields:

$$\Phi (\mathbf{r},t)=\gamma {\int }_0^t{\left({\mathbf{Ar}}_0\right)}^T{\mathbf{g}}_{0}d{t}^{\prime }=\gamma {\int }_0^t{\mathbf{r}}_0^T{\mathbf{A}}^T{\mathbf{g}}_{0}d{t}^{\prime }={\mathbf{r}}_0^T\gamma {\int }_0^t{\mathbf{A}}^T{\mathbf{g}}_{0}d{t}^{\prime }$$ [10]

In general, both A(t) and g₀(t) are time dependent and therefore cannot be separated under the integral. However, for many motion tracking applications it is reasonable to assume that no motion occurs during short (millisecond) periods of gradient encoding; this corresponds to a zero order Taylor approximation in time for A. Therefore, for the remainder of this paper, we assume that A has no time dependence. Consequently, A can be separated from the integral in Eq.[10], which then becomes:

$$\Phi (\mathbf{r},t)={\mathbf{r}}_0^T{\mathbf{A}}^T\gamma {\int }_0^t{\mathbf{g}}_{0}d{t}^{\prime }={\mathbf{r}}_0^T{\mathbf{A}}^T{\mathbf{k}}_0={\mathbf{r}}_0^T\mathbf{k}$$ [11]

The phase evolution is now given as the scalar product of the initial pose r₀ with a transformed augmented k-space vector K = A^Tk₀. Since the phase Φ(r, t) is a scalar, its value based on Eq.[11] has to be identical to that determined with the conventional approach, i.e. using separate rotation and translations. First we calculate the transformed augmented k-space vector k:

$$\mathbf{k}={\mathbf{A}}^T{\mathbf{k}}_0=\left(\begin{array}{cc}\hfill {\widehat{\mathbf{R}}}^T\hfill & \hfill 0\hfill \\ \hfill {\widehat{\mathbf{d}}}^T\hfill & \hfill 1\hfill \end{array}\right)\left(\begin{array}{c}\hfill k_{0x}\hfill \\ \hfill k_{0y}\hfill \\ \hfill k_{0z}\hfill \\ \hfill {\phi }_0\hfill \end{array}\right)=\left(\begin{array}{c}\hfill k_x\hfill \\ \hfill k_y\hfill \\ \hfill k_z\hfill \\ \hfill d_x{k}_{0x}+d_y{k}_{0y}+d_z{k}_{0z}+{\phi }_0\hfill \end{array}\right)=\left(\begin{array}{c}\hfill k_x\hfill \\ \hfill k_y\hfill \\ \hfill k_y\hfill \\ \hfill \phi \hfill \end{array}\right)$$ [12]

Here, (k_x, k_y, k_z)^T are the components of a rotated k-space vector k̂ = R̂^Tk̂₀. The fourth component φ equals the sum of φ₀ plus the scalar product of the translations with the non-rotated k-space vector, as in the case of a translation only. The scalar product for spatial encoding as per Eq. [11] then becomes:

$$\Phi (\mathbf{r},t)={\mathbf{r}}_0^T=(r_{0x},r_{0y},r_{0z},1)\left(\begin{array}{c}\hfill k_x\hfill \\ \hfill k_y\hfill \\ \hfill k_y\hfill \\ \hfill \phi \hfill \end{array}\right)={\widehat{\mathbf{r}}}_0^T\widehat{\mathbf{k}}+\phi$$ [13]

Finally, rewriting the MRI signal equation [6] in terms of homogeneous coordinates yields:

$$s\left(t\right)=s\left(\mathbf{k}\left(\mathbf{t}\right)\right)=\int \rho \left({\mathbf{r}}_0\right)e^{i\Phi (\mathbf{r},t)}dV=\int \rho \left({\mathbf{r}}_0\right)e^{i{\widehat{\mathbf{r}}}_0^T\widehat{\mathbf{k}}+i\phi }dV=e^{i\phi }\int \rho \left({\mathbf{r}}_0\right)e^{i{\widehat{\mathbf{r}}}_0^T\widehat{\mathbf{k}}}dV$$ [14]

Consequently, homogeneous coordinates and homogeneous k-space vectors allow the signal equation in the presence of rigid body motion to be written in a very compact form:

$$s\left(t\right)=\int \rho \left({\mathbf{r}}_0\right)e^{i{\mathbf{r}}_0^T{\mathbf{A}}^T{\mathbf{k}}_0}dV$$ [15]

Affine motion

Changes in reference frames (for instance, from the camera frame to the scanner frame) involves translations and rotations only, and can therefore be represented by rigid body motion only. Consequently, the calculations in the previous sections were based on the assumption of rigid body motion. However, a more general class of movements involves affine transformations; i.e. additional non-rigid motion components such as shear or compression and inflation (scaling). For instance, cardiac and abdominal movements have been approximated using affine transformations (17). Importantly, our theory can be readily generalized to include arbitrary affine transformations. This is achieved by replacing the rotation matrix R̂ in the 4×4 matrix $\mathbf{A}=\left(\begin{array}{cc}\hfill \widehat{\mathbf{R}}\hfill & \hfill \widehat{\mathbf{d}}\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right)$ with a (linear) affine transformation matrix F̂.

Methods

Experiments were performed on 3T Tim Trio scanner (Siemens, Erlangen) using a 12 channel RF coil. Validation of Eqs. [5], [12] and [15] was performed on a structured phantom that was imaged in two different positions using a 3D-GRE sequence (TR/TE = 10/5 ms, 2mm isotropic resolution). The initial scan geometry (FOV) was along the sagittal direction, rotated by 15° around the slice axis with additional off-center shifts of 19.3, 21.0, and 10 mm along the x, y, and z-axes. The vendor specific description of the initial slice position was converted to the homogeneous representation of the slice position and orientation S₀.

Motion between the two phantom positions was recorded using an optical tracking device (in-bore camera system, Metria Innovation, (18)). The motion approximately consisted of a 60° rotation around the scanner’s xy-axis and 10mm translations along all three axes. Retrospective motion correction was implemented using an iterative augmented SENSE (10) reconstruction. The forward model (encoding matrix) was updated incorporating motion feedback according to Eq. [15]. Starting with a Cartesian trajectory, the 3D k-space was rotated using Eq.[12], since no intra-scan motion took place. The starting value of the 4^th component of the augmented k-space vector was set to zero for the original Cartesian trajectory.

Results

Figure 3a shows three orthogonal slices of the phantom in its initial position. After moving (rotating and translating) the phantom, uncorrected images demonstrate substantial movement (Figure 3b). Retrospective motion correction, using image reconstruction according to Eq.[15], results in images that closely match those in the initial position (Figure 3c). This demonstrates that Equation [15] makes it possible to remove the effect of the static inter-scan motion between Figure 3a and 3b.

Figure 3.

Retrospective correction of inter-scan motion based on augmented k-space vectors.

Discussion

We demonstrate that the complete process of transformations between reference frames in MRI, and medical imaging in general, can be described using a homogeneous representation of rigid body motion by 4×4 homogeneous matrices and vectors. This framework models all changes in reference frames, and allows efficient calculation of arbitrary (oblique) volume / slice orientations as well as actual gradient and receiver phase updates for prospective motion correction (by introducing 4D augmented gradients and k-space vectors). Furthermore, it is possible to include non-rigid body motion like shear and scaling motion in this framework.

Assuming that slices are prospectively updated to track object motion, our framework of homogeneous transformations is valid for 2D multi-slice imaging as well because from a signal perspective, slice excitation and encoding are identical to acquiring a thin 3D volume with no phase encoding along the slice direction. In practice, the description of a stack of slices would require an array of initial slice positions S_0i (e.g. with different translational components in case of non-oblique slices) and consequently, an array of logical cross calibrations Y_i as well. However, if slice objects are not updated prospectively, then the disturbance of the steady-state in case of through-plane motion is not addressed by our alternative mathematical framework.”

Our initial motivation for the given formulism was a direct consequence of the need for a cross-calibration between the camera and the scanner in case of optical motion tracking. The derivation, however, applies to all tracking systems with an internal reference frame that is independent from the scanner’s reference frame. Consequently, our same framework is also useful for MR-navigators that are not acquired in the same logical coordinate system as defined by the orientation and position of the imaging field-of-view.

In conclusion, the use of homogeneous vectors and matrices makes it possible to transform motion from the camera into the scanner frame via two simple matrix multiplications. Our new approach is conceptually simpler and computationally more efficient than performing the common two-step process, from camera to physical to logical frames, and than treating rotations and translations separately (although the conventional approach is in no way incorrect ). However, we believe that many aspects of MRI or other medical imaging modalities involving transformations of volumes or slices are best described as a change in reference frames, and are most conveniently formulated in terms of homogeneous transformations and augmented k-space vectors.