Optimizing Locomotion Controllers Using Biologically-Based Actuators and Objectives

Abstract

We present a technique for automatically synthesizing walking and running controllers for physically-simulated 3D humanoid characters. The sagittal hip, knee, and ankle degrees-of-freedom are actuated using a set of eight Hill-type musculotendon models in each leg, with biologically-motivated control laws. The parameters of these control laws are set by an optimization procedure that satisfies a number of locomotion task terms while minimizing a biological model of metabolic energy expenditure. We show that the use of biologically-based actuators and objectives measurably increases the realism of gaits generated by locomotion controllers that operate without the use of motion capture data, and that metabolic energy expenditure provides a simple and unifying measurement of effort that can be used for both walking and running control optimization.

1 Introduction

The development of physics-based locomotion controllers de novo, independent from stock motion data, has been a long-standing objective in computer graphics research and has seen resurgence in recent years. Despite impressive progress, the gaits produced by existing controllers fall short of the natural appearance of human locomotion. For example, physics-based walking controllers that do not rely on motion capture data commonly produce walking motion with exaggerated hip flexion which appears more crouched and less fluid than typical human walking.

One likely cause of these differences is the control force generation mechanism. Biological control systems output neural excitation signals, which then generate musculotendon forces that lead to joint torques. The mapping from excitation to torque is highly complex due to variable moment arms, biarticular muscles, and the dependence of musculotendon forces on fiber length and contraction velocity [Zajac 1989]. On the other hand, state-of-the-art bipedal locomotion control methods directly output joint torques, which ignore constraints and energetic costs imposed by muscle anatomy and physiology. Consequently, to accomplish a motion task, controllers often employ torque patterns that are inefficient or even impossible for humans. These biologically implausible torque patterns diminish the naturalness of the resulting gaits.

The goal of our work is to enhance the realism of locomotion gaits exhibited by physically-simulated humanoids without dependence on motion capture data. To this end, we augment the joint-actuated humanoid model with a set of Hill-type musculotendon units (MTUs). These musculotendon units generate torques for the most important degrees-of-freedom (DOFs) during locomotion—the sagittal plane hip, knee, and ankle DOFs. To actuate these muscles, we define biologically-motivated control functions that map the current state of the body (joint angles, muscle fiber lengths, etc.) to excitation signals. The parameters of these functions are optimized to yield gaits that move the character forward without falling down.

While many sets of parameters are capable of achieving this task, the quality of the resulting motion varies significantly among them. To produce gaits that have a high degree of realism, we employ an objective based on minimization of metabolic energy expenditure, thus choosing the most effortless gait that achieves the task [Alexander 2003]. In living humans and animals, metabolic energy expenditure can be estimated by oxygen consumption. In contrast, it is less clear how metabolic energy expenditure should be modeled for simulated characters. A common substitute is the sum of squared joint torques [Schultz and Mombaur 2010], which does not account for the different effort levels required to generate torques in different joints, directions, and body configurations. More nuanced objectives can be learned from inverse optimization [Liu et al. 2005], but are dependent on training data. Our use of biologically-based actuators enables the estimation of metabolic energy expenditure based on the internal state of the MTUs [Anderson 1999]. The result is a locomotion control optimization procedure that minimizes a physiologically-based objective within a parameter space restricted to biologically plausible torque patterns.

We demonstrate the presented approach by optimizing locomotion controllers for a wide range of speeds. For quantitative evaluation, we collected experimental ground truth data from 20 human subjects walking and running at eight speeds on an instrumented treadmill. Much like human locomotion, our controllers utilize significant ankle torque and generate smooth torque trajectories. The resulting gaits match human ground truth to a greater extent than state-of-the-art walking controllers that do not rely on motion capture data. Furthermore, we show that by simply changing the initialization and target velocity, the same optimization procedure leads to running controllers.

2 Related Work

Animation researchers have been interested in the control of locomotion for 3D humanoid characters for almost 20 years [Hodgins et al. 1995; Laszlo et al. 1996; Faloutsos et al. 2001]. One important recent contribution is SIMBICON [Yin et al. 2007], a remarkably robust 3D humanoid locomotion controller based on the balance control of Raibert and Hodgins [1991]. A number of projects have since focused on expanding the controller repertoire for simulated bipeds [Jain et al. 2009; Coros et al. 2010; de Lasa et al. 2010] and on locomotion in complex environments [Mordatch et al. 2010; Wu and Popović 2010].

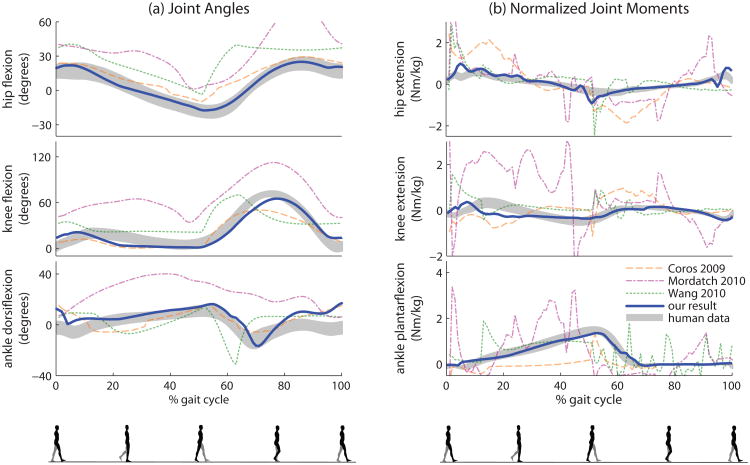
At the same time, efforts have been made to make the synthesized motions more human-like, or “natural.” As discussed by Wang et al. [2009], the original SIMBICON-style controllers tend to produce gaits lacking hip extension with a constant foot orientation. Knee angles lack flexion during swing, but lack extension at heel-strike. More recent controllers improve motions by designing better target trajectories in joint or feature space [Coros et al. 2009; Coros et al. 2010; de Lasa et al. 2010]. While more human-like ankle motions have been produced, differences in the hip and knee angles persist (Figure 6a). Perhaps more importantly, controllers relying on hand-tuned trajectories cannot be easily used to investigate how the control strategies change with respect to new constraints. For example, how would the character's motion style change given a physical disability? Can we synthesize appropriate gaits for older or younger characters?

Figure 6.

Comparison between walking controllers with speeds near 1.0 m/s. The shaded areas represent one standard deviation of the ground truth human data at 1.0 m/s. The hand-tuned SIMBICON-style controller [Coros et al. 2009] matches joint angle data relatively well, but lacks hip extension and relies primarily on hip torques. The robust feature-based controller [Mordatch et al. 2010] walks in a crouch and uses large knee torques. A controller optimized for human-like torque distributions [Wang et al. 2010] fails to generate human-like joint angles and torques. Our result (swalk in Table 1), optimized with a target velocity of 1.0 m/s, best matches human data.

Impressive results have also been achieved by controllers based on tracking motion capture data [da Silva et al. 2008; Muico et al. 2009; Kwon and Hodgins 2010; Lee et al. 2010; Ye and Liu 2010]. However, as with methods that tune joint trajectories or controller parameters by hand, motion capture driven controllers have a limited ability to predict changes in gait.

Alternatively, de novo controller optimization has been used to capture features of human walking [Wang et al. 2009; Wang et al. 2010]. While these methods were shown to produce gaits for a variety of characters and environmental conditions, they do not employ realistic effort measures or biologically-plausible control torques. The resulting torque patterns are highly unnatural (Figure 6b), leading to artifacts such as excessive plantarflexion and sharp changes in kinematics (Figure 6a). In contrast, our approach is to actuate key DOFs using Hill-type MTUs and to measure effort based on metabolic energy expenditure. We demonstrate significantly more human-like kinematic and torque trajectories and show that the same control parameterization and effort objective produce both walking and running.

While locomotion controllers discussed above all operate on joint-actuated models, musculoskeletal models have also been investigated in computer graphics. Such models have been used in facial animation [Waters 1987; Lee et al. 1995; Sifakis et al. 2005], simulation of the human hand [Sueda et al. 2008], neck [Lee and Terzopoulos 2006], torso [Zordan et al. 2006], and the complete upper body [Lee et al. 2009]. Hase et al. [2003] optimize a CPG-based (central pattern generator) locomotion controller [Taga 1995] for 3D musculoskeletal models without tendon or activation dynamics, but their results were not compared to human kinematic and dynamic gait patterns. Moreover, full musculoskeletal models are significantly more difficult to construct than joint-actuated models. Our work demonstrates that measurable increase in locomotion realism can be produced by employing musculotendon actuators for a small subset of the body DOFs.

In the biomechanics literature, abstract planar models have been used to study high-level principles of human locomotion. For example, energy minimization has been suggested as the criterion for humans in determining step length given walking speed [Kuo 2001], as well as in selecting between walking and running [Srinivasan and Ruina 2006]. The spring-loaded inverted pendulum (SLIP) model [Blickhan 1989] has been used as a basis for predicting center-of-mass (COM) movements of human runners [Full and Koditschek 1999]. However, in the absence of knee joints, these models cannot be used to simulate accurate gait patterns. Using a 2D model with knees and musculotendon actuators, Geyer and Herr [2010] showed that patterns of human walking can be generated by a set of simple control laws motivated by muscle reflexes, which inspired our work. We show how their basic ideas can be embedded in a 3D humanoid model and extended to running. Similar 2D models have been used for gait prediction [Ackermann and van den Bogert 2010], and to generate human-like responses to disturbances [Murai and Yamane 2011].

Simulation studies on detailed 3D musculoskeletal models have been employed to understand muscle functions during locomotion tasks [Anderson and Pandy 2001; Liu et al. 2008; Hamner et al. 2010]. In particular, Anderson and Pandy [2001] showed that human-like lower body motor patterns can be found by minimizing metabolic energy expenditure per distance travelled, and we adopt their proposed model of metabolic energy in our work. However, these biomechanical simulations only recovered muscle activation trajectories, and did not produce locomotion controllers that can function beyond the duration of input data.

Finally, our work is complementary of the recent work of Jain and Liu [2011], who showed that simulating soft tissue deformation at contact sites could lead to more robust and realistic character motion. We demonstrate how musculotendon actuators, biologically-motivated control laws, and a more realistic effort term can be used to produce more human-like locomotion gaits.

3 Humanoid Model

Our 3D humanoid model has 30 joint DOFs and mass distributions approximating a 180 cm, 70 kg male [Wang et al. 2010]. From the original model, we adjust the lower-body joint locations and mass distributions to better match human data [Hamner et al. 2010]. We use cylinders to approximate the heel and ball of the foot, which allows for some amount of foot rolling after heel-strike. Unlike previous work, where the model is actuated by setting torques to all joints, we use a model that is partially actuated by Hill-type MTUs (Figure 1). Specifically, control torques for the hip, knee, and ankle joint DOFs in the sagittal plane—key DOFs for gait analysis [Perry and Burnfield 2010]—are exclusively generated by eight MTUs in each leg. In addition, soft joint limit torques as defined by Geyer and Herr [2010] are applied to these DOFs.

Figure 1.

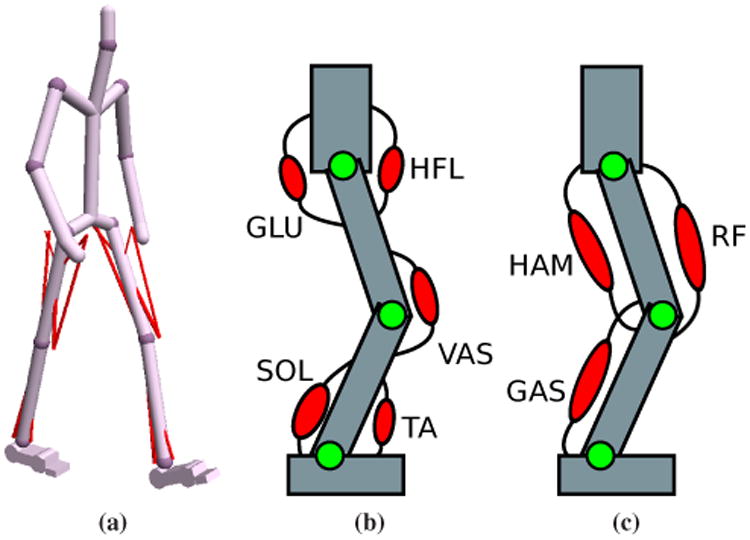
Humanoid model. (a) Sixteen Hill-type MTUs, shown in red, generate torques for the hips, knees, and ankles. Note that the back joint is not rendered for aesthetic reasons. (b) Five uniarticular muscles in each leg produce flexion or extension torques at single joints. (c) Three biarticular muscles in each leg generate torques at pairs of joints. See Section 3 for details.

Figure 1b depicts locations of the uniarticular MTUs and the joints they actuate. The hip joint is extended by the gluteal muscles (GLU) and flexed by the hip flexor muscles (HFL), while the knee joint is extended by the vasti (VAS). The tibialis anterior (TA) and the soleus (SOL) generate dorsiflexion and plantarflexion torques at the ankle, respectively. The biarticular MTUs (Figure 1c) supply torques to two joints simultaneously. We include the hamstring (HAM), which extends the hip and flexes the knee, the rectus femoris (RF), which flexes the hip and extends the knee, and the gastrocnemius (GAS), which flexes the knee and plantarflexes the ankle. The choice of muscles is based on the planar model proposed by Geyer and Herr [2010]. We have added the rectus femoris since we found that it improves the walking knee flexion profile during swing when compared to human data.

3.1 Musculotendon Model

We employ a Hill-type model [Zajac 1989], where each MTU consists of three elements: contractile, parallel-elastic, and serial-elastic. Conceptually, the contractile element (CE) models muscle fibers that can actively generate force (F^CE) depending on the current activation level (a). The parallel-elastic element (PE) models passive forces (F^PE) generated by the muscle fibers, while the serial-elastic element (SE) models the tendon.

In particular, given the length and velocity of CE (l^CE, v^CE), as well as the current muscle activation level (a), we can compute the MTU force (F^MTU) as follows:

$$\begin{array}{c}{F}^{\text{MTU}}=F^{\text{CE}}+F^{\text{PE}},\\ F^{\text{CE}}=a{F}^0{f}_l({\stackrel{\sim }{l}}^{\text{CE}})f_v({\stackrel{\sim }{v}}^{\text{CE}}),\end{array}$$

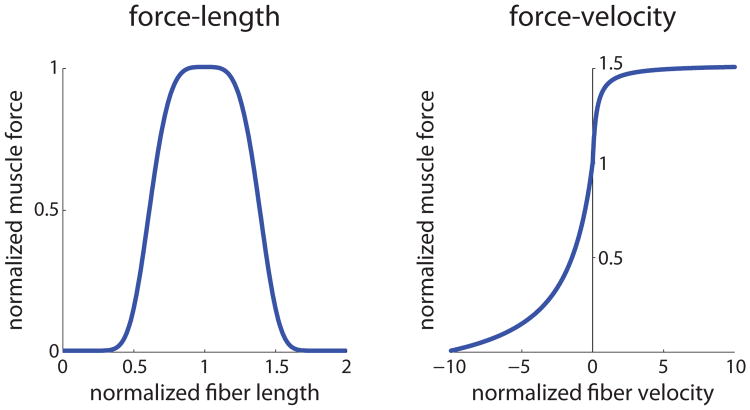
where l̃^CE = l^CE/l^opt and ṽ^CE = v^CE/l^opt. F⁰ and l^opt are muscle-specific maximum isometric force and optimal fiber length parameters. f_l and f_v are the force-length and force-velocity curves (Figure 3). The computation of F^PE and the analytic forms of f_l and f_v are described in the supplemental material.

Figure 3.

Muscle force-length and force-velocity curves used in our model. The force generating capacity of a muscle is dependent on the length of muscle fibers (force-length relationship) and the velocity of muscle fibers (force-velocity relationship). The force-length curve shows that muscles can generate force more efficiently near l^opt, and the force-velocity curve shows that muscles lose ability to generate force as the magnitude of contraction velocity increases.

Intuitively, f_l models the fact that muscles can generate force more efficiently near l^opt, and f_v captures how the muscle loses its ability to generate force as the contraction velocity increases [Zajac 1989]. As to be discussed in Section 4.1, the nonlinearity introduced by these relations is crucial for how simple control laws for muscle excitation can lead to complex force and torque trajectories.

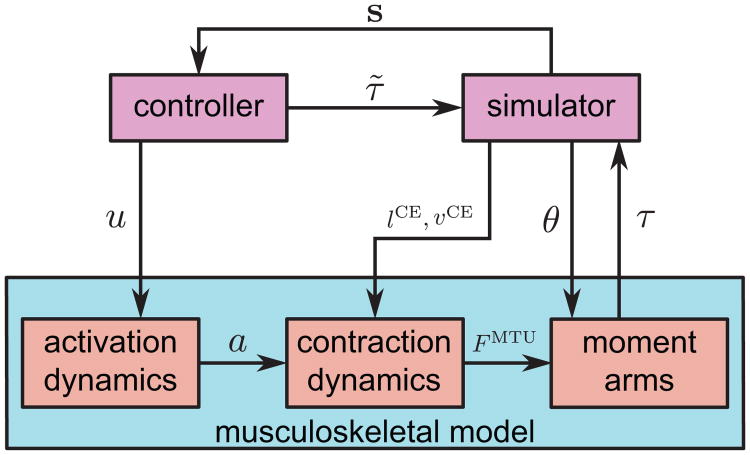
Figure 2 illustrates how the musculotendon model interacts with the controller and the simulator. The controller outputs neural excitation signals (u), which are converted to muscle activations (a). The conversion does not occur instantaneously and is referred to as activation dynamics. The dynamics is modeled by a first-order differential equation [Zajac 1989; Geyer et al. 2003], which can be integrated by a_t+1 = 100h(u_t − a_t) + a_t, where h is the stepsize (1/2400 s) and a_t and u_t are the muscle activation and excitation values at the t-th timestep. A step-response graph for the activation dynamics, as well as details on the l^CE and v^CE computations (contraction dynamics) are given in the supplemental material.

Figure 2.

Relationship between musculoskeletal model, controller, and simulator. The controller takes as input the simulation state (body position, joint configuration, contact state, etc.), denoted by s and outputs neural excitation signals (u) and torques (τ̃). Excitation signals are converted to muscle activations (a), which are then converted to torques τ for the hip, knee, and ankle sagittal DOFs. The remaining DOFs are directly actuated by τ̃. The excitation to torque mapping is a function of the contractile element kinematics (l^CE, v^CE) and hip, knee, and ankle joint configuration (θ).

The joint torques generated by a given MTU is a function of the current body configuration. A simple variable moment arm model is assumed for MTUs attached to the knee or ankle: $\tau =r_{j}cos(\theta -{\phi }_j^M)F^{\text{MTU}}$, where θ is the current knee or ankle angle in the sagittal plane, and r_j is the maximum MTU-joint moment arm, which occurs at the joint angle ${\phi }_j^M$. MTUs attached to the hip are assumed to have a constant moment arm: τ = r_jF^MTU.

The total lower extremity joint torques in the sagittal plane are obtained by summing over contributions from all relevant muscles:

$$\begin{array}{c}{\tau }^{\text{hip}}={\tau }_{\text{GLU}}+{\tau }_{\text{HAM}}^{\text{hip}}-{\tau }_{\text{HFL}}-{\tau }_{\text{RF}}^{\text{hip}},\\ {\tau }^{\text{knee}}={\tau }_{\text{RF}}^{\text{knee}}+{\tau }_{\text{VAS}}-{\tau }_{\text{HAM}}^{\text{knee}}-{\tau }_{\text{GAS}}^{\text{knee}},\\ {\tau }^{\text{ankle}}={\tau }_{\text{GAS}}^{\text{knee}}+{\tau }_{\text{SOL}}-{\tau }_{\text{TA}}.\end{array}$$

4 Control Parameterization

The main part of our control algorithm consists of functions that determine muscle excitation values for each of the lower body MTUs, which actuate the hip, knee, and ankle DOFs in the sagittal plane. For the upper body and the remaining DOFs in the lower body, we rely on a pose-graph controller [Yin et al. 2007].

4.1 Muscle Control

Our control laws for the actuators are based on the muscle-reflex controller introduced by Geyer and Herr [2010]. We will describe the basic formulation and our modifications in this section. Two different sets of control laws apply for each muscle, depending on whether the leg is in stance or swing phase (i.e., foot is on the ground or not). We further define a swing initiation state within the stance phase, and a stance preparation state within the swing phase, where control laws for a subset of MTUs are modified (Figure 4).

Figure 4.

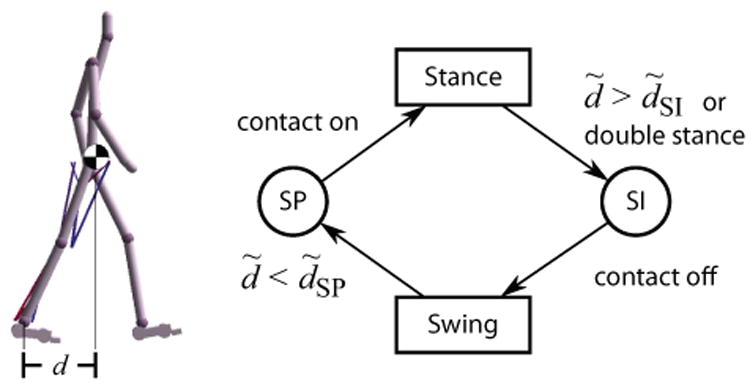
High-level control states for each leg. The stance and swing phases are triggered by ground contact conditions. The signed horizontal distance between the COM and the ankle (d) normalized by leg length (d̃) is compared against two threshold parameters (d̃_SI, d̃_SP) to start swing initiation (SI) and stance preparation (SP), respectively. SI can also be started when the opposing leg makes ground contact (double stance).

The control laws map time-delayed features of the body to muscle excitation signals. The time-delay (Δt) models the time for neural signal propagation, set to 5 ms for MTUs connected to the hip, 20 ms for MTUs connected to the ankle, 10 ms for the VAS and ground contact [Geyer and Herr 2010]. Body features include MTU force, fiber length, joint angle, and segment orientation. Depending on the input feature, three different mappings are defined: positive force feedback, positive length feedback, and muscle-driven proportional derivative (PD) control. These mappings serve as building blocks for the control laws, and we discuss each in turn in this section.

Positive force feedback

Given MTU m, the positive force feedback law is defined as

$$u_m^F=G_m{\stackrel{\sim }{F}}_m^{\text{MTU}}(t-\mathrm{\Delta }{t}_m),$$

where ${\stackrel{\sim }{F}}_m^{\text{MTU}}(t-\mathrm{\Delta }{t}_m)$ is the MTU force normalized by $F_m^0$ with a time-delay of Δt_m. The only free parameter is a positive gain constant G_m, which is different for each MTU. Note that ${\stackrel{\sim }{F}}_m^{\text{MTU}}$ cannot increase indefinitely since the muscle's force generation capacity depends nonlinearly on the length and contraction velocity of the muscle fiber. As ${\stackrel{\sim }{F}}_m^{\text{MTU}}$ starts to decrease due to muscle physiology, $u_m^F$ starts to decrease as well. The force feedback is the main source of activation to the SOL, GAS, and VAS muscles during the stance phase. Figure 5 shows the activation and fiber length of GAS during the stance phase. We can see that $u_{\text{GAS}}^F$ produces a positive feedback during mid-stance, when the muscle activation does not produce a significant change in muscle fiber length, as the foot is planted on the ground. As the heel loses ground contact in late stance, the same muscle activation rapidly shortens the fiber length, which reduces force output and the activation through $u_{\text{GAS}}^F$.

Figure 5.

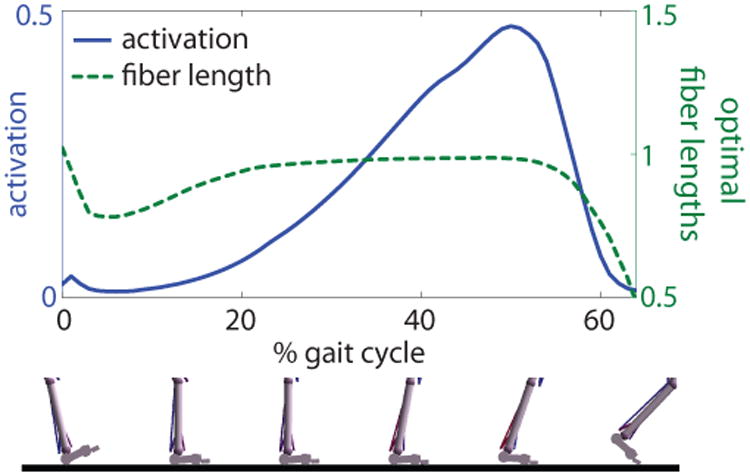
Effects of muscle physiology on activation illustrated by GAS activation and normalized fiber length during the stance phase. Note the nonlinearity of the activation curve generated by the linear force feedback control law (Section 4.1). While the foot is flat on the ground during mid-stance, GAS activation does not significantly change the fiber length, and force feedback leads to an activation build-up. As heel loses contact during late-stance, the fiber rapidly shortens and reduces f_l and f_v (Figure 3). As the generated force decreases, the same force feedback leads to a drop-off in activation.

Positive length feedback

Positive length feedback is defined as

$$u_m^L={\left\{G_m\right({\stackrel{\sim }{l}}_m^{\text{CE}}(t-\mathrm{\Delta }{t}_m)-H_m\left)\right\}}_{+},$$

where ${\stackrel{\sim }{l}}_m^{\text{CE}}(t-\mathrm{\Delta }{t}_m)$ is the length of the muscle fiber normalized by the $l_m^{\text{opt}}$ with a time-delay of Δt_m. G_m and H_m are free positive parameters and {}_± means only positive or negative values (0 otherwise). The positive length feedback effectively models a stretch reflex, which activates the muscle when the fiber is stretched beyond a fixed length. $u_m^L$ is most useful during the swing phase, as the TA must be activated to dorsiflex so that toe-stubbing can be avoided. In addition, the HFL relies on length feedback to generate hip flexion torque during early swing, especially during running.

Muscle-driven PD control

We also define a muscle-driven PD control law with respect to an angular feature θ as

$$u_m^{\theta }=\left|{\{K_m(\theta (t-\mathrm{\Delta }{t}_m)-{\theta }_m)+D_m\dot{\theta }(t-\mathrm{\Delta }{t}_m)\}}_{\pm }\right|,$$

where K_m, D_m, θ_m are free parameters of the PD-controller. The braces sign is positive if torque generated by m is in the opposing direction of θ—e.g., if m is the hip extensor and θ is the hip flexion angle—and negative otherwise. Much like the standard torque-based PD-controller, the muscle-driven PD control aims to adjust θ towards the target angle θ_m while damping its velocity. However, unlike the standard PD-controller, muscles can only activate after a time-delay and each muscle can only generate forces to rotate the angular DOF in one direction. The PD-control laws are employed by the hip muscles during the stance phase to maintain the global upper body orientation, as well as during stance preparation to prepare for ground contact.

4.2 Stance Phase

Each muscle has an initial constant excitation, or pre-stimulation value p_m. These values are initialized close to zero, but are then optimized. The SOL and GAS both rely on positive force feedback and are the main sources of torque during walking. The TA ensures foot clearance during swing using a length feedback ( $u_{\text{TA}}^L$), but the activation is suppressed during stance in proportion to the current force generated from SOL. The suppression allows the generated TA activation patterns to better match human data during locomotion. The force feedback on the VAS creates a strong knee extension torque following ground contact, but excitation is suppressed when the knee flexion angle (θ_k) is extended below an offset ( ${\theta }_k^{\text{off}}$) with an extension velocity (θ̇_k < 0). The suppression prevents hyperextension of the knee during mid-stance. Using muscle-driven PD control laws, the HAM, GLU, and HFL are responsible for maintaining the global orientation of the upper body (Θ), defined as the vector between the COM of the upper body and the COM of the pelvis projected onto the sagittal plane. During double stance, these control laws are only active for the leading leg, denoted as ${\{u_m^{\mathrm{\Theta }}\}}_{\text{lead}}$.

Specifically, control laws during the stance phase are as follows:

$$\begin{array}{c}{u}_{\text{SOL}}=p_{\text{SOL}}+u_{\text{SOL}}^F,\\ u_{\text{TA}}=p_{\text{TA}}+u_{\text{TA}}^L-u_{\text{SOL}}^F,\\ u_{\text{GAS}}=p_{\text{GAS}}+u_{\text{GAS}}^F,\\ u_{\text{VAS}}=p_{\text{VAS}}+u_{\text{VAS}}^F+{\{k_{\theta }({\theta }_k(t-\mathrm{\Delta }{t}_{\text{VAS}})-{\theta }_k^{\text{off}})\}}_{-,{\dot{\theta }}_k<0},\\ u_{\text{HAM}}=p_{\text{HAM}}+{\{u_{\text{HAM}}^{\mathrm{\Theta }}\}}_{\text{lead}},\\ u_{\text{RF}}=p_{\text{RF}},\\ u_{\text{GLU}}=p_{\text{GLU}}+{\{u_{\text{GLU}}^{\mathrm{\Theta }}\}}_{\text{lead}},\\ u_{\text{HFL}}=p_{\text{HFL}}+{\{u_{\text{HFL}}^{\mathrm{\Theta }}\}}_{\text{lead}}.\end{array}$$

Towards the end of the stance phase, the controller enters into the swing initiation, which begins when either the signed horizontal distance between the COM and the ankle normalized by leg length exceeds a constant threshold d̃ > d̃_SI or if the opposing leg has entered into stance phase (double stance). During swing initiation, constant excitation values between 0 and 1 (set during optimization) are added and subtracted to the VAS, RF, GLU, and HFL:

$$\begin{array}{c}{u}_{\text{VAS}}=u_{\text{VAS}}-s_{\text{VAS}},\\ u_{\text{RF}}=u_{\text{RF}}+s_{\text{RF}},\\ u_{\text{GLU}}=u_{\text{GLU}}-s_{\text{GLU}},\\ u_{\text{HFL}}=u_{\text{HFL}}+s_{\text{HFL}}.\end{array}$$

The combination of HFL and GLU excitations creates a large hip flexion torque, while the VAS and RF excitations effectively allow the optimizer to adjust the initial knee swing angle and velocity.

Two main differences between our stance phase control laws compared to Geyer and Herr [2010] lie in how the swing initiation state functions. First, for running we found it necessary to enter into swing initiation using the d̃ > d̃_SI condition, rather than just wait for double stance. Second, we found it unnecessary to modulate the muscle-driven PD-control laws in the hip by ground reaction forces. Instead, the responsibility to maintain upper body orientation is always assigned to the lead leg.

4.3 Swing Phase

Much like in the stance phase, each muscle has an initial constant excitation value (q_m). The leg motion relies significantly on passive dynamics during the swing phase [Collins et al. 2005], as most muscles are only excited at low levels. The main exceptions are the TA, which maintains the length feedback ( $u_{\text{TA}}^L$) to avoid toe-stubbing, and the HAM, which is activated at late swing phase to prevent the knee from being overextended before landing. The HFL introduces a hip flexion torque through a length feedback, which is suppressed when the HAM is stretched in during late swing. The amount of excitation in the HFL also depends on the value of upper body lean at the beginning of the swing phase (Θ_lto): the further the upper body leans forward compared to the reference lean angle (Θ_d), the more excitation is supplied from the HFL during the swing phase. Note that Θ_d is the same as the target angle in $u_{\text{HFL}}^{\mathrm{\Theta }}$.

Non-constant control laws during the swing phase are as follows:

$$\begin{array}{c}{u}_{\text{TA}}=q_{\text{TA}}+u_{\text{TA}}^L,\\ u_{\text{HAM}}=q_{\text{HAM}}+u_{\text{HAM}}^F,\\ u_{\text{GLU}}=q_{\text{GLU}}+u_{\text{GLU}}^F,\\ u_{\text{HFL}}=q_{\text{HFL}}+u_{\text{HFL}}^L-u_{\text{HAM}}^L+k_{\mathrm{\Theta }}({\mathrm{\Theta }}_{\text{lto}}-{\mathrm{\Theta }}_d).\end{array}$$

The controller enters into the stance preparation when d̃ < d̃_SP, where the swing leg enters into a PD-control mode. The GLU, HFL, and VAS work to guide the hip and knee joints toward a desired pose to prepare for ground contact:

$$\begin{array}{c}{u}_{\text{VAS}}=q_{\text{VAS}}+u_{\text{VAS}}^{{\theta }_k},\\ u_{\text{GLU}}=q_{\text{GLU}}+u_{\text{GLU}}^{{\theta }_h},\\ u_{\text{HFL}}=q_{\text{HFL}}+u_{\text{HFL}}^{{\theta }_h}.\end{array}$$

A single desired hip target angle (θ_h) is adjusted according to the SIMBICON balance feedback law [Yin et al. 2007] and is shared by both the GLU and HFL. We found the addition of the stance preparation state to be important for discovering running gaits. The balance feedback law allows robust control strategies to be found in difficult environments (e.g., being pushed by random forces).

4.4 Out-of-Plane and Upperbody Control

The rest of the DOFs are controlled using standard joint-space PD-controllers with state-dependent parameters. Following Wang et al. [2010], the target features for the ankle and hip joints in the coronal plane are the global foot and pelvis orientations, respectively. The coronal swing hip target angles follow the same feedback law as θ_h. Additionally, we set the toe joint to be a spring with spring constant of 30 Nm/rad, target angle 0, and no damping. Unlike in previous work, where a gait cycle is broken down into four states, only two are needed (triggered by left/right foot-strike) since DOFs with the most complex activities are actuated by muscles.

Our upper body control also largely follows Wang et al. [2010], with the exception that the target feature of our back joint in the coronal plane is the global orientation of the torso instead of the local joint angle between the torso and the pelvis. This global target allows our model to better keep the head upright during locomotion. We fix the spring and damper constants for all arm joints to 30 Nm/rad and 3 Nms/rad, respectively, with target angles set to 0. We found that more human-like arm swing can be generated by relating the elbow and shoulder target angles as ${\theta }_s^l={\alpha }_{\text{arm}}({\theta }_h^l-{\theta }_h^r)+\beta {\theta }_e^d$ and ${\varphi }_s^l=\gamma {\theta }_e^d$, where ${\theta }_s^l$ and ${\varphi }_s^l$ are the shoulder angles in the sagittal and transverse planes, respectively; ${\theta }_h^l$ and ${\theta }_h^r$ are the current left and right sagittal hip angles; ${\theta }_e^d$ is the desired elbow angle, β, γ are constants chosen based on human motion data (see supplemental material), and α_arm is a scale constant that determines the magnitude of the arm swing. This formulation captures the tendency to rotate the shoulder backwards and inwards while bending the elbow. The scale constant and the desired elbow angle are among the parameters set by optimization, as described in the next section.

5 Optimization

The control algorithm specified in Section 4 has a large number of parameters, which we set by optimization [Wang et al. 2010]. More specifically, each of the $u_m^F$, $u_m^L$, and $u_m^{\theta }$ laws have one, two, and three parameters, respectively. There are 56 parameters in total (30 stance, 26 swing) for the MTU control laws. For the upper body and the non-sagittal DOFs in the lower body, we optimize the PD-control parameters (spring-damper constants, target angle, balance feedback) for all joints except for arms, where only a target elbow angle and a swing scale parameter are optimized (Section 4.4). When combined with 33 free parameters describing the initial state of the simulation, 124 parameters (w) fully define a simulated motion {s₁ … s_T} over T timesteps. We optimize control parameters and the initial state using Covariance Matrix Adaptation (CMA) [Hansen 2006], with stepsize σ = 0.005 and 50 samples per iteration.

The optimization aims to maximize the following return function:

$$R(\mathbf{w})=(\sum _{t=1}^{T}r({\mathbf{s}}_t))-w_e{J}_{\text{effort}}.$$

Here r is a scalar reward function of the current state s_t, J_effort measures the effort of the synthesized motion, and w_e is set to 0.004 divided by the mass of the model, motivated by Wang et al. [2010].

The reward is defined as the negative sum of a number of task terms (i.e., r(s_t) = − Σ_i K_i(s_t)), which can be thought of as high-priority goals that the controller must satisfy while minimizing effort. In practice, these terms are weighed more heavily than the effort term. The tasks include moving the COM forward at a target velocity while not falling down for 10 seconds, and maintaining head stability and upper body orientation. The task terms are based on Wang et al. [2010] and are defined in the supplemental material. Note that unlike in previous work, we did not need to include human-like speed to step-length ratio and minimal angular momentum about the COM as task terms.

5.1 Effort Term

The main contribution to our effort measurement is the total rate of metabolic energy expenditure (Ė) over all MTUs. To quantify Ė, we implement a model described by Anderson [1999], which is later expanded by Bhargava et al. [2004]. The rate of metabolic energy expenditure for a given muscle can be modeled as the sum of heat released and mechanical work done by the muscle:

$$\dot{E}=\dot{A}+\dot{M}+\dot{S}+\dot{W},$$

where Ȧ is the muscle activation heat rate, Ṁ is the muscle maintenance heat rate, Ṡ is the muscle shortening heat rate, and Ẇ is the positive mechanical work rate.

The muscle activation heat rate models the rate of energy that is converted to heat by a muscle given a certain level of activation, and is a function of both the mass of the muscle and the excitation signal. The maintenance heat rate similarly models the heat rate for the muscle to maintain contraction at a certain level, and depends additionally on the current fiber length. Specifically,

$$\dot{A}=\text{mass}·f_A(u)\text{and}\dot{M}=\text{mass}·g({\stackrel{\sim }{l}}^{\text{CE}})f_M(a),$$

where mass is the muscle mass and l̃^CE is the normalized muscle fiber length. The forms of f_A, f_M, and g are described in the supplemental material. The dependence on muscle mass captures the fact that while larger muscles are generally capable of generating more force, they are also more costly to use.

The muscle shortening heat rate models the heat generated by the shortening of muscle fibers and is proportional to the current force generated by the muscle and the shortening velocity:

$$\dot{S}=0.25F^{\text{MTU}}{\{-v^{\text{CE}}\}}_{+}.$$

Finally, the positive mechanical work rate is the mechanical power produced by the active element of the MTU during contraction:

$$\dot{W}=F^{\text{CE}}{\{-v^{\text{CE}}\}}_{+}.$$

Note that Ṡ is close to one-quarter of Ẇ. The difference is that F^MTU is the net force (both active and passive) produced in the MTU, while F^CE is only the active force.

Let Ė_{m, t} denote the rate of metabolic energy expenditure computed for MTU m at timestep t. We define the average rate of metabolic expenditure due to MTUs as

$$J_M=\dot{B}+\frac{1}{T}\sum _{t=1}^T\sum _{m\in \mathcal{M}}{\dot{E}}_{m,t},$$

where Ḃ is the basal metabolic energy rate, set to 1.51 times body mass [Anderson 1999]. (ℳ) is the set of all sixteen muscles defined in the model.

Additionally, torques generated by the PD-controllers in the rest of the DOFs are penalized by the average sum of torque squared objective:

$$J_R=\frac{1}{T}\sum _{t=1}^T\sum _{j\in {\mathcal{Q}}_r}{\tau }_{j,t}^2,$$

where _r is the set of all joint DOFs except for the sagittal hips, knees, and ankles. We similarly define J_L to penalize the average sum of squared soft joint limit torques for the hip, knee, and ankle joints, specified in Geyer and Herr [2010].

The overall effort of a particular motion is defined as J_effort = w_MJ_M + w_RJ_R + w_LJ_L, a weighted sum between the terms. We empirically set w_M = 100, w_R = 1, and w_L = 0.5 for all experiments.

6 Experiments

The simulations were implemented using Open Dynamics Engine (ODE) with a frequency of 2400 Hz. We simulate for T = 24000 timesteps (10 s) in each evaluation. The optimization is terminated after 3000 iterations, which takes approximately 10 hours using 50 compute cores on a cluster of Dell PowerEdge 1950 servers. An optimized controller can be simulated at interactive rates using standard hardware. We initialize walking parameters of the MTU control laws based on hand-tuned values for 2D walking from Geyer and Herr [2010]. For running, we double the initial gain parameters of GAS and SOL, and initialize ${\theta }_e^d$ to set the elbow in a bent position. The precise initialization values are provided in the supplemental material.

6.1 Ground Truth Data

Human joint moment (torque) curves during locomotion can be computed from motion capture and ground reaction force data. In this work we are particularly interested in comparing our results to the mean and standard deviation curves for the sagittal hip, knee, and ankle joints for multiple subjects over multiple walking and running speeds. While such data for walking is readily available [Perry and Burnfield 2010], only scattered data are available for running [Novacheck 1998; Yokozawa et al. 2007; Hamner et al. 2010]. Instead, we acquired our own ground truth data using an instrumented treadmill with 20 subjects. This data is available from http://graphics.stanford.edu/projects/bio-locomotion.

We acquired kinematics and dynamics data for a range of walking and running speeds (from 1.0 m/s to 5.0 m/s). The supplemental material includes angle and moment plots for all speeds, as well as details on our data collection. Comparing the mean curves for walking speeds from 1.0 m/s to 1.75 m/s, we found that the range of hip angles in our subjects during walking increased by approximately 10°, while the location of maximum ankle plantarflexion shifted slightly earlier in the gait cycle. More pronounced differences are present between running data at different speeds. The hip angle range and maximum knee flexion both increased by 30° as running speed increased from 2.0 m/s to 5.0 m/s, while locations of both the maximum hip extension and ankle plantarflexion shifted earlier by 5% and 10%, respectively. Both the hip and ankle torque outputs increased with speed, though the ankle torque curves did not differ significantly between 4.0 m/s and 5.0 m/s.

6.2 Walking Controllers

We first optimized for a normal walking controller (referred to below as nwalk) with a target velocity of 1.25 m/s, which is approximately the human self-selected walking speed. Initializing with the normal controller, we then optimized for a 1.0 m/s slow walk controller (swalk) and a 1.5 m/s fast walk controller (fwalk). A 1.75 m/s very fast walk controller (vfwalk) is optimized by initializing from fwalk.

Comparison to ground truth

Supplemental figures indicate that our kinematic patterns generally agree with data over a range of speeds and especially at lower speeds. Two main discrepancies are the timing of knee flexion during stance, and ankle dorsiflexion before heel-strike. For higher speeds, the maximum knee flexion angle is lower than human data, and the location of maximum ankle plantarflexion occurs earlier in the gait cycle. All angle and moment curves shown are averaged over multiple cycles. Note that we found time-delays to be important for generating human-like motion given our control model. Optimizing without activation dynamics and with Δt_m = 0 for all MTUs results in a solution where ankle torques build up too quickly in the stance phase, leading to shorter step-lengths compared to human data.

Figure 6a shows the hip, knee, and ankle angles of walking data generated by our 1.0 m/s controller (swalk) compared to controllers of similar speeds presented by previous contributions [Coros et al. 2009; Mordatch et al. 2010; Wang et al. 2010], as well as human data at 1.0 m/s. A major artifact from all of the previous works is the lack of hip extension during mid-gait, which does not occur in our result. The feature-based controller of Mordatch et al. [2010] is robust and flexible, but their basic walking gait shows an obvious crouch. Our result also exhibits a range of knee motion more similar to humans compared to previous works. However, all four controllers show excessive dorsiflexion before heel-strike.

An important advantage of optimization over hand-tuning is the ability to create controllers based on high-level objectives such as walking speed. As demonstrated in supplemental material, our controllers generate more human-like gaits compared to optimized controllers from Wang et al. [2010] at faster walking speeds (Wang10f, Wang10vf) as well. An obvious artifact of all controllers from Wang et al. [2010] is the excessive plantarflexion in the early swing phase, which is not present in our result.¹

Examining differences in torque generation, we can see that the controller presented by Coros et al. [2009] does not employ a human-like torque distribution between the joints (Figure 6b). In particular, as was the case in SIMBICON [Yin et al. 2007], the gait is largely hip-driven, as can be seen by the large hip torques and small ankle torques compared to human data. In turn, controllers from Wang et al. [2010] generated larger amounts of ankle torque by optimizing for a human-like torque ratio, but did not come close to matching the shapes of human torque data. Note that our work does not exhibit unnatural torque spikes due to state switching that are present in the previous works.

Table 1 shows quantitative comparisons between the controllers. We compute the mean standard score against human data over 100 evenly spaced points on the curves. Note that our results show the lowest average standard score for all speeds.

Table 1. Quantitative comparison of walking controllers with human kinematics data in standard score (average number of standard deviations away from the mean).

ref. speed	controller	hip	knee	ankle	average
1.0 m/s	Coros09	1.63	2.04	1.54	1.73
	Mordatch10	5.80	8.10	6.36	6.75
	Wang10s	4.17	3.71	2.40	3.42
	swalk	0.41	1.28	1.41	1.04
1.25 m/s	min_torque	1.35	1.79	4.32	2.49
	min_act	1.51	3.20	3.74	2.82
	nwalk	0.43	1.79	1.34	1.19
1.5 m/s	Wang10f	3.03	3.38	3.46	3.29
	fwalk	0.79	2.53	1.28	1.28
1.75 m/s	Wang10vf	1.37	2.60	3.32	2.43
	vfwalk	1.31	3.19	1.69	2.06

Evaluation of objective

We evaluate the metabolic energy expenditure objective described in Section 5 against the simple sum of squared torques objective, by redefining

$$J_M=\frac{1}{T}{\sum }_{t=1}^T{\sum }_{j\in {\mathcal{Q}}_s}{\tau }_{j,t}^2,$$

where 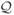_s is the set of sagittal hip, knee, and ankle DOFs (with w_m = 5). Controllers optimized for each of the two objectives (nwalk, min_torque) are demonstrated in the accompanying video. For this comparison, we use a target speed of 1.25 m/s, which is the same as nwalk. The gait resulting from torque minimization exhibits too much knee flexion during the swing phase and too much dorsiflexion before heel-strike. Closer examination reveals that the TA muscle, responsible for dorsiflexion, is highly activated throughout the gait when only torque is being minimized. Since the foot is a relatively light link, the actual magnitude of the dorsiflexion torque is not large even when the TA is fully activated, therefore it does not incur a large penalty in the torque objective. In contrast, the metabolic energy objective captures the fact that activating and maintaining contraction of TA generates significant heat and should therefore be discouraged. Note that unlike dorsiflexion torques, large ankle plantarflexion torques can be generated with relative ease. Simply increasing the penalty on ankle torques does not account for the effort difference between generating torques in different directions.

A simple objective that could approximate effort given a musculoskeletal model is the sum of squared muscle activations, which is commonly used in static optimization—a technique for recovering activations given motion capture and force plate data [Anderson 1999]. However, as demonstrated in the accompanying video, this objective also does not lead to faithful walking kinematics. Here we define

$$J_M=\frac{1}{T}{\sum }_{t=1}^T{\sum }_{m\in \mathcal{M}}{a}_{m,t}^2,$$

where ℳ is the set of MTUs, and a_m,t is the activation level of MTU m at timestep t (with w_M = 60000). In the gait produced by the controller that minimizes this objective (min_act), activations from the GAS/SOL are significantly lowered, while activations from VAS are increased. While the total amount of activations is reduced, the resulting gait walks in a crouch and relies heavily on the knee.

Table 1 includes average standard score values compared against human data at 1.25 m/s. Controllers optimized using the torque and activation objectives both exhibit large errors compared to nwalk, especially at the ankle joint. While noticeable kinematic differences are seen in the gaits produced by different objectives, the torque curves are smooth due to the muscle model and the control parameterization.

Changing muscle properties

The plantarflexors (GAS and SOL) are largely responsible for forward propulsion in normal walking [Liu etal. 2008]. We found that weakening the GAS and SOL to a quarter of their original strength, while keeping all other objectives identical (target speed 1.25 m/s), results in a mild crouch gait characterized by excessive knee flexion (see accompanying video). Our result suggests that under the condition of weakened plantarflexors, the mild crouch gait may be metabolically efficient compared to other gait choices. The crouch gait is commonly found in cerebral palsy patients, and weakness in the plantarflexors is one of many factors thought to contribute to the gait abnormality [Steele etal. 2010].

Knee hyperextension, another common gait abnormality, causes patients to vault the body forward over the extended stance limb, and can result from hamstring lengthening surgery in cerebral palsy patients [Kay et al. 2002]. In the accompanying video, we show that our optimization indeed results in a mild hyperextension gait after weakening HAM to a quarter of its original strength, with a minimum knee flexion angle of 2°. Note that the same angle for the gait generated by nwalk is 9°. Another cause of knee hyperextension is weakened quadriceps, which can be simulated by weakening the VAS in our model. We found that weakening the VAS to one-tenth of its original strength leads to a motion similar to quadriceps avoidance gait, which is seen in patients with quadriceps weakness and anterior cruciate ligament (ACL) deficiency [Timoney et al. 1993].

6.3 Running Controllers

Our controller architecture and objective function is not limited or specific to walking alone. By simply changing the target velocity and initialization (changing the initial velocity from 1.3 m/s to 3.05 m/s, doubling the initial force feedback gains for GAS and SOL, and bending the elbow), the same procedure yields running controllers, without any modifications to the control parameterization. In contrast, previous optimization-based control synthesis methods required including torque ratios specific to walking as part of the objective [Wang et al. 2009] or adding spring elements for running [Wu and Popović 2010]. Our unified approach to both walking and running is consistent with the view that humans select between walking and running by minimizing energy at different speeds [Srinivasan and Ruina 2006].

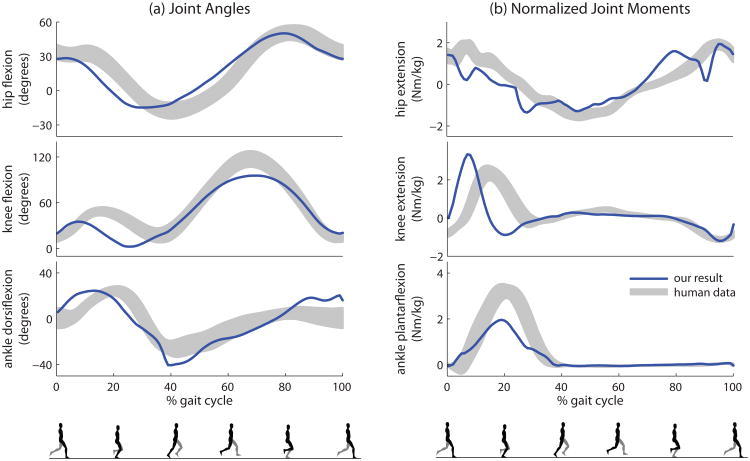
We compare running motions generated by our controller at 4.0 m/s with human running data in Figure 7. Our running kinematic results do not match human data as well as walking, though the basic features of the curves are still present. A main discrepancy is that our hip and knee joints both reach maximum extension earlier than human running data. Similar to our walking results, our knee joint flexes less during the stance phase compared to humans. Our maximum knee flexion is also lower than human data.

Figure 7.

Comparison of running. Our result is optimized with a target velocity of 4.0 m/s. The shaded regions represent one standard deviation of the human running data at 4.0 m/s.

Figure 7b reveals possible causes for the kinematic differences. Our knee extension torque reaches maximum earlier than human data, which can cause the knee to extend too quickly during the stance phase. On the other hand, our plantarflexion torques have a lower peak than human data, resulting in a strategy that relies on the knees more than the ankles. In the supplemental material and the video, we include results for running at speeds ranging from 3.0 m/s to 5.0 m/s. The faster running results are optimized sequentially in 0.5 m/s increments (e.g., 4.0 m/s initialized from 3.5 m/s). As the target velocity increases, finding a satisfactory local minimum appears more difficult. We use 100 samples per iteration and a 0.25 m/s optimization increment for speeds over 4.0 m/s.

6.4 Robustness

In this work, we have chosen to focus on reproducing humanlike kinematics and torque trajectories. Likely due to our modeling of human-like torque generation and activation delays, our controllers cannot tolerate nearly as much external force as recently developed controllers for purely joint-actuated characters [Mordatch et al. 2010; Wang et al. 2010]. However, we can still follow Wang et al. [2010] and optimize explicitly for controllers that can deal with external forces. In particular, we optimized controllers that can tolerate 100 N, 0.4 s pushes to the torso. These controllers chose to walk in a stiff crouch gait, with lowered COM and a constantly dorsiflexed ankle to ensure foot clearance (see accompanying video). Note that 100 N is approximately the weight of a 10 kg object, a significant push to a human. Comparatively, the corresponding 100 N controller presented by Wang et al. [2010], who did not model biological torque generation constraints, did not employ a gait that is significantly different from the undisturbed baseline controller. We also optimized for a 4.0 m/s running controller tolerant of 50 N, 0.4 s pushes, as shown in the video.

7 Discussion

We have presented a biologically-motivated control parameterization that can be used to automatically generate 3D human-like walking and running controllers of different speeds. Controllers are optimized to satisfy a set of high-level task terms while minimizing an effort term based on modeling the rate of metabolic energy expenditure. Notably, walking and running emerge from the same optimization process simply by changing the target velocity and initialization. Through comparisons to kinematic and torque data of human walking, we show that our results adopt a human-like torque generation strategy while producing kinematic data significantly closer to humans than previous work. Our work demonstrates the importance of modeling constraints on torque generation due to muscle physiology, both in restricting the space of possible torque trajectories and in providing a realistic model of effort.

We chose to focus on generating human-like locomotion in a straight line and on flat ground. A natural extension is to investigate whether our control parameterization and effort term can be combined with the popular task-space controllers [Coros et al. 2010; de Lasa et al. 2010; Wu and Popović 2010] and higher-level planning [Coros et al. 2009; Mordatch et al. 2010] to create humanlike motions on uneven terrains [Wu and Popović 2010] or obstacle courses [Mordatch et al. 2010; Ye and Liu 2010]—scenarios that have only been addressed using purely joint-actuated characters.

Finally, an exciting area for future work is to automatically synthesize locomotion controllers for more detailed, fully muscle-actuated human models [Weinstein et al. 2008; Lee et al. 2009]. As we have touched on in Section 6.2, our approach can be used to develop predictive biomechanical models to investigate the effects of muscle and control properties on gait. However, more scientific validation of our simulation results is needed before we can conclude that our results apply to real humans. One clear aspect for improvement is to adopt a more physically-accurate simulation engine [Sherman et al. 2011], as ODE “emphasizes speed and stability over physical accuracy” [Smith 2006]. More accurate simulations and detailed models present additional computational challenges both in simulation speed and in parameter optimization, but are crucial for potential scientific and medical applications.