Primer ID Validates Template Sampling Depth and Greatly Reduces the Error Rate of Next-Generation Sequencing of HIV-1 Genomic RNA Populations

ABSTRACT

Validating the sampling depth and reducing sequencing errors are critical for studies of viral populations using next-generation sequencing (NGS). We previously described the use of Primer ID to tag each viral RNA template with a block of degenerate nucleotides in the cDNA primer. We now show that low-abundance Primer IDs (offspring Primer IDs) are generated due to PCR/sequencing errors. These artifactual Primer IDs can be removed using a cutoff model for the number of reads required to make a template consensus sequence. We have modeled the fraction of sequences lost due to Primer ID resampling. For a typical sequencing run, less than 10% of the raw reads are lost to offspring Primer ID filtering and resampling. The remaining raw reads are used to correct for PCR resampling and sequencing errors. We also demonstrate that Primer ID reveals bias intrinsic to PCR, especially at low template input or utilization. cDNA synthesis and PCR convert ca. 20% of RNA templates into recoverable sequences, and 30-fold sequence coverage recovers most of these template sequences. We have directly measured the residual error rate to be around 1 in 10,000 nucleotides. We use this error rate and the Poisson distribution to define the cutoff to identify preexisting drug resistance mutations at low abundance in an HIV-infected subject. Collectively, these studies show that >90% of the raw sequence reads can be used to validate template sampling depth and to dramatically reduce the error rate in assessing a genetically diverse viral population using NGS.

IMPORTANCE Although next-generation sequencing (NGS) has revolutionized sequencing strategies, it suffers from serious limitations in defining sequence heterogeneity in a genetically diverse population, such as HIV-1 due to PCR resampling and PCR/sequencing errors. The Primer ID approach reveals the true sampling depth and greatly reduces errors. Knowing the sampling depth allows the construction of a model of how to maximize the recovery of sequences from input templates and to reduce resampling of the Primer ID so that appropriate multiplexing can be included in the experimental design. With the defined sampling depth and measured error rate, we are able to assign cutoffs for the accurate detection of minority variants in viral populations. This approach allows the power of NGS to be realized without having to guess about sampling depth or to ignore the problem of PCR resampling, while also being able to correct most of the errors in the data set.

INTRODUCTION

Studies of viral population diversity are increasingly using next-generation sequencing (NGS) technologies to extend the depth of population sampling. Key aspects of understanding within-host viral population diversity are knowing the true depth of template/genome sampling and documenting the accuracy of the sequencing method to validate the detection of rare variants. Current approaches using NGS in viral population studies usually require a preceding PCR amplification step. Thus, PCR errors, including nucleotide misincorporation and PCR-mediated recombination, and errors during the sequencing step introduce artificial diversity into the apparent sequence population (1, 2). In addition, the repetitive sequencing of PCR copies of the original templates (PCR resampling) gives the appearance of artificial homogeneity in the population (3). A corollary of understanding true template sampling depth is then being able to apply statistical tools to define the sensitivity of detecting and the accuracy of quantifying minor variants (4, 5).

We previously showed that including a degenerate nucleotide block (Primer ID) in the cDNA synthesis primer overcomes limitations in deep sequencing protocols that require a preceding PCR step (6, 7). The inclusion of the Primer ID tag allows each original template copy to have its own identifying sequence. When the same Primer ID sequence is observed during the subsequent sequencing step this can be identified as resequencing of the same original cDNA template, i.e., PCR resampling. In addition, once those sequences have been identified as resampled they can be pooled to create a corrected consensus sequence for each original template, a step that removes most method-introduced errors. Finally, the total number of template consensus sequences defines the depth of sampling of the viral population.

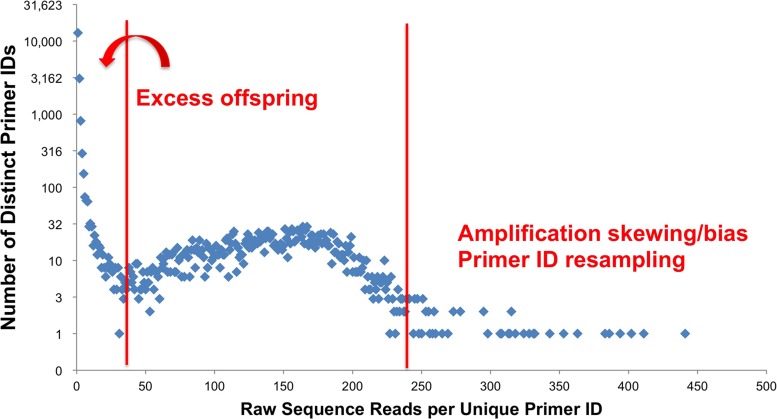
However, we and others (8) have observed several significant technical issues that can confuse the use of the Primer ID approach. There is often a wide range of sequence read numbers for different Primer IDs in the raw data set, with most of the Primer IDs observed present at low frequency (i.e., found in only one or two raw reads), while a few of the Primer IDs are present at very high read numbers (Fig. 1). Due to the relatively high error rate of NGS platforms, it is now clear that one Primer ID can generate “offspring” Primer IDs due to sequencing errors within the Primer ID sequence block itself, which could confound the allelic frequency with low-frequency Primer IDs. Conversely, high-frequency Primer ID reads raises the concern that the Primer ID may cause bias during the PCR step, inducing some templates to be efficiently amplified and thus giving rise to allelic skewing. Finally, chance resampling of the Primer ID sequence from the starting primer library would result in template mixtures during construction of consensus sequences which would reduce template sampling, a problem that would be exacerbated if specific Primer IDs are selected out of the primer library population due to enhanced binding to the template.

FIG 1.

Example of Primer ID distribution. Most of the Primer IDs appear at very low frequency (once or twice), while some of them appear several hundreds of times in the raw read output. Artifacts of mutations within the Primer ID (offspring) and PCR amplification skewing and primer ID resampling are suggested as features that help shape the observed distribution of reads per Primer ID.

We describe here the adaptation of the Primer ID approach to the Illumina MiSeq platform and explore these suggested problems in the use of Primer ID. We also assess the error rate of NGS sequencing when incorporating the Primer ID approach using an authentic virion RNA template and show how we can use this authentic error rate to guide the interpretation of mutations detected at low abundance.

MATERIALS AND METHODS

Cells.

The following reagent was obtained through the AIDS Research and Reference Reagent Program, Division of AIDS, National Institute of Allergy and Infectious Disease, National Institutes of Health (NIH): 8E5/LAV provided by Thomas Folks. Each 8E5/LAV cell contains a single integrated copy of defective HIV-1 DNA. Cells are CD4 negative and produce virions that do not have HIV-1 reverse transcriptase (9). Replication of the viral genome in its DNA form in this cell line is accomplished with the high-fidelity host replication machinery. Thus, these cells can be a source of large amounts of viral particles that should have identical genome sequences for use to estimate the residual error rate. Cells were cultured in RPMI medium containing 10% fetal bovine serum. Cultures were passaged every 2 days at a concentration of 10⁶ cells/ml. To collect virus, the cells were spun down, and supernatants were collected and frozen at −80°C.

Human plasma samples.

Plasma samples were obtained from two individuals infected with subtype B HIV-1. All subjects signed informed consent forms approved by the appropriate institutional review board.

RNA extraction, cDNA synthesis, and MiSeq library construction.

Viral RNA was extracted from plasma samples or 8E5 cell supernatants using a QIAamp viral RNA minikit (Qiagen, Valenicia, CA). cDNA primers were comprised at the 3′ end of an HIV-1 gene-specific primer sequence, followed by a 4-nucleotide spacer and then a 9-nucleotide randomized sequence and, at the 5′ end, a sequence block for PCR priming. The env V1-to-V3 region Primer ID cDNA primer was 5′-GTGACTGGAGTTCAGACGTGTGCTCTTCCGATCTNNNNNNNNNCAGTCCATTTTGCTCTACTAATGTTACAATGTGC-3′ (HBX2 numbering for the gene-specific region: 7238 to 7209). The protease coding domain Primer ID cDNA primer was 5′-GTGACTGGAGTTCAGACGTGTGCTCTTCCGATCTNNNNNNNNNCAGTTTAACTTTTGGGCCATCCATTCC-3′ (HBX2 number for the gene-specific region: 2614 to 2592). All primers were synthesized by Integrated DNA Technologies (Coralville, IA) with hand mixing of random nucleotides and standard desalting for purification.

Based on the viral load tests of an HIV⁺ plasma sample, cDNA reactions were carried out in triplicate with a dilution series of 10,000 copies, 3,333 copies, or 1,111 copies of viral RNA template in each reaction and 370 copies of viral RNA with two repeats in the serial dilution experiment. Serial titrations of 8E5 RNA templates isolated from culture supernatants were made, and the titration generating around 10,000 consensus sequences or fewer was used for the analysis. We used Superscript III reverse transcriptase (Life Technologies, Grand Island, NY) for cDNA synthesis except for the error rate assessment experiment set 3, in which we used AccuScript Hi-Fi reverse transcriptase (Agilent Technologies, Santa Clara, CA) for cDNA synthesis. In the Superscript III set, each cDNA reaction mixture contained 10 U of Superscript III, 2 U of RNaseOut (Life Technologies), 5 mM dithiothreitol (DTT), 0.5 mM deoxynucleoside triphosphates (dNTPs), and 0.25 μM cDNA primer in a total volume of 60 μl. In the AccuScript Hi-Fi set, each cDNA reaction mixture contained 3 μl of AccuScript Hi-Fi reverse transcriptase, 3 μl of RNaseBlock (Agilent Technologies), 10 mM DTT, 0.5 mM dNTPs, and 0.25 μM cDNA primer in a total volume of 60 μl. The primers, dNTPs, and templates were mixed and heated at 65°C for 5 min and then cooled on ice for 1 min (Superscript III sets) or slowly cooled at room temperature for 10 min (AccuScript set). The reaction mixtures were incubated at 50°C for 1 h and then at 55°C for 1 h. Enzymes were inactivated at 70°C for 15 min. We then added 1 μl of RNase H (Life Technologies) to each reaction mixture, followed by incubation at 37°C for 20 min.

cDNA purification.

cDNA was purified using Agencourt RNAClean XP beads (Beckman Coulter, Brea, CA) to remove unused cDNA primer. The ratio of the volume of beads to cDNA reaction was 0.6. The beads were washed four times with 70% ethanol. cDNA was eluted in distilled water.

PCR amplification.

All cDNA was used for amplification after purification. We used KAPA2G Robust Hotstart (Kapa Biosystems, Woburn, MA) or Phusion DNA polymerase (New England BioLabs, Ipswich, MA) as the first-round PCR enzyme. The first-round PCR forward primer was 5′-GCCTCCCTCGCGCCATCAGAGATGTGTATAAGAGACAGNNNNTTATGGGATCAAAGCCTAAAGCCATGTGTA-3′ for the env V1-to-V3 region, and 5′-GCCTCCCTCGCGCCATCAGAGATGTGTATAAGAGACAGNNNNCAGGAGCCGATAGACAAGGAAC-3′ for the protease region. The first-round PCR reverse primer was 5′-GTGACTGGAGTTCAGACGTGTGCTC-3′. The PCR cycling protocol for KAPA2G Robust was initial denaturation at 95°C for 1 min, 25 cycles of 95°C for 15 s, 58°C for 1 min, and 72°C for 30 s, and then a final extension at 72°C for 3 min. The PCR cycling protocol for Phusion was initial denaturation at 98°C for 30 s, 25 cycles of 98°C for 10 s and 72°C for 1 min, and then a final extension at 72°C for 5 min.

First-round PCR products were purified using Agencourt Ampure XP beads (Beckman Coulter). The ratio of volume of beads to PCR volume was 0.6. The beads were washed three times with 70% ethanol. cDNA was eluted in 50 μl of distilled water and stored at −20°C. We used 2 μl of the purified first-round PCR product for the second-round amplification, with the KAPA HiFi PCR Hotstart as a second-round PCR polymerase. The second-round forward primer was 5′-AATGATACGGCGACCACCGAGATCTACACGCCTCCCTCGCGCCATCAGAGATGTG-3′, and the reverse primer was 5′-CAAGCAGAAGACGGCATACGAGATNNNNNNGTGACTGGAGTTCAGACGTGTGCTC-3′. Second-round reverse primers included a 6-nucleotide long index region. We used 24 indexed primers, allowing us to multiplex as many as 24 samples in the same sequencing run. The PCR primer sequences were matched with Illumina sequencing adapters, allowing the Primer ID region to always be sequenced at the second end (R2).

The size of the V1/V3 env amplicon was around 835 bp, covering HXB2 6585-7208 on the HIV-1 genome, and the size of the protease amplicon was 548 bp, covering HXB2 2237-2591 on the HIV-1 genome.

Sequencing.

We used 300-bp paired-end multiplex Illumina MiSeq (San Diego, CA) to sequence the constructed libraries, employing the Illumina pipeline (v1.8.2) for the initial processing of data, including separating raw sequences by their indexes.

Template consensus pipelines.

In-house Ruby (v2.1.2) scripts were used to process raw sequence reads in FASTq format. We initially checked the integrity of the information block, i.e., the Primer ID, spacer, and gene-specific primer region on each sequence read and discarded those without an intact information block. Quality raw sequence reads from both ends (R1 and R2) were then paired. We searched each raw sequence in the R2 region for the Primer ID. All individual Primer IDs were then tabulated for the number of reads with that Primer ID. We used a Primer ID read number cutoff model (described below) to determine the minimum number of reads required to create a template consensus sequence. Primer IDs detected in a number of reads above the cutoff were kept, and template consensus sequences were constructed for both read ends. We used the majority nucleotide at each position to create a consensus nucleotide for that position, and ambiguity nucleotides were also called at positions where there were equal numbers of different nucleotides. Consensus sequences with ambiguity nucleotides were then discarded. Of note, we did not use sequence alignment programs to build a consensus sequence from aligned raw sequences, since insertion/deletion errors are much fewer in MiSeq compared to 454 sequencing (see Ruby scripts in the supplemental material). Since Primer IDs are read at very different frequencies within a data set, when Primer ID resampling occurs, i.e., two templates with the same Primer ID, in most circumstances the templates will have different numbers of Primer ID reads, and the template with fewer Primer ID reads will be lost during the process of making a template consensus sequence.

Combination of template consensus sequences with an overlap region.

There was a 181-nucleotide overlap region of the protease paired-end reads. We first compared the 181 nucleotides of paired consensus sequences (181 nucleotides at the tail of R1 consensus and 181 nucleotides at the head of R2 consensus) and made a combined consensus sequence if they agreed. We used MUSCLE (v3.8.1) (10, 11) to make an alignment of the rest of the paired-end template consensus sequences and, if the actual overlap region was not 181 bp but a 100% match, combined sequences were still made for the subsequent analysis.

Primer ID read number cutoff model.

In the previous pipeline approach for creating a consensus sequence, Primer IDs appearing three times or more were used to create a consensus sequence for that template (6–8). However, when a Primer ID gets amplified and sequenced, a small fraction of the amplified Primer IDs are mutated due to the PCR and sequencing errors, generating offspring Primer IDs. These offspring Primer IDs can be present as different sequences with various frequencies. We used a simulation to develop a new approach to determining the number of Primer ID reads required as a cutoff for creating a consensus sequence. In the simulation, we first generated a parental Primer ID with a random sequence of a certain abundance. We then mutated all of these Primer IDs given a specified mutation rate to generate a pool of offspring Primer IDs. Since the polymerase error rate is at least 2 logs lower than the MiSeq sequencing error rate, we simplified the model by including only a single conservative sequencing error rate (0.02 per site) (12). We further counted the frequencies of each offspring Primer IDs. We performed the process using an abundance of parental Primer IDs from 10 to 20,000, and the whole process was repeated 1,000 times. Finally, we obtained the correlation of the abundance of observed parental Primer IDs (m) and the maximum frequency of a specific offspring Primer ID (N_o) with standard deviation (SN_o).

We calculated the 95% confidence intervals (CI) for N_o. Given an observed m, the cutoff for the offspring Primer ID (c) was determined as the upper limit of 95% CI of N_o, given by c = N_o + 1.96SN_o. We further fit the simulated pairs of mean m value and c into a polynomial regression model. Since N_o had a positive correlation with m, the Primer ID read number cutoff of a sample with multiple parental Primer IDs was determined as the offspring cutoff of the most abundant parental Primer ID. Thus, we obtained the formula to calculate the cutoff to make template consensus sequences based on the most abundant Primer ID in one library.

Primer IDs with a number of reads above the cutoff were used to create a template consensus sequence. We coded this formula into the template consensus creation script and used it to calculate the Primer ID read number cutoff for each sample. We used 8-nucleotide Primer IDs in this simulation model. However, by changing the variables in the provided Ruby script, similar simulations can be performed for other lengths of Primer ID.

Primer ID distribution simulations.

We used Ruby scripts (see the scripts in the supplemental material) to simulate Primer ID distributions. We used three different assumptions. In model 1, we assumed there were no sequencing errors within the 8-nucleotide Primer ID sequence block, and all templates were included in the PCR with 100% amplification efficiency. In model 2, we assumed there were sequencing errors within the Primer ID sequence block (1% substitution rate), and all templates were used with 100% efficiency. In model 3, we included a sampling of 50% of the templates at each of the first 10 rounds of PCR, i.e., we modeled a situation where only 50% of the templates were copied in each cycle, and we included a 1% error rate in the Primer ID sequence block.

In the simulations a certain number of converted templates were first generated by the scripts, and each received a random Primer ID of 8 nucleotides using a pseudorandom number generator (PRNG). In models 1 and 2, the template/Primer ID pairs were directly transferred to the sequencing loops. In model 3 with PCR bias, we simulated the PCR amplification with 50% template utilization in each cycle for 10 cycles and transferred the biased template/Primer ID pairs to the sequencing loops. In models 2 and 3, we mutated the Primer ID sequence with the preset error rate at 1% to generate the mutated template/Primer ID pair. During the sequencing loops, template/Primer ID pools were sampled for a number of times equal to the number of raw sequences using the PRNG. Thus, we obtained the template/Primer ID sample pairs after sequencing. We further ran these pairs through the template consensus pipeline to generate consensus sequences as we did for control and clinical samples. We plotted the Primer ID distributions from the models and compared them with an experiment data set. We further calculated the recovery of templates (using Primer IDs to create template consensus sequences) and the percentage of consensus sequences that included more than one template (Primer ID resampling) under different conditions of number of template and raw sequences using the model 3 assumptions. The recovery rate and Primer ID resampling percentage were the average number of 100 repeats.

Error rate assessment.

We sequenced the HIV-1 env gene V1 through V3 region and the pro gene/protease coding domain for the 8E5 control samples and obtained template consensus sequences using the protocol and pipeline described above. We first tried several titrations of extracted 8E5 RNA template and used the titration that generated around 10,000 unique template consensus sequences per reaction. We further performed an experiment using the three sets of enzyme combinations with the determined RNA titration. After template consensus sequence formation, we used the following algorithm to calculate the error rate. We first obtained a sample consensus sequence as a reference sequence by simple alignment of all template consensus sequences from one sample. We then aligned each of the template consensus sequences with the reference sequence using MUSCLE and annotated each consensus sequence at positions with substitutions, insertions, or deletions. Template consensus sequences with five or more nucleotide differences from the reference sequence were manually examined using the NCBI BLAST sequencing analysis tool (13) and Los Alamos HIV database HIV Sequence Locator tool (http://www.hiv.lanl.gov/content/sequence/LOCATE/locate.html). Consensus sequences with mispriming (defined as at least a 5-nucleotide shift from the priming sites of either end) or undetermined sequences (no match or only a poor match from BLAST) were filtered out. We further filtered out consensus sequences with either in-frame insertions/deletions or frameshift errors. We then calculated the substitution rate and the types of substitutions using the remaining template consensus sequences for each end. In the protease control, we also calculated the substitution rate for the combined template consensus sequences, since there was an overlapping region between the two sequenced ends.

Use of the Poisson distribution in assessing residual errors of template consensus sequences.

Since next-generation sequencing (NGS) has greatly increased the depth of sequencing of viral populations, it is essential to generate validated cutoffs for mutations seen at low abundances from residual method error. One of the approaches is to study how often the random errors appear based on a measured error rate and use this distribution of random error among a known number of sampled genomes as a “floor” or cutoff for rare mutations.

If one sequencing run generates n number of template consensus sequences of m base pairs in length, and the method error from the controls is measured to be p, the probability of observing k mutations at the position due to the method error fits the Poisson distribution. The number of positions with k mutations is given by:

$$f\left(k\right)=t\frac{{\left(np\right)}^k{e}^{-\left(np\right)}}{k!}$$

where k = 0,1,2,3,…n, k! is the factorial of k, e is Euler's number (e = 2.71828…), n is number of template consensus sequences, and t is the length of the sequenced fragment in base pairs.

This approach allows a description of the distribution of method errors. We can observe the number of positions (N_k) with k (k = 0,1,2,3,…) variant(s) from actual sequencing data. If N_k is less or close to f(k), we cannot distinguish true variants from method error. When N_k is significantly greater than f(k), the true variants are more abundant than the method error. Thus, the abundance cutoff for errors is determined as the first k value where N_k is significantly greater than f(k).

Calculation of confidence intervals of minority mutations and detection limits.

We used the Clopper-Pearson method to calculate the 95% binomial confidence intervals for minority mutations in the clinical sample. We used R (v3.0.0) (14) to perform the calculations. We further calculated the probability of detecting a rare mutation above the abundance cutoff for errors based on the Poisson distribution.

Raw sequence reads have been deposited at the NCBI Short Read Archive (experiment accession number SRX844885).

RESULTS

Indexing PCR amplicons for sequencing using MiSeq.

We first adapted the Primer ID approach to the Illumina MiSeq platform (15). Briefly, cDNA was synthesized using primers with a block of degenerate nucleotides (Primer ID), followed by two rounds of PCR amplification to incorporate MiSeq adaptors and 6-nucleotide indexes for multiplexing of different samples for the same sequencing run. In addition, we added a 4-nucleotide degenerate block in the forward PCR primer. Paired-end sequencing started from the degeneracies present at both ends (16), allowing individual amplicons to be detected as distinct sequencing clusters (Fig. 2).

FIG 2.

Adaptation of the Primer ID approach to the MiSeq platform. MiSeq library construction with the Primer ID approach from viral RNA template was used for sequencing. The Primer ID (yellow, N8) is included in the cDNA primer, along with a PCR primer site (brown), and the upstream primer includes four randomized bases to add diversity to the initial sequence read (orange, N4). Illumina indexed primers (green with purple barcode) are included in the last round of PCR. The paired-end sequence of region 1 (R1) and region 2 (R2), which may or may not overlap in the middle, are indicated.

Effect of sequencing errors within the Primer ID sequence.

Sequencing errors within the Primer ID sequence block itself will create a new Primer ID sequence (offspring Primer ID) that will over-represent the original template among the final group of consensus sequences. We examined the sequencing quality score for the Primer IDs that appeared once and those that appeared with the highest frequency from a sample in a template dilution experiment (described below). As shown in Fig. 3a, the Primer IDs that appeared once came from sequence reads that on average had significantly lower quality scores than the scores for the higher frequency reads. This observation suggests that low-abundance Primer ID reads are at least in part the result of misreading of more-abundant Primer IDs that are being resampled (after the PCR amplification step) in the sequencing.

FIG 3.

Assessment of offspring Primer IDs. (a) The Primer ID sequence for “singles” have significantly lower quality scores than the Primer ID sequences at the highest frequency. Primer IDs were 8 nucleotides long. (b) Primer ID distribution and percentages of Primer IDs at low abundance (i.e., read less than 23 times) with one or two nucleotide differences from an abundant consensus Primer ID. Data were generated from the dilution experiment sample RSD11. This example was chosen to highlight the issue of offspring Primer IDs, which is exacerbated when low-input template copies are used. In this case, the total number of consensus sequences above the cutoff was only 121, which is why there is not a symmetrical distribution of raw reads per Primer ID. Symbols for one (red squares) and two (green triangles) nucleotide differences are read on the percentage scale, while the symbol for number of Primer IDs (blue diamonds) is read on the log scale.

We further used one of the dilution experiment samples (one of the two repeats at the 1:27 dilution, estimated 370 input templates) to study the sequence similarity of Primer IDs present at different abundances. In this sample there were 11,208 Primer IDs recovered in the sequencing data, with 8,121 appearing only once, 2,966 appearing more than once but below the calculated Primer ID read number cutoff (c = 54) (Primer ID read number cutoff described below), and 121 appearing above the cutoff (consensus Primer IDs). Figure 3b shows the Primer ID distribution and the percentage of Primer IDs with one or two nucleotide differences from an abundant Primer ID. Among the Primer IDs that appear only once in the raw sequence reads, there are 6 and 43% within one nucleotide or two nucleotides of an abundant Primer ID, respectively. With increasing raw sequence reads per Primer ID, the percentage of Primer IDs with two-nucleotide differences (green triangles) drops quickly to below 20%, while the percentage of Primer IDs with a one-nucleotide difference (red squares) increases quickly above 80%; the analysis was stopped at Primer IDs with 23 raw reads due to the small number of Primer IDs obtained with the limited number of templates used. Overall, among Primer IDs appearing more than once but below the cutoff at 54 raw reads, 57% were different by one nucleotide from an abundant Primer ID, a number that is significantly higher than the number estimated using random Primer IDs selected by chance (4.3%), and an additional 22% were within two nucleotides of an abundant Primer ID. In addition, the one-off nucleotide positions were evenly distributed across the 8-nucleotide Primer ID. This phenomenon suggests that Primer IDs at low abundance are offspring Primer IDs generated from abundantly read Primer IDs, and those at very low abundance can be Primer IDs with multiple changes from an abundant Primer ID due to low sequence quality. These observations provide the rationale for trimming the low-abundance reads to focus on true template consensus sequences.

Primer ID read number cutoff determination.

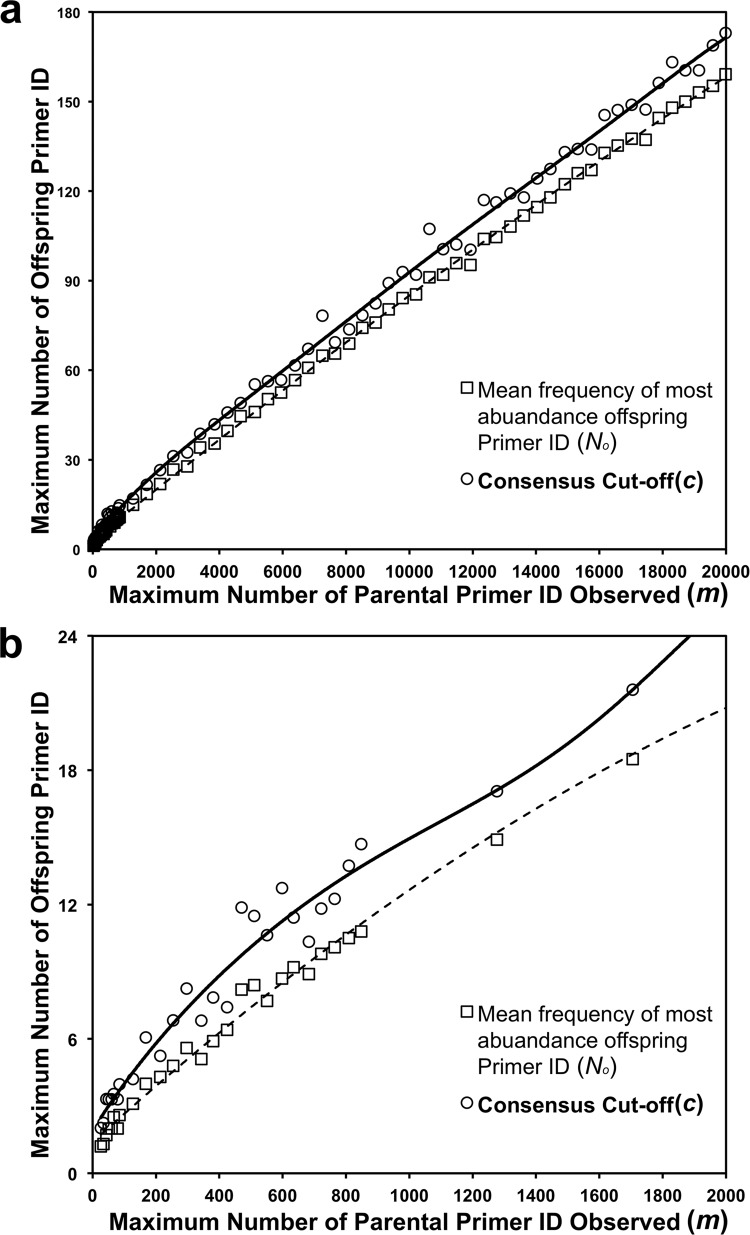
In an effort to correct the offspring Primer ID problem, we have modeled this phenomenon to develop an algorithm to set a cutoff for the number of raw reads needed for a Primer ID to be included as a consensus sequence. In this model we calculated the maximum occurrence of offspring Primer IDs given a specified number of identical Primer ID reads and a combined error rate for PCR misincorporation and sequencing error conservatively set at 2% (see Materials and Methods). For this model the required number of sequence reads with the same Primer ID to make a consensus sequence was designed to be greater than the number of offspring Primer IDs with the highest frequency. Figure 4 shows the simulated number of parental Primer ID and its corresponding maximum number of offspring Primer ID. The Primer ID read number cutoff is determined by the maximum occurrence of offspring Primer IDs of the maximum occurrence of Primer IDs observed in a sequencing library. For instance, if the maximum occurrence of a specific Primer ID (m) in a library is 5,117, the simulated median number of maximum occurrence of an offspring Primer ID (N_o) is 46, and the Primer ID read number cutoff (c) is determined as 55 (46 plus 1.96 times the standard deviation, which is 4.7 in this case). If the maximum occurrence of observed Primer IDs (m) is 292, the Primer ID read number cutoff (c) is estimated at 8.

FIG 4.

Simulated correlation of the abundance of observed parental Primer IDs and the maximum abundance of the offspring Primer ID. Open squares indicate the mean number of maximum abundances of offspring Primer IDs given the observed number of parental Primer IDs. Open circles indicate the upper limit of the 95% confidence intervals of the maximum abundances of offspring Primer IDs, which serve as the Primer ID read number cutoffs for the given abundances of observed maximum parental Primer IDs in a sequencing library. 4a, observed parental Primer ID from 0 to 20,000; 4b, observed parental Primer ID from 0 to 2,000.

The formula of to calculate the Primer ID read number cutoff (c) based on the maximum abundance of Primer ID in one library (m) is as follows: c = (−1.24 × 10⁻²¹m⁶) + (3.53 × 10⁻¹⁷m⁵) − (3.90 × 10⁻¹³m⁴) + (2.12 × 10⁻⁹m³) − (6.06 × 10⁻⁶m²) + 0.018m + 3.15.

The minimum cutoff is 2 since we need at least three raw reads to create a consensus read based on majority rule. There is a corollary of this model. Under circumstances where the same total number of raw reads is obtained, the smaller the amount of template used, the greater the number of reads per template, thus requiring a larger cutoff to avoid offspring.

We examined the cutoff values from the construction of consensus sequences using a serial dilution experiment. A Primer ID cDNA primer, PCR amplification, and MiSeq sequencing were used to sequence the HIV-1 env gene from V1 through V3 using viral RNA extracted from the plasma of an infected subject. Also, a serial dilution series of the starting viral RNA templates (1:1, 1:3, 1:9, and 1:27) was included, and each RNA dilution level was amplified in duplicate/parallel amplifications. As shown in Fig. 5, there was not a strong linear correlation between either the number of input templates and the total number of Primer ID sequences in the raw sequence data set or the number of input templates and the number of Primer ID sequences appearing more than two times (our original strategy for creating a consensus sequence [6]), when we constrained the trend line to cross the origin (without any template no Primer IDs will be generated). However, there was strong linear correlation between the number of input templates and the number of Primer IDs included using the Primer ID read number cutoff model for the number of reads required to build a consensus sequence (R² = 0.99). We further bootstrapped the data 10,000 times and estimated the 95% confidence intervals for R² to be 0.971 to 0.998. In addition, the percentage of raw sequence reads with Primer IDs below the cutoff (discarded sequences) remained relatively constant throughout all dilutions (6.2 to 6.9%) independent of the Primer ID read number cutoff, as expected if offspring Primer IDs are being trimmed from both abundant and less-abundant resampled sequences. Put differently, >90% of the raw sequence data was retained and available to create the consensus sequences based on PCR resampling after removing offspring Primer IDs. Thus, this model for defining the number of raw reads needed for a Primer ID sequence to build a template consensus sequence removes low-abundance offspring Primer IDs (which represent a small fraction of the total sequences but a large fraction of the total Primer IDs) that are the result of sequencing and/or PCR errors.

FIG 5.

Correlation of the number of total Primer IDs, the number of Primer IDs that appear more than twice, and the number of template consensus sequences using the Primer ID read number cutoff model as a function of the number of input templates. Primer ID was 8 nucleotides long. The data are plotted from the experiment shown in the table below the graph, and the percentage of the sequences discarded using the Primer ID read number cutoff model is shown.

PCR versus Primer ID allelic skewing during amplification.

The distribution of the number of reads of Primer IDs in a raw sequence data set typically does not match a normal distribution as would be expected if sequences were being sampled from a population of sequences that were being equally amplified during the PCR step (6). As noted above, this represents offspring Primer IDs at the low end of the distribution, but some sequences are sampled at much higher levels than expected at the high end of the distribution (Fig. 1). We used an analysis of repetitive deep sequencing runs as an approach to address the question of PCR- versus Primer ID-induced skewing. We compared the utilization of Primer ID sequences in several repeat experiments of cDNA synthesis, PCR amplification, and sequencing using viral RNA isolated from the supernatant of the clonal cell line 8E5 cells as the template (9), sequencing both the HIV-1 env V1 to V3 region and the protease coding domain.

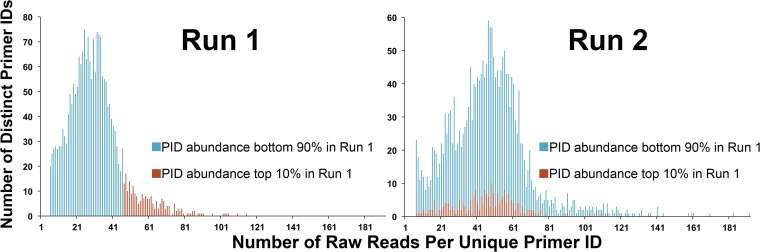
As predicted from random sampling, there was some overlap in the utilization of Primer ID sequence blocks between repeat runs (Fig. 6), which gave us an opportunity to see how these identical sequences were utilized between the runs. We examined the Primer ID sequences that were the most abundantly read in one run (the top 10%) for their distribution of read numbers in a second run. The abundant Primer ID sequences from one run were randomly distributed in the number of reads in the second run (Fig. 6, Run 2), suggesting that it is not the Primer ID sequence itself that is determining the allelic skewing. This comparison was repeated for two more pairs of runs in the HIV-1 env region and seven pairs of runs at the HIV-1 protease coding domain with the same outcome.

FIG 6.

Comparison of Primer ID distribution in two replications of library construction and sequencing of the same template. The distribution of the top 10% (in read abundance) Primer IDs from run 1 (red) and the bottom 90% (blue) that also appeared in run 2 were analyzed for their distribution in run 2.

The Primer ID sequences that were high in one run were randomly distributed in the second run, but there were still a few Primer ID sequences that were high in both runs. To determine whether this was by chance or whether there was something intrinsic to the sequence, we examined the sequences and found no pattern of similarity among the order of nucleotides. When this subset of sequences was placed in a neighbor-joining tree they were widely distributed among a random sampling of Primer ID sequences. Furthermore, we examined nucleotide abundance at each position of the 54 Primer IDs that appeared in the top 10% abundance in both runs from one protease and three env amplification and sequencing runs. The percentage of nucleotides at each position was not significantly different from that expected (calculated from 5,125 Primer IDs used by both runs in total) (Table 1). We also compared homopolymers (defined as a sequence of at least 4 identical nucleotides) in Primer IDs that appeared in top 10% abundance in both runs to the rest of Primer IDs appearing in both runs. The difference was not statistically significant (P = 0.12). Thus, we conclude that the Primer ID sequence itself is not responsible for the skewing.

TABLE 1.

Comparison of nucleotide abundance at each incorporated Primer ID position^a

Positionb	No. (%) of nucleotidesc								Chi-square P value
	A		T		C		G
	Top 10%	All observed	Top 10%	All observed	Top 10%	All observed	Top 10%	All observed
1	12 (22)	1,345 (26)	19 (35)	1,472 (29)	12 (22)	1,105 (22)	11 (20)	1,203 (23)	0.76
2	17 (31)	1,372 (27)	19 (35)	1,481 (29)	7 (13)	1,121 (22)	11 (20)	1,151 (22)	0.35
3	11 (20)	1,371 (26)	21 (39)	1,520 (30)	8 (15)	1,090 (21)	14 (26)	1,144 (22)	0.29
4	10 (19)	1,339 (26)	14 (26)	1,490 (29)	14 (26)	1,121 (22)	16 (30)	1,175 (23)	0.41
5	13 (24)	1,352 (26)	22 (41)	1,476 (29)	8 (15)	1,066 (21)	11 (20)	1,231 (24)	0.26
6	11 (20)	1,351 (26)	14 (26)	1,472 (29)	9 (17)	1,050 (20)	20 (37)	1,252 (24)	0.19
7	8 (15)	1,387 (27)	20 (37)	1,382 (27)	13 (24)	1,075 (21)	13 (24)	1,281 (25)	0.15
8	8 (15)	1,350 (26)	16 (30)	1,504 (29)	10 (19)	943 (18)	20 (37)	1,328 (26)	0.15

^aWe compared the Primer IDs that appeared at the top 10% abundance in both runs to all onserved Primer IDs that appeared in both runs.

^bThat is, from the 5′ end to the 3′ end of the internal Primer ID sequence string.

^cTop 10%, Primer IDs that appeared at the top 10% abundance in both runs (n = 54); all observed, Primer IDs that appeared in both runs (n = 5,125).

Simulation models reveal that PCR skewing and sequencing/PCR errors contribute to skewed Primer ID distributions.

In an effort to understand how PCR might induce skewing in a template number-sensitive way, we modeled Primer ID distribution with three different assumptions. In model 1, we assumed there were no sequencing errors within the 8-nucleotide Primer ID sequence block, and all templates were included in the PCR with 100% efficiency. In model 2, we assumed there were sequencing errors within the Primer ID sequence block (1% substitution rate), and all templates were used with 100% efficiency. In model 3, we included a sampling of 50% of the templates at each round of PCR, i.e., we modeled a situation where only 50% of the templates were copied in each cycle, for the first 10 cycles, and included a 1% error rate in the Primer ID sequence block. Figure 7 shows the modeled distribution under conditions of 300,000 raw sequence reads and 10,000 templates (with 30% conversion of RNA template to cDNA, i.e., 3,000 converted templates) for the three models. We also show the observed distribution (blue diamonds) from the serial dilution experiment sample RSD02, from which 3,076 template consensus sequences were created from 300,000 randomly selected raw sequences (from a total of 334,542 quality raw sequences). Without PCR stochastic sampling or sequencing error in the Primer ID sequence block (Fig. 7; model 1, red squares), there were no Primer IDs at low abundance, and the distribution of Primer ID read abundance was confined to a narrow range; the apparent allelic skewing in high-abundance reads in this model was due to low-level resampling of the Primer ID on two templates where the total number of reads for each template was summed, creating a second “shadow” distribution two times greater than the main distribution (see below). When sequencing error at the Primer ID region was introduced in model 2 (Fig. 7; green triangles), we could now see Primer IDs with low abundance appear due to the offspring Primer ID effect, but the parental Primer IDs were still confined to a similar range of read numbers as seen with model 1. After introducing PCR stochastic sampling at 50% for the early rounds (model 3, purple circles), the model distribution fit well with the observed distribution (Fig. 7; blue diamonds). We further modeled the Primer ID read distribution using model 3 assumptions for different template numbers. Table 2 shows the mean read numbers and standard deviations in the raw sequences for the individual Primer ID sequences (above the Primer ID read number cutoff) from observation of the serial dilution experiment and simulations. The standard deviation was inversely correlated with number of templates from observation and simulation model 3, a finding consistent with greater skewing at a low input template number due to suboptimal template sampling during the PCR step.

FIG 7.

Primer ID distribution as observed and compared to three models. Blue diamonds correspond to the Primer ID distribution from a plasma sample. We modeled Primer ID distributions under three different sets of assumptions. In model 1 (red squares), we assumed that there were no sequencing errors within the 8-nucleotide Primer ID sequence block, and all templates were included in the PCR with 100% efficiency. In model 2 (green triangles), we included 1% PCR/sequencing substitutions at the Primer ID region. In model 3 (purple circle), we assumed that only half of the templates were used in each of the first 10 cycles of PCR before sequencing, in addition to a 1% substitution rate in the Primer ID sequence block.

TABLE 2.

Average number of raw sequences per consensus Primer ID as input template varies for a fixed number of raw reads^a

No. of RNA templatesb	No. of template consensus reads	Avg no. of raw sequences per consensus Primer ID (SD)c
		Observed	Model 1	Model 2	Model 3
370	102	2,756 (2,114)	2,703 (53)	2,497 (45)	2,712 (1,631)
1,111	423	662 (418)	901 (30)	832 (29)	834 (470)
3,333	1,126	247 (124)	302 (29)	278 (25)	284 (161)
10,000	2,911	90 (41)	102 (18)	94 (16)	96 (55)

^aThis analysis used 300,000 quality raw sequences.

^bA 30% conversion rate of RNA templates to cDNA templates was applied in the simulation models.

^cObserved, observed data from the serial dilution experiment; model 1, no PCR bias, no error in the Primer ID region; model 2, no PCR bias, error rate in the Primer ID region = 0.01; model 3, PCR bias (first 10 cycles of PCR, only 50% of templates were used), error rate in the Primer ID region = 0.01.

Template recovery and Primer ID resampling as a function of template input and number of raw reads.

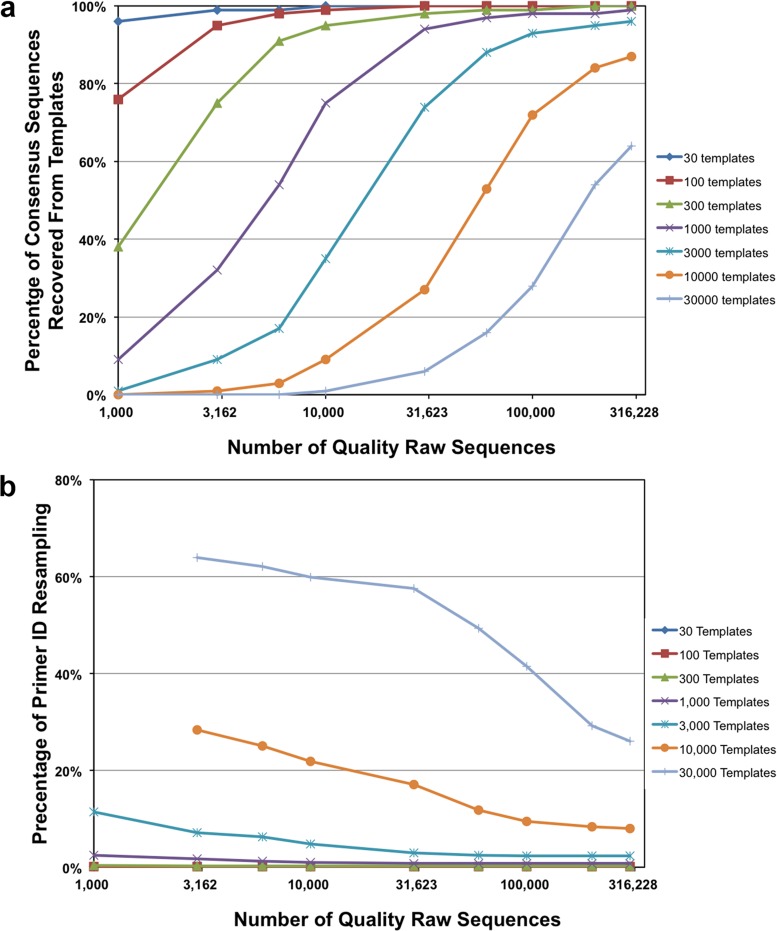
The use of Primer ID allows an estimate of how many input templates get converted into final consensus sequences, and our general experience has been that for different experiments between 10 and 30% of RNA templates used in the cDNA reaction are ultimately converted to consensus sequences (Fig. 5), although this number can be much lower depending on template quality or priming efficiency (7). We modeled the number of raw reads needed to sample most of the template-converted sequences present in the PCR product, in this case assuming that 30% of the RNA input was converted to sequences present in the final PCR product (Fig. 8a). Template recovery increases as the number of raw reads increases and reaches a plateau as the available template sequences approach full recovery. For instance, with 1,000 converted templates 95% of template sequences are recovered with about 30,000 raw reads. With 3,000 converted templates 100,000 raw reads are needed to get 93% of template sequences. Based on this simulation there should be at least 30-fold coverage in raw reads over the number of converted templates to maximize template recovery while minimizing the number of reads committed to each template that are used to build a consensus sequence. The use of 30-fold coverage for each converted template should be a factor in deciding the number of samples to pool for multiplexing given a certain capacity of the sequencing instrument. Greater coverage is not detrimental but does result in the need for a greater Primer ID read number cutoff number and underutilization of the capacity of the sequencing instrument.

FIG 8.

Patterns of Primer ID resampling and template coverage. (a) Relationship between the number of raw sequences and Primer ID resampling (i.e., the percentage of template consensus sequences from more than one template in all of the template consensus sequences recovered) at different levels of converted templates. (b) Relationship between the number of raw sequences and template recovery at different levels of converted templates.

Primer ID resampling can limit the number of templates that can be recovered since two templates with the same Primer ID will be pooled for building the consensus sequence, but the two templates will usually have different numbers of raw reads causing the lower-read template to be lost during the assembly of the consensus sequence. The resampling of the Primer ID from the starting Primer ID sequence library is a statistical problem analogous to the “Birthday Problem” (17). We calculated the percentage of Primer IDs used by more than one template (Primer ID resampling) with different numbers of converted templates and raw sequencing reads with a Primer ID random sequence block of 8 nucleotides (Fig. 8b). Greater numbers of converted templates resulted in a greater extent of Primer ID resampling. Increasing raw reads decreases apparent Primer ID resampling within a certain range, but this is mostly due to the increase in template recovery (denominator). Based on this modeling it is possible to define conditions where there are a sufficient number of raw reads to have most templates recovered with only a small percentage of the Primer IDs resampled. For instance, with 3,000 converted templates and 100,000 raw reads, only 2.4% of template consensus sequences recovered are from Primer IDs that were used for more than one template. Primer ID resampling increased greatly when more than 10,000 converted templates were used as would be expected with the Primer ID sequence library of approximately 65,000 sequences. These limitations on template number are alleviated as the length of the Primer ID is extended beyond the 8-nucleotide length used in this simulation. Also, after removing the reads from offspring Primer IDs and limiting the resampling of Primer IDs by matching template number with Primer ID length, >90% of the raw reads are still available to use in alignments for creating consensus sequences to reduce method-introduced error.

Reduction in PCR and NGS error rate using Primer ID.

We sought an approach to make a direct measurement of the residual reverse transcriptase (RT) PCR/sequencing error rate after correcting errors by creating a consensus sequence. We used the 8E5 clonal cell line which produces HIV-1 particles that are defective for replication and spread (9). Table 3 shows the error rate of template consensus sequences estimated using as the template virion RNA produced by the 8E5 cell line and testing different RT and PCR DNA polymerase pairs. The env V1 to V3 libraries were designed for paired-end sequencing but without overlap. We estimated the error rate for the sequencing of these two regions separately. For the protease sequence libraries there were 181 bp of sequencing overlap between end/region 1 (R1) and end/region 2 (R2). In an additional analyses we discarded sequences with discrepancies within the overlap region to build a combined consensus sequence. The error rate was estimated for the two regions separately and for the combined sequences.

TABLE 3.

Summary of the measured error rates determined for the sequencing of the 8E5 HIV-1 RNA controls

Control variablea	Error rateb
	env (set 1)		env (set 2)		env (set 3)		Protease (set 1)
	V1/V2	C2/V3	V1/V2	C2/V3	V1/V2	C2/V3	R1	R2	combined
Consensus sequences (no.)	23,385	23,385	18,408	18,408	15,205	15,205	14,778	14,778	14,741
Mispriming (no.)	6	41	8	40	4	5	8	15	7
In-frame deletions (no.)	5	12	0	8	1	2	0	0	0
Frameshift (no.)	138	134	151	87	184	25	43	42	55
Consensus sequences (no. without in/del)	23,236	23,198	18,249	18,273	15,016	15,173	14,727	14,721	14,679
Length (no. of nucleotides)	265	256	265	256	265	256	265	256	340
Substitutions (no.)	206	748	73	412	158	311	426	488	565
Substitution rate (%)	0.003	0.013	0.002	0.009	0.004	0.008	0.011	0.013	0.011
Substitutions (%; excluding first and last two positions)		0.009		0.005		0.008

^aFor the number of consensus sequences, the template consensus sequences were pooled from two repeats of library construction and sequencing for each enzyme/region. Mispriming was defined as sequence reads at regions other than the targeted regions. An in-frame deletion was defined as a deletion that could be evenly divided by 3. A frameshift was defined as a deletion that could not be evenly divided by 3. Length was defined as the nucleotide size of the sequenced regions. in/del, insertions and/or deletions.

^bSet 1, Superscript III as the reverse transcriptase and KAPA2G robust as the first-round PCR polymerase; set 2, Supperscript III as the reverse transcriptase and Phusion as the first-round PCR polymerase; set 3, AccuScript as the reverse transcriptase and KAPA2G robust as the first-round PCR polymerase.

We obtained between approximately 15,000 to 23,000 template consensus sequences for each region/enzyme set combined by pooling the data from the two reactions. We observed that there were more (but still at a low level) mispriming events seen in all of the data sets using Superscript III than when using AccuScript reverse transcriptase. In the data sets, ≤1% of the consensus sequences had frameshifts, which we were able to discard in the analysis since they would be nonfunctional as coding domains. A small number of sequences had in-frame deletions from the V1 to the V3 region, and these were not included when estimating the substitution error rate. The substitution error rates for sequencing the V1/V2 region were between 0.002 to 0.004% for the three sets of enzymes. However, we noticed that a significant number of substitutions for reads at the C2/V3 end were clustered at the first nucleotide and last 2 nucleotides of C2/V3 consensus sequences, which could be caused by mis-priming. After these three positions were removed from the analysis, we found that the substitution rates for sets 1 and 2 at the C2/V3 regions were 0.009 and 0.005%, respectively. The substitution rate remained the same for set 3 at 0.008%. The protease R1 and R2 regions had substitution rates of 0.011 and 0.013%, respectively. The substitution rates were consistent between each pair of repeats, and the rate was not lower when we used the overlap region for further correction, indicating that the use of PCR resampling identified by Primer ID to create a consensus sequence was sufficient to remove virtually all of the PCR and sequencing errors. Overall, an error rate of 0.01% (1 in 10,000 nucleotides sequenced) represents an approximate estimate of the error rate using Primer ID and virion RNA, being the result of the combined error rate of host RNA synthesis and cDNA synthesis using RT in vitro. Transitions were the major type of substitution, representing ca. 80% of the substitutions, with A-to-G substitutions being the most common; A-to-T and T-to-A substitutions were the most common transversion substitutions as assessed in the coding strand (data not shown). In addition, the observed error distribution was comparable to the distribution predicted using the Poisson distribution given the measured error rate from each region (Table 4).

TABLE 4.

Poisson distribution of expected substitutions and observed substitutions per position from sequencing the 8E5 viral RNA control samples^a

No. of substitutions per position	RSB14 R1 V1/V2 region (265 bp)b		RSB14 R2 C2/V3 region (253 bp)c
	No. of positions from the Poisson distribution	No. of positions observed	No. of positions from the Poisson distribution	No. of positions observed
0	166	169	89	95
1	78	75	93	89
2	18	18	49	42
3	3	1	17	20
4	0	1	4	5
5	0	0	1	1
6	0	1	0	0
7	0	0	0	1

^aThe total number of consensus sequences was 13,471. The first and last two bases of the C2/V3 region were excluded from this analysis.

^bThe total observed errors were 124 for the V1/V2 region. The Poisson distribution was calculated based on the observed error rate, which for this experiment was measured at 0.003%.

^cThe total observed errors were 265 for the C2/V3 region. The Poisson distribution was calculated based on the observed error rate, which for this experiment was measured at 0.008%.

Using this measured method-induced error rate (0.01%) and the Poisson distribution, the expected number of random errors can be calculated and used to define cutoffs for detecting mutations at low abundance. We constructed a protease sequence data set for a sample from a protease inhibitor-treatment naive subject. We obtained a total of 3,178 consensus sequences, and the sequenced region was 340 nucleotides in length. Table 5 shows the expected distribution of random errors based on the residual error rate and the observed distribution of variants. Based on this measured error rate, we were not able to distinguish positions with one or two mutations as being more abundant than random errors from the method. However, positions with more than two mutations (>0.06% abundance) were likely to be real sequence variants within the viral sequence population. We further searched the template consensus sequences for protease surveillance drug resistance mutations (18). With the cutoff defined above, M46I (0.16%), M46L (0.09%), and I47V (0.13%) were detected at low abundance in the pretherapy viral population present in this plasma sample (Table 6). In addition, we calculated the exact Clopper-Pearson binomial confidence interval (19) for the true abundance of each minority mutation. We can also estimate the probability of detecting a true mutation at a certain abundance based on the Poisson distribution. In this example, we have a 95% chance of detecting a variant in the data set if the true abundance is ≥0.2% given a sampling of 3,178 template sequences.

TABLE 5.

Use of the estimated error rate and the Poisson distribution of errors to make cutoffs for low-abundance mutations in the HIV-1 protease region^a

No. of mutations per position	No. of positions from the Poisson distribution (errors)	No. of positions observed
1	79	68
2	12	35
3	1	20
4	0	13
≥5	0	92

^aFrom a protease inhibitor treatment-naive patient sample. The number of consensus sequences was 3,178. The estimated substitution rate was 0.01%. The length of the sequences was 340 bp.

TABLE 6.

Protease surveillance drug-resistant mutations observed^a

^aMutations with an abundance greater than the error cutoff are shaded.

^bThe total number of template consensus sequences was 3,178.

^cEach 95% confidence interval (CI) for the true abundance was calculated using the Clopper-Pearson method.

DISCUSSION

Advances in the Primer ID approach compared to previous studies.

The technology of using a degenerate block of nucleotides as indexing tags for NGS has been introduced in both DNA template sequencing (20) and RNA virus sequencing (6, 21). However, adoption of this technology has been slowed by several concerns. The cause of the wide distribution of Primer ID reads in the raw sequencing reads (Fig. 1) was unclear when this technology was first introduced. In addition, there is a concern that the random tags could anneal to the template and through this or other mechanisms induce PCR amplification skewing. Conversely, discarding low-abundance tags may cause a bias in interpreting allelic frequency (8, 22).

There are several major differences between our study and previous studies on the use and interpretation of a Primer ID sequence block (6, 8, 20). First, few of the pipelines in the previous studies considered offspring effects of sequencing/PCR errors within the Primer ID region, although this issue was recently addressed by Brodin et al. (23). We have demonstrated that Primer IDs at low abundance are related to abundantly read Primer IDs, but using a sliding cutoff model we observed the expected strong linear correlation between the number of template consensus sequences and the input template number (Fig. 5). Using a fixed cutoff can retain a large proportion of offspring sequences, introducing skewing from rerepresentation of templates with the abundant Primer ID reads as the apparent templates of offspring Primer IDs. Second, previous studies used the Roche 454 platform, which has a much lower throughput compared to the MiSeq platform used in the present study (21, 24, 25), which, along with the Ion Torrent platform, has a high error rate at homopolymer runs (26, 27) that is not a feature of MiSeq platform. When the number of raw sequence reads per template is not sufficient (due either to low capacity or too much multiplexing), the peak of the Primer ID read distribution will be shifted toward the low-abundance error end, making template recovery significantly less than optimal (Fig. 8a), and Primer ID resampling will be more likely to be included (Fig. 8b). Thus, we conclude that using certain platforms and not addressing and discarding offspring Primer IDs in the bioinformatics pipeline significantly compromises the important advantages gained in using the Primer ID strategy. In this regard we found that 30-fold coverage per converted template provides sufficient depth for creating a consensus sequence and allows >90% of the converted templates to be detected in the sequence output.

Advantages of the improved Primer ID approach compared to conventional NGS.

Our improved Primer ID approach has several advantages compared to conventional NGS in viral population studies. The Primer ID approach provides information about initial template sampling, providing the denominator in estimating relative abundance. A standard approach to sequencing viral RNA is to randomly fragment larger PCR amplicons before sequencing and align the sequencing reads with a template sequence (28). With this approach it is difficult to do linkage analysis (due to PCR recombination and the fragmentation) and estimate allelic frequencies (due to PCR amplification skewing, PCR resampling, and PCR and sequencing errors). Here, we show it is possible to construct the MiSeq library directly from the cDNA synthesis product and two rounds of PCR without fragmentation, which provides the opportunity to look at mutation linkages and recombination within the viral population.

A common approach to analyzing population diversity with NGS data is to set an arbitrary cutoff describing polymorphisms at a frequency of 1% or more (29–31). Such an approach assumes that the number of templates queried is well in excess of 100, which can be problematic when only small amounts of a clinical sample are available that are often of unknown viral RNA concentration and/or quality. Given the sensitivity of PCR, amplicons can routinely be generated with fewer than 100 copies of starting template, making an observation of 1% abundance meaningless in the absence of some knowledge of the number of templates queried. At the other extreme, there may be excess templates converted well beyond 100 to make the estimate of 1% accurate, but in this case much of the power of NGS is lost due to the fact that the detection of minor variants could be validated well beyond 1%. Similarly, the inability to use PCR resampling to correct sequencing errors confounds the interpretation of polymorphisms, especially in the case where small template numbers are inadvertently used; for example, an early error during the PCR would be represented in a significant fraction of the population, or stochastic sampling of the starting templates could over- or under-represent the true abundance of a variant.

Strategy for designing NGS using Primer ID.

The simulations and experiments in the present study provide a strategy for designing NGS using Primer ID. As seen in Fig. 8, the key of designing a proper Primer ID sequencing run is to have good template recovery. A typical design would be to have a Primer ID length of 8 nucleotides, with 15,000 RNA templates in a sample with an expectation of 20% conversion to final sequences (i.e., 3,000 templates queried), allocating 30 resampling reads on average per template (i.e., about 90,000 reads per sample), and then having bar codes to allow multiplexing of different samples up to the capacity of the instrument for the number of reads that can be obtained. In this design the recovery of converted templates is high (with 30-fold coverage of quality raw reads), while the number of templates lost to Primer ID resampling is low. The length of the Primer ID determines the number of possible Primer IDs in the cDNA primer library, and it can be lengthened if the number of templates to be sequenced is larger to reduce Primer ID resampling. The Primer ID read number cutoff can be set only after an analysis of the number of reads per template since the cutoff would be relatively low if template utilization were efficient in this design but would be high if template recovery were low, resulting in coverage much greater than 30-fold. Finally, the formation of offspring Primer IDs is not corrected by creating consensus sequences from the resampling; thus, it is directly influenced by the error rate of the platform. The model used to create the cutoff to avoid offspring Primer IDs may therefore vary depending on the sequencing platform.

Meaning of a measured error rate and use of the Poisson distribution.

The 8E5 cell line provides a largely homogenous source of viral RNA templates. The uncorrected error rate is from a combination of human RNA polymerase II errors during the synthesis of viral RNA in the cell, reverse transcriptase errors in the cDNA reaction, PCR errors, and sequencing errors. The corrected error rate, which we could measure directly, was reduced to around 1 in 10,000 nucleotides using the Primer ID approach, close to the reported error rate for reverse transcriptase in an enzyme reaction (32, 33), which cannot be corrected by the Primer ID approach. Using the measured error rate and the Poisson distribution, we can now identify cutoffs for predicting the number of error-introduced minority variants in the final consensus sequence data set of individual genomes that were sequenced. This approach allows the power of NGS capacity to be applied with much greater accuracy to the question of variants present at low abundance while avoiding the use of indirect methods/models to try to account for inferred errors.