Occupational radon exposure and lung cancer mortality: estimating intervention effects using the parametric G formula

Abstract

Background

Traditional regression analysis techniques used to estimate associations between occupational radon exposure and lung cancer focus on estimating the effect of cumulative radon exposure on lung cancer, while public health interventions are typically based on regulating radon concentration rather than workers’ cumulative exposure. Moreover, estimating the direct effect of cumulative occupational exposure on lung cancer may be difficult in situations vulnerable to the healthy worker survivor bias.

Methods

Workers in the Colorado Plateau Uranium Miners cohort (N=4,134) entered the study between 1950 and 1964 and were followed for lung cancer mortality through 2005. We use the parametric g-formula to compare the observed lung cancer mortality to the potential lung cancer mortality had each of 3 policies to limit monthly radon exposure been in place throughout follow-up.

Results

There were 617 lung cancer deaths over 135,275 person-years of follow-up. With no intervention on radon exposure, estimated lung cancer mortality by age 90 was 16%. Lung cancer mortality was reduced for all interventions considered, and larger reductions in lung cancer mortality were seen for interventions with lower monthly radon exposure limits. The most stringent guideline, the Mine Safety and Health Administration standard of 0.33 working level months, reduced lung cancer mortality from 16% to 10% (risk ratio 0.67; 95% confidence interval 0.61, 0.73).

Conclusions

This work illustrates the utility of the parametric g-formula for estimating the effects of policies regarding occupational exposures, particularly in situations vulnerable to the healthy worker survivor bias.

The association between radon gas exposure and lung cancer has been well-documented in cohorts of underground uranium miners.^1-7 However, traditional regression analysis techniques used in these studies focus on quantifying cumulative exposure-response functions that do not directly address the types of questions that concern regulators. The public health impacts of different policy options regarding radon concentrations in the workplace may be more useful to regulators than the estimated change in the excess relative rate of lung cancer per unit increase in cumulative exposure to radon.

We apply the extended parametric g-formula^8,9 to estimate the risk of lung cancer death had several historical radon exposure standards been in place throughout follow-up in an important cohort study of underground miners. The policy interventions that we consider are specified in terms of caps on monthly occupational radon exposure rather than limits on cumulative exposure (i.e., “limit radon exposure to X working level months per month while at work, and set monthly radon exposure to 0 working level months when not at work”). The interventions we consider are “threshold interventions”¹⁰ in which the intervention on radon exposure for a given month depends on the observed exposure for that month.

The extended parametric g-formula has been used to estimate cumulative risk under threshold interventions in diverse substantive areas ^11-15 . This approach was described by Robins⁹ to extend the standard parametric g-formula estimator to allow interventions to depend on the natural value of exposure. A formal discussion of the identifying conditions under which the extended parametric g-formula estimator can have a causal interpretation can be found in recent work by Richardson and Robins ¹⁶ and Young.¹⁷ Our implementation of the parametric g-formula also accommodates competing risks, as outlined by Taubman ¹¹ and Cole.¹⁵

Here, we use the g-formula to estimate cumulative incidence of lung cancer mortality under various intervention scenarios and compute risk difference and risk ratio measures, which are often the most relevant estimates to present to the lay public and policy makers. These effect measures have intuitive interpretations as the estimated difference (or ratio) in cumulative incidence that would have been seen had the same population of miners been exposed to different dynamic exposure regimes corresponding to hypothetical industry guidelines.

Estimates of attributable risk due to lung cancer derived in previous reports, such as the Biological Effects of Ionizing Radiation (BEIR) IV and BEIR VI reports, and life table calculations also aim to facilitate communication of the public health impact of radon exposure. However, the BEIR reports estimate the attributable fraction of radon-related excess lung cancer deaths, which conforms to change in risk given complete elimination of radon, while we focus on public health impacts of plausible policy interventions (i.e., reduction in radon exposure to specific limits, rather than elimination of radon exposure).

In this work, we use the extended parametric g-formula to compare observed lung cancer mortality in the Colorado Plateau Uranium Miners cohort to estimated lung cancer mortality if radon exposure had been limited to three historical radon exposure standards in the U.S.

METHODS

Study population

The Colorado Plateau uranium miners’ cohort includes 4,137 men who worked in an underground uranium mine on the Colorado Plateau for at least 1 month prior to January 1, 1964 and agreed to a health screening between 1950 and 1960. Miners began follow-up at the midpoint of the year of age in which their first health screening occurred or, if the miner was under age 18 at their first health screening, age 18. Miners were followed until death or December 31, 2005 as described in a previous report.⁷ Age, calendar year at cohort entry and race were ascertained during the health screening. In the current study we administratively censor workers at 90 years of age to avoid imprecise estimates at older ages when few miners were alive and at risk for lung cancer mortality (n=84; 5 lung cancer deaths). Three miners whose estimated cumulative radon exposure exceeded an implausible level of 10,000 working level months were excluded.

As an analysis of existing de-identified data, this study was granted an exemption by the University of North Carolina's Institutional Review Board.

Outcome ascertainment

Vital status was ascertained using Social Security Administration, Internal Revenue Service, National Death Index, and Health Care Financing Administration records.^3,7 For follow-up through 1990, death certificates were reviewed by a nosologist and underlying cause of death was coded using the International Classification of Diseases (ICD) codes in use at the time of death.^3,4 Additional follow-up through 2005 was performed through linkage to the National Death Index and the Social Security Administration mortality file.⁷ Miners who were confirmed alive in 1979 (when the National Death Index began) and not found in these databases were presumed to be alive at the end of follow-up. Fourteen miners were lost to follow-up prior to 1979 and no cause of death was reported for 22 miners. Lung cancer mortality was defined as an ICD code for malignant neoplasm of trachea, bronchus, and lung: ICD-6 codes 162-163; ICD-7 codes 162.0, 162.1, 162.8, and 163; ICD-8 code 162; ICD-9 code 162; and ICD-10-CM codes C33-C34.

Radon exposure assessment

Details of radon exposure assessment in this cohort have been described previously. ^3,4,7 Briefly, radon levels in Colorado plateau uranium mines were measured between 1951 and 1968. During this time period, 43,000 measurements were made in 2,500 mines. These measurements were used to estimate annual average radon concentrations in each mine; if multiple measurements were available in the same year for a mine, those measurements were averaged to produce a summary measurement¹⁸.

The cumulative radon exposure for each miner was estimated based on the mine-specific annual radon concentration estimates and the miner's employment history. Cumulative exposure to radon progeny was expressed in units of the working level month, which is equivalent to experiencing one “working level” for 170 hours. A working level is the combination of radon decay products in one liter of air that would result in emission of 20.8 microjoules of potential alpha energy exposure per cubic meter of air. Occupational radon exposure was assumed to be 0 after cessation of employment. Cumulative radon exposure prior to study entry was assigned to the day prior to study entry.

Statistical methods

We use the parametric g-formula to estimate the proportion of miners experiencing lung cancer mortality under four exposure scenarios: 1) no intervention on exposure; 2) monthly radon exposure capped at the radiation protection guideline recommended by the first report of the Federal Radiation Council in 1960 (3 rems per 13 weeks = 2 working level months)¹⁹; 3) monthly radon exposure limited to the Federal Radiation Council's 1967 recommendation, which was the basis for the U.S. Environmental Protection Agency's 1971 guidance on radiation protection for underground uranium mining (12 working level months per year/12 months = 1 working level month)^20,21; and 4) monthly radon exposure capped at the U.S. Mine Safety and Health Administration exposure standard adopted in the 1970s and still used in 2013 (4 working level months per year/12 months = 0.33 working level months).²² Using the g-formula, we estimate the lung cancer mortality under the following dynamic treatment regime: if at work, radon exposure level is not allowed to exceed the intervention level, and if not at work, radon exposure level is set to 0.

The steps to implement the extended parametric g-formula have been described in detail elsewhere. ^11-15 First, we parametrically model the conditional probabilities of the exposure, outcomes, and work status using the observed data (see the eAppendix for details). We use the estimated conditional probabilities to predict work status, exposure, other death, and lung cancer mortality under the “natural course”, an intervention that prevents censoring due to drop out but does not intervene on exposure status, in a Monte Carlo sample of 50,000 miners drawn with replacement from the existing cohort. The large Monte Carlo sample is used to minimize simulation error. We estimate the distributions of baseline covariates nonparametrically using the empirical distribution in the Monte Carlo sample. We compare these predicted values with the observed data to assess the fit of the parametric models.²³

Next, in the same Monte Carlo sample of miners, we estimate the cumulative incidence of lung cancer had each of the 3 historical radon exposure guidelines described above been in place from cohort entry through the end of employment. Note that exposure accrued prior to entry is not influenced by the policy interventions under study. For each of these scenarios, if a miner's estimated monthly exposure exceeds the monthly exposure limit, the miner's exposure for that month is set to the intervention exposure limit. If the miner's estimated monthly exposure is below the monthly limit, no intervention occurs for that miner in that month. This might be conceptualized as an intervention under which the miner is removed from the mine when the limit is reached for the month and allowing him to return to work the following month.

The parametric g-formula uses the following process to estimate lung cancer mortality under each intervention scenario. 1) Exposure and work status are assigned using the conditional probabilities estimated from the parametric models above. 2) If the miner is not at work during that month, exposure is set to 0. If the miner is at work, exposure is estimated using the conditional probabilities estimated from the parametric models discussed above. If the predicted dose for any month exceeds the intervention level, it is set to the intervention level, otherwise, the miner's exposure is not intervened on for that month. 3) The probability of lung cancer mortality is estimated based on the joint distribution of covariates. 4) An indicator of lung cancer death is drawn from a Bernoulli distribution with the probability estimated from Step 3. 5) The cumulative incidence of lung cancer mortality is estimated in the simulated cohort.

We estimate cumulative lung cancer mortality for each intervention scenario using an extension of the Kaplan-Meier approach that accommodates competing risks and yields an estimate of the cumulative subdistribution of lung cancer mortality. ^11,24 Lung cancer mortality is compared between each intervention scenario and the natural course using risk differences and risk ratios, and 95% confidence intervals are computed using standard errors estimated by the standard deviation from results of the procedure conducted using 200 nonparametric bootstrap resamples. SAS version 9.3 (SAS Institute, Inc., Cary, North Carolina) was used for all analyses.

RESULTS

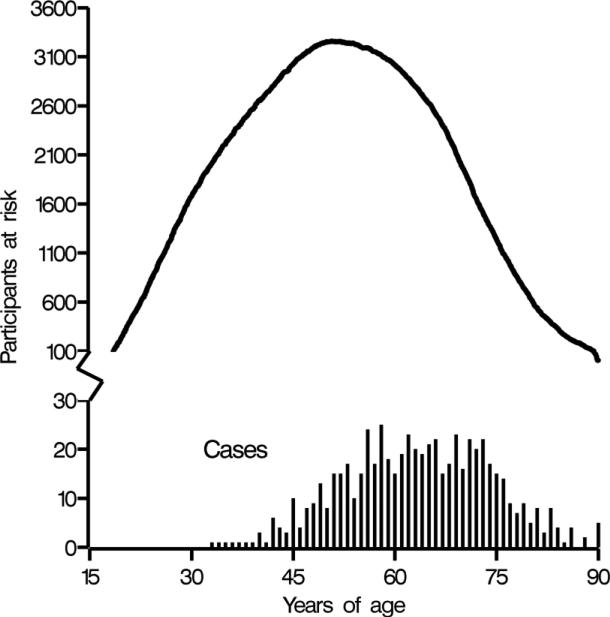
In total, 4,134 male miners entered follow-up between 1950 and 1964. Table 1 describes the characteristics of the study population at baseline. Most of the cohort had been occupationally exposed to radon prior to study entry (94%) with a median cumulative radon exposure of 154 working level months. The median time between hire and cohort entry was 1.5 years (interquartile range: 0.3 – 3.9). The cohort was followed for 135,275 person-years and experienced 617 lung cancer deaths and 14 losses to follow-up. The median (interquartile range) age at lung cancer death was 71 (63–90) years, with the youngest death occurring at 33 years (Figure 1).

TABLE 1.

Characteristics of the Colorado Plateau Uranium Miners Cohort at Study Entry (n = 4,134)

Characteristica
Age	33 (25–43)
Calendar year	1958 (1955–1958)
White; no. (%)	3,358 (81)
Smoked; no. (%)
Never	962 (23)
Ever	3,165 (77)
Missing	10 (<1)
Radon exposure prior to study entry
Previously exposed; no. (%)	3,899 (94)
Working-level monthb	154 (51–485)

^aMedian (interquartile range), unless otherwise noted.

^bWorking-level months of cumulative prior radon exposure among previously exposed miners.

Figure 1.

Number of cohort members at risk for lung cancer mortality and number of lung cancer deaths by age in the Colorado Plateau Uranium Miners cohort between 1950 and 2005

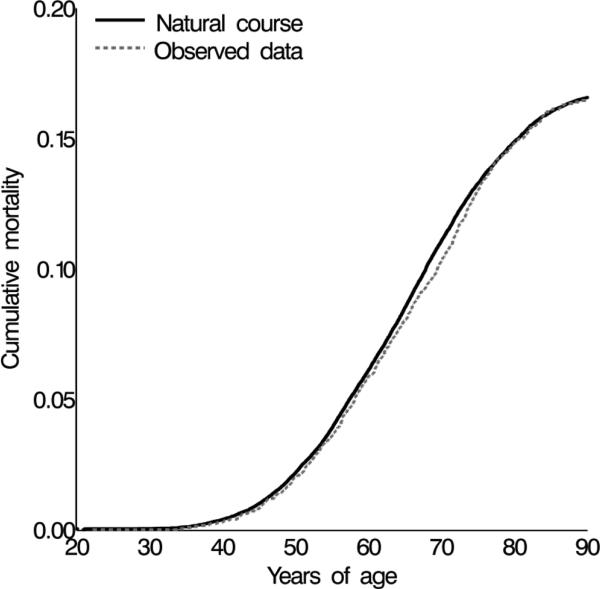
The natural course replicates the observed data closely. Differences in the distribution of person-months by age, calendar year, race, smoking status, employment, and radon exposure between the natural course and the observed data were negligible (Table 2). Figure 2 illustrates the similarity in predicted lung cancer mortality between the observed data and the model estimates from the natural course.

TABLE 2.

Distribution of Person-Months for Observed Data and Simulated Scenariosa in the Colorado Plateau Uranium Miners Cohort (n = 4,134) over 135,275 Person-Years of Follow-Up Between 1950 and 2005

			Intervention Exposure Level
Characteristicb	Observed Data	Natural Course	≤ 2 Working-level months	≤ 1 Working-level month	≤ 0.33 Working-level months
Age	52 (41–63)	53 (41–65)	54 (42–66)	54 (42–66)	54 (42–66)
Calendar year	1975 (1965–1986)	1975 (1965–1988)	1976 (1966–1989)	1976 (1966–1989)	1976 (1966–1990)
White; %	80	79	79	79	79
Ever smoked; %	74	73	74	74	74
Radon exposure
Employed; %	16	14	11	9	5
Working-level monthsc	3.42 (1.60–7.04)	3.47 (1.53–8.23)	1.34 (0.84–1.92)	0.81 (055–1.00)	0.31 (0.23–0.33)

^aSimulated interventions correspond to historical radon exposure guidelines.

^bMedian (interquartile range), unless otherwise specified.

^cMedian (interquartile range) dose in working-level months during exposed person-months.

SD, standard deviation.

Figure 2.

Cumulative lung cancer mortality in the observed data and simulated natural course in the Colorado Plateau Uranium Miners cohort between 1950 and 2005

Radon exposure was reduced from a median of 3.47 working level months per month under the natural course to 1.34, 0.81, and 0.31 working level months per month, under the intervention limits of 2, 1, and 0.33 working level months, respectively. Because the interventions caused miners to live longer, the distribution of person-months shifted toward older ages, later calendar years, and a smaller proportion of months employed (Table 2).

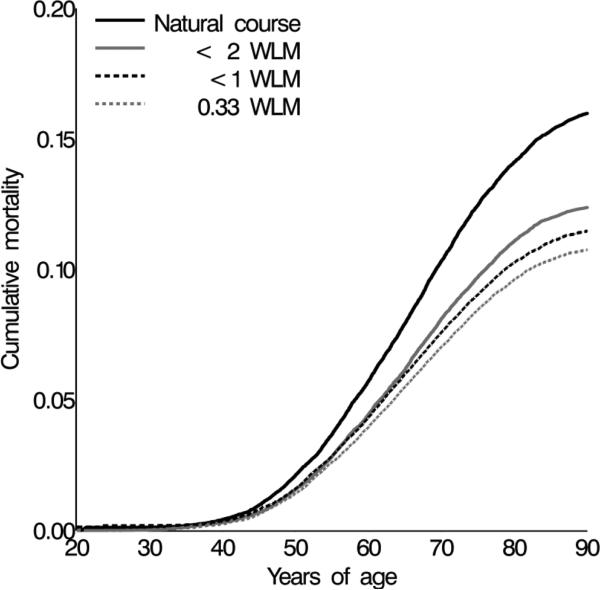
With no intervention on radon exposure, estimated lung cancer mortality by age 90 was nearly 16%. Interventions limiting radon exposure to historical radon exposure guidelines resulted in lower cumulative lung cancer mortality by age 90. With incremental decreases in radon exposure limits, there was a corresponding reduction in lung cancer mortality under the three interventions (Figure 3). The risk of lung cancer death by age 90 decreased by 23% (risk ratio = 0.77: 95% CI = 0.72, 0.81), 28% (risk ratio = 0.72: 95% CI = 0.68, 0.77), and 33% (risk ratio = 0.67: 95% CI = 0.61, 0.73), when each miner's monthly radon exposure was capped at 2, 1, and 0.33 working level months, respectively (Table 3). In the simulated cohort, we estimate that capping exposure at the Federal Radiation Council guidelines of 2 and 1 working level months would have prevented 149 and 187 lung cancer deaths by age 90, respectively, while capping exposure at the Mine Safety and Health Administration standard of 0.33 working level months would have prevented 216 lung cancer deaths over the study period.

Figure 3.

Cumulative lung cancer mortality in the simulated natural course and intervention scenarios in the Colorado Plateau Uranium Miners cohort between 1950 and 2005, WLM is working level months

TABLE 3.

Cumulative Lung Cancer Mortality by Age 90 Years Under each Radon Exposure Scenarioa in the Colorado Plateau Uranium Miners Cohort Between 1950 and 2005

Intervention Exposur Levelb	% Risk of Lung Cancer	Risk Difference	(95% CI)	Risk ratio	(95% CI)
Natural course	15.98	0		1.00
≤2 Working-level months	12.37	–3.6	(–4.4 to –2.8)	0.77	(0.72 to 0.81)
≤1 Working-level months	11.47	–4.5	(–5.3 to –3.7)	072	(0.68 to 0.77)
≤0.33 Working-levele months	10.75	–5.2	(–6.1 to –4.3)	0.67	(0.61 to 0.73)

^aSimulated interventions correspond to historical radon exposure guidelines.

^bInterventions were implemented by limiting monthly radon exposure to the intervention level while the miner was at work; when the miner was not at work exposure was set to 0.

DISCUSSION

We applied the parametric g-formula to estimate the effect of radon exposure interventions on lung cancer mortality in the Colorado Plateau Uranium Miners cohort. By limiting monthly radon exposure to 2, 1, and 0.33 working level months, we estimated that lung cancer mortality would have been reduced by 23%, 28%, and 33%, respectively. These reductions are notable given that 77% of the cohort was classified as ever smokers. Had the most stringent of the guidelines, the Mine Safety and Health Administration standard of 0.33 working level months, been in place (and followed) throughout the study period, we estimate that 216 fewer lung cancer deaths would have occurred than were observed under the actual history of regulation. Our findings support historical recommendations to lower radon exposure limits and suggest that the Mine Safety and Health Administration standard prevents a substantial number of lung cancer deaths among people who are occupationally-exposed to radon.

The parametric g-formula provides estimates of the cumulative incidence of lung cancer death for exposure scenarios under several assumptions. The first assumption, sometimes called the consistency assumption, requires that exposure levels set by investigators in the counterfactual scenarios correspond to well-defined interventions. For our study interventions, we capped monthly radon exposure at a specified number of working level months. This scenario could be achieved by using personal radon monitoring devices and removing the worker from the mine when the limit is reached and then returning him to work the following month. One could imagine other scenarios, such as job sharing/switching, respirator use, improving ventilation with ambient monitoring, or gradually reducing exposure by limiting the number of hours worked when a miner's exposure approaches the intervention level. Our analysis assumes that these methods of capping exposure would produce equivalent results.

We also assumed that miners’ potential outcomes were independent of the exposure they received, conditional on observed variables. This assumption, known as the exchangeability assumption, implies no unmeasured confounding or selection bias, and means that experiences of participants receiving low exposures represent the potential outcomes of participants receiving high exposures, had they received low exposures. Because we did not have information on time-varying smoking status, we included smoking as a fixed variable at study entry under the assumption that most workers started smoking prior to their employment in the mine. The exchangeability assumption may have been violated if there were differences in smoking status over time between miners with high and low radon exposure. It is also possible that an unobserved variable such as health status or exposure to silica may have been associated with exposure intensity or duration and lung cancer mortality. In addition, the estimates presented here are conditional on miners surviving exposure between the date of hire and cohort entry. Although this could result in selection bias, it is unlikely that radon exposure would have caused lung cancer deaths during this brief period.

This version of the parametric g-formula assumes that the parametric models used to predict relevant variables are correctly specified. To obtain a consistent point estimate, we must correctly specify four parametric models (for work status, exposure, death, and lung cancer death). We used monthly linear models to predict the natural log of radon dose and logistic models for work status, non-lung cancer deaths, and lung cancer deaths. We assume no interaction between radon and smoking, that the effects of radon persist over time, and that there is no variation in the effect of radon on lung cancer mortality with time since exposure or exposure rate. Relaxing this assumption to allow interaction between cumulative radon exposure and exposure rate in the model to predict lung cancer mortality (as discussed in the BEIR VI report) did not alter the results. Covariate distributions and cumulative incidence functions in the observed data closely matched our predicted natural course, suggesting that the models may be adequately specified, but the modeling assumptions are not testable. Confidence intervals are narrow partly because this method is fully parametric, and the additional modeling assumptions reduce the variance of the estimate.

Estimates of lung cancer mortality in the intervention scenarios may be subject to error from at least two sources. First, lung cancer mortality under the intervention scenarios is predicted based on observed lung cancer mortality for miners who were exposed to low doses of radon. There was a substantial proportion of exposed person-time with radon exposures below the intervention levels (31% of exposed miners had radon levels ≤2 working level months). However, results may be biased if miners who received low doses of radon exposure were systematically different from miners who received higher doses, beyond measured variables. Second, larger exposure measurement error at low doses of exposure could imply that the dose-response relationship between radon exposure and lung cancer mortality is incorrectly specified.

Studies of the health effects of occupational exposures are subject to the healthy worker survivor bias, in which work status is both a time-varying confounder and a mediator of the relationship between exposure and outcome. In addition, traditional analyses of occupational data are often subject to bias due to nonpositivity, or zero probably of exposure within strata of a confounder (here, when participants are not at work). Naimi et al. demonstrated that Cox proportional hazards models with or without adjustment for work status and marginal structural Cox proportional hazards models fit using inverse probability weights produced biased estimates in situations characterized by the healthy worker survivor effect. ²⁵

The g-formula appropriately accounts for time-varying confounding by work status by allowing investigators to set exposure at each time point. In addition, the g-formula allows estimation of the effects of interventions that avoid violations of the positivity assumption. The positivity assumption is violated if 1) radon exposure is impossible when the miner is not working; 2) time-varying work status is a confounder; and 3) the interventions under consideration require that an individual have non-zero exposure when not at work. The interventions considered here did not require the miners to be exposed when they were not at work and therefore did not induce bias due to nonpositivity.²⁶

The parametric g-formula is subject to the g-null paradox, in which it will reject the null hypothesis (of no causal effect of exposure on outcome) even when true when the sample is sufficiently large. However, because the existing literature provides strong evidence that the causal null hypothesis is false (i.e., that radon does affect lung cancer mortality),^{2-4,6,7,27-31} use of the parametric g-formula is justified in this setting.

This work estimates the effect of reducing occupational radon exposure to specific monthly doses on lung cancer mortality. Instead of estimating the reduction in mortality per unit of cumulative radon exposure (as in standard regression models) or the reduction in mortality if no miners had been exposed to radon (as in attributable fraction calculations), we used the g-formula to compare mortality under interventions on radon exposure that correspond to potential (and, in this case, historical) regulatory limits. The estimated reduction in mortality associated with applying various policy guidelines demonstrates the parametric g-formula's ability to estimate intervention effects and provide intuitive results for policy makers.