Abstract
Objective
We present a proof of concept for a novel method of predicting the onset of pathological tremor using non-invasively measured surface electromyogram (sEMG) and acceleration from tremor-affected extremities of patients with Parkinson’s disease (PD) and Essential tremor (ET).
Approach
The tremor prediction algorithm uses a set of spectral (fourier and wavelet) and non-linear time series (entropy and recurrence rate) parameters extracted from the non-invasively recorded sEMG and acceleration signals.
Main results
The resulting algorithm is shown to successfully predict tremor onset for all 91 trials recorded in 4 PD patients and for all 91 trials recorded in 4 ET patients. The predictor achieves a 100% sensitivity for all trials considered, along with an overall accuracy of 85.7% for all ET trials and 80.2% for all PD trials. By using a Pearson’s chi-square test, the prediction results are shown to significantly differ from a random prediction outcome.
Significance
The tremor prediction algorithm can be potentially used for designing the next generation of non-invasive closed-loop predictive ON-OFF controllers for deep brain stimulation (DBS), used for suppressing pathological tremor in such patients. Such a system is based on alternating ON and OFF DBS periods, an incoming tremor being predicted during the time intervals when DBS is OFF, so as to turn DBS back ON. The prediction should be a few seconds before tremor re-appears so that the patient is tremor-free for the entire DBS ON-OFF cycle as well as the tremor-free DBS OFF interval should be maximized in order to minimize the current injected in the brain and battery usage.
1. Introduction
Parkinson’s disease (PD) and Essential tremor (ET) are the two most common progressive neurological movement disorders. No cure is available at present for either of the diseases. The main symptoms in PD include tremor, rigidity, imbalance, and slowness of movement. PD tremor is generally a mild resting tremor with slow, regular oscillations of 4–6 Hz. It might also be present during posture or voluntary movements (postural/action tremor) which is typically in the 7–11 Hz frequency range. Dopamine replacement therapy, using the dopamine precursor levodopa is the mainstay of therapy in early stage PD. However, for advanced PD patients a surgical procedure called deep brain stimulation (DBS) can provide significant benefit for all motor symptoms while reducing or eliminating dyskinesias and improving quality of life [1, 2]. The Food and Drug Administration (FDA) approved DBS for PD in 2001.
ET is characterized by a tremor of 4–12 Hz, that is present only when the affected muscle is exerting effort (postural/kinetic tremor)[3]. Treatments that give relief and improve quality of life in ET patients include drug therapies such as propranolol and primidone as well as surgical procedures, such as thalamotomy (an irreversible lesion in a small part of the thalamus) [4] and deep brain stimulation (DBS) [5]. The FDA approved DBS as a treatment for ET in 1997.
DBS uses a surgically-implanted battery-operated medical device that delivers high frequency electrical stimulation (HFS) through implanted electrodes to target areas in the brain that control movement [6]. A DBS system consists of three components: the lead, the extension, and the neurostimulator. The lead contains 4 thin insulated electrodes whose tips are positioned within the targeted brain area (electrodes 0, 1, 2, 3). The neurostimulator, similar to a cardiac pacemaker, is implanted under the skin below the collarbone or over the abdomen. The extension is an insulated wire that is passed under the skin and connects the lead to the neurostimulator. The preferred targets in the brain for placement of a DBS lead are the internal segment of globus pallidus (GPi) and the subthalamic nucleus (STN) for PD patients, and the ventral intermediate nucleus (VIM) of the thalamus for ET patients.
The only FDA approved DBS system for PD/ET is manufactured by Medtronic, Inc. Their Activa system operates open-loop. The clinician chooses the optimal electrode combination and sets the stimulation parameters (pulse amplitude, duration and frequency), based on subjective and objective clinical observations to ensure that the patient receives maximal benefit and minimal side effects. DBS is provided continuously over time and the stimulation parameters remain constant over time until the next visit of the patient to the clinician. Thus, the current DBS technology is neither adaptive to the patients’ needs nor to the patients’ disease progression over time.
In order to adapt to the patients’ condition, current DBS systems must be redesigned so as to include a closed-loop feedback control where the patients’ symptoms are continuously monitored and the stimulation is adapted in response to its variations. To design a closed-loop DBS system, it is necessary to find a suitable physiological signal that can be easily measured and has predictive information on tremor reappearance once DBS is OFF. One such feedback signal could be the actual neuronal brain activity measured from individual neurons (micro-recording) represented by the cell firing, or a group of neurons (macro-recording) represented by the local field potential, at the site where the DBS electrodes are implanted. However, the measurement of these signals by means of DBS electrodes (during DBS OFF times) require changes to the current FDA approved DBS electrode and pulse generator system. It would also require decoding brain activity and simultaneous sensing-stimulation protocols. Alternatively, muscular and kinematic signals measured by means of surface-electromyogram (sEMG) and acceleration (acc) can be recorded non-invasively from the patients’ symptomatic extremities. These signals are known to carry predictive information on tremor reappearance [7, 8] and can thus be potentially used for closed-loop ON-OFF control of DBS.
The design of a closed-loop DBS controller has been a highly pursued field over the past decade because of the fact that although the current paradigm is highly successful, it is not adaptive to the patients’ condition. Some of the significant work towards this goal [9] include optimizing the stimulation pattern, such as phase resetting and delayed feedback [10, 11, 12], using a pulse train with random frequency [13] and use of local field potentials as feedback for the design of a closed loop DBS system [14] . However the results of these efforts are solely based on computational models and if tested on human subjects, would require measurement of neuronal signals from the implant site in the brain, which has the drawbacks discussed earlier. In a study on two parkinsonian (MPTP treated) non-human primates [15], the authors showed that cortico-pallidal closed-loop DBS has a significantly greater effect on akinesia and on cortical and pallidal discharge patterns than standard open-loop DBS. In all the trials, the stimulus was applied through two electrodes located within the GPi in response to an action potential in GPi or primary motor cortex (M1). Hence this system involves multiple electrodes instead of the usual clinically used one electrode.
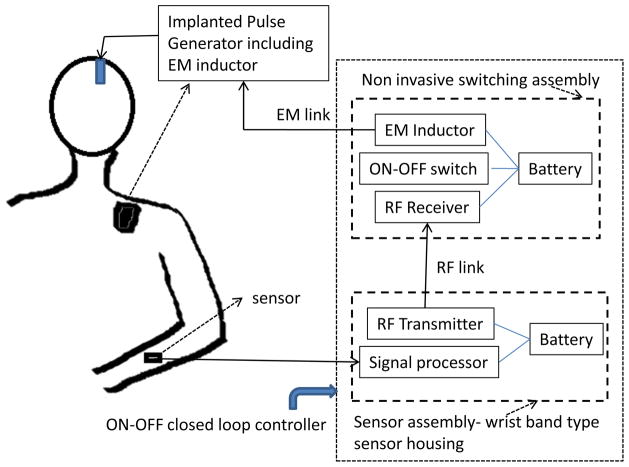
Our approach consists of updating the existing FDA approved DBS system by using external non-invasively measured signals, such as sEMG and acc, as feedback signals to predict re-emergence of tremor when DBS is OFF. Since this does not modify the actual stimulation generator and the implanted electrodes, it can be implemented as an add-on subsystem for the FDA-approved DBS systems. A schematic of such a system is shown in figure 1 in which, the signal acquisition, processing and ON/OFF command generation can be integrated in a microchip housed inside the sensor assembly of figure 1 [16] mounted non-invasively over the measurement site as a wrist-band type housing (protected under patent application 8391986 approved in December 2012). The control ON/OFF command is sent via radio frequency (RF) link to the switch assembly which, in turn, switches DBS ON and OFF via an elecrtromagnetic (EM) induction coupling to the EM inductor coil commonly used in all present implanted pulse generator (IPG) devices (for receiving ON-OFF manual commands from physician or patient, from a manual switching device such as Medtronic therapy controller Model 7438).
Figure 1.
A schematic of a closed loop ON-OFF DBS system that uses external non-invasively measured signals for control. The ON-OFF switch turns DBS OFF at pre-determined delay (optimized per each patient) and turns it ON when tremor is predicted via a command through the RF link from the signal processing unit. The switching assembly is non-invasively placed above implanted pulse generator, at location where physician/patient presently performs manual ON-OFF switching as required. Note: EM - Electromagnetic.
In this paper, we explore the possibility of an external signal based closed loop ON-OFF type DBS system by designing a tremor prediction algorithm which can be implemented in the signal processing unit of such a system as outlined in figure 1. Such a tremor predictor must achieve the following objectives:
Goal 1: Tremor onset should be predicted just a few seconds before it is actually detected so that the patient does not experience any discomfort due to tremor.
Goal 2: Voluntary movement and posture initiation in the absence of tremor should not be predicted as tremor.
This will produce a novel non-invasive add-on system to the existing DBS device, that will turn the stimulation ON for a fixed time interval (optimized for each patient), switch it OFF and track a set of parameters calculated from the sEMG and acc in real time. It will automatically turn DBS back ON before the tremor re-appears such that the tremor-free DBS-OFF duration is maximized. We chose to use tremor as an indicator for turning DBS ON because it is the only symptom in ET and the symptom that re-appears the fastest after switching DBS OFF in PD patients with dominant tremor [17].
Our algorithm uses a set of parameters extracted from sEMG and acc signals to predict tremor onsets. It is to be noted that our objective is to predict tremor and not detect it. Hence, we require more than basic spectral parameters which can predict tremor before it actually occurs. At the same time, we also need to avoid movements being predicted as tremor. We show that the designed prediction algorithm successfully predicts tremor (Goal 1) during DBS-OFF period for all the trials considered (with data collected from human subjects). At the same time it does not predict too early (Goal 2) for 85.7% of the ET trials and 80.2% of the PD trials.
Previously, we have shown that the lower frequency bands of the sEMG signal, reconstructed by using a discrete wavelet transform, contains predictive information about tremor re-appearance in an ET patient with DBS implants, after the stimulation is switched OFF [8]. We also showed that by using a combination of two types of entropy measures, tremor onset could be successfully predicted from sEMG recordings from an ET patient [18]. While both [8] and [18] are concerned with ET patients only, the present work also covers PD patients. Furthermore, in our previous work [8],[18] we did not have acceleration data, we did not describe the prediction algorithm in full detail and used only simple preprocessing (wavelet coefficient [8], wavelet entropy and approximate entropy [18]). An extended Kalman filter approach was used in [19] to estimate the amplitude and phase of pathological tremor. The objective was to design a real time tremor detection algorithm in an ET patient using sEMG and acc. Although this work was for tremor compensation using functional electrical stimulation of the muscles, it has the same flavor as our work. This approach was able to suppress tremor by 57% and was tested in only one ET patient. Limited number of parameters in the above mentioned work are not enough to predict tremor for a wider patient population with different pathologies and varying extents of tremor. Hence we extend our previous work by employing additional parameters, as described in section 2.4. This not only extends our previous prediction algorithm to PD but also allows for improving performance in ET. To the best of our knowledge, this is the first study with a considerable number of patients with varying degrees of tremor, tested for such an application.
2. Methods
2.1. Subjects
Eight patients were recruited for this study. Four PD and two ET patients were recruited from the Movement Disorder Clinic at Rush University Medical Center and two ET patients from the University of Illinois at Chicago hospital. Patient details are listed in table 1. Informed consents for this study’s protocol approved by the IRB of respective institutes were obtained from all patients. The four PD patients had DBS electrodes (Medtronic DBS lead model 3389) stereotactically implanted in the STN while the four ET patients had the electrodes placed in the VIM of the thalamus. All patients had significant tremor in one or both arms and their symptoms were well controlled by a combination of stimulation and medication. All of them have their stimulation on for the entire day as well as at night while sleeping.
Table 1.
Patient details.
| Patient# | age | gender | DBS parameter | active contacts | DBS implant | hand tested | ||
|---|---|---|---|---|---|---|---|---|
| amplitude (Volts) | frequency (Hz) | pulse width (μs) | ||||||
| PD1 | 46 | M | 2.8 | 180 | 80 | 1-0+ | 2008 | R |
| PD2 | 45 | M | 2.5 | 185 | 60 | 1-2-C+ | 2002 | L |
| PD3 | 52 | F | 2.8 | 185 | 120 | 0-C+ | 2004 | R |
| PD4 | 60 | F | 2 | 145 | 60 | 1-3-C+ | 2009 | R |
| ET1 | 64 | M | 2 | 150 | 90 | 2-C+ | 2002 | L |
| ET2 | 67 | M | 1,1.4 (L,R) | 130 | 120 | 1-C+(L), 5-6-C+(R) | 2010 | L,R |
| ET3 | 51 | M | 2.3 | 185 | 60 | 9-C+ | 2010 | R |
| ET4 | 62 | F | 2 | 185 | 90 | 0-C+ | 2007 | R |
2.2. Experimental setup
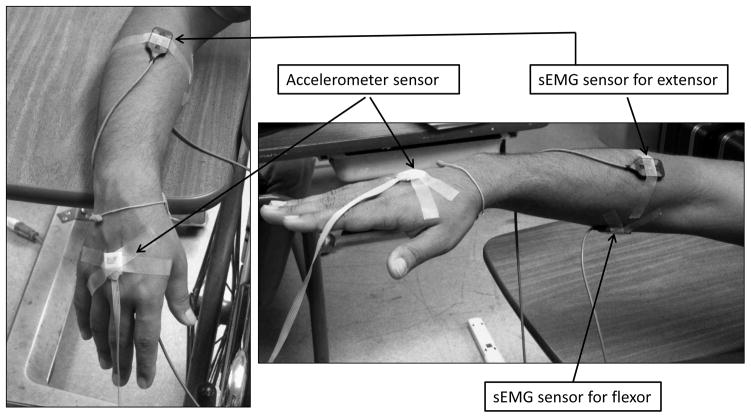
All PD patients and three ET patients had one recording session each and one ET patient had two recording sessions (one for each arm) in the Neural Control of Movement Laboratory (NCML) at the University of Illinois at Chicago. On the testing day, the patients were on their usual medication and a series of sEMG recordings were obtained from the extensor digitorum communis (EDC) and the flexor digitorum profundus (FDP) of the forearm with worst tremor. For one ET patient, sEMG was recorded from both forearms (over two recording sessions). The EDC is the muscle that produces extension at the wrist and fingers, and muscle activity in the FDP results in wrist and finger flexion. Electrode placement was determined by muscle palpation during active wrist and finger extension and flexion. Correct placement was confirmed by inspecting sEMG output on a digital oscilloscope. The recording setup was as in [20, 21]. The sEMG signal was amplified (gain set to 1,000) and bandpass filtered between 20Hz and 450Hz (Delsys Inc., Boston, MA). The high pass filter at 20 Hz is an in-built feature of the sEMG sensor in order to reject low frequency noise and movement artifacts. This setting however, does not filter out the tremor signal since the tremor bursts are at 5–12 Hz which can be easily recovered by an envelop detection. Along with sEMG, acc data were recorded with a calibrated Coulbourn type V94–41 miniature solid-state piezoresistive accelerometer. It was taped to the hand (2 cm proximal to the middle of the first metacarpophalangeal joint). The accelerometer resolution was 0.01g. Both sEMG and acc were sampled at fs = 1000Hz.
In the beginning of the experiment, the patient was comfortably seated in an upright position on a chair. A table with an adjustable height was positioned by the side of the chair and served as the supportive surface for the subject’s forearm. The height of the table was adjusted to be level with the subject’s hand when the wrist and fingers were extended parallel with the floor. The table served as the visual target to enable the subject to maintain the wrist in a neutral position. sEMG and acc were measured with the patients in the following 3 states:
R: Resting, with the forearm and hand muscles completely relaxed and the hand dangling unsupported over the edge of the supportive surface as in figure 2(left).
P: Posture, by maintaining the wrist and hand in a neutral, extended position while keeping it level with the table surface as in figure 2(right).
A: Action, performing some voluntary action/movement, such as reaching for the opposite shoulder and/or extension and flexion of the wrist.
Figure 2.
Hand position with sEMG and acc sensors during rest (R) (left) and posture (P) (right).
2.3. Experimental protocol
Two types of trials were recorded for each patient in R, P and A:
Baseline data: At the start of a recording session, 3 baseline trials each of 30 seconds were recorded with the patient in R, P and A, with DBS ON.
Experimental data: After that DBS was switched OFF for sometime and then a total of 15 to 32 experimental trials were recorded in R, P and A. Each experimental trial was of 50–100 seconds in duration and consisted of an interval with DBS ON (20–50 seconds) followed immediately by the rest of the trial interval with DBS OFF. During DBS-OFF periods, the first instant when tremor visibly re-appeared was noted. This was also verified using a threshold of 0.15 – 0.2mm/s2 on the acceleration data for states R and P.
PD patients were tested under all 3 conditions (R, P, A) whereas ET patients only performed P and A since none of the ET patients had resting tremor. In P and A, the posture holding/movement was initiated either before or after switching the stimulation OFF.
2.4. sEMG and acc data preprocessing
For final analysis, only the extensor sEMG was used as by visual inspection of the data it had a higher signal to noise ratio (SNR) than the flexor sEMG especially in the R and P state. During A, extensor sEMG bursts precede flexor bursts, hence any predictive information is expected to be obtained from the extensor sEMG before the flexor sEMG. This was also verified by considering parameters calculated from the flexor sEMG, whose addition did not improve the algorithm’s performance. The raw extensor sEMG signal (indicated as x(τ)) was first smoothed by calculating its power over windows of 50ms (equivalent to 50 samples) duration that slid over every sample. The smoothed sEMG signal will be denoted as xs(τ). The sEMG was smoothed to extract the lower frequency tremor bursts by averaging out the higher frequency oscillations inside the sEMG bursts. This is equivalent to rectification and low pass filtering. A set of parameters were calculated using windows of 1s (equivalent to 1000 samples) of xs(τ) with an overlap of 0.75s thus producing a sample every 0.25s after an initial delay of 1.05 s for the first parameter sample. Following is a description of all the parameters that were calculated for PD and/or ET dataset:
2.4.1. Spectral parameters
Fourier analysis
Let Pk be the power of a 1 second window of xs(τ) at frequency bands centered around fk, k ∈ {1, …, N } calculated by using a 512 point Fourier transform, where (fN − f1) is the bandwidth of xs(t). Then the mean frequency ( ) was calculated as:
| (1) |
It represents the expected value of the frequency distribution over the spectrum range considered. Since depends on the distribution of power at the different frequency points considered, in presence of tremor or just before tremor starts, we would expect that this average frequency ( ) would have a lower value than the one in the absence of any tremor.
Let (fB − f1) be the bandwidth of interest with B < N . Let j★ be the index of frequency with maximum power in this bandwidth of interest:
| (2) |
Power ( ) at peak frequency ( ) were calculated as:
| (3) |
| (4) |
Since, the smoothed sEMG signal had most of its power concentrated in the (0–40) Hz range and we are interested in the 3–18 Hz range (encompassing the typical tremor frequency range), only frequency components in the (2–40) Hz band were considered, that is N = 37 and B = 16 in equation (3). We omit the 0–2 Hz band to account for the DC value and very low frequency movement artifacts. is the frequency in the 3–18 Hz range with the largest power, while is the power at . We are interested in the low frequency contents of the smoothed sEMG signal as tremor components are expected to lie in this band [22]. Note that in equation (3) is normalized by the power of the recorded data signal outside the main signal bandwidth of interest. This is so because the power at must be compared over different trials/recordings, which might have significantly different power outside the range of interest. In a way, the quantity in equation (3) can be interpreted as a ratio between the maximum power in the bandwidth of interest (3–18 Hz) and the total power in the frequency band that we are not interested in (18–40 Hz).
Wavelet Analysis
xs(τ) was decomposed into M = 10 frequency bands using a Daubechies4 discrete wavelet transform (DWT). Let xj(τ) represent xs(τ) in the j-th frequency band, j ∈ {1, …, M}. Mean power in the j-th wavelet band, is defined as:
| (5) |
captures the average signal content in the j-th frequency band over each window of duration ΔT = 1s. The mean power in the (8–16) Hz band was computed using equation (5) which will be referred to as . This particular band was considered because it was seen to contain the most predictive information [8] which can distinguish between tremor and voluntary movement. Moreover this band also overlaps with the typical action/postural tremor frequency band.
2.4.2. Entropy parameters
Wavelet Entropy
The (Shannon) entropy is a measure of unpredictability and is often used to quantify the amount of order/disorder in a signal. In information theory, the entropy of a discrete random variable (RV) X is defined as [23]:
| (6) |
where pi = ℙ[X = xi], i ∈ {1, …, K}, is the probability mass function and K is the number of possible outcomes for X. Based on equation (6), the Wavelet Entropy, Hwt(τ) of xs(τ), is calculated as [24]:
| (7) |
where,
| (8) |
x̄j(t) represents the normalized power of xj(t) and hence can be treated as a probability mass function whose (Shannon) entropy is estimated by Hwt(τ). This parameter was calculated only for PD sEMG. For each window of xs(τ), the wavelet entropy was calculated as the average of Hwt(τ) over the time window.
Sample Entropy
Sample Entropy is calculated as the negative logarithm of an estimate of the conditional probability that a data series of a given length that match point-wise within a given tolerance also match when the length is increased by one. The computation of the sample entropy, denoted as SpEn(U, m, r), for a given time series U = {x(i), i ∈ {1, …, L}} of length L involves two input parameters m and r, which are the pattern length and the similarity criterion, respectively. SpEn(U, m, r) is evaluated as follows. Let xm(i) = [x(i), …, x(i + m − 1)] for i ∈ {1, …, L − m + 1} be a set of length m vector sequences constructed from U. The ℓ∞ distance between two such sequences x(i) and x(j) is
Let:
| (9) |
for i, j ∈ {1, …, L − m}, i = ≠ j and let:
| (10) |
SpEn(U, m, r) is then defined as:
| (11) |
where Am(r)/Bm(r) is the conditional probability that two sequences that are similar for m points remain similar within a tolerance r at the next point. A lower SpEn(U, m, r) value reflects a higher degree of regularity.
Each window of xs(τ) was used to calculate sample entropy SpEn(U, m, r) according to equation (11) with U = xs(τ), m = 2, r = 0.15σ, where σ is the standard deviation (std) of the signal window considered. Since the number of samples in the 1s window (L = 1000) should be 10m – 30m [25], m = 2 was chosen. For m = 2, values of r range from 0.1 to 0.25 times the std [26].
2.4.3. Recurrence quantification parameters
Recurrence Quantification Analysis (RQA) [27] involves the computation of a recurrence matrix (RM) with elements, Ri,j, (i, j) ∈ {1, …, P }, P = L − (E − 1)τ, for U = {x(i), i ∈ {1, …, L}} of length L involves the following parameters: The embedding dimension E, a time delay τ, a norm || · || (which could be minimum norm, maximum norm, and Euclidean norm), and radius r. RM is then calculated as:
| (12) |
| (13) |
| (14) |
where, Θ is the Heaviside function and xi is a vector of length m constructed as:
From Ri,j, the recurrence rate R is calculated as:
| (15) |
Each window of xs(τ) was used to calculate R according to equation (15) with E = 5, τ = 3, r = 0.33. These values were chosen based on guidelines for parameter selection outlined in the “crptool” MATLAB toolbox [28]. E was estimated using the nearest-neighbor methodology, that is the minimum embedding dimension value which maximizes system information; t was estimated by finding the first minimum in the mutual information function and r was chosen such that R < 1 [27].
The acc signal was used to calculate the mean frequency ( in equation (1)) and power ( in equation (3) at peak frequency ( in equation (4)) and used for tremor prediction in PD.
2.5. Tremor Prediction Algorithm
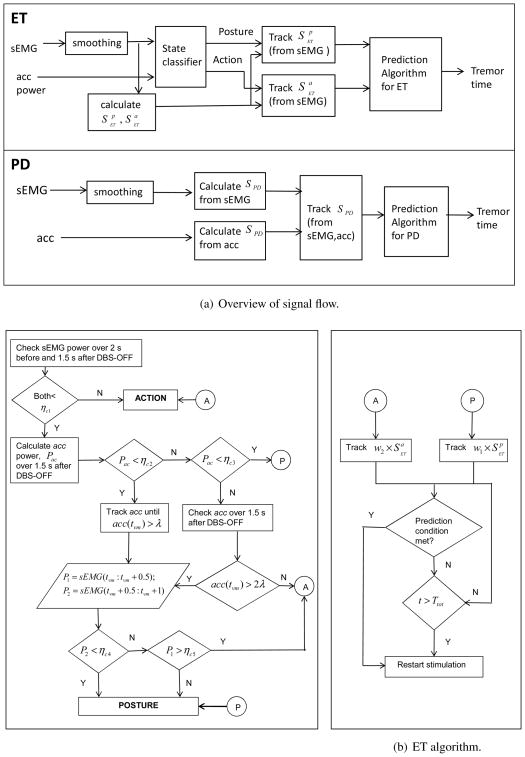
For both PD and ET, DBS is ON for a fixed time during each DBS ON-OFF cycle. This fixed stimulation duration for each patient can be estimated as the DBS-ON duration that maximizes the average ratio of the delay in tremor re-appearance to the total DBS ON-OFF duration [8]. This ratio, Rdt is described later in section 2.7. In practice, an optimum DBS-ON period can be estimated either during a patient’s clinic visit or during programming of the DBS device. When DBS switches OFF after this fixed ON duration, the prediction algorithm starts operating. Figure 3(a) shows an overall block diagram of the signal flow for the entire prediction process. The smoothed sEMG and acc are used as inputs to the entire algorithm block as shown in Figure 3(a). In ET, the smoothed sEMG and acc are first used to classify which state (P/A) the patient is in just before and immediately after DBS is OFF and based on the classifier outcome, a set of parameters calculated from the smoothed sEMG are tracked until one of them meets a prediction criterion or the DBS OFF interval exceeds a preset value, when DBS is switched ON. In PD, both smoothed sEMG and acc are used to calculate a set of parameters which are tracked. Whenever one of the parameters satisfies its corresponding prediction criterion or the DBS OFF interval exceeds the preset value, DBS is turned back ON. Following is a detailed description of the algorithm steps.
Figure 3.
(a): A block diagram showing how the two signals, sEMG and acc are used in the algorithm for ET (top) and PD (bottom) (b): Classification (left) and prediction (right) for the ET algorithm described in Section 2.5.1 and shown in (a).
2.5.1. Prediction Algorithm for ET
For ET patients, the prediction involves two steps:
-
Classification of patient’s state (P/A): This is done based on the sEMG and acc signal power by setting some thresholds, [ηc1, ηc2, ηc3, ηc4, ηc5, λ] as shown in figure 3. The basic premise is that the power of sEMG and acc signals is greater while performing an active motion than during holding a posture, which in turn is higher than at rest. Additionally, there will be an abrupt change in these signals when there is a change in state. In particular, the following steps are done:
If the power of sEMG (xs(t)) over 2s just before and 1.5s immediately after DBS is switched OFF is less than ηc1, then go to ii). Else the state is A.
Calculate the power of acc (indicated with Pac) over 1.5s immediately after DBS is switched OFF. If Pac ∈ [ηc2, ηc3], the state is P. If Pac < ηc2, go to iii) else go to v).
The sEMG and acc are tracked until acc(tvm) > λ where tvm is the time instant when acc exceeds threshold λ.
Calculate power of sEMG(xs(t)) over intervals [tvm, tvm+0.5] and [tvm+0.5, tvm+1] which are denoted as P1 and P2 respectively. If either P2 < ηc4, or if P2 > ηc4 and P1 < ηc5, state is P. If P2 > ηc4 and P1 > ηc5, state is A.
Over the 1.5s interval after DBS is switched OFF, find if at any instant, {tvm: acc(tvm) > 2λ}. If there is such an instant then go to iv) else the state is A.
Based on the classifier output, proceed as follows: If holding a posture (state P), the parameter ( ) is tracked. If performing an action/movement (state A), the parameter ( ) is tracked as shown in figure 3(b). Here I is the indicator function, w1 and w2 are weights and can either be 0 or 1. are the set of parameters as described in table 2 and are a subset of the parameters introduced in the sEMG and acc data preprocessing (section 2.4). Whenever, one of the parameters in (for P) or (for A) meets its corresponding prediction criterion or the DBS-OFF time exceeds a preset value, the stimulation is turned ON. The two sets of parameters and their corresponding prediction criterion are listed in table 2 and is described in section 2.5.4. A default preset value is a safety measure to ensure that the stimulation turns ON after sometime in case the algorithm does not predict any tremor event. This value can be decided based on the average time the tremor takes to come back for a particular patient.
Table 2.
Parameter Set for ET.
| # | Parameter Set, | Predict tremor at time t |
|---|---|---|
| 1 | SpEn and | Let (i − 1) is a local min and k < i is a local max over (k − 1, i), if SpEn(k) ∈ (ηl1, ηh1) & SpEn(k) − SpEn(i − 1) ∈ (ηl2, ηh2) & , l ∈ (k − 6, i + 4), t = max(i, l) |
| 2 | R | Let (i − 1) is a local max and k < i is a local min over (k − 1, i), R(i − 1) − R(k) ∈ (ρl, ρh),t=i |
| 3 | and | If and , t = i |
| # | Parameter Set, | Predict tremor at time i | |
|---|---|---|---|
| 1 | R | Let (i − 1) is a local max and k < i is a local min over (k − 1, i), R(i − 1) − R(k) ∈ (ρl, ρh), t = i | |
| 2 |
|
If , t = i |
2.5.2. Prediction Algorithm for PD
For PD, the prediction is done similarly to that proposed for ET. The main difference is that there is no preceding classification step as in ET and a set of parameters extracted from the acc signal is also used in the prediction. Omission of a state classification is to avoid confusion between rest tremor and change in state from R to P/A. Moreover, we would also have to determine three sets of parameters for the three states in PD thus complicating the algorithm further. Hence for the PD cases, 1s after stimulation is turned OFF, (Iw=1 × SPD) is tracked; whenever a prediction criterion is met or the DBS OFF time exceeds a preset value the stimulation is turned ON. The set of parameters SPD and their corresponding prediction criterion are tabulated in table 3.
Table 3.
Parameter Set for PD.
| # | Parameter Set, | Predict tremor at time t |
|---|---|---|
| 1 | SpEn & | Let (i − 1) is a local min and k < i is a local max over (k − 1, i), if SpEn(k) ∈ (ηl1, ηh1) & (SpEn(k) − SpEn(i − 1)) ∈ (ηl2, ηh2) & , l ∈ (k − 6, i + 4), t = max(i, l) |
| 2 | R | Let (i − 1) is a local max and k < i is a local min over (k − 1, i), R(i − 1) − R(k) ∈ (ρl, ρh),t=i |
| 3 | & | If and , t = i |
| 4 | and | If and , t=i |
| 5 | Hwt | Let Hwt(i − 1) and Hwt(i) ∈ (hl, hh), t = i |
2.5.3. Algorithm parameters and threshold values
All the trials recorded from each patient were divided into two groups: a) training trials consisted of the baseline trial data (30s DBS-ON condition in R, P and A) and around 40% of the total experimental trial data (consists of recordings with DBS-ON followed by DBS-OFF) as in section 2.3, b) testing trials consisted of experimental trials that were not used for training. The algorithm was tested using just the testing trials as well as all experimental trials.
For each patient the threshold values for the classification (ET) and those for parameters used in the prediction algorithm were chosen as follows: The threshold values for the state classification in ET were chosen by comparing the sEMG power and acc magnitude in all 3 states during DBS-ON and DBS-OFF intervals of the training trials. All parameter values as described in section 2.4, were first calculated for the sEMG and acc signals recorded during the training trials. The calculated parameters for intervals of no tremor (entire baseline data duration and tremor-free intervals of the rest of the training trials) were compared with those in the DBS-OFF intervals of the training trials when tremor started to build up. Based on the difference between the parameter values with and without tremor, a threshold was decided for each parameter such that each of the training trial produced a desired prediction output (TP or TN defined in section 2.6). For parameters with two thresholds, the second one was estimated based on difference in the parameters in state R and during movement initiation. Only those parameters were included in the set as in table 5, which produced desired output for the maximum number of training trials using the same threshold.
Table 5.
Patient specific parameter set for tremor prediction algorithm in PD and ET.
| PD Patient# | Parameters used for prediction |
|---|---|
| PD1 | SpEn, , R, and |
| PD2 | SpEn, , Hwt |
| PD3 | Hwt, and |
| PD4 | SpEn, , Hwt, and |
| ET Patient# | Parameters used for prediction in P(w1 = 1) and A(w2 = 1) |
|---|---|
| ET1 | P: SpEn,
and
A: R, |
| ET2(left) | P:
A: R |
| ET2(right) | P: SpEn,
A: |
| ET3 | P: SpEn,
A: R, |
| ET4 | P: SpEn,
and
A: R |
2.5.4. Prediction Criterion
Tables 2 and 3 list the prediction criterion that each parameter should meet in order for a tremor to be predicted. Following is a brief description of the criteria and the underlying logic:
Sample entropy and power in the 8–16 Hz wavelet band (SpEn, ): At each time instant i, the algorithm searches for the most recent local maximum and minimum of sample entropy. If the maximum precedes the minimum and each of them or their difference lie between thresholds, ηh1, ηl1 and ηh2, ηl2, then the algorithm checks if simultaneously over this entire period the power in the 8–16 Hz wavelet band exceeds a threshold, η4 and predicts a tremor if all the 3 conditions are satisfied. This criterion relies on the fact that during a tremor buildup, the sEMG will increasingly become more synchronized, hence leading to a decrease in the sample entropy and an increase in the 8–16 Hz sEMG signal power.
Wavelet entropy (Hwt): This parameter is used only for PD dataset. The algorithm predicts a tremor if the wavelet entropy value at that time instant and the one immediately preceding it lie within the thresholds hh, hl. The underlying logic is similar to that for sample entropy.
Recurrence rate (R): At each time instant i, the algorithm searches for the most recent local maximum and minimum of recurrence rate. If the minimum precedes the maximum and the increase between these values lies between thresholds, ρl, ρh, a tremor is predicted. This criterion is based on the increase in sEMG recurrence during tremor buildup.
Power at peak frequency ( ): The algorithm predicts a tremor if at that instant, the frequency of the sEMG or acc signal, that has the maximum power lies between certain thresholds and the power exceeds a threshold as listed in tables 2, 3. The frequency range defined by the thresholds is the typical tremor frequency. This criterion checks if the spectral component of the sEMG/acc which has the maximum power is the tremor frequency band as well as if this power exceeds a certain value.
Mean frequency ( ): This parameter is used only for predicting ET kinetic tremor. The instant when the mean frequency value lies in between thresholds fh, fl, a tremor is predicted. It is based on the fact that mean frequency was observed to lie in a certain frequency band before tremor starts.
Use of a lower threshold for entropy and spectral parameters and an upper threshold for R help reduce false predictions due to voluntary movements. This is based on the assumption that a movement initiation causes a higher degree of synchronization and hence a greater magnitude of decrease/increase in parameter values than tremor. It was also seen that the 8–16 Hz band carried more tremor information than movement artifact. On the other hand, both tremor and movement cause an increase in the lower frequency band (1–8 Hz) power. Hence, the wavelet band power along with sample entropy also serves to discriminate voluntary movements from tremor. Thus, the lower threshold on sample entropy, wavelet entropy, mean and peak frequency; the upper threshold on recurrence rate and the 8–16 Hz wavelet band power are used to discriminate between voluntary movement and tremor.
2.6. Classification of prediction outcomes
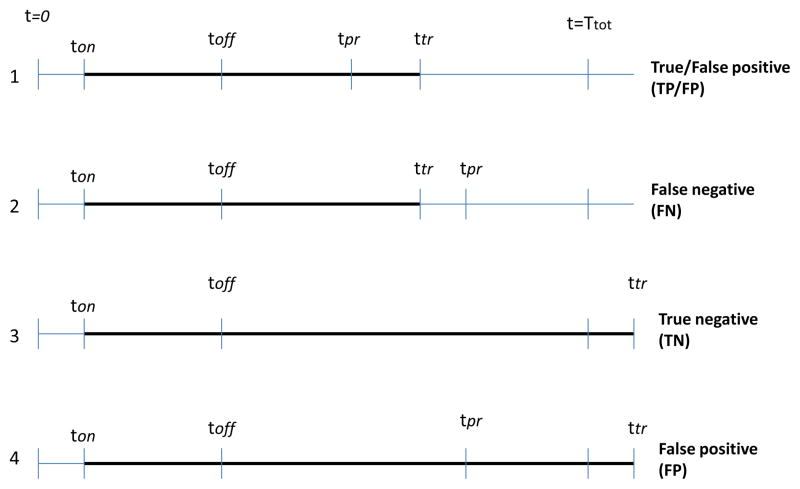
To analyze the prediction performance, each trial is classified based on the prediction outcome as follows. Let Ttot be the total duration of a trial, and ton and toff be the times when stimulation was switched ON and OFF, respectively. Furthermore, let ttr and tpr be the times when tremor was detected during the DBS-OFF period and tremor was predicted using the algorithm, respectively as in figure 4. The trials were then classified as:
Figure 4.
Timing points for events from DBS-ON time (ton) to tremor detection time (ttr) marked in bold line. There are 4 possible scenarios: 1,2 are TD trials, in 1 the tremor is predicted before its detection (TP/FP) and in 2 tremor is predicted after its detection (FN); 3,4 are NTD trials, in 3 tremor is not predicted over the entire interval TN and in 4 tremor is predicted FP. Notation: Ttot is the total duration of a trial, ton and toff are the times when DBS was switched ON and OFF respectively, ttr and tpr are the times when tremor was detected and predicted using the algorithm, respectively.
-
TD (Tremor Detected): These are trials where tremor was detected over the recorded interval after stimulation was OFF, i.e ttr < Ttot.
If [(ttr > tpr) and (ttr−tpr) < max(5s, 0.4(tpr−toff))] or [(ttr < tpr) and (tpr−ttr) < 1s], then the algorithm successfully predicts tremor and this outcome is classified as a true positive(TP).
If (ttr > tpr) and (ttr − tpr) > max(5s, 0.4(tpr − toff)], then the prediction is too early and the outcome is classified as false positive (FP)
-
If (ttr < tpr) and (tpr − ttr) > 1s, then the prediction is too late and the outcome is classified as false negative (FN)
The TP definition is a bit different from the classical one, in that we require that the prediction be at most 40% of the tremor free DBS-OFF period or 5s (whichever is greater) before actual tremor reappears. This allows penalizing too early prediction outcomes. The maximum between 40% of (tpr − toff) and 5s is considered to account for trials where the tremor delay is very short (< 10s) for which a prediction 5s ahead in time is good enough to be classified as a TP. We also allow for prediction at most 1s after detection. This will take care of situations when the tremor re-appears almost immediately (within 1–2 seconds) after stimulation is switched OFF.
-
NTD (No-Tremor Detected): These are trials where tremor was not detected over the recorded DBS-OFF interval, i.e ttr ≥ Ttot.
If the algorithm does not predict any tremor over the entire interval Ttot − toff, then its classified as true negative (TN)
If the algorithm predicts tremor over the entire interval Ttot − toff, then its classified as false positive (FP)
2.7. Statistical analysis of prediction outcomes
For the algorithm to perform well, the total number of TP and TN must be maximized while minimizing FP and eliminating FN. This would achieve the maximum “tremor-free” DBS-OFF interval. To quantify this, the following performance metrics are defined:
| (16) |
| (17) |
| (18) |
| (19) |
A in equation (16) is the accuracy of the prediction algorithm, which is the ratio of the correctly predicted trials to the total number of trials. For our application, we aim to have a high accuracy (above 80%). S in equation (17) defines the sensitivity of the prediction algorithm. It relates to the algorithm’s ability to correctly predict tremor in TD trials. This value has to be very high (as close to 100% as possible) for the application since we want to avoid missing any tremor event. FA in equation (18) is the false alarm rate, which expresses the ratio of NTD trials that are falsely predicted. This relates to the algorithm’s ability to correctly identify the absence of tremor when there is no tremor. We aim to have a low FA value so that the tremor-free DBS-OFF interval is maximized. mcc in equation (19) is the Matthews correlation coefficient [29], which is a measure of the quality of a binary classifier. It is generally regarded as a balanced measure and is used even if the classes are of very different sizes. It has a value in the range −1 to 1, where 1 represents a perfect prediction, 0 no better than random prediction and −1 indicates total disagreement between prediction and observation. It is related to the chi-square statistic for a 2 × 2 contingency table
| (20) |
where the χ2 statistic can be used to calculate the p-value in order to accept/reject the null hypothesis that the predictions were completely random. The p-value is the probability that X > |χ2|, where X is a random variable with a χ2 distribution with 1 degree of freedom. A p-value less than α indicates the the prediction outcome is significantly different from a random prediction with α being the significance level and is often chosen to be 5% or less.
For this application, S should be very high (over 90%) because we want to avoid missing any tremor event. At the same time, we also want to have high A and a low FA. This ensures that the algorithm not only correctly predicts tremor events, but also avoids early predictions. The mcc value should be close to 0.5 or higher and should produces a p-value that is less than 5%.
For each patient, A, S, FA in equations (16), (17), (18) and mcc in equation (19) were calculated for all experimental trials as well as for the testing trials. A χ2 statistic and the corresponding p-value was calculated only when the number of trials exceeded 10 [30]. For patients with NTD< 5, FA was not calculated (NC). An overall A, S, FA and mcc were calculated based on all experimental and testing trials in PD and in ET . Additionally, three ratios are calculated for each patient which are defined as:
| (21) |
| (22) |
| (23) |
where the summation is over all the experimental trials for each patient. Since for the NTD trials the exact time when tremor would come back is not known, we set ttr = Ttot and tpr = min(Ttot, tpr). In a practical scenario, Ttot would be the time when the stimulation switches ON automatically in the absence of a tremor prediction. Hence, to determine the fraction of time the stimulation is OFF, we can consider Ttot − toff to be the time interval when stimulation is OFF for NTD trials.
Furthermore, Rpt is calculated only for trials where the DBS-ON duration, , is the one that maximizes the ratio, and is denoted as:
| (24) |
Rpd is the ratio between the predicted delay to the actual delay in tremor, hence Rpd provides a measure of how good the prediction is, i.e., a higher value indicates that the predicted delay is closer to the actual delay which is desirable. In a similar way, Rdt and Rpt provide a measure of the fraction of time the stimulation is OFF with an ideal predictor (which would predict the exact time when tremor re-appeared) and the one designed. Rdt values can be used to assess if a particular patient is well suited for this type of application. If Rdt is very low, i.e., if the stimulation is OFF for just 10% of the total time then it is better just to have DBS-ON continuously. provides a measure of the fraction of total trial time that the stimulation would be OFF if the predictor worked only for the optimum stimulation duration, . The goal of our tremor predictor is to maximize Rpd as well as since with a higher , the patient will have a high percentage of “tremor-free” DBS-OFF interval. can be chosen as outlined in [8].
3. Results
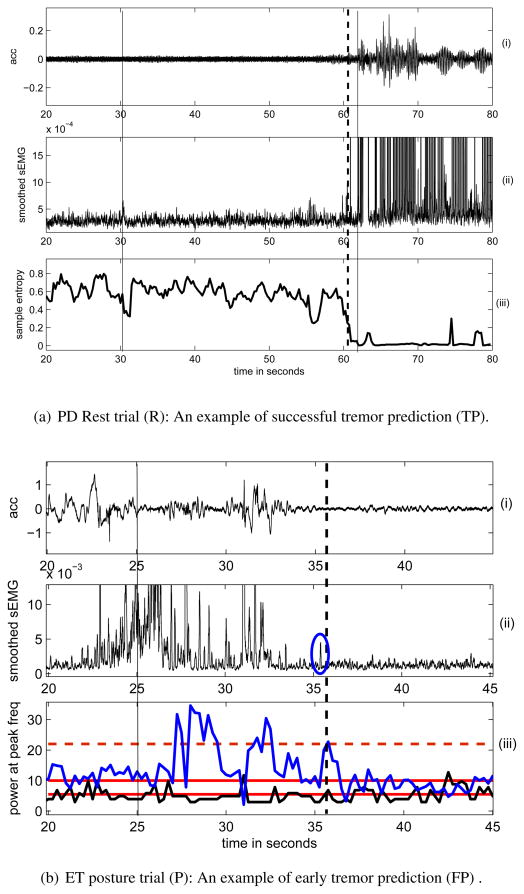
The parameters and corresponding thresholds used in the prediction algorithm were determined for each patient based on training trial data as described in section 2.5.3. The prediction parameters used for each patient are listed in table 5 and the threshold values are listed in tables A1, A2 and A3. The data in figure 5(a) shows (i) the acc signal and (ii) smoothed sEMG which was recorded from PD1 in R, with a total recording duration, Ttot = 80s. DBS was OFF at 31s and tremor re-appeared at 62 s which is also seen from the acc data (indicated by a solid black line). The sample entropy, SpEn calculated from the smoothed sEMG was the parameter that met the tremor prediction criterion the earliest (at 60.75s) amongst the others considered as listed in table 5. This is shown in figure 5(a) (iii). The tremor prediction time is shown with black dotted line. Figure 5(a) thus represents a TP trial since the tremor is predicted just a few seconds before it actually re-appears.
Figure 5.
(i) acceleration, (ii) smoothed extensor sEMG recorded from (a) a PD patient at rest. Sample entropy (bottom) calculated from the smoothed sEMG was used for predicting tremor. The vertical solid lines show instants of DBS-OFF (31 s) and tremor appearance (62 s), dashed line shows instant (60.75 s) when tremor was predicted using (iii) sample entropy. (b) an ET patient while holding a posture (initiated at 22s). DBS was OFF at 25s and there was no tremor during the entire trial of 50s.(iii) (in blue) and (in black)were used to predict tremor. The red horizontal solid lines show the thresholds for while the one in dashed line shows the threshold for . The vertical dashed line shows the instant (37.5s) when tremor was predicted exceeds threshold and falls in the prediction range simultaneously) due to an artifact circled in blue.
The trial shown in figure 5(b) was recorded from ET4 in P and shows a case of a FP, that is the algorithm predicted a tremor when there was actually no tremor for the entire recording interval (Ttot = 50s). DBS was OFF at 25s and the patient initiated a posture at 22s. From the (i) acc and (ii) smoothed sEMG signal in figure 5(b), it can be seen that there were some movements during the 22–34 s interval after the posture initiation, but no tremor after that. The prediction parameters shown in (iii), (in blue) and (in black) met the prediction criterion at 37.5 s ( and at the same time instant), thus resulting in a false alarm. The y-axis of the smoothed sEMG has been enlarged to show the small artifact after 35s which probably caused a false alarm at 37.5s.
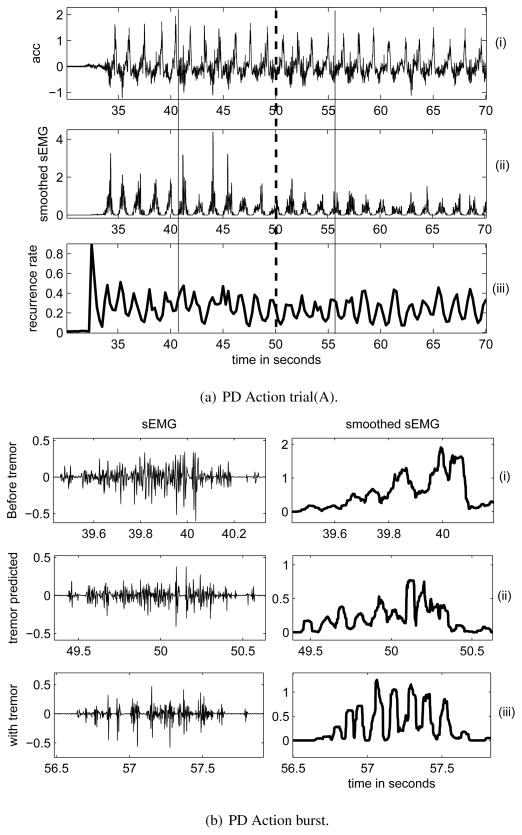
A trial recorded from PD1 in A is shown in figure 6(a) and consists of (i) acc, (ii) smoothed sEMG and (iii) the prediction parameter, recurrence rate (R) calculated from the smoothed sEMG. DBS was OFF at 41s and tremor re-appeared visually at 56 s (indicated by a solid black line). Since figure 6(a)(ii) lacks the resolution to show each sEMG action burst, portions of it are enlarged and shown in figure 6(b). The sEMG (left) and corresponding smoothed signal (right) during different intervals of the trial as in figure 6(a)(ii) are shown in figure 6(b): (i) when there was no tremor, (ii) when tremor was predicted and (iii) after tremor was detected (bottom). It can be seen that the burst with tremor (iii) and the one when tremor is predicted (ii) has a more regular structure than the one without it (i) which is captured by a greater increase in R.
Figure 6.
(a)(i)acceleration and (ii) smoothed extensor sEMG (middle) recorded from a PD patient while performing a voluntary movement initiated around 33s. (iii) Recurrence rate calculated from the smoothed sEMG was used for predicting tremor. The vertical solid lines show instants of DBS-OFF (41 s) and tremor appearance (56 s), dashed line shows instant (50 s) when tremor was predicted using recurrence rate. (b)an enlarged view of raw extensor sEMG (left), smoothed extensor sEMG (right) during the trial as in 6(a), (i) burst without tremor, (ii) tremor was predicted (iii) after tremor was detected visually.
A, S, FA in equations (16), (17), (18), mcc in equation (19) and the corresponding p-values were calculated for all experimental trials and for all testing trials corresponding to each patient and are listed in table 6. An overall A, S, FA and mcc based on all experimental and testing trials in PD and in ET are also included in table 6. The ratios, Rpd, Rpt, Rdt in equations (21), (23), (22); the optimum DBS-ON duration and the corresponding were also calculated for each patient based on all experimental trials which are listed in table 7. It also lists for each patient, the average of the actual delay in tremor re-appearance (ttr − toff) and the predicted delay (tpr − toff), over all experimental trials with the optimum DBS-ON duration.
Table 6.
Statistical analysis of the prediction outcomes, A, S, FA in %. The first row for each patient corresponds to the metrics calculated on all experimental trials (all) while the second row shows the same calculated for testing trials (test) which were not used for training.
| Patient# | Trial | N,NTD | TP,TN,FP,FN | A | S | FA | mcc, p-value |
|---|---|---|---|---|---|---|---|
| PD1 | all | 16,2 | 14,1,1,0 | 93.8 | 100 | NC | 0.68, 0.006 |
| test | 9,1 | 7,1,1,0 | 88.9 | 100 | NC | 0.66,NC | |
|
| |||||||
| PD2 | all | 26,4 | 16,3,7,0 | 73.1 | 100 | NC | 0.46, 0.02 |
| test | 16,2 | 10,2,4,0 | 75.0 | 100 | NC | 0.49,0.05 | |
|
| |||||||
| PD3 | all | 17,0 | 15,0,2,0 | 88.2 | 100 | NC | NA |
| test | 10,0 | 9,0,1,0 | 90.0 | 100 | NC | NA | |
|
| |||||||
| PD4 | all | 32,11 | 16,8,8,0 | 75.0 | 100 | 27.3 | 0.53, 0.003 |
| test | 20,7 | 10,5,5,0 | 75.0 | 100 | 28.6 | 0.58, 0.01 | |
|
| |||||||
| All PD | all | 91,17 | 61,12,18,0 | 80.2 | 100 | 29.4 | 0.56, 10−10 |
| test | 55,10 | 36,8,11,0 | 80.0 | 100 | 20.0 | 0.57, 10−4 | |
|
| |||||||
| ET1 | all | 15,3 | 10,2,3,0 | 80.0 | 100 | NC | 0.55, 0.03 |
| test | 9,2 | 5,2,2,0 | 77.8 | 100 | NC | 0.6, NC | |
|
| |||||||
| ET2 | all | 30,14 | 13,14,3,0 | 90.0 | 100 | 0 | 0.82, 0.0001 |
| test | 18,7 | 9,7,2,0 | 88.9 | 100 | 0 | 0.8, 0.0007 | |
|
| |||||||
| ET3 | all | 16,6 | 10,5,1,0 | 87.5 | 100 | 16.7 | 0.87, 0.0005 |
| test | 10,5 | 5,4,1,0 | 90.0 | 100 | 20 | 0.82, NC | |
|
| |||||||
| ET4 | all | 30,20 | 7,17,6,0 | 80.0 | 100 | 15 | 0.63, 0.0005 |
| test | 18,12 | 4,11,3,0 | 83.3 | 100 | 8.3 | 0.67, 0.005 | |
|
| |||||||
| All ET | all | 91,43 | 40,38,13,0 | 85.7 | 100 | 11.6 | 0.71, 0 |
| test | 55,26 | 23,24,8,0 | 85.5 | 100 | 7.7 | 0.75, 10−8 | |
Note: NC means not calculated; mcc could not be calculated for PD3 (NA) due to an indeterminate form (TN=FN=0); a p-value was calculated only when N > 10; FA for PD4 and for overall PD are not same because although FA was not calculated for PD(1-3), PD(1-2) had a few NTD trials which were included in the calculation of overall FA
Table 7.
Optimum DBS-ON time, average DBS-OFF time without tremor (in seconds) and ratios expressed in % for all experimental trials.
| Patient# | Rpd | Rpt, Rdt |
|
|
Average (ttr − toff) | Average (tpr − toff) | ||
|---|---|---|---|---|---|---|---|---|
| PD1 | 77.6 | 28.6,34.1 | 30–32 | 34.1 | 21.25 | 16.06 | ||
| PD2 | 67.0 | 28.5,37.7 | 20–37 | 31 | 20.64 | 13.02 | ||
| PD3* | 68.8 | 11.5,15.9 | 42–55 | 11.5 | 9.56 | 6.96 | ||
| PD4 | 80.7 | 34.3,39.3 | 22–37 | 42.4 | 24.11 | 20.03 | ||
| ET1 | 80.2 | 35.2,40.4 | 28–38 | 37.4 | 24.03 | 19.0 | ||
| ET2 | 89.8 | 36.8,39.3 | 20–40 | 39.1 | 18.67 | 15.53 | ||
| ET3 | 79.1 | 32.8,38.1 | 30–42 | 32.8 | 22.18 | 17.53 | ||
| ET4 | 88.7 | 48.3,51.3 | 17–30 | 45.7 | 27.49 | 24.22 |
Note: PD3* indicates that is the range of all DBS-ON intervals recorded and not necessarily the optimum one.
4. Discussion
The aim of this study was to design an algorithm for predicting pathological tremor in patients with PD and ET, using non-invasively measured sEMG and acc signals from the tremor affected limbs. The designed algorithm achieves a 100% sensitivity for all trials considered, along with an overall accuracy of 85.7% for all ET trials and 80.2% for all PD trials. A Pearson’s chi-square test shows that the prediction results significantly differ from a random prediction outcome. Following is a brief discussion about the algorithm parameters and prediction results.
4.1. Algorithm parameters
The set of parameters considered for predicting tremor consists of some basic spectral measures such as mean frequency, power at maximum frequency and the power in a particular frequency band as well as a few non-linear measures such as a couple of entropy measures and a recurrence measure. The FFT based spectral measures are commonly used parameters [31] for sEMG analysis. Classical spectral characteristics of sEMG have some diagnostic value for quantification of motor unit synchronization [32]. However, sEMG signals are nonlinear in nature and hence nonlinear time-series analyses of sEMG can potentially provide additional information on the underlying motor strategies [33]. Wavelet Entropy has been widely used for analyzing electroencephalogram (EEG) signals to measure degree of similarity between different segments of the signal [24] and for detecting different events such as seizures in epileptic patients [34]. It has been shown that tremor is characterized by an increased regularity in the corresponding sEMG signal as compared to sEMG without tremor which can be captured by the Approximate Entropy measure [20]. It has also been used for similar analysis of EEG signals [35] and heart rate signals [26]. Sample Entropy was developed to overcome some shortcomings of the Approximate Entropy statistics such as bias, relative inconsistency and dependence on the sample length [36]. Based on these two types of entropy measures, we used Wavelet Entropy to capture information relating to power shifts in different frequency bands and Sample Entropy to quantify the regularity and complexity of a time series signal [36]. These two measures are however not directly comparable. RQA has been extensively used for analysis of sEMG for detecting hidden characteristics that cannot be detected by linear analysis [31, 33]. Different variables can be extracted from a recurrence plot [37] which has been shown to correlate with synchronization in the signal and is more sensitive to changes in the degree of synchronization than linear variables such as mean/median frequency [33].
From table 5, it can be seen that the sample entropy along with the power in the (8–16 Hz) wavelet band are the parameters that have been used for 6 out of 8 patients which indicates that it has high predictive information. The recurrence rate and mean frequency are the only parameters used for predicting action tremor in all ET patients. Wavelet entropy (Hwt) is useful only in PD patients but not for ET. This might be due to the fact that parkinsonian tremor has a more well defined and narrow range of frequency than in ET. Although acc is used in the state classification for ET, its not used in the actual prediction algorithm. acc was most useful for predicting rest tremor in PD. However, it is not useful in predicting action tremor. Hence a set of parameters from both these signals were essential to predict all three types of tremor, which could not have been achieved by using either of them alone.
Since PD and ET have very different pathologies with different types of tremor, it can be expected that we would require different parameters to predict tremor in the two disorders. The variance of parameters within the PD group may be higher than that in the ET group due to the fact that PD patients do not all exhibit the same symptoms. Some have more tremor while others have more rigidity than tremor. In ET patients, some have more tremor during holding a posture while some have more tremor while performing an active movement. All these factors could have contributed to the different set of parameters required to predict tremor.
4.2. Prediction performance based on A, S, FA
The predictor does not miss any tremor event (S = 100%) and it achieves a high accuracy (A > 80) for 6/8 patients as shown in table 6. Out of the 8 patients, PD1 and PD3 had high tremor amplitude with a lower value of Rdt, as is also reflected from the values of NTD. For both of them, the A and S are quite high, which is desirable. PD4 was the only PD patient who had long delays in tremor with 11/32 NTD trials. The lower A and relatively high FA is because of the fact that the algorithm predicted a tremor either in the NTD cases or predicted a tremor too early for the TD cases. PD2 had moderate tremor amplitude and all the FP’s except one are due to early prediction in the TD cases. ET3 and ET4 had almost no postural tremor (in state P) but had tremor while performing an active movement (state A). ET2 had very low amplitude tremor on the right hand. The FA could not be calculated for every patient because some of them had very few or no NTD trials. Hence an overall FA value was also calculated for ET and PD by considering all ET and PD trials respectively. It should be noted that for this application, we aim to achieve S as close to 100% as possible. Hence, for patients who have relatively higher delays in tremor re-appearance and/or lower tremor amplitude, the algorithm predicts early tremor events for some of the trials resulting in a higher value of FA. The values of A, S, FA for each patient are not very different when considering all the experimental trials or just the testing trials. Some of the metrics actually show better values when considering only the testing trials. This is because while training, we tried to maximize the number of training trials producing desired output using the same threshold values. This however does not mean that all the training trials actually had 100% accuracy.
4.3. Statistics based on mcc
The mcc value was calculated for each patient, except PD3 due to an indeterminate form produced by TN=FN=0. For all the 7 patients, the mcc value was close to or greater than 0.5 and the overall mcc for both PD and ET were above 0.5. This indicates 50% or higher correlation between predicted and actual classification for each patient(PD/ET) and for overall PD and ET trials. The mcc was further used to calculate the χ2 test statistics according to 20 in order to determine the corresponding p-value. With all experimental trials, each p-value (both individual and overall) was less than α = 5%, which indicates that the null hypothesis that the prediction is completely random can be rejected. When considering the testing trials alone, the χ2 test statistics could not be calculated for all patients since the number of trials for PD1, ET1 and ET3 were not sufficient for a reliable estimate [30]. In general, for all patients the p-value increases when considering the testing trials alone due to a reduction in the sample size.
4.4. Overall performance
The overall S for both ET and PD is 100% which means that for all TD trials in ET and PD, the predictor does not miss any tremor event during the DBS-OFF interval. The overall A for ET is 85.7% while for PD is 80.2%, which indicates that in 85.7% of all ET trials and in 80.2% of all PD trials, the algorithm correctly predicts tremor. Correct tremor prediction means that, in the TD trials, tremor is predicted not too early while in the NTD trials, tremor is not predicted. The overall FA for ET is 11.6% and for PD is 29.4%, which means that in 11.6% of the ET NTD trials and in 29.4% of the PD NTD trials, the algorithm predicts tremor.
The performance for ET is in general better than that for PD with higher overall A and lower FA because of a preceding classification step that allowed to choose different parameters for each state. A classification in PD is more challenging due to the fact that a change in power in the sEMG/acc from the rest state could either be due to tremor or movement while for ET it is certain that there is no tremor during rest and hence an increase in power is certainly due to some movement initiation which might be accompanied by tremor.
4.5. Practical considerations
If the tremor prediction algorithm were implemented in practice, this would definitely be patient specific in terms of the degree of benefit that it would provide. It might not be beneficial to certain patients with severe tremor and short delays in tremor, such as PD3, who had the lowest value of Rdt as in table 7. For all other patients, which means that with the optimal stimulation duration, , the proposed adaptive ON-OFF DBS controller achieves a “tremor free DBS-OFF period” that is greater than 30% of the total ON-OFF duration as shown by the values in table 7. That is, with such a system, the battery life will be extended by a factor of . Although PD4 has the highest FA, the average prediction delay is 20 s for an ON-DBS period of 22–37 s and . This means that if this patient had a battery life of 5 years with the stimulator ON continuously, then with the new system, the battery would last for (1 + 0.72) × 5 = 8.6 years.
The tremor prediction algorithm requires determining an optimal set of parameters and setting their thresholds for each patient which requires some training and manual intervention. This can be easily overcome by using similar parameter set as inputs to a neural network [38] which can train itself at regular intervals of time as the thresholds might change over longer time periods due to disease progression. Initial prediction results using such a neural network on a subset of the PD data set has been published [39].
We acknowledge that this type of DBS controller takes into account only the tremor symptom while PD patients also suffer from rigidity and slowness of movement. However, for most PD patients who have tremor, it is the symptom that re-appears the earliest after the DBS is switched OFF [17]. In many PD patients speech performance is worsened during simulation at the STN [40]. For such cases, it is reasonable to assume that such worsening will not occur during DBS-OFF periods under our proposed control. For ET patients, this type of DBS controller may have additional benefit beyond just extending battery life, as it has been shown that for some ET patients the stimulation benefits decrease over time [41]. It was also seen that for some such ET patients, restarting the stimulation after its temporary discontinuation resensitized them to stimulation [42]. Hence lesser and discontinuous current injection might actually help in prolonging the therapeutic effects of DBS in ET.
Electric jolts that a patient might experience during switching DBS ON can be minimized by using a gradual ramping of the current (which is generally used) and is of lesser concern to patients with bipolar stimulation than monopolar.
5. Conclusion
In this paper, we have designed an algorithm for predicting pathological tremor by using a set of frequency related and entropy type parameters calculated from non-invasively measured sEMG and acc signals. This can be used to successfully predict a tremor event during a DBS-OFF interval, before it occurs. Hence, this method can potentially be used for closed-loop on-demand ON-OFF DBS paradigm which can be added on to the existing system as in figure 1. The recording and processing of data and transmitting the control ON/OFF information to the pulse generator can be done within the sEMG/acc sensor which will be powered by a separate battery incorporated in the sensor electrodes on patient’s muscles and will not affect the IPG battery. The battery in the sensor and switching assembly can be easily replaced and do not require any surgical intervention. Moreover, they do not contribute to current injected in the brain. Thus, the proposed system will achieve lower current injection and reduced frequency of IPG replacement.
Table 4.
Description of thresholds used for state classification and tremor prediction in ET and PD.
| Symbol | Description |
|---|---|
| ET state classification | |
| ηc1, ηc4, ηc5 | upper thresholds on sEMG power |
| ηc2, ηc3 | lower and upper thresholds on acc power |
| λ | lower threshold on acc signal |
|
| |
| ET tremor prediction | |
| ηl1, ηh1 | lower and upper thresholds for local maximum of SpEn |
| η2, ηh2 | lower and upper thresholds for local minimum of SpEn |
| ηp | lower threshold for |
| ρl, ρh | lower and upper thresholds for increase in R |
| fl, fh | lower and upper thresholds for or |
| fp | lower threshold for |
|
| |
| PD tremor prediction | |
| ηl1, ηh1 | lower and upper thresholds for local maximum of SpEn |
| ηl2, ηh2 | lower and upper thresholds for decrease in SpEn |
| ηp | lower threshold for |
| ρl, ρh | lower and upper thresholds for increase in R |
| fl1, fh1, fp1 | lower and upper thresholds for , lower threshold for |
| fl2, fh2, fp2 | lower and upper thresholds for , lower threshold for |
| hl, hh | lower and upper thresholds for consecutive Hwt samples. |
Acknowledgments
The authors would like to thank Dr Fabian Jude David, Dr Julie Robichaud and Dr Cynthia Poon from NCML for helping with the equipment setup and data collection. The work of Ishita Basu, Pitamber Shukla, Daniela Tuninetti and Daniel Graupe was partially funded by NSF under award number 1134296. The data collection, patient payment was partially funded by NIH under award number R56 NS 040902-11 and the Parkinson’s Disease Foundation. Dr Leo Verhagen Metman gratefully acknowledges the support from the Parkinson’s Disease Foundation, educational support and consultation fees from Medtronic, Inc.
Appendix A. Thresholds on parameters for classification and prediction
Table A1.
Threshold for state classification in ET.
| Patient# | threshold |
|---|---|
| ET1 | ηc1 = 0.3, ηc2 = 0.6, ηc3 = 1.2, ηc4 = 0.15, ηc5 = 0.2, λ = 0.2 |
| ET2 | ηc1 = 0.06, ηc2 = 0.5, ηc3 = 3, ηc4 = 0.4, ηc5 = 0.15, λ = 0.2 |
| ET3 | ηc1 = 0.1, ηc2 = 0.6, ηc3 = 3, ηc4 = 0.07, ηc5 = 0.01, λ = 0.1 |
| ET4 | ηc1 = 0.5, ηc2 = 1.1, ηc3 = 1.6, ηc4 = 0.1, ηc5 = 0.15, λ = 0.2 |
Table A2.
Parameter threshold for prediction algorithm for ET.
| Patient# | Parameter with w1, w2 = 1 | threshold |
|---|---|---|
| ET1 | SpEn and
and R(w2) |
(ηl1, ηh1) = (0.25, 0.3); (ηl2, ηh2) = (0.18, 0.22); ηp = 10; fp = 22; (fl, fh) = (5, 10) (ρl, ρh) = (0.3, 0.35) (fl, fh) = (10, 11) |
| ET2(left) | and | fp = 20; (fl, fh) = (4, 10) |
| R(w2) | (ρl, ρh) = (0.3, 0.4) | |
| ET2(right) | SpEn and
|
(ηl1, ηh1) = (0.45, 0.5); (ηl2, ηh2) = (0.1, 0.2); ηp = 10; (fl, fh) = (11, 12) |
| ET3 | SpEn and
R(w2) |
(ηl1, ηh1) = (0.3, 0.4); (ηl2, ηh2) = (0.16, 0.18); ηp = 50; (ρl, ρh) = (0.4, 0.48) |
|
|
(fl, fh) = (11, 12) | |
| ET4 | SpEn and
and |
(ηl1, ηh1) = (0.78, 0.98); (ηl2, ηh2) = (0.38, 0.48); ηp = 20; fp = 22; (fl, fh) = (5, 10) |
| R(w2) | (ρl, ρh) = (0.3, 0.34) |
Table A3.
Parameter threshold for prediction algorithm for PD.
| Patient# | Parameter with w = 1 | threshold |
|---|---|---|
| PD1 | SpEn and
SpEn and R and |
(ηl1, ηh1) = (0.2, 0.35); (ηl2, ηh2) = (0.11, 0.2); ηp = 15; (ηl1, ηh1) = (0.35, 0.4); (ηl2, ηh2) = (0.14, 0.34); ηp = 15; (ρl, ρh) = (0.2, 0.22) fp1 = 28; (fl1, fh1) = (4, 10) |
| PD2 | SpEn and
Hwt |
(ηl1, ηh1) = (0.2, 0.32); (ηl2, ηh2) = (0.1, 0.16); ηp = 28; (hl, hh) = (0.31, 0.35) |
| PD3 |
Hwt and |
(hl, hh) = (0.32, 0.36) fp2 = 30; (fl2, fh2) = (4, 7) |
| PD4 | SpEn and
Hwt and |
(ηl1, ηh1) = (0.25, 0.34); (ηl2, ηh2) = (0.15, 0.22); ηp = 25; (hl, hh) = (0.275, 0.295) fp2 = 30; (fl2, fh2) = (4, 7) |
References
- 1.Lozano AM, Dostrovsky J, Chen R, Ashby P. Lancet Neurol. 2002;1:225–231. doi: 10.1016/s1474-4422(02)00101-1. [DOI] [PubMed] [Google Scholar]
- 2.Metman LV, Konitsiotis S, Chase TN. Movement Disorders. 2000;15:3–8. doi: 10.1002/1531-8257(200001)15:1<3::aid-mds1003>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- 3.Benito-León J, Louis ED. The Lancet. 2007;369:1152–1154. doi: 10.1016/S0140-6736(07)60544-3. [DOI] [PubMed] [Google Scholar]
- 4.Shahzadi S, Tasker RR, Lozano AM. Stereotactic and Functional Neurosurgery. 1995;65:11–17. doi: 10.1159/000098890. [DOI] [PubMed] [Google Scholar]
- 5.Pahwa R, Lyons KL, Wilkinson SB, Carpenter MA, Troster AI, Searl JP, Overman J, Pickering S, Koller WC. Neurology. 1999;53:1447–1450. doi: 10.1212/wnl.53.7.1447. [DOI] [PubMed] [Google Scholar]
- 6.Volkmann J, Herzog J, Kopper F, Deuschl G. Movement Disorders. 2002;17:S181–S187. doi: 10.1002/mds.10162. [DOI] [PubMed] [Google Scholar]
- 7.Graupe D, Cline W. Systems, Man and Cybernetics, IEEE Transactions on. 1975:252–259. [Google Scholar]
- 8.Graupe D, Basu I, Tuninetti D, Vannemreddy P, Slavin KV. Neurological Research. 2010;32:899–904. doi: 10.1179/016164110X12767786356354. [DOI] [PubMed] [Google Scholar]
- 9.Leondopulos SS, Micheli-Tzanakou E. Computational Neuroscience. 2010:227–253. [Google Scholar]
- 10.Popovych OV, Hauptmann C, Tass PA. Biological cybernetics. 2006;95:69–85. doi: 10.1007/s00422-006-0066-8. [DOI] [PubMed] [Google Scholar]
- 11.Tass PA. Phase Resetting in Medicine and Biology: Stochastic Modeling and data Analysis. Springer; Berlin Heidelberg New York: 2006. [Google Scholar]
- 12.Hauptmann C, Roulet JC, Niederhauser JJ, Döll W, Kirlangic ME, Lysyansky B, Krachkovskyi V, Bhatti MA, Barnikol UB, Sasse L, et al. Journal of neural engineering. 2009;6:066003. doi: 10.1088/1741-2560/6/6/066003. [DOI] [PubMed] [Google Scholar]
- 13.Feng XJ, Greenwald B, Rabitz H, Shea-Brown E, Kosut R. J Neuroengineering. 2007;4:L14–21. doi: 10.1088/1741-2560/4/2/L03. [DOI] [PubMed] [Google Scholar]
- 14.Santaniello S, Fiengo G, Glielmo L, Grill WM. Neural Systems and Rehabilitation Engineering, IEEE Transactions on. 2011;19:15–24. doi: 10.1109/TNSRE.2010.2081377. [DOI] [PubMed] [Google Scholar]
- 15.Rosin B, Slovik M, Mitelman R, Rivlin-Etzion M, Haber SN, Israel Z, Vaadia E, Bergman H. Neuron. 2011;72:370–384. doi: 10.1016/j.neuron.2011.08.023. [DOI] [PubMed] [Google Scholar]
- 16.Graupe D, Basu I, Tuninetti D, Slavin K. ASSFN Biennial Meeting; San Francisco. 2012. [Google Scholar]
- 17.Temperli P, Ghika J, Villemure JG, Burkhard PR, Bogousslavsky J, Vingerhoets FJG. Neurology. 2003;60:78–81. doi: 10.1212/wnl.60.1.78. [DOI] [PubMed] [Google Scholar]
- 18.Basu I, Tuninetti D, Graupe D, Slavin KV. Adaptive control of deep brain stimulator for essential tremor: Entropy-based tremor prediction using surface-emg. Conference proceedings:International Conference of the IEEE EMBC; 2011. p. 7711. [DOI] [PubMed] [Google Scholar]
- 19.Widjaja F, Shee CY, Ang WT, Wing LA, Poignet P. Journal of Mechanics in Medicine and Biology. 2011;11:1347–1371. [Google Scholar]
- 20.Vaillancourt DE, Sturman MM, Verhagen-Metman L, Bakay RAE, Corcos DM. Neurology. 2003;61:919–925. doi: 10.1212/01.wnl.0000086371.78447.d2. [DOI] [PubMed] [Google Scholar]
- 21.Sturman MM, Vaillancourt DE, Verhagen-Metman L, Bakay RAE, Corcos DM. Brain. 2004;127:2131–2143. doi: 10.1093/brain/awh237. [DOI] [PubMed] [Google Scholar]
- 22.O’Suilleabhain P, Matsumoto J. Brain. 1998;121:2127–2134. doi: 10.1093/brain/121.11.2127. [DOI] [PubMed] [Google Scholar]
- 23.Shannon CE. ACM SIGMOBILE Mobile Computing and Communications Review. 2001;5:3–55. [Google Scholar]
- 24.Rosso OA, Blanco S, Yordanova J, Kolev V, Figliola A, Schurmann M, Basar E. Journal of neuroscience methods. 2001;105:65–75. doi: 10.1016/s0165-0270(00)00356-3. [DOI] [PubMed] [Google Scholar]
- 25.Pincus SM. Proceedings of the National Academy of Sciences of the United States of America. 1991;88:2297–2301. doi: 10.1073/pnas.88.6.2297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Pincus SM, Goldberger AL. American Journal of Physiology-Heart and Circulatory Physiology. 1994;266:H1643. doi: 10.1152/ajpheart.1994.266.4.H1643. [DOI] [PubMed] [Google Scholar]
- 27.Webber CL, Jr, Zbilut JP. Tutorials in contemporary nonlinear methods for the behavioral sciences. 2005:26–94. [Google Scholar]
- 28.Marwan N. http://tocsy.pik-potsdam.de/index2.php.
- 29.Baldi P, Brunak S, Chauvin Y, Andersen C, Nielsen H. Bioinformatics. 2000;16:412–424. doi: 10.1093/bioinformatics/16.5.412. [DOI] [PubMed] [Google Scholar]
- 30.Roscoe JT, Byars JA. Journal of the American Statistical Association. 1971;66:755–759. [Google Scholar]
- 31.Farina D, Fattorini L, Felici F, Filligoi G. Journal of Applied Physiology. 2002;93:1753–1763. doi: 10.1152/japplphysiol.00314.2002. [DOI] [PubMed] [Google Scholar]
- 32.Semmler JG, Nordstrom MA. Journal of neuroscience methods. 1999;90:47–55. doi: 10.1016/s0165-0270(99)00069-2. [DOI] [PubMed] [Google Scholar]
- 33.Filligoi GC, Felici F. Medical engineering & physics. 1999;21:439–448. doi: 10.1016/s1350-4533(99)00073-9. [DOI] [PubMed] [Google Scholar]
- 34.Zelmann R, Mari F, Jacobs J, Zijlmans M, Chander R, Gotman J. Automatic detector of High Frequency Oscillations for human recordings with macroelectrodes. EMBC 2010, Annual International Conference of the IEEE (IEEE); 2010. pp. 2329–2333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ocak H. Expert Systems with Applications. 2009;36:2027–2036. [Google Scholar]
- 36.Richman JS, Moorman JR. American Journal of Physiology-Heart and Circulatory Physiology. 2000;278:H2039. doi: 10.1152/ajpheart.2000.278.6.H2039. [DOI] [PubMed] [Google Scholar]
- 37.Marwan N, Carmen Romano M, Thiel M, Kurths J. Physics Reports. 2007;438:237–329. [Google Scholar]
- 38.Graupe D. Principles of artificial neural networks. Vol. 6. World Scientific Pub Co Inc; 2007. [Google Scholar]
- 39.Shukla P, Basu I, Graupe D, Tuninetti D, Slavin KV. A neural network-based design of an on-off adaptive control for deep brain stimulation in movement disorders. 2012. submitted to the IEEE EMBC. [DOI] [PubMed] [Google Scholar]
- 40.Klostermann F, Ehlen F, Vesper J, Nubel K, Gross M, Marzinzik F, Curio G, Sappok T. Journal of Neurology, Neurosurgery & Psychiatry. 2008;79:522–529. doi: 10.1136/jnnp.2007.123323. [DOI] [PubMed] [Google Scholar]
- 41.Pilitsis JG, Metman LV, Toleikis JR, Hughes LE, Sani SB, Bakay RAE. Journal of neurosurgery. 2008;109:640–646. doi: 10.3171/JNS/2008/109/10/0640. [DOI] [PubMed] [Google Scholar]
- 42.Kumar R, Lozano AM, Sime E, Lang AE. Neurology. 2003;61:1601–1604. doi: 10.1212/01.wnl.0000096012.07360.1c. [DOI] [PubMed] [Google Scholar]