Abstract
Studies that used conflict paradigms such as the Eriksen Flanker task show that many individuals with Parkinson’s disease (PD) have pronounced difficulty resolving the conflict that arises from the simultaneous activation of mutually exclusive responses. This finding fits well with contemporary views that postulate a key role for the basal ganglia in action selection. The present experiment aims to specify the cognitive processes that underlie action selection deficits among PD patients in the context of variations in speed-accuracy strategy. PD patients (n = 28) and healthy controls (n = 17) performed an arrow version of the flanker task under task instructions that either emphasized speed or accuracy of responses. Reaction time (RT) and accuracy rates decreased with speed compared to accuracy instructions, although to a lesser extent for the PD group. Differences in flanker interference effects among PD and healthy controls depended on speed-accuracy strategy. Compared to the healthy controls, PD patients showed larger flanker interference effects under speed stress. RT distribution analyses suggested that PD patients have greater difficulty suppressing incorrect response activation when pressing for speed. These initial findings point to an important interaction between strategic and computational aspects of interference control in accounting for cognitive impairments of PD. The results are also compatible with recent brain imaging studies that demonstrate basal ganglia activity to co-vary with speed-accuracy adjustments.
Keywords: Parkinson’s disease, Reaction time, Speed-accuracy tradeoff, SAT, Flanker interference, Cognitive control, Executive control
1. Introduction
Parkinson’s disease is a neurodegenerative condition that involves progressive loss of the dopamine-producing substantia nigra neurons of the basal ganglia. The disease is diagnosed by the presence of overt motor symptoms (e.g., bradykinesia, rigidity, and tremor), but also alters qualitative aspects of information processing (Cools, 2006; Robbins & Brown, 1990; Taylor & Saint-Cyr, 1995). Some of the cognitive deficits produced by PD can be related to how dopamine depletion alters functional interactions between the frontal cortex and the basal ganglia. The basal ganglia receive extensive afferents from the frontal cortex, thus bridging the established role of frontal cortex in executive cognitive control and the complementary pathways within the basal ganglia architecture that are hypothesized to implement, among several functions, the focused selection and inhibition of competing motor programs (Hikosaka, 1998; Mink, 1996). This functional connectivity has generated considerable interest in studying how PD might disrupt top-down, executive cognitive control processes that guide and optimize voluntary selection of appropriate actions in response to external stimuli (Hikosaka, 1998; Jackson & Houghton, 1995; Rolls & Treves, 1998; van den Wildenberg et al., 2006). In the present study, we investigate the effects of PD on two important aspects of cognitive control that operate and often interact during action selection: interference control and speed-accuracy strategy.
1.1. The effect of PD on interference control
In a dynamic, changing environment, the information conveyed by certain stimuli may be more relevant to action selection than other stimuli. Situations in which optimal performance calls for a novel or less familiar response but the environment or past learning strongly impels an alternative, but incorrect response, cause interference because conflicting responses are activated simultaneously. Interference control describes the cognitive mechanism(s) engaged to resolve this conflict situation and to select the appropriate action. One of the conflict tasks that have been used widely to study cognitive processes involved in interference control is the Eriksen flanker task (Eriksen & Eriksen, 1974). Here, participants are required to respond to a visual target while ignoring distractors, or flankers, positioned about the target that signal either the same response as the target (i.e., are congruent) or the opposite response (i.e., are incongruent). While performing this task, it is difficult to ignore the task-irrelevant flankers completely, especially on incongruent trials in which target and flankers signal opposite responses (Miller, 1991). For example, when a subject responds to a right-pointing target arrow that is surrounded by left-pointing flanker arrows, accuracy rates decrease and reaction time (RT) increases compared to when a response is made to a target arrow that is surrounded by flanker arrows pointing in the same direction. This observation is referred to as the flanker interference effect. In the case of incongruent flankers, the performance decrements are attributed to the conflict that arises from the simultaneous activation of opposing response alternatives.
According to dual-route models of information processing, the target, which guides selection of the preferred response, dominates processing along a slower, more controlled stimulus–response translation route (i.e., the deliberate route) so as to ensure correct response selection. In contrast, fast, automatic activation of responses associated with the flanker array is thought to occur along a direct route. The direct activation, or ‘response capture’, is closely related to the saliency of the flanker array. Because flankers dominate the visual array, response capture along the direct activation route is greater for the response signaled by the flankers, a finding supported by psychophysiological investigations that show stronger and earlier bias of activation over motor areas that control the response hand signaled by incongruent flankers (Bashore, 1990; Coles, Gratton, & Donchin, 1988; Gratton, Coles, Sirevaag, Eriksen, & Donchin, 1988). Flanker interference on incongruent trials results from direct response capture by the flankers that conflicts and competes with the deliberate selection of the response signaled by the target (e.g., Eimer, Hommel, & Prinz, 1995; Kornblum, Hasbroucq, & Osman, 1990; Ridderinkhof, van der Molen, & Bashore, 1995).
According to the ‘activation–suppression hypothesis’, the conflict that arises from the simultaneous activation of response alternatives can be resolved through selective suppression of initial response capture, as an act of top-down inhibitory control. The term ‘selective response suppression’ is used here descriptively to refer to mechanisms that serve to reduce interference between competing actions. RT distribution analyses are a useful tool to quantify the temporal dynamics and individual proficiency of selective response suppression. More specific, delta plots can be constructed by plotting the interference effect as a function of response speed (de Jong, Liang, & Lauber, 1994; Ridderinkhof, 2002; Wiegand & Wascher, 2007). In accordance with the dual-route architecture, delta plots reveal that flanker interference effects are reduced for relatively slow responses, and more so for groups of participants that are proficient at suppressing unintended responses.
Because the basal ganglia are argued to play an important role in action selection, individuals with PD can be expected to show larger flanker interference effects compared to age-matched healthy controls (e.g., Praamstra, Stegeman, Cools, & Horstink, 1998). Several studies of medicated and medication-withdrawn PD patients supported this prediction (Praamstra, Plat, Meyer, & Horstink, 1999; Praamstra et al., 1998; Wylie, Bashore, & Stout, 2005; Wylie et al., 2009), whereas other studies showed similar interference effects among PD and healthy control groups (Cagigas, Filoteo, Stricker, Rilling, & Friedrich, 2007; Falkenstein, Willemssen, Hohnsbein, & Hielscher, 2006; Lee, Wild, Hollnagel, & Grafman, 1999). In the study with by far the largest sample size (50 PD patients), the PD group displayed larger mean flanker interference effects compared to a healthy control group, and this difference remained for a subset of PD patients that was matched to the healthy control group on the basis of baseline RT (Wylie et al., 2009). Distributional analyses of RT revealed that the PD patients, particularly those with the largest interference effects, displayed stronger response capture by the irrelevant flankers coupled with poorer inhibitory control of this capture. An important, yet unexamined, issue concerns how individual differences in task strategy may influence these action selection deficits in PD patients. This led us to the present experiment, which considers an important strategic variable known to affect task performance in situations of response conflict, namely, speed-accuracy strategy.
1.2. Speed-accuracy strategy and PD
The strategic tradeoff between speed and accuracy is well known to studies of mental chronometry and certainly evident in a variety of applied settings. As an example, consider the adjustments to speed-accuracy strategy that might be made by a neurosurgeon. During the placement of intracranial electrodes, the surgeon will likely favor precision at the expense of speed. However, an emergency situation might compel the same surgeon to sacrifice some precision in order to quickly stop an aneurysm. As this example suggests, speed-accuracy strategy and adjustments can be deliberate and under the control of the individual (Niemi & Naatanen, 1981; Pachella, 1974; Wickelgren, 1977). Thus, individuals (or groups of individuals) can approach a task by focusing on the speed of performance (often at the expense of making more errors), or on the accuracy of performance (often at the expense of slowing RT). Relevant to the present investigation, it has been hypothesized that changes in response activation and inhibitory processes play an important role in speed-accuracy adjustments and may depend on intact frontal–basal ganglia circuits (Band, Ridderinkhof, & van der Molen, 2003; Frank, 2006; Van Veen, Krug, & Carter, 2008).
Conflict tasks, including the flanker task, are ideal for investigating the interaction between interference control and speed-accuracy strategy (Osman et al., 2000). On incongruent trials, error rates increase when task instructions emphasize speed compared to when task instructions emphasize accuracy. Thus, an individual who pushes to respond quickly is more susceptible to initial response capture that is induced by the incongruent flankers. Conversely, fewer overt response selection errors are made when accuracy of performance is emphasized. In terms of RT, an emphasis on speed of performance decreases RT, but studies of healthy adults have mostly shown that the magnitude of the flanker interference effect remains unchanged (Osman et al., 2000; Rinkenauer, Osman, Ulrich, Muller-Gethmann, & Mattes, 2004; Ullsperger, Bylsma, & Botvinick, 2005). Thus, even though healthy participants are more susceptible to making an initial fast error when emphasizing speed, emphasis on speed or on accuracy does not change the magnitude of the RT interference effect.
1.2.1. The current study
Because (1) the basal ganglia dysfunction caused by PD is argued to compromise action selection/inhibition processes and (2) speed-accuracy adjustments may involve basal ganglia activity, we tested a large, new sample of PD and healthy control participants on a flanker task that concurrently manipulated speed-accuracy instructions. Our central prediction was that the increased levels of response capture induced by speed pressure would produce greater interference for PD patients relative to healthy controls. That is, we expected PD patients to be more sensitive than healthy controls to the interaction between interference effects and speed-accuracy strategy. Specifically, the PD group was expected to more often select the prepotent, but incorrect, response in error and show increased flanker interference under the speed instructions compared to healthy controls. We were less specific about predictions when task instructions emphasized accuracy of performance.
To capture the temporal dynamics of direct response activation and its subsequent suppression, we used distributional analysis techniques guided by the activation–suppression hypothesis (Ridderinkhof, 2002). According to this model, the proportion of fast errors reflects the strength of initial response capture by the incongruent flankers. We expected speed instructions to increase response capture. If PD affects the dynamics of response capture, a higher proportion of fast errors relative to healthy controls was expected. According to the activation–suppression hypothesis, the engagement and build up of selective suppression of direct response activation can be observed by plotting the interference effect as a function of the entire RT distribution (i.e., delta plots). In particular, the modulation of the interference effect at the slowest segments of the distribution, where inhibition is expected to be fully engaged, is sensitive to group differences in the efficiency of inhibitory control (Bub, Masson, & Lalonde, 2006; Ridderinkhof, Scheres, Oosterlaan, & Sergeant, 2005; Wylie, Ridderinkhof, Eckerle, & Manning, 2007). Guided by this framework and the proposed role of the basal ganglia during action selection, we predicted that PD patients would show reduced selective suppression of incongruent responses when instructions emphasized speed of responding.
2. Methods
2.1. Participants
Twenty-eight individuals diagnosed with PD and 17 healthy controls similar in age (p > .05) and education (p > .05) comprised the final sample (see Table 1 for participant information). The data from three additional PD patients and two controls were excluded because of excessively slowed responses and highly variable error rates (i.e., >3 standard deviations from the group mean) that suggested poor attention or comprehension of the task. We note that the PD and healthy control participants used in the current study comprised a new sample of participants that did not overlap with those participants used in our previous study of flanker effects in PD. The groups comprising the final sample did not differ on a measure of global cognitive status (p > .05) (Mini-Mental Status Exam; Folstein, Folstein, & McHugh, 1975). The PD participants were recruited from the Movement Disorders Clinic at the University of Virginia, diagnosed with PD by a neurologist specializing in movement disorders, and voluntarily completed the study. All PD patients were of mild to moderate disease severity as rated by the Hoehn and Yahr Scale (i.e., stage I–III), with stage II the most common rating (Hoehn & Yahr, 1967). All but six of the PD patients were taking medications to improve dopaminergic function and tested during the “on” state of their medication cycle. The six patients had not yet initiated dopaminergic pharmacotherapy and had shorter disease duration than the patients on dopaminergic therapy (about 3 years versus about 7 years), but the two groups were of similar age (about 65 years) and disease severity based on the motor subscore of the UPDRS and the Hoehn and Yahr (p > .10). Five PD patients and one healthy control participant were taking anti-depressant medications, but reported stable mood functioning.
Table 1.
Demographic and flanker task data for PD and HC groups.
| HC | PD | P-value | |
|---|---|---|---|
| Sample size | 17 | 28 | |
| Age (years) | 62.3 (9.5) | 65.5 (9.5) | 0.27 |
| Education (years) | 17.2 (3.7) | 15.8 (2.6) | 0.15 |
| Gender (M:F) | 9:8 (53% male) | 17:11 (61% male) | – |
| Depression rating (CES-D) | 12.4 (4.1) | 14.6 (6.1) | 0.32 |
| UPDRS motor total | – | 19 (1.68) | – |
| AMNART (estimated IQ) | 118.9 (9.1) | 115.6 (10.4) | 0.30 |
| MMSE (raw score) | 29 (0.9) | 28.6 (1.6) | 0.37 |
| Flanker task | |||
| Accuracy instructions | |||
| Congruent (Cg) Flankers | |||
| RT (ms) | 475 (81) | 492 (59) | |
| Accuracy (%) | 99.8 (0.6) | 98.9 (1.1) | |
| Incongruent (Ig) Flankers | |||
| RT (ms) | 546 (91) | 567 (74) | |
| Accuracy (%) | 98.6 (1.6) | 97.0 (2.4) | |
| Flanker effect (Ig–Cg) | |||
| RT (ms) | 72 (24) | 76 (34) | |
| Accuracy (%) | –1.1 (1.5) | –1.4 (1.8) | |
| Speed instructions | |||
| Congruent (Cg) Flankers | |||
| RT (ms) | 422 (58) | 456 (67) | |
| Accuracy (%) | 99.5 (0.7) | 98.5 (1.4) | |
| Incongruent (Ig) Flankers | |||
| RT(ms) | 494 (59) | 546 (87) | |
| Accuracy (%) | 94.9 (3.5) | 94.3 (4.9) | |
| Flanker effect (Ig–Cg) | |||
| RT (ms) | 72 (25) | 91 (43) | |
| Accuracy (%) | –4.6 (3.6) | –4.1 (5.2) | |
Healthy elderly controls were spouses or family members of PD patients as well as individuals recruited from the local community via advertisement. Exclusion criteria included the following: history of other neurological condition; unstable or untreated mood disorder; history of bipolar affective disorder, schizophrenia, or other psychiatric condition known to compromise executive cognitive functioning; untreated or unstable medical condition known to interfere with cognitive functioning (e.g., diabetes and pulmonary disease). All participants provided informed consent prior to participating in the study, which was fully compliant with standards of ethical conduct in human research as governed by the University of Virginia human investigation committee.
2.2. Task design and procedures
The flanker task was programmed using E-prime software (www.pstnet.com; Psychology Software Tools, Inc.) and implemented on an IBM-compatible computer with a 17-in. digital display computer screen. The computer screen, placed at a distance of 91 cm, was positioned so that stimuli, white arrows (pointing in the left or right direction) against a black background, appeared at eye level. Responses were registered via a button box so that the right and left thumbs rested comfortably on corresponding right and left response buttons. Subjects were instructed to respond to the direction of a centrally located target arrow according to the following rules: left pointing target arrow = left button press; right pointing target arrow = right button press.
Within blocks of trials, each trial began with the presentation of the word “ACCURACY” (for the Accuracy Instruction Set) or the word “SPEED” (for the Speed Instruction Set) for 750 ms. For blocks of trials containing the word “ACCURACY” at the beginning of each trial, participants were instructed to focus on making an accurate response without losing too much speed. For blocks containing the word “SPEED” at the outset of a trial, participants were instructed to focus on speeding their responses and be less concerned about making errors, but not to the point of simply guessing a response. Participants completed equal numbers of speed and accuracy blocks, which alternated throughout the task.
After the word “SPEED” or “ACCURACY” was extinguished, a fixation point appeared in isolation in the center of the screen for 750 ms. Participants were instructed to focus on the fixation point as a target arrow would appear in the same location. The fixation point was then replaced by a stimulus array consisting of a target arrow and flanking arrows that remained on the screen until the participant made a response or 2000 ms elapsed. If no response was issued by 2000 ms, the trial was terminated, and the next trial epoch began. Each array consisted of five horizontally aligned arrows, a target arrow located in the same center location as the fixation point and two flanker arrows located on each side of the target arrow. The entire arrow array spanned 22.5 cm (visual angle = 14°), and each arrow measured 3.5 cm in height and 4.0 cm in width (visual angle = 2.5°). Less than 1° visual angle separated the edges of the target arrow and the edges of the nearest flanker arrows. After each response, the screen was cleared for an intertrial interval of 1600 ms before the next trial began with the presentation of the word “ACCURACY” or “SPEED.”
In addition to defining each block of trials on the basis of Instruction Set (speed versus accuracy), each trial within a block was defined by the correspondence of the flanking arrows to the target arrow, what we call Flanker Congruence. This factor had two levels, congruent and incongruent. Congruent arrays consisted of flanker arrows pointing in the same direction as the target arrow, thus corresponding to the same response as the target (Fig. 1). For incongruent arrays, flanker arrows pointed in the opposite direction of the target arrow (Fig. 1). Each flanker array and direction (right, left) appeared randomly and with equal probability within a block of trials. Participants completed a block of 20 practice trials under each Instruction Set prior to completing 10 blocks of 40 experimental trials that alternated between the two Instruction Sets. Thus, each participant completed a total of 400 experimental trials, with 100 trials corresponding to each combination (i.e., cell) of the factors Instruction Set and Flanker Congruence.
Fig. 1.

Example of congruent (upper configuration) and incongruent (lower configuration) stimulus arrays used in the flanker task.
2.3. Data analyses
The design was mixed with one between-subjects factor, Group (PD, HC), and two within-subject factors, Instruction Set (accuracy, speed) and Flanker Congruence (congruent, incongruent). Instruction Set varied across blocks of trials, whereas Flanker Congruence was mixed randomly within blocks of trials. For each subject, extreme RT values in each condition were discarded, accounting for fewer than 1% of trials per flanker condition per subject. We applied an initial search for RT values that were 3 standard deviations above or below the mean and also eliminated anticipatory responses (i.e., RT < 100 ms). Visual inspection of discarded trials confirmed that only extreme, outlying values were eliminated from the analysis. RT and accuracy rates were the dependent variables of interest. Mean RT and square-rooted accuracy data were analyzed using repeated-measures analysis of variance to determine the effects of Instruction Set (accuracy, speed), Flanker Congruence (congruent, incongruent), and Group (PD, HC).
2.4. RT distributional analyses
The effects of accuracy versus speed instructions on accuracy rates and on interference effects were plotted against mean RT using, respectively, the conditional accuracy function (CAF) and the delta-plot technique. CAFs depict accuracy rates as a function of the underlying RT distribution. Specifically, each participant’s RTs for a particular cell were rank-ordered and partitioned into 7 equal size bins (septiles; bins 1–7). Accuracy rates were calculated separately for each bin and plotted against the average RT for that bin. To construct delta plots, each participant’s RTs for a particular cell were also rank-ordered and partitioned into 7 equal size bins (septiles; bins 1–7). Next, mean RT was calculated for each bin. Interference effect sizes (delta values) were generated for each Instruction Set by subtracting mean RT for the congruent condition from the incongruent condition for each bin. Delta plots for RT were then constructed by plotting interference effect sizes (i.e., delta values) as a function of average RT for the corresponding bin.
3. Results
3.1. Response accuracy
3.1.1. Mean accuracy data
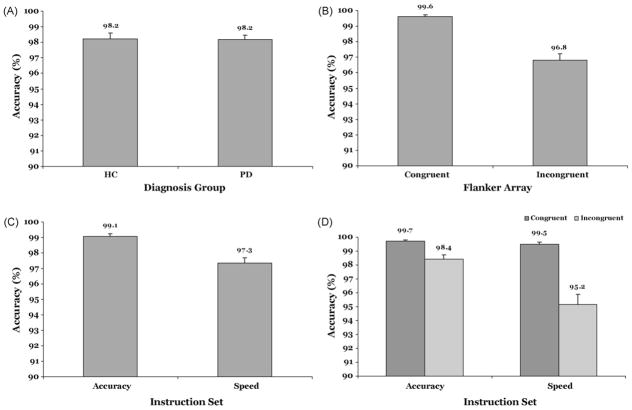
Overall, accuracy rates did not differ between the two groups, Group, F(1, 43) = 0.01, p = .93. However, accuracy was lower for incongruent than that for congruent flanker arrays, (Flanker Congruence, F(1, 43) = 44.01, p < .001) and under speed as opposed to accuracy instructions (Instruction Set, F(1, 43) = 25.69, p < .001). These main effects are depicted in Fig. 2A–C. Moreover, as illustrated in Fig. 2D, the reduction in accuracy seen with incongruent flankers was greater under speed than accuracy instructions (Flanker Congruence × Instruction Set, F(1, 43) = 19.01, p < .001). That the two groups had similar accuracies across all factor levels is suggested by our finding that the pattern of effects on accuracy rates associated with variations in Flanker Congruence and Instruction Set did not differ across groups. That is, all of the group interactions with these two factors were at p > .10.
Fig. 2.
Mean accuracy rates (%) as a function of (A) Group, (B) Flanker Congruence, (C) Instruction Set, and (D) the Instruction Set by Flanker Congruence interaction.
3.1.2. Conditional accuracy functions
According to the activation–suppression hypothesis, changes in initial response capture induced by the incongruent flankers can be measured by the pattern of errors exposed in conditional accuracy functions (CAF). In conflict tasks, the strength of initial response capture is reflected in the frequency of fast errors, with higher error rates associated with stronger initial capture. Fig. 3 shows the CAFs for healthy controls and PD patients under accuracy (Panel A) and speed (Panel B) instructions. The slope value between the two fastest RT segments of the CAF has been used as a measure of the strength of initial response capture, with steeper slopes revealing a higher proportion of fast errors suggestive of stronger initial activation of the incorrect response (Ridderinkhof, 2002). We predicted that PD patients would show more fast errors under speed instructions (i.e., steeper positive slope between the fastest two segments of the RT distribution), indicating a vulnerability to stronger response capture when pressed for speed.
Fig. 3.
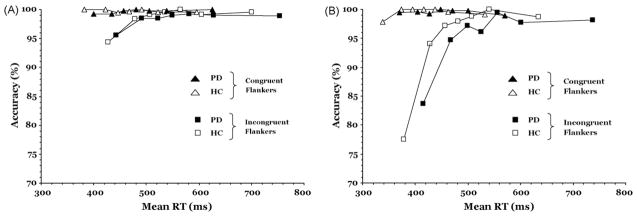
Conditional accuracy functions (CAF) for PD and HC groups: (A) CAF for congruent and incongruent flankers under the instructions to emphasize accuracy of responding; (B) CAF for congruent and incongruent flanker conditions under the instructions to emphasize speed of responding.
To test this hypothesis, the slope between the first two (i.e., the fastest) segments of the CAF was submitted to repeated-measures ANOVA with Instruction Set and Flanker Congruence as within-subject factors and Group as the between-subject factor. The slope was modulated significantly by variations in flanker congruence as suggested in our finding that incongruent flankers produced significantly more fast errors (i.e., a steeper positive slope) than did congruent flankers (Flanker Congruence, F(1, 43) = 21.55, p < .001). Fast errors were also more prevalent under speed than accuracy instructions (Instruction Set, F(1, 43) = 23.46, p < .001). However, this effect varied with the congruency between target and flanker stimuli (Flanker Congruence × Instruction Set, F(1, 43) = 10.51, p < .01). As reflected in Fig. 3A and B, a steeper positive-going slope (i.e., stronger response capture) was induced by incongruent flankers than by congruent flankers under accuracy instructions, F(1, 43) = 24.69, p < .001, and under speed instructions, F(1, 43) = 34.82, p < .001. However, the interaction showed that this effect was greater under speed compared to accuracy instructions. It is important to note that the steepness of the initial slopes of the CAFs did not differ between PD and HC for variations in either Flanker Congruence or Instruction Set (all Group influences on the two other factors were at p > .10). The absence of any such interactions indicates that variations in Flanker Congruence induced similar patterns of initial response capture in the two groups across speed and accuracy instructions.
3.2. Reaction time
3.2.1. Mean RT data
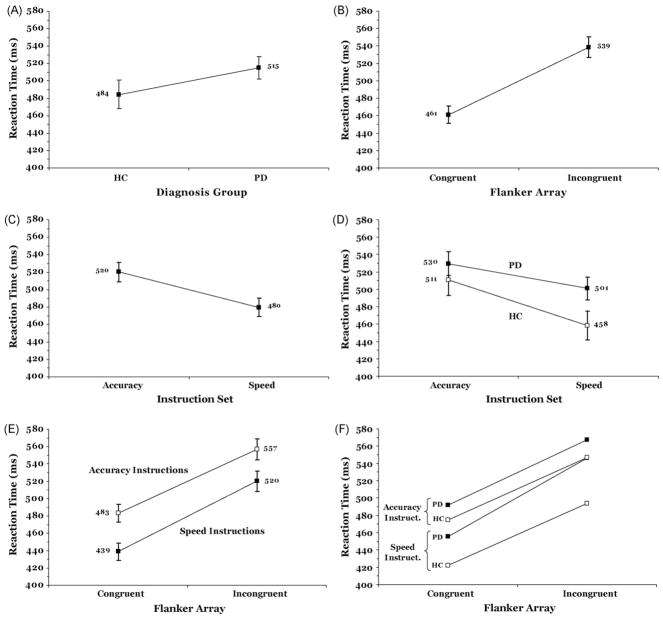
As shown in Fig. 4A, the two groups did not differ in overall RT (Group, F(1, 43) = 2.19, p > .10). RT differed, however, with variations in Flanker Congruence (F(1, 43) = 239.72, p < .001) and Instruction Set (F(1, 43) = 38.03, p < .001). As is evident in Fig. 4B and C, RT was slower when incongruent rather than congruent flankers appeared (B) and when accuracy rather than speed of responding was emphasized (C). Overall, the increase in RT apparent for incongruent arrays did not differ between the two groups (Group × Flanker Congruence, F(1,43) = 1.34, p > .10). However, there was a trend in the data, shown in Fig. 4D, suggesting that HC may increase their speed more than PD under speed instructions (Group × Instruction Set, F(1, 43) = 3.31, p = .07). Under accuracy instructions, both groups had equivalent RTs, F(1, 43) = 0.70, p = .68, whereas under speed instructions, HC had faster RTs than PD, F(1, 43) = 4.09, p < .05. In addition, as illustrated in Fig. 4E, the increase in RT associated with responding to an incongruent flanker array was larger under speed than accuracy instructions (Instruction Set × Flanker Congruence, F(1, 43) = 5.92, p < .05). However, it is evident in Fig. 4F that this increase was not shared among both groups. A three-way interaction indicated that there was no change in the magnitude of the interference effect among healthy controls between accuracy and speed instructions, whereas there was a marked interference effect increase in the PD group when they were pressed for speed (Group × Instruction Set × Flanker Congruence, F(1, 43) = 5.72, p = .02; group comparison, p < .05). From Fig. 4F, the source of this interaction is quite clear. Under speed compared to accuracy instructions, HC individuals speeded up their responses for congruent and incongruent arrays alike, whereas PD patients lagged behind in speeding up their responses on incongruent trials compared to congruent trials. Of note, to address the role of global reaction speed as a potential explanatory factor, we ran the same analysis with overall RT included as a covariate. Importantly, the significant three-way interaction between group, instruction set, and Flanker Congruence remained unchanged.
Fig. 4.
Mean RT (ms) as a function of (A) diagnosis group, (B) Flanker Congruence, (C) Instruction Set, (D) the Instruction Set by Group interaction, (E) the Instruction Set by Flanker Congruence interaction, and (F) the three-way interaction among Group, Instruction Set, and Flanker Congruence.
We conducted a follow-up analysis to rule out the possibility that these effects depended on how much participants sped their RT under speed instructions compared to accuracy instructions. We calculated the average RT difference between trials under the accuracy instruction and those under the speed instruction for each individual. Next, we ranked-ordered participants on the basis of this average RT difference. We applied separate median splits to the HC and PD groups, creating ‘Acceleration Subgroups’ with comparatively smaller and larger speeding of their RTs due to speed instructions. For the HC group, the Acceleration Subgroups sped their RTs by 18 and 90 ms, respectively, whereas the PD Acceleration Subgroups shortened their RTs by 3 and 54 ms, respectively. We examined flanker interference effects (incongruent RT – congruent RT) using repeated-measures ANOVA to determine the effects of Instruction Set (accuracy, speed), Group (HC, PD), and Acceleration Subgroups (small increase, large increase). These effects are plotted in Fig. 5. Consistent with the main analysis, flanker interference effects were influenced by Instruction Set, F(1, 40) = 5.01, p < .05, with speed instructions associated with larger interference effects compared to accuracy instructions. However, this effect varied by Group, (Group × Instruction Set, F(1, 40) = 6.57, p < .05), indicating that PD patients showed a greater increase in the flanker interference effect than did HC participants. Importantly, this effect was independent of how much faster individuals sped their responses under speed stress, (Acceleration Subgroup × Group × Instruction Set, F(1, 40) = 0.36, p = .55). In fact, the Acceleration Subgroup factor did not influence interference effects independently or interact with Group or Instruction Set (all p > .10). These results suggest that the exacerbated interference effects under speed stress among PD patients are independent of how much they actually sped their RTs.
Fig. 5.
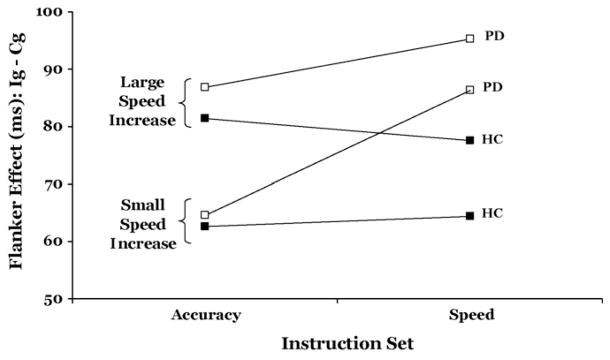
Mean Flanker interference effect (ms) for Acceleration Subgroups (small versus large speed increase) as a function of Instruction Set (accuracy versus speed). Ig = incongruent and Cg = congruent.
3.2.2. Delta plots
The analysis of mean RT showed that, relative to healthy controls, PD patients experienced greater flanker interference effects when pressing for speed. Among HC participants, on the other hand, the interference effect did not vary as a function of the Instruction Set. One possible explanation for the increased effect among PD patients is that they had greater difficulty overcoming the early response capture (i.e., suppressing the initial incorrect response activation) induced by the incongruent flankers which, in turn, delayed their selection and activation of the correct response. Previous studies have utilized the delta plot technique on RT data as a way of measuring the efficiency of inhibitory control during response conflict tasks (Forstmann, van den Wildenberg, & Ridderinkhof, 2008a; Ridderinkhof et al., 2005; Wiegand & Wascher, 2007; Wylie et al., 2009). According to the activation–suppression hypothesis, the initial activation of the incorrect response signaled by incongruent flankers is eventually suppressed by a top-down inhibitory control process. Because inhibition takes time to buildup, its effects are best observed for slower responses in an RT distribution. Delta plots display interference effects (RT incongruent – RT congruent) across the entire RT distribution. Consistent with the initial buildup of incorrect response activation, interference effects generally show an increase across the fastest segments of an RT distribution (i.e., a positive delta slope). However, the engagement of inhibitory control processes reduces the slope of this increase and in some tasks (e.g., the Simon task) actually produces a strong negative-going delta slope as the size of the interference effect decreases over time (see also Burle, Possamaï, Vidal, Bonnet, & Hasbroucq, 2002). In fact, individual and group differences in the delta slope value between the slowest segments of the RT distribution are associated with the effectiveness of inhibitory control, with more effective inhibition revealed by less positive-going (or more negative-going) delta slopes (Ridderinkhof, 2002).
We applied the delta plot method to determine if the increased flanker interference effect among PD patients under speed instructions relates to less efficient selective suppression. Guided by the activation–suppression hypothesis outlined above, we compared the effects of Instruction Set on the delta slopes of the RT distribution. Fig. 6 depicts the interference effects (i.e., RT delta values) across the entire RT distribution for healthy controls and PD patients under either accuracy (A) or speed (B) instructions. To test the predictions of the activation–suppression hypothesis, we submitted the slope values to a repeated-measures ANOVA with Instruction Set (speed, accuracy) and Delta Slopes (corresponding to the six slopes between bins 1–7) as within-subject factors and Group (PD, HC) as a between-subject factor. This analysis revealed one significant main effect, that of Instruction Set (F(1, 43) = 5.69, p = .02), indicating that the delta slope was larger for speed (m = .32) than for accuracy instructions (m = .25). Thus, the interference effect increased at a steeper rate when speed was emphasized. However, the steepness of the slope did not vary between the two groups (Group, F(1, 43) = 0.56, p = .46), whether as a function of Instruction Set (Group × Instruction Set, F(1, 43) = 0.84, p = .36), or as a function of the three-way interaction between Group, Instruction Set, and Delta Slope, F(1, 43) = 0.37, p = .87. None of the remaining interactions were significant.
Fig. 6.
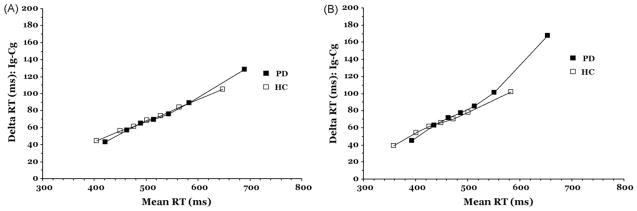
Delta plots for PD and HC groups when instructions emphasize (A) accuracy of responding and (B) speed of responding.
The omnibus analysis of delta slopes did not reveal group interactions with Instruction Set. However, we proceeded with separate group analyses of delta slopes for a few reasons. First, only the PD group showed an overall mean RT change in the flanker interference effect as a function of Instruction Set. This suggested that delta slope analyses may only be sensitive to a within-subject analysis of the PD group. In fact, inspection of the delta plot Fig. 6A and B further suggested this possibility. The delta slope between the slowest bins of the RT distribution appears to differ according to accuracy and speed instructions for the PD group only. We also suspected that the sensitivity of the omnibus test to PD effects at the last segment of the RT distribution may have been masked by the added variance from the delta slopes associated with the first five segments of the RT distribution, which were not expected to differ between groups or as a function of Instruction Set. According to the activation–suppression model, the 6th and last segment of the RT distribution should be most sensitive to the effects of group or Instruction Set on the suppression mechanism. Thus, we focused the following analysis on the delta slope associated with the slowest segment of the RT distribution, expecting that this analysis would reveal important effects of Instruction Set on this delta slope within the PD group.
Based on Fig. 6A and B, we expected that an analysis of the HC group would show no effects of Instruction Set on delta slopes. This turned out to be the case as the overall delta slope for speed (m = .28) and for accuracy (m = .24) instruction sets did not differ among healthy controls, F(1, 16) = 0.81, p = .38. As expected, the overall delta slope for speed (m = .35) was significantly larger than for accuracy (m = .25) among PD patients, F(1, 27) = 7.50, p = .01. Zooming in on the slowest segments of the RT distribution where, according to the activation–suppression model, inhibitory control is expected to be maximal, a paired t-test confirmed a significantly larger delta slope between these segments for speed instructions (m = .54) compared to accuracy instructions (m = .29) in PD, t(27) = −2.66, p < .01, one-tailed hypothesis test). This finding suggests that PD patients had greater difficulty suppressing the initial incorrect response capture when pressing for speed.
3.3. Relationships to clinical features of PD
Correlational methods were used to determine if the increase in the interference effect under speed instructions was related to disease severity (motor scores of the UPDRS) or years since disease onset. Neither the magnitude of the effect under the speed instructions nor its increase for speed relative to accuracy instructions was correlated with disease duration or motor symptom severity (p > .10).
4. Discussion
We investigated the influence of variations in speed-accuracy strategy on response conflict resolution between patients with Parkinson’s disease and healthy controls. In separate blocks of trials, subjects were instructed either to emphasize speed or accuracy in their responding. Both patients and controls complied with our instructions in that their response latencies and accuracy levels decreased significantly under speed as compared to accuracy instructions.
The flanker task used also successfully produced response interference in both groups as evidenced by poorer accuracy and slower RTs when a target arrow was flanked by incongruent as opposed to congruent arrows. However, the most important finding concerned differences between the PD and healthy control groups in terms of the interaction between speed-accuracy strategy and flanker interference effects. When accuracy was emphasized, RTs and accuracy rates were equivalent in the two groups as were the effects of incongruent flankers on these two measures (i.e., the flanker interference effect). Thus, when PD patients were more concerned about being accurate than fast in their processing and responding to the stimulus array, they were able to resolve response interference as effectively as did their age-matched peers.
Consistent with our prediction, however, a different pattern of flanker interference effects emerged for PD patients when instructions emphasized speed of performance. Relative to healthy control participants, PD patients did not increase their speed of responding as much under the speed instructions (PD = 28 ms; HC = 53 ms), but nonetheless showed an equivalent increase in fast errors under the incongruent flanker condition. Whereas the flanker effect in the HC group was equal between Instruction Sets, the PD patients showed an increased cost of responding to incongruent flankers under speed instructions compared to instructions that emphasized accuracy. This effect held regardless of how much faster patients sped up their performance under speed instructions than under accuracy instructions. Interestingly, a subset of PD patients who minimally sped their RTs under instructions of speed stress on the order of a few milliseconds still showed an increase in flanker interference. This suggests the intriguing hypothesis that merely the perception of speed pressure is sufficient for disrupting action selection processes among some PD patients. This has clear clinical relevance if future studies confirm this idea.
To examine the underlying processing dynamics of these augmented interference effects in PD in more detail, we used distributional analyses guided by the activation–suppression hypothesis. Specifically, we considered differences in the strength of the initial response activation of the incorrect response channel by the incongruent flankers (i.e., response capture) versus differences in the selective suppression of this activation. This analysis indicated that, relative to accuracy instructions, speed instructions led to a significant increase in fast errors in both HC and PD groups, supporting the inference that stronger initial response capture by the incongruent flankers had occurred. Notably, the PD and healthy control groups did not differ in their patterns of response capture for accuracy or speed instructions. This was somewhat surprising, particularly under the speed stress condition, given a demonstrated difference in this measure between PD and healthy controls in a recent flanker task study (Wylie et al., 2009). In that study, the PD group showed stronger response capture than the HC group, even when the two groups were matched on the basis of baseline RT. Notably, the HC group from that study showed an accuracy rate of about 92% for the fastest RT segment, whereas speed instructions led the current HC group to perform at 78% accuracy. We therefore suspect that the discrepancy between studies lies in the fact that the HC group sped up their reactions more under the speed instruction set than the PD group, which would be expected to produce stronger response capture. A baseline condition (e.g., neutral flanker condition) was not used in the current study in order to keep the length of the task reasonable for PD patients. It seems necessary to include a baseline RT measure in future studies of PD that vary speed-accuracy strategy.
Guided by the activation–suppression hypothesis, we used delta plots on the RT data to characterize the flanker interference effect. According to the model, slower responses benefit more from the buildup of inhibition to suppress the activation of the incongruent response. For HC, the slopes representing the change in flanker interference effects at the slowest segments of the distribution did not vary with Instruction Set. This suggests that speed-accuracy strategy may not normally influence the selective suppression mechanism in conflict tasks. Notably, a similar finding in healthy adults was observed by Band et al. (2003) who studied the effect of speed-accuracy instructions on selective suppression using a response-priming task. They also found evidence for strong effects of speed-accuracy strategy on response capture as revealed by conditional accuracy functions, but no effects on selective suppression of an incorrectly primed conflict response. Only the PD group showed changes in overall flanker interference effects as a function of strategy. Looking within the PD group, we found a significant effect of speed-accuracy strategy on the delta slope corresponding to the slowest segment of the RT distribution. Specifically, the slope was significantly larger under speed instructions compared to accuracy instructions, suggesting less effective suppression of the incorrect response activation when instructions stressed speed.
While the present results point to the possible role of reduced inhibitory control as one explanation of the PD effects, other explanations cannot be ruled out by the current study and represent important areas for future research. Several factors have been hypothesized to play a role in speed-accuracy tradeoff effects. An early study of speed-accuracy effects by Kutas, McCarthy, and Donchin (1977) indicated that under speed stress less time is given to the evaluation of the imperative stimulus prior to selecting a response. Thus, differences in the timing of stimulus evaluation with respect to stimulus onset and the onset of the response might be important to developing a more complete understanding of how speed-accuracy strategy affects the performance of PD patients under response conflict.
Others have argued that speed-accuracy adjustments involve response-end processes. Essential to this idea is a hypothetical distance between baseline levels of response system preparation and the threshold for selecting a response (Bogacz, 2007; Osman et al., 2000; Rinkenauer et al., 2004; Van der Lubbe, Jaskowski, Wauschkuhn, & Verleger, 2001; Van Veen et al., 2008). Recent evidence suggests that variations in response preparation and/or adjustments to the response threshold may be dependent on intact basal ganglia function (Bogacz & Gurney, 2007; Forstmann et al., 2008b; Frank, 2006; Lo & Wang, 2006). For example, using the Simon task as a measure of response conflict, Van Veen et al. (2008) showed increased baseline activation in frontal-basal ganglia circuits preceding trials that emphasized speed of performance relative to trials in which instructions emphasized performance accuracy. Upon the presentation of the imperative stimulus, the change in activation from these baseline levels was smaller under speed stress relative to accuracy stress, consistent with the idea that less activation is required to reach the response threshold under speed instructions. Whether these patterns are altered by PD is unknown and represents an important direction for future studies.
It has also been conjectured that tonic levels of dopamine may play a key role in speed-accuracy adjustments performed by the basal ganglia system (Bogacz & Gurney, 2007; Gurney, Humphries, Wood, Prescott, & Redgrave, 2004). If true, the performance of PD patients off and on their dopaminergic medications should be particularly sensitive to speed-accuracy instructions. In the current study, all PD patients performed the task while taking their usual dopmaminergic medications with the exception of six patients who had not yet started taking dopaminergic medications and had a shorter duration of disease (about 3 years versus about 7 years for patients on dopaminergic medications). This small subgroup of PD patients showed a trend toward a larger overall flanker interference effect compared to PD patients taking dopaminergic medications (106 ms versus 77 ms; p = .08). Importantly, the subgroup of patients not yet taking dopaminergic medications showed a similar increase in flanker interference (19 ms) as the patients on medications (14 ms) when pressing for speed. A comparison of patient performance during “on” and “off” medication states would be particularly helpful in determining a role for dopamine in speed-accuracy adjustments.
The study shows that PD patients can resolve response interference as effectively as healthy peers when focusing on performance accuracy and being less concerned about the speed of their responses. In fact, when performance accuracy was emphasized, both groups achieved comparably high levels of accuracy at equivalent response speeds. We note that error rates were relatively low under both sets of instructions at all factor levels for both groups. This pattern is consistent with other studies that have demonstrated a tendency for older adults to prefer accuracy over speed relative to young adults (Botwinick, 1984; Rabbitt, 1979; Salthouse, 1979; Smith & Brewer, 1995). However, as noted by Pachella (1974), small changes in error rates, particularly when accuracy is quite high, can produce rather appreciable changes in RT. This, in fact, was true for PD patients. The roughly 5% error rate increase under speed instructions was associated with a measurable increase in the RT flanker interference effect among these patients.
The finding in PD of poor inhibitory control under speed stress coupled with normal interference control when emphasis is on response accuracy raises the possibility that strategy may be an important factor in accounting for the mixed findings in the literature concerning flanker interference effects in PD. We looked carefully at instructions and data patterns in previous studies for clues that might further support this notion, but found that most studies emphasized performance speed. Thus, it is difficult to determine how much patients complied with speed instructions or adjusted their speed and accuracy without inclusion of a comparison set of instructions that emphasized accuracy. It is notable that in two studies that reported no differences in flanker effects among PD and HC groups, the PD group showed slower overall RT with equivalent or higher error rates. In contrast, studies reporting higher interference effects among PD patients found overall RT to be similar among groups. Given the variation in task instructions and designs (see Falkenstein et al., 2006; Wylie et al., 2009, for detailed discussion of design issues), the current findings highlight the need for future studies that sample performance from a broader range of speed-accuracy levels.
As a final point of discussion, it is notable that previous studies of motor control have considered the possibility that slowed movement associated with PD reflects a compensatory slowing to improve movement accuracy (Mazzoni, Hristova, & Krakauer, 2007; Montgomery & Nuessen, 1990; Phillips, Martin, Bradshaw, & Iansek, 1994). According to this hypothesis, we would expect PD patients to show greater slowing of RT in order to perform at equivalent accuracy rates to healthy controls, even when instructions emphasized performance accuracy. This was generally not the case, and PD patients did not appear to have a pervasive deficit resolving response interference at all levels of strategy. PD patients showed equivalent RTs and accuracy rates when accuracy of performance was emphasized. However, when speed was emphasized, both HC and PD patients similarly tolerated about a 5% decrease in accuracy, even though PD patients did not speed their reactions to incongruent stimuli as much as did healthy controls. This pattern, however, does not rule out the possibility that PD patients constrained their speed in order to maintain a comfortable accuracy rate, which happened to coincide with that tolerated by healthy controls.
An alternative to the compensatory slowing hypothesis of motor control has recently been advanced by Mazzoni et al. (2007) who propose that PD patients are as capable at pressing for speed with similar accuracy costs as healthy controls, but poorly regulate the energy or effort expenditure necessary to consistently press for speed. In their study, PD patients showed equivalent speed-accuracy adjustments and dynamics in a reaching task, but took more trials to achieve criterion under speed instructions. Furthermore, the measure of trials-to-criterion was positively associated with a measure of the energy cost of making the movement among PD patients. This was interpreted as evidence that PD patients implicitly choose not to move faster due to the higher energy expenditure associated with movement. To weigh on this intriguing possibility, future studies of response conflict effects could sample a broad range of speed-accuracy adjustments and calculate the number of trials required by PD and HC groups to achieve a criterion performance level within each range. Comparing self-selected versus criterion-guided speed-accuracy ranges might also provide support to the idea that PD patients tend to rely on strategies that minimize energy expenditure more than healthy controls when making adjustments during psychomotor performance.
5. Conclusion
The interaction between speed-accuracy strategy and interference control is well established. The current study shows that, relative to healthy peers, individuals with PD who are pressing for performance speed take longer to resolve the interference that arises from the activation of an unintended response. Although in need of replication, this result suggests that the study of PD and basal ganglia dysfunction would benefit from investigations that consider the dynamic interactions between strategic and computational aspects of cognitive control.
Acknowledgments
The work of KRR and WPMvdW is supported, respectively, by a VICI grant and a VENI grant from the Netherlands Organization for Scientific Research (NWO).
References
- Band GPH, Ridderinkhof KR, van der Molen MW. Speed-accuracy modulation in case of conflict: The roles of activation and inhibition. Psychological Research. 2003;76:266–279. doi: 10.1007/s00426-002-0127-0. [DOI] [PubMed] [Google Scholar]
- Bashore TR. S–R compatibility viewed from a cognitive psychophysiological perspective. In: Proctor RW, Reeves TG, editors. Stimulus–response compatibility: An integrative perspective. Amsterdam: North Holland; 1990. pp. 183–224. [Google Scholar]
- Bogacz R. Optimal decision making theories: Linking neurobiology with behaviour. Trends in Cognitive Sciences. 2007;11:118–125. doi: 10.1016/j.tics.2006.12.006. [DOI] [PubMed] [Google Scholar]
- Bogacz R, Gurney K. The basal ganglia and cortex implement optimal decision making between alternative actions. Neural Computation. 2007;19:442–477. doi: 10.1162/neco.2007.19.2.442. [DOI] [PubMed] [Google Scholar]
- Botwinick J. Aging and behavior. 3. New York: Springer; 1984. [Google Scholar]
- Bub DN, Masson ME, Lalonde CE. Cognitive control in children: Stroop interference and suppression of word reading. Psychological Science. 2006;17:351–357. doi: 10.1111/j.1467-9280.2006.01710.x. [DOI] [PubMed] [Google Scholar]
- Burle B, Possamaï CA, Vidal F, Bonnet M, Hasbroucq T. Executive control in the Simon effect: An electromyographic and distributional analysis. Psychological Research. 2002;66:324–339. doi: 10.1007/s00426-002-0105-6. [DOI] [PubMed] [Google Scholar]
- Cagigas XE, Filoteo JV, Stricker JL, Rilling LM, Friedrich FJ. Flanker compatibility effects in patients with Parkinson’s disease: Impact of target onset delay and trial-by-trial stimulus variation. Brain and Cognition. 2007;63:247–259. doi: 10.1016/j.bandc.2006.09.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coles MG, Gratton G, Donchin E. Detecting early communication: Using measures of movement-related potentials to illuminate human information processing. Biological Psychology. 1988;26:69–89. doi: 10.1016/0301-0511(88)90014-2. [DOI] [PubMed] [Google Scholar]
- Cools R. Dopaminergic modulation of cognitive function-implications for L-DOPA treatment in Parkinson’s disease. Neuroscience and Biobehavioral Reviews. 2006;30:1–23. doi: 10.1016/j.neubiorev.2005.03.024. [DOI] [PubMed] [Google Scholar]
- de Jong R, Liang CC, Lauber E. Conditional and unconditional automaticity: A dual-process model of effects of spatial stimulus–response correspondence. Journal of Experimental Psychology: Human Perception and Performance. 1994;20:731–750. doi: 10.1037//0096-1523.20.4.731. [DOI] [PubMed] [Google Scholar]
- Eimer M, Hommel B, Prinz W. S–R compatibility and response selection. Acta Psychologica. 1995;90:301–313. [Google Scholar]
- Eriksen BA, Eriksen CW. Effects of noise letters upon the identification of target letters in a non-search task. Perception & Psychophysics. 1974;16:143–149. [Google Scholar]
- Falkenstein M, Willemssen R, Hohnsbein J, Hielscher H. Effects of stimulus–response compatibility in Parkinson’s disease. A psychophysiological analysis. Journal of Neural Transmission. 2006;113:1449–1462. doi: 10.1007/s00702-005-0430-1. [DOI] [PubMed] [Google Scholar]
- Folstein MF, Folstein SE, McHugh PR. Mini-mental state. Journal of Psychiatric Research. 1975;12:189–198. doi: 10.1016/0022-3956(75)90026-6. [DOI] [PubMed] [Google Scholar]
- Forstmann BU, van den Wildenberg WP, Ridderinkhof KR. Neural mechanisms, temporal dynamics, and individual differences in interference control. Journal of Cognitive Neuroscience. 2008;20:1854–1865. doi: 10.1162/jocn.2008.20122. [DOI] [PubMed] [Google Scholar]
- Forstmann BU, Dutilh G, Brown S, Neumann J, von Cramon YD, Ridderinkhof KR, Wagenmakers EJ. Striatum and pre-SMA facilitate decision-making under time pressure. Proceedings of the National Academy of Science. 2008;105:17538–17542. doi: 10.1073/pnas.0805903105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank MJ. Hold your horses: A dynamic computational role for the subthalamic nucleus in decision making. Neural Networks. 2006;19:1120–1136. doi: 10.1016/j.neunet.2006.03.006. [DOI] [PubMed] [Google Scholar]
- Gratton G, Coles MG, Sirevaag EJ, Eriksen CW, Donchin E. Pre- and poststimulus activation of response channels: A psychophysiological analysis. Journal of Experimental Psychology: Human Perception & Performance. 1988;14:331–344. doi: 10.1037//0096-1523.14.3.331. [DOI] [PubMed] [Google Scholar]
- Gurney K, Humphries M, Wood R, Prescott TJ, Redgrave P. Testing computational hypotheses of brain systems function: a case study with the basal ganglia. Network. 2004;15:263–290. [PubMed] [Google Scholar]
- Hikosaka O. Neural systems for control of voluntary action—A hypothesis. Advances in Biophysics. 1998;35:81–102. [PubMed] [Google Scholar]
- Hoehn MM, Yahr MD. Parkinsonism: Onset, progression, and mortality. Neurology. 1967;17:427–442. doi: 10.1212/wnl.17.5.427. [DOI] [PubMed] [Google Scholar]
- Jackson S, Houghton G. Sensorimotor selection and the basal ganglia: A neural network model. In: Houk J, Davis J, Beiser D, editors. Models of information processing in the basal ganglia. Cambridge, MA: MIT Press; 1995. pp. 337–368. [Google Scholar]
- Kornblum S, Hasbroucq T, Osman A. Dimensional overlap: Cognitive basis for stimulus–response compatibility—A model and taxonomy. Psychological Review. 1990;97:253–270. doi: 10.1037/0033-295x.97.2.253. [DOI] [PubMed] [Google Scholar]
- Kutas M, McCarthy G, Donchin E. Augmenting mental chronometry: The P300 as a measure of stimulus evaluation time. Science. 1977;197:792–795. doi: 10.1126/science.887923. [DOI] [PubMed] [Google Scholar]
- Lee SS, Wild K, Hollnagel C, Grafman J. Selective visual attention in patients with frontal lobe lesions or Parkinson’s disease. Neuropsychologia. 1999;37:595–604. doi: 10.1016/s0028-3932(98)00081-5. [DOI] [PubMed] [Google Scholar]
- Lo CC, Wang XJ. Cortico-basal ganglia circuit mechanism for a decision threshold in reaction time tasks. Nature Neuroscience. 2006;9:956–963. doi: 10.1038/nn1722. [DOI] [PubMed] [Google Scholar]
- Mazzoni P, Hristova A, Krakauer JW. Why don’t we move faster? Parkinson’s disease, movement vigor, and implicit motivation. Journal of Neuroscience. 2007;27:7105–7116. doi: 10.1523/JNEUROSCI.0264-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller J. The flanker compatibility effect as a function of visual angle, attentional focus, visual transients, and perceptual load: A search for boundary conditions. Perception & Psychophysics. 1991;49:270–288. doi: 10.3758/bf03214311. [DOI] [PubMed] [Google Scholar]
- Mink JW. The basal ganglia: Focused selection and inhibition of competing motor programs. Progress in Neurobiology. 1996;50:381–425. doi: 10.1016/s0301-0082(96)00042-1. [DOI] [PubMed] [Google Scholar]
- Montgomery EB, Nuessen J. The movement speed/accuracy operator in Parkinson’s disease. Neurology. 1990;40:269–272. doi: 10.1212/wnl.40.2.269. [DOI] [PubMed] [Google Scholar]
- Niemi P, Naatanen R. Foreperiod and simple reaction time. Psychological Bulletin. 1981;89:133–162. [Google Scholar]
- Osman A, Lou L, Muller-Gethmann H, Rinkenauer G, Mattes S, Ulrich R. Mechanisms of speed-accuracy tradeoff: Evidence from covert motor processes. Biological Psychology. 2000;51:173–199. doi: 10.1016/s0301-0511(99)00045-9. [DOI] [PubMed] [Google Scholar]
- Pachella RG. The interpretation of reaction time in information processing research. In: Kantowitz BH, editor. Human information processing: Tutorials in performance and cognition. Hillsdale, NJ: Erlbaum; 1974. pp. 41–82. [Google Scholar]
- Phillips JG, Martin KE, Bradshaw JL, Iansek R. Could bradykinesia in Parkinson’s disease simply be compensation? Journal of Neurology. 1994;241:439–447. doi: 10.1007/BF00900963. [DOI] [PubMed] [Google Scholar]
- Praamstra P, Stegeman D, Cools A, Horstink M. Reliance on external cues for movement inititation in Parkinson’s disease: Evidence from movement-related potentials. Brain. 1998;121:167. doi: 10.1093/brain/121.1.167. [DOI] [PubMed] [Google Scholar]
- Praamstra P, Plat EM, Meyer AS, Horstink MW. Motor cortex activation in Parkinson’s disease: Dissociation of electrocortical and peripheral measures of response generation. Movement Disorders. 1999;14:790–799. doi: 10.1002/1531-8257(199909)14:5<790::aid-mds1011>3.0.co;2-a. [DOI] [PubMed] [Google Scholar]
- Rabbitt PMA. How old and young subjects monitor and control responses for accuracy and speed. British Journal of Psychology. 1979;70:305–311. [Google Scholar]
- Ridderinkhof KR, van der Molen MW, Bashore TR. Limits on the application of additive factors logic: Violations of stage robustness suggest a dual-process architecture to explain flanker effects on target processing. Acta Psychologica. 1995;90:29–48. [Google Scholar]
- Ridderinkhof KR. Activation and suppression in conflict tasks: Empirical clarification through distributional analyses. In: Prinz W, Hommel B, editors. Common mechanisms in perception and action. Attention & performance. Oxford: Oxford University Press; 2002. pp. 494–519. [Google Scholar]
- Ridderinkhof KR, Scheres A, Oosterlaan J, Sergeant JA. Delta plots in the study of individual differences: New tools reveal response inhibition deficits in AD/HD that are eliminated by methylphenidate treatment. Journal of Abnormal Psychology. 2005;114:197–215. doi: 10.1037/0021-843X.114.2.197. [DOI] [PubMed] [Google Scholar]
- Rinkenauer G, Osman A, Ulrich R, Muller-Gethmann H, Mattes S. On the locus of speed-accuracy trade-off in reaction time: Inferences from the lateralized readiness potential. Journal of Experimental Psychology: General. 2004;133:261–282. doi: 10.1037/0096-3445.133.2.261. [DOI] [PubMed] [Google Scholar]
- Robbins TW, Brown VJ. The role of the striatum in the mental chronometry of action: A theoretical review. Reviews in the Neurosciences. 1990;2(4):181–213. doi: 10.1515/REVNEURO.1990.2.4.181. [DOI] [PubMed] [Google Scholar]
- Rolls ET, Treves A. Motor systems: Cerebellum and basal ganglia. In: Rolls ET, Treves A, editors. Neural networks and brain function. Oxford: Oxford University Press; 1998. pp. 189–226. [Google Scholar]
- Salthouse TA. Adult age and the speed-accuracy trade-off. Ergonomics. 1979;22:811–821. doi: 10.1080/00140137908924659. [DOI] [PubMed] [Google Scholar]
- Smith GA, Brewer N. Slowness and age: Speed-accuracy mechanisms. Psychology and Aging. 1995;10:238–247. doi: 10.1037//0882-7974.10.2.238. [DOI] [PubMed] [Google Scholar]
- Taylor A, Saint-Cyr J. The neuropsychology of Parkinson’s disease. Brain & Cognition. 1995;28:281. doi: 10.1006/brcg.1995.1258. [DOI] [PubMed] [Google Scholar]
- Ullsperger M, Bylsma L, Botvinick MM. The conflict adaptation effect: It’s not just priming. Cognitive, Affective, and Behavioral Neuroscience. 2005;5:467–472. doi: 10.3758/cabn.5.4.467. [DOI] [PubMed] [Google Scholar]
- van den Wildenberg WPM, van Boxtel GJM, van der Molen MW, Bosch DA, Speelman JD, Brunia CHM. Stimulation of the subthalamic region facilitates the selection and inhibition of motor responses in Parkinson’s disease. Journal of Cognitive Neuroscience. 2006;18:626–636. doi: 10.1162/jocn.2006.18.4.626. [DOI] [PubMed] [Google Scholar]
- Van der Lubbe RHJ, Jaskowski P, Wauschkuhn B, Verleger R. Influence of time pressure in a simple response task, a choice-by-location task, and the Simon task. Journal of Psychophysiology. 2001;15:241–255. [Google Scholar]
- Van Veen V, Krug MK, Carter CS. The neural and computational basis of controlled speed-accuracy tradeoff during task performance. Journal of Cognitive Neuroscience. 2008;20:1–14. doi: 10.1162/jocn.2008.20146. [DOI] [PubMed] [Google Scholar]
- Wickelgren WA. Speed-accuracy tradeoff and information processing dynamics. Acta Psychologica. 1977;41:67–85. [Google Scholar]
- Wiegand K, Wascher E. The Simon effect for vertical S–R relations: Changing the mechanism by randomly varying S–R mapping rule? Psychological Research. 2007;71:219–233. doi: 10.1007/s00426-005-0023-5. [DOI] [PubMed] [Google Scholar]
- Wylie SA, Bashore TR, Stout JC. Activation of conflicting responses in Parkinson’s disease: Evidence for degrading and facilitating effects on response time. Neuropsychologia. 2005;43:1033–1043. doi: 10.1016/j.neuropsychologia.2004.10.008. [DOI] [PubMed] [Google Scholar]
- Wylie SA, Ridderinkhof KR, Eckerle MK, Manning CA. Inefficient response inhibition in individuals with mild cognitive impairment. Neuropsychologia. 2007;45:1408–1419. doi: 10.1016/j.neuropsychologia.2006.11.003. [DOI] [PubMed] [Google Scholar]
- Wylie SA, van den Wildenberg WPM, Ridderinkhof KR, Bashore TR, Powell VD, Manning CA, Wooten GF. The effect of Parkinson’s disease on interference control during action selection. Neuropsychologia. 2009;47:145–157. doi: 10.1016/j.neuropsychologia.2008.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]