Skip to main content
PMC home page
Nature Portfolio logoLink to Nature Portfolio
. 2015 Jul 22;6:7803. doi: 10.1038/ncomms8803

Interaction-induced decay of a heteronuclear two-atom system

Peng Xu 1,2, Jiaheng Yang 1,2,3, Min Liu 1,2, Xiaodong He 1,2, Yong Zeng 1,2,3, Kunpeng Wang 1,2,3, Jin Wang 1,2, D J Papoular 4, G V Shlyapnikov 1,5,6,7, Mingsheng Zhan 1,2,a
PMCID: PMC4525158  PMID: 26199051

Abstract

Two-atom systems in small traps are of fundamental interest for understanding the role of interactions in degenerate cold gases and for the creation of quantum gates in quantum information processing with single-atom traps. One of the key quantities is the inelastic relaxation (decay) time when one of the atoms or both are in a higher hyperfine state. Here we measure this quantity in a heteronuclear system of 87Rb and 85Rb in a micro optical trap and demonstrate experimentally and theoretically the presence of both fast and slow relaxation processes, depending on the choice of the initial hyperfine states. This experimental method allows us to single out a particular relaxation process thus provides an extremely clean platform for collisional physics studies. Our results have also implications for engineering of quantum states via controlled collisions and creation of two-qubit quantum gates.

Inline graphicUnderstanding the behaviour of trapped two-atom systems is interesting for engineering quantum gases, and one of the key quantities to determine is the inelastic relaxation time from hyperfine states. Here, the authors measure this quantity for heteronuclear systems of 87Rb and 85Rb in a micro optical trap.

The studies of two-atom systems in small traps attract a great deal of interest, in particular for engineering of quantum states via controlled collisions and creation of quantum gates in quantum information processing with a set of single-atom traps1,2. The crucial points are the decoherence time and the lifetime related to the interaction-induced inelastic decay of a higher hyperfine state. On the other hand, this type of inelastic processes, in particular heteronuclear ones, are important for the creation of multi-species quantum degenerate systems3, for obtaining ultracold heteronuclear molecules4, and for ultracold chemistry5. In homonuclear systems, the inelastic processes have been well studied from large ensembles of atoms to a few and even two atoms6,7,8. However, in the studies of inelastic heteronuclear collisions in a trapped gas9 the main obstacle is the simultaneous presence of a large variety of loss mechanisms, which complicates the analysis. In magneto-optical traps where many heteronuclear systems have been studied10,11,12,13,14,15,16, aside from collisional processes one has radiative escape. In optical dipole traps there are homonuclear inelastic collisions17,18,19, and at sufficiently large densities, three-body recombination becomes important20. It is thus crucial to perform experiments allowing one to single out a particular inelastic process.

This is done in the present paper. We study a two-atom system of different isotopes of rubidium (single 85Rb and single 87Rb) in a micro optical trap. One of them or both are in a higher hyperfine state, and we measure the corresponding rate of inelastic relaxation accompanied by the loss of the atoms. The homonuclear collisions are absent and our measurements give pure loss rates of specific hyperfine heteronuclear collisions. The experiments are done at temperatures close to the border of the ultracold limit (tens of microkelvins) and are supported by finite temperature coupled channel calculations. Our work can be easily extended to other alkali atoms, even to atom–molecule collisions21,22, thus allowing further understanding of heteronuclear collisions, a precise test of atomic collisional theory, and applications to quantum information processing.

Results

Experimental setup and results

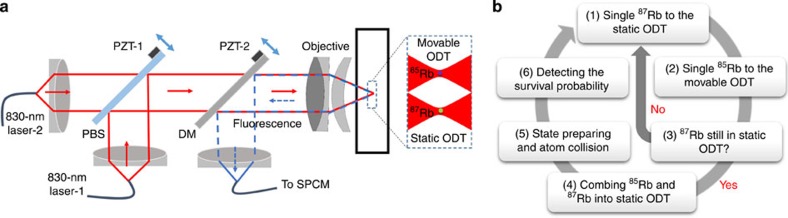
Our two-atom heteronuclear system is composed of a single 85Rb and a single 87Rb in a micro optical dipole trap (ODT), and there are three important points in the experiment. The first one is a sequential trapping of a single 87Rb in a static ODT and a single 85Rb in a movable ODT23, and we make sure that two atoms of different isotopes are actually trapped (see Fig. 1 and Methods). Second, we shift the movable ODT to overlap with the static one, and adiabatically turn off the movable trap. We get 87Rb and 85Rb in one trap with probability of about 95%. The third point is that the collisional blockade24 does not allow us to detect the presence of 87Rb or 85Rb when both of them are in the same trap. Therefore, we first have to kick out one of the atoms to detect the presence of the other one. By optimizing this procedure we have minimized unwanted atom losses to <3%.

Figure 1. Experimental setup and measurement time sequence.

Figure 1

Open in a new tab

(a) Schematic diagram of the experimental setup. Two 830-nm lasers are collimated, combined by a polarizing beam splitter (PBS) and then strongly focused by an objective (Linos, HALO30) into the vacuum chamber to form two ODTs. The movable ODT is from 830-nm laser-1 and can be shifted to overlap with the static ODT (from 830-nm laser-2) by controlling piezoelectric ceramic transducer (PZT)-1. The fluorescence of trapped single atoms is collected by the same objective, separated from dipole lasers by a dichroic mirror (DM) and guided to single-photon-counting module (SPCM) for detection. PZT-2 controls the fluorescence-collecting region. A detailed description can be found in Methods. (b) Time sequence in the experiment. Each survival probability in our experiment is the result from 300 repeated measurements.

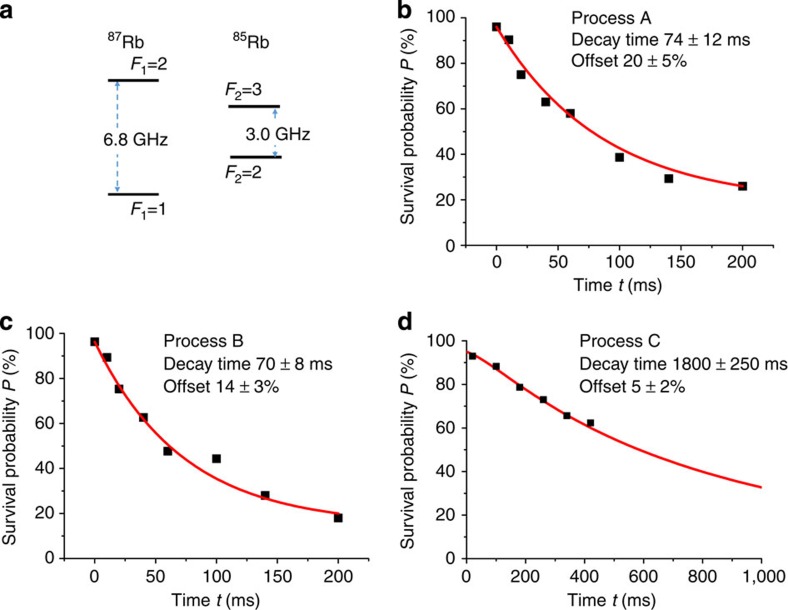
Depending on the hyperfine states of 87Rb and 85Rb, there are three inelastic decay processes:

graphic file with name ncomms8803-m1.jpg
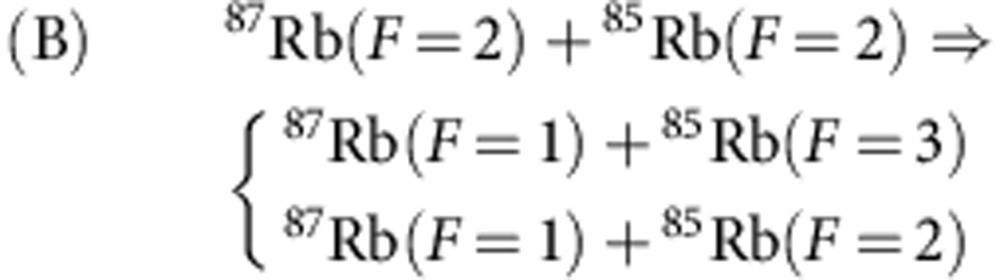graphic file with name ncomms8803-m2.jpg
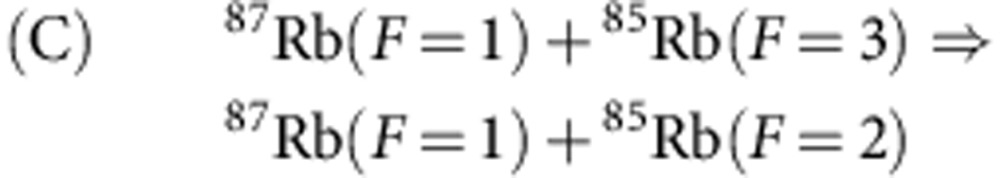graphic file with name ncomms8803-m3.jpg

We have not set a magnetic field, and for each atomic spin F in the initial state of the collision the states with all possible values of the spin projection MF are likely equally populated. The energy released in the inelastic processes A, B and C is about several GHz and it exceeds the trap depth U0 by more than two orders of magnitude. Therefore, both atoms are ejected from the trap as a result of the inelastic relaxation. In most of our experiments the trap depth is U0=0.6 mK, which in our configuration provides the radial trap frequency ωρ/(2π)=38.8±0.1 kHz and the axial trap frequency ωz/(2π)=3.2±0.1 kHz.

We measure the survival probability P(t) for the atoms to remain in the trap at time t (see Fig. 2). For each t we execute 300 repetitions of the loop sequence of Fig. 1b. In the case of A and B processes the decay is strongly dominated by the interaction-induced spin relaxation. The probability P(t) is then described by an exponential time dependence. Within <10% of uncertainty the experimental data can be fitted with an exponential function P=w exp(−t/τ)+w0. The presence of the offset w0 has several reasons discussed in detail in Methods. First of all, the two-atom system is obtained with 95% probability, and there are traps with only one atom that remains trapped on a much longer timescale (about 11 s (ref. 25)) than the collisional lifetime τ. Second, for the A and C processes doubly polarized pairs (for each atom the spin projection is equal to the spin) can decay only due to weak spin–spin or spin–orbit interactions that may change the spin projection of the pair, and the polarized pairs practically remain stable on the timescale of our experiment. For the B process, however, the doubly polarized pairs efficiently relax due to the channel leading to the formation of 87Rb(F=1) and 85Rb(F=3).

Figure 2. Experimental data for the decay rates.

Figure 2

Open in a new tab

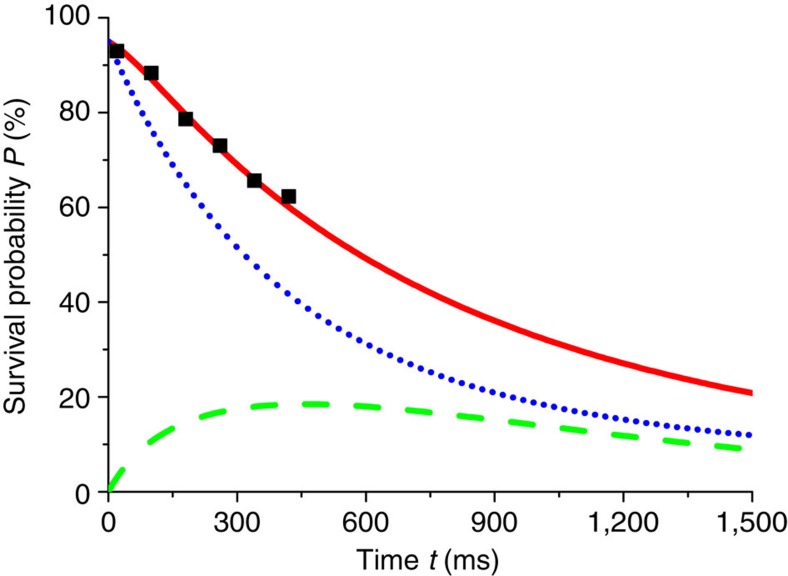
(a) Energy levels of hyperfine states of 87Rb and 85Rb. (b–d) Survival probability P versus time t for the A, B and C collisions, respectively. The measurements are done for the survival probability of 87Rb after kicking out 85Rb. The black squares are experimental data, with each point being the result from 300 repeated measurements. In (b,c) the solid curves show a fit by the formula P=w exp(−t/τ)+w0, and the error in the decay time indicates the s.d. when using the fit of P(t) by the exponential formula. In (d) the solid curve is a fit with the numerical solution of the rate equations including single-atom spin relaxation. The error in the decay time shows the uncertainty originating from the uncertainty in the single atom spin relaxation time τr entering the rate equations (see Methods). The data are collected at the trap depth U0=0.6 mK and the initial temperatures T87=35±3 μK, T85=15±1 μK.

The process C is much slower than A and B, and our measurements for this process have been made on a timescale of about 500 ms. In this case the decay is significantly influenced by single-atom spin relaxation, and we have to take it into account in the rate equations for extracting τ from our measurements (see Methods).

The measured τ has about 15% of statistical uncertainty that decreases with increasing the executed loop numbers. Aside from single-atom spin relaxation, the value of τ is influenced by single-atom loss events. The heating rate in the dipole trap is about 20 μK s−1 (ref. 26) and it increases the collisional volume, thus slightly increasing the decay time τ. We estimate the overall uncertainty in our values of τ as about 20%.

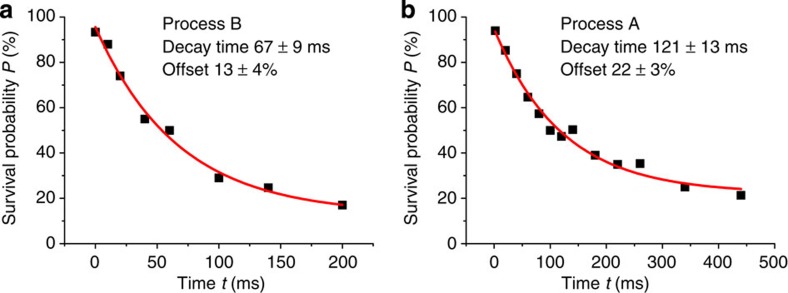
We also test that the result for τ does not depend on whether we kick out 85Rb or 87Rb for measuring P(t). Comparing Fig. 2c with Fig. 3a it is easy to conclude that not only relaxation times are very close to each other (see also Table 1) but also the functions P(t). We then vary the temperature for the A collisional process to test the dependence of τ on the effective volume (density) of atoms in the trap. As expected, the time τ increases with temperature and one can see this from the comparison of the results in Figs 2b and 3b.

Figure 3. The decay under different conditions.

Figure 3

Open in a new tab

(a,b) Survival probability P versus time t for the B and A collisions, respectively. The black squares are experimental data collected at the trap depth U0=0.6 mK, with each point being the result from 300 repeated measurements. The solid curves show a fit by the formula P=w exp(−t/τ)+w0, and the error in the decay time indicates the s.d. when using the fit of P(t) by the exponential formula. In (a) The measurements are done for the survival probability of 85Rb after kicking out 87Rb, and the initial temperatures are T87=35±3 μK and T85=15±1 μK. In (b) 85Rb is kicked out, and the survival probability of 87Rb is measured with the initial temperatures T87=47±3 μK and T85=27±2 μK.

Table 1. Summary of the experimental and calculated results. The experiment is done with the trap depth U 0=0.6 mK (ω ρ /(2π)=38.8 kHz, ω z/(2π)=3.2 kHz).

Collisional process Experimental parameters: temperature (μK) Decay time (ms) Experimental α(cm3 s−1) Calculated α(cm3 s−1) Calculated αT=0(cm3 s−1)
A T87=35±3, T85=15±1, kick out 85Rb τA=74±12 (5.9±1.1) × 10−11 5.6 × 10−11 5.7 × 10−11
  T87=47±3, T85=27±2, kick out 85Rb τA=121±13 (6.5±0.8) × 10−11 5.9 × 10−11  
B T87=35±3, T85=15±1, kick out 85Rb τB=70±8 (6.3±0.9) × 10−11 6.8 × 10−11 1.1 × 10−10
  T87=35±3, T85=15±1, kick out 87Rb τB=67±9 (6.6±1.0) × 10−11    
C T87=35±3, T85=15±1, kick out 85Rb τC=1,800±250 (2.4±0.4) × 10−12 3.2 × 10−12 0.8 × 10−12
Open in a new tab

Theory and analysis

The rate equations for the inelastic decay processes A, B and C can be written as

graphic file with name ncomms8803-m4.jpg

where P(t) is the probability that at time t the atoms are still present in the trap, and τ is the relaxation (decay) time that we measure. These processes occur at interatomic distances of the order of or smaller than the radius of the interaction potential Re=(mC6/ħ2)1/4≈80 Å (C6 is the Van der Waals constant). At our trap frequencies and temperatures from 15 to 55 μK we have 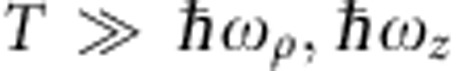Inline graphic, and the motion of atoms in the trap is surely quasiclassical. In our trap configuration the extension of the wavefunction of the trapped atoms is the shortest in the radial direction 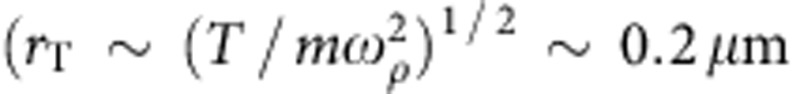Inline graphic, where m and ωρ are the atom mass and radial trap frequency, respectively), and we still have the inequality

graphic file with name ncomms8803-m7.jpg

Therefore, the decay (relaxation) time τ can be expressed through the relaxation rate constant α in free space:

graphic file with name ncomms8803-m8.jpg

where

graphic file with name ncomms8803-m9.jpg

is the effective volume, Teff=μ(T1/m1+T2/m2) is the effective temperature, with m1, m2 and T1, T2 being the masses and temperatures of 87Rb and 85Rb, respectively, and μ is the reduced mass. The rate constant α in equation (3) is averaged over the Boltzmann distribution of relative momenta k at effective temperature Teff:

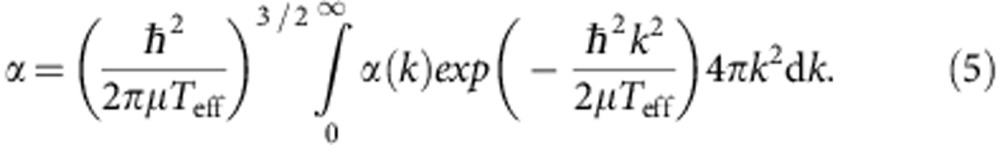graphic file with name ncomms8803-m10.jpg

Note that due to elastic collisions between the atoms, the two-atom system eventually acquires an equilibrium temperature (T1+T2)/2. However, it is different from the initial effective temperature Teff by <1%, and so will be the effective volume and the average value of α.

At our temperatures, the quantity kTRe∼0.5, where kT=(mT/ħ2)1/2 is the thermal momentum, so that we are close to the border of the s-wave-scattering limit. Therefore, in addition to the s-wave scattering, we took into account the scattering with higher orbital angular momenta. The rate constants αA, αB and αC for the processes A, B and C were calculated using the coupled channel method4,27 at finite collision energies (see Methods). In the centre of mass reference frame, the Hamiltonian governing the collisions has the form

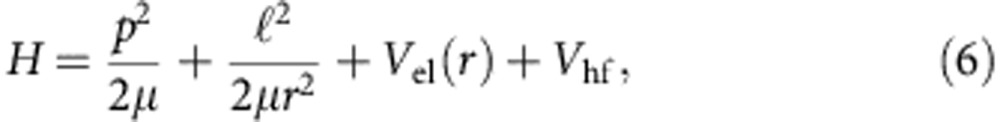graphic file with name ncomms8803-m11.jpg

where r is the interatomic distance, p is its conjugate momentum and ℓ is the orbital angular momentum operator. The interatomic interaction operator is given by Vel(r)=Vs(r)Ps+Vt(r)Pt, with Ps and Pt being projectors onto the electronic singlet and triplet states of the colliding pair of atoms. The term Vhf=a1S1·I1+a2S2·I2 is the hyperfine interaction, where S1, I1, a1 and S2, I2, a2 are the electron and nuclear spin operators and hyperfine constants for 87Rb and 85Rb, respectively. The total spin operators of the atoms are F1=S1+I1 and F2=S2+I2, and the total spin operator of the pair is F=F1+F2. The Hamiltonian H of equation (6) conserves both the total spin F and its projection MF. It also conserves the orbital angular momentum ℓ and its projection Mℓ.

The rate of inelastic spin relaxation occurring when at least one of the colliding atoms is in a higher hyperfine state can be expressed through the real and imaginary parts of the elastic scattering amplitude. The well-known formula for the inelastic rate constant28, averaged over the initial spin projections, is transformed to (see Methods):

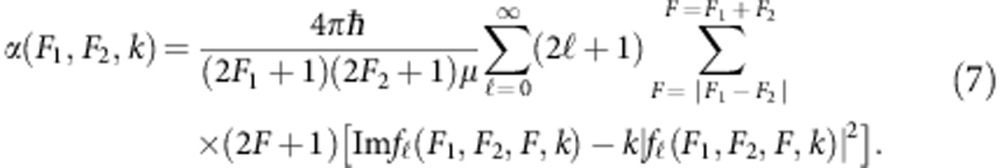graphic file with name ncomms8803-m12.jpg

Accordingly, αA≡α(2, 3), αB≡α(2, 2), and αC≡α(1, 3). The quantity fℓ(F1, F2, F, k) in equation (7) is the amplitude of elastic ℓ-wave scattering of these atoms at the total spin F.

We apply the accumulated-phase method (see Methods) and calculate the accumulated-phase parameters from the known properties of homonuclear 87Rb87Rb and 85Rb85Rb collisions using mass scaling27. The main inaccuracy of our calculations stems from the choice of the accumulated phase, and we have checked that our results are stable within 5% when the value of this phase is varied by a few percent. The p-wave (ℓ=1) contribution at our temperatures is comparable to the s-wave (ℓ=0) one, but the contributions of the d-wave and higher partial waves are below 1%. Therefore, in the following we confine ourselves only to the s-wave and p-wave scattering.

In Table 1 the results of the calculations for the processes A, B and C are compared with the experimental data. To show that finite temperature effects are important in our experiment we also present the rate constants calculated at T=0. For the fast A and B processes one sees an agreement between experiment and theory within the error bars of the experimental data. For the slow C process the calculated α is near the upper bound of the experimental value accounting only for statistical uncertainties. The reason for this small discrepancy is that the heating effect, although fairly small, still increases the effective volume so that the measured τ actually corresponds to slightly higher temperatures than the initial ones. This means that the experimental value of α at the initial temperatures should actually be slightly (by about 15%) higher than the one in Table 1.

Discussion

The relaxation rates obtained in our work are rather high. In interesting experiments with spinor heteronuclear mixtures29, this places an upper limit of about n∼1012 cm−3 on the density if a higher hyperfine atomic state is involved. We should note, however, that the rate constant αC has a pronounced temperature dependence. At the temperatures used in this experiment, it is larger by about a factor of 4 than at T=0 (see Table 1). Our zero temperature result αC=0.8 × 10−12 cm3 s−1 is somewhat below the lower bound of the interval (1.2–4.5) × 10−12 cm3 s−1 found for the C process with 87Rb(F1=1, M1=−1) and 85Rb(F2=3, M2=3) in ref. 30, which used old data for the interaction potentials. In experiments with ultracold clouds containing many atoms, the common temperature is ∼100 nK, which practically corresponds to T=0 limit in our calculations. We thus expect that an admixture of 85Rb(F2=3) can be collisionally stable on a timescale of 100 ms in the gas of 87Rb(F1=1) at densities approaching 1013 cm−3.

Two-atom systems in small traps are convenient for the creation of heteronuclear molecules. In the gas mixture, Feshbach molecules of 87Rb(F1=1, M1=−1) and 85Rb(F2=2, M2=−2) have already been created31 and they were undergoing losses due to collisional relaxation. In the two-atom system in a trap, the Feshbach molecule can be created by sweeping the magnetic field across the resonance like in experiments in an optical lattice32. For 87Rb–85Rb, Feshbach resonances have been observed in the fields of hundreds of Gauss31 and also predicted in the fields below 10 G ref. 33. The rate of a spontaneous decay (dissociation) of a single Feshbach molecule in a trap due to spin relaxation34,35 is proportional to α/〈r〉3, where α is the rate constant of relaxation in binary collisions and 〈r〉 is the size of the molecule35. With our relaxation rate constants α∼10−10 to 10−12 cm3 s−1 the decay time can be made on the level of tens of milliseconds, like in the case of 85Rb–85Rb Feshbach molecules35. This is sufficient for using the two-photon-stimulated Raman adiabatic passage and transferring this molecule to the ground rovibrational state36.

Our results may also have implications for engineering of quantum states and creation of two-qubit quantum gates based on controlled collisions in a system of single-atom traps1,2,37, in particular with respect to a proper selection of hyperfine atomic states. In our system, the relaxation time is τ=Veff/α and it strongly decreases with temperature, so that for atoms in the ground vibrational state τ may become of the order of the single-atom decoherence time τdc. For collisional quantum gates the time τdc and, hence, τ should be at least four orders of magnitude larger than the operational time τop (ref. 38). The latter cannot be much smaller than the inverse interaction energy of the two atoms in the trap, and for atoms in the ground vibrational state one has τop∼ħVeff/g, where g=4πħ2a/m is the coupling constant for the elastic interaction, and a is the scattering length (this leads to τop of about tens of microseconds at our trap frequencies, although for our present temperatures it is on the millisecond level). We thus have the condition:

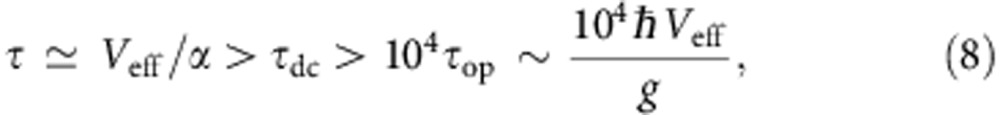graphic file with name ncomms8803-m13.jpg

which immediately leads to the inequality

graphic file with name ncomms8803-m14.jpg

For common values of g/ħ from 10−9 to 10−11 cm3 s−1 equation (9) can be satisfied for doubly polarized atomic states, such as 87Rb(F=2, MF=2) where g/ħ∼10−10 cm3 s−1, and the relaxation is caused only by weak spin–spin or spin–orbit interactions32 leading to α<10−14 cm3 s−1 Another option would be to increase g by using a Feshbach resonance, although this can also increase inelastic losses.

The advantage of our work is that we study collisions in a two-atom system, which allows us to single out a particular collisional process. In upcoming experiments we intend to trap single atoms with a farer detuned dipole laser (1,064 nm) to suppress the single-atom spin relaxation. We then prepare atomic states with given spin projections MF and cool the atoms down to the ground vibrational state39,40 to execute the possibility of creating a quantum gate. Our work also paves a way to the creation of single heteronuclear molecules and to the studies of atom–molecule and molecule–molecule binary systems.

Methods

Details of experimental methods

In our experiment single atoms are trapped in micro ODTs that are formed by strongly focusing 830-nm lasers to a beam waist of about 2.1 μm. The dipole lasers follow the paths shown in Fig. 1a by the red solid lines. The movable ODT is initially 5 μm away and it can be shifted to overlap with the static ODT by changing the voltage of piezoelectric ceramic transducer-1. We detect trapped atoms by collecting the fluorescence in the trap region as shown by blue dashed lines. The fluorescence is coupled into a polarization-maintaining single-mode fibre (with the core diameter of 5 μm) for spatial filtering and is then guided to a single-photon-counting module (AQRH-14-FC). Owing to a moderate core diameter of the fibre and to a fairly large distance between the two traps, we can selectively collect the fluorescence from one of them. The disturbance from the other trap (crosstalk effect) is eliminated by properly adjusting the voltage of piezoelectric ceramic transducer-2.

The experiment is executed following the time sequence shown in Fig. 1b. We first trap 87Rb in the static ODT. During this step the movable ODT is off to prevent the loading of 87Rb. Then we turn off the magneto-optical trap (MOT) of 87Rb, and turn on the movable ODT and the 85Rb MOT to execute step 2. The loading of a single 85Rb may occur not only into the movable ODT but also into the static ODT, which leads to the loss of both 85Rb and 87Rb due to collisional blockade. Therefore, we do an extra check of the 87Rb presence in the static trap in step 3. Only when 87Rb is still trapped, we record the final result of the collision, otherwise we go back to step 1 and start loading again. To check that only 87Rb is in the static trap and meanwhile only 85Rb in the movable trap, we first detect the absence of the fluorescence of 87Rb from the movable trap and the absence of fluorescence of 85Rb from the static trap. This is followed by the fluorescence detection of 87Rb and 85Rb in the static and movable traps, respectively.

In step 4 we first prepare 85Rb in F2=2 and 87Rb in F1=1 states to eliminate the unwanted collisional losses when switching off the MOT repumping lasers 1 ms before the MOT cooling lasers. For minimizing the heating effect we have optimized the process of transferring 85Rb to the static trap. The transfer efficiency can go up to 98% and is limited by the detection efficiency and heating losses. The probability that 87Rb survives when the movable trap approaches the static one and then is adiabatically switched off is also about 98%. The temperature is measured in this type of process by using the release and recapture technique41,42 when one of the traps (either static or movable) is empty.

In this way we create a heteronuclear two-atom system. After a certain time, we kick out one of the atoms from the trap using resonant lasers. Optimizing the laser intensities and shortening the pulse duration to 0.1 ms, we have minimized the unwanted losses to <3%. Eventually, we have succeeded in trapping two heteronuclear single atoms in the static ODT with about 95% probability.

Analysis of the experimental data

To confirm that the decay times τA and τB can be extracted by a simple exponential fit of the experiment data in Figs 2b,c and 3a,b, we numerically solved the rate equations taking into account single-atom spin relaxation. These are linear equations for the quantities 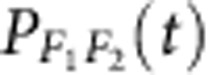Inline graphic representing the probabilities that both 87Rb with spin F1 and 85Rb with spin F2 are present in the trap at time t:

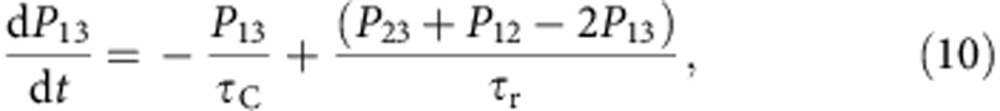graphic file with name ncomms8803-m16.jpg
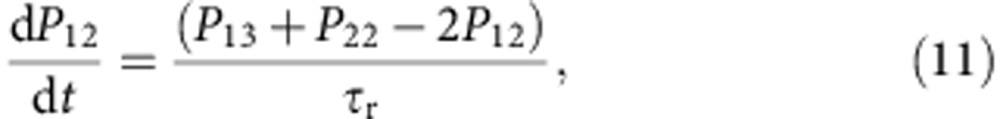graphic file with name ncomms8803-m17.jpg
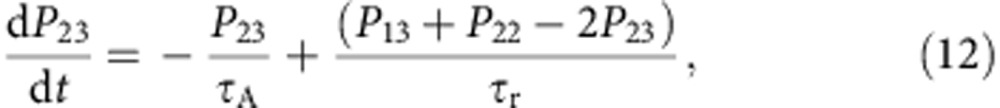graphic file with name ncomms8803-m18.jpg
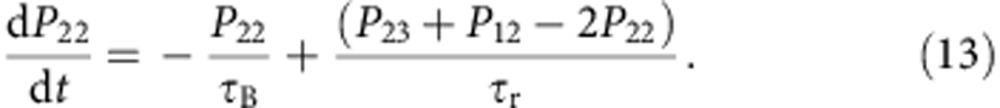graphic file with name ncomms8803-m19.jpg

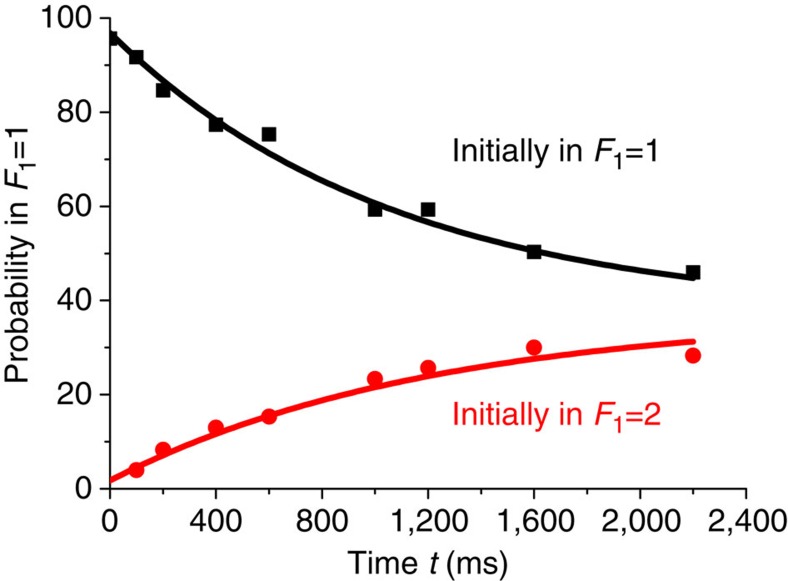
We do not include single-atom loss in the rate equations, as the related loss time is about 11 s and it changes the simulated survival probability by <2% even at times t approaching 1,000 ms. For the time of single-atom spin relaxation we did an independent measurement, and the measured value is τr=1,100±150 ms (see Fig. 4).

Figure 4. Spin-relaxation measurement.

Figure 4

Open in a new tab

We first prepare a single 87Rb atom in the state F1=1 (black squares) or F1=2 (red circles). After a time t we kick out atoms that are populated in the state F1=2 by using a resonant laser and then detect the survival probability of single atoms. Each data is averaged over 300 single atoms. The solid curves show a fit by the exponential formula: dP/dt∝exp(∓t/τr −t/τs), where the sign − is related to the black curve, the sign + to the red one, and the single-atom loss time is τs=11,000 ms. The fitted spin-relaxation time is τr=1,100±150 ms.

The best fit with the experimental data for the process A in the conditions of Fig. 3b is obtained with τA=129.5±1.5 ms at τB=115±15 ms, τC=1,800 ms and τr=1,100 ms. The obtained τA is consistent with the decay time of 121±13 ms given in Fig. 3b from the simple exponential fit. The simulations in the conditions of Figs 2b,c and 3a show that the best fitted τA and τB are larger than the exponential-fit decay times indicated in these figures by not more than 2 ms.

The offsets of the fitted decay curves for the A and B processes in Figs 2 and 3 originate from several effects. They include the probability that there is only one atom in the trap ((5±2)%), the probability that 87Rb(F1=2) undergoes a transition to the state with F1=1 due to Raman scattering of the dipole laser (about 5% for Figs 2b,c and 3a, and about 7% for Fig. 3b), and for the A process the 6% probability that atom pairs are prepared in a doubly polarized state. All the offsets can be explained by these effects within our measurement uncertainty.

For the slow process C the timescale is longer and the single-atom spin relaxation is more important, so that the time τC can be extracted only from the best fit of the numerical solution of the rate equations with the experimental data. In Fig. 5 we display the results of the simulations in the conditions of Fig. 2d up to t=1,500 ms. The best numerical fit deviates from the experimental data by <10%.

Figure 5. Numerical fitting for the process C.

Figure 5

Open in a new tab

We fit the experimental data (black squares) by numerical results from the rate equations for the process C. The red solid curve shows the survival probability of 87Rb, the blue dotted curve shows the probability P13, and the green dashed curve is the probability P23+P22+P12.

Calculation of the inelastic rate constants

At low temperature the inelastic spin relaxation occurs when at least one of the colliding atoms is in a higher hyperfine state. The rate constant of this process is given by28

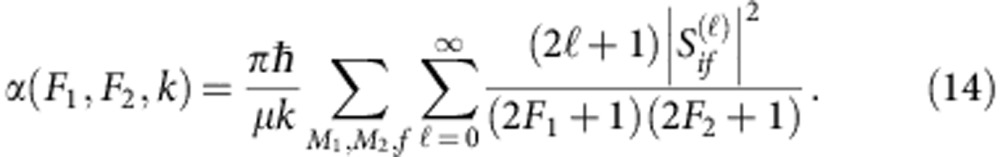graphic file with name ncomms8803-m20.jpg

The quantity 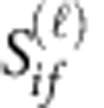Inline graphic is the S-matrix element for the ℓ-wave scattering from the initial state i characterized by the atom spins F1, F2 and their projections M1, M2 to a final state f that has a lower internal (hyperfine) energy, so that there is an energy release in the inelastic scattering process. In equation (14) we also averaged over the initial spin projections M1 and M2. Owing to the unitarity condition for the S-matrix elements we have:

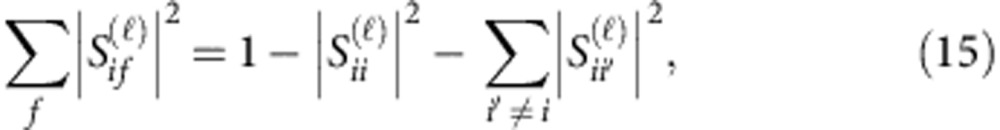graphic file with name ncomms8803-m22.jpg

where Sii is the S-matrix element for elastic scattering in which the spin projections M1, M2 remain the same, and Sii′ is the S-matrix element for elastic scattering, which changes M1, M2 to 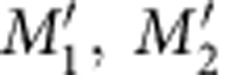Inline graphic. Expressions for the S-matrix elements through the corresponding scattering amplitudes read28:

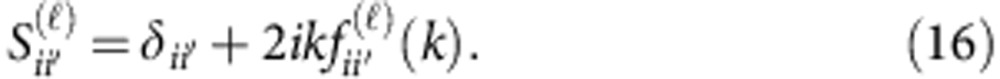graphic file with name ncomms8803-m24.jpg

The amplitudes 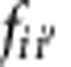Inline graphic are conveniently expressed through the amplitudes fℓ(F1, F2, F, k) of elastic scattering of atoms with spins F1, F2 at the total spin F of the pair:

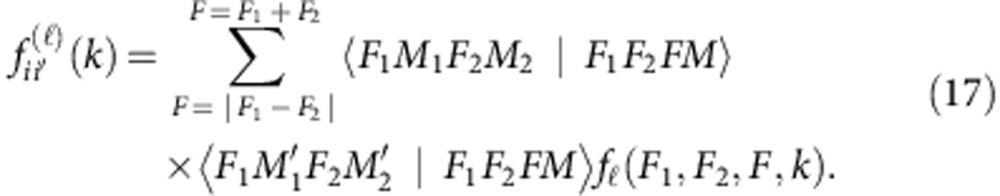graphic file with name ncomms8803-m26.jpg

In the absence of a magnetic field the amplitudes fℓ(F1, F2, F, k) do not depend on the total spin projection M. The Clebsch–Gordan coefficients, which appear in equation (17), satisfy the summation rule:

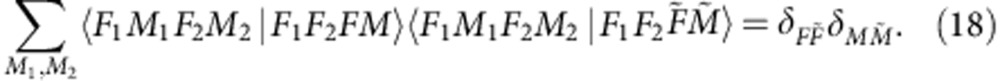graphic file with name ncomms8803-m27.jpg

Substituting equations (16) and (17) into equation (14), and making use of equation (18), we arrive at equation (7) of the main text:

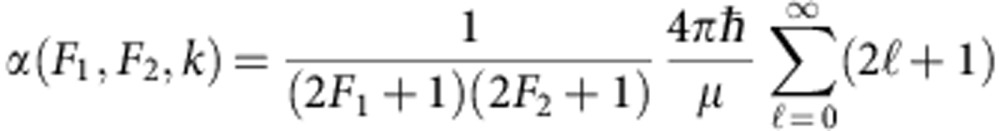graphic file with name ncomms8803-m28.jpg
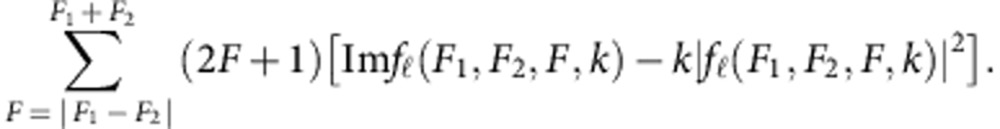graphic file with name ncomms8803-m29.jpg

The amplitudes fℓ(F1, F2, F, k) were calculated numerically using the coupled channel method4. Our implementation of this method is described in ref. 43. The asymptotic behaviour of the scattering states is enforced at a distance of 1,000a0, with a0 being the Bohr radius. The accumulated-phase boundary condition is applied at r0=16a0. It summarizes the short-range physics in the region of distances r<r0, where the triplet and singlet interaction potentials are poorly known, into six phase parameters. We calculate these parameters for heteronuclear 87Rb85Rb collisions starting from the known data for homonuclear 87Rb87Rb and 85Rb85Rb collisions and using the mass scaling technique27, which exploits the fact that the Born–Oppenheimer electronic potentials Vs and Vt do not depend on the type of isotopes. The hyperfine coefficients a1 and a2 were taken from ref. 44. Solving the coupled differential equations for the wavefunctions within the subspaces characterized by the conserved quantum numbers F, M we calculated all scattering amplitudes fℓ(F1, F2, F, k) as functions of the incident relative momentum k. The calculated rate constants α(F1, F2, k) are then averaged over the thermal distribution of k according to equation (5).

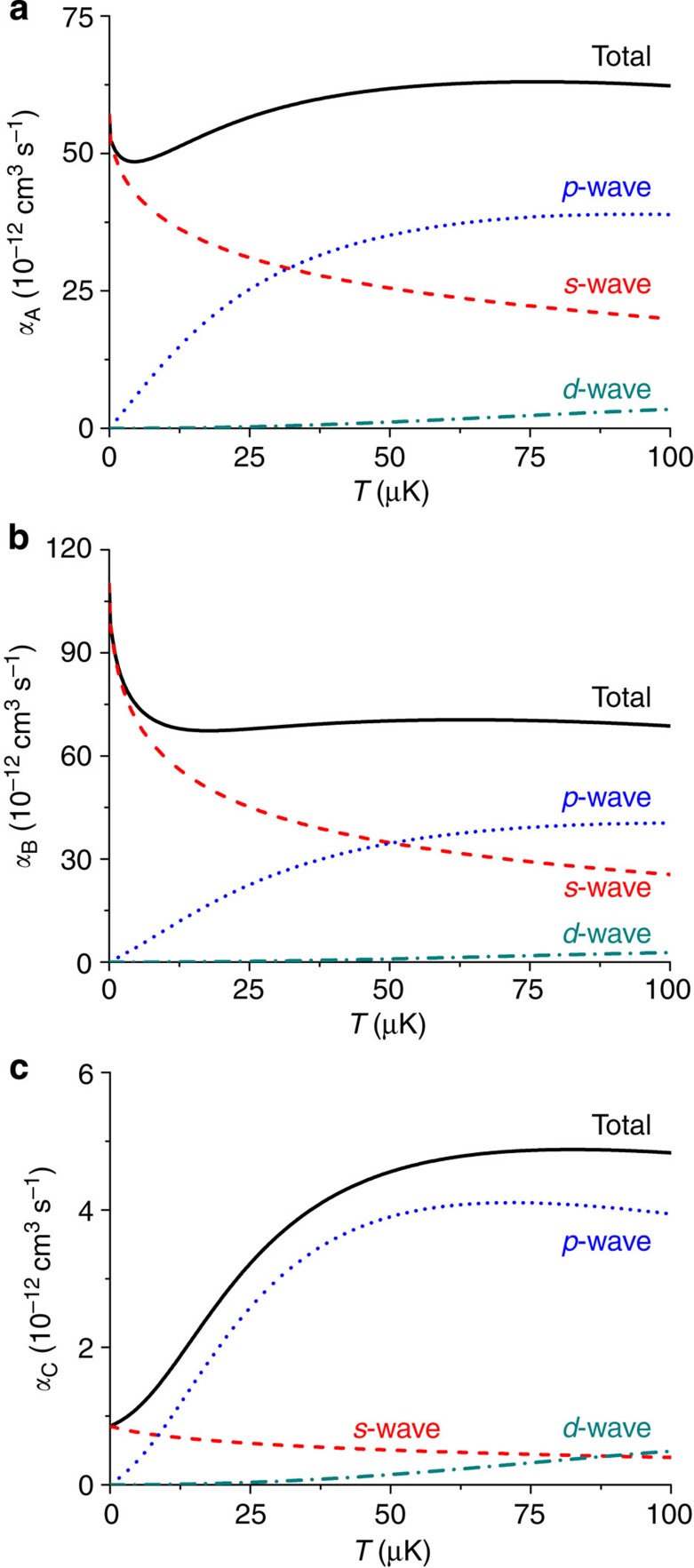
In Fig. 6 we present the calculated rate constants at temperatures from 0 to 100 μK and specify the s-wave, p-wave and d-wave contributions (the latter is below 1% at temperatures of our experiment, but at T=100 μK it is 4–5% for the A and B processes, and 10% for the C process). As one can see, the s-wave contribution slowly decreases with increasing temperature. However, the p-wave contribution significantly grows with T, which is expected. The role of the p-wave scattering is especially important for the C process, where it starts to dominate over the s-wave scattering already at T∼15 μK. As a result, the total αC significantly increases with temperature. For the A and B processes the total α does not change much with increasing T as the decrease in the s-wave contribution is compensated by the p-wave contribution.

Figure 6. Calculated rate constants.

Figure 6

Open in a new tab

(a–c) The rate constants αA, αB and αC are calculated at temperatures ranging from 0 to 100 μK, respectively. The black solid curves show the total rate constant, and the red dashed, blue dotted and dark cyan dash–dotted curves show the s-wave, p-wave and d-wave contributions, respectively.

Additional information

How to cite this article: Xu, P. et al. Interaction-induced decay of a heteronuclear two-atom system. Nat. Commun. 6:7803 doi: 10.1038/ncomms8803 (2015).

Acknowledgments

We acknowledge fruitful discussions with Jiaming Li, Antoine Browaeys and Philippe Grangier. This work has been supported by the National Basic Research Program of China under Grant No. 2012CB922101 and the National Natural Science Foundation of China under Grant Nos. 11104320 and 11104321. G.V.S. acknowledges support from IFRAF and from the Dutch Foundation FOM. D.J.P. and G.V.S. emphasize that the research leading to their results in this paper has received funding from the European Research Council under European Community's Seventh Framework Programme (FR7/2007–2013 Grant Agreement no.341197).

Footnotes

Author contributions X.D.H., P.X. and M.S.Z. designed the experiments; M.S.Z. supervised the project; J.H.Y, Y.Z. and K.P.W. did the experiment; P.X. and J.W. analysed the experimental data; D.J.P., G.V.S., and M.L. performed the theoretical calculation; P.X., G.V.S. and M.S.Z. wrote the paper.

References

  1. Jaksch D., Briegel H.-J., Cirac J. I., Gardiner C. W. & Zoller P. Entanglement of atoms via cold controlled collisions. Phys. Rev. Lett. 82, 1975–1978 (1999). [Google Scholar]
  2. Mandel O. et al. Controlled collisions for multi-particle entanglement of optically trapped atoms. Nature 425, 937 (2003). [DOI] [PubMed] [Google Scholar]
  3. Taglieber M., Voigt A.-C., Aoki T., Hänsch T. W. & Dieckmann K. Quantum Degenerate two-species fermi-fermi mixture coexisting with a Bose-Einstein Condensate. Phys. Rev. Lett. 100, 010401 (2008). [DOI] [PubMed] [Google Scholar]
  4. Kohler T., Goral K. & Julienne P. S. Production of cold molecules via magnetically tunable Feshbach resonances. Rev. Mod. Phys. 78, 1311–1361 (2006). [Google Scholar]
  5. Bell M. T. & Softley T. P. Ultracold molecules and ultracold chemistry. Mol. Phys. 107, 99–132 (2009). [Google Scholar]
  6. Ueberholz B., Kuhr S., Fresen D., Meschede D. & Gomer V. Counting cold collisions. J. Phys. B: At. Mol. Opt. Phys. 33, L135 (2000). [Google Scholar]
  7. Fuhrmanek A., Bourgain R., Sortais Y. R. P. & Browaeys A. Light-assisted collisions between a few cold atoms in a microscopic dipole trap. Phys. Rev. A 85, 062708 (2012). [Google Scholar]
  8. Sompet P., Carpentier A. V., Fung Y. H., McGovern M. & Andersen M. F. Dynamics of two atoms undergoing light assisted collisions in an optical microtrap. Phys. Rev. A 88, 051401(R) (2013). [Google Scholar]
  9. Weiner J., Bagnato V. S., Zilio S. & Julienne P. S. Experiments and theory in cold and ultracold collisions. Rev. Mod. Phys. 71, 1 (1999). [Google Scholar]
  10. Santos M. S. et al. Simultaneous trapping of two different atomic species in a vapor-cell magneto-optical trap. Phys. Rev. A 52, R4340(R) (1995). [DOI] [PubMed] [Google Scholar]
  11. Santos M. S. et al. Erratum: simultaneous trapping of two different atomic species in a vapor-cell magneto-optical trap. Phys. Rev. A 54, 1739 (1996). [DOI] [PubMed] [Google Scholar]
  12. Telles G. D. et al. Inelastic cold collisions of a Na/Rb mixture in a magneto-optical trap. Phys. Rev. A 59, R23(R) (1999). [Google Scholar]
  13. Shaffer J. P., Chalupczak W. & Bigelow N. P. Trap loss in a two-species Na-Cs magneto-optical trap: intramultiplet mixing in heteronuclear ultracold collisions. Phys. Rev. A 60, R3365(R) (1999). [Google Scholar]
  14. Telles G. D. et al. Trap loss in a two-species Rb-Cs magneto-optical trap. Phys. Rev. A 63, 033406 (2001). [Google Scholar]
  15. Schlöder U., Engler H., Schünemann U., Grimm R. & Weidmüller M. Cold inelastic collisions between lithium and cesium in a two-species magneto-optical trap. Eur.Phys. J. D 7, 331 (1999). [Google Scholar]
  16. Weber C., John S., Spethmann N., Meschede D. & Widera A. Single Cs atoms as collisional probes in a large Rb magneto-optical trap. Phys. Rev. A 82, 042722 (2010). [Google Scholar]
  17. Mudrich M. et al. Hyperfine-changing collisions in an optically trapped gas of ultracold cesium and lithium. Phys. Rev. A 70, 062712 (2004). [Google Scholar]
  18. Gorges A. R., Bingham N. S., DeAngelo M. K., Hamilton M. S. & Roberts J. L. Light-assisted collisional loss in a 85/87Rb ultracold optical trap. Phys. Rev. A 78, 033420 (2008). [Google Scholar]
  19. Hamilton M. S., Gorges A. R. & Roberts J. L. Inter-isotope effects in optimal dual-isotope loading into a shallow optical trap. J. Phys. B: At. Mol. Opt. Phys. 45, 095302 (2012). [Google Scholar]
  20. Spethmann N. et al. Dynamics of single neutral impurity atoms immersed in an ultracold gas. Phys. Rev. Lett. 109, 235301 (2012). [DOI] [PubMed] [Google Scholar]
  21. Staanum P., Kraft S. D., Lange J., Wester R. & Weidemüller M. Experimental investigation of ultracold atom-molecule collisions. Phys. Rev. Lett. 96, 023201 (2006). [DOI] [PubMed] [Google Scholar]
  22. Zahzam N., Vogt T., Mudrich M., Comparat D. & Pillet P. Atom-molecule collisions in an optically trapped gas. Phys. Rev. Lett. 96, 023202 (2006). [DOI] [PubMed] [Google Scholar]
  23. Beugnon J. et al. Two-dimensional transport and transfer of a single atomic qubit in optical tweezers. Nat. Phys. 3, 696 (2007). [Google Scholar]
  24. Schlosser N., Reymond G. & Grangier P. Collisional blockade in microscopic optical dipole traps. Phys. Rev. Lett. 89, 023005 (2002). [DOI] [PubMed] [Google Scholar]
  25. Yu S. et al. Single atoms in the ring lattice for quantum information processing and quantum simulation. Chin. Sci. Bull. 57, 1931–1945 (2012). [Google Scholar]
  26. Yu S. et al. Qubit fidelity of a single atom transferred among the sites of a ring optical lattice. Phys. Rev. A 90, 062335 (2014). [Google Scholar]
  27. Verhaar B. J., van Kempen E. G. M. & Kokkelmans S. J. J. M. F. Predicting scattering properties of ultracold atoms: adiabatic accumulated phase method and mass scaling. Phys. Rev. A 79, 032711 (2009). [Google Scholar]
  28. Landau L. D. & Lifshitz E. M. Quantum Mechanics Vol. III, Pergamon (1991). [Google Scholar]
  29. Papp S. B., Pino J. M. & Wieman C. E. Tunable miscibility in a dual-species Bose-Einstein condensate. Phys. Rev. Lett. 101, 040402 (2008). [DOI] [PubMed] [Google Scholar]
  30. Burke J. P., Bohn J. L., Esry B. D. & Greene C. H. Prospects for mixed-isotope Bose-Einstein Condensates in rubidium. Phys. Rev. Lett. 80, 2097 (1998). [Google Scholar]
  31. Papp S. B. & Wieman C. E. Observation of heteronuclear Feshbach molecules from a 85Rb–87Rb gas. Phys. Rev. Lett. 97, 180404 (2006). [DOI] [PubMed] [Google Scholar]
  32. Chin C., Grimm R., Julienne P. S. & Tiesinga E. Feshbach resionances in ultracold gases. Rev. Mod. Phys. 82, 1225 (2010). [Google Scholar]
  33. Li Z., Singh S., Tscherbul T. V. & Madison K. W. Feshbach resonances in 85Rb–87Rb and 6Li–87Rb mixtures. Phys. Rev. A 78, 022710 (2008). [Google Scholar]
  34. Thompson S. T., Hodby E. & Wieman C. E. Spontaneous dissociation of 85Rb Feshbach molecules. Phys. Rev. Lett. 94, 020401 (2005). [DOI] [PubMed] [Google Scholar]
  35. Köhler T., Tiesinga E. & Julienne P. S. Spontaneous dissociation of long-reange Feshbach molecules. Phys. Rev. Lett. 94, 020402 (2005). [DOI] [PubMed] [Google Scholar]
  36. Yan B. et al. Observation of dipolar spin-exchange interactions with lattice-confined polar molecules. Nature 501, 521 (2013). [DOI] [PubMed] [Google Scholar]
  37. Anderlini M. et al. Controlled exchange interaction between pairs of neutral atoms in an optical lattice. Nature 448, 452 (2007). [DOI] [PubMed] [Google Scholar]
  38. DiVincenzo D. P. The physical implementation of quantum computation. Fortschr. Phys. 48, 771 (2000). [Google Scholar]
  39. Kaufman A. M., Lester B. J. & Regal C. A. Cooling a single atom in an optical tweezer to its quantum ground state. Phys. Rev. X 2, 041014 (2012). [Google Scholar]
  40. Thompson J. D., Tiecke T. G., Zibrov A. S., Vuletic V. & Lukin M. D. Coherence and Raman sideband cooling of a single atom in optical tweezer. Phys. Rev. Lett. 110, 133001 (2013). [DOI] [PubMed] [Google Scholar]
  41. Reymond G., Schlosser N., Protsenko I. & Grangier P. Single-atom manipulations in a microscopic dipole trap. Phil. Trans. R. Soc. Lond. A 361, 1527 (2003). [DOI] [PubMed] [Google Scholar]
  42. Tuchendler C., Lance A. M., Browaeys A., Sortais Y. R. P. & Grangier P. Energy distribution and cooling of a single atom in an optical tweezer. Phys. Rev. A 78, 033425 (2008). [Google Scholar]
  43. Papoular D. J. Manipulation of Interactions in Quantum Gases: A Theoretical Approach PhD thesis Univ. Paris–Sud (2011). [Google Scholar]
  44. Arimondo E., Inguscio M. & Violino P. Experimental determinations of the hyperfine structure in the alkali atoms. Rev. Mod. Phys. 49, 31 (1977). [Google Scholar]

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES