A Probabilistic Reasoning Method for Predicting the Progression of Clinical Findings from Electronic Medical Records

Abstract

In this paper, we present a probabilistic reasoning method capable of generating predictions of the progression of clinical findings (CFs) reported in the narrative portion of electronic medical records. This method benefits from a probabilistic knowledge representation made possible by a graphical model. The knowledge encoded in the graphical model considers not only the CFs extracted from the clinical narratives, but also their chronological ordering (CO) made possible by a temporal inference technique described in this paper. Our experiments indicate that the predictions about the progression of CFs achieve high performance given the COs induced from patient records.

Introduction

The narrative clinical notes in electronic medical records (EMRs) mention clinical findings (CFs) related to patients, and thus are a very important source of information which captures the progression of the patients’ overall clinical picture. An additional important aspect of the information available from clinical narratives is provided by temporal information, which enables temporal inference related to CFs. The clinical information about CFs, and their associated temporal information, is not structured; thus, it is available only when automatic extraction techniques based on natural language processing are employed. As extraction techniques become available, they make possible the development of prediction methods that can evaluate the likelihood that a certain patient develops a new condition or clinical risk factor. These predictions can be used in the clinical management of the patients, being essential in personalized medicine as they inform individual diagnostic and treatment decision making.

Automated extraction techniques that are able to identify CFs as well as their temporal information were developed in the recent 2014 Informatics for Integrating Biology and the Bedside (i2b2) Challenges addressing Language Processing for Clinical Data1. This task made possible the development of multiple approaches which were able to recognize CFs related to coronary artery disease (CAD). These CFs include diagnoses of related diseases, such as CAD itself, and diabetes, as well as certain risk factors, such as hypertension, hyperlipidemia, and obesity. As information about these risk factors related to CAD along with associated temporal information can now be identified automatically from the narrative portion of EMRs, we are in a position to be able to (1) perform temporal inference, which enables and informs (2) prediction techniques based on state-of-the-art probabilistic knowledge representation and reasoning.

Our contributions in this paper are as follows. First,we have used the annotations provided by the 2014 i2b2/UTHealth shared task that tackled the recognition of CFs for CAD in order to perform temporal inference which resulted in chronological orderings (COs) of the CFs. Second, we have produced a probabilistic knowledge representation which captures information about (a) clinical findings (CFs), (b) the COs that resulted from temporal inference, and (c) the statistical inter-dependencies which model all possible progressions of CFs over time. Third, we have used the probabilistic graphical model to perform predictions about the progressions of CFs relying on probabilistic inference. Fourth, we performed detailed experiments evaluating the predictions against the COs we inferred from the 2014 i2b2/UTHealth dataset. These experiments validate the accuracy of our prediction model and show that itproduces state-of-the-art results, especially when compared with other methods of prediction currently used.

Related Work

Clinical prediction rules have been developed to reduce the uncertainty inherent in medical practice by defining how to use CFs to make predictions [1]. However, these rules do not capture the temporal aspects of the change in CFs, and thus cannot predict their progression. A vast literature on mining association rules from patient records (PRs) has been published [2, 3], but it has been documented that these methods often produce many superfluous rules, and even those that are useful for prediction do not rely on any form of temporal inference. In consequence, they capture only a small portion of the medical knowledge that can be inferred from PRs, and only produce predictions that do not consider temporal information. Most prediction models for Coronary Artery Disease (CAD) rely on statistical methods based on Cox regression, as illustrated by the GRACE postdischarge prediction model [4]. As reported in[5], the results of this prediction model on development and validation patient cohorts were promising but may be further improved by probabilistically modelling the statistical inter-dependencies between risk factors and co-morbidities. The model presented in this paper is, to our knowledge, the first prediction model that uses an undirected probabilistic graphical model capable of representing such inter-dependencies and enabling the prediction of progressions of CFs. Although Bayesian networks have been used for many years in predictive medicine [6, 7], they operate on an underlying causal assumption: that the probabilistic influence between two random variables is represented by conditional probabilities. The model presented in this paper leverages an alternative class probabilistic graphical models, known as Markov networks, which only assume correlation between random variables (represented by joint probabilities) and allow for bi-directional influence. Because we are interested in predicting the likely progression of CFs for any patient,we rely both on the temporal information and on the bi-directional influence between any pair of CFs discovered in the PRs, thus Markov networks are ideal for our probabilistic representation.

Dataset

In this work we consider a dataset of 790 fully de-identified narrative patient records (PRs). These reports were provided by the 2014 Informatics for Integrating Biology and the Bedside (i2b2) and the University of Texas Health Science Center at Houston (UTHealth) shared-tasks on Challenges in Language Processing for Clinical Data. This dataset documents the progression of heart disease over longitudinal PRs for 128 diabetic patients where the number of PRs for each patient varied between three to five. Each PR was manually annotated to indicate the presence of certain clinical findings (CFs) deemed clinically relevant to heart disease or diabetes and include both diseases and their associated risk factors. Table 1 illustrates examples of CFs annotated as well as the criteria used for identifying them in PRs. There were 6,302 such annotations: 16,95 for DIABETES, 433 for OBESITY, 1,926 for HYPERTENSION, 1,062 for HYPERLIPIDEMIA, and 1,186 for CAD. Each of the CFs was also annotated with a temporal signal (TS) which indicates when the CF was inferred. Three temporal signals were used; their definitions and examples are provided in Table 2.

Table 1:

Clinical findings related to heart disease, based on risk factors annotated in the i2b2/UTHealth 2014 dataset.

Clinical Finding	Criteria		Example
CF1 = DIABETES (DBS)	(1)	diagnosis of type 1 or 2 diabetes	patient has h/o DMII
	(2)	A1c test over 6.5	7/18: A1c: 7.3
	(3)	two fasting blood glucose measures over 126	(8:00AM) glu: 145 …(8:00PM) glu: 139
CF2 = CAD	(1)	diagnosis of coronary artery disease (CAD)	PMH: significant for CAD
	(2)	myocardial infarction (MI, STEMI, NSTEMI)	s/p STEMI in 2004
	(3)	revascularization, cardiac arrest or ischemic cardiomyopathy	CABG in 1999
	(4)	stress test showing ischemia	dolbutamine stress test revleaing ischemia
	(5)	abnormal cardiac catherization showing coronary stenoses	cath. of LAD revealed 50% lesion
	(6)	chest pain consistent with angina	treated for stable angina
CF3 = HYPERLIPIDEMIA (HLA)	(1)	diagnosis of Hyperlipidemia or Hypercholesterolemia	control of his hypercholersterolemia
	(2)	total cholesterol measure of over 240	result of latest chol. test is 250
	(3)	LDL measurement of over 100 mg/dL	latest LDL: 135
CF4 = HYPERTENSION (HTN)	(1)	diagnosis of Hypertension	PMH: HTN
	(2)	blood pressure measurement of over 140/90 mm/hg	at admit, bp 140/100
CF5 = OBESITY (OBY)	(1)	a description of the patient as being obese	57y/o obese white male
	(2)	a body mass index (BMI) over 30	recommending lowering BMI (31.4 last August)
	(3)	a waist circumference > 40 in. for males or 35 in. for females	42in waist

Table 2:

Temporal signals associated with risk factors in the i2b2/UTHealth 2014 dataset.

Temporal Signal	Definition	Example
DURING	finding was present at the time this PR was created	today’s lab values: Chol. 247
BEFORE	finding was present before the creation of this PR	lab values from previous visit: LDL: 135
AFTER	finding is present after the creation of this PR	confirmed as diabetic

Approach

We developed a probabilistic reasoning technique which is able to predict the progression of CFs for any individual patient. To enable such predictions,we needed to encode knowledge about CFs, temporal information that allows for a chronological ordering (CO),as well as the statistical inter-dependencies between CFs. Although we have used the i2b2/UTHealth dataset, our method can operate on any set of PRs with any arbitrary set of CFs as long as they have been extracted with their associated TSs. The probabilistic knowledge that we encoded relied on (1) the CFs that were extracted from the annotations available in the data; (2) the COs that resulted from a form of temporal inference which assigned CFs to time intervals; and (3) statistical inter-dependencies which were estimated based on the COs produced on the entire dataset. This knowledge was cast in a graphical model on which probabilistic inference allowed us to produce predictions at any time during the health management of a patient. To summarize, our approach consists of three steps: (1) infer COs of CFs, (2) encode knowledge in a graphical model and (3) use probabilistic inference on the graphical model to make predictions.

Chronological Ordering of Clinical Findings

The PRs in our dataset document the clinical findings (CFs) for each patient at different times. As such, there is an implicit temporal ordering between the PRs for an individual patient. Moreover, in each PR, temporal signals (TSs) provide additional temporal information for each CF. For example, when encountering a clinical finding CF_i associated with the TS BEFORE within PR_j, we can infer that CF_i was present in the time interval beginning at the creation of PR_j–1 and ending when PR_j was created. These creation times (CTs) were parsed from PRs.

By analyzing the dataset that was created for the 2014 i2b2/UTHealth Shared Task, we noticed that the distribution of TSs associated with mentions of CFs is as follows: BEFORE was the most predominant, associated with 37% of CFs, whereas DURING was observed for 35% of the CFs, while AFTER was associated with 28% of the CFs. Moreover, we observed that the same CF may be mentioned multiple times in the same PR and that each of these mentions may be associated with a different TS. In this way, the TSs associated with each CF vary within a single PR, across PRs for the same patient, and between different patients from the population. When analysing the association between mentions of CFs and TSs, we discovered that 89% of the CFs mentioned in a PR were associated with all three possible TSs and only a very small percentage of the CFs annotated in our dataset were associated with only one or two TSs. Motivated by these observations, we based our chronological ordering on temporal inference which operates according to the following assumptions:

• [A1] If a CF_i from PR_j for a patient is associated with TS = after, we temporally infer that CF_i was present in the time interval TI(CT(PR_j), CT(PR_j+1)), denoting the time interval (TI) between the creation times (CTs) of two successive PRs for the same patient.

• [A2] In the first PR created for a patient, all CFs associated with TS = before are inferred to have been present in the special time interval before-all.

• [A3] In the last PR created for a patient, all CFs associated with TS = after are inferred to have been present in the special time interval after-all.

• [A4] A CF_i associated with TS = during is processed in the same way as if it were annotated with TS = after (as described in [A1]). Very few CFs occur only during the medical visit (6%), while the vast majority of CFs (83%) occur both during and after (and even before) the creation time of their PRs. Hence, given that the TS during does not represent a statistically significant distribution in our data, we cast the temporal inference for it to be similar to the one dictated by the TS after. Clearly, for a different temporal distribution of CFs, this assumption may not hold and additional temporal inference may be required.

Based on these assumptions, we automatically inferred the CO of the CFs for each patient. Figure 1 illustrates the temporal inference for one patient documented in the dataset and the resulting CO of CFs induced for that patient.

Figure 1:

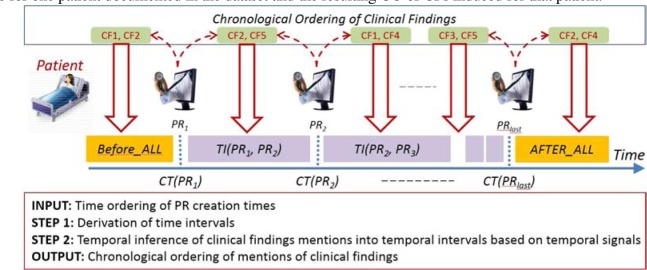
Chronological ordering (CO) of clinical findings (CFs) for a patient.

To devise the chronological order of CFs,we first take into account the creation times (CTs) of each pr. Given all the PRs generated for a patient, we order the PRs as shown in Figure 1. This allows us to produce N+1 time intervals where N is the number of PRs produced for the patient. These time intervals (TIs) are represented as: [ before-all; ti(ct(pr₁), ct(pr₂)); ti(ct(pr₂), ct(pr₃)); …; after-all]. In the next step, we applied the assumptions [A1-4], in order to determine which CFs should be associated with each ti. For each PR_i, we map each cf with TS= BEFORE into the time interval ti(ct(pr_i–1), ct(pr_i)), and each CF with TS= AFTER into the time interval ti(ct(pr_i), ct(pr_i+1)). As illustrated in Figure 1, a chronological ordering (CO)is a temporally-ordered sequence of sets, where each set S_i represents the combination of CFs which were temporally inferred as belonging to the i-th time interval (ti_i). For example, the co produced for the patient illustrated in Figure 1 consists of the following sets: ${\mathbb{S}}_0=\left\{\text{DIABETES},\text{CAD}\right\}$; ${\mathbb{S}}_1=\left\{\text{CAD},\text{OBESITY}\right\}$; ${\mathbb{S}}_2=\left\{\text{DIABETES HYPERTENSION}\right\}$, ${\mathbb{S}}_3=\left\{\text{HYPERLIPIDEMIA},OBESITY\right\}$; and ${\mathbb{S}}_4=\left\{\text{CAD},\text{HYPERTENSION}\right\}$. When we infer the COs for all patients in the dataset, we enable the probabilistic representation of the knowledge about CFs from the clinical dataset.

A Graphical Model for Representing Knowledge about Clinical Findings

We encoded knowledge using a probabilistic graphical model (PGM), illustrated in Figure 2. In our PGM, nodes correspond to CFs and are represented as binary random variables. Our PGM also encodes knowledge about the CO of CFs. COs are sequences of sets of CFs, denoted as ${\mathbb{S}}_0,{\mathbb{S}}_1,\dots ,{\mathbb{S}}_L$ where L is the longest CO inferred from our dataset. Because the PGM encodes knowledge about the entire patient population documented in the dataset, the PGM needed to encode all the possible sets of CFs for each ${\mathbb{S}}_i$ where 0 ≤ i ≤ L. This was achieved by assigning a value of 1 to the random variable of a CF which was observed in the same ${\mathbb{S}}_i$ and a value of 0 to any CF which was not observed in that same ${\mathbb{S}}_i$. An advantage of the knowledge representation using the PGM stems from the ability to also assign a probability to the random variables, which encapsulates the statistical distribution of the CFs corresponding to the COs across all patients. A second advantage of this knowledge representation stems from the ability to capture statistical dependencies between the random variables, which are represented as edges in the graph. Any edge from a CF_x in ${\mathbb{S}}_i$ to a CF_y in ${\mathbb{S}}_i{}_{+1}$ indicates such a dependency. The statistical dependencies between CFs across successive sets $\left({\mathbb{S}}_i\text{to}{\mathbb{S}}_{i+1}\right)$ allows us to represent all the possible ways in which CFs may progress from one time interval to the next based on the properties of our clinical dataset. Because we are only considering five different CFs in our dataset, there are 25 = 32 possible statistical dependencies between any ${\mathbb{S}}_i$ to ${\mathbb{S}}_{i+}{}_1$.

Figure 2:

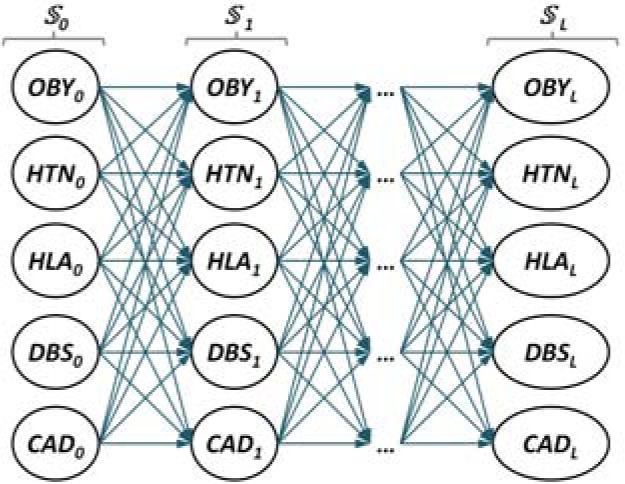
A probabilistic graphical model encoding the likelihood of any possible progression of clinical findings.

Predictions as Probabilistic Inference

To make predictions about the progression of CFs of any patient, we used probabilistic inference to estimate the most likely assignment of CFs, $\widehat{\mathbb{S}}$, given the observed sets of CFs and their COs encoded in the sets ${\mathbb{S}}_0,{\mathbb{S}}_1,\dots ,{\mathbb{S}}_i$ by finding the most likely assignment to the set ${\mathbb{S}}_{i+1}$. When i = 1, we make predictions about the progression of CFs given knowledge documented only in the first PR, whereas when i = LAST, we make predictions about the progression of CFs after the last visit (documented in the last PR) of the patient. Since there are 32 possible transitions from any ${\mathbb{S}}_i$ to ${\mathbb{S}}_i{}_{+1}$, we define $\mathbb{X}$ as the set of all 32 possible values for ${\mathbb{S}}_{i+1}$. In this way, probabilistic inference used the maximum a posterior (MAP) assignment which predicts the most likely progression, i.e. the set of CFs ${\mathbb{S}}_{i+1}$ provided by the assignment $\widehat{\mathbb{S}}$:

$$\widehat{\mathbb{S}}=\underset{{\mathbb{S}}^{\prime }\in \mathbb{X}}{\text{argmax}}P({\mathbb{S}}_{i+1}={\mathbb{S}}^{\prime }|{\mathbb{S}}_0,\dots ,{\mathbb{S}}_i)$$ (1)

To compute the MAP estimation, we also needed to estimate (a) the transition probability between a set of CFs ${\mathbb{S}}_i$ to a set ${\mathbb{S}}_{i+1}$; and (b) the prior probability of any set ${\mathbb{S}}_i$ which indicates the likelihood that the combination of CFs represented by ${\mathbb{S}}_i$ was observed in any CO produced by temporal inference in the patient population. To estimate the transition probability, $P\left({\mathbb{S}}_{i+1}|{\mathbb{S}}_i\right)$ we evaluated two functions: (a) ${\mathbb{Q}}_1\left({\mathbb{S}}_i,{\mathbb{S}}_{i+1}\right)$ representing the number of times in which all CFs observed in the set ${\mathbb{S}}_i$ were temporally mapped to some time interval TI_j in a CO, while all the observed CFs from ${\mathbb{S}}_{i+1}$ were temporally mapped to the next time interval TI_j+1 in the same CO; and (b) ${\mathbb{Q}}_2\left({\mathbb{S}}_i\right)$ representing the number of times the CFs from ${\mathbb{S}}_i$ were temporally mapped to the same time interval in any of the COs for the entire patient population. This allowed us to estimate $P\left({\mathbb{S}}_{i+1}|{\mathbb{S}}_i\right)={\mathbb{Q}}_1\left({\mathbb{S}}_i,{\mathbb{S}}_{i+1}\right)/{\mathbb{Q}}_2\left({\mathbb{S}}_i\right)$. Similarly, to estimate $P\left({\mathbb{S}}_i\right)$, we define the number ${\mathbb{Q}}_3$ which represents the total number of COs induced for the entire dataset. Then, $P\left({\mathbb{S}}_i\right)={\mathbb{Q}}_2\left({\mathbb{S}}_i\right)/{\mathbb{Q}}_3$. Given the definitions of the transition probability and the prior probability of any set of CFs, we can compute the likelihood of any progression of CFs. We define the progression of CFs as a sequence of sets of CFs, ${\mathbb{S}}_0,{\mathbb{S}}_1,\dots ,{\mathbb{S}}_j$, where j represents the number of time intervals in the documented care of the patient. This enables us to compute the likelihood of any progression of CFs as:

$$P({\mathbb{S}}_0,\dots ,{\mathbb{S}}_j)=P({\mathbb{S}}_0)\times {\displaystyle \prod _{i=0}^{j-1}P({\mathbb{S}}_{i+1}|{\mathbb{S}}_i)}$$ (2)

As we were able to compute the likel.ihood of any arbitrary progression of CFs from the dataset, we were also capable of predicting the progression of a new, unseen set of CFs, i.e. ${\mathbb{S}}_{j+1}$ using Eq. 3.

$$P({\mathbb{S}}_{j+1}|{\mathbb{S}}_0,\dots ,{\mathbb{S}}_j)=\frac{P({\mathbb{S}}_0,\dots ,{\mathbb{S}}_{j+1})}{{\displaystyle \sum _{{\mathbb{S}}^{\prime }\in \mathbb{X}}P({\mathbb{S}}_0,\dots ,{\mathbb{S}}_j,{\mathbb{S}}^{\prime })}}$$ (3)

As the probability of a new progression of CFs is defined by Eq. 3, the probabilistic inference through MAP as given in Equation 1 makes predictions about the progression of CFs in the dataset used in our experiments and allowed us to evaluate the model we have constructed. To exemplify the probabilistic inference enabled by our model, we use the CO illustrated in Figure 1 to instantiate the five sets of CFs ${\mathbb{S}}_0$, ${\mathbb{S}}_1$, ${\mathbb{S}}_2$, ${\mathbb{S}}_3$, and ${\mathbb{S}}_4$. This allows us to determine the probability that the CFs for this patient will progress such that only HYPERTENSION is present in the future by defining ${\mathbb{S}}_5=\left\{HT{N}_5=1,OB{Y}_5=0,HL{A}_5=0,DB{S}_5=0,CA{D}_5=0\right\}$. Using Eq. 3, we can compute the posterior probability for the CFs in ${\mathbb{S}}_5$ as 09.8%, meaning that, for the patient, there is an approximately 10% chance that he or she will no longer present with CAD in the next hospital visit and will instead present with only hypertension. We can additionally predict the most probable progression of CFs for the same patient, by determining (a) the most probable assignment of random variables from ${\mathbb{S}}_5$ and (b) the likelihood of that assignment. The most probable next set of CFs is HYPERTENSION and CAD with probability 17.5%, and the next most likely assignment is HYPERTENSION at 9.8%. This shows that although there are many possible combinations of CFs for the next time-step, our model predicts that the combination of both HYPERTENSION and CAD is 78.6% more likely than just HYPERTENSION.

Experimental Results

We conducted an extensive set of experiments with the purpose of evaluating the qualityof the predictions of CF progressions. We considered predictions performed after any number of time intervals had been observed, i.e. we evaluated the predictions for each possible value of 1≤ j ≤ L, where L is the length of the longest CO obtained for any patient. It is to be noted that the accuracy of our model is always very high (above 80%) while the F₁-measure improves as more information from the COs of CFs becomes available. Table 3 details the evaluations of the predictions produced by our system for all COs of length j from the entire patient population. As shown, the highest precision for the prediction of any type of CF was obtained when considering only a single previous time-interval. This confirms the conclusions hypothesized in [8] which suggest that the presence of CFs in the immediately proceeding PR is the best predictor for the presence of a CF. Note, however, that when considering COs of greater length, the Recall tends to improve. This suggests that considering more chronological information allows for more complex and rarer combinations of CFs to be predicted. A more detailed evaluation of the prediction of the progression for each individual CF is illustrated in Figure 3. Across all five CFs, our probabilistic model has the best F₁ measure when predicting DIABETES, with an F₁=94.57. Coronary Artery Disease, CAD, was a close second at F₁=92.31, followed by HYPERTENSION with F₁ =93.24, HYPERLIPIDEMIA at F₁ =85.42, and OBESITY at F₁ =78.8. We believe that the difference in predictive performance for these CFs can be attributed to differences in the distribution of how often each type of CF was observed in our dataset. For example, DIABETES, HYPERTENSION and CAD are the most frequently occurring CFs (26%, 30%, and 19% respectively), while HYPERLIPIDEMIA and OBESITY are the least frequently occuring CFs (accounting for 16% and 7%, respectively). Further, we notice that for the most common CFs (HYPERTENSION and DIABETES), the F₁-measure tends to improve consistently as COs of longer lengths are considered, while for less common CFs (OBESITY) the trends are not as clear. This implies the need for additional data to balance the distribution of CFs. It also shows that, for any given problem-based patient cohort, the progression of certain CFs may be better predicted as more PRs documenting that CF are provided.

Table 3:

Performance results over all CFs for COs of length j, where Acc = Accuracy, PPV = positive predictive value (Precision), FNR = false negative rate, FPR = false positive rate, TNR = true negative rate (Specificity), TPR = true positive rate (Recall), F1 = F₁-measure defined as $2\times \frac{PPV\times TPR}{PPV\times TPR}$, TP = true positives, FP = false positives, FN = false negatives, TN = true negatives.

j	Acc	PPV	FNR	FPR	TNR	TPR	F1	TP	FP	FN	TN
1	84.94	94.22	22.84	05.69	94.31	77.16	84.84	375	23	111	381
2	81.91	86.63	17.80	18.51	81.49	82.20	84.35	434	67	94	295
3	86.18	91.13	13.20	14.91	85.09	86.80	88.91	493	48	75	274
4	86.71	85.21	06.27	23.38	76.62	93.73	89.26	478	83	32	272
5	88.92	85.29	02.52	22.60	77.40	97.48	90.98	232	40	6	137

Figure 3:

Experimental results for the prediction of the progression of CFs for chronological orderings of lengths 1 ≤ j ≤ 5, where A denotes the Accuracy, P denotes the Precision, R denotes the Recall, and F1 denotes the F₁-measure.

Conclusion

This paper has introduced a novel method of predicting the progression of CFs. The predictions are based on probability inference operating on a graphical model that encodes knowledge about CFs extracted from PRs as well as their inferred chronological orderings. Our method provided promising results in extensive experiments.