How Comorbidities Co-Occur in Readmitted Hip Fracture Patients: From Bipartite Networks to Insights for Post-Discharge Planning

Abstract

Although a majority of 30-day readmissions of hip-fracture (HFx) patients in the elderly are caused by non-surgical complications, little is known about which specific combinations of comorbidities are associated with increased risk of readmission. We therefore used bipartite network analysis to explore the complex associations between 70 comorbidities (defined by hierarchal condition categories as critical in this population) and (a) cases consisting of all 2,316 HFx patients without hospital complications in the 2010 Medicare claims database who were re-admitted within 30 days of discharge, and (b) controls consisting of an equal number of matched HFx patients who were not readmitted for at least 90 days since discharge. A network-wide analysis revealed nine patient/comorbidity co-clusters, of which two had a significantly different proportion of cases compared to the rest of the data. A cluster-specific analysis of the most significant co-cluster revealed that a pair of comorbidities (Renal Failure and Diabetes with no Complications) within the co-cluster had significantly higher risk of 30-day readmission, whereas another pair of comorbidities (Renal Failure and Diabetes with Renal or Peripheral Circulatory Manifestations), despite having a relatively more serious comorbidity, did not confer a higher risk. This counter-intuitive result suggests that HFx patients with more serious comorbidities may have better follow-up that reduces the risk of 30-day readmission, whereas those with specific relatively less-serious comorbidities may have less stringent follow-up resulting in unanticipated incidents that precipitate readmission. These analyses reveal the strengths and limitations of bipartite networks for identifying hypotheses for complex phenomena related to readmissions, with the goal of improving follow-up care for patients with specific combinations of comorbidities.

Introduction

Several studies have shown that hip fractures (HFx) in the elderly are a leading cause of morbidity, long term functional impairment, and mortality1. Furthermore, a large scale study2 in the veteran population revealed that the risk of mortality within a year doubled if there was a readmission within 30 days of hospital discharge after surgery. These statistics explain the high personal and financial burden3 resulting from HFx in the elderly, a situation which will likely worsen with the rapid aging of the US population.

Unfortunately, much remains to be discovered about the factors that precipitate readmission within 30 days. For example, a recent study4 revealed that 30-day readmissions of HFx patients are associated with mainly non-surgical causes, suggesting that existing comorbidities are exacerbated after hip fracture surgery. However, the existing research has either used (1) univariate statistics to determine the risk of single comorbidities4, but which cannot reveal how they interact, (2) multivariate statistics like regression to determine which combination of comorbidities best distinguish cases from controls2, but which cannot reveal co-clusters and their inter-relationships, or (3) combinatorial methods that identify a large number of patient clusters characterized by combinations of comorbidities5 (all dyads, triads, etc.), but which cannot reveal interactions among such combinations (e.g., how a dyad of comorbidities interacts with a triad of a different set of comorbidities).

We therefore explored the use of bipartite networks to conduct a multivariate analysis of how comorbidities co-occur across readmitted and not readmitted HFx patients with the goal of (1) understanding interactions across all comorbidities, and (2) specific interactions of a subset of comorbidities that confer high risk for 30-day readmission. Similar to most visual analytical methods, our primary goal was to identify hypotheses for complex phenomena requiring a global and specific understanding of interactions, which are more difficult to derive from many of the methods that have been attempted.

Method

Our research began with the question: How do comorbidities co-occur across 30-day readmitted HFx patients compared to similar patients who were not readmitted for at least 90 days? To address our research question, we made critical decisions related to data selection, and data analysis as discussed below:

Data Selection

As is commonly done in analytical studies of claims data, we used MS-DRG codes to define our population. We operationally defined hip fracture patients as those who were discharged from hospital with MS-DRG code 480, but without hospital complications. This subset of the total hip fracture patient population was designed to isolate the association of comorbidities to readmission. Using the Medicare claims data for 2010, we extracted (1) all HFx cases (n=2,316 with MS-DRG=480) without hospital-acquired complications that were readmitted within 30 days of discharge, and (2) an equal number (n=2,316 with MS-DRG=480) of controls matched by age, gender, and race, who were not re-admitted (defined as patients not readmitted for at least 90 days since discharge). This 90-day window of no re-admittance was used to ensure that the controls were substantially free of complications that precipitate readmission to enable an effective comparison with the cases. For each of the above patients, we extracted their status on 70 high-level comorbidities as defined by hierarchal condition categories6 (HCC) which represents the range of conditions typically encountered by this population. As our index condition was HFx, we excluded it resulting in a total of 69 HCC comorbidities across 4,632 cases and matched controls.

Data Analysis

Our analysis consisted of two steps: (1) exploratory visual analysis to identify emergent bipartite relationships between patients and comorbidities; and (2) quantitative analysis suggested by the emergent visual patterns. This two-step method was motivated by our earlier studies7,8, which have demonstrated that bipartite networks can reveal complex associations each prompting the use of quantitative methods that make the appropriate assumptions about the underlying data.

1. Exploratory Visual Analysis was conducted using network visualization and analysis9. Networks are increasingly being used to analyze a wide range9 of complex molecular, clinical, and social phenomena such as gene and protein-protein interactions, how symptoms co-occur across toxic chemical exposure, and how infections spread across a social group. A network consists of nodes and edges; nodes represent one or more types of entities (e.g., patients or genes), and edges between the nodes represent a specific relationship between the entities. Figure 1A shows a bipartite network where edges exist only between patients (circles) and comorbidities (triangles).

Figure 1.

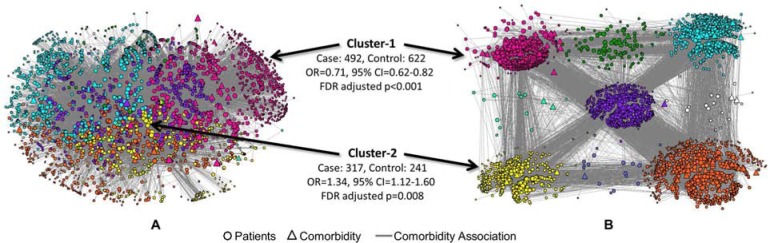
A bipartite network of 4,632 patients (cases and controls) and 69 HCC comorbidities displayed using a 3D layout (A), and an exploded 2D layout (B) to show the size and spread of the nodes in each cluster. Cluster-1 (magenta nodes in the upper left corner) and Cluster-2 (yellow nodes in the lower left corner) had significantly lower and higher risk respectively of 30-day readmission compared to the risk of readmission in rest of the data.

Node color was used to distinguish between different types of nodes (members of a cluster; cases versus controls). Node shape was used to distinguish between patients and comorbidities (patients=circles, comorbidities=triangles). Finally, node diameter was used to represent the sum of the edge weights connected to it (also referred to as degree centrality). These graphical representations of the data, and of analysis results, enabled a rapid visual inspection to determine for example, which patients have overall higher comorbidities, and how such patients relate to the rest of the network. Global patterns between subjects and genes in the network were visualized and analyzed using the Fruchterman-Reingold layout algorithm10 in Pajek11 (version 3.13). This algorithm results in pulling together nodes that have a similar pattern of connections, and pushing apart nodes that do not. As shown in Figure 1, we used the 3D version of this algorithm as the extra degree of freedom provided by the z-plane enables a more accurate layout of the nodes11. This algorithm is fast but approximate and well-suited for large networks consisting of >1000 nodes.

A key advantage of a network representation is the simultaneous visualization of multiple raw values (patient-comorbidity associations), aggregated values (sum of patients across comorbidities), and emergent global patterns (clusters) in a uniform visual representation. Such a representation enables the rapid generation of hypotheses based on complex multivariate relationships, which can be verified through appropriate quantitative methods.

2. Quantitative Analysis was conducted using two measures to verify the insights derived from the exploratory visual analysis. These methods were selected based on their appropriateness to the emergent patterns in the network.

(a) Degree of Clusteredness

Because the network layout suggested distinct co-clusters (patients plus cormobidities), we used modularity12 to determine (1) the degree of clusteredness, (2) the number of co-clusters in the network, and (3) the members of each co-cluster. Modularity (a standard measure used to analyze networks) quantifies the notion that there are more edges between nodes in a cluster than can be expected by random chance, and fewer edges between nodes across clusters than can be expected by random chance. Modularity values range from −1 to +1, where high values (>0.3) represent substantial clustering12. We used a bipartite version of modularity to identify the co-clusters of patients/comorbidities. As shown in Figure 1A/1B, the co-cluster boundaries identified by modularity were superimposed onto the network by using identical node color to denote cluster membership.

(b) Cluster Significance

To identify which co-cluster had significantly different risk of readmission, we compared the proportion of cases in a co-cluster to the proportion of cases in the rest of the data using chi-square (adjusted for multiple testing), and report the FDR-adjusted p-value. Then we measured the magnitude of risk of readmission in the statistically significant co-clusters using odds ratio (OR), and report the OR and the 95% confidence interval for each cluster. (Henceforth we refer to “co-clusters” simply as “clusters”).

Results

The analysis revealed associations at the network-wide level, and at the cluster-specific level as described below:

Network-Wide Associations

As shown in the 3D layout in Figure 1A, the bipartite network, despite being fairly dense, had substantial clusteredness of patients and comorbidities (modularity = 0.369) consisting of 9 clusters (denoted by different colors). The presence of these clusters was most salient when the 3D model was rotated. Unfortunately, the comprehension of this clustered topology is lost in the static 2D image shown in Figure 1A. We therefore re-laid out the network in 2D, and created an exploded view of the network by pulling apart each cluster. As shown in Figure 1B, this exploded view does not preserve the distance between the clusters, but preserves the distance among nodes within each cluster, enabling comprehension of its size and spread. As shown, some clusters (e.g., the magenta cluster) were large and dense, whereas others (e.g., the white cluster) were small and sparse providing a simultaneous understanding of the prevalence and co-occurrence of comorbidities across the data.

Next, we analyzed which of these clusters had a statistically significant risk for readmission compared to the rest of the data. The results identified two significant clusters. Cluster-1 (colored magenta in Figure 1A and 1B) had 1,114 patients (492 cases and 622 controls) and 19 comorbidities: (Renal Failure, Dialysis Status, Diabetes w/o Complication, Diabetes w/Renal or Peripheral Circulatory Manifestation, Diabetes w/Neurologic Manifestation, Diabetes w/Ophthalmologic Manifestation, Nephritis, Proliferative Diabetic Retinopathy, HIV/AIDS, Major Cancers, Inflammatory Bowel Disease, Disorders of Immunity, Quadriplegia and Other Extensive Paralysis, Muscular Dystrophy, Polyneuropathy, Multiple Sclerosis, Chronic Ulcer of Skin, Major Organ Transplant, Amputation Complications). This cluster had low risk (OR=0.71, 95% CI=0.62–0.82, FDR adjusted p<0.001) where the p-value denotes the significance (based on chi-square) of the difference in proportion of cases compared to the rest of the data after FDR correction. This result was counter-intuitive as 8 comorbidities (bolded in the above list) were directly related to renal or diabetes conditions, which generally are known on their own to confer high risk for readmission.

In contrast, Cluster-2 (colored yellow in Figure 1A and 1B) had 558 patients (317 cases and 241 controls) and 3 comorbidities all directly or indirectly related to heart disease (Acute Myocardial Infarction, Unstable Angina and Other Acute Heart Disease, Major Complications of Medical Care and Trauma). Furthermore, as this cluster had high risk (OR=1.34, 95% CI=1.12–1.60, FDR adjusted p=0.008), the result was comprehensible as conditions such as Acute Myocardial Infractions have unanticipated onsets, which are likely to result in high rates of readmission. Therefore, while Cluster-2 was comprehensible, we needed to analyze Cluster-1 in more depth to understand why the cluster as a whole had significantly lower risk.

Cluster-Specific Associations

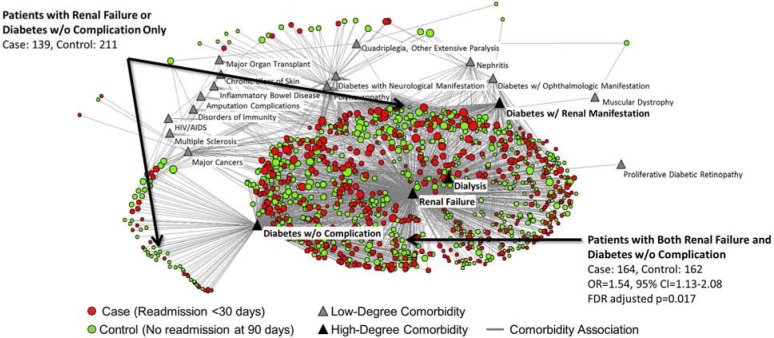
As shown in Figure 2, Cluster-1 had four comorbidities (Renal Failure, Diabetes w/o Complication, Diabetes w/Renal or Peripheral Circulatory Manifestation, and Dialysis Status) that were connected to the majority (97.6%) of the patients within the cluster, and which had the four highest node degrees (total number of coincident edges). Because Cluster-1 had the highest significance of all the clusters, and the above four comorbidities were highly connected to a majority of the patients, we analyzed the odds ratio (OR) and significance for all combinations of these four comorbidities with respect to the other comorbidities in Cluster-1. The results revealed that only the combination of Renal Failure and Diabetes w/o Complications compared to either alone (with no other comorbidities) conferred high risk (OR=1.54, 95% CI=1.13–2.08, FDR adjusted p=0.017), whereas all other combinations did not. For example, even though Diabetes w/Renal or Peripheral Circulatory Manifestation and Dialysis constitute high risk for complications, they were not associated with significantly higher OR of readmission in any combination. Finally, the association between Renal Failure and Diabetes w/o Complications also conferred high risk (OR=1.54, 95% CI=1.01–2.36, p=0.044) when considering all 69 comorbidities in the entire network.

Figure 2.

Bipartite network of only Cluster-1 showing the four comorbidities (black triangles), which were associated with a majority of the patients. Patients with both Renal Failure, and Diabetes w/o Complications had a significantly higher risk of 30-day readmission compared to either alone with respect to the other comorbidities in this cluster. This relationship was also significant when considering all the patients in the full network.

Discussion

The bipartite network analysis helped to identify a complex but comprehensible phenomenon. At the network-wide level, it helped to identify two clusters which were significantly different for risk of 30-day readmission compared to the rest of the data. However, at this level of analysis, only Cluster-2 had a comprehensible association: Hip fracture patients with ischemic heart disease or related conditions are at higher risk for readmission because this combination of comorbidities could lead to unanticipated events like a heart attack, resulting in a higher risk for readmission.

However, Cluster-1, despite being dominated by renal- and diabetes-related comorbidities, had a significantly lower risk of readmission. What could explain this reversal? A cluster-specific analysis revealed that among the four most dominant comorbidities in the cluster, no combination had a higher risk for readmission except Renal Failure and Diabetes w/o Complications. This was surprising as other combinations such as Renal Failure and Diabetes w/Renal or Peripheral Circulatory Manifestation are regarded as more serious conditions, and therefore could be expected to result in more complications and consequently higher risk for readmission.

Two plausible explanations for this reversal include: (1) Patients that have advanced conditions might already have closely monitored follow-up, which would continue or be enhanced after a hip fracture. In contrast, patients who have more easily controlled conditions (and therefore perceived to be of low risk for complications), do not receive as much scrutiny during follow-up. When unanticipated interactions occur, such patients are unprepared resulting in a readmission. (2) Medications, procedures, and stressors related to HFx surgeries could trigger a complex biochemical imbalance in patients with renal failure and diabetes13, resulting in unanticipated events, which in turn precipitates readmission. Regardless of the causation, the results suggest that this specific subpopulation possibly requires follow-up care that is equivalent to what patients with more serious conditions typically receive.

Based on these analyses, we believe that the bipartite network analysis approach enabled the identification and integration of four separate and significant associations: (1) identification of a cluster that had a significantly higher risk of readmission, (2) identification of a cluster that had a significantly lower risk of readmission, (3) one pair of comorbidities without progression to complications, but with a higher risk of readmission compared to either alone, and (4) comorbidities that were more developed but which did not have a significantly higher risk of readmission. Because these associations were derived from a unified network representation, it enabled a domain expert to quickly integrate them into a complex but comprehensible hypothesis for the phenomenon at work.

Conclusions and Future Research

Although several different methods have been used to analyze risks involved in hospital readmission, to the best of our knowledge there has been no prior attempt to use bipartite networks to shed light on this significant and time-sensitive problem. By using bipartite networks to analyze HFx patients, we have demonstrated how they helped to (1) identify multiple associations at different levels, and (2) integrate them into a hypothesis for a complex but comprehensible phenomenon related to readmission. A limitation of the study is that we analyzed only those patients with an MS-DRG 480 code, but without hospital complications in order to isolate the association of comorbidities with readmission. Future studies should analyze the interactions of hospital complications and comorbidities to obtain a more complete understanding of the risk related to HFx readmissions.

Methodologically it is important to note that the visualization and clustering methods we have demonstrated do not scale up well to handle millions of nodes in a network. Modularity algorithms use search methods to optimize the separation of nodes into clusters, and therefore have performance problems if the network exceeds ~1000 variables. Furthermore, network layout algorithms also use heuristic search methods and therefore when processing a large number of nodes often generate suboptimal layouts, which tend to be less useful for analysis. In our future research, we therefore intend to use more scalable methods such as (1) using bipartite networks to analyze a random sample of patients to generate specific hypotheses of high-risk comorbidity combinations, and (2) testing those hypotheses without using networks on the entire dataset. We also intend to analyze inter-cluster associations such as the proportion of cases or controls in one cluster that are connected to other clusters, and to validate our results from another fiscal year of Medicare claims data. Such methodological advances should accelerate the identification and validation of complex phenomena in “big data” related to readmissions, with the goal of reducing the high personal and financial burden resulting from HFx in the elderly.