Rediscovering drug side effects: the impact of analytical assumptions on the detection of associations in EHR data

Abstract

Large clinical datasets can be used to discover and monitor drug side effects. Many previous studies analyzed symptom data as discrete events. However, some drug side effects are inferred from continuous variables such as weight or blood pressure. These require additional assumptions for analysis. For example, we can define positive/negative thresholds and time windows within which we expect to see the side effect. In this paper, we discuss the impact of such assumptions on the ability to detect known continuous drug side effects using statistical and visualization techniques. Taking the case of prednisone exposure and weight gain reflected in real EHR data, we found that temporal windowing greatly affected the ability to detect the expected effect. Categorization of the exposure variable improved side effect detection but negatively impacted model fit. To avoid false positive and false negative conclusions from clinical data reuse, studies reusing clinical data should determine the sensitivity of their findings to alternative analytic assumptions.

Introduction

Adoption of electronic health records (EHRs) has led to large clinical data warehouses (CDWs) that can be used to answer clinically-relevant research questions (1,2). Clinical data reuse complements traditional research methods such as randomized controlled trials (RCTs), which are time consuming and costly (1–4). Post-marketing discovery and surveillance of drug side effects is a particularly attractive use of large clinical datasets (5,6). For example, Brownstein et al. were able to retrospectively link COX-2 inhibitors to myocardial infarction (7).

Most prior studies focused on side effects that were defined as discrete events occurring at a specific point in time. However, many drug side effects are tracked and recorded by continuous variables such as weight and blood pressure (8). Although one can define an event from a set of sampled continuous descriptors (e.g., weight gain), information is lost when this variable is categorized (e.g., patients whose weight increased by more than 10% or less than or equal 10%) and such classification is dependent on the cut point that may impact the analytical outcome of the study. Moreover, when exploring data, researchers must make additional assumptions to address issues related to data repurposing such as heterogeneity (9), data accessibility (10) and unknown sampling conditions (11).

For this study, we attempted to “rediscover” the known association between prednisone, a commonly prescribed corticosteroid, and weight gain. We chose this association because it is well-accepted by clinicians (12) and common in our data. Notably, “patient taking prednisone” is a time varying event – i.e., prednisone is prescribed at some or varying dose over time. Often the dose changes during the prescription period (e.g., prednisone taper), which complicates analysis. Similarly, weight gain occurs over time against a background of ordinary trends. For example, patients generally gain weight changes with age at a rate of approximately half a pound per year (13). Thus, reuse of such continuous EHR data requires the researcher to make multiple assumptions. Hypothesizing that these assumptions may impact the detection of a known association, we explored the effect of assumptions on the outcome of data analysis.

Methods

We employed longitudinal statistical regression methods as well as interactive data visualizations to analyze the known relationship between prednisone and weight gain using real electronic health record data extracted from a CDW. The study was deemed exempt by the UTHealth Committee for the Protection of Human Subjects.

Our dataset was extracted from an outpatient clinic’s EHR production database and contained 105,660 observations, for 10,915 patients with at least one prednisone prescription, spanning from April 2004 to January 2014. We filtered out patients under 21 years of age and extreme outliers for weight (i.e., weight>400 kg). A second round of filtering was performed on the weight variable by removing measurements more than three standard deviations on both sides of its mean. No missing values were found for age, and sex variables. After the previously-described filtering, the final dataset contained 93,617 records for 9,767 patients which were analyzed in this study. Drug exposure was calculated as the cumulative number of milligrams prescribed of which 15.4% were missing (i.e. 0 or null values in the database). Because the distribution of exposure was not normal, we converted exposure into a binary variable (i.e., high/low as above or below mean exposure=300mg).

Statistical Analysis

We used summary statistics such as mean, median and extreme values to screen the data for outliers, missing values and erroneous input. As an example, one patient in the dataset had a recorded weight of 112,552.70 kg; roughly the weight the largest mining trucks in existence today. We verified normality of continuous variables using histograms. To detect weight gain (our continuous main outcome variable) over time, we built a longitudinal regression model using generalized estimating equations (GEE). Statistical significance was set at p=0.05. The model was built on weight, time and exposure (cumulative prednisone dose in mg) or exposure group (cumulative prednisone dose below or above the mean=300mg). We included known covariates: sex and age. Time windowing was varied around the time of prescription to optimize effect detection. We used SAS (version 9.0, SAS Institute Inc., Cary, NC) for statistical analysis.

Continuous signal visualization analysis

Our continuous variable visualizations were built using Tableau (Version 8.1, Tableau Software, Seattle, WA). Tableau allows the user to explore data by rapidly creating and iteratively modifying graphs using quantitative and qualitative data. The data were studied as weight measurements over time aligned on the first prednisone prescription for each patient. Weight data were averaged using different time resolutions (i.e., days, weeks and months) to reduce high-frequency noise and to better visualize the effect (14). We normalized relative to each patient’s starting weigh by visualizing percentage weight gain over time.

Sensitivity analysis

To explore the impact of assumptions, we ran the regressions varying the lower and higher temporal thresholds of our data. We also evaluated the impact of cateorizing the exposure variable of our dataset. For the visualization method, we explored the same assumptions in the context of creating graphs for each scenario. To evaluate the impact of assumptions, we looked at the degree of statistical significance (i.e., p-value) and the Quasi-likelihood under Independence Model Criterion (QIC)(15). QIC is a generalization of Akaike’s information criterion which represents the goodness of fit of statistical models typically employed with GEE and informs model selection.

Accounting for baseline weight trends

To account for changes in patients weight not related to prednisone, we compared patients prescribed prednisone to patients who were on aspirin and ACE-inhibitors. Neither aspirin, nor ACE-inhibitors are thought to cause weight gain. We extracted weight information for patients with at least one prescription for aspirin (selected through prescriptions with drug names containing the string ‘aspirin’) or ACE-inhibitors including: benazepril, lotensin, captopril, capoten, enalapril, vasotec, fosinopril, monopril, lisinopril, prinivil, zestril, perindopril, aceon, quinapril, accupril, ramipril, altace, trandolapril or mavik. Notably, the goal was not to identify all patients prescribed any form of aspirin or ACE-inhibitor, as long as the groups were not biased with respect to weight change. We have no reason to think that patients prescribed different forms of aspirin or different ACE-inhibitors differ with respect to weight change. We analyzed the data using the previously described continuous signal visualization technique. Regression lines and slopes were used to estimate rate of weight change. The slope values were then compared to previous results. We used the assumptions yielding the most appropriate results in the statistical analysis to ensure comparability.

Results

Statistical analysis

Of the 9,767 patients analyzed, 35.03% were male. The average and standard deviation (SD) of age to receive a first prednisone prescription were 54.79±15.62 with a median of age of 55 years. Mean and standard deviation of weight were 84.23±22kg. Mean and standard deviation of exposure were 312.77±697.31 mg.

Our GEE model predicted the main outcome (weight) based on drug exposure (high/low), the number of days from the first prescription (time), the patient’s age at the time of first prescription, the patient’s sex taking into account the interaction between time and exposure. An autoregressive correlation structure was used, due to the likelihood of adjacent measurements having higher associations. We built the longitudinal linear regression model on the whole dataset, not finding any variables to be significant. Different time windows were explored between 10 days prior and 120 days after taking the drug. The largest effect size and significance were found for a window set 7–90 days after the prednisone prescription (Table 1), which matches what is clinically expected (i.e., patients gain weight 7–90 days after starting prednisone).

Table 1.

Regression results for varying assumption parameters. Model fit improves (i.e., QIC reduces) as conditions are included to improve the model. Categorization improves significance (p-values) but negatively impacts fit. Temporal windowing improves both.

Analysis Of GEE Parameter Estimates
Empirical Standard Error Estimates
	Overall Regression (after prescription)			Classification of exposure		Upper Time Limit (90 Days)		Fully Windowed (7–90 days)		Windowed Unclassified
Parameter		Estimate	p-value	Estimate	p-value	Estimate	p-value	Estimate	p-value	Estimate	p-value
Intercept		83.5748	<.000l	83.4507	<.0001	82.0536	<.0001	84.2715	<.0001	84.2508	<.0001
Days From Presc.		−0.0002	0.3078	−0.0000	0.9004	0.0048	0.0038	0.0104	<.0001	0.0111	<.0001
Age		−0.0945	<.0001	−0.0878	<.0001	−0.0729	<.0001	−0.1008	<.0001	−0.1017	<.0001
Sex	M	14.5919	<.0001	14.4329	<.0001	14.7893	<.0001	14.1036	<.0001	14.1146	<.0001
Sex (Ref.)	F
Exposure (mg)		−0.0001	0.8211							−0.0010	0.0645
Exposure (Classified)	Hi			−0.5607	0.3890	−1.4034	0.0266	−1.6381	0.0616
Exposure (Ref.)	Lo
Days*Exposure(mg)		−0.0000	0.6170							0.0000	0.0261
Days*Exposure(Class)	Hi			−0.0003	0.2370	0.0158	<.0001	0.0156	0.0055
Days*Exposure(Ref.)	Lo
QIC Value		53904.1566		79020.4751		15669.6750		7335.3435		7335.9024

We explored the impact of exposure variable categorization, temporal windowing and boundary setting on reaching statistical significance and the goodness of fit of each model (Table 1). Running an overall regression, without categorization or specified time boundaries (i.e., all data after prescription) yielded no statistical significance for time (p=0.308), exposure (p=0.821) or the interaction between these two variables (p=0.617). The model also showed a very high QIC=53,904 indicating a very poor fit of the model to the data. Stratification of the exposure variable reduced p-values for exposure (p=0.389) and the time-exposure interaction term (p=0.237) but did not reach statistical significance. P-value for time dramatically increased to 0.9; fit also worsened (QIC=79,020). Setting an upper temporal boundary at 90 days from first prescription brought all variables beyond the significance threshold (time: p<0.0001, exposure: p=0.0266, interaction: p<0.0001), dramatically improving the fit (QIC=15,669). The final coefficient estimate value for time was 0.0104, which reveals a positive correlation between time and weight increase in patients prescribed with prednisone. Setting a delayed lower time limit where the data considered for the regression started at 7 days after the first prescription dramatically increased the goodness of fit (QIC=7335), preserving statistical significance for all variables but classified exposure (p=0.0645). A continuous exposure variable under the same assumptions showed significance for all variables but exposure (p=0.645) with a similar fit (QIC=7,336). Interestingly, the interaction between time and exposure was still significant with this continuous variable (p=0.0261).

Continuous signal visualization analysis

Exploring our CDW dataset visually was challenging. At first, weight vs. time graphs did not reveal any clearly visible slopes. We averaged at each time point to reduce high-frequency noise, yet again saw no clear signal. We calculated weight change from measurement at the time of prednisone prescription and found a significant upward trend (p=0.012). We plotted percentage change to take patient’s pre-prescription weight into account and stratified by prednisone exposure (high/low), filtering out patients with unknown dosages (and thus unknown exposure).

The raw visualization showed a downward trend when the considered data spanned over several years (Fig. 1); stratifying this graph by exposures (high-low) also yielded downward trends for both groups. Thus, this set of assumptions would lead us to conclude that prednisone led to weight loss. Setting up an upper limit to 90 days after the first prescription reversed this phenomenon (Fig. 1), revealing a slope of 0.00012%/day increase (p=0.0004). Stratifying by exposure, we found significant positive slopes for both groups (Fig 2). For high exposure, we found a slope of 0.000388%/day (p<0.0001) and low exposure revealed a slope of 0.000175%/day (p=0.0001).

Figure 1.

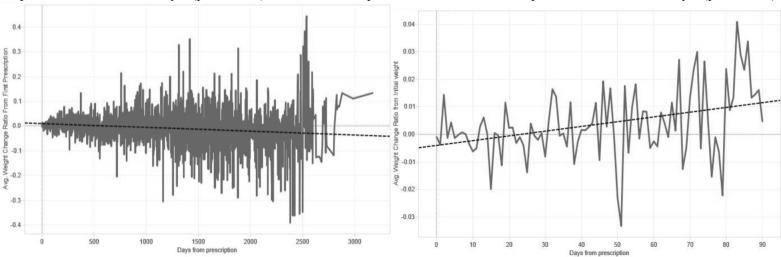
The absence of windowing may mask relationships. Adding temporal window constraints impacts visualization of the effect of drug in weight over time. Left: All weight data available after prednisone prescription is shown. The data shows a downward trend, which is contrary to the expected outcome. Right: When the data are windowed within the first 90 days after prescription, a clear upward trend is detectable.

Figure 2.

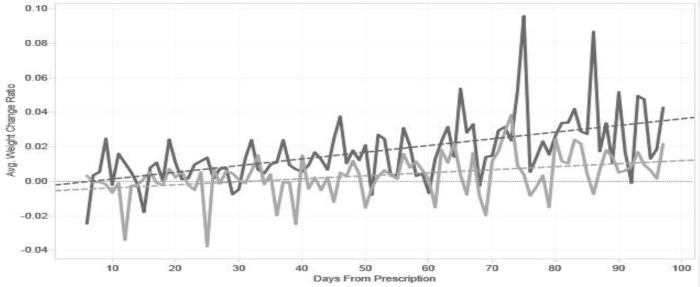
Continuous signal visualization of CDW data after cleaning and categorization by prednisone dose levels. High dose group is represented in dark gray. Low dose group is represented in light gray.

Accounting for baseline weight-gain trends

The aspirin dataset contained 22,757 patients with 208,954 weight observations (mean±SD=84.2±25kg) after filtering (weight>400kg). The ACE-Inhibitor dataset contained 24,880 patients with 395,897 weight observations (mean±SD=86.7±27kg). Visualizing weight change patterns for Aspirin and ACE inhibitors, we found regression slopes of 0.0000481%/day (p=0.0003) and −0.0000156%/day (p>0.05) respectively for patient timelines aligned on the first prescription using the same assumptions as in the prednisone study (i.e., window=days 7–90). These values reveal that the average percent weight gain in patients taking prednisone is over an order of magnitude larger than in patients taking aspirin. Though not statistically significant, we found a negative trend for ACE-inhibitors. Thus, prednisone was associated with greater weight gain than aspirin or ACE-inhibitors.

Discussion

We employed statistical and visualization methods to explore the impact of different analytical assumptions on our ability to rediscover a known drug side effect within a large clinical data set. We found that in statistical analysis as well as visualization of EHR-extracted continuous side effect data (i.e., weight gain), analytical assumptions such as the choice of temporal window and variable categorization can change conclusions (Table 2). Assumptions affected variable significance, estimate values and goodness of fit in statistical regressions as well as slopes and p-values of regression lines in continuous visualizations. Although we were able to demonstrate that prednisone was associated with weight gain, we had to leverage significant domain knowledge and make multiple assumptions.

Table 2.

Weight gain findings by method and assumption. Analytical assumptions impacted the finding of weight gain in the data, independent of the method. Temporal constraints had a greater impact than classification.

	Weight Change Found by method
Test Conditions (Assumptions)	Statistical analysis	Continuous signal visualization
Full Dataset (All data after prescription)	➘	➘
Full Dataset with Classified Exposure	–	➘
Upper Time Limit (0–90 Days)	➚	➚
Fully Windowed (7–90 Days)	➚	➚
Windowed and Unclassified	➚	➚

We also found that assumptions impacted the significance of interaction terms. Failure to include interaction terms in a model can lead to misleading results (16). Thus, interactions should also be considered while exploring assumptions. For a similar reason, we included age and sex in all models to control for potential confounding effects.

Our study has several limitations. We chose the assumptions to review (temporal windowing and variable categorization) and ignored multiple other potentially important assumptions such as the choice of variables to include. For example, the reason why prednisone was prescribed might be a significant factor (e.g., asthma vs. rheumatoid arthritis). Also, considering concurrent clinical events such as other clinical conditions, drugs taken or surgical procedures, would be useful to validate the hypothesis. Indeed, there are a very large number of variables that could be included in our model some of which may be difficult to accurately assess (e.g., compliance with medications). Although these issues are clearly important, our goal was to assess the impact of analytic assumptions rather than to build an optimal model or to discover new biology. Similarly, the analytic methods selected were also not comprehensive. We chose two examples of common approaches to data exploration: statistical testing and analytical data visualization (17).

Many studies have explored issues related to EHR data quality and bias (2,9,10,18). These are important issues. Clinical data reflect workflow, convention and multiple other confounders in addition to biology (6,7,18). Also, the assumptions required to convert data from its native state to an analyzable form, can change the outcome. Exploring all possible assumptions and their combinations is impractical. However, it is important to assess the robustness of the conclusions drawn from analyses of clinical data. This can involve evaluation of the sensitivity of the findings to alternative analytic approaches, replication of the findings across data sets and institutions, looking for “dose-response” effects (i.e., higher dose associated with greater effect) and other approaches (17,19).

Though it may be possible to make reasonable assumptions based on clinical knowledge, the true power of data reuse lies in finding new meaningful and actionable information while keeping assumptions to a minimum (1,4). Our findings suggest caution regarding the ability of automated “Big Data” approaches to find previously unrecognized side effects. In the case of prednisone and weight gain, we had to rely on knowledge regarding the side effect (i.e., that patients will gain weight 7–90 days after starting prednisone) to identify the side effect. Hripcsak et al. (20) describe a method to deal with temporal data with minimal assumptions. Their approach allows automated exploration of assumptions, while the user sets the boundaries of exploration. Such tools may help reduce the sensitivity of analyses to assumptions. That being said, assumptions will always have to be made and it is crucial to communicate reasonable alternatives and their impact on the outcome of an analysis.

Conclusion

The conclusions drawn from analyses of large clinical data sets depend on the choices (i.e., assumptions) made by the analyst. It is difficult to identify known side drug side effects without leveraging what we know about the side effect (e.g., timing relative to exposure). Therefore, surveillance for novel side effects using large clinical data sets is challenging. To increase the reliability and reproducibility of findings derived from the analysis of large clinical datasets, researchers must determine whether their findings are robust under an appropriate range of assumptions.