Abstract
Continuous phylogeography is a growing approach to studying the spatiotemporal origins of RNA viruses because of its realistic spatial reconstruction advantages over discrete phylogeography. While the generalized linear model has been demonstrated as an effective tool for simultaneously assessing the drivers impacting viral diffusion in discrete phylogeography, there is no similar testing method in the continuous phylogeographic framework. In this paper, we take a step toward bridging that gap by conceptualizing a novel quasi-continuous approach which enables the addition of discrete locations beyond the known sampling locations of the virus. Our model, when fully developed into phylogeographic software, will enable spatiotemporal hypothesis testing of viral diffusion without being strictly limited to observed sampling locations. This model can still assess the impact of local epidemiological variables on virus spread and could provide public health agencies with more realistic estimates of key predictors and locations by utilizing a more continuous landscape.
Introduction
Understanding the spread of disease is one of the most fundamental principles of an effective public health system. This includes the ability to track the spread of disease from location to location while keeping a timescale with respect to the emergence and divergence of viral strains. Phylogeography is an emerging field that has potential for improving public health surveillance. In particular, virus phylogeography considers molecular evolution over geography and has been used to study viral epidemics and pandemics related to influenza1, West Nile Virus2, and rabies3 among others.
The spatial diffusion approach to phylogeography has two main underlying methods: discrete4 and continuous3, 5 models. While both are used to estimate virus spread, there are major differences. In discrete phylogeography, ancestral state reconstruction is estimated over observed locations. For example, if viruses are collected in states A, B, C, and D, the model will only consider these when estimating spread. Conversely, in a continuous model spread can be estimated over any sampled or unsampled location, thus alleviating this constraint. In this sense, each ancestral node in a continuous model can have a unique latitude and longitude while the discrete model limits the ancestral nodes to be drawn from the originally defined discrete sites.
In epidemiology, understanding the local variables that play a role in the overall diffusion process of the disease is as vital as the genetic and geographic mechanisms by which they evolve and spread. The rapid development and mutation of viruses, especially those that are RNA-based, makes them especially challenging to fully comprehend. Zoonotic RNA viruses are particularly concerning due to their elevated transmissibility6, 7 across multiple host species. Aside from the genetic principles alone, there are a variety of variables that have been shown to be risk factors for zoonotic diffusion such as longitude, temperature, and humidity8, elevation9, livestock10, 11 and human population densities11. Recent work in the discrete setting has focused on spatiotemporal hypothesis testing for identifying significant predictors of virus spread. For example, work by Lemey et al.12 demonstrated the use of a generalized linear model (GLM) to identify predictors that contributed to the global spread of H3N2 influenza. The group used a log-linear GLM13 within a Bayesian framework as seen in (1), below, to reconstruct virus history while simultaneously assessing local predictor variables including passenger flux, population size and density, and latitude.
| (1) |
To evaluate this, data for each predictor variable p was obtained for each discretized location, which can be a state, county, country, or other geographic boundary. A common approach is to utilize the centroid coordinates at each location and gather all predictor data from that point, creating uniformity in the model, and these data are used for hypothesis testing. This group included a binary indicator, δ, to govern the inclusion or exclusion of each given predictor. The specified predictors can be tested for support in the model by a formal Bayes factor test14 as seen in (2).
| (2) |
Here, p is the posterior probability obtained via BEAST15 for a predictor and q is the prior probability. In this work, the group specified q in which there was a 50% likelihood of no predictor being included in the model. Unsurprisingly, but yet an affirmation of the concept, was the revelation that air travel networks accounted for the most contribution to the diffusion model while other local predictors such as latitude were identified as significant contributors. This demonstrated the usefulness of a GLM while also analyzing the evolutionary history of the virus in a discrete phylogeographic framework and Magee et al.16 utilized this approach in studying H5N1 in Egypt.
While the GLM has been used successfully in the discrete setting, there are limitations to its implementation for continuous phylogeography. In discrete Bayesian phylogeography, each branch in a phylogeny is suggested to be an independent continuous-time Markov Chain (CTMC)4 which emit discrete outcomes over a function of continuous time. For K discrete sites in the phylogeny there exists an infinitesimal rate matrix to characterize the CTMC having the distinct property of being stochastic upon exponentiation of the matrix. An eigen decomposition of this matrix can yield the transition probabilities of the rates in finite-time. Continuous phylogeography does not have a defined number of sites, so the K × K matrix does not exist and the GLM principles fail. Instead there is a rate scalar ϕb for each branch b of the phylogeny, and the overall precision matrix P is scaled to this ϕb. The precision matrix P has two parameters for bivariate diffusion, p1 and p2, and also a variable r. Here p1 and p2, represent the precision in each spatial dimension, respectively, while r is the correlation coefficient between them. This forms a relaxed random walk model which overcomes a restrictive Brownian diffusion process where each branch in a phylogeny has the same evolutionary rate3.
A Brownian diffusion model in phylogeography requires all branches of the tree to evolve at the same rate. This assumption is unrealistic and constraining in terms of evolution and needed to be outfitted to better demonstrate evolutionary principles. To overcome this limitation Lemey et al.3 introduced a bivariate Brownian random walk into the Bayesian framework that accompanies widely used phylogeographic models. This relaxed random walk enabled the individual branches of the phylogeographic trees to have their own evolutionary rate to more accurately portray the underlying evolutionary principles. Furthermore, this avoided an overparameterization issue in the eigen decomposition that comes with having too many sparse discrete locations while allowing additional geographic locations that the observed discrete states.
In a GLM, the number of parameters is dependent upon the number of predictors rather than the number of discrete locations. This avoids the overparameterization issue exhibited with a large set of sparse discrete locations. The roadblock toward incorporating a GLM in the continuous model is the lack of parameters as rates between locations when dealing with continuous space. To incorporate the predictors for the continuous model, we would need a statistical sample from each potential location’s geographic coordinates, which is clearly not possible over a continuous landscape where any location could serve as the ancestral node’s origin. To address this problem, we propose a novel conceptual model for a quasi-continuous approach to phylogeography.
Proposed Method
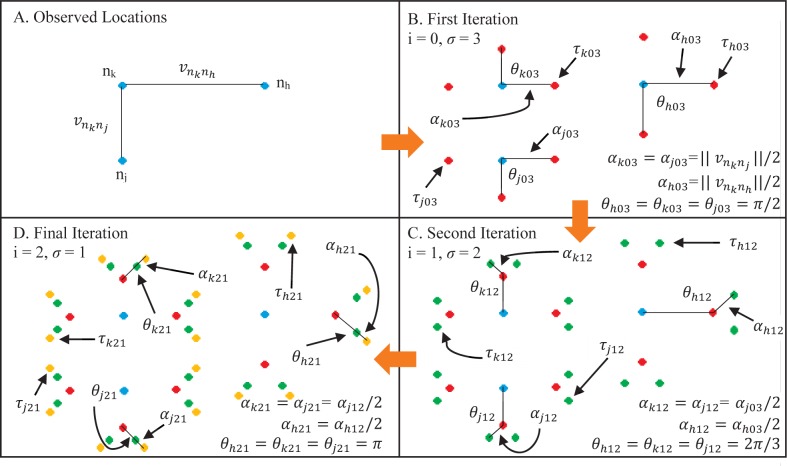
We address the current gap between discrete and continuous phylogeography by introducing a quasi-continuous model in which additional discrete locations are added to the original observed locations of sequences. For the set K of n observed discrete locations where n ϵ ℕ, the user may specify an amount of new nodes, τ, where τ ϵ ℕ including 0, to be added for each nk where nk ϵ K and k ϵ [1, 2, …, n]. Let us define στ = τ, στ − 1 = τ – 1, …, στ − (τ − 1) = 1 to represent the current value of τ as the algorithm proceeds and i = 0 to represent the iteration of the algorithm. That is, i increases in increments of 1 from 0 to τ − 1 while σ decreases in increments of 1 from τ to 1. From each of the first new nodes, τk0τ, there will be στ −1 = τ − 1 new nodes, τ k1(τ − 1). Each τ k1(τ − 1) has στ − 2 = τ − 2 new nodes, and this process continues until τ = 1 when there will be no more new nodes to add. That is, each new node τ kiσ will have στ = τ − (i + 1) new nodes. The τk0τ nodes will be dispersed equally about nk at an angle θk0τ where θk0τ = [ 2π (τ + 1)] radians relative to the vector connecting nk and its nearest neighbor nj where nj ϵ K. The distance of each τk0τ node from nk will be a length αk0τ where αk0τ is half the distance between observed locations nk and nj, that is . The τk1(τ − 1) nodes will be dispersed about τk0τ in a similar manner such that the distance αk1(τ − 1) is half the distance between τk0τ and nk and at an angle θk1(τ−1) where θk1(τ−1) = [ 2π / ((τ + 1) + 1] radians relative to the vector connecting nk and τk0τ.
This dispersal pattern will continue for all i, σ, and nk such that the angle and distance of each node to be added distributed by (3), (4), and (5). Box 1 shows the pseudocode of this algorithm and one example is shown in Figure 1.
| (3) |
| (4) |
| (5) |
Box 1. Pseudocode for algorithm to create new locations for each node nk in the set of original locations K.
| Prompt user to enter τ, the desired number of new locations to be added per observed discrete location nk in K For each observed discrete state nk in K |
| Determine the nearest neighbor nj |
| For σ = τ to σ = 1 |
| Draw σ new nodes, p, from nk at a distance αp from nk where αp = || nk ± nj || / 2 |
| Space each node p at θp = [2π / σ+1)] radians from each other p relative to a vector from nk to nj |
| For m = σ − 1 to m = 1 |
| Draw m new nodes, q, from each node p at a distance αm where αm = αp / 2 |
| Space each node q at θq = (2π / m+1) radians from each other q relative to a vector from p to nk |
| m = m− 1 |
| σ = σ – 1 |
| Move to the next observed discrete state |
Figure 1.
A step-by-step visual representation of the algorithm in Box 1 on a network of K = 3 observed discrete sampling locations with τ = 3. A) The three observed sampling locations (nh, nj, nk) are shown as blue circles and the corresponding shortest vectors are and . B) Each observed location is given σ = 3 nodes (τh03, τj03, τk03) shown as red circles. These nodes are distributed by (3) and (4). C) Each red node is given σ = 2 nodes (τh12, τj12, τk12) shown as green circles, distributed by (3) and (5). D) Each green circle is given σ = 1 node, (τ h21, τj21, τk21) shown as yellow circles, distributed by (3) and (5). At this point there are no new nodes to add and the algorithm exits. There are ϕ(3, 3) = 48 total nodes in the new set by (6) and (7). The distances and angles between nodes are shown by αxyz and θxyz, respectively, where x is the node (h, j, k), y is the ith step in the iteration, and z is the count of σ nodes added during the step. Note that all α and θ values are equal for each node for each step in the algorithm.
In this algorithm, the distance between nodes will quickly decrease at the nodes added during the last several iterations. This will result in a high density of nodes near the outermost locations (high values of i) but the continuous revolution of angles from outer node to outer node and halving of the distance as ensures that the additional nodes will not occur at the same geographic location. It is also important to note that in this method, the total number of locations, ϕ, rapidly increases as τ and K increase. Table 1 demonstrates this trend, which is summarized by (6) and (7).
| (6) |
| (7) |
Table 1.
Numerical summary of the first 10 cases of additional locations, τ, to add to each state k in the original set of discrete locations K. Here ϕ represents the total number of locations given τ and set K.
| Case | τ | ϕ | τ, K = 1 | ϕ | τ K = 2 | ϕ | τ, K = 3 | ϕ | τ, K = 4 | ϕ | τ K = 5 | ϕ | τ K = 6 |
|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 1 | 2 | 4 | 6 | 8 | 10 | 12 |
| 3 | 2 | 5 | 10 | 15 | 20 | 25 | 30 |
| 4 | 3 | 16 | 32 | 48 | 64 | 80 | 96 |
| 5 | 4 | 65 | 130 | 195 | 260 | 325 | 390 |
| 6 | 5 | 326 | 652 | 978 | 1,304 | 1,630 | 1,956 |
| 7 | 6 | 1,957 | 3,914 | 5,871 | 7,828 | 9,785 | 11,742 |
| 8 | 7 | 13,700 | 27,400 | 41,100 | 54,800 | 68,500 | 82,200 |
| 9 | 8 | 109,601 | 219,202 | 328,803 | 438,404 | 548,005 | 657,606 |
| 10 | 9 | 986,410 | 1,972,820 | 2,959,230 | 3,945,640 | 4,932,050 | 5,918,460 |
Here, (7) represents the base case for any (τ, K). This is intuitive, as with just one discrete state and zero additional locations to disperse about nk there remains exactly one node. This base case, with just one discretized location, cannot provide any phylogeographic insight but each observed location nk in K will scale on that base case and τ.
Results
Since this model is conceptual, it has yet to be implemented with phylogeographic software packages or tested for accuracy in Bayesian inference with a real set of discrete sites. Instead we provide a visualization of a specific application of this algorithm (Figure 1) and demonstrate the expansion of the observed sampling locations (Table 1) in our proposed novel quasi-continuous model.
Discussion
Our novel quasi-continuous model allows us to utilize the GLM for spatiotemporal hypothesis testing outside of a traditional Bayesian discrete setting. For each new location, the corresponding coordinate pair can mapped to see which discretized location it would fall in under the GLM. The predictor data for that location can then be that of the defined initial observed locations as seen in Lemey et al.12 and Magee et al.16 and be tested for Bayes factor support via (2). As previously mentioned, it is likely that as we reach the nodes for the smaller values of σ they will all fall in the same discretized location defined by the model because of their decreasing separation; however this will not be constraining for studies across a wider area where discretized locations are whole countries or global regions. With the increased locations that we have introduced in this quasi-continuous model, we will also be able to eliminate poorly reconstructed trees from consideration if an ancestral node lies in an unlikely geographic location such as an ocean, mountain range, or uninhabited desert. This increases the reliability of inferred ancestral states produced in phylogeographic software packages such as BEAST.
Incorporating landscape heterogeneity into a phylogeographic framework would undoubtedly yield dividends in accuracy, confidence, and reliability among inferred results. This challenging task is aided by publically available software and services such as Google Earth that can provide detailed information on global terrain. Although this integration has yet to be achieved, the impact on public health would be immediate as it would provide insight on the true origins of viral diffusion. It will also allow a more focused analysis on the local predictors associated with the dispersal of these viruses which could help identify the most plausible disease drivers via the GLM. Furthermore, data on climate, agriculture, livestock, and population demographics are becoming increasingly available via sources such as the National Oceanic and Atmospheric Administration and Food and Agricultural Organization of the United Nations. Reliable data sources such as these can provide the necessary inputs for the GLMs and the ability of the GLM to identify drivers of viral diffusion increases as the number of predictor variables increases.
There are limitations with this model, including the lack of hypothesis testing on actual data that would demonstrate how our model can be visualized, analyzed, and interpreted. In addition, the model will be computationally intensive for larger sets of observed locations and larger values of τ. The eigen decomposition of the rate matrix between the increased number of locations may cause problems with these software packages. For a large number of discrete, sparse locations a continuous model is generally the better option, but due diligence should be performed to analyze the performance of this conceptual model in our quest for the incorporation of the GLM into continuous space.
Although this quasi-continuous model does not quite complete the desired task of integrating a GLM within a continuous Bayesian phylogeographic model but does improve upon the established discrete GLM by including more nodes at the request of the end user. Future work will include incorporating these concepts into the BEAST framework such that they become accessible to users, allowing a specific value of τ for each observed sampling location, and eliminating added nodes from consideration prior to hypothesis testing if they fall in an unlikely location. In addition, we will be able to statistically analyze the effect of τ on the model and identify an optimal value for computer performance and Bayesian inference. Once completed, we will have the capability to test this model, identify flaws, and strengthen the algorithm to expand and improve the field of phylogeography.
Acknowledgments
The project described was supported by award number R00LM009825 from the National Library of Medicine to Matthew Scotch. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Library of Medicine, the National Institutes of Health. The authors would like to thank Philippe Lemey, Ph.D., for his suggestions regarding a GLM approach for a large number of observed sampling locations.
References
- 1.Scotch M, Mei C, Makonnen Y, et al. Phylogeography of influenza a H5N1 clade 2.2.1.1 in Egypt. BMC Genomics. 2013;14(1):871. doi: 10.1186/1471-2164-14-871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.May FJ, Davis CT, Tesh RB, Barrett ADT. Phylogeography of West Nile Virus: from the Cradle of Evolution in Africa to Eurasia, Australia, and the Americas. Journal of Virology. 2011. 2011 Mar 15;85(6):2964–74. doi: 10.1128/JVI.01963-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lemey P, Rambaut A, Welch JJ, Suchard MA. Phylogeography Takes a Relaxed Random Walk in Continuous Space and Time. Molecular Biology and Evolution. 2010. 2010 Aug 1;27(8):1877–85. doi: 10.1093/molbev/msq067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lemey P, Rambaut A, Drummond AJ, Suchard MA. Bayesian Phylogeography Finds Its Roots. PLoS Comput Biol. 2009;5(9):e1000520. doi: 10.1371/journal.pcbi.1000520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lemmon AR, Lemmon EM. A Likelihood Framework for Estimating Phylogeographic History on a Continuous Landscape. Systematic Biology. 2008. 2008 Aug 1;57(4):544–61. doi: 10.1080/10635150802304761. [DOI] [PubMed] [Google Scholar]
- 6.Krauss H. Zoonoses: Infectious Diseases Transmissible from Animals to Humans: ASM Press; 2003. [Google Scholar]
- 7.Chen Y, Liu T, Cai L, Du H, Li M. A One-Step RT-PCR Array for Detection and Differentiation of Zoonotic Influenza Viruses H5N1, H9N2, and H1N1. Journal of Clinical Laboratory Analysis. 2013;27(6):450–60. doi: 10.1002/jcla.21627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.He D, Dushoff J, Eftimie R, Earn DJD. Patterns of spread of influenza A in Canada. Proceedings of the Royal Society B: Biological Sciences. 2013 2013 Nov 7;280(1770) doi: 10.1098/rspb.2013.1174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Loth L, Gilbert M, Wu J, Czarnecki C, Hidayat M, Xiao X. Identifying risk factors of highly pathogenic avian influenza (H5N1 subtype) in Indonesia. Preventive Veterinary Medicine. 2011 Oct 1;102(1):50–8. doi: 10.1016/j.prevetmed.2011.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Pfeiffer DU, Minh PQ, Martin V, Epprecht M, Otte MJ. An analysis of the spatial and temporal patterns of highly pathogenic avian influenza occurrence in Vietnam using national surveillance data. The Veterinary Journal. 2007 Sep;174(2):302–9. doi: 10.1016/j.tvjl.2007.05.010. [DOI] [PubMed] [Google Scholar]
- 11.Gilbert M, Xiao X, Pfeiffer DU, et al. Mapping H5N1 highly pathogenic avian influenza risk in Southeast Asia. Proceedings of the National Academy of Sciences. 2008. 2008 Mar 25;105(12):4769–74. doi: 10.1073/pnas.0710581105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lemey P, Rambaut A, Bedford T, et al. The seasonal flight of influenza: a unified framework for spatiotemporal hypothesis testing. 2012;arXiv(12105877v1) [Google Scholar]
- 13.McCullagh P. Generalized linear models. European Journal of Operational Research. 1984 Jun;16(3):285–92. [Google Scholar]
- 14.Suchard MA, Weiss RE, Sinsheimer JS. Models for Estimating Bayes Factors with Applications to Phylogeny and Tests of Monophyly. Biometrics. 2005;61(3):665–73. doi: 10.1111/j.1541-0420.2005.00352.x. [DOI] [PubMed] [Google Scholar]
- 15.Drummond AJ, Suchard MA, Xie D, Rambaut A. Bayesian phylogenetics with BEAUti and the BEAST 1.7. Mol Biol Evol. 2012 Aug;29(8):1969–73. doi: 10.1093/molbev/mss075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Magee D, Beard R, Suchard MA, Lemey P, Scotch M. Combining phylogeography and spatial epidemiology to uncover predictors of H5N1 influenza A virus diffusion. Archives of Virology. 2014 Oct 30; doi: 10.1007/s00705-014-2262-5. [DOI] [PMC free article] [PubMed] [Google Scholar]