Cumulative Time Series Representation for Code Blue prediction in the Intensive Care Unit.

Abstract

Patient monitors in hospitals generate a high number of false alarms that compromise patients care and burden clinicians. In our previous work, an attempt to alleviate this problem by finding combinations of monitor alarms and laboratory test that were predictive of code blue events, called SuperAlarms. Our current work consists of developing a novel time series representation that accounts for both cumulative effects and temporality was developed, and it is applied to code blue prediction in the intensive care unit (ICU). The health status of patients is represented both by a term frequency approach, TF, often used in natural language processing; and by our novel cumulative approach. We call this representation “weighted accumulated occurrence representation”, or WAOR. These two representations are fed into a L1 regularized logistic regression classifier, and are used to predict code blue events. Our performance was assessed online in an independent set. We report the sensitivity of our algorithm at different time windows prior to the code blue event, as well as the work-up to detect ratio and the proportion of false code blue detections divided by the number of false monitor alarms. We obtained a better performance with our cumulative representation, retaining a sensitivity close to our previous work while improving the other metrics.

1. Background

Modern technology enables us to access in real-time the patient’s medical history, as well as a continuous stream of physiological measurements, often paired with alarms generated by the devices capturing these signals. All these developments brought unintended consequences, namely, an excess of data. Clinicians are often overwhelmed by all the continuously streaming information. False alarm rates of 88.8% have been reported [1], which have led to alarm fatigue; a growing problem that decreases the quality of care of the patient. Numerous efforts have been made in order to take a more integral approach for real-time patient assessment [2–6].

In [7], Hu et al introduced a data-driven approach, which consists in finding meaningful combinations of monitor alarms that are present in code blue patients but not in control patients. These patterns were called SuperAlarms. In [8], this work was expanded to include laboratory test results, and a different approach to find these combinations, resulting in less redundant patterns. A sensitivity of 93% was achieved in the independent dataset, where we say a code blue is predicted if at least one SuperAlarm is triggered in a given time window.

We propose to generate a time series that encodes the cumulative effects of each SuperAlarm, dependent on time elapsed between the current time and the previous time each SuperAlarm patterns were triggered. This novel representation encodes both frequency and proximity in time, and could be easily used in any application concerned with time series classification. We compare this representation to a term frequency representation (TF), a commonly used technique in natural language processing (NLP).

2. Methods

2.1 SuperAlarm patterns

The extraction of our SuperAlarm patterns is described in [7,8] SuperAlarm patterns are combinations of frequently co-occurring monitor alarms and laboratory test results that were capable of predicting code blue events in hospitalized patients. The SuperAlarm patterns were discovered using a maximal frequent itemsets mining algorithm (MAFIA). The dataset used to extract the SuperAlarm patterns was extracted from a central repository of comprehensive data elements archived for patients hospitalized at the UCLA Ronald Regan Medical Center, admitted from March 2010 to June 2012. The patients included in this study came from either ICUs or other acute care areas, see [8]. The control set was determined as patients without code blues or unplanned ICU transfers. For each code blue patient, a cohort of control patients was selected following certain criteria [8]. A total of 1766 control patients and 176 code blue patients were included in the training set, and 440 control and 30 code blue patients in the test set.

2.2 Representation of the time series

Let there be m different SuperAlarm patterns. We propose representing each patient, at a given time t, via an m-dimensional vector p(t). Hence, each patient is represented by a multidimensional time series {p(t)}.

One possibility for extracting this vector p(t) is given by a term frequency (TF) approach, which consists on pre-defining a window of a specific length L, and, given a time t, and building the frequency vector:

$$p_{TF}(t,L)=\left(\begin{array}{c}\#\text{of times SuperAlarm 1 is triggered is time interval [t}-\text{L,t]}\\ ⋮\\ \#\text{of times SuperAlarm}m\text{is triggered is time interval [t}-\text{L,t]}\end{array}\right).$$

We used three values for L in our study: L = 2 hrs, 4 hrs and 6 hrs. We refer to their corresponding representations p_TF(t, L) as TF₂, TF₄ and TF₆; respectively. However, this approach has a few drawbacks. First, a fixed window of time may arbitrarily remove the influence of a SuperAlarm in the future. Also, the importance of a SuperAlarm trigger should depend on how close to the current time t it was triggered. We propose a continuous, cumulative representation of the lingering effect a Super Alarm trigger should have. We call our approach “weighted accumulated occurrence representation”, or WAOR. In this representation, the i-th entry will describe the cumulative value, up to time t, of the i-th SuperAlarm:

$$p_{WAOR}(t,w)=\left(\begin{array}{c}{y}_1(t)\\ ⋮\\ y_m(t)\end{array}\right)=\left(\begin{array}{c}{\displaystyle {\sum }_{t^{\prime }\le t}{w}_1(|t-t^{\prime }|){\chi }_1(t^{\prime })}\\ ⋮\\ {\displaystyle {\sum }_{t^{\prime }\le t}{w}_m(|t-t^{\prime }|){\chi }_m(t^{\prime })}\end{array}\right),$$

where the indicator function χ_i(t′) is defined as 1 if the i-th SuperAlarm is triggered at time t’, and 0 otherwise. Also, w_i(|t − t′|) is a decreasing function of |t − t′|, the difference between the current time t and the time the i-th SuperAlarm was triggered, t'. This is because, if a SuperAlarm is triggered, we want it to influence the i-th entry of p(t) for minutes, or hours. The three functions w we used are given by $w\left(|t-t^{\prime }|\right)=\frac{1}{\sqrt{|t-t^{\prime }|}+1}$, $w(|t-t^{\prime }|)=\frac{1}{|t-t^{\prime }|+1}$ and $w(|t-t^{\prime }|)=\frac{1}{{|t-t^{\prime }|}^2+1}$, and their corresponding representations p_cont(t, w) are referred to as WAOR_sqrt, WAOR_abs and WAOR_sq, respectively, throughout the text.

2.2.1 Sampling the patients in the training set

From here onward we drop the subindex “TF” or “WAOR” indicating the time series representation in this text. The following analysis was carried out for all six representations described in the previous section. For every patient, we chose a sequence p(t) = {p(t₁), p(t₂), _…, p(t_N)|t_i ∈T_SA}, where T_SA = {t_i such that a SuperAlarm was triggered at time t_i}. Since we had far more controls than cases, we handled the class imbalance by oversampling the cases. For control patients, no particular time carries more importance. Hence, up to three time points t_i for each control patient were sampled uniformly from T_SA, with a total of 4,126 samples. For a case patient, time points closer to a code blue event should be preferred, since they give us vectors p(t) that carry more descriptive power for a code blue event. The number of time points t_i sampled depended on their closeness to the code blue event − points close to the event had a higher probability of being sampled, and up to 60 timepoints were sampled for each case patient. The training set consists of 6,880 observations. The training dataset was scaled to the range [0,1].

2.2.2 Sampling the patients in the test set

Both control and code blue patients in the test set will be sampled every time a SuperAlarm was triggered. We obtained a total of 60,604 code blue and 239,665 control vectors. The transform that achieved the [0,1] scaling in the training set was applied to the test set as well.

2.3 Classification

Feature selection was achieved by applying a L1 regularized logistic regression (L1-LR) model to the entire training set. In L1-LR, the probability of a sample x being labeled as a code blue (y=1) is given by p(y = 1|x; θ) = σ(θ^Tx), where x is, in our case, the vector p(t) with the information about the patient, and σ is a sigmoid function, and θ is a vector of weights to be learned by the classification algorithm, given by the solution to:

$$\underset{\theta }{\min }{\displaystyle \sum _{i=1}^M-\log p(y^{(i)}|x^{(i)};\theta )}subjectto{\Vert \theta \Vert }_1\le C$$

All vectors extracted from a code blue patient will be labeled as y = 1, and all of those extracted from control patients as y = 0. Linear models penalized with the L1 norm have sparse solutions: many of their estimated coefficients are zero. The features retained are those that were assigned non-zero coefficients.

Afterwards, L1-LR classification was used. The hyper parameter C, as well as the class weights, were chosen via a grid search and 10-fold cross validation on the training set. The value C chosen is so that it maximizes the mean of a given performance metric across all the folds in cross validation in the training set. However, different performance metrics produce different results in the hyper-parameters of the classifiers. We performed our analysis with two performance metrics: Precision, given by TP / (TP + FP) where TP = true positive, FP = False positive; and f1 score, given by f1 = 2 TP / (2TP + FP + FN), where FN = False negative.

3. Results

Both control and code blue patients in the test set will be sampled every time a SuperAlarm is triggered, producing a sequence p(t) = {p(t₁), p(t₂), _…, p(t_N)|t_i ∈ T_SA}. Afterwards, the classifier trained in the training stage will convert this sequence into a sequence of decisions, {y₁, y₂, _…, y_N}, where y = 0 or y = 1, with y = 0 corresponding to the classifier labeling the observation as “control”, and y = 1 to the classifier labeling the observation as “code blue”.

We present the following performance metrics; all have significance in a clinical setting and are defined in [7]:

• SensitivityL@(T): The proportion of code blue patients to have at least one y = 1 in the time window [T hours before the code blue − 12 hours, T hours before code blue event].

• Work-up to detection ratio: Defined as WTDR = (a + b)/a, where a is the number of code blue patients that our algorithm labeled correctly as “code blue”, and b is the number of control patients that our algorithm labeled incorrectly as “code blue”.

• Alarm frequency reduction rate: Defined as AFRR=1 − FSAR, where FSAR, or False SuperAlarm ratio, is computed in the control population. It is given by the mean and standard deviation (std) of number of SuperAlarm triggers in one hour divided by number of monitor alarms in that hour, computed throughout the patient’s stay.

In computing the WTDR we specified windows of 12 hours, corresponding to a usual nursing shift. We say our algorithm labeled a “code blue” patient as true if at least one y is equal to 1, from the time of the code blue up to 12 hours before the code blue. To determine if our algorithm labeled a control patient as a “code blue”, we randomly select 100 windows of 12 hours throughout the patient’s stay. For each window, if there was at least one y = 1 in each time window, the patient was labeled as a “code blue”. We obtained the mean and std of times each control patient is labeled as a “code blue”, and combined them all to report the mean and std of b. We show results for the test set when optimizing two metrics in cross validation: Precision (Table 1) and f1 score (Table 2).

Table 1.

Results of online classification using precision score as the performance metric for cross validation during training.

SuperAlarm type	Sensitivity@L(t) (%)					AFRR (mean ± std)	WTDR (mean ± std)
	30 min	1 hr	2 hrs	6 hrs	12 hrs		12 hrs
TF2	20.0%	20.0%	20.0%	16.6%	13.3%	99.3 ± 4.8	1.9 ± 0.3
TF4	23.3%	23.3%	23.3%	20.0%	16.6%	99.1 ± 5.1	1.83 ± 0.26
TF6	26.6%	26.6%	26.6%	20.0%	23.3%	99.2 ± 4.9	1.53± 0.21
WAORsq	36.6%	36.6%	36.6%	33.3%	26.6%	99.1 ± 7.1	1.47 ± 0.18
WAORabs	40.0%	40.0%	40.0%	30.0%	30.0%	98.3 ± 9.5	1.98 ± 0.16
WAORsqrt	40.0%	40.0%	36.6%	30.0%	26.6%	97.7 ± 10.7	2.6 ± 0.18

Table 2.

Results of online classification using f1 score as the performance metric for cross validation during training.

SuperAlarm type	Sensitivity@L(t) (%)					AFRR (mean± std)	WTDR (mean ± std)
	30 min	1 hr	2 hrs	6 hrs	12 hrs		12 hrs
TF2	46.6%	46.6%	46.6%	43.3%	40.0%	96.7 ± 11.6	2.90 ± 0.25
TF4	43.3%	43.3%	43.3%	43.3%	43.3%	97.1 ± 10.8	2.65 ± 0.29
TF6	43.3%	43.3%	43.3%	33.3%	33.3%	97.2 ± 10.4	2.71 ± 0.32
WAORsq	90.0%	90.0%	90.0%	86.6%	70.0%	88.5 ± 21.4	4.75 ± 0.14
WAORabs	50.0%	50.0%	50.0%	43.3%	36.6%	95.7 ± 13.0	3.56 ± 0.22
WAORsqrt	46.6%	46.6%	43.3%	36.6%	33.3%	96.6 ± 11.9	3.04 ± 0.26

4. Discussion

We introduced a novel time series representation of our previously developed SuperAlarm patterns that reduces false positives while retaining the sensitivity of code blue prediction in our dataset. Our WAOR time series representation carries advantages over a TF approach: temporality is included, and events happening closer to the current time carry more weight. Off-the-shelf techniques used in NLP that express a document of words as a vector just based on their frequencies may not be suitable for the problem of monitoring patients in time, as they do not leverage the temporal nature of the data. Our WAOR representation can be applied to any other timeseries datasets for event prediction. There are other existing methods to detect patient deterioration [2–6]. We did not compare their performance with the proposal algorithm in this study. This is partly due to the fact that none of these existing methods for patient deterioration detection uses alarm data and our current data set does not contain vital signs that are frequently used in some of the existing methods. We acknowledge that a direct comparison between our algorithm and the existing methods. However, we argue that the appropriate performance metrics such as sensitivity and work-up to detection ratio that are reported in this study can be readily communicated to clinical users.

In our application, we have far more control patients than code blue patients. We balanced the training dataset by oversampling the code blue patients, drawing more samples as the patient approached the code blue event. Moreover, we optimized the class weights during cross validation. Better results in the test set were obtained after optimizing the class weights. Even though a priori we assume all SuperAlarm patterns carry equal importance, the coefficients found by our classifier assign more importance to more predictive patterns.

Using the f1 score as a performance metric, we see the WAOR_sq approach clearly outperforms the other ones, in terms of SensitivityL@(T) and with a WTDR of 4.75 and a AFRR of 88.5%. Our approach retains a sensitivity compared to that in [7], while reducing both the WTDR and AFRR. When we use the precision as a performance metric, the sensitivity drops significantly for all six approaches. However, the WAOR representations have a higher sensitivity than the TF ones, while keeping comparable WTDR and AFRR. A parameter yet to be exploited in the WAOR representations is the constant term in the denominator added to ensure it will be non-zero. In our application, we set this parameter to be equal to one, however, in future work we will optimize this parameter in cross validation.

Figure 1.

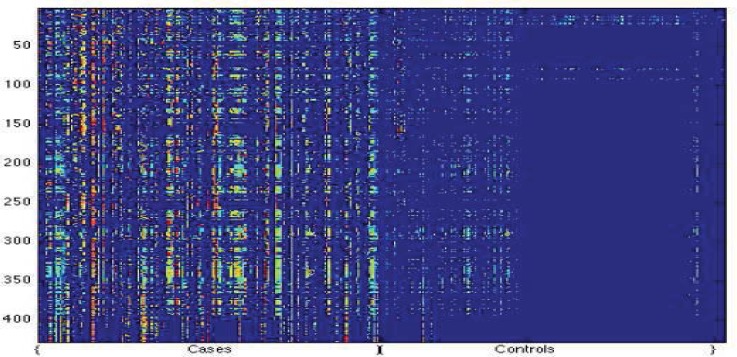
A comparison of code blue cases and control patients. In this image, each column represents one sample p(t), and the i-th row the i-th value of the vector p(t), that is, how represented the i-th SuperAlarm is at the time t, using the representation WAOR_abs.