How the unstable eye sees a stable and moving world

Abstract

Eye motion, even during fixation, results in constant motion of the image of the world on our retinas. Vision scientists have long sought to understand the process by which we perceive the stable parts of the world as unmoving despite this instability and perceive the moving parts with realistic motion. We used an instrument capable of delivering visual stimuli with controlled motion relative to the retina at cone-level precision while capturing the subjects' percepts of stimulus motion with a matching task. We found that the percept of stimulus motion is more complex than conventionally thought. Retinal stimuli that move in a direction that is consistent with eye motion (i.e., opposite eye motion) appear stable even if the magnitude of that motion is amplified. The apparent stabilization diminishes for stimulus motions increasingly inconsistent with eye motion direction. Remarkably, we found that this perceived direction-contingent stabilization occurs separately for each separately moving pattern on the retina rather than for the image as a whole. One consequence is that multiple patterns that move at different rates relative to each other in the visual input are perceived as immobile with respect to each other, thereby disrupting our hyperacute sensitivity to target motion against a frame of reference. This illusion of relative stability has profound implications regarding the underlying visual mechanisms. Functionally, the system compensates retinal slip induced by eye motion without requiring an extremely precise optomotor signal and, at the same time, retains an exquisite sensitivity to an object's true motion in the world.

Introduction

Motion detection is one of the hyperacuities with optimal thresholds measured in arc seconds (McKee, Welch, Taylor, & Bowne, 1990). To achieve such performance, it is necessary that the moving target lie near a stationary reference so that relative, rather than absolute, motion is being judged (Legge & Campbell, 1981; Levi, Klein, & Aitsebaomo, 1984; Murakami, 2004; Tulunay-Keesey & VerHoeve, 1987; Whitaker & MacVeigh, 1990). The presence of the reference is thought to aid in the compensation for retinal image motions due to eye motion (Raghunandan, Frasier, Poonja, Roorda, & Stevenson, 2008).

Our eyes are in constant motion even when we fixate steadily on an object, and the amplitude of the drifts and saccades of fixation are typically several minutes of arc (Krauskopf, Cornsweet, & Riggs, 1960), large enough that the motion should be clearly visible if not for compensation. Images that fall on the retina have motion due to both object motion and eye motion, yet we generally do not perceive the eye motion component.

Past investigations of the compensation for eye motion in our perception of the world have often addressed the effects of saccades, which produce a dramatic sudden shift of the retinal image, on the perceived positions of objects (Bridgeman, Hendry, & Stark, 1975; Deubel, Schneider, & Bridgeman, 1996). Other studies have examined the effect of smooth pursuit on the perceived velocity of objects (Freeman, Champion, & Warren, 2010; Wertheim, 1987). In both paradigms, investigators often address the question of how much of the compensation comes from inflow (retinal image information and/or proprioceptive information from extraocular muscles) and how much comes from outflow (efference copy information generated centrally as part of the eye movement control). For large and fast eye motion, there is good evidence for a primary role for outflow (Bridgeman & Stark, 1991).

In this study, we examine perceptual compensation for the minute drifts of the eye that accompany fixation, which have also been the subject of other recent investigations (Murakami & Cavanagh, 1998; Poletti, Listorti, & Rucci, 2010). Murakami and Cavanagh reported that prior adaptation to jittering motion allows subjects to perceive the retinal image motion produced by fixation. Unresolved in these studies was whether the compensation would suppress all retinal image motions on the scale of the eye motion (Murakami, 2004) or whether it is specific to the ongoing direction and speed of drift. Ideal compensation would consist of a subtraction of the instantaneous velocity of eye motion from all retinal motions, leaving only world motion. This would require a precise eye velocity estimate, whether from analysis of all retinal motions or from an efference copy.

We asked the question: How would subjects perceive stimuli that moved across the retina in different directions and amplitude relationships to actual eye motion? If eye motion is compensated by suppressing all retinal motions smaller than fixation jitter, then stimuli with motion amplitudes consistent with eye motion but direction independent of eye motion should appear steady. On the other hand, if compensation is based on a moment-by-moment estimate of eye motion, then only stimuli having the exact opposite direction of eye motion should appear stable. This might occur whether the eye motion is obtained from an efference copy (Helmholtz, 1924) or from the retinal image motion itself (Poletti et al., 2010; Olveczky, Baccus, & Meister, 2003).

To move stimuli across the retina in different directions and speeds relative to eye motion, we used an adaptive optics scanning laser ophthalmoscope (AOSLO) with real-time retinal tracking and targeted stimulus delivery. In the AOSLO, the tracking errors for drift are less than 1 min of arc (Yang, Arathorn, Tiruveedhula, Vogel, & Roorda, 2010). The methods are described in detail in the Methods section.

For all experiments reported here, subjects reported the perceived motion of stimuli under different retinal motion conditions using a simple matching task (i.e., adjusting the jitter amplitude of a similar target to produce the same overall impression of motion). Subjects always had a world-stationary frame of reference for judging target motion, so the adjustment task was to match the relative motion of target and background. If relative motion is all that matters, then the perceived jitter amplitude should always scale with the amount of relative motion in the AOSLO display regardless of the direction of motion with respect to eye jitter. If absolute retinal image motion is all that matters, then motion in directions that increase retinal motion should be more evident, and motions that decrease retinal motion should appear more stable.

The results came as a surprise, following neither of these patterns. Perceived motion was proportional to neither relative motion nor to retinal motion. Retinally stabilized stimuli appeared to have motion whereas some stimuli with exaggerated motion appeared to be stable. Specifically, stimuli that moved in a direction that was roughly consistent with eye motion (± ∼20°) always appeared to be stable even if the amplitude was larger than the natural slip caused by eye motion. As the direction of stimulus motion diverged from this sector, perceptual stability diminished rapidly, and the percept of motion became rapidly more intense. This perceived stability persisted even in the presence of a world-stable frame of reference. Despite the presence of multiple targets with relative motions that should be above the threshold for detection, subjects reported all as unmoving as long as they were within this range of directions. The dependence on direction is inconsistent with a general suppression of retinal image motion below some criterion speed. The relative insensitivity to retinal slip velocity is inconsistent with subtraction of a single precise eye motion signal.

Methods

Subjects

Subjects were three members of the lab group (two males, one female), including one author. Subjects were aware of the purpose of the study and the manipulations being used, but they were not told what particular manipulations were made for each trial and were not able to deduce them from the appearance of the display. All procedures adhered to the tenets of the Declaration of Helsinki and were approved by the University of California Institutional Review Board. Informed consent was obtained from the subjects after explanation of the nature and possible consequences of the study.

The task

The subject's task was to fixate on a small fixation cross midway between two red fields (see Figure 1) and adjust the amplitude of the motion in the right LCD display to match the overall perception of relative motions in the left AOSLO display (see details below in the section on LCD display for motion matching). Motion in the AOSLO display was always derived from the subject's own fixation eye movements but with various transformations of speed (“gain”) and direction (“angle”) as elaborated in later sections. Within each experimental condition, the gain and angle states were presented in a pseudorandom order, and subjects had no knowledge of which condition was being tested. Subjects were given as much time as they needed to make a motion setting but typically did so in just a few seconds. Individual motion settings were recorded for each trial in each stimulus condition.

Figure 1.

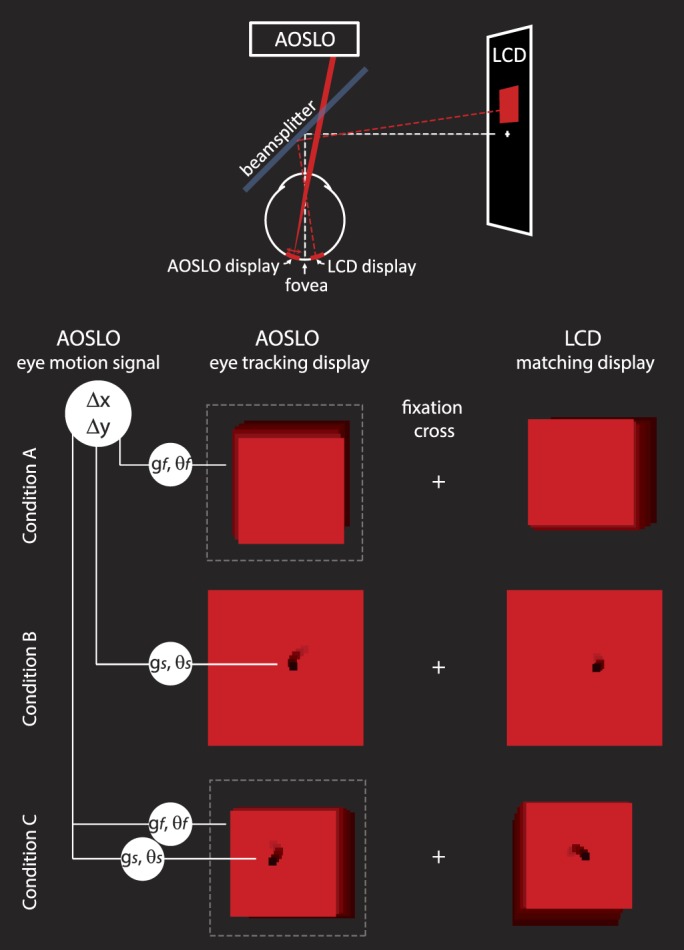
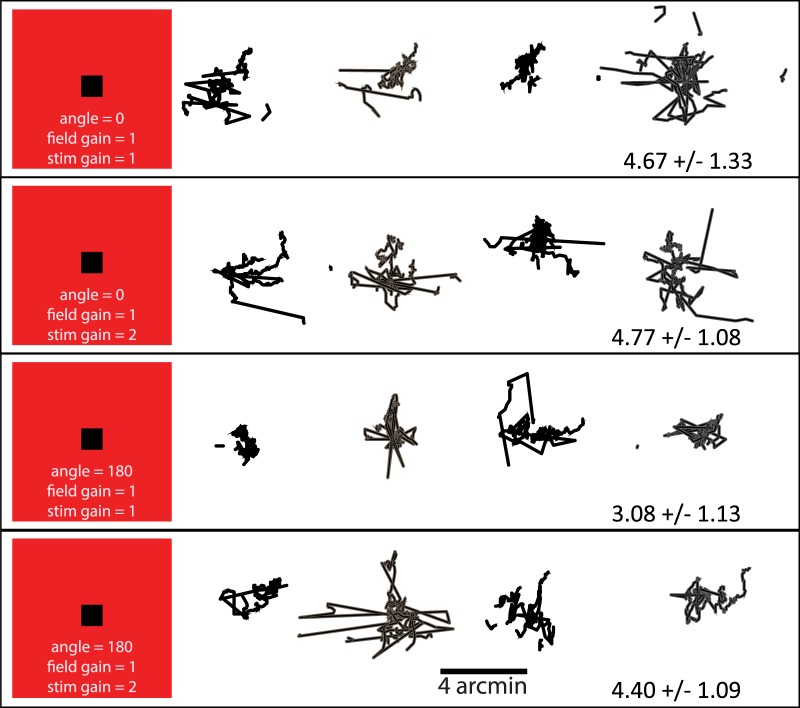
Experimental methods: The physical configuration of the system is shown schematically at the top of the figure. The subject saw two fields against a dark background, each with a size of 2° or smaller and positioned 2° on either side of a fixation cross. The left display was generated by the AOSLO scanning beam and was projected directly onto the retina. The motion of the stimulus and/or the field in the AOSLO display was computed directly from eye motion after applying a transformation of gain, g, and/or angle, θ. The right display was a conventional LCD computer screen display that was used for the matching task. The stimulus and/or the field on the right jittered randomly with an amplitude that was controlled by the subject. For conditions A and C, the AOSLO scanning beam was modulated to generate a smaller field within the full extent of the raster scan (indicated by the dashed line). In condition B, only the black stimulus moved. In condition C, both the field and the stimulus were moved with independent gain and angle transformations. Example motion of stimulus and field are illustrated here as motion trails.

Display configuration

The fixation cross presented via an LCD display (as shown in the schematic on Figure 1) was always world-stationary and so provided a frame of reference against which other motions could be judged. There were also other world-stationary features that were visible to the subject because we could not control for all reflections and light leakage in the room. The red fields were about 2° in size and 2° on either side of fixation. Each field contained a small, black, 0.1° square stimulus with the exception of condition A, in which only the red field was visible. One red field was the projection of the AOSLO raster-scanning beam directly onto the retina. The wavelength of the scanning beam was 840 nm. Because it was scanning a raster at 30 frames per second, it appeared as a red square as illustrated in Figure 1 with a luminance of about 4 candelas per square meter. The black stimulus (Figure 1, conditions B and C) was generated within the raster by using an acousto-optic modulator to turn off the stimulus at the appropriate times to form a 0.1° black square at the target location. The other red field was produced on the LCD monitor and was matched for size, color, and luminance to the AOSLO raster (Figure 1, right side).

AOSLO display for retinal imaging, eye tracking, and stimulus delivery

The AOSLO was set to record a high-resolution 512 × 512 pixel video of a 2° square patch of the retina with cellular-level resolution (Roorda et al., 2002). High resolution was obtained by using adaptive optics, which dynamically measures and corrects for the ocular aberrations of the eye during imaging (Liang, Williams, & Miller, 1997). To correct for eye motion, we implemented a set of techniques whereby we tracked the retina in real time by analyzing the distortions within each scanned image (Arathorn et al., 2007; Sheehy et al., 2012; Yang et al., 2010) and placed the stimulus at a targeted retinal location within each frame. The eye tracking was accomplished by acquiring each image as a series of narrow 3.75 arc min (16 pixel) strips or subimages and cross-correlating the strips against a reference frame, which was acquired earlier in the imaging session. The X- and Y-displacements of each strip that were required to conform it to the reference frame were a direct measure of the eye motion that occurred during each frame. Visible stimuli were presented to the subject by modulating the laser beam as it scanned across the retina, much in the same way as an image is projected onto the surface of a cathode-ray-tube television screen (Poonja, Patel, Henry, & Roorda, 2005). To stabilize the stimulus, we used the eye position signal to guide the timing for the modulation of the scanning laser in order to place it at a targeted location. The original intended use of this capability was to stabilize a stimulus on a particular cone or area regardless of eye motion for neurophysiological experimentation (e.g., Sincich, Zhang, Tiruveedhula, Horton, & Roorda, 2009) or for targeted visual function testing (e.g., Tuten, Tiruveedhula, & Roorda, 2012). But because this stabilization is determined from computed eye motion, other stimulus motions relative to the retinal mosaic can be computed and delivered with high precision. We refer to it as a retina-contingent retinal display. The motion of the stimulus and/or the red field that was delivered directly to the retina with the AOSLO was controlled with a direction and a magnitude that were a computed function of the eye's own motion, according to gain and angle. The gain refers to the speed of the motion applied to the stimulus relative to the actual eye motion. The angle refers to the direction of the motion relative to the actual eye motion at any given moment. For example, a gain of 1 and an angle of 0 generates the stabilized stimulus condition because the stimulus is moved an amount equal to the motion of the eye (gain 1) in a direction that is the same as the eye motion (angle 0). A gain of 0 refers to a stimulus that is fixed relative to the field but one that naturally slips across the retina in a direction that is opposite to the eye's motion. A gain of 1 with an angle of 180 doubles the retinal slip of the stimulus caused by eye motion, and a gain of 2 and an angle of 0 mean that the stimulus will move across the retina ahead of eye motion. Other angles will cause the stimulus to move with components that are not in line with the eye's motion. Regardless of angle, any gain greater than 0 produces relative motion between the target and the fixation cross.

Accuracy of AOSLO-based targeted stimulus delivery

The accuracy with which we can place the stimulus at its targeted location depends on the accuracy of the eye tracker and the delay, or lag, between the prediction and the actual delivery of the stimulus. For experimental condition B, which only required movement of the central dark stimulus, the tracker ran with a 2–4 msec lag between eye motion prediction and stimulus delivery. The reduced lag combined with high-accuracy eye tracking (owing to the high resolution of the AOSLO image) allowed for targeted placement of the stimulus with an accuracy of 0.15 min of arc (Yang et al., 2010). However, our approach precluded using the same small lags for experimental conditions in which the entire scanned field was moved (conditions A and C). For those conditions, the average delay between measurement and delivery was the time taken to acquire one AOSLO frame or ∼33 msec. The tracking system allows for stabilization of slow drifts during fixation but sometimes loses lock during saccades or larger excursions. Eyeblinks, large saccades, or deviations of ∼0.75° or more from fixation occasionally caused the tracking and stimulus delivery to fail, resulting in a red field with no target until tracking resumed. Subjects who had higher than normal rates of microsaccades were difficult to track and were not used for this experiment. The higher frequency components of fixation (e.g., tremor) were unstabilized but were too small to have influenced our results.

LCD display for motion matching

In the other red field, provided by the LCD display, the amplitude of a jittery motion in the stimulus and/or field was controlled directly by the subject using keyboard inputs. The purpose of the LCD display was to allow the subject to make adjustments to match the perceived amplitude of motion of the AOSLO display. The motion of the matching field and the stimulus within it were given similar motion statistics to normal eye motion (approximated with a 1/f power spectrum; Eizenman, Hallet, & Frecker, 1985; Findlay, 1971; Stevenson, Roorda, & Kumar, 2010). Specifically, the motion of the comparison target was calculated as the sum of sinusoids with frequencies from 1 to 30 Hz and amplitudes that were inversely proportional to frequency. Phase was randomized, and new random phases were chosen every 2 s so that the target did not continually repeat the same complex Lissajous trajectory. The value produced by the adjustment was the overall standard deviation of the motion in arc minutes. Subjects all reported that this motion was a fairly close match to the overall subjective appearance of the jitter they saw in the AOSLO targets and were comfortable making the settings.

Experiment protocol

Three experimental conditions were tested. The three experimental conditions were chosen to subsume both a number of stimulus conditions and the variation in the inherent lag of our experimental equipment. Each subject's response was an average of five trials for each gain and angle state that was tested. The three conditions are illustrated in Figure 1 and are described here.

Condition A: Field yoked to eye motion

In this condition, we moved the entire scanned field according to the eye's motion. This was accomplished by modulating the laser to “crop” the scanned raster pattern to a set position within the full envelope of the raster scan. The size of the cropped raster was necessarily smaller than the original raster but had to be large enough to contain enough information to maintain a suitable image for eye tracking. In this configuration, the raster was cropped to 350 × 350 pixels (1.37°) from the original 512 × 512 pixel dimension (2°), allowing for a range of motion of ±80 pixels (20 arc min). Condition A had no fixed frame of reference near the stimulus although the fixation cross still provided a reference for motion. When the full raster was used as the stimulus, the latter's motion had to be derived from motion estimates captured during the presentation of the previous frame with an average latency of 33 msec. Because of the larger field size, the range of gains for stimulus motion was limited to 1.5.

Condition B: Stimulus yoked to eye motion, field fixed in world coordinates

In this condition, a small black square stimulus was moved within a world-stationary red field. The purpose of this case was to establish a frame of reference close to the stimulus to elicit any differences from condition A in motion perception due to the presence of the surrounding frame of reference as opposed to only the relatively distant fixation cross and dimly illuminated room. Because the stimulus moved within the red field, the lag of its motion with respect to eye motion was very short, 2–4 msec. Hence, condition B provided two differences from condition A: a surrounding fixed frame and shorter lag. If the results from condition A were to differ significantly from condition B, one would have to attribute the difference to either (a) the presence of a surrounding reference or (b) the shorter lag. If the perception of motion in condition B were not to differ significantly from condition A, we could conclude that neither the surrounding reference nor the difference in lag affects the observed behavior. The black stimulus was moved with a range of gains and angles spanning 0° to 180° in 20° steps.

Condition C: Stimulus and field yoked to eye motion but with independently controlled gains and angles

In this condition, we presented two stimuli moving with respect to each other as well as the world-referenced fixation cross: One stimulus was the raster and the other the dark square within the raster. The lag between eye motion prediction and stimulus delivery for both the black box and the red field was an average of 33 msec as in condition A. The purpose of condition C was dual: (a) to distinguish the effect of a moving reference on the perception of motion of the interior stimulus or (b) in the absence of any difference in the perception of motion of the interior stimulus from the stimulus in condition B, to determine any possible relationship of two independently moving stimuli in close proximity. That is, if the perception of motion of the interior stimulus (black square) as a function of its motion with respect to eye motion were to be unaffected by the motion or absence of motion of the surrounding red field, one could then treat the moving field as effectively a separate stimulus. In these trials, various configurations of relative motions between the field and the black square stimulus were presented. To keep the number of trials down, we restricted the range of gains and limited the angles tested to 0° and 180°. In this condition, the matching task involved two steps: first, adjusting the LCD display to match the motion of the red field, then adjusting the relative motion of the black stimulus within the field.

Recorded videos

The AOSLO videos that were used to track the retina were saved for each trial. Because the scanned field as well as the black stimulus were generated by modulating the scanning laser, their positions were also encoded directly onto the video. These videos were used to evaluate the eye motion during the task and to assure the fidelity of the eye tracking and delivery of the retinal stimulus. Movies 1 through 3 in Appendix 3 show actual videos recorded for each experimental condition.

Assessment of eye motion during the task

Estimating eye motion during the actual matching task was not straightforward because we could not be certain of the times when the subject was actually attending to the task. To get the most accurate measurement, we evaluated eye motion for the first 3.33 s (100 frames) at the beginning of each trial. Because the subject initiated each trial, we felt that these early periods were when the subject was most likely attending to the task. Two parameters were extracted from the eye motion traces. First, we determined the average standard deviation of fixation from the videos. Second, we estimated the number of microsaccades per second. A microsaccade was defined as a jump of more than 3 min of arc over a 33 msec interval. To test whether the different experimental conditions affected the eye's fixation behavior, we performed a series of longer trials on one subject in experiment condition C in which we recorded eye motion during each trial.

Data analysis

Motion-matching estimates for each individual showed similar trends but had different magnitudes between the three subjects (Appendix 1). To account for that, we normalized each subject's results before combining them. For data from experimental conditions A and B, we divided each subject's motion estimates by their average motion estimate from the gain = 1 and angle = 40, 60, and 80 conditions. These gain and angle settings were selected for normalization because they were conditions for which reliable motion estimates were made and no fading occurred. For experimental condition C, each subject's motion estimates were divided by the average motion estimates for the field under the stabilized condition.

Results

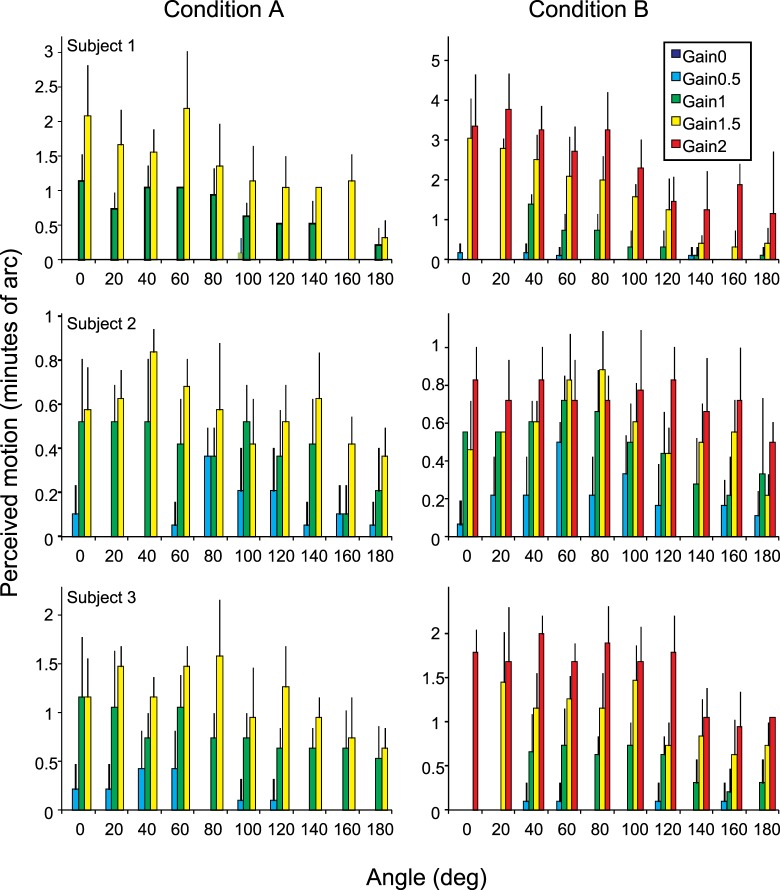
The experiments revealed that the percept of motion bears a more complex relationship to actual eye motion than we expected. We found that stimulus motions with directions that are consistent with eye motion but largely independent of amplitude of that motion produce the most stable percepts. As long as all objects in the field slip in roughly the same direction, opposite eye motion, they are perceived as stationary despite having different speeds of retinal slip. The maximum stabilization takes place for motion at a range of angles within a sector (±∼20°) around the 180° direction and then becomes less effective as the angle continues to increase. This phenomenon is revealed under experimental conditions A and B, and the data are shown in Figure 2. The radial plots of motion versus angle and gain (dashed lines in the 180°–360° sector are reflected versions of data from 0°–180°) show that the perceived motion roughly takes the form of a cardioid function. Objects moving in the 0° direction are perceived to be moving much more than objects in the 180° direction. Even though some relative motion is seen for all gains other than 0, the cardioid shape of the function is maintained for gains as high as 2, showing that the perceived motion is much reduced when retinal slip is opposite the eye's drift. This means that the visual system works to stabilize its percept of stimuli moving opposite to eye motion even if they are moving across the retina more than the eye's own motion would make them move.

Figure 2.

Results from experimental conditions A and B. Left: Polar plots of perceived motion versus gain and angle. Right: Bar charts of the same data. The average responses (based on five trials) from each of three subjects were first normalized then averaged as described in the Methods section. Error bars indicate standard deviation of normalized motion estimates. Actual motion estimates from each individual subject are provided in Appendix 1. The angle and gain indicate the direction and magnitude of motion of the field itself (condition A) or the 10′ stimulus within a stationary field (condition B) relative to actual eye motion. Because the large, bright raster field itself was used as the stimulus in condition A, no fading was observed even when the field was stabilized on the retina (small dotted circles on polar plots). The smaller stimulus in condition B, however, often faded whenever the stimulus was close to stabilized (i.e., small angles and gains that were close to 1). For conditions in which fading occurred, the percentage of faded trials is listed above the bar on the figure. Because of the smaller stimulus size, more extreme gains could be tested under condition B. Preliminary trials indicated that the full range of results is essentially symmetrical around the 0–180 axis, so data was collected for only one half of the range. The polar plots show that data reflected around the 0–180 axis using dashed lines, leading to the exact symmetry of the polar figures. The least perceived motion was encountered when the field (condition A) or the black stimulus (condition B) moved 180° relative to true eye motion (i.e., retinal image motion that was consistent with eye motion) as was to be expected. However, what was not expected was that the perceived stabilization for angles around 180° would persist for gains up to 1.5 (condition A) and 2.0 (condition B). If responses were based simply on relative motion of target and fixation, data should fall on a circle centered on the origin in the polar plots and have equal height bars in the histograms.

A two-way ANOVA (Matlab, Natick, MA) was used to test the significance of the results. We could reject the null hypothesis for effects of gain on motion, of angle on motion, and for the interaction of gain and angle with motion for both conditions A and B.

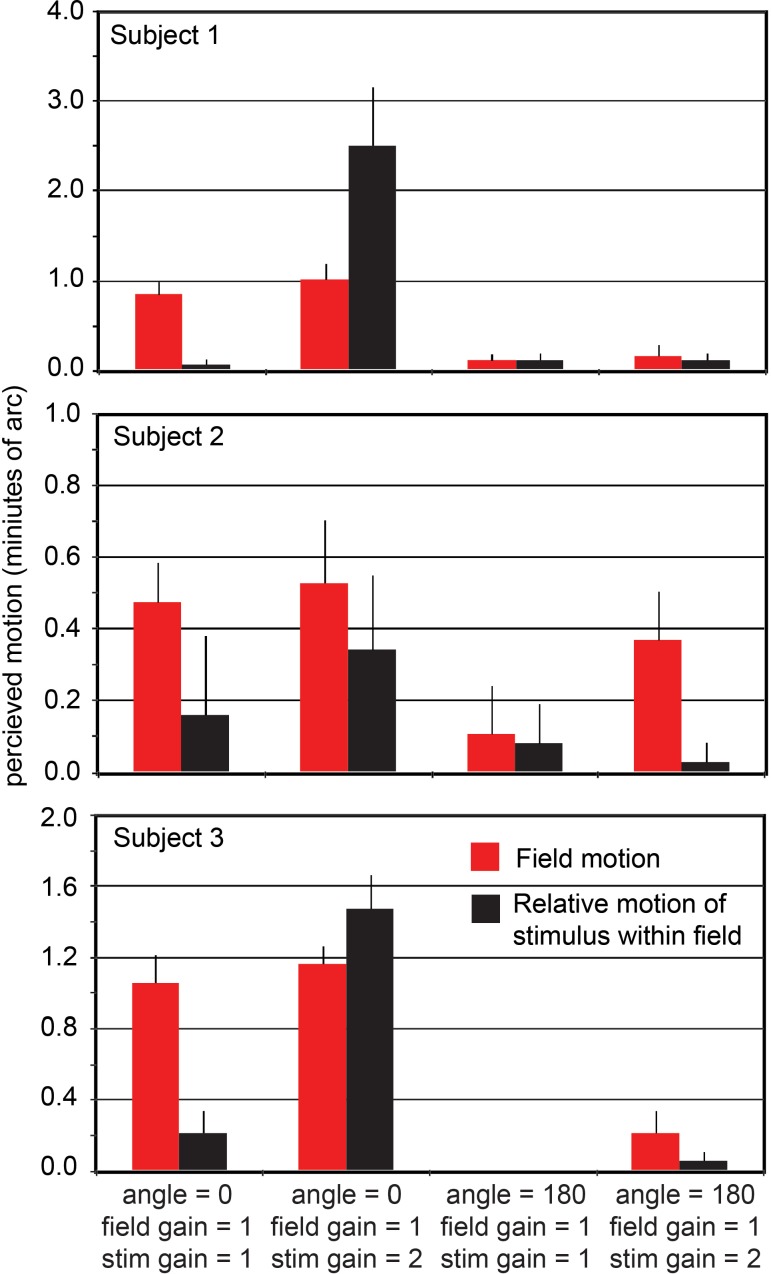
Condition C (Figure 3) gave the most striking outcome: If two stimuli moving with different retinal speeds have directions that are both opposite the direction of eye drift, they appear fixed with respect to each other even though their veridical position relative to each other is constantly changing. The subject has an illusion of relative stability. This phenomenon is revealed best in experimental condition C in which the subject sees three objects, each moving with a different gain (category 4 in Figure 3). The fixation cross has a gain of 0 and therefore slips across the retina in a direction and at a rate that is consistent with eye motion. The retinal slip of the field and the stimulus are doubled (angle 180, gain 1) and tripled (angle 180, gain 2), respectively, relative to eye motion. Despite the fact that these three objects are moving at different rates, they all appear to be fixed and moving very little relative to each other. If the same relative motions of stimulus and field are presented with, instead of against, the eye motion direction (category 2), the motions are clearly perceived.

Figure 3.

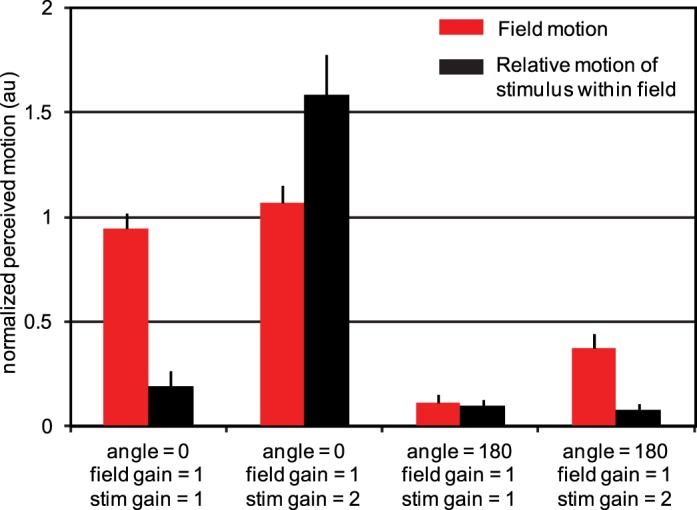
Results from experimental condition C. Perceived motion of the field (red) and the relative motion of the stimulus within the field (black). The average responses (based on five trials) from each of three subjects were first normalized then averaged as described in the Methods section. Data from each individual subject are provided in Appendix 1. Error bars indicate standard error of the mean of the 15 normalized motion estimates for each category. Stabilized fields (field angle = 0, field gain = 1, two left categories) are seen as moving whereas fields moving in a direction consistent with eye motion but with twice the retinal slip (field angle = 180, field gain = 1, right two categories) appear nearly stable. As expected, a stimulus that is not moving relative to the raster appears as such (first and third categories). For unequal gains in the angle = 0 direction (second category), large relative motion was observed. However, when the field was moving at two times the retina slip and the stimulus was moving within it at three times the retinal slip (rightmost category), there was nearly no apparent relative motion. The same relative motion is perceived very differently, depending on its overall relationship to eye motion.

Results from all three conditions show that the perception of relative motion of retinal images is dramatically reduced whenever the direction of motion of those images is opposite to ongoing eye motion direction, regardless of gain.

Discussion

Our results with the small drifts of the eye during fixation contribute to the larger body of evidence that the visual system incorporates estimates of eye motion into the perception of motions and positions of world objects. Studies of this phenomenon have included perceived position of objects flashed at various time points relative to saccadic shifts of gaze (Bridgeman et al., 1975; Freeman et al., 2010; Pola, 2011; Wertheim, 1987). These larger eye motions are typically imperfectly compensated, resulting in misperceptions of position or motion under conditions designed to reveal them (Raghunandan et al., 2008). Here we add to this body of work the finding that the minute drifts of fixation are also compensated in perceived motion of targets. The results show that retinal slips that are roughly consistent with moment-to-moment eye motion during fixation are not perceived as object motion.

Our results for fixation drift show compensation for a small range of motion directions relative to eye motion but a relatively large range of speeds in that direction. A similar phenomenon has been described for smooth pursuit, in which the compensation for eye motion is tuned for direction but not for speed (Festinger, Sedgwick, & Holtzman, 1976; Morvan & Wexler, 2009). In the case of these larger, faster eye movements, some combination of efference copy and retinal image motion may also be responsible for the compensation.

Insensitivity to retinal slip in only the appropriate direction has obvious functional advantages. Complete suppression of small motions, regardless of direction, would leave us with no percept of target motion until its motion exceeded a certain threshold, and then it would appear to start moving with a combination of eye motion and its own motion. Instead, retinal motion induced by stimulus motion in any direction other than in the stabilized sector (±∼20° from eye motion–induced slip as seen in Figure 2) is perceived as motion in the world. Because fixation jitter direction is approximately random, this means any objects moving in the world ought to be perceived even if occasionally they are aligned with eye motion–induced slip. We thus retain an exquisite sense of actual motion of objects in the world despite continual fixation eye motion.

The illusion of relative stability

Not only did we find that the perceived stability of retinal images moving in a direction consistent with eye motion held for a range of amplitudes of motion, but objects moving with different gains were perceived as stable with respect to each other. We call this the illusion of relative stability. In natural viewing, a very small difference in image motions does occur due to parallax effects as the pupil translates with eye rotation. Near objects slip more rapidly across the retina than distant ones, but velocity ratios never approach those used in our experiment. An object has to be touching the cornea for it to slip twice as fast as an object at infinity. It seems unlikely that the mechanism behind this illusion exists to deal with this very small parallax effect. Rather, we postulate that this illusion simply reveals the mechanism for motion compensation that is sufficient for the human visual system to properly sense world motion. That is, the visual system senses and compensates for the direction of motion, rather than the actual position of objects on the retina. To our knowledge, the only other experimental encounter with one of the unnatural motion settings in our experiments was briefly mentioned in Riggs, Ratliff, Cornsweet, and Cornsweet (1953) in a study of the effects of retinal slip on acuity and persistence of visibility. Using a system of compensating mirrors and a reflective contact lens, they were able to stabilize a retinal stimulus (equivalent to our angle = 0, gain = 1 setting), but they also reconfigured the optics to make the stimulus move opposite to eye motion with a doubled amplitude, a condition that they called “exaggerated” motion (equivalent to our angle = 180, gain = 1 setting). The extent of their observation was that the stimulus, under the exaggerated motion condition, appeared “locked in place.” However, they did not further explore the range of conditions under which this perceived stabilization occurred.

The experimental design ensured that the eye fixation behavior remained the same for all conditions. First, the presentations were made about 2° away from fixation, and attention had to be paid to either side of fixation simultaneously for the matching task. Second, the stimulus was only present when the eye was fixating on the fixation cross. Whenever the eye drifted ∼0.75° or more, the tracking would fail. As such, the subject could never make a motion assessment while looking directly at the AOSLO display. Finally, all conditions were presented in pseudorandom order, so the subject could never anticipate the next experimental condition. To confirm that fixation behavior was not affected by the experimental condition, we had one subject perform the matching task for all settings of experimental condition C four times each and recorded 10-s AOSLO videos for each trial. The subject was instructed to attend to the task for the entire period. We used offline software to extract the eye motion for each trial. Figure 4 shows plots of each eye motion trace. These plots indicate normal fixation behavior with no systematic fixation differences between the experimental conditions.

Figure 4.

Typical fixation behavior during the matching tasks of experimental condition C. Plots show eye traces from four 10-s trials for one subject. Gain and angle settings are labeled on the left of each row. The standard deviation is typical for a fixating eye, and there are no apparent differences in fixation behavior for the different conditions.

The delay between the capture of the eye motion and the execution of the stimulus must be considered in interpreting these results. In experimental condition B, in which the only moving stimulus is the dark square, this delay is 4 msec or less and, hence, shorter than the highest frequency components of the jitter and drift. Consequently, we take the results of experimental condition B to be closest to describing the actual behavior. For experimental condition A, in which the entire field moves, the delay is one frame or 33 msec. This interval is three times as long as the highest frequency components of jitter and drift and, consequently, is physiologically significant. Despite this difference in latencies, the perceived motion for the two conditions shown in Figure 2 is substantially the same. This indicates that the neuronal stabilization mechanism is robust enough to be unaffected by any direction noise introduced by the longer delay for experimental condition A. For experimental condition C, both the field and stimulus used a prediction delay of 33 msec. Again, the results are insensitive to the extra delay. Non-retina–contingent motion was also caused by tracking errors, particularly under the most extreme gain conditions. As such, the motion estimates reported here should be considered as an upper bound on what might actually be perceived under ideal conditions.

One of the goals of our study was to determine whether and the extent to which the visual system has knowledge of its motion during fixation. Our results clearly rule out an overall insensitivity to motion, in which jittery retinal images are seen as stable regardless of direction. There must also be a signal indicating at least the direction of eye motion that is then used to perceptually stabilize individual targets based on their retinal slip direction. The experimental configuration imposed the necessity of presenting at least one spatially fixed stimulus: a white cross for the subject to fixate. Other spatially fixed features were also visible across the field because we were unable to eliminate all light reflections within the system. The movement of the world-referenced features across the retina could be the source of the eye motion signal used for computing the percept of motion for all parts of the retinal image. Alternatively, an efference copy signal of the eye drift might be available although these drifts are only a few arc minutes in extent. Drifts have long been thought to be the result of small instabilities in the oculomotor system (Cornsweet, 1956) although some subjects are able to control them to maintain fixation (Epelboim & Kowler, 1993). It seems unlikely that efference copy of these tiny drifts could carry the precision required to produce our results (Royden, Banks, & Crowell, 1992). In either case, it appears to be sufficient that the eye motion signal have only enough precision to roughly specify direction of drift with much less precision for the speed of drift.

Speculation on the neural mechanisms that account for visual stability go back at least as far as Von Helmholtz. Two camps evolved: efferent theories positing a motion correction signal derived from an optomotor source (Helmholtz, 1924) and retinal theories positing a correction signal derived from the motion of the image on the retina (Gibson, 1954). Until the incorporation of instruments capable of controlling the motion of a stimulus with respect to the motion of the eye, hence controlling the position of the stimulus on the retina in real time, experimental data was limited to clever manipulations of natural viewing conditions. Interpretations of the observed psychophysics led to support of both theoretical camps. The Purkinje eye tracker coupled with computer-generated displays and, most recently, the AOSLO equipped with a retina-contingent retinal display have allowed a more controlled approach to the question and, as can be seen from our results, broaden the question itself to include the detailed behavior of that stabilization.

Our results affect the interpretation of earlier results obtained with such devices. While the relevant literature is vast, we present as examples the implications of our results on several recently reported results by other investigators. Gur and Snodderly (1997), using a dual Purkinje eye tracker and recording from V1, concluded that V1 receptive fields do not move to follow, and thereby stabilize, a moving stimulus. However, because the direction of motion of their stimulus is independent from the direction of eye motion, their results necessarily pool over all theta (angles between stimulus motion and eye motion). Because for random theta stimulus motion is outside the stabilized anti–eye motion direction sector 90% of the time, such pooling necessarily hides the stabilized regime. In a sense, Gur and Snodderly's results are consistent with ours but, in light of ours, do not support the neuroanatomical neurophysiological conclusion they assert. The only time the translation of RFs in V1 (by whatever means) would be distinguishable is when the stimulus motion is within the stabilized sector. It should be noted that this methodological issue raised by our results is not limited to Gur and Snodderly but would affect all methods that do not plot percept motion as a function of how the stimulus moves relative to eye motion. For example, Tulunay-Keesey and VerHoeve (1987) examined natural and motion-controlled perception of motion near the threshold of detectability. They found that with background reference (more relevant to conditions in our experiment), the threshold for motion visibility is somewhat higher for the stabilized condition than for the natural condition. The authors concluded that eye motion facilitates motion detection. But interpreting their results in light of our experiment, approximately 90% of the time their stimulus motion was not in the stabilized direction sector and consequently would be seen as veridical or nearly veridical. Because the motion in their experiment is near threshold, their stabilized case is equivalent to a small random motion superimposed on g = 1, θ = 0. Because such retinally stabilized stimuli are perceived as moving, it is not surprising that the threshold for detecting a random motion superimposed should be greater than when the eye-motion–induced component is erased perceptually by whatever mechanism is involved.

Poletti et al. (2010) coupled a dual Purkinje eye tracker with a high refresh-rate computerized display to deliver similar stimuli to those reported here, and addressed the question of whether stabilization is driven from retinal or extraretinal data. Their experiment was constructed as a two-alternative forced choice wherein subjects were asked to report whether they observed the target stimulus to be moving or still. The stimuli were similarly categorized into moving or still with respect to the “normal” or stabilized frame of reference. The subjects' responses were presented as probability of correct categorizations. Their experiments included the additional dimension of referenced (light) versus unreferenced (dark) conditions. Because the methodology here requires a fixation target, only Poletti et al.'s referenced condition is comparable to the results reported here, but as a result of the “binarization” of both stimuli and response categories, Poletti et al. are analyzing a small space in the larger space analyzed here. Within this small space, their results are consistent with ours, including the finding that stimuli that are retinally stabilized are perceived to move. This particular observation has been made at least since the 18th century in the context of afterimage motion (see Wade, Brozek, & Hoskovec, 2001). Poletti et al. conclude from a variety of tests that perceptual stabilization is entirely driven from retinal data rather than efferent eye motion data. Their methodology precluded the observation made here that the percept of motion is, in fact, a function of both eye motion and world reference–stimulus motion. Our methodology precluded any conclusion as to whether the eye-motion input to this function is derived from optomotor sources or from analysis of the motion of the fixation cross (or other inadvertent world-frame features) on the retina. The combined results might be taken to suggest that the eye-motion input to the motion percept is, in fact, also retinally derived. The experiments are sufficiently different that this conclusion should be taken, at best, tentatively.

In some species, it has been suggested that the analysis of relative motion may begin in retinal ganglion cells (Olveczky et al., 2003). Recordings from salamander and rabbit retinas showed a suppression of motion responses in ganglion cells unless the surround motion was different from the center motion. While this enhances relative motion over full-field motion, by itself it is not sufficient to produce our eye motion contingent percepts.

Although the stimulus motions we use are quite small, they are well above typical minimum motion thresholds (McKee et al., 1990). The relative retinal slip velocities are also well above typical velocity discrimination thresholds of 10% and so should be easily detected (Kowler & McKee, 1987). Hence, the perception of relative stability for targets moving in directions opposite eye drift is likely the result of a neuronal mechanism for eye movement compensation rather than being a near-threshold artifact.

The results of the experiment raise the question about the neuronal mechanisms that implement the observed behavior. One such mechanism might involve a selective inhibition of motion mechanisms, analogous to the motion threshold increase proposed by Murakami (2004) but with selectivity for the moment-to-moment direction of overall retinal slip. A more sophisticated mechanism might involve an active stabilization of the targets based on individual motion estimates for each stimulus pattern. A behavioral computational model of the latter kind of mechanism is provided in Appendix 2. While there are several long-standing neuronal models consistent to various degrees with the proposed model, we are not aware of any neuroanatomical or neurophysiological evidence supporting any particular circuitry or architecture.

Conclusion

In summary, several surprising results and implications have arisen from these experiments. Apparently, perceptual stabilization is a subtle function of the moment-by-moment direction of the eye's inadvertent drifts in combination with the actual motion of a pattern on the retina. Motions of an image on the retina that lie approximately in the direction opposite eye motion are perceptually stabilized, despite differences in the speed of that motion on the retina. As the motion of the image on the retina diverges from the direction that would be produced by eye motion, the percept of motion becomes increasingly veridical. More remarkably, parts of the retinal image that have different motions on the retina are independently stabilized or not, depending on the relationship of their motions to the momentary eye motion. This overall system behavior satisfies the need for stabilized vision and provides representation of veridical target motion, particularly when the background does not provide useful reference and more particularly when the entire visual scene is composed of elements moving with respect to one another, such as encountered when the observer's path lies through clusters of branches and foliage. Such scenes often present no stable reference frame, yet the multiplicity of observer-induced velocities of the various elements of the scene is essential in reconstructing the 3-D spatial relationship of those physical elements. A visual mechanism that extracts separate veridical velocities while rejecting the image velocity components that would be introduced by eye motion would seem to be ideally adapted to such a visual environment.

Appendix 1: Individual data

Figure A1.

Individual data for each subject for experimental conditions A and B. Error bars are standard deviation based on five trials for each gain and angle setting. A two-way ANOVA was used to reject the null hypothesis for dependence of motion on gain and dependence of motion on angle for all subjects. The null hypothesis for the interaction of gain and angle could be rejected for all subjects and conditions with the exception of subject 2, condition B (p = 0.3689) and subject 3, condition A (p = 0.3544).

Figure A2.

Individual data for each subject for experimental condition C. Error bars are standard error of the mean for the five trials in each category.

Table A1.

Eye motion statistics. Notes: The overall eye motion of the three subjects during this task is consistent with typical fixation statistics reported in the literature (see review by Martinez-Conde, Macknik, & Hubel, 2004).

	Subject 1		Subject 2		Subject 3
	Eye motion X, Y (SD in arc min) (time in s)	Saccade freq (Hz)	Eye motion X, Y (SD in arc min) (time in s)	Saccade freq (Hz)	Eye motion X, Y (SD in arc min) (time in s)	Saccade freq (Hz)
Condition A	2.0, 1.5 (t = 413)	0.26	2.5, 2.3 (t = 167)	0.35	3.1, 2.0 (t = 376)	0.60
Condition B	2.6, 2.6 (t = 603)	0.41	3.9, 2.3 (t = 420)	0.46	2.5, 1.5 (t = 649)	0.23
Condition C	2.2, 1.5 (t = 17)	0.36	2.4, 2.1 (t = 17)	0.24	2.8, 2.3 (t = 47)	0.47

Appendix 2: Behavioral model of the observed results

We developed a computational model of the behavior reported in the main body of the paper for two purposes: to try to understand the kinds of computations that might underlie the relationship between the actual stimulus motion and the percept of that motion and to generate simulations of the percept for different stimulus motion conditions because the percepts are otherwise only available to subjects of the experiment.

Contingent stabilization with the observed characteristics appears to involve a nontrivial transformation from the input image to the percept involving three steps: (1) segregation of the retinal image into its constituent components or “stimulus patterns” and computing the retina-relative group velocity vector for each pattern, (2) computing a percept velocity for each stimulus pattern as a function of its own retina-relative velocity and eye motion, and (3) computing an aggregate percept combining all the stimulus patterns.

Because the experiments strongly suggest independent velocity computation for each coherently moving pattern, the requirement for the first step appears to preclude purely local processing. Due to the well-known aperture effect, local motion estimates along the vertical and horizontal edges of the stimulus and the field patterns in these experiments are ambiguous, particularly when the retinal motion is oblique to those edges, and cannot be readily converted into a group velocity vector for the whole pattern. The independent processing of each pattern therefore suggests that the displacement of each pattern as a coherent figure is being used to compute its group velocity. We therefore use correlation (e.g., by FFT or map seeking circuit; Arathorn, 2002) to identify and isolate each independently moving pattern. Whether this corresponds to a neuronally plausible step is outside the scope of this paper.

By whatever means each pattern's group velocity signal is computed, the next step involves a computation combining that velocity and the eye-motion signal to produce the cardioid-like perceptual response observed in the experiment.

Finally, the perceptual velocities computed for each pattern must be used to assemble the aggregate percept reported by the subjects. There are two scenarios for this stage. The model presented here explicitly constructs the full percept image by combining the segregated stimulus patterns mapped into position on a single “canvas.” The resulting motion of the mapped stimuli on the “canvas” is what the subjects perceive. (Movies generated from the model of the observed signal versus the percept corresponding to the experimental conditions listed above are provided in Appendix 3). The alternative scenario would encode the group velocity of each pattern as a quantitative signal of direction and magnitude, which would then be interpreted by some integrative process. Because the nature of the latter process is not apparent to us, we do not pursue the latter stage in this scenario.

In the experiment, the motion v_i,tj of the stimuli that are projected onto the retina are computed by rotating the direction (by θ_i) and scaling the magnitude (by g_i) of the measured eye-motion vector v_ref,tj, which is determined by displacement of the retinal mosaic in the AOSLO image. Both stimulus motion v_i,tj and eye motion v_ref,tj are relative to the world frame

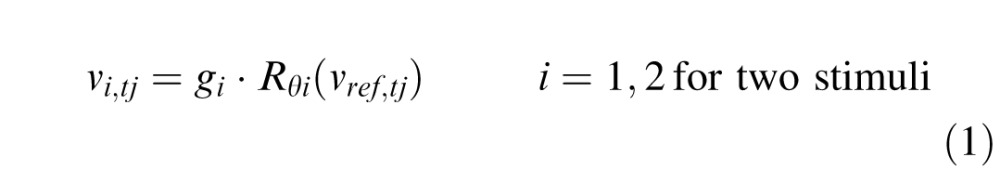The experiment applies independent motion as described above to both stimuli. We describe motion as a sequence of displacements from the t_j–1 loci.

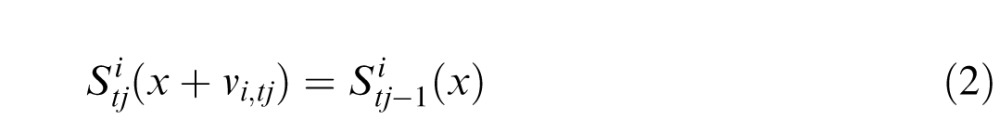The motion of the stimulus on the retina ṽ_i,tj is a combination of the opposite of eye motion and the stimulus motion

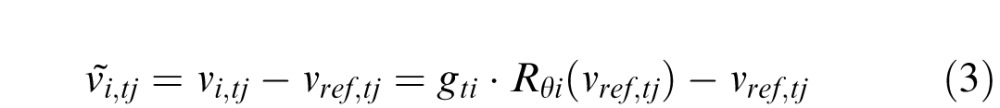The stimulus motion combined with the eye motion in the same interval v_ref,tj produces a retinal image of each stimulus pattern

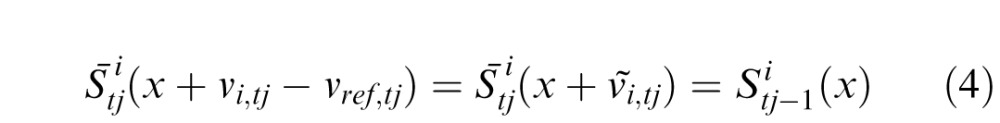Or, more simply,

First input image at t0 is composed of different stimuli

The first input image is captured as the initial memory

The next input image, Ī_t1, is then correlated with the memory M_t0. Because there are two independent motions, the circuit obtains two correlation peaks

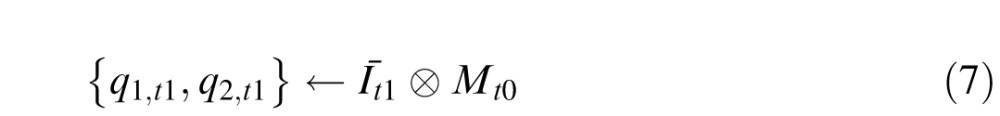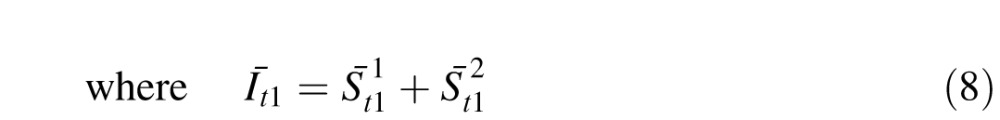Correlation peaks are measurements of retinal displacements d_1,tj and d_2,tj between the current position and the position of the pattern in memory M_t0. These peaks are associated with mappings that “undo” those displacements.

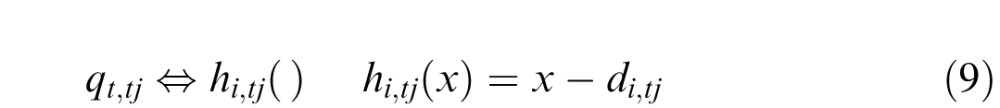Separate memories are created for each correlation peak by intersecting memory at t_j–1 with two translations of input image at t_j. Each translation registers one of the stimuli patterns in I_t with the same stimulus in the reference memory M_t0

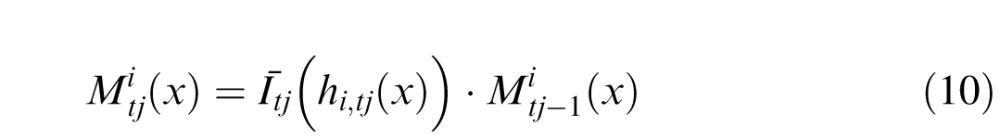For j = 1, both memories 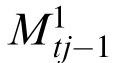= = 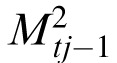M_t0

(Note that the model as presented predicts that if two stimuli are congruent, two correlation peaks will be produced for each matching memory pattern. To eliminate this, the model must include one extra step to select the correspondence peak associated with the least motion between time periods.)

Next input images j = 2, …, n are formed by more independent motion as in Equations 2–5 above. Each input image is correlated with the two memories

The measured velocity vector v̄_i,tj for each stimulus in each time step is the difference between successive measured displacements

And so forth for each time period. After several iterations, the two stimuli patterns are completely separated in the two memories M¹ and M², and the motion tracks of each have been computed.

If there is a stimulus pattern s_ref, which from context can be assumed to be fixed in the world, such as the fixation point in the experiments, eye motion v_ref can be computed just as above. Alternatively, v_ref may be an efferent-copy signal.

The percept P_tj is now reassembled from the separate memories and the motion information by mapping each memory pattern by a function of its estimated world displacement 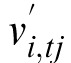and eye motion v_ref.

The brain has no direct access to world stimulus motion but can compute an estimate 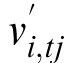from eye motion v_ref,tj and stimulus motion on the retina v̄_i,tj. For simplicity, we assume the eye is in motion in every interval, i.e., |v_ref,tj| ≠ 0.

From the same data, it can compute an estimate of the angle between eye motion and stimulus motion in the world frame

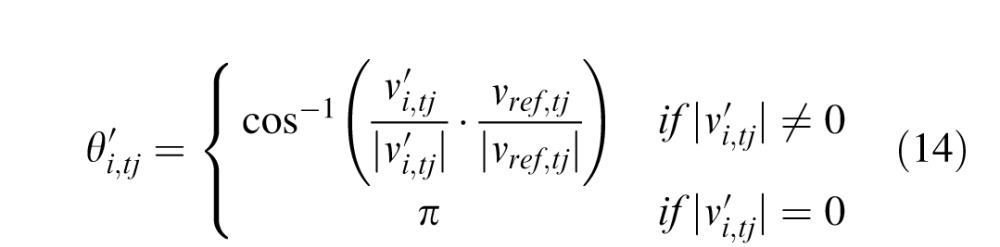From these, it can now compute the apparent or percept motion V_i,tj

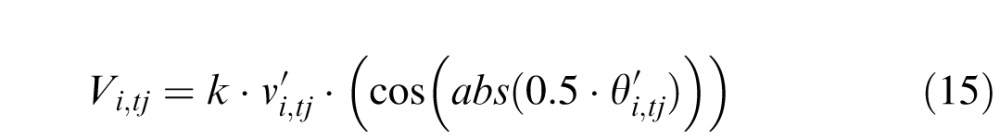Note that the apparent displacement function is here idealized to be a cardioid whose radius is zero when θ′ = π. When θ′ = 0, the apparent displacement is the estimate of the actual displacement . The constant coefficient k is introduced to account for the differences in reported scale of motion among different experimental subjects. Note also that the direction of the apparent stimulus motion is “veridical,” i.e., a scaled estimate of the world motion of the stimulus.

The percept P_tj is created by inversely mapping the isolated stimulus patterns M¹ and M² to their apparent displacements D_i,tj

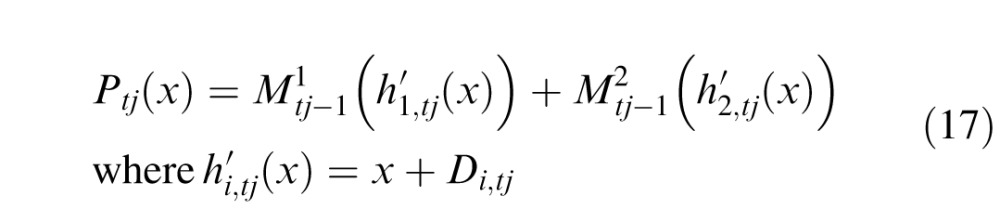Due to the small range of displacements possible in the experiment, it was impossible to determine if the perceived stabilized location corresponded to one of the samples or the average location. If the latter, then the percept is mapped first to the average location

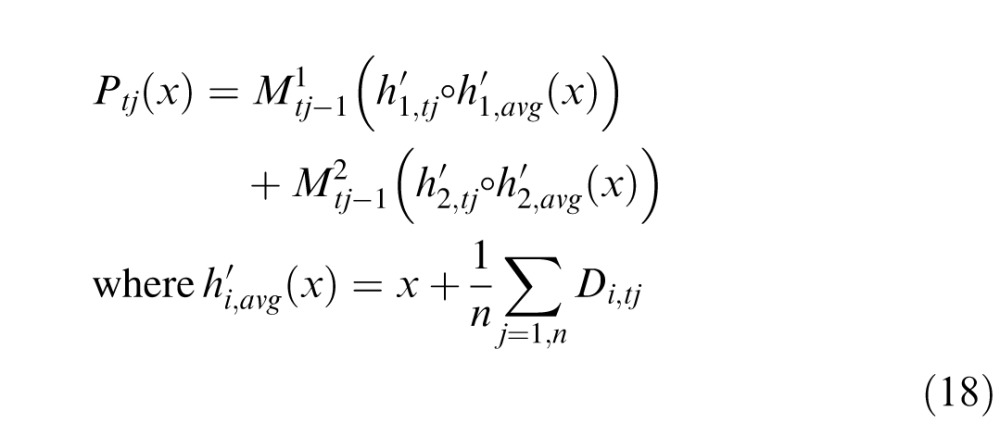Videos of simulated stimuli and percepts modeled as described above are provided in Movies 1 through 6.

The cardioid function in Equation 15 is only intended to be indicative of the role that the angle theta plays in generating the percept of motion. A variety of other functions would approximate the data equally well and could have been used. The function used is one of the simplest to visualize.

An alternative to the above model that ignores motion in assembling the stabilized percept must decide which mappings to use based on some other characterization of the relationship of the two stimuli. We do not offer a suggestion as to how this decision is made.

The computation of q₁ and q₂ can be implemented by neuronal circuits that compute global shifts, such as Olshausen, Anderson, and Van Essen (1995) and Arathorn (2002). The isolation of a stimulus amid background (or other stimuli) by intersection is demonstrated in Arathorn.

Appendix 3: Movies

Movie 1.

Download video file ^{(1.1MB, mov)}

DOI: 10.1167/13.10.22.M1

Actual retinal videos recorded from one subject while performing motion judgments for experimental condition A. The movie comprises three 50-frame video segments from the following angle:gain conditions 0:1, 180:1.5, and 100:1. In this movie, the 300 × 300 pixel frame border (which is the field seen by the subject) is moving relative to the instantaneous retinal position, which is indicated by the white cross.

Movie 2.

Download video file ^{(1.7MB, mov)}

DOI: 10.1167/13.10.22.M2

Actual retinal videos recorded from one subject while performing motion judgments for experimental condition B. The movie comprises three 50-frame video segments from the following angle:gain conditions 0:1, 0:2, and 180:2. In this movie, the 512 × 512 pixel frame border (which is the field seen by the subject) is fixed while the black stimulus is moving relative to the instantaneous retinal position, which is indicated by the white cross.

Movie 3.

Download video file ^{(902KB, mov)}

DOI: 10.1167/13.10.22.M3

Actual retinal videos recorded from one subject while performing motion judgments for experimental condition C. The movie comprises three 50-frame video segments from the following angle:gain(field):gain(stim) conditions 0:1:1, 0:1:2, and 180:1:2. In this movie, both the 300 × 300 pixel frame border and the black stimulus are moving relative to the instantaneous retinal position, which is indicated by the white cross.

Movie 4.

Download video file ^{(74.6KB, mov)}

DOI: 10.1167/13.10.22.M4

The left panel shows the motion of the field and the stimulus relative to the retina. A retinal landmark is indicated by the white diamond. The right panel indicates how the field and stimulus are perceived to move as per the model in the supplementary discussion section. Settings: field: gain = 1, angle = 0; stimulus: gain = 1, angle = 0. In this simulation, both the field and the stimulus are stabilized on the retina and not moving relative to each other. This condition was tested in experimental condition C.

Movie 5.

Download video file ^{(62.5KB, mov)}

DOI: 10.1167/13.10.22.M5

The left panel shows the motion of the field and the stimulus relative to the retina. A retinal landmark is indicated by the white diamond. The right panel indicates how the field and stimulus are perceived to move as per the model in the supplementary discussion section. Settings: field: gain = 1, angle = 180; stimulus: gain = 1, angle = 180. In this simulation, both the field and the stimulus are slipping across the retina in a direction that is consistent with eye motion but at double the rate of eye motion. They are not moving relative to each other. This condition was tested in experimental condition C.

Movie 6.

Download video file ^{(74.1KB, mov)}

DOI: 10.1167/13.10.22.M6

The left panel shows the motion of the field and the stimulus relative to the retina. A retinal landmark is indicated by the white diamond. The right panel indicates how the field and stimulus are perceived to move as per the model in the supplementary discussion section. Settings: field: gain = 1, angle = 0; stimulus: gain = 2, angle = 0. In this simulation, the field is stabilized, but the stimulus is moving in advance of eye motion. This condition was tested in experimental condition C.

Movie 7.

Download video file ^{(62.3KB, mov)}

DOI: 10.1167/13.10.22.M7

The left panel shows the motion of the field and the stimulus relative to the retina. A retinal landmark is indicated by the white diamond. The right panel indicates how the field and stimulus are perceived to move as per the model in the supplementary discussion section. Settings: field: gain = 1, angle = 180; stimulus: gain = 2, angle = 180. In this simulation, both the field and the stimulus are slipping across the retina in a direction that is consistent with eye motion, but the field has a rate of two and the stimulus a rate of three times the eye motion. This condition was tested in experimental condition C.

Movie 8.

Download video file ^{(61.8KB, mov)}

DOI: 10.1167/13.10.22.M8

The left panel shows the motion of the field and the stimulus relative to the retina. A retinal landmark is indicated by the white diamond. The right panel indicates how the field and stimulus are perceived to move as per the model in the supplementary discussion section. Settings: field: gain = 1, angle = 200; stimulus: gain = 2, angle = 160. In this simulation, the field and the stimulus are moving in different directions relative to each other, but both are close to a direction that is consistent with eye motion. The field has a rate of two and the stimulus has a rate of three times the eye motion. This corresponds to percepts reported for these stimulus parameters in earlier experiments not reported here.

Movie 9.

Download video file ^{(73.2KB, mov)}

DOI: 10.1167/13.10.22.M9

The left panel shows the motion of the field and the stimulus relative to the retina. A retinal landmark is indicated by the white diamond. The right panel indicates how the field and stimulus are perceived to move as per the model in the supplementary discussion section. Settings: field: gain = 1, angle = 340; stimulus: gain = 2, angle = 20. In this simulation, the field and the stimulus are moving in different directions relative to each other and relative to eye motion. The field is nearly stabilized on the retina, and the stimulus is moving in a direction that is nearly in advance of eye motion. This corresponds to percepts reported for these stimulus parameters in earlier experiments not reported here.