Properties of Switch-like Bioregulatory Networks Studied by Simulation of the Hypoxia Response Control System

Abstract

A complex bioregulatory network could be more easily comprehended if its essential function could be described by a small “core” subsystem, and if its response characteristics were switch-like. We tested this proposition by simulation studies of the hypoxia response control network. We hypothesized that a small subsystem governs the basics of the cellular response to hypoxia and that this response has a sharp oxygen-dependent transition. A molecular interaction map of the network was prepared, and an evolutionarily conserved core subsystem was extracted that could control the activity of hypoxia response promoter elements on the basis of oxygen concentration. The core subsystem included the hypoxia-inducible transcription factor (HIFα:ARNT heterodimer), proline hydroxylase, and the von Hippel-Lindau protein. Simulation studies showed that the same core subsystem can exhibit switch-like responses both to oxygen level and to HIFα synthesis rate, thus suggesting a mechanism for hypoxia response promoter element-dependent responses common to both hypoxia and growth factor signaling. The studies disclosed the mechanism responsible for the sharp transitions. We show how parameter sets giving switch-like behavior can be found and how this type of behavior provides a foundation for quantitative studies in cells.

INTRODUCTION

Understanding the dynamic behavior of bioregulatory networks is critical for future progress in biology and therapeutics, but the complexity and high interconnectivity of these networks often make it difficult to comprehend directly how the systems function. Understanding the dynamic function of a bioregulatory network therefore will often require simulation by computer. It is questionable however whether the present state of knowledge is sufficient for computational simulations of large systems to yield useful results. In the present work, we took an alternative approach, based on the premise that essential behavior is already encoded in small “core” subsystems. Further complexity may then serve to modulate this behavior. Functional organization around core subsystems is a concept akin to the functional modularity discussed by Hartwell et al. (1999) and the modular response analysis developed by Kholodenko and colleagues (Bruggeman et al., 2002). A second premise in the present work was that the response characteristics of the fundamental subsystems are often switch-like (Bluthgen and Herzel, 2003). This type of model may reflect how the networks evolved and became robust, and it may help link theory with experiment. The selection of a core subsystem could be guided, in part, by its conserved function in widely separated species of organisms. Subsystems characterized by a combination of theory and experiment could be combined later to model larger networks.

In the current work, we investigated the network that controls the induction of a set of genes in response to hypoxia (Bruick, 2003; Semenza, 2003). This is an attractive subject for theoretical study, because there is extensive information about relevant molecular and biological behavior and because there is a clearly defined dependence of an output on an input. The input is the concentration of molecular oxygen; the output is the activation of promoters that are under the control of hypoxia-regulated elements (HREs). We prepared a molecular interaction map of the hypoxia control network and selected from it a core subsystem that is evolutionarily conserved between nematodes and mammals (Caenorhabditis elegans, Drosophila, and humans) (Shen and Powell-Coffman, 2003). The core subsystem focuses on the HIFα and ARNT components of the heterodimeric transcription factor that binds and activates HRE-containing promoters. (HIFα includes the HIF-1α and/or HIF-2α subunits of the transcription factor; ARNT is also known as HIF-1β.) The subsystem also includes proline hydroxylases (PHDs) that hydroxylate HIFα in an oxygen-dependent manner, thereby targeting HIFα for degradation via binding to the von Hippel-Lindau protein (VHL), a component of a ubiquitin-dependent degradation pathway. Our presumption of switch-like behavior is consistent with the impression that there is a critical oxygen concentration above which the HIFα protein is undetectable (Hofer et al., 2002), although we have found no definitive published experiments that either confirm or refute this impression.

We were surprised to find that this small core subsystem can have switch-like behavior, even in the absence of feedback. The same system produced switch-like dependence on oxygen level and on HIFα synthesis rate, thus linking the regulation of HRE-dependent genes by hypoxia and by growth factors to the same mechanism. The simulation results also disclosed the origin of the switch-like behavior. We show how a subsystem can be encoded for computer survey of parameter space, how switch-like behavior can be found, and how this behavior predicts response characteristics that could provide powerful linkage between theory and experiment.

MATERIALS AND METHODS

Selection of a Core Subsystem from a Molecular Interaction Map of the Hypoxia Response Network

The first step was to assemble the known molecular interactions in the form of a map, by using previously described notation (Kohn, 1999, 2001) (Figure 1). We first summarize some of the key interactions shown on the map and then explain how we selected interactions for inclusion in the core subsystem for simulation (Bruick, 2003; Semenza, 2003). Oxygen dependence is conferred by enzymes that hydroxylate HIFα at prolines-402 and -564, and at asparagine-803. The function of the proline hydroxylase is better understood than the asparagine hydroxylase. Therefore, we chose the former as the major player in the core subsystem. We assume that the activity of the hypoxia-regulated genes is mainly governed by stimulatory occupancy of the HRE promoter elements by HIFα-containing transcription factors. We assumed initially that the transcription factors are equally effective whether or not the HIFα component is proline-hydroxylated; in later analyses (Figures 9 and 10), we modified this assumption. The transcription factors are heterodimers consisting of an HIFα component bound to ARNT. The availability of HIFα is largely dependent on the VHL gene product, which binds specifically to proline-hydroxylated HIF and leads to HIFα degradation. These features of the hypoxia response system are conserved in C. elegans and Drosophila, as well as mammals. We assume that the selected core subsystem is the major pathway for HIFα degradation and further that HIFα is synthesized at a constant rate and that ARNT concentration is constant (Bruick, 2003). In some of the simulations (Figure 7), we include in the core subsystem the fact that the expression of the proline hydroxylase gene(s) is governed by an HRE, creating a negative feedback loop.

Figure 1.

(A) Molecular interaction map of the network that governs the expression of hypoxia-dependent genes activated by HRE elements in the promoters. (B) Definitions of molecular interaction. Detailed explanations can be accessed at http://discover.nci.nih.gov/mim/index.jsp and http://ccr.cancer.gov/labs/lab.asp?labid=47.

Figure 9.

Comparison of VHL dependence of oxygen response in the original model (A) with a modified model in which hydroxylated HIFα was assumed to be inactive (B) or 50% active (C). Parameters were set to k-set1, and the monitored species was initiated transcript (species 8 in Figure 2A). The feedback loop was not included.

Figure 10.

Dependence on HIFα synthesis rate (k1 in Figure 2A). The simulation conditions and parameter settings were the same as in Figure 9C with VHL = 2.0. (A) HRE-dependent transcript initiation versus k1 for various oxygen concentrations. (B) HRE-dependent transcript initiation versus oxygen level for various values of k1.

Figure 7.

mRNA kinetics in response to various oxygen levels (marked on the plots); rate constants were as shown in k-set3 of Table 3. (A) No feedback from HRE elements in the proline hydroxylase genes PHD2 and 3; k7 = k8 = k9 = k10 = k11 = 0.04; k32 = 0; k33 = 0 (Figure 3). (B) As in A, except with feedback set at k32 = 0.04. (C) As in A, except with feedback set at k32 = 0.40. (D) As in panel C, except with proline hydroxylase degradation added (k33 = 0.04).

Display of the Core Subsystem as an “Explicit” Interaction Diagram That Defines the System for Simulation

An explicit interaction diagram (Figure 2A) shows the reactions that make up the core subsystem to be simulated and displays the reactions as molecular association/dissociation or as stoichiometric conversions; thus, the diagram represents a “microworld” model (Kholodenko and Westerhoff, 1995) based exclusively on mass action law terms describing the individual interactions (see Figure 1B for symbol definitions). This diagram defines the reaction steps in a manner that allows direct translation into the input to a computer program (Kohn, 1998, 2001). Enzymatic reactions are represented by three rate constants, which govern enzyme:substrate association, enzyme:substrate dissociation, and conversion of enzyme:substrate complex to products, respectively.

Figure 2.

(A) Explicit diagram of the assumed essential “core” subsystem derived from the network shown in Figure 1. Explicit diagrams define inputs for computer simulation (Kohn, 1998, 2001). Rate constants (k values) are defined next to interaction lines; for binding interactions, the k values for association and dissociation rates are denoted in that order. The underlined numbers next to the molecular species symbols correspond to the species identification numbers in the first column of Table 1. Unless otherwise specified, the simulations monitored the dependence of total HRE occupancy (molecular species 23, the output) on oxygen level (species 20, the input) in the absence of feedback stimulation of proline hydroxylase synthesis (i.e., k32 = 0). The simulations in Figure 7 added feedback and monitored mRNA (species 11) as output. The simulations in Figures 9 and 10 combined full activity for HRE occupied by nonhydroxylated HIFα:ARNT (species 7) with 50% activity for HRE occupied by hydroxylated HIFα:ARNT (species 22); the monitored output was initiated transcripts (species 8). (B) Summary block diagram of the input, output, and core subsystem components.

HRE-bound transcription factor has two forms that we initially assumed to be equally stimulatory: unhydroxylated HIFα:ARNT bound to HRE (species 7 in Figure 2A) and hydroxylated HIFα:ARNT bound to HRE (species 22). This assumption was relaxed in the studies described in Figures 9 and 10. A negative feedback loop is formed by the control of at least some proline hydroxylase genes by HRE elements; this feedback was included only in the simulations in Figure 7. The monitored output was HRE promoter occupancy, unless otherwise indicated in the figure legends. Except in Figures 9 and 10, promoter occupancy is assumed to correspond to gene activation. (Details are given in the figure legends.)

A summary block diagram (Figure 2B) shows the input (molecular oxygen), which governs the core subsystem, which in turn governs the output (HRE occupancy/activation or HRE-dependent mRNA). The core subsystem (feedback loop excluded) consists of five primary monomolecular species, 12 total molecular species, and 12 independent rate constants (some of the rate constants were linked as described below).

Coding the Subsystems as Reaction Files for Input to a Computer Program

The operation essentials of the simulation program used here were described previously (Kohn, 1998, 2001). The program and a description of its mode of operation are available at http://discover.nci.nih.gov or on request (kohnk@dc37a.nci.nih.gov). In brief, the program iterates a set of finite difference equations, each equation expressing one interaction in the diagram (Figure 2A). Thus, each equation corresponds to a term in a set of ordinary differential equations. The program is similar to a differential equation solver, except that we do not require convergence to a final state in all cases. Although convergence to a final state was usually achieved, there were exceptions, usually within the switch transition zone, where convergence sometimes was extremely slow. Our imposed limitation on the time we allow for convergence is not unrealistic, because the cell may undergo global changes faster than the time required for some reactions to reach steady state. In any case, our imposed time limitations did not affect the essential system behavior we describe.

The reaction files used for program input are shown in Tables 1 and 2 (in simplified form). Some of the rate constants were linked as follows. The rate constants for the association and dissociation of hydroxylated HIFα and ARNT (k21 and k22) were automatically set equal, respectively, to the rate constants for the association and dissociation of unhydroxylated HIFα and ARNT (k3 and k4) (Figure 2A). Similarly, the program was set to automatically set k15 = k12, k16 = k13, and k17 = k14, because we assume that proline hydroxylase acts on HIFα the same way whether or not the HIFα is bound to ARNT. Also, k29 = k5 and k30 = k6, because we assume that the binding to HRE is independent of whether the HIFα is hydroxylated or unhydroxylated. Thus, in the absence of the mRNA loop, there are 12 independent rate constants.

Table 1.

Molecular species file

Species no.	Initial concentration	Species identifier
1	1	Hif precursor
2	0	Degradation products
3	5	Hif
4	5	Arnt
5	0	Hif:Arnt
6	1	Hre
7	0	Hif:Arnt:Hre
8	0	Transcript intermediate-1
9	0	Transcript intermediate-2
10	0	Transcript intermediate-3
11	0	mRNA
12	10	Proline hydroxylase (PH)
13	0	Hif:PH
14	0	HifOH
15	0	Hif:Arnt:PH
16	0	HifOH:Arnt
17	10	Vhl
18	0	HifOH:Vhl
19	0	HifOH:Arnt:Vhl
20	1	Oxygen
21	0	Hif:Arnt:Hre:PH
22	0	HifOH:Arnt:Hre
23	0	Species 7 + 22

Table 2.

Reaction file

Reaction	Input species		Output species		Rate constant
1	− 1	0	3	0	0.1930
2	3	0	2	0	0.0007
3	3	4	5	0	0.0148
4	5	0	3	4	1.6733
5	5	6	7	0	0.2681
6	7	0	5	6	0.0809
7	− 23	0	8	0	0.0400
8	8	0	9	0	= k7
9	9	0	10	0	= k7
10	10	0	11	0	= k7
11	11	0	2	0	0.0400
12	3	12	13	0	1.5478
13	13	0	3	12	0.0416
14	13	− 20	12	14	0.0226
15	5	12	15	0	= k12
16	15	0	5	12	= k13
17	15	− 20	12	16	= k14
18	14	17	18	0	0.4738
19	18	0	14	17	0.1392
20	18	0	17	0	0.2144
21	4	14	16	0	= k3
22	16	0	4	14	= k4
29	6	16	22	0	= k5
30	22	0	6	16	= k6
31	− 7	− 22	0	23	c23=c7+c22
32	− 11	0	12	0	0.0400

These files (Tables 1 and 2) were used as input for the simulations shown in Figure 7B. The numbers under the columns headed input species and output species correspond to the reaction identifiers (underlined numbers in Figure 2A). The number preceded by “c” refers to the concentration of that species. A minus sign before a species identifier number flags the program not to decrement that species during the reaction. It is used when a species concentration, such as oxygen, is to be held constant. An equal sign in the right-most column signals the indicated linkage of rate constants. The rate constants shown here are similar to k-set3 in Table 3, with k7-11 and k32 all set equal to 0.04 (see Figure 2A).

When the mRNA loop is included, the first-order rate constants for the sequence of steps leading to mRNA were automatically set equal: k7 = k8 = k9 = k10 (Figure 3). (Thus, when k7 is changed during a scan, k8, k9, and k10 are automatically set equal to it.) The sequence of steps simulates a time delay in the production of mRNA. The program coding allows these rate constants to be linked automatically, a useful feature for simulations with a series of different rate constant values.

Figure 3.

(A) Automated search for sets of rate constants (k-sets) giving progressively higher oxygen-response ratios. Oxygen-response ratio is defined as HRE-occupancy at oxygen level = 0.5 divided by HRE-occupancy at oxygen level = 1.0 (arbitrary units); HRE-occupancy is the fraction of the HRE elements that are occupied by HIF-1α:ARNT complexes (hydroxylated plus nonhydroxylated HIF-1α complexes, species 7 plus 22 in Figure 2A) and is taken to be equivalent to HRE activation. Feedback stimulation of proline hydroxylase synthesis was excluded (k32 = 0) in this set of simulations. The figure shows the results of a sequence of 978 simulations, iteratively selected for progressively higher oxygen response ratios. (B) Switch-like oxygen dependence of HRE-occupancy/activation obtained with the rate constant set that gave the highest response ratio in the search shown in A (k-set1 in Table 3).

Search of Parameter Space for Switch-like Responses to Oxygen

The previously described program (Kohn, 1998, 2001) was modified to permit searching of parameter space for switch-like responses of the output species (e.g., HRE occupancy) as a function of the concentration of input species (e.g., oxygen). To carry out this search, two simulations were run for each set of rate constants (the parameters k), one at oxygen level 0.5, and one at oxygen level 1.0 (arbitrary units). When near steady state was achieved, the ratio of HRE occupancy (species 23, the “output”) for the two oxygen levels was determined. The program searched iteratively for progressively higher values of this ratio (the “criterion”). The total amount of HRE was set at 1.0. To avoid high ratios arising from very small denominators, a floor was set, such that output values <0.05 were automatically elevated to 0.05. The ratio therefore was confined to values between 1 and 20. In biological terms, the floor implies that there is a background level below which gene expression will never go (at steady state), regardless of oxygen level. If the criterion ratio is greater than 10, there must necessarily be some nonlinearity (sharpness) in the oxygen dependence.

Distributions in “k-Space”

A “k-set” is a set of rate constants (k values) that define a point in a k-dimensional space (k-space). Actually, the values used were LOG(k). A distance measure in this logarithmic k-space is the Euclidean SQRT(SUM(LOG (k))^2). A suitable distribution of points in this space was obtained over a 12-dimensional hypersphere volume of radius LOG(r) centered about a point defined by a given k-set. The procedure was as follows:

First, a random subradius was obtained as

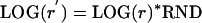Eq. 1

where LOG is natural logarithm and RND is a random number between 0 and 1. A new random point was obtained by modifying each k individually as

Eq. 2

(a new RND being selected for each k). This procedure selects a random point separated from the center point (the original k-set) by a distance of

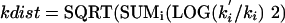Eq. 3

(The reason for the two random steps is that it facilitates exploration of the region near the center, as well as far from the center.)

An intuitive meaning of kdist can be obtained by calculating the factor by which all of the k values would have to be changed to give that value of kdist. The factor is

Eq. 4

where n is the number of k values that are changed. For example, if kdist = 0.8 and n = 12, then a = 1.069. That is, a 6.9% change in all 12 k values gives kdist = 0.8. We use this calculation to provide a measure of robustness.

Robustness of an optimized k-set depends on how much one can change the k values (how far away one can go in k-space) before the response is substantially lost. A measure of robustness is the kdist at which the median oxygen response ratio is reduced by 50% (we call this the kdist50). Because we use median values, we can make the following interpretation: if kdist > kdist50, then more than half of the simulations will give results <50% of optimum. If 50% loss of response is considered to be system “failure,” then kdist50 is the distance at which the system fails half the time.

Median values were obtained as follows. The k-sets obtained in each set of simulations were sorted in Microsoft Excel on the basis of increasing kdist. Median values for successive ranges of kdist were obtained for groups of ∼100 simulations each; the median values for both oxygen response ratio and kdist in each group were obtained using the MEDIAN function in Excel.

RESULTS

A Core Subsystem Can Produce Switch-like Oxygen Response Transitions

The rate constant parameter space was searched iteratively for progressively higher oxygen response ratios (ratio of HRE occupancy at oxygen = 0.5 relative to oxygen = 1.0), as described under MATERIALS AND METHODS. In this model, feedback is excluded (k32 = 0; Figure 2A), and HRE occupancy is taken to be equivalent to promoter activation. Figure 3A shows the progressive increase in the oxygen-response ratio criterion in the course of 978 successive simulation runs. The highest response ratio achieved was 14.7. As explained under MATERIALS AND METHODS, the highest ratio that can be achieved is 20, and any ratio above 10 implies a nonlinear response with some degree of sharpness. The set of rate constants that gave the highest response ratio (14.7) is shown in Table 3 (k-set1).

Table 3.

Selected rate constant sets that give sharp transitions

Reaction	k-set1	k-set2	k-set3
1	0.2321	0.1069	0.1929
2	0.0017	0.0013	0.0007
3, 21	0.0121	0.0060	0.0148
4, 22	0.6163	1.7740	1.6732
5, 29	0.1693	0.6213	0.2681
6, 30	0.0566	0.0165	0.0809
12, 15	0.8326	2.1959	1.5478
13, 16	0.0196	0.0442	0.0416
14, 17	0.0361	0.0142	0.0226
18	0.5722	1.5914	0.4738
19	0.2667	0.0208	0.1392
20	0.4591	3.6871	0.2144

Using this set of “optimized” k values, an oxygen response curve was obtained (Figure 3B). (The initial concentrations were as in Table 1.) A sharp response transition is seen, centered at oxygen = 0.65 (arbitrary units). Under these conditions (VHL = 10), HRE occupancy was almost entirely by nonhydroxylated HIFα:ARNT (species 7; our unpublished data).

A second independent search of parameter space led to a new and substantially different set of optimized rate constants (Table 3, k-set2), which achieved a response ratio of 17.8. As with k-set1, k-set2 produced a sharp response transition, in this case centered at oxygen = 0.75.

Dependence of the Theoretical Oxygen Response Curve on ARNT

Oxygen response curves for various amounts of ARNT in the system (k-set1) are shown in Figure 4A. We see that HRE occupancy (promoter activation) at low oxygen levels increases as total ARNT is increased. At high oxygen, HRE occupancy remains low even at high ARNT. Notably, the response transition occurs at the same oxygen level, independent of total ARNT.

Figure 4.

Dependence of the oxygen response curves on the amounts of protein components in the system. The rate constants were those of k-set1 in Figure 3. (A) Dependence on total ARNT. (B) Dependence on total VHL. (C) Dependence on total proline hydroxylase (PHD2 and 3). “Total” includes all of the complexes in which that molecule exists.

Dependence of the Theoretical Oxygen Response Curve on VHL

Oxygen response curves for various amounts of total VHL are shown in Figure 4B. We see that HRE occupancy at high oxygen levels decreases as total VHL is increased. At low oxygen, HRE occupancy is high, independent of VHL. As in the case of ARNT, VHL did not affect the oxygen levels at the response transition.

Dependence of the Theoretical Oxygen Response Curve on Proline Hydroxylase

Oxygen response curves for various amounts of total proline hydroxylase protein are shown in Figure 4C. Contrary to what we have seen with ARNT and VHL, the oxygen response transition is markedly dependent on the amount of proline hydroxylase in the system. HRE occupancy becomes very low at sufficiently high oxygen levels, independent of proline hydroxylase content. The maximum achievable HRE occupancy at low oxygen, however, decreases as proline hydroxylase content increases.

Distribution of Oxygen Response Ratios in k-Space

To gauge the uniqueness of the optimized set of rate constants (k-set1) described above, we explored a region of the logarithmic k-space centered about this k-set point (see MATERIALS AND METHODS). We see that the oxygen-response ratio remains high within a region close to the optimized k-set (Figure 5). The response ratio then drops increasingly often as distance is increased. However, even at large distances, occasional (albeit rare) k-sets have high response ratios. We do not know whether there are isolated pockets of “good” k-sets, or whether these regions are connected by linear or branched channels.

Figure 5.

Distribution of oxygen response ratios (HRE occupancy at oxygen level = 0.5 divided by HRE occupancy at oxygen level = 1.0) over a spherical volume of logarithmic k-space centered at k-set1 (see MATERIALS AND METHODS). For 3010 random points in k-space, oxygen response ratios were obtained and plotted against Euclidean distance from the point defined by k-set1. (Each point in k-space defines a set of rate constants.)

Robustness

Because regulatory networks must function correctly over a range of local conditions, it is useful to gauge model networks for “robustness.” We measured robustness from data similar to that described above for k-set1. Starting from an optimized k-set, the rate constants (k values) were subjected to random changes. Simulations were carried out with the modified k-sets, which were randomly distributed in k-space (see MATERIALS AND METHODS). The distance of each modified k-set from the starting optimized k-set was determined. For each distance interval (containing 100-200 simulations), the median response ratio for the k-sets that fell within that distance interval was plotted against the distance (Figure 6). Figure 6 includes four independent data sets, two for optimized k-set1 and two for k-set2. (The oxygen response ratios were normalized, setting the maximum ratio to 1.) Figure 6 shows agreement among all four data sets, and shows a half-maximum value, kdist50 = 0.79 (see MATERIALS AND METHODS). (log₁₀(kdist) = -0.1 in Figure 6 corresponds to kdist = 0.79.) As a measure of robustness, this value means that the 50% failure threshold occurs when all of the rate constants (k values) are altered by 6.8% (see equation 4 and subsequent discussion under MATERIALS AND METHODS).

Figure 6.

Robustness plots for k-set1 and k-set2 (Table 3). Two independent scans of the volumes of k-space centered at k-set1 (open symbols) and two centered at k-set2 (filled symbols) are shown. The median value of the normalized oxygen response ratio was plotted against log(k-distance) from k-set1 or k-set2. Oxygen-response ratio was normalized by setting the optimum for each k-set (14.7 for k-set1 and 17.8 for k-set 2) equal to 1.0. We measure robustness by the distance at which the median oxygen response ratio has declined to half its maximum value.

Effect of the Feedback Loop from HRE Activation to Proline Hydroxylase

The proline hydroxylase genes (PHD2 and PHD3) are thought to be regulated, at least in part, by an HRE in the promoters (Figure 2A). We looked at how this feedback affects the response of HRE-regulated mRNA to oxygen.

The production of mRNA was modeled as a sequence of four reaction steps, all of whose rate constants (k7-k10) were linked to be equal. This sequence models a time delay in mRNA production. A new set of optimized rate constants (k-set3 in Table 3) was obtained by searching parameter space, varying the same 12 k values as before and holding the new k values constant at k7 = k8 = k9 = k10 = 0.2; k11 = 1; k32 = 0.1.

As a baseline for comparison, the time course of mRNA response to various oxygen levels in the absence of feedback is shown in Figure 7A. As in all of the preceding simulations, the final values of the output species rose to near steady-state plateaus, and there was a sharp oxygen-dependent transition of mRNA response.

However, when a low level of feedback was added (Figure 7B), the oxygen response kinetics in the transition zone became biphasic, with mRNA levels rising for a period of time and then declining. Thus, the response to intermediate levels of oxygen becomes transient, its duration increasing with degree of hypoxia. In accord with this general picture, del Peso et al., 2003 recently reported that hypoxia increases PHD2 and three mRNA levels by increasing the expression of their genes in a HIFα-dependent manner and that 1% oxygen caused the amount of HIF2α to rise and then fall (del Peso et al., 2003).

When the strength of feedback was increased 10-fold (Figure 7C), elevated mRNA concentrations persisted even at high oxygen levels and exhibited damped oscillations. The oscillations were reduced when degradation of proline hydroxylase was added as a step in the network (Figure 7D).

What Features of the Core System Are Responsible for the Switch-like Transitions?

To gain insight into mechanisms that can give rise to sharp transitions in simple systems without feedback loops, we carried out ∼15,000 simulation runs at random points in a volume of parameter space encompassing the two previously found optima: k-set1 and k-set2, listed in Table 3. The endpoint monitored was HRE occupancy ratio for an oxygen level of 0.5 relative to 1.0, and the mRNA loop was excluded (k32 = 0). The general conditions were the same as in the previous simulations without feedback.

A sharp oxygen-response transition (HRE occupancy ratio >10) was found in 0.84% of the simulation runs. It seemed that high HRE occupancy ratio required a high k12/k13 ratio and/or low k3/k4 ratio (Figure 8). By referring to Figure 2A, we can see what this observation implies. It means that HIFα must bind with high affinity to proline hydroxylase and with relatively low affinity to ARNT. The mechanism, or at least part of it, is thus revealed. When oxygen level is high, HIFα is rapidly degraded (via VHL), and proline hydroxylase is continually regenerated and available to bind and sequester newly formed HIFα in an enzyme-substrate complex that is incapable of promoter binding. When oxygen level is low enough to allow HIFα to accumulate to levels that exceed the amount of available free proline hydroxylase, the excess HIFα suddenly becomes available for binding ARNT to produce the active transcription factor. For this to work, the HIFα must have substantially higher affinity for proline hydroxylase(s) than for ARNT. (A subsidiary requirement is that the rate of degradation of hydroxylated HIFα, governed by k18, k19, and k20, is fast enough.)

Figure 8.

Dependence of oxygen-response ratio on HIFα affinity for ARNT (k3/k4) and HIFα affinity for proline hydroxylase (PH) (k12/k13) (association constant/dissociation constant; see Figure 2A for definition of k values). Oxygen response ratio is HRE occupancy (activation) at oxygen = 0.5 divided by HRE occupancy at oxygen = 1.0 (arbitrary units). Oxygen-response ratios were determined in the absence of feedback (k32 = 0). Simulations (15,182) were carried out for random sets of rate constants (k-sets) over a volume of k-space encompassing the two previously determined optima (k-set1 and k-set2). Each rate constant was randomly chosen over a range of sixfold decrease to sixfold increase from the selected centerpoint in k-space. (The randomization was logarithmically uniform.) Oxygen-response ratios: >13.5, red circles; 10-13.5, orange triangles; 5-10, green squares; 1.5-5.0, blue dots (simulations that gave oxygen response ratios <1.5 were omitted from the plot).

Alternative Models

To see how alternative models could be distinguished, we examined a subtle, but plausible, modification of the model. Instead of allowing transactivation to be independent of HIFα hydroxylation, we assumed that hydroxylation prevents or reduces transactivation potency. This is plausible in light of recent evidence that hydroxylated HIFα could diminish histone acetylation, thereby reducing the ability of chromatin to be transcribed. The original and modified models both assume that hydroxylation does not affect the binding of HIFα to ARNT.

We carried out a new set of simulations, monitoring as output the level of initiated transcripts (species 8 in Figure 2A). As a control, Figure 9A repeats the simulation conditions used in Figure 4B and shows that essentially the same results are obtained whether the monitored output is HRE occupancy or transcript initiation. (The small upward hooks of the response curves at low VHL have no special significance: they arise merely due to our omission of a small background degradation rate for hydroxylated HIFα.)

Using the same conditions, we then examined a modified model that assumed hydroxylated HIFα to be transcriptionally inactive. The result (Figure 9B) is that the effect of VHL is entirely different from that seen when hydroxylated HIFα is fully active (Figure 9A). The reason for the difference is that the inactive hydroxylated HIFα now competes with the active nonhydroxylated HIFα for occupancy of HRE sites. As a result, VHL deficiency reduces HRE expression at low oxygen levels and fails to increase expression at high oxygen levels. This modified model thus contradicts the fact that loss of VHL function increases the expression of HRE-dependent genes under normoxia.

We then tested a model in which hydroxylated HIFα activates HRE-dependent genes 50% as effectively as nonhydroxylated HIFα (the binding to HRE remaining unaltered). The result (Figure 9C) is consistent with what we know, but makes a new prediction. The expected effect of VHL deficiency to increase HRE activity under normoxia is seen, but the increase does not reach the levels achieved under hypoxia. Moreover, the effect of VHL deficiency under hypoxia would be to reduce HRE activity, a seemingly paradoxical prediction that could be tested.

HIF1α Synthesis Rate as an Avenue for Control of HRE-dependent Gene Expression

HRE-dependent genes can be activated under normoxia by growth factor signaling, particularly from insulin and insulin-like growth factors. Recent findings indicate that this activation is not due to increased HIF1α stability but rather is due to increased rate of HIF1α production (Bardos et al., 2004). We therefore investigated the effect of HIF1α production rate (k1 in Figure 2A).

Figure 10A shows that using the same conditions as in Figure 9C with VHL = 2.0, the initiation of HRE-dependent transcripts respond to HIF1α production rate (k1) in switch-like manner and that the production rate required to turn on transcription increases with oxygen level. This suggests that the same network model that produces switch-like responses to hypoxia can also produce switch-like responses to growth factors. In addition, it predicts that reducing oxygen tension will reduce the growth factor signal strength required to turn on HRE-dependent genes.

Figure 10B complements Figure 10A. It shows how the hypoxia response curves depend on HIF1α production rate. The oxygen level of the transition sensitively increases with increased HIF1α production rate.

The implications of these observations will be considered further in DISCUSSION.

DISCUSSION

In this study, we took the view that the essential behavior of a complex bioregulatory network is already encoded through evolution in a small part of the network, which we call the “core” subsystem. Although there may be many other connections that would modulate the behavior of the network, the essential behavior may already be apparent in a core subsystem. An advantage of small model systems is that the potential mechanisms revealed can more easily be comprehended. The findings of the current investigation indeed suggested a testable mechanism that, moreover, could have general applicability to other systems.

We selected a core subsystem of the cell's hypoxia response network by scrutinizing a molecular interaction map of the complex network that controls the HIF transcription factors. The selected core subsystem is conserved between nematodes and mammals (C. elegans, Drosophila, and humans). The test of this selection was whether it could show biologically plausible behavior with appropriate choices of parameter values.

We have little or no information about the numerical values of most of the relevant parameters. However, a biological system must be robust, so as to preserve its essential behavior over a range of parameter values (Bluthgen and Herzel, 2003). Moreover, evolution may have settled on one of the more easily discovered suitable parameter sets. Therefore, searches of parameter space by simulation could mimic evolution and have a chance of finding conditions relevant to biological reality.

To carry out this kind of search of parameter space, we needed a numerical criterion that would measure the “goodness” of any given set of parameters, with respect to how well it mimicked the target biological behavior. For the hypoxia response system, such a criterion is readily available, namely, the ratio of HRE-dependent promoter activation in the presence of low versus high oxygen. We hypothesized that this “activation ratio” would show a sharp oxygen-dependent transition, such that gene activation would switch between high and low relatively abruptly at a critical oxygen level. We studied two independently optimized parameter sets that gave sharp oxygen-dependent transitions and determined how these transitions depend on the amount of each molecular component of the system.

The results give us a clear basis for comparison with experiment, as follows. 1) Dependence of promoter activation on ARNT should be strongly positive at oxygen concentrations below the switch-like transition, should be weak above the transition, and should not affect the oxygen concentration at which the transition occurs (Figure 4A). 2) Dependence on VHL should be strongly negative at oxygen concentrations above the transition, should be weak below the transition, and, again, should not affect the oxygen concentration at which the transition occurs (Figure 4B). 3) Dependence on proline hydroxylase should show a marked effect on the oxygen concentration at which the transition occurs (Figure 4C). The oxygen concentration at the transition should decrease as proline hydroxylase is increased. In addition, the maximum response to hypoxia may decrease at high proline hydroxylase levels (Figure 4C). 4) As a function of time after the institution of a moderate degree of hypoxia, there should be a transient response of HRE-dependent genes, and the duration of the response should increase with the severity of hypoxia (Figure 7B). Physiologically, this would correspond to adaptation to reduced (but survivable) oxygen levels. 5) Sharp transitions should also be seen as a function of HIFα synthesis rate at fixed oxygen concentration (including normoxia), and the HIFα synthesis rate at which the transition occurs should be increase with increased oxygen concentration (Figure 10A). 6) The deduced mechanism of the switch-like behavior suggests that HIFα would have substantially greater affinity for HIF proline hydroxylase(s) than for ARNT (Figure 8).

Very few quantitative studies have been reported that show the shape of the curve depicting hypoxia response as a function oxygen concentration. Jiang et al. (1996) found in HeLa cells that HIF-1 protein levels and DNA-binding capacity remained nearly unchanged down to 3% oxygen and rose rapidly with further reduction of oxygen down to 0.5%. The reported oxygen dependence does not seem to be as sharp as in our simulations; however, no measurements were reported between 0.5 and 2%. More detailed studies are needed to determine the sharpness of the transition.

It should be stressed that a great deal has been left out of our current model. This was intentional. In the absence of adequate data to distinguish more detailed models, we kept our present model in the simplest form, which provides a starting point from which to guide forthcoming quantitative experiments. Molecular interactions would be added to the model as we are compelled to do so by experimental results. Of particular interest is the interaction between HIF1α and the p53-Mdm2 system (Ravi et al., 2000; Chen et al., 2003). Although the oxygen-independent action of PHD1 (Bruick, 2003) was omitted from the model (Figure 2), we found that the addition of PHD1 to the model reduced the oxygen concentration at which the transition occurs without changing the shape of the oxygen dependence curve (our unpublished data). It remains to be determined how the system will be affected by the presumed inhibitory action of HIF-3α (Makino et al., 2002). Further details that remain to be elucidated, both by experiment and theory, include the effects of hydroxylation at different HIFα sites, the action and regulation of the asparagine hydroxylase, and the effects of the different HIFα family members. Some of these factors may vary among types of cells and tissues.

The sensitivity to hypoxia (and activation of HIFα) varies from one tissue to another, presumably due to differences in the forms of PHD and HIFα that are predominantly expressed. Our inferences pertain to cells that express predominantly one functional form of either PHD2 or PHD3, which we believe to be the case in most normal cell types. Tissues may differ in quantitative details. For example, in the oxygen concentration of the transition, but the essential behavior we describe in our model should be preserved. Thus, different tissues expressing different enzyme family members or variants may correspond to different instances of parameter sets in Figure 8. Many widely different sets of rate constants can give sharp transitions and similar qualitative behavior. Such differences may correspond to differences among tissues expressing different isoforms of proline hydroxylase and/or HIFα.

Regardless of the extent to which experiment will prove to agree or disagree with the simulations of the particular system reported herein, our results suggest quantitative experiments (such as those enumerated above) suited for testing various models. We have shown how switch-like transitions yield predictive power for experiments. It would therefore be useful to look for sharp transitions in various systems and focus on them for theoretical and quantitative experiments. When experiment shows clear deviation from a simple model, it will compel the addition of known or hypothesized interaction steps to the model until adequate fit with experiment is attained.

In the current analysis, all concentrations are necessarily described in arbitrary units. If sharp transitions are found experimentally, some of these arbitrary units could be calibrated to correspond to real values. Moreover, depending on the degree of agreement with the phenomena seen in the simulations, it may be possible to estimate some of the rate constant parameters.

Mechanism and Implications of the Switch-like Transition

The α subunits of the HIF transcription factors are up-regulated by hypoxia and by growth factors. Hypoxia increases the stability of the HIFα proteins without changing their synthesis rate, whereas growth factors increase the production rate of these proteins without changing their stability (Bardos et al., 2004). We now find that the same network model, with the same parameter settings, can produce switch-like gene activation both in response to hypoxia (increased stability) and in response to growth factor (increased production).

The switch-like behavior of our model requires a high enzyme-substrate affinity between HIFα and proline hydroxylase (Figure 8). High enzyme-substrate affinity is also the basis for the Goldbeter-Koshland model for switch-like behavior (Goldbeter and Koshland, 1981), although our model lacks the reciprocal reactions that are fundamental to their model. Nevertheless, the same principle may be involved, fitting under their rubric of “zero-order ultrasensitivity.” Next, we will explain what we mean by this, and how our model seems to operate.

The amount of HIFα in the system depends on the balance between production and consumption (hydroxylation followed by degradation). When HIFα production (synthesis) is relatively slow, almost all of the protein binds to proline hydroxylase and becomes hydroxylated and degraded before it can bind ARNT; therefore, very little active transcription factor (HIFα:ARNT heterodimer) is formed. When production exceeds consumption, the proline hydroxylase becomes saturated with HIFα, and HIFα consumption rate is maximized. Further HIFα production can no longer increase the hydroxylation rate; the consumption kinetics thus becomes zero-order with respect to HIFα concentration. Free HIFα then becomes available to bind ARNT and to form active transcription factor (HIFα:ARNT heterodimer). The formation of HIFα:ARNT heterodimer thus is switch-like as HIFα production is increased or hydroxylation/degradation is decreased, because, either way, a threshold will be passed where HIFα production suddenly exceeds consumption. As this threshold is passed, the production of HIFα:ARNT heterodimer is switch-like, because of the assumed high affinity of HIFα for proline hydroxylase, which makes HIFα unavailable to ARNT until the hydroxylase becomes saturated, which occurs when HIFα production exceeds consumption.

This mechanism of switch-like behavior is consistent with the observed short half-life of HIF-1α (∼5 min) in the presence of oxygen (Kallio et al., 1999). The mechanism also implies a high rate of HIFα synthesis, consistent with the observed rapid increase in HIF-1α protein (detectable within 2 min) in response to hypoxia (Jewell et al., 2001). The rapid oxygen-independent synthesis and rapid oxygen-dependent degradation of HIF-1α permit rapid responses to changes in available oxygen.

Our model suggests how the controls on HRE-dependent gene expression via hypoxia and growth factor may be interrelated. Tissues, or cell types within tissues, differ in their normal degree of oxygenation and in the oxygen levels where hypoxic response is expected. As we have seen, the model shows how the “thermostat setting” for hypoxic response could depend on the rates of HIFα synthesis and hydroxylation/degradation. HIFα synthesis rate depends on the strength of growth factor signaling; hydroxylation/degradation rates depend on which proline hydroxylase and HIFα isotypes predominate in particular cell types. These factors therefore could modulate the hypoxia response in different cell types in a manner predicted by the model.

Perspective

It is becoming recognized that understanding bioregulatory network function requires computer simulation. It remains to be determined, however, how to go about this in a useful way. Not only are the systems extremely complicated but also their function may depend critically on the details of the assumed models. Rather than attempting to include all the known interactions in one global simulation, our approach is to look for simplifications that could give a starting point from which more complex models can be explored by stepwise addition of modifier interactions.

The current study may justifiably be viewed as a bold oversimplification. However, if we are eventually to comprehend these highly complex systems, we must hope that at least some of them can be approximated by simplified models. Indeed, it is striking how even simple models can generate complex behavior. When theory raises well-defined questions, experimentalists may be encouraged to assemble, perhaps from purified components, the relevant simple networks for insightful study.