Comparison of Three Parametric Models for Glaucomatous Visual Field Progression Rate Distributions

Abstract

Purpose

To compare parametric models for fitting published distributions of visual field progression rates (in dB/yr) for glaucoma.

Method

We fitted a modified Gaussian model, a modified Cauchy model and a modified hyperbolic secant model to previously published distributions of visual field progression rates from Canada, Sweden, and the United States. The modification allowed the shape of the model's distribution either side of the mode to be independently varied to allow for the asymmetric tails seen in visual field progression rate distributions.

Results

Summing likelihoods across datasets, the modified hyperbolic secant was strongly favored (by 26.7 log units) compared with the next best-fitting model, the modified Cauchy. The modified hyperbolic secant was not the best fit for the Canadian dataset, however. Best-fitting modified hyperbolic secant parameters were broadly similarly between datasets, with parameter variances being less than those expected to negate the benefits of a previously described Bayesian method for improving individual visual field progression rate estimates in glaucoma.

Conclusions

Although the optimum model differed depending upon the particular dataset, a modified hyperbolic secant performed well for all distributions investigated and was strongly favored when evidence was summed across datasets.

Translational Relevance

Despite differences in the progression rate distributions between studies, the use of an “average” distribution may still be of benefit for improving individual visual field progression rate estimates in glaucoma using Bayesian methods.

Introduction

The overall rate of visual field loss in glaucoma (in dB/yr) can be estimated by linear regression of the perimetric summary index mean deviation (MD),¹ or by averaging the individual rates of loss at each point in the visual field.² It is a common finding that the distribution of glaucoma progression rates is skewed, with a longer tail for negative rates of progression (i.e., worsening visual fields over time) than for positive rates.^2–5 The ability to quantify such distributions allows rates of progression to be compared between different glaucoma types³ or between different groups with the same glaucoma type (e.g., study populations versus general clinical populations).⁵ More specifically, fully quantifying distributions allows for differences other than those in central tendency (e.g., mean or median rate) or spread (e.g., the interquartile range) to be explored. This may be particularly important when trying to examine differences within the tails of distributions: for example, the number of very fast progressors in a group.⁵ Quantifying progression distributions is also needed for Bayesian methods that use population data to constrain estimates of rates in individuals^6–9 and so help to reduce the wide variation in rates seen when the amount of longitudinal data available is limited.¹⁰

One way to efficiently quantify distributions is by fitting them with parametric models. Glaucoma progression rate distributions have previously been parametrically modelled using a modified hyperbolic secant,⁶ which allows for the slopes of the upper and lower tails to be specified, along with the mode of the distribution. This model was selected because it fitted the general shape of the distribution well enough for the simulation studies then performed, and so no attempt was made to see whether other models might provide substantially better fits.⁶ There has been an increased use of nonparametric methods to quantify aspects of the visual field,^11,12 particularly given the ubiquitous access to fast computing required to generate these analyses. Therefore, it may be questioned why parametric models are required at all, at least for statistical quantification purposes. We believe that parametric models are useful for several reasons. Firstly, simple parametric models for progression rate distributions efficiently summarizes the entire shape of the distribution in a way that simple metrics such as the mode and interquartile range cannot. Secondly, the frequency of rapid rates of progression is relatively small and so it is not uncommon for histograms of empirical progression data to have some bins with a zero frequency in one range, yet have nonzero frequencies at lower and higher ranges. This can occur despite large cohort sizes (e.g., 583 patients in Heijl et al.¹³). Presuming that the distribution of glaucoma is a continuous function, these zero frequencies reflect sampling variability rather than that glaucoma never produces progression rates within the missing range. Conventional nonparametric bootstrapping procedures, where new datasets are generated by sampling with replacement from the original data, will also always have zero frequencies at the same ranges, and so do not solve the problem. It is possible to smooth the data using a spline curve or moving average⁵ and so fill in these gaps, although the degree of smoothing selected is commonly ad hoc and such techniques necessarily widen the frequency distribution and flatten its peak. Modelling the distribution parametrically avoids intermediate zero frequency bins. There is also no inherent reason for such models to bias a distribution in a particular direction (e.g., always widen or narrow) or to systematically reduce the peak of the distribution, although a specific model may indeed create a bias if it is always found to be either too compact or too broad relative to the empirical data. Bootstrap data may still be generated from fitted distributions in order to determine probability limits, a procedure known as a parametric bootstrap. Finally, empirical data is often presented in histograms with markedly differing binning strategies (e.g., regular 0.1-dB/yr wide bins⁵ vs. 0.5-dB/yr bins with open ended-bins for distribution tails²) making a comparison of distributions between different studies challenging. Parametric models of these data can be presented using a common binning strategy and so avoid distortions introduced by different histogram binning strategies.

Here, we examine three candidate models for fitting the distribution of glaucomatous visual field progression rates, and apply them to recent distributional data published in the literature. In addition to employing standard goodness-of-fit assessments, we use statistical methods to investigate whether one of the models is better supported by the data.

Methods

Candidate Models

We investigated three candidate models: a modified hyperbolic secant, a modified Gaussian, and a modified Cauchy distribution. In all cases, the principal modification was to allow for separate parameters to alter the width of the distribution either side of the mode. A Gaussian and a Cauchy distribution represent two extremes of the t distribution, the former having many degrees of freedom and the later having one degree of freedom,¹⁴ thereby representing a compact and a wide distribution, respectively. A Cauchy distribution is sometimes used in robust regression methods to account for outliers in the data not well modelled by a Gaussian distribution.¹⁵

The modified Gaussian was as follows:

where r is the progression rate, A gives the height of the function at its peak, mode gives the position of the peak, and B and C alter the width of the distribution to the more positive and more negative side of the mode, respectively.

The modified Cauchy distribution was as follows:

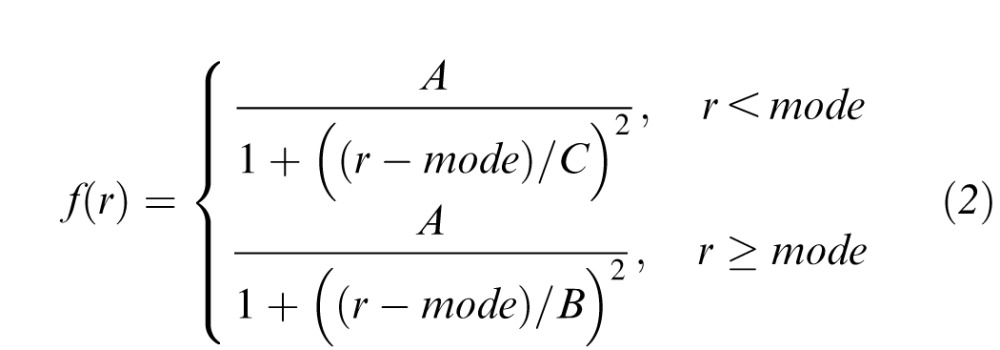with terms defined as per the modified Gaussian distribution.

The modified hyperbolic secant was as described in King-Smith et al.¹⁶ and as previously used to model glaucoma progression rate distributions.⁶ Its parameters were defined as per the modified Gaussian distribution, with mode being equivalent to parameter t in the original equation by King-Smith et al.¹⁶

For this paper, parameter A was set to give an area of one under each function, as calculated by summing the bin heights at 0.1-dB/yr wide intervals between −10 and +10 dB/yr. All three distributions therefore had only three free parameters (i.e., mode, B, C).

Empirical Data and Fitting

We estimated the distribution of visual field progression rates (in dB/yr) in glaucoma from previously published histograms: 2324 glaucoma and glaucoma suspect patients drawn from a tertiary-care setting in Canada (≥5 SITA-Standard 24-2 Humphrey Field Analyzer [Carl Zeiss Meditec, Inc., Dublin, CA] fields, tested every 4 months),⁵ 587 eyes with treated glaucoma from the New York Glaucoma Progression Study (≥8 SITA-Standard 24-2 Humphrey Field Analyzer II fields, tested each 6 to 12 months; data from progressing and non-progressing patients combined),² and 583 patients with primary open-angle glaucoma or pseudoexfoliation glaucoma in Sweden (≥5 Humphrey SITA-Standard fields over ≥5 years).¹³ The Canadian and Swedish studies determined progression rates from linear regression of the summary index MD, whereas the US study determined the overall rate of visual field loss from the average of pointwise linear regression slopes. The variability in each dataset was estimated using a bootstrap procedure, with 10,000 new random datasets produced by sampling (with replacement) from the original distribution and 2.5% and 97.5% limits for histogram bin frequencies then calculated.

Candidate models were fitted to these data using a maximum likelihood procedure. In brief, an initial estimate of a model's parameters was made and the likelihood of obtaining each progression rate in the empirical dataset then determined. The log of these likelihoods were then summed, creating a value that gave the log-likelihood of obtaining the set of progression rates in the dataset given the model. The model parameters were then systematically adjusted (Solver module, Version 14.3.6; Microsoft Excel for Mac 2011, Microsoft, Redmond, WA) in order to maximize this likelihood. Even with optimum model parameters such likelihoods are typically very small (i.e., a large negative value in log units), reflecting that the particular empirical data represents just one example of the many combinations that could be drawn from the same underlying distribution. The absolute likelihood is not a direct measure of goodness of fit therefore, and is heavily influenced by the size of the sample (and, therefore, the number of potential other combinations that exist). Of most importance is the relative likelihoods between models, which quantifies the relative support obtained for each model from the data. These relative likelihoods are mathematically equivalent of those calculated using an Aikaike's Information Criterion (AIC),¹⁴ which are in turn equivalent to the version of the AIC corrected for finite samples (AIC_C) given that both the number of data points and the number of free parameters are identical for the models being compared. We also quantified absolute goodness of fit by calculating the coefficient of determination R² (i.e., the fraction of the total variance in the y-direction that is explained by our nonlinear models, similar to the r² value used in linear regression) for the maximum likelihood fit.¹⁴

To average fits across datasets, we took the average of the fitted parameters for each dataset, consistent with the mean coefficient technique described by Anastasi and coworkers.¹⁷

Results

Figure 1 shows the fit of the three models to the Canadian data, along with the corresponding coefficients of determination. Log₁₀ likelihoods for the modified Gaussian, modified Cauchy and modified hyperbolic secant models were −3036.8, −2891.1, −2893.9, respectively, indicating that the modified Cauchy model fitted best and was 583 times (−2891.1 minus −2893.9 = 2.8 log units) more likely than the next best fitting model, the modified hyperbolic secant. While the shape of the modified Cauchy distributions well captures the extended tails of the empirical data, the modified Gaussian distribution must substantially increase its spread in order to encompass these tails, resulting in a comparatively poor representation of the more central portion of the distribution. The modified hyperbolic secant improves the representation of the central portion of the fit while retaining broad tails, although still underestimates the peak of the data.

Figure 1.

Maximum-likelihood fits of the three parametric models to the distribution of visual field progression rates for a clinical cohort of glaucoma patients and suspects, derived from data reported by Chauhan et al.⁵ Each model (thick line) is in histogram bins identical to those of the empirical data although, for ease of reading, line segments are drawn between the model height at each bin-midpoint. Bootstrap limits (2.5% and 97.5%) on the empirical histogram frequencies are represented by the thin lines, drawn as continuous functions for ease of reading.

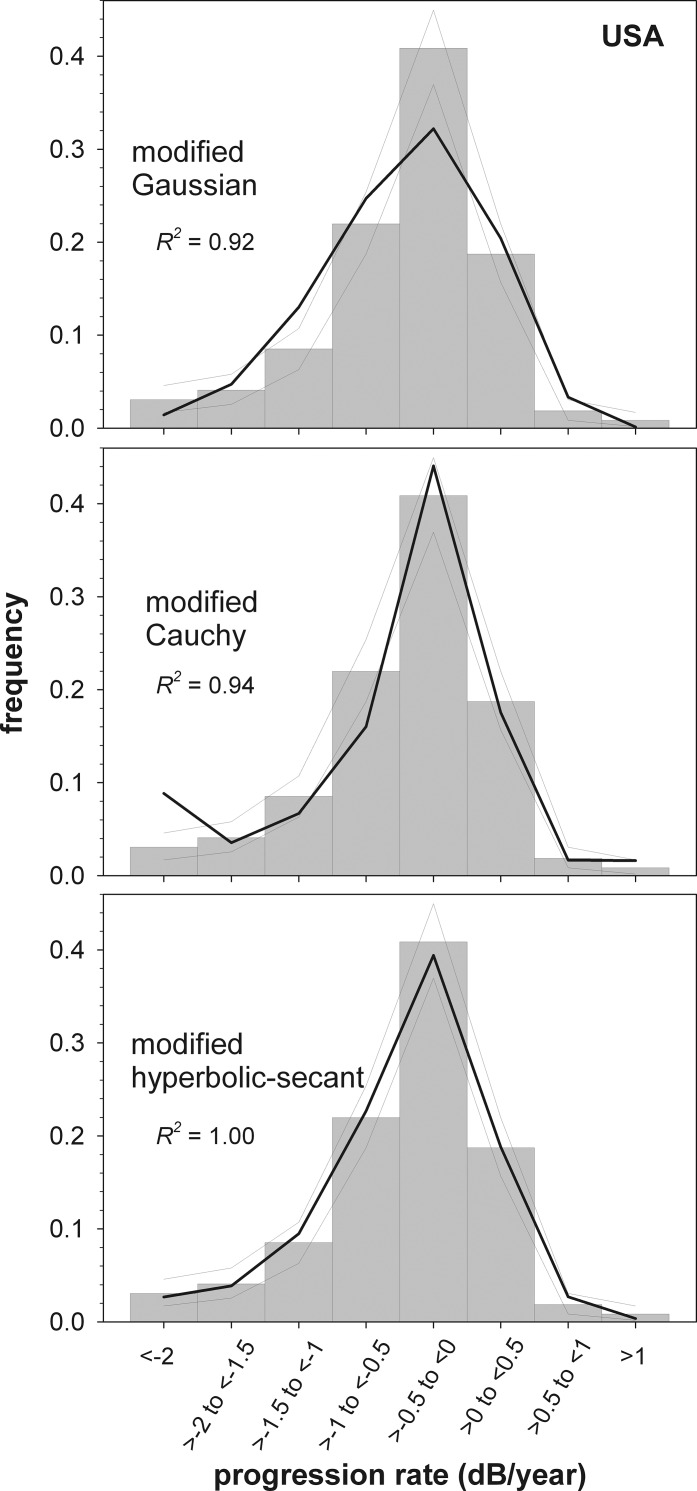
The Swedish dataset (Fig. 2) had a more extended tail for negative progression rates than the Canadian dataset. Log-likelihoods for the best-fit model to the Swedish data were −695.2, −701.3, and −684.1, indicating the modified hyperbolic secant gave the best fit (by 1.0 × 10⁶ times, compared with the modified Cauchy distribution). For the US data (Fig. 3), log-likelihoods were −412.3, −412.1, and −402.8, indicating the modified hyperbolic secant gave the best fit (by 2.8 × 10⁹ times). Summing likelihoods across datasets, the hyperbolic secant was strongly favored (by 26.7 log units) compared with the next best-fitting model, the modified Cauchy. For all three datasets, the modified Gaussian distribution fit had the lowest likelihood and the lowest goodness of fit R² values.

Figure 2.

Maximum-likelihood fits of the three parametric models to the distribution of visual field progression rates for a clinical cohort of glaucoma patients (primary open-angle and pseudoexfoliation glaucoma) from data reported by Heijl et al.¹³ Remaining details are as given for Figure 1.

Figure 3.

Maximum-likelihood fits of the three parametric models to the distribution of visual field progression rates patients from the New York Glaucoma Progression Study, derived from data reported by De Moraes et al.² The upturn in the leftmost point of the modified Cauchy results from the unequal bin widths used for these data: for this model, more people are predicted to have progression rates between −2 and −10 dB/yr (the limit to which rates were calculated in the current paper) than between −2 and −1.5 dB/yr. Remaining details are as given for Figure 1.

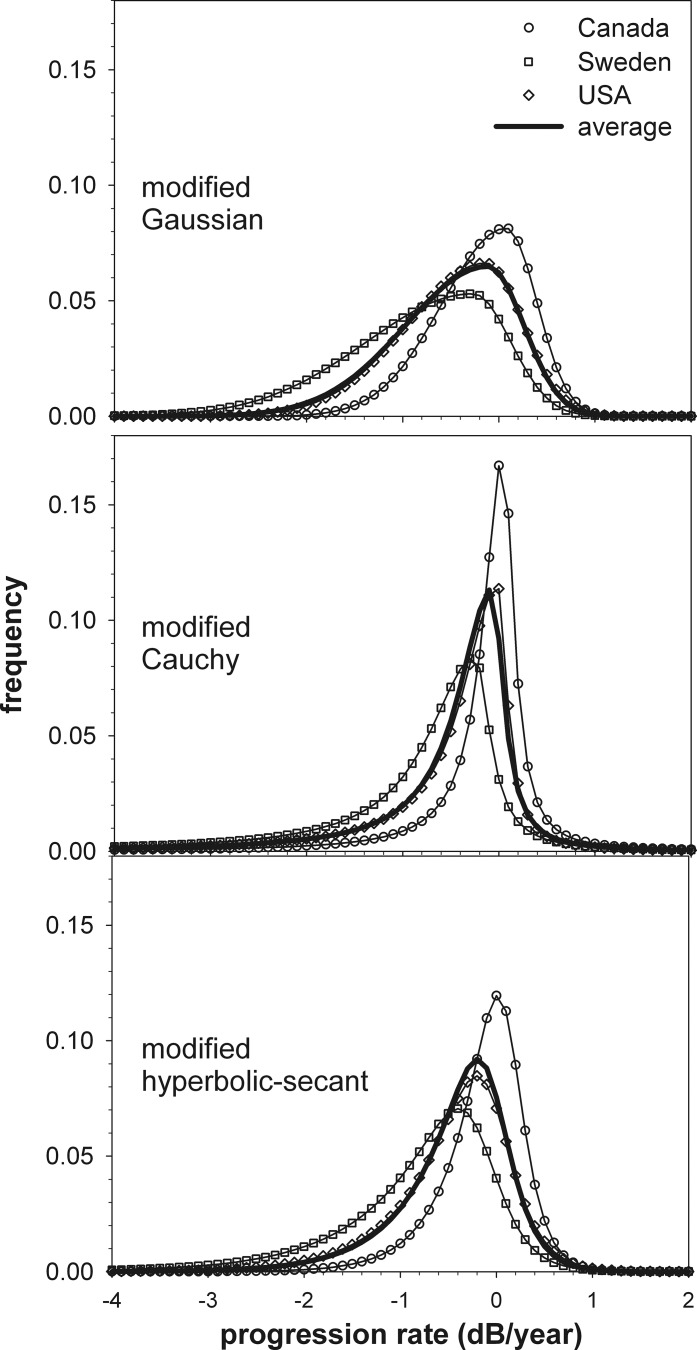
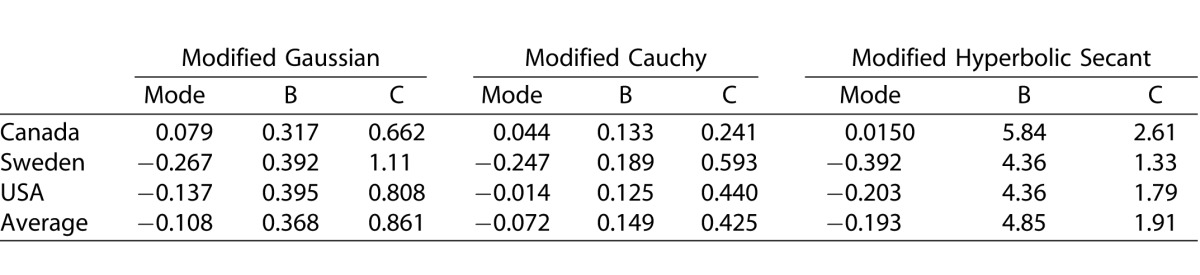
The three dataset analyzed are represented in the literature with different histogram bin widths. Figure 4 shows the best-fit models presented with identical binning strategies (0.1-dB/yr bin widths) to aid comparison. For all datasets the upper limit on positive progression rates is similar. The peaks and negative tails of the distributions differ, however, with the Canadian dataset showing the lowest amount of progression and the Swedish dataset the highest. For all models, the average fit is similar to that for the US data, which is also seen in the similarity between the USA best-fit parameters and the average parameters (Table 1).

Figure 4.

Comparison of the maximum likelihood fits for the three datasets and the three models, along with models using the average parameters of the fits to the three datasets. Model fits for the Sweden and US data sets are as given in Figures 2 and 3 except with histogram frequencies represented in 0.1-dB/yr wide bins.

Table 1.

Free-Parameters for the Maximum Likelihood Fits

Discussion

Our results show that parametric models can describe well the distribution of visual field progression rates in treated glaucoma, with the best-fitting model achieving an R² never less than 0.96 for the three datasets analyzed. The best-fitting model differed depending upon the dataset fitted, but was either the modified Cauchy and modified hyperbolic secant. In each situation, these two models returned fits with R² of at least 0.94. In contrast, the modified Gaussian provided a comparatively poor fit to the Canadian data (Fig. 1) and was never the best-fitting model. When evidence was summed across datasets, the modified hyperbolic secant model was strongly favored.

Differences in how data is binned^2,5 can make the comparison of empirical distributions difficult. By applying a common binning strategy to our parametric models, the differences between datasets can be readily appreciated however (Fig. 4). The Canadian dataset had a comparatively narrow distribution and a high modal progression rate. The high mode may reflect that this distribution includes glaucoma suspects⁵ who by definition would show little or no progression and so should shift the distribution's mode to the right. In addition, a robust regression technique was used to determine progression rates,⁵ which would be expected to reduce the number of very extreme rates arising from statistical variability alone and so narrow the distribution of rates for the population. In comparison, the Swedish dataset contained over one-third of patients with pseudoexfoliation glaucoma.¹³ This likely contributes to the long tail of rapid progression rates in this distribution, given that extremely rapid progression can occur in pseudoexfoliation glaucoma.³ Analyzing glaucomatous progression rates using linear regression of MD may also be influenced by other factors such as cataract, learning, or physiological aging at a rate other than that predicted by average values¹⁸: while such nonglaucomatous factors might be well controlled in clinical trials, their influence may be expected to be more marked in data collected from general clinical populations.

Both the Canadian (Fig. 1) and Swedish (Fig. 2) datasets well demonstrate how bins with zero frequency can occur in the histogram tails of progression rate distributions, despite investigating large numbers of patients. Such zero frequencies present a problem for nonparametric bootstrapping procedures (e.g., note that the bootstrapped 2.5% and 97.5% limits are similarly zero for these bins), although performing a parametric bootstrap (i.e., generating bootstrap samples based on the fitted model) solves this problem. Zero frequency bins also create problems for Bayesian methods that use population information to improve progression rate estimates for an individual,⁶ as such methods cannot return a progression rate within this bin as the a priori probability of such an event is zero (hence, the posterior probability given via Bayes theorem must also be zero). This problem is avoided when a parametric model of the empirical data, rather than empirical data itself, is used to estimate glaucoma progression rates in the population.

Creating an “Average” Distribution: Is it Worth it?

Our current investigation shows that population distributions are broadly similar across three recent, large investigations of visual field progression rates (Fig. 4) despite differences in the specific details of each study, although it is clear that a single model is not the best description of all the datasets analyzed. Is having a model that performs well “on average,” such as the modified hyperbolic secant in the current study, of any benefit, given these distributional differences? In empirical Bayes methods, the distribution of the population (the prior distribution) is estimated from the empirical data itself⁸ and so is therefore very well matched to the particular cohort of patients analyzed in terms of such factors as glaucoma type, ethnicity, and testing procedure. While producing very encouraging results, empirical Bayes probably represent an upper boundary on what performance benefits might be expected, as any commercially developed, widely-implemented progression tool will almost certainly assume a population distribution that differs from that of the patients the tool is eventually applied to. Indeed, outside of a research environment, the precise distribution of glaucoma rates in a given clinical population is almost certainly unknown and so recourse to some form of “average” distribution is required, at least initially. Our data gives some idea of what variation might be expected between populations of different geography and patient inclusion criteria (Fig. 4, Table 1), and it has been argued that at least one of our hospital-based datasets does not represent a selected subgroup of glaucoma patients distinct from that in the wider community.¹³ Previous work suggests that modest performance benefits of Bayesian methods still persists despite discrepancies between the lower tail of the prior distribution and the patient data (each modelled with a modified hyperbolic secant) that were slightly greater than those seen in Table 1, suggesting that use of our distribution defined by average parameters (Fig. 4, thick line) may still have some benefits in improving individual visual field progression rate estimates. An average prior could then be made to better reflect the particular patient group to which it is applied by progressively updating the prior to incorporate information from each patient's test result, in an approach similar to that proposed for determining perimetric thresholds.¹⁹ Improvements from Bayesian methods are likely to be modest, however, owing to the fact that the distribution of progression rates in the population is quite broad and so does not constrain individual progression rate estimates much.⁶ Even if a parametric model were found that fitted the population distribution perfectly (as is very nearly the case for the modified Cauchy distribution fit to the Canadian data, and the modified hyperbolic secant fit to the Swedish data), the broad nature of the fit remains: hence, the goodness of fit of a model is not a guarantee of its use in a Bayesian method.

Summary

We find that parametric models can well describe the distribution of visual field progression rates in glaucoma despite only three free parameters. Aside from efficiently summarizing the entire shape of the distribution, such models can be used to compare incompatibly binned empirical data, perform parametric bootstrap procedures, as well as generate prior distributions for Bayesian progression rate estimators. Models based on distributions broader than a conventional Gaussian distribution are better able to capture the long tails in progression rate distributions. A modified hyperbolic secant found the greatest overall support from the empirical data, but was not the best fit in all cases. Distributions were sufficiently similar that an “average” distribution may still be of use in Bayesian methods to improve the reliability of individual estimates of visual field progression.