Evaluation of a Cone Beam Computed Tomography Geometry for Image Guided Small Animal Irradiation

Abstract

The conventional imaging geometry for small animal cone beam computed tomography (CBCT) is that a detector panel rotates around the head-to-tail axis of an imaged animal (“tubular” geometry). Another unusual but possible imaging geometry is that the detector panel rotates around the anterior-to-posterior axis of the animal (“pancake” geometry). The small animal radiation research platform (SARRP) developed at Johns Hopkins University employs the pancake geometry where a prone-positioned animal is rotated horizontally between an x-ray source and detector panel. This study is to assess the CBCT image quality in the pancake geometry and investigate potential methods for improvement. We compared CBCT images acquired in the pancake geometry with those acquired in the tubular geometry when the phantom/animal was placed upright simulating the conventional CBCT geometry. Results showed signal-to-noise and contrast-to-noise ratios in the pancake geometry were reduced in comparison to the tubular geometry at the same dose level. But the overall spatial resolution within the transverse plane of the imaged cylinder/animal was better in the pancake geometry. A modest exposure increase to two folds in the pancake geometry can improve image quality to a level close to the tubular geometry. Image quality can also be improved by inclining the animal, which reduces streak artifacts caused by bony structures. The major factor resulting in the inferior image quality in the pancake geometry is the elevated beam attenuation along the long axis of the phantom/animal and consequently increased scatter-to-primary ratio in that orientation. Notwithstanding, the image quality in the pancake-geometry CBCT is adequate to support image guided animal positioning, while providing unique advantages of non-coplanar and multiple mice irradiation. This study also provides useful knowledge about the image quality in the two very different imaging geometries, i.e., pancake and tubular geometry, respectively.

INTRODUCTION

There has been increasing interest in image-guided radiotherapy in preclinical cancer research. Several systems mimicking human treatment methodologies have been developed to facilitate accurate focal irradiation for small target in laboratory animals (Wong et al., 2008, Clarkson et al., 2011, Graves et al., 2007). One such system is the small animal radiation research platform (SARRP) developed at Johns Hopkins University (Wong et al., 2008). The capabilities of the SARRP have been characterized and reported, including its mechanical calibration, beam modeling, and ability of irradiating a target to within 0.2 mm accuracy (Matinfar et al., 2009, Tryggestad et al., 2009, Armour et al., 2010). Since SARRP became available in 2008, it has been employed in many preclinical studies that take advantage of the precision focal irradiation (Duan et al., 2008, Ford et al., 2011, Karikari et al., 2007, Purger et al., 2009, Cao et al., 2011, Zhou et al., 2011).

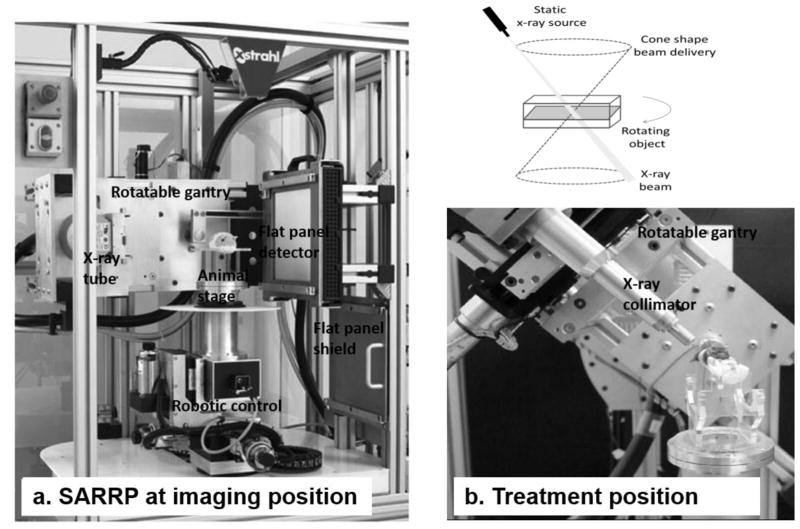
In typical computed tomography (CT) guided small animal radiation systems, a gantry with an opposite x-ray source and image detector is usually rotated around the longitudinal axis of a stationary animal for image acquisition (Clarkson et al., 2011, Graves et al., 2007). However, SARRP employs an unusual imaging geometry for cone beam CT (CBCT) acquisition where the animal atop a stage is rotated between a horizontally opposite, but stationary, x-ray source and flat panel detector (Figure 1(a)). This imaging setup is denoted as “pancake” geometry, describing the horizontal positioning of x-ray beam during CBCT of a prone or supine animal subject. The intent of this geometry is to provide non-coplanar irradiation on the SARRP where the beam isocenter lies on the axis of the rotating stage (Figure 1(b)). However, the pancake geometry results in uneven x-ray transmission from one angle to another during CBCT projection acquisition, particularly between the beam paths along the length and width of the animal object, which can possibly degrade the image quality. This study is to evaluate the SARRP CBCT image quality and propose potential methods for improvement. We compared CBCT images acquired in the pancake geometry with those acquired when the phantom/animal was placed upright simulating the conventional CBCT geometry (denoted as “tubular” geometry). This study provides useful knowledge about the image quality in the two very different imaging geometries, i.e., pancake and tubular geometry.

Figure 1.

The SARRP. (a) demonstrates SARRP configuration in imaging position. The gantry is in horizontal position, and the animal stage rotates for CBCT acquisition. (b) shows the noncoplanar irradiation where the mouse stage is rotating while the gantry is set at 60° angle with radiation collimator attached. The track of radiation beams resembles a conical shell relative to the irradiated object, as shown in the top panel.

METHODS

We compared CBCT images acquired in the pancake geometry and those acquired in the conventional, i.e., tubular geometry, while keeping all parameters for image acquisition, reconstruction and analysis identical for paired comparisons. The significance level is determined at p < 0.05 for student t test. All animal experiments were performed with the approval of the Johns Hopkins Animal Care and Use Committee.

Image Acquisition

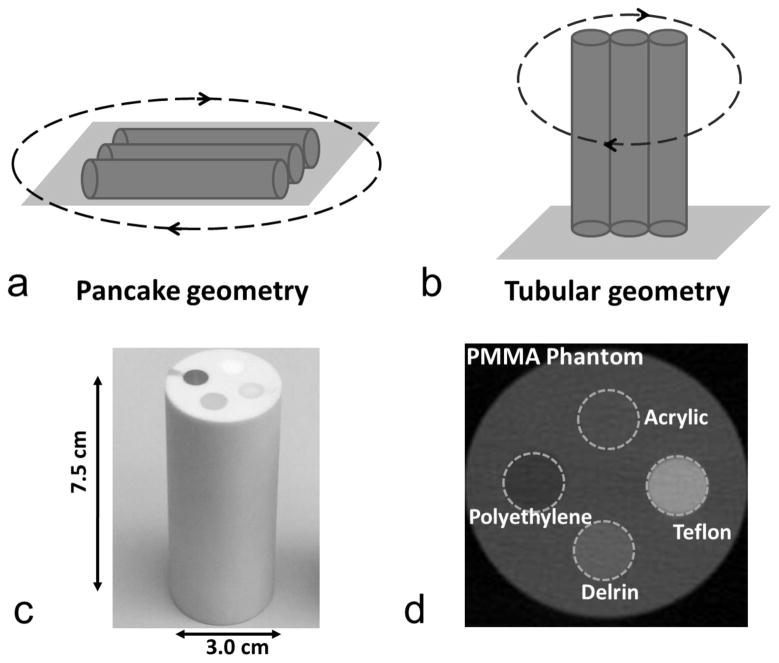
The SARRP x-ray source is mounted on a gantry with a 35 cm source-to-isocenter distance and a 53 cm source-to-detector distance. On-board CBCT is acquired by rotating the imaged object in the horizontal plane between a stationary x-ray source and a 20 cm × 20 cm flat panel detector of 1024 × 1024 pixels. In the pancake geometry, CBCT was acquired with the phantom placed flat or animal placed in prone position. In the tubular geometry, the phantom or animal was placed upright mimicking conventional CT geometry. The two imaging geometries were demonstrated in Figure 2 (a) and (b). CBCT projections were acquired with 65 kVp, 1.6 mA, a 0.1 mm-thick brass filter and a 0.4 mm x-ray focal spot (nominal value per IEC336 standard) for all studies. No automatic tube current modulation was used in this study. We used filtered back projection, i.e., FDK algorithm with Hamming filter, for CBCT reconstruction (Feldkamp et al., 1984).

Figure 2.

Imaging geometries and phantom for SNR and CNR measurement. (a) illustrates the pancake geometry where the stage is rotated with phantoms lying flat. (b) illustrates the tubular geometry where the stage is rotated with phantoms standing upright. (c) shows a photo of the PMMA phantom. (d) shows a CBCT transection marked with four heterogeneities. (a) and (b) represent the phantom arrangement for triple phantom study.

Signal-to-Noise Ratio and Contrast-to-Noise Ratio

To obtain signal-to-noise ratio (SNR) and contrast-to-noise ratio (CNR), we used cylindrical polymethyl methacrylate (PMMA, 1.18 g/cm³, background material) phantoms similar to mouse dimension (3 cm wide and 7.5 cm long) embedded with four heterogeneities: teflon (2.20 g/cm³), delrin (1.42 g/cm³), acrylic (1.20 g/cm³) and polyethylene (0.93 g/cm³). The phantom compositions are illustrated in Figure 2 (c) and (d). CBCT of a single phantom, three phantoms placed side-by-side, or a euthanized mouse, was acquired in the pancake and tubular geometry, respectively, and reconstructed with 0.2 mm × 0.2 mm × 0.2 mm voxels. The triple phantom arrangement is shown in Figure 2 (a) and (b). To examine the improvement by increasing radiation exposure, the imaging doses varied from 1 fold (1x, 1.6 cGy) to 2 folds (2x, 3.2 cGy) and 4 folds (4x, 6.4 cGy), by increasing the number of projections from 360 to 720 and 1440, correspondingly. In addition, CBCT of the PMMA phantom or euthanized mouse inclined at 14° and 28° were acquired to examine the effect of inclining the imaged object on the SNR and CNR. Image acquisition or measurement was repeated three times for each setup.

An in-house program developed in MATLAB (MathWorks, Natick, MA, USA) was used for the SNR and CNR analysis. A volumetric region of interest (ROI) was drawn at the center of each inhomogeneity with a diameter of 20 pixels and a length of 70 pixels (approximately 22000 pixels in total). Comparisons of SNR and CNR for all ROIs were made between the two imaging geometries. The SNR is defined as SI_x/σ_x, where SI_x is the mean signal intensity (SI) of ROI_x and σ_x is the corresponding standard deviation. The CNR is defined as (SI_x − SI_bkg)/σ_bkg, where SI_bkg is the SI of a reference volumetric ROI located in the PMMA background with similar size, and σ_bkg is the standard deviation of the reference ROI. For data analysis on animal CBCT, the volumetric ROIs were drawn in the liver and brain, respectively. The liver ROIs had a diameter of 20 pixels and length of 20 pixels, and brain ROIs had a diameter of 10 pixels and length of 10 pixels. SNR and CNR Data were reported in the format of mean ± standard deviation.

Spatial Resolution

To estimate the spatial resolution, a cylindrical phantom of 30 mm diameter and 70 mm length was fabricated with a straight steel wire of 50 μm diameter stretched inside a cylindrical hole. The phantom was made of acrylic and embedded with teflon, delrin, and polyethylene rods. The CBCT transection of the phantom is shown in Figure 3 (a) where the thin steel wire is shown as a bright dot in the dark air space. The CBCT was acquired with 720 projections and reconstructed with 0.25 mm × 0.25 mm × 0.25 mm voxels. The spatial resolution was measured in the transverse plane of the cylinder phantom, along radial and tangent directions, respectively, with an over-sampling method as described by Kwan et al (Kwan et al., 2007). The radial and tangent directions were defined in the coordinates of the transverse plane of the phantom, as shown in Figure 3 (a). To obtain line spread functions with over-sampling method, the wire was slightly tilted to a 5–15° angle away from the radial or tangent direction, by inclining the phantom. The resolution was measured in both pancake and tubular geometry, with single and triple phantoms, respectively. For the triple phantom study, the resolution phantom was positioned at center or side as shown in Figure 3 (a), to examine whether the resolution is dependent on the location within the reconstruction volume. Another two homogeneous acrylic cylinder of 30 mm × 70 mm were placed along with the resolution phantom. Modulation transfer functions (MTFs) were derived and plotted, and the frequency at 10% amplitude (f_0.1) was used for comparison.

Figure 3.

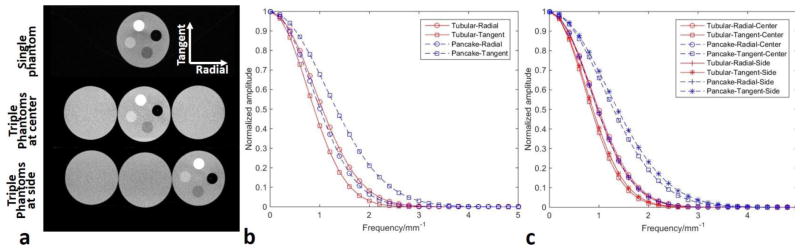
Spatial resolution at different setups. (a) shows the transverse sections obtained for single phantom, triple phantom with resolution phantom at center, and triple phantom with resolution phantom at side. Spatial resolution was measured in the radial and tangent directions, respectively, as defined in the top right. (b) shows the MTFs for single phantom studies. (c) shows the MTFs for triple phantom studies. The radial MTF at center (Pancake-Radial-Center) and at side (Pancake-Radial-Side) for pancake geometry, and radial MTF at side for tubular geometry (Tubular-Radial-Side) are almost overlapped with each other. The radial MTF at center for tubular geometry (Tubular-Radial-Center) is slightly better than the above three MTFs.

Scatter-to-Primary Ratio

Scatter-to-primary ratio (SPR) was measured in the pancake and tubular geometry, along the long and short axis of imaged phantoms, respectively. The definitions of the long and short axis are shown in Figure 4 (a). In the single phantom pancake geometry, the long axis setup is defined as the beam central axis passes through the long axis of the cylinder, and the short axis setup defined as the beam central axis passes through the diameter of the cylinder. In the single phantom tubular geometry, the long axis and short axis setup are identical, both referring to that the beam central axis passes through the cylinder diameter. In the triple phantom studies, the long axis setup is defined as the beam central axis passes through three phantoms, and the short axis setup as the beam central axis passes through the center phantom only. A tungsten wire of 1 mm diameter and10 mm length was attached along the long axis of a homogeneous acrylic cylinder of 30 mm diameter and 70 mm length to block part of primary x-ray beam as shown in Figure 4 (b). The wire was positioned on the cylinder phantom at beam entrance and exit, respectively. A projection image of 1024 × 1024 pixels (0.2 mm pixel size) was acquired with the shadow of the tungsten wire shown at the image center. Dark current was subtracted from the image, but image lag correction was not performed because single image was acquired instead of an image sequence. The x-ray attenuation caused by the tungsten wire resulted in a dip in the measured signal profile as shown in Figure 4(c). The x-ray path through the diameter of the tungsten wire is equivalent to approximately 40 tenth value layers at the mean energy of the 65 kVp beam. Therefore, the x-ray transmission through the wire was negligible, and the signal intensity at the dip was considered contributed solely from scatter (SI_scatter=SI_bottom, Figure 4(c)). The signals measured on the shoulders of the dip (SI_left and SI_right) can be averaged and approximated as the total signal (SI_total) at the dip otherwise without the wire in place. The total signal SI_total is the summation of the primary SI_primary and scatter SI_scatter components. The SPR is calculated as

Figure 4.

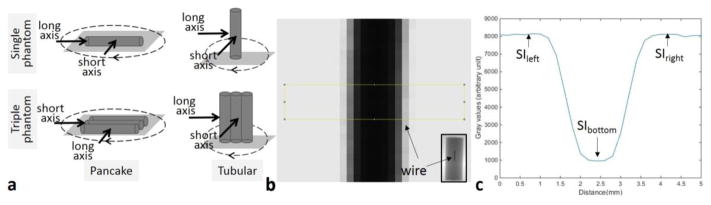
SPR measurement. (a) shows the definition of the measurement geometry, i.e., the long and short axis setup in the single and triple phantom study. (b) shows an enlarged x-ray image of the 1 mm-diameter tungsten wire. A 25 pixel x 5 pixel (5 mm × 1 mm) box was drawn across the wire to generate a profile. The insert at bottom right shows the planar image of the entire phantom with the wire attached. (c) shows the profile obtained by averaging the pixels along the short side of the box in (b). SI_bottom is the signal at the dip referring to the scatter component. SI_left and SI_right are the signal at the left and right shoulder of the dip. The SPR was calculated according to equation (1).

$$\begin{array}{l}\mathit{SPR}=\frac{{SI}_{\mathit{scatter}}}{{SI}_{\mathit{primary}}}\\ =\frac{{SI}_{\mathit{bottom}}}{({SI}_{\mathit{left}}+{SI}_{\mathit{right}})/2-{SI}_{\mathit{bottom}}}\end{array}$$ (1)

Angular-Dependent Transmission

The average x-ray transmission, defined as the mean value of all the pixels within a large ROI that contoured the entire phantom or mouse on two-dimensional projection images, was measured in both tubular and pancake geometries at stage rotation angles of 0°, 90°, 180° and 270°. In the pancake geometry, rotation angle 0° or 180° is defined at the position where the long axis of the imaged object is perpendicular to the beam central axis. In the tubular geometry, rotation angle 0° or 180° is defined at the position where the beam central axis passes through all three phantoms in the triple phantom study, and at the position where the beam central axis passes laterally in the single mouse study. There is no angular difference in the single phantom tubular geometry.

RESULTS

SNR and CNR

Single Phantom Study

The SNR and CNR measurement results are shown in Table 1 and 2 respectively. The SNR and CNR in the pancake geometry were inferior to their counterparts in the tubular geometry at the same dose level. The SNRs in the pancake geometry were 17.3±2.7, 20.7±2.9, 23.1±4.1 and 26.0±5.6, for polyethylene, acrylic, delrin and teflon, respectively, versus 23.2±1.8, 26.3±0.5, 33.9±1.2, and 48.5±3.0 in the tubular geometry (p < 0.05 for all comparisons). The most dramatic discrepancy occurred in the high density heterogeneity teflon. At 2x exposure, the SNRs in the pancake geometry were superior or nearly equal to those in the tubular geometry at 1x exposure, for all heterogeneities except the teflon. The SNR for the teflon was recovered when the exposure was increased to 4x. Besides increasing exposure, inclining the phantom also enhanced the SNR. With a modest 14° inclination, the SNRs were improved by 16.5%, 17.3%, 22.8% and 55.1% for polyethylene, acrylic, delrin and teflon, respectively, compared to the pancake geometry without inclination. The most significant improvement by inclination occurred for the teflon.

Table 1.

The SNRs for the single phantom study

ROI	Tubular 1x	Pancake 1x	Pancake 2x	Pancake 4x	Pancake 14°, 1x
Teflon	48.5±3.0	26.0±5.6	36.7±3.6	48.7±3.6	40.4±2.2
Delrin	33.9±1.2	23.1±4.1	33.7±1.0	45.9±2.0	28.3±1.0
Acrylic	26.3±0.5	20.7±2.9	30.0±0.5	39.5±1.0	24.3±0.8
Polyethylene	23.2±1.8	17.3±2.7	24.9±2.1	34.2±1.5	20.1±1.2
PMMA	20.0±1.5	17.3±2.2	25.3±1.5	33.0±1.0	20.6±1.0

Table 2.

The CNRs for the single phantom study

ROI	Tubular 1x	Pancake 1x	Pancake 2x	Pancake 4x	Pancake 14°, 1x
Teflon	21.5±2.0	12.0±1.3	17.5±0.9	22.5±1.4	18.6±1.8
Delrin	5.8±0.9	4.0±0.3	5.8±0.7	7.6±1.0	5.3±0.7
Acrylic	1.0±0.3	0.7±0.3	1.1±0.6	1.4±0.8	0.7±0.3
Polyethylene	−3.7±0.3	−2.6±0.3	−3.8±0.2	−4.8±0.2	−3.1±0.3

The CNRs in the pancake geometry at 1x exposure were −2.6±0.3, 0.7±0.3, 4.0±0.3, and 12.0±1.3, for polyethylene, acrylic, delrin and teflon, respectively, versus −3.7±0.3, 1.0±0.3, 5.8±0.9, and 21.5±2.0 in the tubular geometry (p < 0.05 for all comparisons except the acrylic). Similar to the SNR results, the largest discrepancy occurred for the teflon. We increased the CNRs to −3.8±0.2, 1.1±0.6, 5.8±0.7 and 17.5±0.9, respectively, by doubling the exposure in the pancake geometry. The CNRs in the pancake geometry at 2x exposure were superior or nearly equal to those in the tubular geometry at 1x exposure, for all heterogeneities except the teflon. The CNR for the teflon was recovered when the exposure was increased to 4x. Again, inclining the phantom to 14° improved the CNRs in the pancake geometry for all the four heterogeneities.

Triple Phantom Study

The SNR and CNR measurement results for the triple phantom study are shown in Table 3 and 4, respectively. The SNR and CNR in the pancake geometry were inferior to those in the tubular geometry. The SNRs in the pancake geometry were 13.1±1.0, 12.9±1.4, 14.8±1.5, and 18.5±1.4, for polyethylene, acrylic, delrin and teflon, respectively, versus 17.1±1.3, 23.2±1.1, 27.5±0.4 and 39.5±2.5 in the tubular geometry (p < 0.05 for all comparisons). The CNRs in the pancake geometry were −1.8±0.2, 0.5±0.1, 2.9±0.2, and 8.7±0.8, versus −3.4±0.3, 1.6±0.1, 6.1±0.3 and 20.5±1.3 in the tubular geometry (p < 0.05 for all comparisons). Similar to the single phantom study, increasing exposure improved the SNR and CNR in the pancake geometry. The SNRs in pancake geometry were recovered at 4x exposure level for all heterogeneities except the teflon. The CNRs, however, required more than 4x exposure to achieve a level identical to the tubular geometry.

Table 3.

The SNRs for the triple phantom study

ROI	Tubular 1x	Pancake 1x	Pancake 2x	Pancake 4x
Teflon	39.5±2.5	18.5±1.4	25.1±2.7	32.5±4.3
Delrin	27.5±0.4	14.8±1.5	20.0±2.3	29.0±4.2
Acrylic	23.2±1.1	12.9±1.4	17.5±2.4	23.9±2.5
Polyethylene	17.1±1.3	13.1±1.0	17.6±1.8	23.9±3.7
Background	20.0±1.5	11.9±1.3	16.1±2.1	21.9±3.6

Table 4.

The CNRs for the triple phantom study

ROI	Tubular 1x	Pancake 1x	Pancake 2x	Pancake 4x
Teflon	20.5±1.3	8.7±0.8	11.7±1.4	15.7±2.3
Delrin	6.1±0.3	2.9±0.2	3.9±0.4	5.3±0.8
Acrylic	1.6±0.1	0.5±0.1	0.7±0.1	0.9±0.0
Polyethylene	−3.4±0.3	−1.8±0.2	−2.5±0.3	−3.3±0.6

We also compared the SNR and CNR between the phantom at center and side in the pancake geometry at 1x exposure. The SNRs at side were better than those at center by 16.0%, 21.8%, 26.2%, and 14.1%, and the CNRs at side were better than those at center by 17.0%, 16.3%, 29.9%, and 21.8%, for teflon, delrin, acrylic and polyethylene, respectively. The non-uniformity, defined as the maximum percentage difference between the mean signal intensity of ROIs at center and side, was 1.5±0.1%.

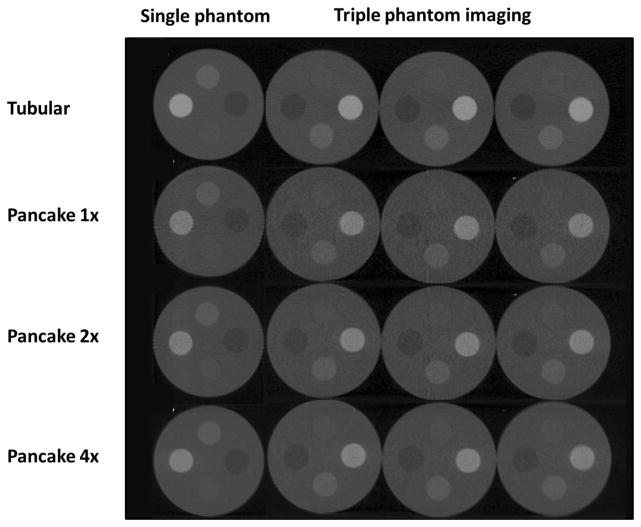
The images from both pancake and tubular geometries at different exposures are shown in Figure 5. Although the SNRs and CNRs in the pancake geometry were inferior to those in the tubular geometry, they were adequate for visual differentiation of all four heterogeneities from the background.

Figure 5.

CBCT transection images. The transection of single phantom (column 1) and triple phantom (column 2–4) acquired in the tubular geometry at 1x exposure (row 1), pancake geometry at 1x exposure (row 2), pancake geometry at 2x exposure (row 3) and pancake geometry at 4x exposure (row 4). The blur in the bottom right image might be caused by loosening of the phantom which was taped to a styrofoam plate during CBCT acquisition.

Animal Imaging

Mouse CBCTs acquired at different imaging geometries are shown in Figure 6. Images acquired in the pancake geometry have noticeable streak artifacts in brain and thoracic regions, owing to increased x-ray attenuation by bony structures. The streak artifacts in brain was more severe than other anatomical sites due to abundance of bony structures in mouse brain. We reduced the streak artifacts by inclining the animal. The SNR analysis in brain and liver showed that either doubling the radiation exposure or inclining the animal could improve image quality in the pancake geometry, as shown in Table 5. The SNRs in the pancake geometry at 2x exposure approached to those in the tubular geometry at 1x exposure (25.6±1.0 versus 26.1±0.6 in brain and 23.6±1.0 versus 26.9±0.1 in liver, p < 0.05 for both comparisons). At 28° inclination, the SNR in the pancake geometry at 1x exposure was 22.4±1.3 in brain and 26.8±1.5 in liver, and improved by 42.7% and 21.8%, respectively, compared to the 14° inclination (p = 0.01 and 0.89, respectively). No obvious SNR improvement was observed at 14° inclination compared to the non-inclination.

Figure 6.

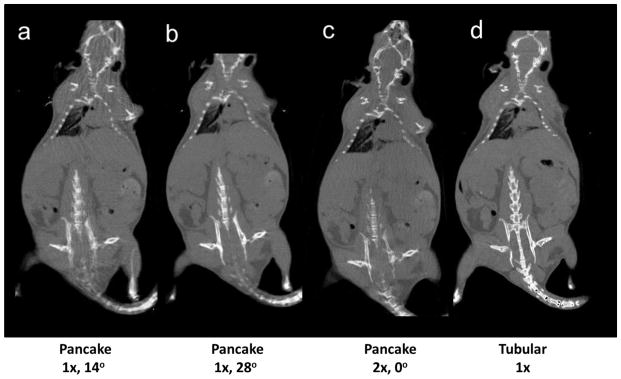
The coronal images of a mouse CBCT. Images were acquired (a) in the pancake geometry at 1x exposure and 14° inclination; (b) 1x exposure and 28° inclination; (c) 2x exposure and no inclination; and (d) in the tubular geometry at 1x exposure and no inclination.

Table 5.

The SNRs for the mouse CBCT

ROI	Tubular 1x	Pancake 14°, 1x	Pancake 28°, 1x	Pancake 2x	Pancake 14°, 2x
Brain	26.1±0.6	15.7±0.4	22.4±1.3	25.6±1.0	25.2±0.9
Liver	26.9±0.1	21.8±1.4	26.8±1.5	23.6±1.0	23.5±1.4

Spatial Resolution

Single Phantom Study

The MTFs for single phantom study are shown in Figure 3 (b). The tangent resolution in the pancake geometry (f_0.1 = 2.4 mm⁻¹) is better than either resolution (f_0.1 = 1.6 mm⁻¹ for the tangent resolution and 1.9 mm⁻¹ for the radial resolution) in the tubular geometry. The radial resolution in the pancake geometry (f_0.1 = 1.8 mm⁻¹) is similar to its counterpart in the tubular geometry.

Triple Phantom Study

The MTFs for triple phantom study are shown in Figure 3 (c). Similar to the single phantom study, the resolutions in the pancake geometry are either similar or better than those in the tubular geometry. In the pancake geometry, the tangent resolutions (f_0.1 = 2.4 mm⁻¹ at center and 2.5 mm⁻¹ at side) are better than the radial resolutions (f_0.1 = 1.8 mm⁻¹ for both center and side). In the tubular geometry, the radial resolutions (f_0.1 = 1.8 mm⁻¹ for both center and side) are slightly better than the tangent ones (f_0.1 = 1.6 mm⁻¹ for both center and side). The location of the phantom, either at center or side, has minimal effect on the resolution. The resolution at side is not worse, at least, than that at center. The spatial resolutions in the triple phantom study were very similar to their counterparts in the single phantom study.

Angular Dependent Transmission

The angular dependent transmission data for phantom studies are shown in Figure 7 (a) and (b). In the single phantom pancake geometry, the amount of radiation transmitting through the single phantom was dependent on the x-ray projection angle. The transmission was smallest at the projection angles 90° and 270°, where x-ray beam central axis aligned with the long axis of the cylinder. In the single phantom tubular geometry, the transmission was similar at all projection angles owing to the axial symmetry of the phantom rotation. The reverse was observed when transmission was measured in the triple phantom study. The transmission was nearly independent of projection angles in the pancake geometry. In the tubular geometry, the transmission was smallest when the beam central axis passed through three phantoms, and was greatest when it only passed through one phantom.

Figure 7.

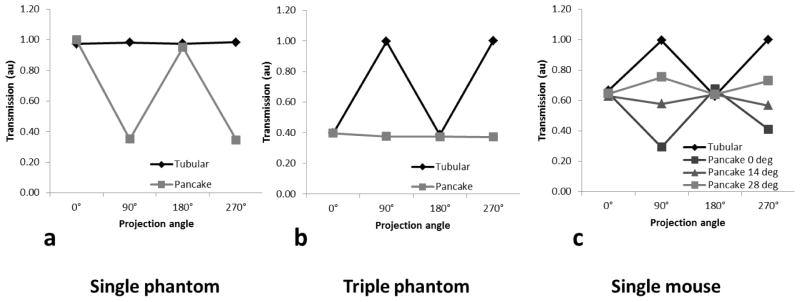
Angle dependent x-ray transmission. (a) is for the single phantom study, (b) the triple phantom study, and (c) the single mouse study.

The transmission data for the single mouse study are shown in Figure 7(c). In the pancake geometry, the transmission shows strong angle dependency at no inclination. The greatest transmission occurred when the beam central axis passed the animal body laterally, and smallest when the beam central axis passed along the craniocaudal direction. The transmission uniformity over projection angles was improved by animal inclination in the pancake geometry. The tubular geometry can be viewed as the extreme case of the pancake geometry at 90° inclination, which resulted in maximal transmission along the anterior-posterior direction and minimal transmission along the lateral direction in the single mouse study. Animal inclination in the pancake geometry improved transmission uniformity, approaching that in the tubular geometry with increasing inclination angles.

Scatter-to-Primary Ratio

The SPRs measured at x-ray beam entrance and exit were almost identical. Therefore the mean values were used and shown in Table 6. The primary and scatter x-ray passing through the imaged object at any project angle in the tubular geometry were similar to those in the pancake geometry when the beam central axis was perpendicular to the phantom long axis, resulting in similar SPRs (0.14 and 0.13 in the tubular geometry, versus 0.14 for the short axis setup in the pancake geometry). When the beam central axis penetrated through the long axis in the pancake geometry, the primary x-ray intensity deceased by 68.6%, and the SPR increased by 64.3% to 0.23. In the triple phantom tubular geometry, the SPR was greater when the beam central axis penetrated through three phantoms (0.30 in the long axis setup versus 0.16 in the short axis setup). In the pancake geometry, the SPR was 0.27 when the beam central axis penetrated through single phantom (the short axis setup), and 0.33 when it penetrated through three phantoms (the long axis setup). Increased scatter portion at certain projection angles is one of the major causes that worsen the image quality in the pancake geometry.

Table 6.

The SPRs for different geometries

Geometry	Single Phantom		Triple phantom
	Tubular	Pancake	Tubular	Pancake
Short axis	0.14	0.14	0.16	0.27
Long axis	0.13	0.23	0.30	0.33

Note: the standard deviations are not presented because they are negligible.

DISCUSSION

This study investigated the image quality of the CBCT acquired in an unconventional geometry, i.e., pancake geometry and compared it with the conventional geometry, i.e., tubular geometry. At the same exposure level, the SNR and CNR in the pancake geometry were inferior to those in the tubular geometry. The degradation in the SNR and CNR is expected owing to appreciable non-uniformity in the x-ray transmission over projection angles when an elongated mouse-like object is rotated in the stationary x-ray beam, as demonstrated in the angular dependent transmission study. The transmission can be up to two times difference in one rotation in the single phantom pancake geometry. When the x-ray penetrates through the long axis, particularly of a high density material such as a teflon rod in a phantom or the spinal column in an animal, the large attenuation would significantly limit the transmission of the primary photons and result in considerable SPR increase. Such elongated objects are usually of substantial contrast and thus would not deter visualization. They would, however, impart streak artifacts caused by the increased scatter portion and beam hardening effect. To decouple the two effects warrants nontrivial effort and is beyond the scope of this study. Overall, CBCT acquired with the pancake geometry appears to be adequate to provide image guidance for small animal radiation therapy. Images of the contrast phantom shown in Figure 5 illustrate that 5 mm objects at a low 2% contrast, such as acrylic embedded in PMMA, can be detected. It should be noted that a SNR value of five was achieved for all the objects in the phantom imaging study at all exposure levels which satisfied the simple SNR Rose Criteria for visualization (Rose, 1973).

The SNR and CNR in the pancake geometry can be improved by either increasing the exposure or inclining the imaged object. Doubling the exposure can increase SNR and CNR to the level approaching the tubular geometry. The imaging dose is about 3.2 cGy at 2x exposure level, which is still lower than the 10 cGy threshold, below which neither deterministic nor stochastic effect due to radiation has ever been demonstrated (Mole, 1957, ICRP, 2007). Inclining the imaged objects can effectively reduce the streak artifact caused by elongated bony structures. This method is attractive because it does not incur additional dose to the animal, although more involved image manipulation utility, such as image tilting, is needed to allow visualization in customary orientation. On the other hand, while inclination of the imaged mouse can improve CBCT image quality, it may need extra efforts to ensure a reproducible animal setup for fractionated radiation treatment. A special animal holder with a properly tilted bed is needed to incline the mouse. Additional attention should be paid to ensure a steady fixation while taping the animal to the holder. Notwithstanding, with the CBCT guidance, the animal positon can always be adjusted to best reproduce the simulation or initial treatment setup. Another option is to hang up the animal vertically, which mimics the tubular geometry. Sharma et al has successfully delivered fractionated radiation treatment to rats by hanging up animals with a custom-made holder (Sharma et al., 2014). There are other potential methods for reducing the streak artifacts caused by bony structures, one of which is using higher energy photon beams which are considered less susceptible to bone attenuation. The general image quality can also be improved by implementing automatic current modulation technique to offset the angular dependent variation of x-ray transmission in the pancake geometry.

One concern of using pancake CBCT for image guidance is whether or not the non-conventional imaging geometry induces imaging artefacts that detract from targeting accuracy, particularly in multiple mice irradiation. Our group performed a study that investigated the capability of image guidance with the pancake geometry (Armour et al., 2010). The positioning error for repeated alignments with bony structures in the pancake CBCT was −0.18±0.05 mm for translation and −0.4±0.9° for rotation, better than that when mouse was setup without CBCT guidance, which was 0.8±0.49mm for translation and 0±2° for rotation. Therefore, we think the image quality of pancake CBCT is sufficient for image guidance purpose. In the triple phantom study, we found that the image quality, including SNR, CNR and spatial resolution, at side was not worse, if not better, than that at center, and the signal intensity non-uniformity was < 2% between center and side. In addition, the spatial resolution was not degraded by the increased scatter in the triple phantom study. Therefore, the targeting accuracy in multiple mice study should not be compromised by the location of the irradiated mouse.

We used a tungsten wire of 1 mm diameter to block the primary radiation beam in the SPR estimation in this study. A more typical approach is using small blocks of decreasing diameter, and then extrapolate the scatter contribution. However, one study by Niu et al (Niu et al., 2011) showed that scatter was estimated within 5% around the object center with single-width lead blockers of 2 mm thickness positioned at the beam entrance. Therefore our method should be sufficient to estimate and relatively compare the scatter contribution between the two imaging geometries.

It should be noted that the imaging quality in either pancake or tubular geometry is dependent on the shapes of the imaged objects. It is possible for pancake geometry to be more advantageous for certain object shapes/setups, although CBCT of cylindrically shaped objects can be aptly acquired with the conventional, i.e. tubular, geometry. One gain from the pancake geometry is the reduced cone angle that can fully cover the imaged animal, which may improve the vertical spatial resolution along the cone-opening direction. Previous studies have shown the spatial resolution along this direction deceases with increased cone angle (Mettivier et al., 2011). Based on our study, the spatial resolution along certain direction in the pancake geometry was actually better than that in the tubular geometry. Spatial resolution in CBCT varies depending on the direction along which it is measured (Mettivier et al., 2011). Usually it can be measured in three directions: the beam central axis direction, the cathode to anode direction, and the third direction perpendicular to the above two directions. In our study, the measurement directions were defined in the image coordinates, particularly in the transverse plane, the most common plane in image browsing, of the imaged phantom or animal. In the pancake geometry, the radial resolution was defined along the beam central axis direction, and the tangent resolution defined along the direction perpendicular to both the beam central axis and cathode to anode direction. In the tubular geometry, the radial resolution was defined along the beam central axis, and the tangent resolution defined along the cathode to anode direction. This probably explains why the radial resolutions were similar between the two imaging geometries. Comparing the single phantom study with triple phantom study, the corresponding resolutions were almost the same, indicating that the increased scatter in the triple phantom study does not degrade spatial resolution. We recognized, however, that the above conclusions drawn upon the high contrast resolution used in this study do not necessarily apply to low contrast resolution.

The pancake geometry on the SARRP is chosen primarily for its irradiation advantages. In image guided radiation therapy, with the axes of its translation and rotation stages readily aligned with the isocenter of the x-ray gantry, delivery of non-coplanar beams is simplified with conical beam tracks as shown in Figure 1(b). To mimic human radiotherapy situation, we need deliver focal radiation to the tumor target while sparing normal tissues. One example requiring precision focal irradiation is to model the radiation induced lung injury by mimicking clinical stereotactic radiotherapy often delivered with CyberKnife non-coplanar radiation beams (Bibault, et al., 2012, Gibbs, et al., 2010). Another example is to investigate the synergetic effect of combining radiotherapy and immunotherapy (Zeng et al., 2013, Burnette et al., 2013). It is highly desired to minimize the immune response induced by unnecessary irradiation of normal tissues. SARRP can deliver stereotactic radiation with non-coplanar beams in a simplified conical beam path, and has the ability of even better sparing normal tissues by adding several layers of conical beam paths. Another advantage of the pancake setup is its ability to support image guided multiple mice non-coplanar irradiation which is difficult, if not impossible, to achieve for the conventional geometry with a non-rotating animal stage. The pancake arrangement can accommodate non-coplanar irradiation of a target in each mouse, such as using a conical beam trajectory, provided that beam paths do not traverse the other mice. This is useful because efficient multiple mice irradiation is most desirable for preclinical radiation experiments that require a large number of animals.

COCLUSION

The SNR and CNR in the pancake geometry were inferior to those in the conventional, i.e., tubular geometry, for both single and triple phantom imaging. But the overall spatial resolution within the transverse plane of the imaged cylinder/animal in the pancake geometry was better. A modest exposure increase by a factor of two in the pancake geometry improved and produced SNR and CNR comparable to those in the tubular geometry. The image quality in the pancake geometry can also be enhanced by inclining the animal, which improves x-ray transmission and reduces streak artifacts caused by bony structures. The major factor contributing to the inferior image quality in the pancake geometry is the escalated primary beam attenuation along the long axis of the phantom/animal and consequently increased SPR. Notwithstanding, the CBCT acquired in the pancake geometry is adequate for image guided animal positioning, while this geometry provides advantages of non-coplanar and multiple mice irradiation.

Abbreviations

CBCT

Cone Beam Computed Tomography

CNR

Contrast to Noise Ratio

MTF

Modulation Transfer Function

PMMA

Polymethyl Methacrylate

ROI

Regions of Interest

SARRP

Small Animal Radiation Research Platform

SI

Signal Intensity

SNR

Signal to Noise Ratio

SPR

Scatter to Primary Ratio