Improved Energy Bound Accuracy Enhances the Efficiency of Continuous Protein Design

Abstract

Flexibility and dynamics are important for protein function and a protein’s ability to accommodate amino acid substitutions. However, when computational protein design algorithms search over protein structures, the allowed flexibility is often reduced to a relatively small set of discrete side-chain and backbone conformations. While simplifications in scoring functions and protein flexibility are currently necessary to computationally search the vast protein sequence and conformational space, a rigid representation of a protein causes the search to become brittle and miss low-energy structures. Continuous rotamers more closely represent the allowed movement of a side chain within its torsional well and have been successfully incorporated into the protein design framework to design biomedically relevant protein systems. The use of continuous rotamers in protein design enables algorithms to search a larger conformational space than previously possible, but adds additional complexity to the design search. To design large, complex systems with continuous rotamers, new algorithms are needed to increase the efficiency of the search. We present two methods, PartCR and HOT, that greatly increase the speed and efficiency of protein design with continuous rotamers. These methods specifically target the large errors in energetic terms that are used to bound pairwise energies during the design search. By tightening the energy bounds, additional pruning of the conformation space can be achieved, and the number of conformations that must be enumerated to find the global minimum energy conformation is greatly reduced.

1 Introduction

Computational structure-based protein design (CSPD) algorithms use a protein’s three-dimensional structure to predict mutations to the native protein sequence that will confer a desired function [1]. Because protein conformational space is vast, CSPD algorithms often limit their search space to highly-populated discrete side-chain positions curated from protein crystal structures, called rigid rotamers [2, 3]. Rigid rotamers approximate a region of side-chain space using a single conformation, causing the protein design search to become brittle [4–9], and ignore proteins’ inherent flexibility [10–12] and ability to make small adjustments in response to a side-chain mutation [13, 14]. We have shown previously that the common practice of subsampling rigid rotamers does not adequately recover side-chain movements within their rotameric wells [4]. However, allowing rotamers to continuously minimize during the design search can discover unique low-energy sequences that are missed by rigid rotamer techniques. The use of continuous rotamers was critical to successfully design a change in specificity of a non-ribosomal peptide synthetase adenylation domain [15], predict resistance mutations in MRSA DHFR [16, 17], design peptide inhibitors of a cystic fibrosis agonist [18] and design improved HIV antibodies [19].

The only CSPD software that is able to take advantage of continuous rotamers is the open-source package OSPREY [20]. In addition to using continuous rotamers, OSPREY utilizes provable techniques, meaning that it is guaranteed to find the global minimum energy conformation (GMEC) with respect to the protein design input model (i.e., the input structure, rotamer library, energy function, and allowed flexible degrees of freedom in the protein). OSPREY divides the CSPD problem into two separate steps: pruning and conformation enumeration (Fig 1). The initial pruning step uses the precomputed rotamer energies to prune rotamers from the search that are guaranteed not to be part of the GMEC or any low-energy conformations. OSPREY uses several dead-end elimination (DEE) criteria to efficiently prune as many rotamers as possible [21–24]. The conformation enumeration step searches through the remaining unpruned rotamers to find the low-energy protein conformations. OSPREY uses the best-first search algorithm, A^*, to enumerate conformations in order of their lowest energies [25].

Fig. 1. OSPREY Protein Design Overview.

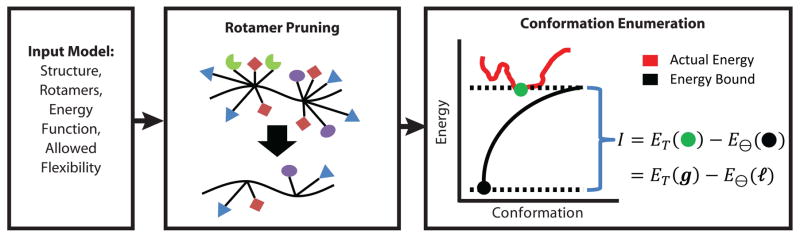
The OSPREY protein design software [20] takes as input an initial protein structure, a rotamer library, an energy function to rank conformations, and the allowed flexibility of the protein during the search. OSPREY uses DEE criteria to prune rotamers from the search that are guaranteed to not participate in any low energy conformations. The rotamers remaining after pruning are input to the conformation enumeration step where conformations are enumerated in order of lowest energy, or in the case of continuous rotamers, in order of lowest energy bound.

While vital to finding the low-energy conformations predicted by the CSPD input model, continuous rotamers increase the CSPD conformational search space and computational complexity of a design. Traditionally, CSPD algorithms evaluate the actual energies of discrete rotamer pairs and optimize these energies to find the GMEC. However, continuous rotamers introduce an infinite number of discrete conformations to the search problem, so it is no longer feasible to calculate actual energies for the discrete rotamer pairs. Instead, the continuous rotamer CSPD algorithms, minDEE [26], iMinDEE [4] and DEEPER [27], calculate energy bounds over a voxel of conformation space for each intra-rotamer and pairwise rotamer interaction.

The difference between the energy bounds used during the design search and the actual energies of full protein conformations (the bound error) introduces specific challenges to the CSPD problem. Specifically, the pruning power of the DEE criteria are reduced because they must account for the bound error and cannot prune rotamers that are within this error window. The A^* enumeration step is lengthened because A^* must enumerate conformations in order of low-energy bounds instead of actual energies. Therefore, all conformations with low-energy bounds less than the GMEC energy must be computed and fully minimized. In addition to these specific challenges, the inherent difficulty of CSPD increases when allowing minimization because flexibility increases the number of viable rotamers compared to a rigid approach that uses a similar rotamer library.

Previously, we developed the iMinDEE algorithm [4], which greatly increases the ability of osprey to efficiently prune continuous rotamers. Here we focus on methods to improve the conformation enumeration step by reducing the number of conformations that must be enumerated before the GMEC is found. We present two new algorithms that can solve more complex protein designs and reduce the number of conformations that must be enumerated with continuous rotamers. First, we present a divide-and-conquer strategy, PartCR, that partitions continuous rotamers to reduce the bound error for loosely (i.e., poorly) bounded rotamers. PartCR takes advantage of the weighted constraint satisfaction problem (WCSP) formulation of the CSPD problem [28] to create an efficient search over continuous rotamers. Second, we present the HOT algorithm that specifically targets higher-order partial rotamer conformations with large bound errors and improves these bounds. HOT utilizes a novel modified version of the integer linear programming (ILP) protein design formulation [29] to incorporate higher-order energy costs into the search. Both of these novel methods have been implemented and tested in the OSPREY CSPD software suite.

2 Methods

2.1 Continuous Rotamers

Side-chain conformations observed in high-resolution protein structures cluster in specific regions of dihedral space [2, 3]. The rigid rotamers used in CSPD represent these highly populated regions as a single side-chain conformation. Using the rigid rotamer model, a protein conformation a can be represented as a vector of n rotamers:

$$\mathbf{a}=(a_1,a_2,\dots ,a_n),$$ (1)

where n is the number of residue positions allowed to mutate during the design search. The total energy for the conformation, a, is defined as

$$E_T(\mathbf{a})=E_{\text{templ}}+\sum _{i=0}^{n}E(a_i)+\sum _{i=0}^n\sum _{j=i+1}^{n}E(a_i,a_j),$$ (2)

where E_templ is the template energy (i.e., the energy of the backbone atoms and side-chain residues that are not allowed to move or mutate), E(a_i) is the internal energy of rotamer a_i plus the energy of a_i with the template, and E(a_i, a_j) is the pairwise energy between rotamers a_i and a_j. Protein energies are very sensitive to small changes in protein atom coordinates, so using rigid rotamers can make the CSPD search brittle [4]. Continuous rotamers can be used to make the search more robust and identify lower energy sequences. A single continuous rotamer represents a region of side-chain dihedral space known as a voxel. In comparison, a traditional rigid rotamer would only be a single point within this voxel. Given a pair of continuous rotamers, (i_r, j_s), their voxels are known, but their positions within their voxels cannot be determined until all rotamers in a conformation (Eq. 1) are assigned. Thus, the pairwise decomposition of a protein conformation’s energy with assigned continuous rotamers can no longer be broken down into a pairwise sum. Instead, CSPD algorithms must use energetic bounds over the rotamer voxels. The minimum energy bound of a conformation can be written as:

$$E_{\ominus }(\mathbf{a})=E_{\text{templ}}+\sum _{i=0}^n{E}_{\ominus }(a_i)+\sum _{i=0}^n\sum _{j=i+1}^n{E}_{\ominus }(a_i,a_j),$$ (3)

where E_⊖(a_i) is the minimum energy of a_i within its voxel and E_⊖(a_i, a_j) is the minimum energy of the rotamer pair (a_i, a_j) within their voxels [26, 4]. Because continuous rotamers allow side chains to minimize within their voxels, for a design with the same rotamer library, the GMEC using rigid rotamers can differ greatly from the GMEC using continuous rotamers in both conformation and sequence [4, 20, 27]. To distinguish the rigid rotamer GMEC from the continuous rotamer GMEC, we use the terms rigidGMEC and minGMEC, respectively.

2.2 A* Conformation Enumeration with Continuous Rotamers

The A^* algorithm used by OSPREY to enumerate conformations requires an admissible heuristic that can bound the energy of any partial protein conformation during the search [25, 30]. Since the protein conformation energy with continuous rotamers cannot be pairwise decomposed, the energy lower bounds E_⊖(a_i) and E_⊖(a_i, a_j) are used during the A^* enumeration step [26, 4]. Therefore, protein conformations are enumerated in order of their lower energy bound E_⊖(a) instead of their actual energy E_T(a), as was the case for rigid rotamers. However, once a full protein conformation with continuous rotamers is generated from A^*, its actual energy E_T (a) can be computed by minimizing all rotamers at once. Let g be the minGMEC and ℓ be the conformation with the lowest energy bound. A^* can guarantee that the minGMEC, g, is found when the stopping criterion is satisfied [26, 4], i.e. the lower bound of the m^th conformation generated by A^* is greater than any conformation found so far:

$$E_{\ominus }({\mathit{\ell }}_m)>\underset{q\in \{1,\cdots ,m-1\}}{min}{E}_T({\mathit{\ell }}_q).$$ (4)

All conformations D = {a | E_⊖(a) ≤ E_T(g)} with a lower energy bound less than the minGMEC energy must be enumerated before the minGMEC is guaranteed to be found. It is unknown how to efficiently determine exactly how many conformations are in D, but the overall number is related to the energy gap between the minGMEC energy and the conformation with the lowest energy bound, I = E_T (g) − E_⊖(ℓ). If I is large for a protein design system, a large number of conformations must be enumerated before the minGMEC is found. Therefore, it is important to understand what characteristics of a CSPD system cause large I values and develop techniques that reduce the value of I.

Since E_T (g) is defined by the CSPD system and is constant during the design search, the only way to improve I is to increase the value of E_⊖(ℓ). The quantity ε(ℓ) = E_T (ℓ) − E_⊖(ℓ), called the bound error, represents the discrepancy between the actual energy and the pairwise energy bounds for conformation ℓ. By increasing E_⊖(ℓ) to more tightly bound E_T (ℓ), the bound error is reduced and I is improved. When g ≠ ℓ, we know that E_T (g) < E_T (ℓ). If the energy bound of ℓ is increased such that E_T (g) < E_⊖(ℓ) ≤ E_T (ℓ), ℓ would be removed from D and would no longer need to be enumerated by OSPREY. After improving E_⊖(ℓ), the I value for the CSPD system becomes I = E_T (g) − E_⊖(ℓ′), where ℓ′ ∈ D − {ℓ} is the conformation in D − {ℓ} with the lowest-energy bound. Continually improving the lower bounds of conformations in D will reduce I and reduce the number of conformations OSPREY must enumerate.

The I value is also present in the iMinDEE pruning criterion [4] used by HOT and PartCR:

$$E_{\ominus }(i_r)-E_{\ominus }(i_t)+\sum _{j\ne i}\underset{s}{min}(E_{\ominus }(i_r,j_s)-E_{\ominus }(i_t,j_s))>I_{m+1}.$$ (5)

Similar to iMinDEE, the rotamer pruning that HOT and PartCR can accomplish is directly related to the current estimate of I, $I_{m+1}=E_T({\mathbf{g}}_m^{\prime })-E_{\ominus }({\mathit{\ell }}_m)$. As I_m+1 decreases, more rotamers can be pruned from the search.

2.3 Understanding Large Bound Errors

To improve the bound error for a given conformation, it is critical to understand where the error comes from. Because the bounds are pairwise, when E_⊖(i_r, j_s) is determined, side chains at other mutable residue positions are excluded from the calculation. This leads to two general situations that can cause bounds to be overoptimistic (Fig. 2). First, it is possible that when calculating E_⊖(i_r, j_s), i_r minimizes to the dihedral angles (χ₁, χ₂, χ₃, χ₄), but for E_⊖(i_r, k_t), i_r minimizes to another dihedral position ( ${\chi }_1^{\prime },{\chi }_2^{\prime },{\chi }_3^{\prime },{\chi }_4^{\prime }$). Therefore, when the partial conformation (i_r, j_s, k_t) is chosen, it is impossible for i_r to simultaneously optimize its interaction with both j_s and k_t. Second, rotamers i_r and j_s might both minimize to similar Cartesian positions when their interaction with k_t is optimized, but cannot both occupy the same space when the partial rotamer assignment (i_r, j_s, k_t) is chosen. In both situations, when rotamers i_r, j_s, and k_t are simultaneously minimized they are prevented from choosing their optimal pairwise positions, leading to a difference between the pairwise bounds and the actual energy.

Fig. 2. Two possible ways for large bound errors to occur during the design search.

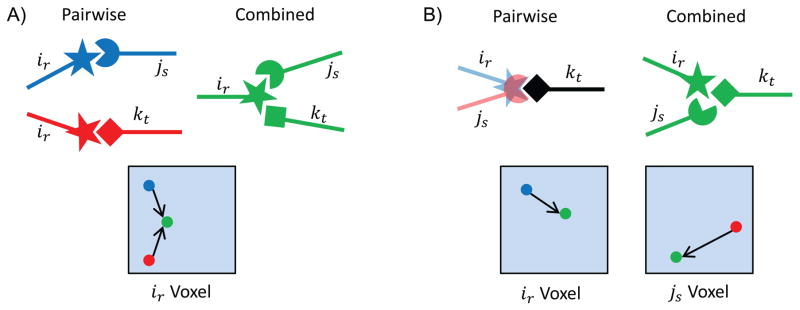
A) When i_r is pairwise minimized with two different rotamers, j_s and k_t, the optimal position of i_r is different for the two pairwise interactions. When all three rotamers are minimized simultaneously, i_r cannot be in two places at once, so the globally optimal positioning of the rotamers is suboptimal with respect to the pairwise interactions. Therefore, the global minimum for all three rotamers is higher than the optimal pairwise minima. The shaded box represents the continuous voxel for continuous rotamer i_r. The colored dots show schematically the movement of the i_r rotamer within its voxel from its pairwise optimal positioning (with j_s, blue; with k_t, red) to its globally optimal positioning (green). B) Two rotamers, i_r and j_s, may minimize to the same real space position, but when minimized simultaneously protein sterics does not allow the rotamers to occupy the same Cartesian coordinates. As in A), the global minimum for all three rotamers is suboptimal relative to the pairwise bounds, resulting in a global minimum that is higher than the pairwise minima. The shaded boxes represent the continuous voxels for rotamers i_r and j_s. The colored dots show schematically the movement of the i_r and j_s rotamers within their voxel from their pairwise optimal positioning (blue and red) to their globally optimal positioning (green).

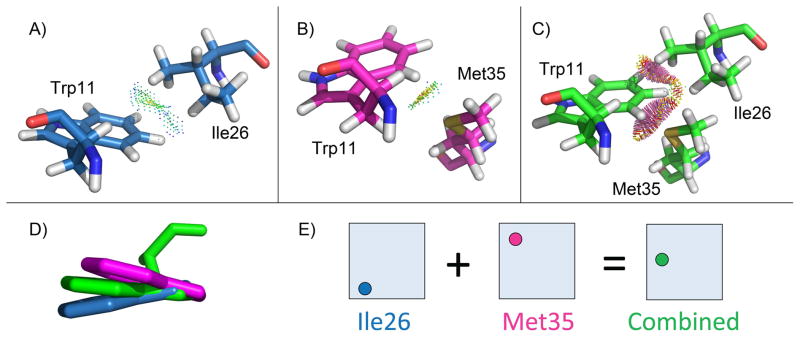
Figure 3 describes an example from the protein core design of S. pneumoniae PhtA histidine triad (PDB id: 2CS7) where the bound error of the conformation with the lowest energy bound, ε(ℓ), is very large. The design allowed 14 residue positions to mutate, which resulted in a search space with over 10²³ continuous rotamer conformations. The figure shows three rotamers from the conformation with the lowest energy bound that create a situation where all pairwise bounds look favorable (Panels A and B), but the full conformation results in several clashes (Panel C). To accurately quantify this error, the actual rotamer energy contributions, $E_T(i_r)=E_T(i_r)+{\displaystyle \sum _{j\ne i}}0.5E_T(i_r,j_s)$, were compared to the rotamer energy bounds, $E_{\ominus }(i_r)=E_{\ominus }(i_r)+{\displaystyle \sum _{j\ne i}}0.5E_{\ominus }(i_r,j_s)$, to compute the per rotamer error bounds ε(i_r) = E_T (i_r) − E_⊖(i_r). Pairwise energies are symmetric, so each pairwise term occurs in two pairwise rotamer terms. Therefore, pairwise terms were halved when calculating the rotamer energy contributions to avoid double counting. The rotamer error bounds from the three problem rotamers account for 66% of ε(ℓ), while the other 11 rotamers account for an average of only 3% each. Therefore, improving the pairwise bounds for these three problem rotamers would greatly reduce ε(ℓ). Importantly, the partial conformation consisting of these three rotamers is not only present in ℓ, but in ${\displaystyle \prod _{i\in U}}\mid Q_i\mid$ conformations, where |Q_i| is the number of available rotamers at position i, and U is the set of all mutable positions not in the triple with poor bounds. Since the bound is very optimistic (i.e., loose), it is likely that many of these conformations are in D for the 2CS7 design system. If the bound for these three rotamers was specifically corrected, a combinatorial number of conformations would be removed from D that would otherwise appear extremely favorable. We hypothesize that compared to the number of partial rotamer conformations that exist in a CSPD problem, the number with large overoptimistic bounds is small. If we are able to target only the partial rotamer conformations with the worst bounds, we can quickly exclude those conformations from the search and efficiently find the minGMEC. We present two methods, PartCR and HOT, that improve large error bounds during the design search (Fig. 4).

Fig. 3. Example of large bound error from a protein core design.

For the protein core design of S. pneumoniae PhtA histidine triad (PDB id: 2CS7), the triple of rotamers, Trp11, Ile26, and Met35, account for 66% of the error between the actual minimized energy and the pairwise lower energy bounds for ℓ, the conformation with the lowest energy bound. Panels A) and B) show the minimized pairwise interactions between Trp11 and Ile26, and Trp11 and Met35 respectively. In both of these cases blue and green contact dots show that the rotamers interact favorably (contact dots generated by Probe [34] using Protein Interaction Viewer [35]). C) While the rotamers had favorable pairwise interactions, when all three rotamers are minimized simultaneously the rotamers clash (shown by red and yellow contact dots). Therefore, the global minimum energy is much higher than the local pairwise bounds. D) Alignment of the Trp11 conformation when minimized with Ile26 (blue), Met35 (magenta), or both Ile26 and Met35 (green). E) Schematic of Trp11 rotamer minimization. Shaded blue boxes represent the voxel of the Trp11 continuous rotamer, and the colored dots represent the optimal placement of Trp11 when minimized in the presence of the different rotamers.

Fig. 4. Overview of HOT and PartCR algorithms.

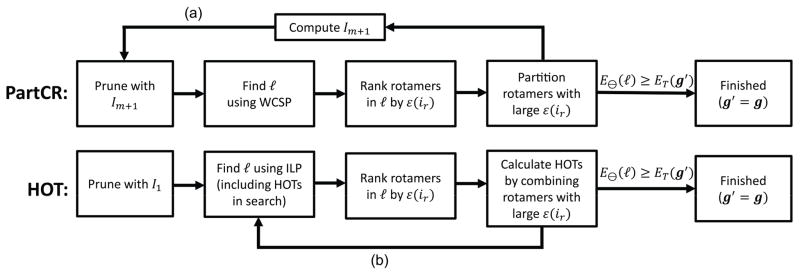
Top) The overall scheme for using partitioned rotamers to improve CPSD with continuous rotamers. First, the standard iMinDEE protocol [4] is used to prune rotamers and find the conformation, ℓ, with the lowest bound. Next, bound errors (ε(i_r) = E_T(ir) − E_⊖(i_r)) are computed for each rotamer in ℓ. The rotamers with the largest (worst) bounds are split into two or more partitioned rotamers. If the lower bound of ℓ is greater than the best energy that has been found so far, the search is finished. Otherwise, the $I_{m+1}\leftarrow E_T({\mathbf{g}}_m^{\prime })-E_{\ominus }({\mathit{\ell }}_m)$ pruning value can be calculated and can be used to prune additional rotamers with DEE. Note that when a rotamer is partitioned the pairwise bounds can increase, which increases the E_⊖(ℓ) from the previous iteration. Therefore, re-pruning rotamers (a) has the ability not only to prune rotamers that weren’t originally pruned, but also to prune partitioned rotamers that were just created. The process of pruning rotamers, enumerating conformations, and partitioning rotamers continues until the stopping criterion (Eq. 4) is reached, which guarantees that the minGMEC has been found. Bottom) The HOT algorithm proceeds similarly to the PartCR algorithm. The main difference is that higher-order terms (HOTs) are used to improve the search instead of partitioning rotamers. Since traditional DEE criteria cannot utilize these higher-order terms, the HOT algorithm only performs DEE once and the loop (b) returns directly to the enumeration stage to compute the next conformation with the lowest energy bound.

2.4 Partitioning Continuous Rotamers

As described in Section 2.3, one main reason that pairwise bounds can be overoptimistic is that a single rotamer, i_r, participates in many pairwise bounds and can minimize to a different location within its voxel, V, for each pairwise bound. If rotamer i_r was forced to minimize within a smaller voxel V′, which is contained within V, the pairwise bounds with respect to V′ would always be greater than or equal to the original bounds (i.e., E_⊖(i_r, j_s|V′) ≥ E_⊖(i_r, j_s|V) for all j_s). Therefore, one way to improve the bounds for a given rotamer is to decrease the voxel size it can minimize within. However, the voxel size represents the allowed flexibility of the side chain during the protein design, so directly reducing the voxel size does not maintain the flexibility defined by the input model. Alternatively, the same effect can be achieved by partitioning a rotamer’s voxel into several smaller disjoint voxels, V₁, V₂, …, V_n, and creating a new partitioned rotamer, i_r1, i_r2, …, i_rn, for each new voxel such that the new voxels completely cover the space of the original voxel V, V₁ ∪ V₂ ∪ … ∪ V_n = V. A new bound can be computed for each new rotamer with respect to its new voxel. The smaller voxels allow the bounds to be tighter than the original bound for i_r, but the new bounds still remain valid lower bounds. This partitioning comes at the cost of adding n new rotamers to the protein design search so it is important to only partition rotamers when the difference between the original bounds and the new bounds, $E_{\ominus }(i_r,j_s\mid V)-\underset{k}{min}{E}_{\ominus }(i_r,j_s\mid V_k)$, is large.

The rotamer partitioning search scheme shown in Figure 4 and Algorithm 1 details the divide-and-conquer method PartCR that uses partitioned rotamers to improve pairwise bounds and increase the efficiency of a continuous rotamer design search. Once the conformation with the lowest bound, ℓ, is found, the conformation enumeration is paused and the rotamers i_r within ℓ are ranked by their bound error, ε(i_r). The rotamers with the largest error are split into partitioned rotamers (Fig. 5A; Alg. 1, Line 10) and new bounds for the partitioned rotamers are calculated. Since the algorithm targets the rotamers with the worst bounds, it is likely that the pairwise bounds will significantly increase, causing the lower bound of the next enumerated conformation ℓ_m+1 to increase as well: E_⊖(ℓ_m) ≤ E_⊖(ℓ_m+1) (Fig. 5B). Since E_⊖(ℓ_m) ≤ E_⊖(ℓ_m+1), we know that I_m+1 ≤ I_m and now I_m+1 can be used to potentially prune additional rotamers. The algorithm continues by iteratively enumerating conformations and partitioning rotamers from those conformations with the largest error bounds. After each partitioning step, the I_m+1 value can be calculated and if I_m+1 < I_m, DEE can be used to prune additional rotamers. These steps can be repeated until E_⊖(ℓ_m) ≥ E_T (g), which guarantees that the minGMEC is found.

Fig. 5. Rotamer Partitioning Scheme and Benefits of Partitioned Rotamers.

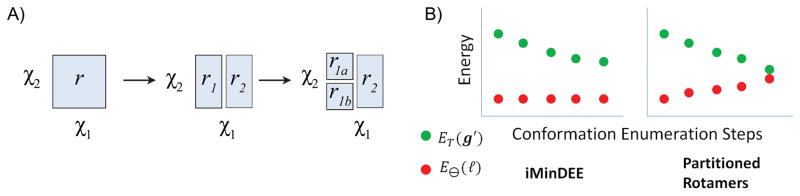
A) An example of how a rotamer is partitioned. In this example the rotamer r with two dihedrals is first partitioned along the χ₁ dimension to create two new rotamers r₁ and r₂. Next the partitioned rotamer r₁ is further split along the χ₂ dimension to create the partitioned rotamers r_1a and r_1b. B) In the original iMinDEE protocol, as conformations are enumerated the pairwise bounds are never updated so E_⊖(ℓ) remain constant. However, during a partitioned rotamer design the bounds are updated, which increases E_⊖(ℓ) during the run. Since the iMinDEE I value is defined as I = E_T (g′) − E_⊖(ℓ), the I_m+1 value continuously shrinks during the partitioned rotamer conformation enumeration, allowing for additional rotamers to be pruned as more rotamers are partitioned.

Algorithm 1.

Partitioning Continuous Rotamers (PartCR) Algorithm

1:	Ebest ← ∞, I ← ∞
2:	while I > ECUT do
3:	Prune and remove rotamers using I
4:	Find ℓ using WCSP framework
5:	Ebest ← min(Ebest, ET(ℓ))
6:	I ← Ebest − E⊖(ℓ)
7:	L ← {ℓ}
8:	while E⊖(L) ≤ Ebest do
9:	Find the rotamer ir ∈ ℓ with the largest bound error, ε(ir)
10:	newRots ← PartitionRotamer(ir)
11:	Replace ir with newRots in Emat
12:	Recalculate energies for newRots
13:	L ← newConfs(newRots, ℓ)
14:	end while
15:	end while
16:	Enumerate remaining conformations with modified A* until minGMEC is found (See text)

Algorithm 1 describes in detail the PartCR algorithm used for the partitioning continuous rotamers. The PartCR algorithm takes as input ECUT, which defines the energy cutoff where the algorithm switches from improving the energy bounds by partitioning rotamers to enumerating conformations. In Line 4, ℓ is the conformation with the lowest bound. E_best is the energy of the best conformation found so far, E_T (ℓ) is the minimized energy of conformation ℓ, and E_⊖ (L) is the lower bound for all conformations in L. The function PartitionRotamer takes as input a rotamer, i_r, and returns a set of partitioned rotamers that partition the voxel of i_r. The function newConfs takes as input a parent rotamer, i_r, a set of partitioned rotamers, and the current set of conformations L and returns a new set of conformations where the parent rotamer has been replaced by each partitioned rotamer. Therefore, L is repeatedly updated to reflect all the conformations created by partitioning the rotamer dihedral space.

Several improvements can be made to Algorithm 1 to make it run faster in practice. First, to reduce the number of rotamers the weighted constraint satisfaction problem search at Line 4 must search through, rotamers can be temporarily pruned immediately before the conformation search using I = 0 and then immediately unpruned once ℓ has been found. Next, an additional criterion can be added to the loop at Line 8 to ensure that rotamers are not split unnecessarily. Splitting a rotamer that already has a tight bound will likely just add a rotamer and complicate the conformation search without any improvement in bounds. Therefore, we can stop splitting rotamers when the majority of the bound error has been ameliorated. In our implementation, rotamers were partitioned until the split rotamers cumulatively accounted for more than 75% of the bound error or if the bound error E_T (ℓ) − E_⊖(L) becomes less than 70% of the original bound error E_T (ℓ) − E_⊖(ℓ).

In the last step of the PartCR design protocol (Line 16), the A^* heuristic has been modified so that all partitioned rotamers that came from the same parent rotamer are considered part of the same conformation. For example, if node x is expanded at residue position i and there are six available rotamers, normally six nodes will be added to the queue. However, if three of the six rotamers _ir1, i_r2, and i_r3are partitioned rotamers that all came from the same parent rotamer, i_r, all three rotamers will be assigned to the same A^* node, resulting in only four new nodes added to the A^* tree. Therefore, each leaf node will correspond to a parent rotamer conformation, but several partitioned rotamers can be assigned to the conformation. Once the leaf node is extracted from the A^* tree, a quick WCSP search over the allowed partitioned rotamers can find the actual rotamer assignment with the lowest bound. osprey was modified to use the WCSP solver Toulbar2 for the WCSP searches [28, 31].

2.5 Bounding Higher Order Rotamer Tuples

As illustrated in Section 2.3, when the lower bound for a given conformation is loose, this is usually because a subset of rotamers in the conformation have poor pairwise bounds. By identifying these poorly bounded rotamers during conformation enumeration, a new bound can be be obtained for the higher-order partial rotamer conformation to improve the bound for subsequent conformations. The HOT algorithm calculates higher-order bounds and incorporates them into the design search to efficiently reduce the number of conformations that must be enumerated to find the minGMEC (Fig. 4).

When a conformation is enumerated from A^* based on its lower bound and is fully minimized, ε(i_r) can be determined for every rotamer. A new bound for the three rotamers with the largest ε(i_r) values can be calculated by minimizing those three rotamers together while ignoring the energy contributions from all other mutable residues. This is analogous to calculating pairwise bounds, except that three rotamers are present instead of two. This ternary bound will be tighter than the individual pairwise bounds: E_⊖(i_r, j_s, k_t) ≥ E_⊖(i_r, j_s) + E_⊖(i_r, k_t) + E_⊖(j_s, k_t), which can improve the bounds of all conformations in D that contain these three rotamers. This new bound can be incorporated into the enumeration search to create a more accurate energy landscape. Once new bounds are computed, the conformation enumeration can resume, alternating between enumerating conformations based on their lower bound and computing higher-order bounds. As more higher-order bounds are included in the search, only conformations with tight bounds will be enumerated, which uncovers a quick path to the minGMEC. If needed, even higher-order bounds (quaternary, quinary, up to n-ary) can be obtained by minimizing partial rotamer conformations that contain four or more rotamers. In practice, the HOT algorithm uses a heuristic (Algorithm 2 Line 13) to determine when to stop increasing the size of the partial conformation used to calculate additional higher-order bounds and switch back to enumerating the next protein conformation with the lowest energy bound.

Algorithm 2 describes in detail how the HOT algorithm improves poor energy bounds by incorporating higher-order minimization of rotamer tuples into the design search. The function pop is the standard function for a queue that removes and returns the first element in the queue. The partial conformation s is minimized to calculate a higher-order term that provides a much tighter energy bound on the conformation ℓ. Finally, the function newBound recalculates the energy bound on the conformation ℓ given the energy of the partial conformation s.

HOT and ILP

The HOT algorithm is similar to PartCR, but it calculates higher-order bounds rather than partitioning rotamers. These higher-order bounds cannot be easily incorporated into the DEE pruning step because traditional DEE criteria only consider single and pairwise rotamer terms. However, the higher-order terms can be incorporated into the conformation search at Line 4 of the HOT algorithm (Algorithm 2). We developed enhancements for both the A^* [25] and integer linear program (ILP) [29] CSPD conformational search methods that allows the methods to account for higher-order terms during the search. These enhancements were implemented in OSPREY and used to test the HOT algorithm. Here we focus on how we modified the traditional ILP CSPD formulation [29] to incorporate higher-order terms.

Algorithm 2.

Higher-Order Terms Algorithm

1:	Ebest ← ∞, I ← ∞
2:	while True do
3:	Prune rotamers with I using iMinDEE [4]
4:	Find the conformation ℓ with the lowest energy bound
5:	Ebest ← min(Ebest, ET(ℓ))
6:	if I < Ebest − E⊖(ℓ) then
7:	Exit ▷ The minGMEC has been found
8:	else if E⊖(ℓ) > Ebest then
9:	I ← min(ET(ℓ) − E⊖(ℓ), 2I)
10:	end if
11:	rots ← Rotamers of ℓ in order of largest bound error, ε(ir)
12:	s ← {rots.pop()}
13:	while E⊖(ℓ|s) < E⊖(ℓ) + I and E⊖(ℓ|s) < Ebest do
14:	s ← s ∪ {rots.pop()}
15:	Minimize the partial rotamer conformation s
16:	Add s to the list of calculated higher-order bounds
17:	E⊖(ℓ|s) ← newBound(ℓ, ET(s))
18:	end while
19:	end while

Integer linear programming is a general mathematical technique to optimize an objective function given a set of linear constraints where all the variables must be integers. Many standard techniques and software packages exist for solving ILP problems [32, 33], which CSPD can exploit when the CSPD problem is represented as an ILP. To convert CSPD into an ILP, the protein design problem can be represented as a graph search problem [29]. In this framework, the graph G is an undirected p-partite graph with node sets V₁, …, V_p for each residue position, where V_i includes a node u for each rotamer i_r at position i. Each internal node is assigned a weight equal to the intra-rotamer energy E(i_r) and an edge is placed between every interacting rotamer pair i_r and j_s where the weight of the edge is E(i_r, j_s). The GMEC is determined by finding a single node u per V_i that minimizes the weight of the induced subgraph.

This graph problem can be formulated as an integer linear program (ILP) as follows [29]:

$$\text{Minimize}:\sum x(i_r)E(i_r)+\sum x(i_r,j_s)E(i_r,j_s)$$ (6)

subject to

$$\begin{array}{ll}\sum _{r\in i}x(i_r)=1\hfill & \hfill \text{For}\text{all}i\\ \sum _{s\in j}x(i_r,j_s)=x(i_r)\hfill & \hfill \text{For}\text{all}(i_r,j)\text{pairs}\end{array}$$

where x(i_r), x(i_r, j_s) ∈ {0, 1}. When the decision variable x(i_r) or x(i_r, j_s) is set to 1, this corresponds to choosing rotamer i_r or rotamer pair (i_r, j_s) respectively.

We modified the standard CSPD ILP framework to incorporate higher-order energy terms as follows. Let H be the set of all partial rotamer conformations for which higher-order bounds have been calculated. To modify the CSPD ILP to include higher-order bounds, a new decision variable, x(t), can be added to the ILP for every higher-order rotamer conformation t ∈ H. Every new decision variable x(t) has an associated cost function c(t) such that the new ILP objective function is:

$$\sum x(i_r)E_{\ominus }(i_r)+\sum x(i_r,j_s)E_{\ominus }(i_r,j_s)+\sum _{\mathbf{t}\in H}x(\mathbf{t})c(\mathbf{t}).$$ (7)

In addition, corresponding constraints must be added to the ILP to require x(t) = 1 if and only if all the rotamers in t are selected as part of the GMEC:

$$\begin{array}{c}\left(\sum _{i_r\in \mathbf{t}}x(i_r)\right)-x(\mathbf{t})\le \mid \mathbf{t}\mid -1\\ x(\mathbf{t})-x(i_r)\le 0\text{For}\text{all}{i}_r\in \mathbf{t}.\end{array}$$ (8)

The partial conformation t can be represented as a subset of a fully assigned conformation a (Eq. 1). Hence, we use |t| to denote the number of elements in t, and we use i_r ∈ t to denote an assigned rotamer in t. The second set of constraints in Eq. (8) ensure that x(t) cannot be set to 1 if any of the rotamers in t are not chosen.

In this framework, the decision variables for the intra-rotamer and pairwise energies in t are still turned on in the ILP objective function when a conformation a is chosen that contains the partial conformation t. To avoid double counting energies, c(t) should not be the energy of the partial conformation, but rather a correction term that represents the added cost of simultaneously minimizing all the rotamers in the partial conformation t. Specifically, c(t) is the energy difference between the pairwise bound of conformation t and the conformation’s higher-order bound: $c(\mathbf{t})=E_{\ominus }(\mathbf{t})-{\displaystyle \sum _{i_r\in \mathbf{t}}}{E}_{\ominus }(i_r)-{\displaystyle \sum _{i_r\in \mathbf{t}}}{\displaystyle \sum _{j_s\in \mathbf{t},j>i}}{E}_{\ominus }(i_r,j_s)$. However, this term still double counts energetic contributions when multiple smaller partial conformations are contained in (i.e., have the same rotamers as) a larger partial conformation, t₁, t₂, ···, t_m ∈ t. To prevent this double counting, c(t) must be modified to include the costs from all the other higher-order bounds that are contained within it. Finally, c(t) should never be negative, because it is the cost associated with moving from pairwise terms to higher-order terms. Using all of this information, we have

$$c(\mathbf{t})=max(0,E_{\ominus }(\mathbf{t})-\sum _{{\mathbf{t}}^{\prime }\subset \mathbf{t},{\mathbf{t}}^{\prime }\in H}c({\mathbf{t}}^{\prime })-\sum _{i_r\in \mathbf{t}}{E}_{\ominus }(i_r)-\sum _{i_r\in \mathbf{t}}\sum _{j_s\in \mathbf{t},j>i}{E}_{\ominus }(i_r,j_s)).$$ (9)

This newly constructed ILP can be used at Line 4 to incorporate the higher-order terms into the conformation search. This ILP framework was implemented in OSPREY and solved using the Gurobi optimization suite application programming interface (Version 5.6) [32].

Rotamer Combination Methods

In Step 14 of the HOT algorithm, rotamers i_r are added to the partial conformation s in order of their bound error, ε(i_r). This ordering was chosen because rotamers with the largest bound error provide the greatest opportunity for improving the bound. This approach assumes that the rotamers with large ε(i_r) values all affect each other during minimization, so if they are minimized together the overall bound will be improved. This is a likely scenario because a large bound error implies that two or more rotamers minimize to similar positions in 3D space and are prevented from doing so when all rotamers are minimized together. However, this is not the only scenario that can result in a large ε(i_r) value.

Consider the scenario in Figure 6 where two rotamers (i_r, k_t) minimize favorably with one another (Note, this scenario is a specific instantiation of the general case shown in Figure 2B). It is possible that a third rotamer, j_s, interacts with i_r and k_t but has no bound error (i.e., E_T(k_t) − E_⊖(k_t) = 0), meaning that its conformation stays the same between pairwise and global minimizations. If j_s is located in between i_r and k_t in the protein conformation, minimizing the partial conformation (i_r, j_s, k_t) reveals that j_s disrupts the favorable interactions between (i_r, k_t). The disruption of the favorable pairwise minimization of (i_r, k_t) means that both of these rotamers would have relatively large bound errors. Because of their large bound errors, i_r and k_t will be quickly added to the higher-order term used by HOT. However, since j_s has a bound error of zero, it would be the last rotamer added to the higher-order term, yet j_s would improve the bound the most. Therefore, for this particular case another strategy is needed to correctly build useful higher-order terms for HOT. One such strategy is described below.

Fig. 6. A problematic scenario can occur if rotamers are combined to form higher-order terms based solely on bound error.

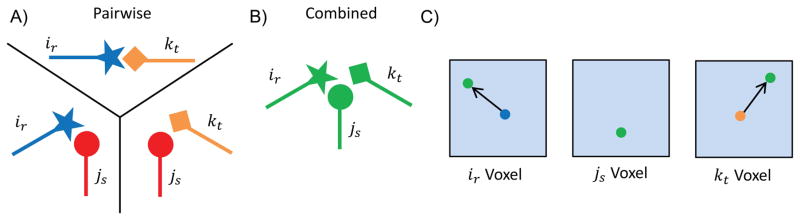
A) Pairwise minimizations for three pairs of rotamers. Note that when calculating pairwise bounds, i_r and k_t minimize favorably with one another. B) Conformation of all three rotamers from A) when they are globally minimized together. When globally minimized, j_s maintains the same conformation as when pairwise minimized, but i_r and k_t no longer interact favorably with one another. C) The three shaded boxes represent the continuous voxels for i_r, j_s, and k_t. The colored dots schematically show the movement of each rotamer from its pairwise minimized conformation (blue and orange) to its globally optimal conformation (green). Rotamer j_s does not change conformations, which means that ε(j_s) = 0. However, i_r and k_t both have large movements, which suggests their bound errors are much greater than zero. If rotamers are added to higher-order terms based on bound error, j_s would be the last rotamer added to the higher-order term, yet minimizing i_r and k_t with j_s would improve the bound the most.

An amino acid generally interacts most strongly with the side chains that are closest to it in Cartesian space, implying that rotamer minimization is most impacted by rotamers that are in the closest proximity. Therefore, an alternative approach for adding rotamers to the higher-order term is to add additional rotamers based on their distance to the rotamer with the largest ε(i_r). This fixes the problem described above, where the crucial rotamer k_t was the last rotamer to be included in the higher-order term. Adding rotamers to the higher-order term in order of their proximity to the rotamer with the largest bound error constructs partial conformations where each rotamer in the partial conformation is likely to affect the minimization of the others. In practice, however, we find that ordering rotamers 17 based on their error bounds works well, so we do not further analyze the distance-based method in the results.

2.6 Protein Core Design Tests

The 73 protein core designs from [4] were used to compare the iMinDEE algorithm to the new PartCR and HOT algorithms. The energy function weights are the same as those used in the native sequence recovery portion of [4]. Continuous rotamers were defined using the Lovell rotamer library [2] as in [26, 4], where each rotamer voxel was defined as ±9° to each rotamer dihedral. Each design was run on a single processor and given 4GB of RAM.

3 Results

The iMinDEE algorithm for CSPD with continuous rotamers must enumerate many con- formations before it can identify the minGMEC. The large number of conformations causes the A* tree to become large, which slows down the design search and can ultimately cause the design to require large amounts of memory. The algorithms presented here specifically target and reduce loose pairwise bounds to reduce the number of conformations that must be enumerated to find the minGMEC.

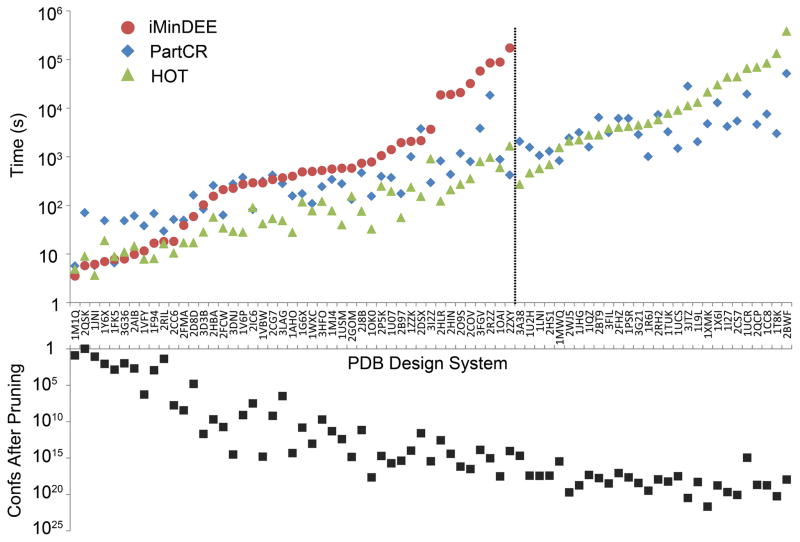
The original iMinDEE algorithm was compared to the novel HOT and PartCR algorithms for 73 protein core designs. The iMinDEE algorithm was unable to complete 28 of the 73 design systems tested. Both the HOT and PartCR algorithms were able to successfully find the minGMEC for every design system in the test set. If the design systems are sorted by the minimum time it takes any of the three algorithms to complete, there appear to be three different regimes. For easy protein design problems (problems where at least one algorithm finished within 15 seconds), iMinDEE and HOT are often able to complete the designs faster than PartCR (Fig. 7). In this regime, the median time to completion for iMinDEE and HOT is 7.8 and 8.9 seconds, respectively, while PartCR increases to 48 seconds. For all but these easiest problems, PartCR and HOT solve the problem faster than iMinDEE. For problems of medium difficulty (those that take greater then 15 but less than 975 seconds) HOT dominates PartCR and iMinDEE with a median completion time of 118 seconds, compared to 354 seconds and 579 seconds, respectively. However, on the most difficult problems, PartCR outperforms HOT with a median completion time of 4576 seconds compared to 9000 seconds (iMinDEE does not complete for any of these systems). When looking at individual designs, PartCR was able to obtain as much as a 44-fold speedup over HOT, and PartCR solved the most complex design 3.8 days faster than HOT.

Fig. 7. Comparison of runtime for iMinDEE vs. two new algorithms that improve pairwise bounds during the CSPD search.

iMinDEE, PartCR, and HOT were tested on 73 protein core designs. iMinDEE failed on 28 of the designs (designs to the right of the dotted line), while PartCR and HOT completed all of the designs successfully. The bottom inverted graph shows the number of conformations that remained after iMinDEE pruning for each design system.

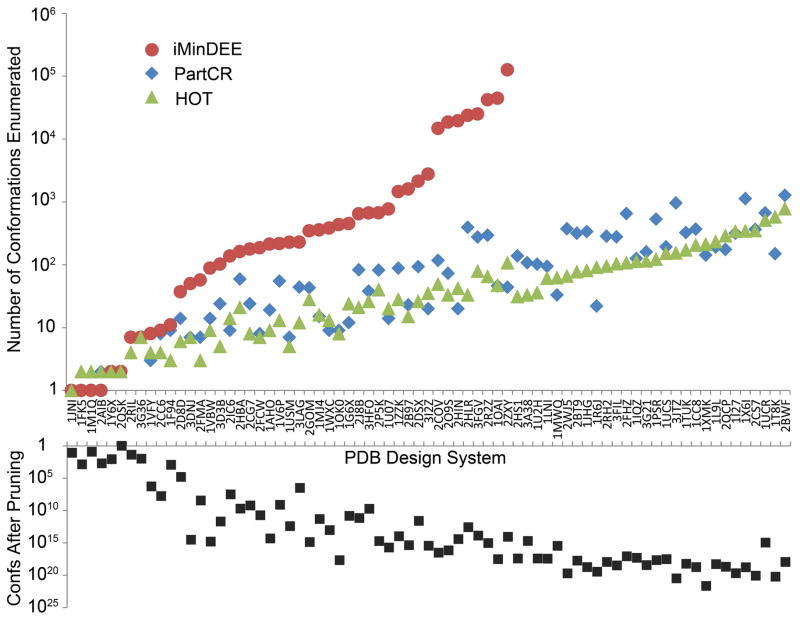
The new CSPD algorithms are able to speed up the CSPD search because they improve the energy bounds over the pairwise bounds used by iMinDEE. By improving the bounds, the number of conformations that must be enumerated before the GMEC is found is reduced, which speeds up the overall run. Figure 8 shows the reduction in enumerated conformations for the 73 protein design systems tested. For all but the most simple designs, PartCR and HOT greatly reduce the number of conformations that must be enumerated. For the 28 designs that were unable to complete with iMinDEE, PartCR and HOT never enumerated more than 1269 or 776 conformations, respectively. That is two orders of magnitude smaller than what iMinDEE required to complete the simpler design systems. For the design systems that iMinDEE did complete, the average fold decrease in the number of enumerated conformations was 135- and 132-fold for PartCR and HOT. While the runtime of the design correlates with the number of conformations that must be enumerated, PartCR and HOT must do additional work for every enumerated conformation. On average, PartCR and HOT take 16 and 40 seconds per conformation, while iMinDEE only takes 2 seconds per conformation. Therefore, the new algorithms take longer per conformation than iMinDEE, but the large reduction in the number of conformations greatly outweighs this extra required work.

Fig. 8. Number of conformations that were enumerated by iMinDEE, PartCR and HOT.

PartCR and HOT greatly reduce the number of conformations that must be enumerated to find the minGMEC. This reduction in the number of conformations corresponds with the improvement in runtime achieved by the new algorithms. The bottom inverted graph shows the number of conformations that remained after iMinDEE pruning for each design system.

The HOT and PartCR algorithms both rely on the principle that only a few rotamer combinations with a large bound error must be improved to find the minGMEC. Even if a small fraction of all partial conformations had to be improved, this would be prohibitively expensive. For all of the systems tested, the number of rotamer partitions and higher-order terms that needed to be calculated were very small (Fig. 9). The design systems had a maximum conformation space of 10²⁵ potential conformations, but the maximum number of rotamer partitions and higher-order terms needed for any design were merely 1078 and 2577, respectively. This shows the power of only improving the rotamer interactions with the worst bounds.

Fig. 9. Comparison of the number of partial rotamer conformations that were computed by PartCR and HOT.

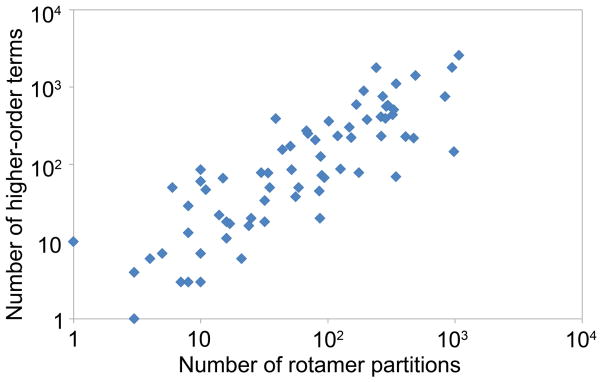
PartCR and HOT only needed to target a small number of partial rotamer conformations with large error bounds to find the minGMEC. For the design test cases there were as many as 10²⁵ conformations possible for a single design problem. PartCR only needed at most 1078 rotamer partitions to find the minGMEC. Similarly, HOT only needed to compute at most 2577 higher-order terms. Thus, the number of partial conformations needed is only a small fraction (always less than 10⁻¹⁶% for difficult systems) of the total conformational search space. Additionally, the number of partitions and higher-order terms that PartCR and HOT must calculate correlate with each other. This suggests that both algorithms need to do a similar amount of work as the complexity of the CSPD system increases.

Specifically, consider the design system for Cytochrome c555 from A. aeolicus (PDB id: 2ZXY), which has 14 mutable positions and 174 continuous rotamers remaining after iMinDEE pruning for a total of 10¹⁴ possible conformations. In order to find the minGMEC, iMinDEE had to enumerate over 125,000 conformations. The PartCR algorithm was able to find the minGMEC after only enumerating 44 conformations and splitting 39 rotamers. Similarly, HOT had to enumerate only 107 conformations and calculate higher-order bounds for only 390 partial rotamer conformations. This demonstrates that only a fraction of the pairwise bounds in the design system must be improved to generate full conformation bounds that are tight and can be used to directly find the minGMEC.

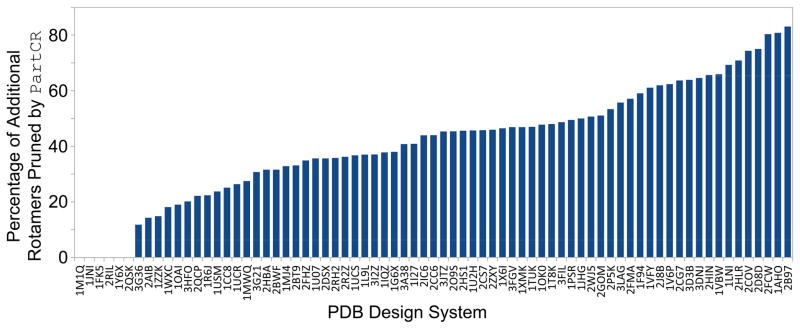
HOT and PartCR both increase the speed of CSPD with continuous rotamers by improving large error bounds that arise during the search. One key difference between the two algorithms is that PartCR maintains the pairwise nature of the design by not adding any higher-order terms to the search. By partitioning the search space into rotamers with reduced voxel sizes, the partitioned rotamers can be analyzed by DEE to prune additional rotamers (Fig. 4). Partitioning rotamers increases the value of E_⊖(ℓ) (see Section 2.4), which reduces the I value in the iMinDEE pruning criterion, ultimately strengthening its pruning capability. After rotamers are partitioned and DEE is run with the new I_m+1 pruning value, not only can newly added partitioned rotamers be pruned, but original parent rotamers can be pruned that were unpruned in previous DEE steps. During the PartCR designs, up to 83% more rotamers were pruned over the initial iMinDEE pruning (Fig. 10). As with all DEE pruning, this removal of additional rotamers exponentially reduces the number of conformations that the conformation enumeration step searches over. By not adding higher-order terms to improve the search, PartCR can take advantage of advanced DEE pruning methods to quickly narrow the search space.

Fig. 10. Percentage of rotamers pruned by PartCR after pruning by iMinDEE.

PartCR prunes additional rotamers after iMinDEE pruning has been conducted. Up to 83% additional pruning can be achieved over the stringent iMinDEE criteria in [4]. For five of the six systems with no improvement in pruning, PartCR was able to solve the problem by enumerating at most two conformations, indicating that these problems were relatively easy to solve and most of the pruning was likely done by iMinDEE.

4 Discussion

A clear challenge in CSPD is to incorporate realistic protein flexibility into the design search so that low-energy conformations/sequences are not missed by the search. Rigid rotamers neglect a side chain’s movement within its rotameric well. This flexibility can be recovered in CSPD with the use of continuous rotamers and has been shown to be crucial for success in several protein designs. Continuous rotamers introduce specific challenges to protein design because the energy of continuous rotamer interactions can only be bounded and not computed exactly. These bounds weaken both the pruning and conformation enumeration steps of CSPD. If the pairwise bounds are loose, a large number of conformations must be enumerated before the minGMEC is guaranteed to be found. The new algorithms presented here, HOT and PartCR, specifically improve partial rotamer interactions that have large energy bound errors. These new methods are both able to solve more complex problems than previously possible.

The bound errors of continuous rotamers stem from the pairwise nature of the bounds calculation. PartCR and HOT target partial rotamer conformations with poor bounds, but in different ways. HOT calculates energy bounds for progressively higher-order partial rotamer conformations. Because the pruning step in CSPD relies on pairwise interactions, the newly computed higher-order terms can only be incorporated during the conformation enumeration step. Alternatively, PartCR partitions a rotamer with poor bounds into smaller voxels to better bound the rugged energy landscape. This maintains the pairwise nature of the problem and allows for both increased pruning and a reduction in the number of conformations that must be enumerated. The ability of PartCR to take advantage of further rounds of DEE pruning is likely why it performs better on the most difficult problems.

While it is possible to use higher-order DEE criteria [27] to incorporate the higher-order bounds calculated by HOT into the rotamer pruning step, it is unclear if this would improve the speed of the design search. First, HOT only needs to calculate a small number of higher-order bounds, whereas m-tuple DEE searches over all m-tuple partial rotamer conformations. Second, the runtime of the more complex m-tuple DEE criteria is exponential with respect to m, so while the pruning might increase, the overall runtime of the design search might significantly increase to accommodate the additional pruning. Third, m-tuple pruning cannot directly prune individual rotamers, but rather only prune (m 1)-tuples. As m grows, an increasingly large number of partial conformations must be pruned before a single rotamer can be pruned. Therefore, it is likely unproductive to enhance time-consuming higher-order DEE criteria with only a small number of higher-order terms calculated by HOT.

The protein design test cases we used focused on continuous rotamers with only side-chain flexibility. However, PartCR and HOT can be applied to both side-chain and backbone flexibility. The DEEPER algorithm has already demonstrated the ability to use continuous rotamers to model side-chain and backbone flexibility simultaneously [27]. Combining either PartCR or HOT with the DEEPER protocol for residue conformations (RCs) will allow efficient side-chain and backbone flexibility to enable accurate and detailed protein designs.

The field of CSPD holds much promise for therapeutics and biological diagnostics. Methods that improve the computational design search to allow more realistic protein flexibility are crucial to the accuracy of CSPD. The methods presented here make continuous rotamer design applicable to large, complex protein design systems and extend the impact of computational protein design.

5 Software Availability

The PartCR and HOT algorithms were implemented in the osprey CSPD software suite. osprey is free and open source under a Lesser GPL license. The program, user manual, and source code are available at www.cs.duke.edu/donaldlab/osprey.php.